随着海上经济的发展, 海上交通也日益复杂, 海上事故后的海上搜救资源调度优化问题也一直是应急管理领域研究的研究热点. 由于不同水域的特性不同, 当人员落水后, 受风、浪、流等环境因素的影响, 处于动态漂移的状态, 给海上搜救带来很大的困难, 尤其是对搜救资源的合理调度及分配, 能够影响搜救的成功率, 因此需要计划、协调、控制和指挥搜救行动以应对紧急情况.

目前, 针对海上搜救资源调度的研究, 主要可以分为单目标和多目标模型两个方向. 针对单目标模型, 主要是采用遗传算法、遗传模拟退火算法求解. 文献[1]以时间为目标建立海上搜寻船舶单目标模型, 通过改进的遗传算法对模型进行求解. 文献[2]在搜救成功率中加入救助概率设计目标函数, 建立搜救调度单目标模型, 采用遗传模拟退火算法求解. 文献[3]分析在不同船舶数量限制情况下时间与搜救成本的关系, 结合搜救力量覆盖待搜救区域的覆盖面积所用时间, 得到经济可行的搜救力量方案.

针对多目标模型, 多采用NSGA-II算法求解, 文献[4]通过建立以搜救成功率和搜救成本的多目标模型, 采用NSGA-II对模型进行求解. 文献[5]通过以时间、成本为目标函数, 建立多目标优化模型, 采用NSGA-II算法和多目标粒子群优化算法对模型进行求解.

综上, 目前大多采用遗传算法和NSGA-II算法进行求解, 本文拟采用改进的NSGA-II算法进行求解. 因此本文建立以搜救成功率和搜救成本为目标的多目标优化模型, 设计基于改进NSGA-II算法的海上搜救调度方法, 通过对黄渤海海域船舶事故案例进行分析验证, 验证了所设计方法在海上搜救调度问题中的可行性和有效性.

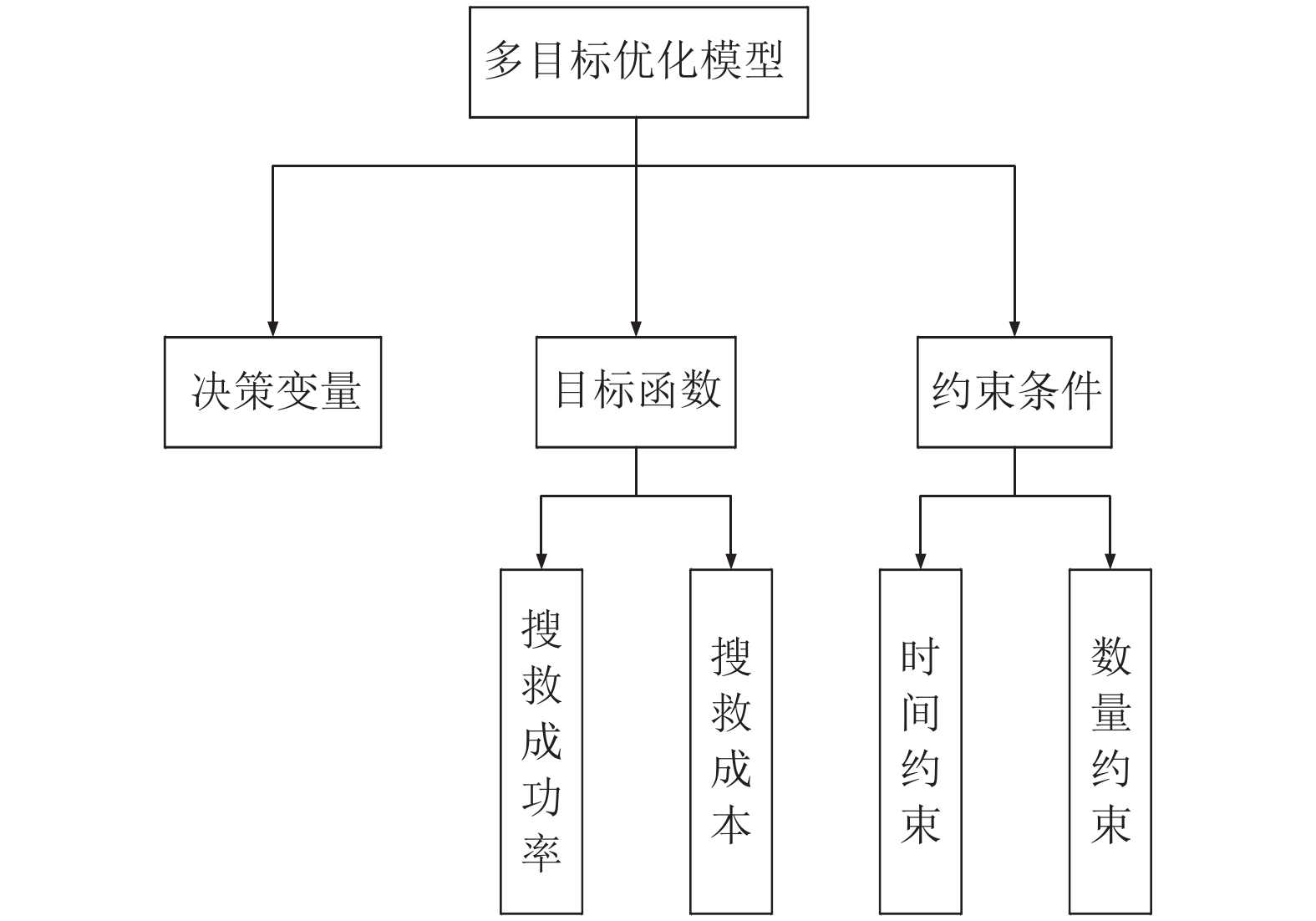
1 海上搜救资源配置的多目标模型构建

依据AIS及北斗数据, 建立多目标优化模型, 如图1所示, 具体设计分为输入变量、决策变量、中间变量、目标函数以及约束条件设计.

1.1 输入变量设计

输入变量主要包括待搜寻区域面积, 周围船舶数量, 船舶距离事故点的距离, 船舶的最大航速、扫海宽度、航线间距、搜救成本. 具体设计如表1所示.

1.2 决策变量设计

根据AIS及北斗数据, 设计多目标模型中的决策变量为搜救资源选择 ${x_i}$ ( $i = 1, 2, 3, \cdots, M$ ), 其中, ${x_i}$ 表示参与搜救资源 $i$ 的数量, 设计如下.

$ {x}_{i}=\left\{\begin{array}{l}1,\;如果船舶i参与搜寻行动\\ 0,\;如果船舶i不参与搜寻行动\end{array} \right.$

(1)

1.3 中间变量设计

根据对海上搜救资源已知信息进行分析, 可以计算出一些后文可以用到的中间变量, 搜救船舶赶往搜寻区域的时间 $T_i^0$ , 假设整个搜寻行动所用时间为 $T$ , 可以计算出搜寻船舶在待搜寻区域作业的时间以及在所完成搜寻区域面积.

(1)第 $i$ 艘船舶赶往搜寻区域的时间:

$ T_i^0{\text{ = }}\frac{{{D_i}}}{{{V_i}}} $

(2)

(2)第 $i$ 艘船舶在搜寻区域作业的时间:

$ {T_i}{\text{ = }}T - T_i^0 $

(3)

(3)第 $i$ 艘船舶所完成的搜寻面积:

$ {S_i} = {T_i} \times {W_i} \times {V_i} $

(4)

其中, 搜救面积的为第 $i$ 艘搜救船舶搜寻时间乘以第 $i$ 艘搜救船舶的扫海宽度乘以第 $i$ 艘船舶的最大航速. 时间乘以最大航速即为有效航程, 有效航程乘以扫海宽度即为搜救面积. 扫海宽度的物理意义指的是探测器能够发现搜救目标的有效距离, 是船舶搜寻能力的一种衡量, 因其受海洋环境、搜寻设备、遇险目标特征的影响, 通常是根据大量的实验数据进行统计分析得出.

1.4 目标函数设计

搜救成功率的目标函数设计如下:

$ {f_1} = 1 - POS $

(5)

其中, $POS$ 表示搜救成功率, 是搜救过程的主要衡量指标, 通常由包含概率 $POC$ 和发现概率 $POD$ 所决定, 这三者是海上搜寻理论中的3个重要部分.

$ S - \sum\limits_{j = 1}^n {{S_j}} > 0 $

(6)

$ PO{S_j}\left( A \right){\text{ = }}\sum\limits_{i = 1}^M {PO{C_i} \times PO{D_i}} $

(7)

其中, $j$ 表示当前处于第 $j$ 阶段的搜寻, $A$ 表示当前搜寻区域, ${S_j}$ 表示第 $j$ 个阶段的搜寻面积, $PO{S_j}$ 表示第 $j$ 个阶段的搜救成功率, $PO{C_i}$ 表示第 $i$ 个搜救资源的包含概率, $PO{D_i}$ 表示第 $i$ 个搜救资源的发现概率.

成本的目标函数设计如下:

$ {f_2} = \min \left[ {\sum\limits_{j = 1}^n {{C_j}\left( A \right)} } \right] $

(8)

$ {C_j}\left( A \right){\text{ = }}\sum\limits_{i = 1}^M {{x_i}{C_i}{T_i}} $

(9)

$ {T_i} = \frac{{{S_i}}}{{{x_i}{V_i}{R_i}}} $

(10)

其中, ${C_j}$ 表示第 $j$ 个阶段的搜救成本, ${x_i}$ 表示参与搜救的搜救资源 $i$ 的数量, ${T_i}$ 表示第 $i$ 个搜救资源的搜索时间, ${S_i}$ 表示第 $i$ 个搜救资源的搜寻面积.

1.5 约束条件设计

对所提出的海上搜救多目标模型, 由于搜救资源本身存在一些限制, 需要结合实际环境情况、搜救资源状况, 算法设计需要满足以下约束条件.

(1)搜救资源的数量小于能够在相应搜寻时间内完成搜寻任务的能力最弱搜救资源的数量.

$ \sum\limits_{i = 1}^M {{x_i}} \leqslant {n_i} $

(11)

(2)搜救资源到达待搜寻区域的时间要小于总搜寻时间.

$ T_i^0 \leqslant T $

(12)

综上所述, 考虑整个搜救过程搜寻对象受多种因素的影响具有动态性, 因此把搜救过程划分为多个时段, 通常情况下只考虑搜救成功率这一单目标问题, 本文中加入搜救资源的总成本, 但由于海上搜救具有强紧急性和弱经济性, 因此搜救成功率和总成本之间存在优先级, 在满足搜救成功率最优的情况去求总成本最低, 建立了海上搜救资源多目标优化模型.

2 基于改进NSGA-II多目标优化算法的海上搜救资源调度设计 2.1 多目标优化求解

对多目标模型的求解主要有2种方法, 第1种是传统目标法, 即转化法, 利用加权和将多目标问题转化为单目标问题. 第2种是对多目标直接求解, 通过采用智能优化算法求解, 例如NSGA-II算法, 它克服了NSGA计算复杂度高和缺乏精英策略的缺点^[6], 是一种强大的、鲁棒的多目标进化算法, 适用于解决具有2个或3个目标的问题^[7].

2.2 正态分布交叉 (NDX)算子设计

传统的模拟二进制交叉算子 (SBX)搜索能力较差, 正态分布交叉 (NDX)算子的搜索能力更强, 能够跳出局部最优, 达到一个全局最优的效果. 同样假设两个父代个体 ${p_1}$ 和 ${p_2}$ , 使用NDX算子^[8]产生两个子代个体 ${c_1}$ 和 ${c_2}$ 对于第 $i$ 个变量, 其交叉的过程为:

$ \left\{ \begin{gathered} {c_{1, i}} = \frac{{{p_{1, i}} + {p_{2, i}}}}{2} \pm \frac{{1.481\left( {{p_{1, i}} - {p_{2, i}}} \right)\left| {N\left( {0, 1} \right)} \right|}}{2},\;\mu \leqslant {\text{0}}{\text{.5}} \\ {c_{2, i}} = \frac{{{p_{1, i}} + {p_{2, i}}}}{2} \mp \frac{{1.481\left( {{p_{1, i}} - {p_{2, i}}} \right)\left| {N\left( {0, 1} \right)} \right|}}{2},\;\mu > 0.5 \\ \end{gathered} \right.{\text{ }} $

(13)

其中, ${c_{1, i}}$ 、 ${c_{2, i}}$ 代表子代染色体上对应的第 $i$ 个变量; ${p_{1, i}}$ 、 ${p_{2, i}}$ 代表父代染色体上对应的第 $i$ 个变量; $\;\mu $ 是均匀分布在区间 (0, 1)的随机数, $\left| {N\left( {0, 1} \right)} \right|$ 代表正态分布随机变量.

2.3 改进NSGA-II算法的海上搜救资源调度方法设计

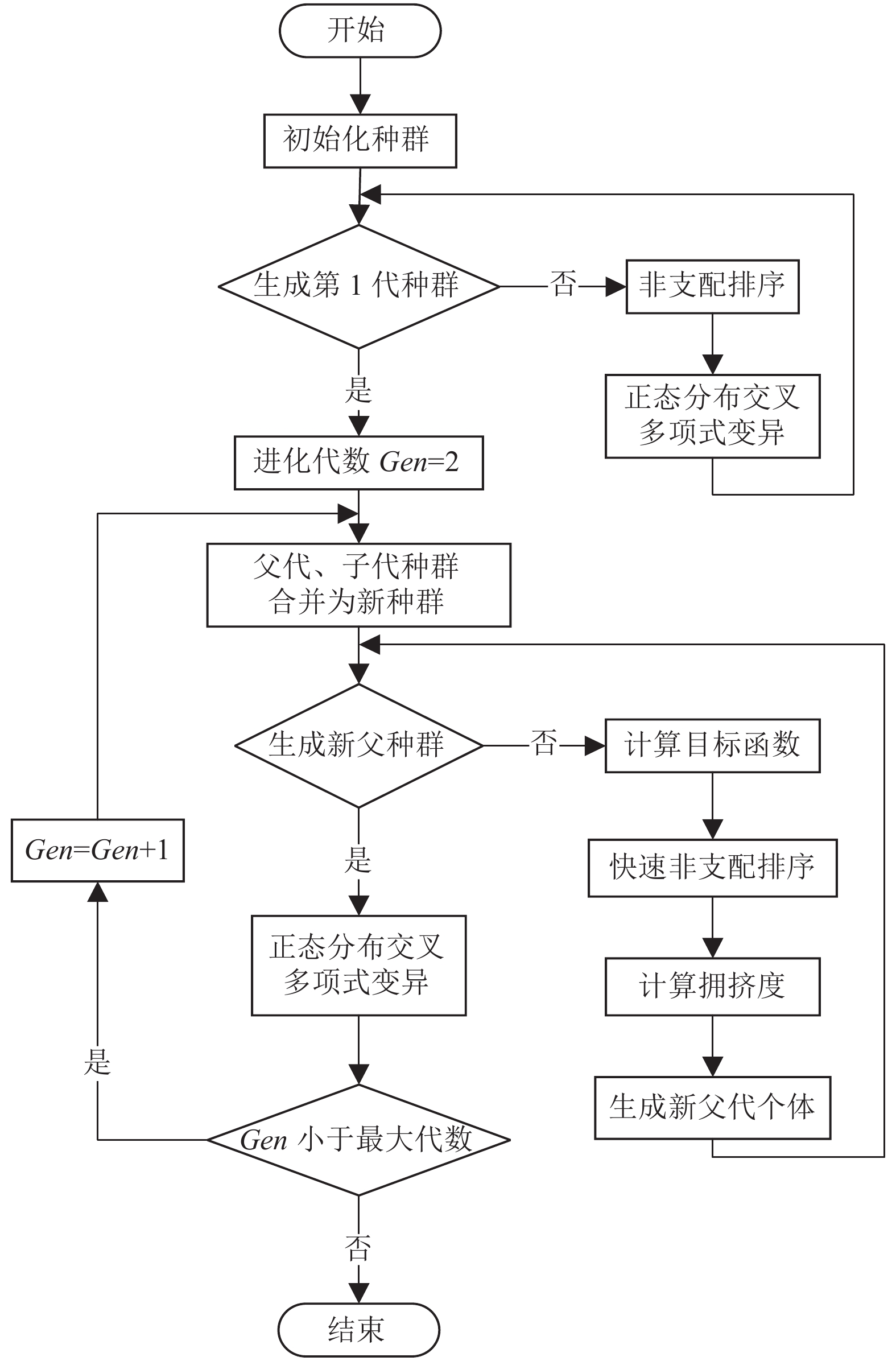
将NDX算子引入到NSGA-II算法中, 得到改进的NSGA-II算法, 利用改进的NSGA-II算法对多目标模型进行求解, 最终得到多目标模型中的Pareto解集, 进而对Pareto解集采用TOPSIS方法^[9]获取折衷解, 即海上搜救调度方案. 具体的算法流程图如图2所示.

(1) 初始化种群设置进化代数Gen=1, 这里的初始种群即为所有的搜救船舶组合方案.

(2) 判断是否生成了第1代种群, 如果是, 则进化代数Gen=2, 否则对初始的种群采用非支配遗传排序和正态分布交叉多项式变异使得生成第1代种群, 从而进化代数Gen=2.

(3) 将父代、子代种群合并为新的种群.

(4) 判断是否生成新的父种群, 如果是, 则执行步骤(5), 如果否, 则计算新种群中个体的目标函数, 并采用快速非支配排序并计算拥挤度生成新父代种群.

(5) 对生成的新父代种群采用正态分布交叉多项式变异生成子代种群.

(6) 判断Gen是否小于最大代数, 如果是, Gen=Gen+1, 继续执行步骤(3), 否, 运行结束.

3 仿真及结果分析

青岛市海上搜救中心接到报警信息, 黄海海域发生事故, 两艘船舶相撞, 船上共有6名船员逃生. 海上搜救中心接到报警信息后划定搜救区域的面积为1000 平方海里, 船舶的搜寻航线间距统一设为0.2 海里. 根据海上落水人员生存分析算法得出失事人员存活时间为4 h. 根据当前时刻AIS及北斗信息显示, 周边有16艘可用船舶, 各船舶性能参数表如表2所示, 考虑到面积为1000 平方海里的区域内最多可以同时容纳的船舶数量为8艘. 综合上述信息, 选择合适的搜救船舶组成最优海上搜救力量配置方案.

在Windows 10操作系统下, 软件平台为Matlab R2019a, 利用改进的NSGA-II算法对海上搜救调度进行优化, 分别与NSGA-II算法和贪婪算法进行对比, 算法具体的参数设置如表3所示.

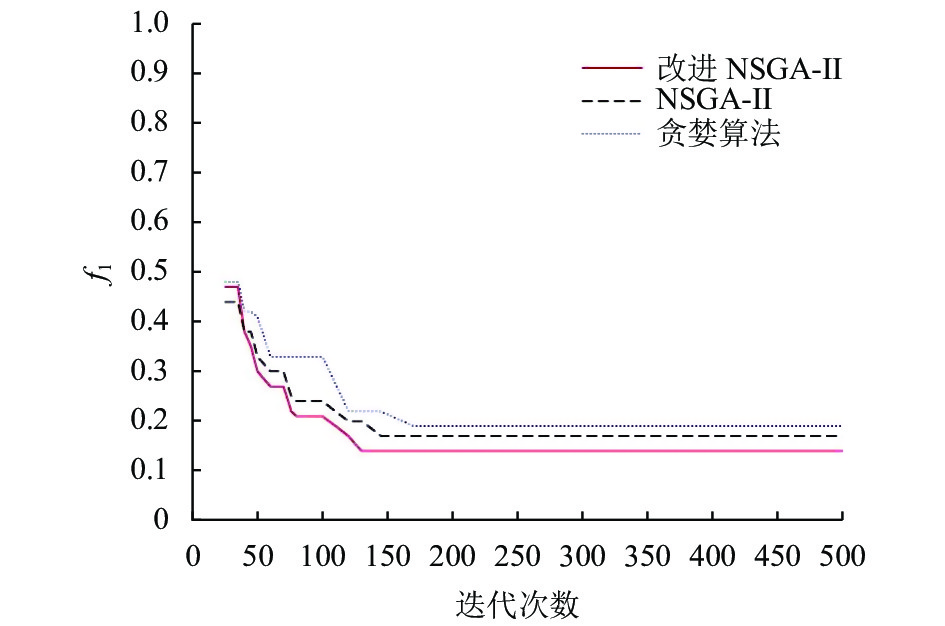
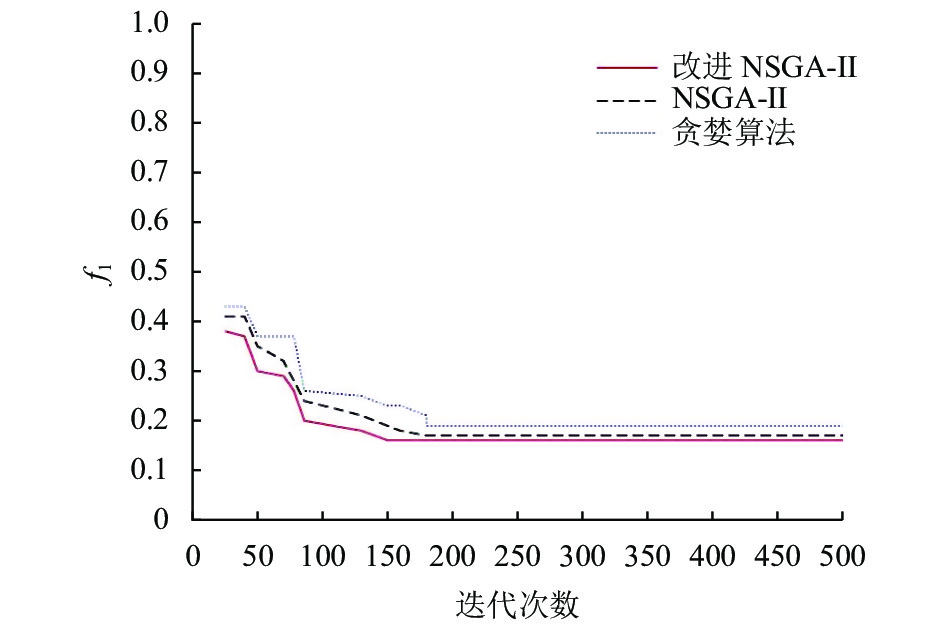
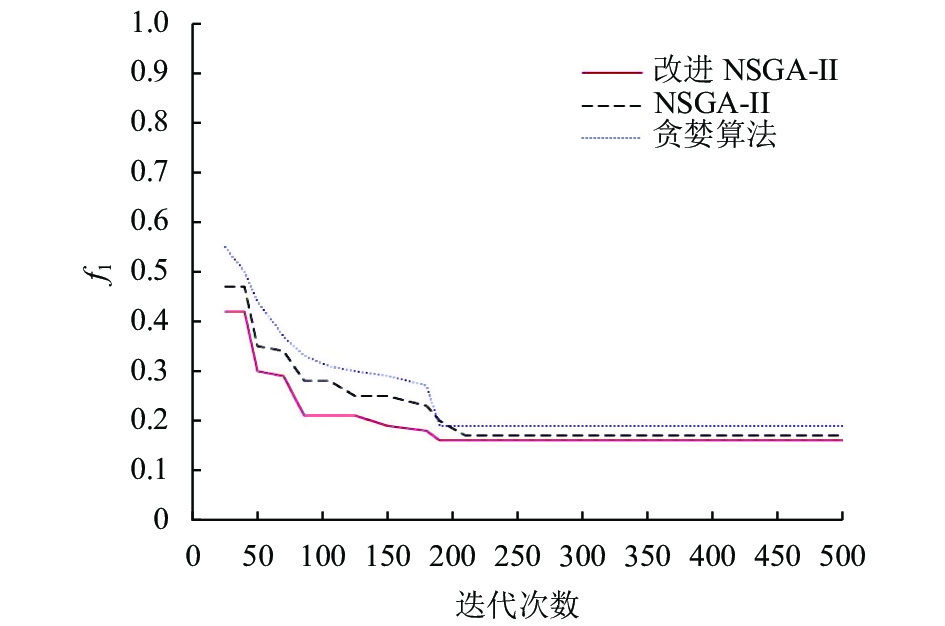
为了更好地进行对比实验, 将表2数据代入多目标模型中的式(5)和式(8), 在3个不同的时间段内, 算法的参数设定一致, 分别运行3种算法10次, 记录下每种算法下的一个最优曲线. 最佳搜救力量结果如表4所示, 对应的3个时间段内进化曲线如图3、图4、图5所示.

对表4的结果进行分析, 在13:00–15:00时之间, 贪婪算法和NSGA-II算法得出需要4艘船舶, 而改进NSGA-II算法只需3艘船舶, 对应的搜救成功率更高, 成本更低; 在15:00–17:00时以及17:00–19:00时之间, 3种算法得出的搜救力量组合数量相同, 但改进NSGA-II算法所求得的搜救成功率更高, 成本更低.

从图3、图4可以看出, 改进NSGA-II算法的目标曲线值相比于贪婪算法和NSGA-II算法以较快的速度达到最优收敛解, 并且f₁值低于贪婪算法和NSGA-II, 即搜救成功率高. 从图5可以看出, 虽然3种算法基本以相同的迭代次数达到收敛, 搜索的速度基本相同, 但是改进的NSGA-II算法达到的f₁最低, 即搜救成功率最高, 这证明了改进的NSGA-II算法引入了NDX算子具有良好的效果, 相比于其他2种算法, 提高了收敛速度, 增加全局搜索能力, 能够达到一个全局优化的效果. 综上, 改进NSGA-II算法不仅保证了搜救成功率, 也相对降低了一些经济成本, 优化决策的结果更加合理, 也验证了该算法在海上搜救调度中的合理性.

4 结论

针对海上搜救调度建立多目标模型, 建立以搜救成功率和搜救成本为目标函数, 本文设计一种基于改进的NSGA-II算法的海上搜救调度方法, 该方法中引入了NDX算子, 扩大搜索能力和搜索范围, 能够跳出局部最优, 得到全局最优, 基于最优Pareto解集得到最优海上搜救调度方案. 通过实验验证分析, 改进的NSGA-II算法相比于贪婪算法和NSGA-II, 能够以较快的速度达到收敛值, 在保证搜索效率的同时达到全局优化的效果, 在一定程度上提高了搜救成功率同时降低了搜救成本, 得到了高效且经济可行的搜救决策方案, 同时也验证了本文算法对于求解海上搜救多目标优化模型的可行性和有效性.