1 引言

随着现代信息科技的发展, 人工智能技术突飞猛进, 人们着手于将人工智能应用于机器人来解决诸如物流等领域中的问题. 在物流系统中, 货物一般通过托盘这一载体进行运输, 移动托盘是自动化仓储中AGV设备的常见任务. 2022年《中共中央国务院关于加快建设全国统一大市场的意见》中也提到了“推广标准化托盘带板运输模式”^[1]. 因此, 托盘定位是自动化仓储中不可或缺的环节.

根据采集数据所使用的传感器类型不同, 托盘定位可以分为以下两类.

(1)基于激光雷达的托盘定位. 赵俊宏等人^[2]采用2D激光雷达获取数据, 然后使用模板匹配的方法进行位姿估计, 鲁棒性较差. Mohamed等人^[3]采用深度学习结合2D激光雷达进行托盘定位, 但因为激光数据不够密集, 托盘位姿估计精度低. Bellomo等人^[4]使用点云图像与激光雷达相结合的形式, 由于点云数据处理需要耗费大量的时间, 难以保证算法的实时性. 并且激光雷达价格相对高昂, 难以大规模普及.

(2)基于视觉的托盘定位. 基于视觉的方法主要可以分为传统图像处理方法和基于深度学习的方法. 在传统图像处理上Chen等人^[5]将图像从RGB空间转换到HSV空间, 利用托盘的几何形状确定托盘位置. Cui等人^[6]通过分析托盘的颜色、边缘、角点等信息直接检测托盘, 这种方法只能适用于特定形状和颜色的托盘. 武文汉^[7]使用ToF相机和纸标签进行3D点云模板匹配来进行托盘定位, 虽然能保证准确性和鲁棒性, 但无法满足实时性. Xiao等人^[8]先对点云数据进行平面分割再使用模板匹配来估计托盘的位姿, 但该算法对于相应的视觉传感器性能要求严格. 利用传统图像算法来进行托盘定位鲁棒性低, 实际场景下容易受到环境噪声干扰导致实用性不高. 深度学习的方法主要是使用深度卷积神经网络完成对于托盘的检测. Mok等人^[9]采用多任务分类的方式进行托盘的定位, 将托盘按照偏转角度和距离分为多个类别, 该方法只能用于特定场景, 不具备实用性. 叶伟^[10]使用了深度学习结合传统方法的想法, 先使用YOLOv4^[11]算法对托盘进行目标检测, 得到托盘在图像中的位置后, 再使用GrabCut^[12]进行分割, 以此来定位托盘, 虽然该方法的托盘检测效果较好, 但是无法获得空间信息. 朱丹平等人^[13]采用了改进CenterNet^[14]的方法检测托盘, 并利用托盘几何约束估计托盘偏转方向, 效果较好, 但关键点数量较少, 无法得到托盘的距离和倾角信息.

在实际的托盘运输过程中, 叉车需要完成对于托盘的精准对接, 这就需要知道托盘与叉车之间的距离以及托盘与叉铲的倾角, 保证叉车可以正确调整车身实现对于托盘的安全叉取. 针对此问题, 本文提出了一种基于目标和关键点检测的单目托盘定位方法. 由目标检测和关键点检测得到托盘的轮廓信息, 通过轮廓信息与几何约束计算托盘的距离和倾角.

使用传统图像的方法在进行托盘检测容易受到光照等环境因素影响, 导致检测鲁棒性低, 托盘检测失败的情况发生. 而深度学习的托盘检测由于使用深度神经网络提取特征, 整体鲁棒性高, 检测效果好. 如图1所示, 当有光照造成阴影在托盘表面时, 传统方法的模板匹配无法检测托盘, 而基于深度学习的YOLOv5网络在训练好模型后可以很好地进行托盘的检测. 因此本文在选取托盘检测算法时, 采取基于深度神经网络的YOLOv5算法.

本文的贡献如下: (1)针对托盘轮廓提取, 本文提出了目标检测加关键点检测的方法, 并设计了边缘自适应调整, 得到高精度的轮廓信息. (2)针对托盘定位任务, 本文根据轮廓信息和几何关系提出托盘的距离和倾角计算方法, 并采用RANSAC算法^[15]提高计算精度和稳定性. (3)使用RGB摄像头拍摄并制作了托盘数据集.

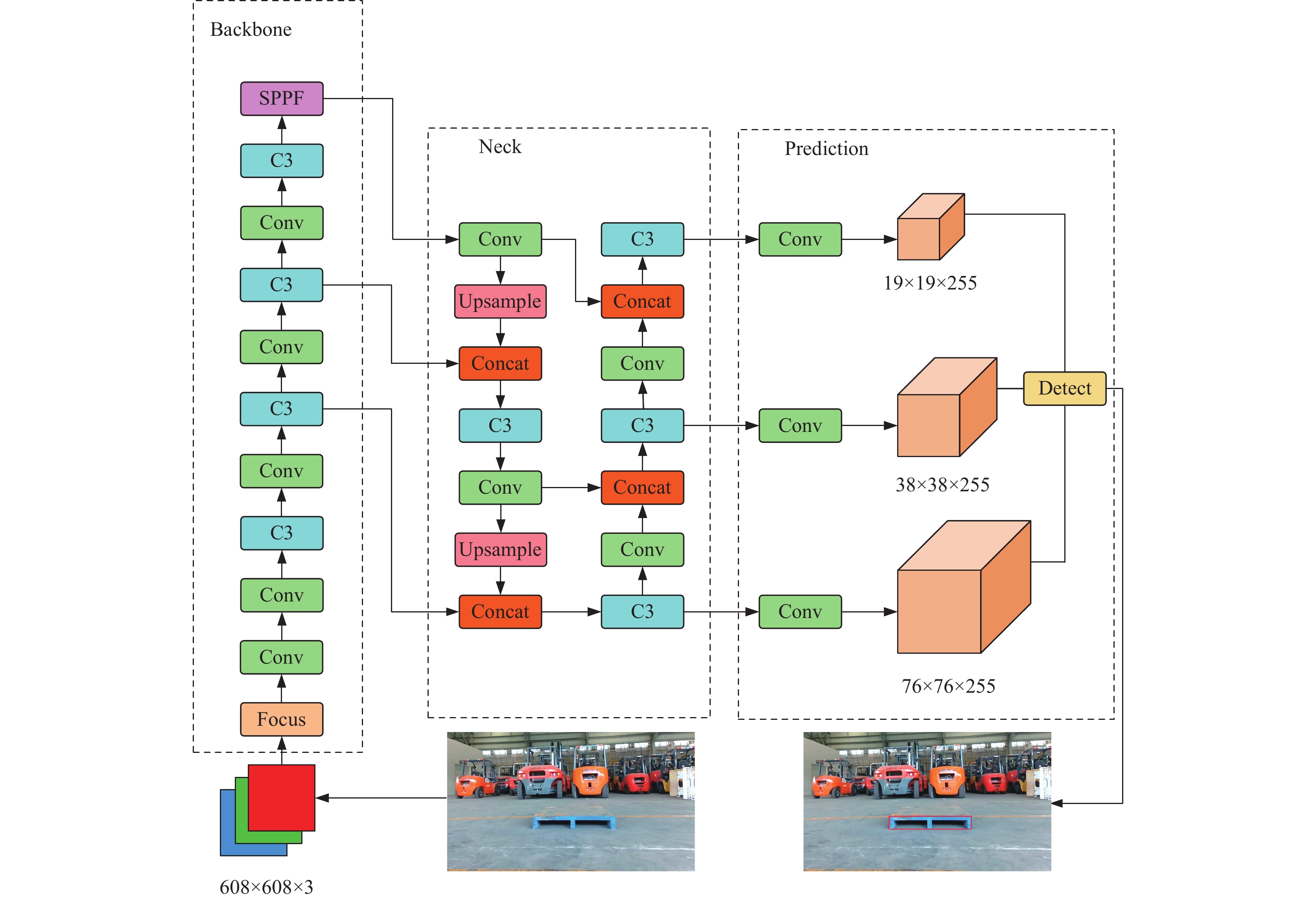
2 相关工作 2.1 YOLOv5目标检测算法

YOLOv5^[16]根据模型的深度和宽度不同可以分为YOLOv5s、YOLO5m、YOLO5l、YOLO5x. 其中从硬件条件和推理速度与精度等方面考虑, YOLOv5s适用性更广, 所以本文选取YOLOv5s为基础检测模型. YOLOv5模型在网络结构上可以分为以下4个部分: 输入端、Backbone、Neck、Prediction. 整体的网络结构如图2所示. 在输入端对输入图像采用Mosaic数据增强, 通过对于训练图像进行随机排布、随机剪裁的方式进行拼接, 同时采用随机缩放增加小目标的数据, 丰富了训练时的数据集, 让网络的鲁棒性有了进一步的提升. 增加了自适应图片缩放, 通过对图像填充最小黑边的方式, 减少了冗余信息, 提升了网络的推理速度. 在Backbone中通过Focus模块对608×608×3样本进行切片拼接, 变成304×304×12的特征图, 后经过32个卷积核的卷积运算后将特征图转换为304×304×32大小. 经过多个Conv与C3层, 提取图像的特征信息, 给后续的模块使用. 在Neck阶段, 采用FPN+PAN上下采样结构, 使得模型的特征信息更加丰富; 同时借鉴了CSPnet的设计, 使用了CSP2_X结构, 加强了网络融合特征的能力. 在Prediction阶段, 网络输出3种不同尺度的特征图用于不同尺寸物体的预测, 通过NMS进行筛选. YOLOv5训练时使用了损失函数 $CIoU\_{\textit{LOSS}}$ 作为Bounding box的损失, 计算公式如下所示:

$ CIoU\_{\textit{LOSS}} = 1 - \left(IoU - \frac{{Dis\_{2^2}}}{{Dis\_{C^2}}} - \frac{{{v^{^2}}}}{{(1 - IoU) + v}}\right) $

(1)

$ v = \frac{4}{{{{\text{π}} ^2}}}{\left( {\arctan \frac{{{w^{gt}}}}{{{h^{gt}}}} - \arctan \frac{{{w^p}}}{{{h^p}}}} \right)^2} $

(2)

其中, $Dis\_2$ 是模型预测框与真实标注框中心点之间的欧式距离, $Dis\_C$ 是包含上述两个框的最小外接矩形对角线的距离, $v$ 是用于衡量长宽比一致性的参数.

2.2 关键点检测

在关键点检测上, 本文采用了KPDA-Net^[17], 基于FCN (full convolution network)^[18]构建而成. 该算法相较于其他关键点检测算法, 可以更灵活的调整算法的输出结构来适应新的对象类别, 迁移能力较强, 所以本文选用KPDA-Net作为关键点检测网络. 该网络模型主要有以下3个部分构成: Stage1, Stage2和Back Propagation. Stage1主要是提取输入图像的数据特征. 模型从经典的ResNet^[19]中借鉴了short-cut connection结构, 解决了训练时反向传播过程中出现梯度退化的问题, 保证了参数之间的区分度. Stage2阶段进行特征图的数值坐标回归. 主要包括计算输出特征图 $S_j^t(p)$ 与热图标签的损失和特征图回归对象的关键点与对象的对应关系. Back propagation进行关键点坐标预测值和真实值之间的损失计算. 将关键点预测坐标与真实坐标之间的L2范数定义为 $f_S^t$ , 关系定义为 $f_L^t$ , 损失函数的计算方式如下:

$ f_S^t = \sum\nolimits_{j = 1}^J {\sum\nolimits_p {W(p) \cdot ||S_j^t} } (p)S_j^*(p)||_2^2 $

(3)

$ f_L^t = \sum\nolimits_{c = 1}^C {\sum\nolimits_p {W(p) \cdot ||L_c^t} } (p)L_c^*(p)||_2^2 $

(4)

$ {\textit{Total}}\_loss = average\_loss(f_S^t + f_L^t) $

(5)

其中, $S_j^*(p)$ 是实际关键点的坐标位置, $L_c^*(p)$ 是实际标签中坐标中心位置生成的矢量图, $W(p)$ 是二值化掩码矩阵, 当 $p$ 位置标签缺失时为1, 否则为0.

3 算法 3.1 算法框架

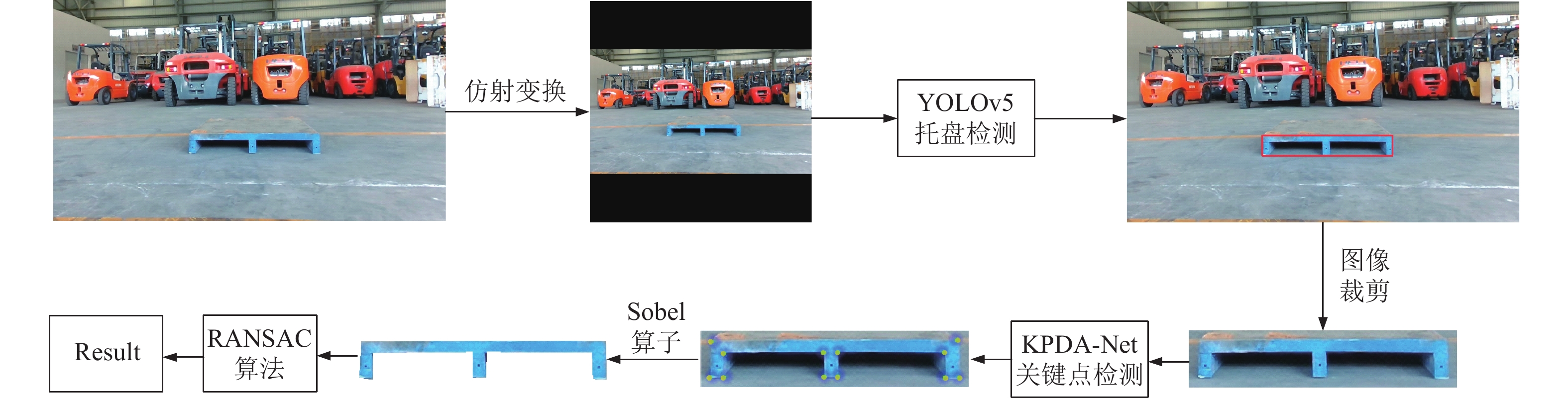
单目视觉的托盘定位算法可分为3部分: 托盘检测, 关键点检测与轮廓提取, 托盘距离与倾角计算. 设YOLOv5的模型为YOLOv5det, 检测类别为托盘(pallet), 返回信息为托盘的在图像中的位置信息(x, y, w, h, 分别表示目标框的中心点和宽高); KPDA-Net模型为KPDA, 输入图像img, 返回关键点(keypoints)的坐标(coords), 具体算法流程如算法1所示, 整体的算法框架如图3所示.

算法1. 托盘定位算法

输入: 摄像头采集的图片

输出: 托盘在图像中的位置(x, y, w, h)与托盘的距离D与倾角θ

1.　使用仿射变换将图像转换成608×608×3

2.　 if YOLOv5det[‘pallet’] != None then

3.　　 x, y, w, h = YOLOv5[‘pallet’]

4.　　根据x, y, w, h对图像进行裁剪

5.　　keypoints = KPDA(img)

6.　　基于几何关键初步得到托盘轮廓信息

7.　　使用Sobel算子自适应调整得到轮廓

8.　　根据式(14)和式(15)使用RANSAC算法计算距离D倾角θ

9.　 end if

10. return x, y, h, w, D, θ

3.2 K-means++预设锚框的托盘检测

在托盘检测的问题上, 本文使用了YOLOv5作为目标检测网络. YOLOv5是有锚框(anchor box)的目标检测模型, 合理的锚框设置能够训练出效果更好的检测器. YOLOv5中的预设锚框是在COCO数据集上使用K-means聚类算法计算得到, 而托盘检测作为特定的任务, 预设锚框在大多数情况下并不适用. 所以本文使用K-means++算法对于托盘数据集中的标签进行聚类, 得到更适用于托盘检测任务的锚框预设值进行训练. K-means++算法修改了K-means算法中初始化k个聚类中心的选取方法, 在K-means++算法中, 距离已经选取聚类中心更远的点被选取为新的聚类中心的概率更大, 这让中心点在随机选取的过程中更趋于全局最优解而不是局部最优解. 通过K-means++算法计算网络初始化的锚框大小, 使其与托盘的真实标记框大小更符合.

对托盘进行目标检测后, 按照检测结果, 对检测框四周各拓宽0.25h像素值对图像进行剪裁 (h表示目标框在y方向的宽度), 输入关键点检测网络中进行关键点检测. 这样既可以保证剪裁过程中保留托盘的关键点以及轮廓信息, 同时又去除大量无关背景, 减少关键点检测网络的训练, 提升关键点的检测速度和准确率.

3.3 关键点检测与轮廓提取

KPDA-Net进行关键点检测由两部分组成, 首先使用特征提取模块KeyPointsModel对输入图像(img)进行特征提取, 得到热图(heatmap); 再使用数值坐标回归模块dsntnn对热图中的数组坐标(coords)进行回归得到关键点的坐标. 由于托盘具有固定的几何外形, 通过热力图回归得到的关键点按照一定顺序相连将直接获得托盘初步的轮廓信息. 但较差的关键点结果会影响托盘的轮廓信息进而影响最终的角度和距离测算. 针对此问题, 本文对边缘点设计了自适应调整的方法. 因为轮廓边缘是梯度变化最大的点, 所以本文采用10×10大小的采样框在初步轮廓连线上移动, 将采样框中图像转化为灰度图后对托盘的上下边缘计算Sobel算子Y方向梯度, 左右边缘计算Sobel算子X方向梯度, 按照梯度最大值自适应调整边缘, 如图4所示.

Sobel算子是在边缘检测中常用的一种离散微分算子, 由两个3×3的卷积核构成, 分别是水平方向内核 $ {G_x} $ 和竖直方向内核 $ {G_y} $ .

$ {G_x} = \left( {\begin{array}{*{20}{c}} { - 1}&0&{ + 1} \\ { - 2}&0&{ + 2} \\ { - 1}&0&{ + 1} \end{array}} \right) $

(6)

$ {G_y} = \left( {\begin{array}{*{20}{c}} { - 1}&{ - 2}&{ - 1} \\ 0&0&0 \\ { + 1}&{ + 2}&{ + 1} \end{array}} \right) $

(7)

具体算法流程如算法2所示.

算法2. 关键点检测与轮廓提取的算法

输入: 根据YOLOv5返回结果剪裁后的图片

输出: 托盘的轮廓信息

1.　heatmap = KeyPointsModel(img)

2.　coords = dsntnn(heatmap)

3.　将关键点按照几何位置相连得到初步轮廓边缘

4.　 for point in keypoints connection do

5.　　point = sobel(point range)

6.　 end for

7.　return 托盘轮廓信息

3.4 基于几何约束的托盘倾角和距离计算方法

无人叉车在叉取托盘的过程中, 相机会安装在叉车上的固定位置, 托盘会摆放在地面或者货架上, 与地面平行. 根据以上条件, 将像素坐标系与叉车相机坐标系进行映射, 就可以对单目相机采集的托盘图像进行位姿估计. 像素坐标系与叉车相机坐标系的关系如图5所示. 根据针孔相机模型, 在叉车相机坐标系中, xz平面平行于地面, z轴方向为相机正前方, $y$ 轴垂直于地面朝下. 归一化平面是相机前方 ${\textit{z}} = 1$ 位置的平面. $P$ 是托盘上的任意一点, 在叉车相机坐标系中的坐标为 $\left( {X, Y, Z} \right)$ . $p$ 是 $P$ 在归一化平面中所对应的点, 像素坐标为 $\left( {x, y} \right)$ . $P$ 与 $p$ 有如下映射关系:

$ \left( {\begin{array}{*{20}{c}} x \\ y \\ 1 \end{array}} \right) = \frac{1}{Z}\left( {\begin{array}{*{20}{c}} {{f_x}}&0&{{c_x}} \\ 0&{{f_y}}&{{c_y}} \\ 0&0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} X \\ Y \\ Z \end{array}} \right) \triangleq \frac{1}{Z}KP $

(8)

其中, ${f_x}, {f_y}$ 为归一化焦距, ${c_x}, {c_y}$ 为像主点的坐标, $K$ 为相机的内参矩阵. 托盘在空间中的位姿如图5所示. $H$ 为托盘的物理高度, $h$ 为叉孔上边缘的厚度, $L$ 为托盘的长度, 定义角度 $\theta $ 为托盘正面与坐标系 $x$ 轴到地面投影所成夹角, 定义距离 $D$ 为托盘正面中心位置

到相机的水平距离, ${P_l}, {P_r}$ 是托盘上边缘的左右端点, 坐标为 $\left( {{X_l}, {Y_l}, {Z_l}} \right), \left( {{X_r}, {Y_r}, {Z_r}} \right)$ , ${p_l}, {p_r}$ 为 ${P_l}, {P_r}$ 在归一化平面内的映射点, 坐标为 $\left( {{x_l}, {y_l}} \right), \left( {{x_r}, {y_r}} \right)$ , ${P_{i1}}, {P_{i2}}$ 是托盘上下边缘 ${\textit{z}}$ 值相等的一对点, 坐标为 $\left( {{X_{i1}}, {Y_{i1}}, {Z_{i1}}} \right), \left( {{X_{i2}}, {Y_{i2}}, {Z_{i2}}} \right)$ , ${p_{i1}}, {p_{i2}}$ 为 ${P_{i1}}, {P_{i2}}$ 在归一化平面内的映射点, 坐标为 $\left( {{x_{i1}}, {y_{i1}}} \right), \left( {{x_{i2}}, {y_{i2}}} \right)$ . 当点对 ${P_{i1}}, {P_{i2}}$ 处在非插孔所在边缘时, 有如下空间关系:

$ \left( {\begin{array}{*{20}{c}} {{X_{i2}}} \\ {{Y_{i2}}} \\ {{Z_{i2}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{X_{i1}}} \\ {{Y_{i1}}} \\ {{Z_{i1}}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} 0 \\ H \\ 0 \end{array}} \right) $

(9)

在托盘轮廓上任取两对点 ${P_{11}}, {P_{12}}$ 和 ${P_{21}}, {P_{22}}$ , 对点 ${P_{11}}$ 和 ${P_{21}}$ , 有如下空间关系:

$ \left( {\begin{array}{*{20}{c}} {{X_{21}}} \\ {{Y_{21}}} \\ {{Z_{21}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{X_{11}}} \\ {{Y_{11}}} \\ {{Z_{11}}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {W\cos \theta } \\ 0 \\ {W\sin \theta } \end{array}} \right) $

(10)

$ W = L\frac{{{x_{11}} - {x_{21}}}}{{{x_1} - {x_2}}} $

(11)

其中, $W$ 为点 ${P_{11}}$ 和 ${P_{21}}$ 的空间距离. 根据式(8)反向求解 $Y$ 可得:

$ Y = \frac{Z}{{{f_y}}}\left( {y - {c_y}} \right) $

(12)

将式(12)带入式(9)求解 $Z$ 可得:

$ {Z_{i1}} = {Z_{i2}} = \frac{{{f_y}H}}{{{y_{i2}} - {y_{i1}}}} $

(13)

将式(13)带入式(10)可得:

$ \theta = \arcsin \left( {\frac{{{f_y}H\left( {{x_1} - {x_2}} \right)}}{{L\left( {{x_{11}} - {x_{21}}} \right)}}\left( {\frac{1}{{{y_{22}} - {y_{21}}}} - \frac{1}{{{y_{12}} - {y_{11}}}}} \right)} \right) $

(14)

将式(13)和式(14)带入式(10)可得:

$ D = \frac{{{f_y}H}}{{\Delta {y_i}}} + \frac{{{f_y}H\left( {{x_{i1}} - 0.5\Delta x} \right)}}{{L\left( {{x_{11}} - {x_{21}}} \right)}}\left( {\frac{1}{{\Delta {y_2}}} - \frac{1}{{\Delta {y_1}}}} \right) $

(15)

$ \Delta {y_i} = {y_{i2}} - {y_{i1}} $

(16)

$ \Delta x = {x_1} - {x_2} $

(17)

由式(14)和式(15)即可算出托盘当前与摄像头之间的距离和倾角.

3.5 基于RANSAC算法的托盘倾角和距离计算

如果只取检测的关键点用于计算, 样本数据量小, 微小的误差就可能导致不准确的计算结果, 针对此问题, 本文根据轮廓信息, 采用RANSAC算法提高计算精度, 算法流程如图6所示.

通过选取多组点对进行计算增加样本的数据量, 同时使用RANSAC算法剔除错误的点对. 由于通过点对计算得到的倾角和距离是估计值而非固定值, 所以就必须考虑存在误差. 设定算法阈值为:

$ \left| {d\theta } \right| \leqslant 3^\circ $

(18)

$ \left| {dD} \right| \leqslant 0.2 \; {\text{m}} $

(19)

其中, $d\theta $ 为最优角度与当前计算角度的差, $dD$ 为最优距离与当前计算距离的差.

4 实验分析 4.1 数据集

本文采用的数据集是笔者自己采集并建立的数据集. 考虑到目前没有公开托盘检测数据集, 笔者自己使用1980×1080分辨率的RGB摄像头拍摄了一个托盘数据集. 整个数据集分别在室内和室外多个场景下拍摄放置于地面和货架上的托盘, 采集总时长为70 min的视频. 剔除质量不高和变化不大的图片, 选取1680帧图像作为实验数据集. 其中训练集占比80%, 验证集占比10%, 测试集占比10%.

4.2 实验过程

本实验所用机器配置如表1所示. 为了提高目标检测的鲁棒性, 本文训练时对输入图像进行随机反转, 并加入一个服从正太分布的随机噪声, 将数据增强后的2688张图像输入网络进行训练.

实验有以下评价指标: 对于托盘的目标检测, 使用召回率Recall和平均AP值mAP. 召回率越高, 表示托盘被正确检测的概率越高; mAP越高, 表示托盘检测精度越高. 对于托盘倾角和距离计算, 使用平均角度误差 ${\theta _{{\rm{average}}}}$ 和最大角度误差 ${\theta _{\max }}$ 作为角度计算的评价指标; 使用平均距离误差 ${D_{{\rm{average}}}}$ 和最大距离误差 ${D_{\max }}$ 作为距离计算的评价指标.

$ {\theta _{{\rm{average}}}} = \frac{{\displaystyle\sum\nolimits_{j = 1}^J {\left| {{\theta _j} - \theta } \right|} }}{J} $

(20)

$ {\theta _{\max }} = MAX\left(\left| {{\theta _j} - \theta } \right|\right) $

(21)

$ {D_{{\rm{average}}}} = \frac{{\displaystyle\sum\nolimits_{j = 1}^J {\left| {{D_j} - D} \right|} }}{J} $

(22)

$ {D_{\max }} = MAX \left(\left| {{D_j} - D} \right|\right) $

(23)

其中, ${\theta _j}$ 为第j帧图像中托盘角度计算值, $\theta $ 为托盘实际角度, ${D_j}$ 为第j帧图像中托盘距离计算值, $D$ 为托盘实际距离.

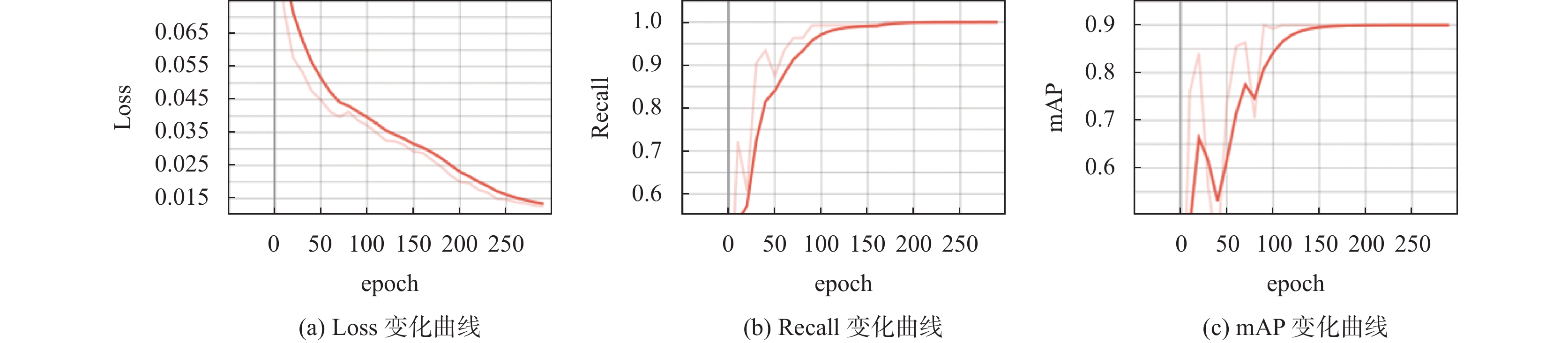
经过K-means++算法对托盘数据集进行聚类后得到的9个锚框的大小分别为(62, 19), (68, 22), (76, 27), (80, 23), (89, 34), (91, 27), (102, 30), (112, 31), (119, 35). 学习率设置为0.0032, 模型训练的epoch设置为300, 模型每次迭代一个epoch都会在验证集上进行验证, 并保存效果最好的一个模型. 由于数据集数量较小, 为了防止出现过拟合的情况, 当训练过程中Loss不再下降时笔者会停止训练. 利用YOLOv5的预训练权重作为初始训练权重, 使用自己的数据集进行训练. 训练过程中Loss, Recall和mAP的变化曲线如图7所示, 其中, 深色曲线为当前坐标轴的曲线变化，浅色曲线为放大坐标轴的曲线变化.

由图7可知, 随着训练的进行, Loss值逐渐下降, Recall和mAP值逐渐上升. 当训练到一定的程度时, 模型收敛, 此时Loss, Recall和mAP的值在一个稳定的区间, 停止训练, 得到训练好的模型.

4.3 实验结果及分析

将设定锚框后的网络与经典的目标检测网络Faster R-CNN^[20], YOLOv5s^[16]以及文献[10]和文献[13]中的方法在测试集上进行实验结果比对, 如表2所示. 表中对比不同网络的召回率和平均精度, 从表中可以看出, 本文方法对比其他目标检测网络效果较好, 更利于后续对于托盘的位姿计算.

为了验证本文对于托盘倾角和距离计算方法及其改进的有效性, 选取室内放置于地面场景下的托盘, 角度为−60°~60°, 每间隔10°为一组图片; 距离为1600– 3200 mm, 每间隔100 mm一组图片进行实验验证. 笔者使用 ${\theta _{{\rm{average}}}}$ , ${\theta _{\max }}$ , ${D_{{\rm{average}}}}$ 和 ${D_{\max }}$ 作为评价指标, 对算法自身进行了纵向对比实验. 将关键点检测后直接进行倾角和距离计算设为原算法, 自适应边缘调整设为改进1, 使用RANSAC算法设为改进2. 实验所得角度与真实角度的误差如表3所示, 表中所有数据单位为°; 所得距离与真实距离的误差如表4所示, 表中所有数据单位为mm.

根据表3和表4的实验结果可知, 改进后的算法精度和稳定性显著提升, 对于托盘的角度计算误差均值小于5°, 最大值不超过10°; 距离计算误差均值小于110 mm, 最大值不超过130 mm, 不足真实距离的5%. 实验结果, 本文方法的托盘距离和倾角计算对于单目相机而言具有较高的精度, 能够提供有效的托盘位姿信息.

5 结论与展望

本文提出了一种基于目标和关键点检测的托盘定位方法. 首先通过目标检测网络YOLOv5对于托盘进行目标检测, 将得到的结果剪裁后输入KPDA-Net中进行关键点检测. 然后根据托盘的几何外形, 设计了自适应边缘调整提取轮廓. 在得到托盘轮廓的基础上, 提出了托盘倾角与距离的计算方法并进行了实验验证. 与其他托盘定位的方法对比, 本文解决了目前托盘定位中目标检测算法无法得到托盘空间信息的问题, 算法表现优异, 下一步计划将本文方法部署在无人叉车系统上, 更好更精确的实现托盘的叉卸.