常减压蒸馏设备作为炼油厂的龙头装置, 产出油品的质量直接影响炼油厂的经济效益. 闪点是常一线航空煤油等一类产品的重要质量指标, 为了保证航空煤油产品合格, 控制闪点值是主要技术手段. 目前, 常一线航空煤油闪点的数据都是通过实验室化验得到, 此方法具有很大的时滞性, 为了准确及时得到闪点值, 只能通过软测量技术解决这个问题. 软测量是过程控制领域中用于解决难测参数检测的一种常用技术, 近年来广泛运用于工业中[1, 2]. 软测量建模主要分为数据驱动建模、机理建模、混合建模3类[3]. 因其简单好求解, 所以目前大部分建模使用的是数据驱动建模. 基于数据驱动的软测量方法目前有人工神经网络[4]、回归分析[5]和支持向量机[6].
目前已经有很多学者在该领域进行了深入的研究. 文献[7]利用人工神经网络 (artificial neural network, ANN)建模方法, 对轻质油闭口闪点值进行预测, 并利用现场采集的5种轻质油品的化验值检验模型的预测能力. 文献[8]针对原油闪点的在线预测, 采用主成分分析法对输入变量进行降维, 分别采用多元线性回归 (multiple linear regression, MLR)、RBF (radial basis function)神经网络和BP (back propagation)神经网络3种建模方法对原油闪点进行预测, 并对预测结果进行对比. 文献[9]提出了一种基于粒子群优化算法 (particle swarm optimization, PSO)-BP神经网络的软测量模型, 用于精制柴油闪点值的预测, 以此来控制柴油的生产质量. 文献[10]提出一种利用支持向量机 (support vector machine, SVM)建模的方法实现轻柴油的闪点、95%馏出温度和凝点3个关键指标的在线预测. 文献[11]使用核偏最小二乘法 (kernel partial least squares, KPLS)进行数据压缩和特征提取, 采用混沌粒子-模拟退火方法 (CPSO-SA)优化最小二乘支持向量机 (least squares support vector machine, LS-SVM)的模型方法对航煤闪点和干点值进行在线预测. 尽管软测量技术在石油闪点值预测方面有不少的研究成果, 但目前的研究工作仍然存在着预测精度不高、时滞性较大及模型复杂等问题.
近年研究成果表明, 极限学习机作为一种单层前馈神经网络, 具有结构简单、泛化性能良好以及较快的学习能力, 目前广泛应用于软测量方向. 但ELM的初始权重和偏置是随机产生的, 导致其每次运行结果具有较大的随机性, 因此, 在常压塔航空煤油闪点值预测中一般加入优化算法来对ELM寻找最优的初始权阈值, 提高预测模型的泛化能力.
本文为了保证航空煤油闪点在线预测的可靠性和准确性, 故提出了一种基于灰色关联分析法并利用改进鲸鱼优化算法对极限学习机进行优化的预测模型来进行在线估计[12]. 首先采用GRA方法对辅助变量进行相关性分析并挑选出相关性较大的变量, 这样不仅提高了模型训练速度, 还降低了输入变量的维数[13]; 然后将筛选出的6个辅助变量输入到ELM中; 由于ELM的权阈值对模型的适用性和拟合精度都有很大的影响, 所以通过 IWOA的全局搜索和局部寻优能力来优化ELM的参数. 最后, 利用常压塔蒸馏过程对此进行了验证, 证明了其可行性.
1 常压塔工艺流程常压塔是一个复合塔, 利用原油各成分的挥发度不同, 通过常压蒸馏过程来进行分割. 通过对某炼油厂的常压塔工艺机理分析可知, 原油首先进行严格的脱盐、脱水、换热进入到初馏塔中, 由常压炉加热到指定温度后进入常压塔, 从上至下依次分割出汽油、航空煤油、轻柴油、重柴油及重油. 重油经水蒸气提炼出轻组分后, 通过转油线作为进料输送到减压塔中[14], 图1为常压系统工艺流程图.

|
图 1 常压系统工艺流程图 |
2 灰色关联分析法
灰色关联分析法是对一个系统发展变化态势的定量描述和比较的方法, 通过确定参考数据与比较数据的几何形状相似程度来进行辅助变量的选取[15]. 下面以常一线航空煤油闪点辅助变量选取为例进行说明.
对常一线航空煤油闪点数据利用均值法进行归一化处理, 设辅助变量 (对比数列)矩阵为
利用式(1)计算关联系数
| εi(j)=mini,jΔij+ρmaxi,jΔijΔij+ρmaxi,jΔij | (1) |
其中,
最后, 计算各比较数列灰色关联度
| Ri=n∑j=1εi(j) | (2) |
通过GRA筛选出与预测变量相关度高的辅助变量, 本数据集一共23个辅助变量, 选取前6个变量作为输入, 分别为初底油进料温度、塔底温度、常压炉出口温度、塔底出口温度、常三汽提塔液位、常一中流量.
3 鲸鱼算法 3.1 算法原理鲸鱼优化算法 (WOA)[16]是基于座头鲸捕食行为的启发, 提出的一种结构简单、收敛快、容易实现的新型启发式算法. 该算法是以“气泡网络”捕食策略为基础的, 将其分成包围、泡泡网、搜寻猎物3个阶段.
3.1.1 包围猎物阶段该算法以座头鲸的觅食行为为基础, 构建了一种新的数学模型. 在不知道猎物位置的情况下, 该算法假定最优候选解是 (最靠近)目标猎物位置, 并在此基础上不断地进行更新. 这种行为用式(3)、式(4)表示:
| D=|C⋅X∗(t)−X(t)| | (3) |
| X(t+1)=X∗(t)−A⋅D | (4) |
其中, D为
A和C由式(5)–式(7)得出:
| A=2ar1−a | (5) |
| C=2r2 | (6) |
| a=2−2ttmax | (7) |
其中,
(1)收缩包围机制: 这种机制的实现是通过降低a的值来达到的, 使鲸鱼个体不断更新位置来完成猎物的包围[17].
(2)螺旋更新位置: 这种方法首先计算位于当前位置的鲸鱼和位于目标位置的猎物之间的距离. 然后在二者之间的位置建立一个螺旋方程, 通过此方程来进行围捕. 公式如下:
| D′=|X∗(t)−X(t)| | (8) |
| b=−1−ttmax | (9) |
| X(t+1)=D′⋅ebl⋅cos(2πl)+X∗(t) | (10) |
其中,
若
| X(t + 1) = \left\{ {\begin{array}{*{20}{l}} {{X^*}(t) - A \cdot D{\text{ }}}, \\ {D' \cdot {{\rm{e}}^{bl}} \cdot \cos (2 {\text{π}} l) + {X^*}(t)} , \end{array}} \right.{\text{ }}\begin{array}{*{20}{c}} {p < 0.5} \\ {p \geqslant 0.5} \end{array} | (11) |
当
| D = |C \cdot {X_{{\rm{rand}}}}(t) - X(t)| | (12) |
| X(t + 1) = {X_{{\rm{rand}}}}(t) - A \cdot D | (13) |
其中,
WOA在种群初始化、全局搜索和局部寻优存在不足, 针对这些问题进行了如下改进.
3.2.1 改进的Tent混沌映射种群初始化种群初始化不但会影响算法的精度, 而且对其收敛速率也会产生一定的影响. 一般情况下, 基础的WOA在求解最优问题时, 往往会使用随机的方式来生成初始群体, 这会导致种群分布不均匀, 以至于种群多样性较差, 从而导致寻找不到最优解. 由此, 本文在原始Tent混沌映射初始化种群公式中增加了一个扰动分量[19], 以此来加强Tent混沌映射的抗干扰能力, 使种群初始化更加稳定及分布更加均匀, 来提高算法的寻优精度. 原初始化公式如下:
| {x_{n + 1}} = \left\{ {\begin{array}{*{20}{l}} {0.5{x_n}} , \\ {0.5\left( {1 - {x_n}} \right)}, \end{array}} \right.{\text{ }}\begin{array}{*{20}{c}} {0 \leqslant {x_n} \leqslant 0.5} \\ {0.5 \lt {x_n} \leqslant 1} \end{array} | (14) |
改进后的公式如下:
| {x_{n + 1}} = \left\{ {\begin{array}{*{20}{l}} {0.5{x_n} + 1} , \\ {0.5\left( {1 - {x_n}} \right) + 1} , \end{array}} \right.{\text{ }}\begin{array}{*{20}{c}} {0 \leqslant {x_n} \leqslant 0.5} \\ {0.5 \lt {x_n} \leqslant 1} \end{array} | (15) |
其中,
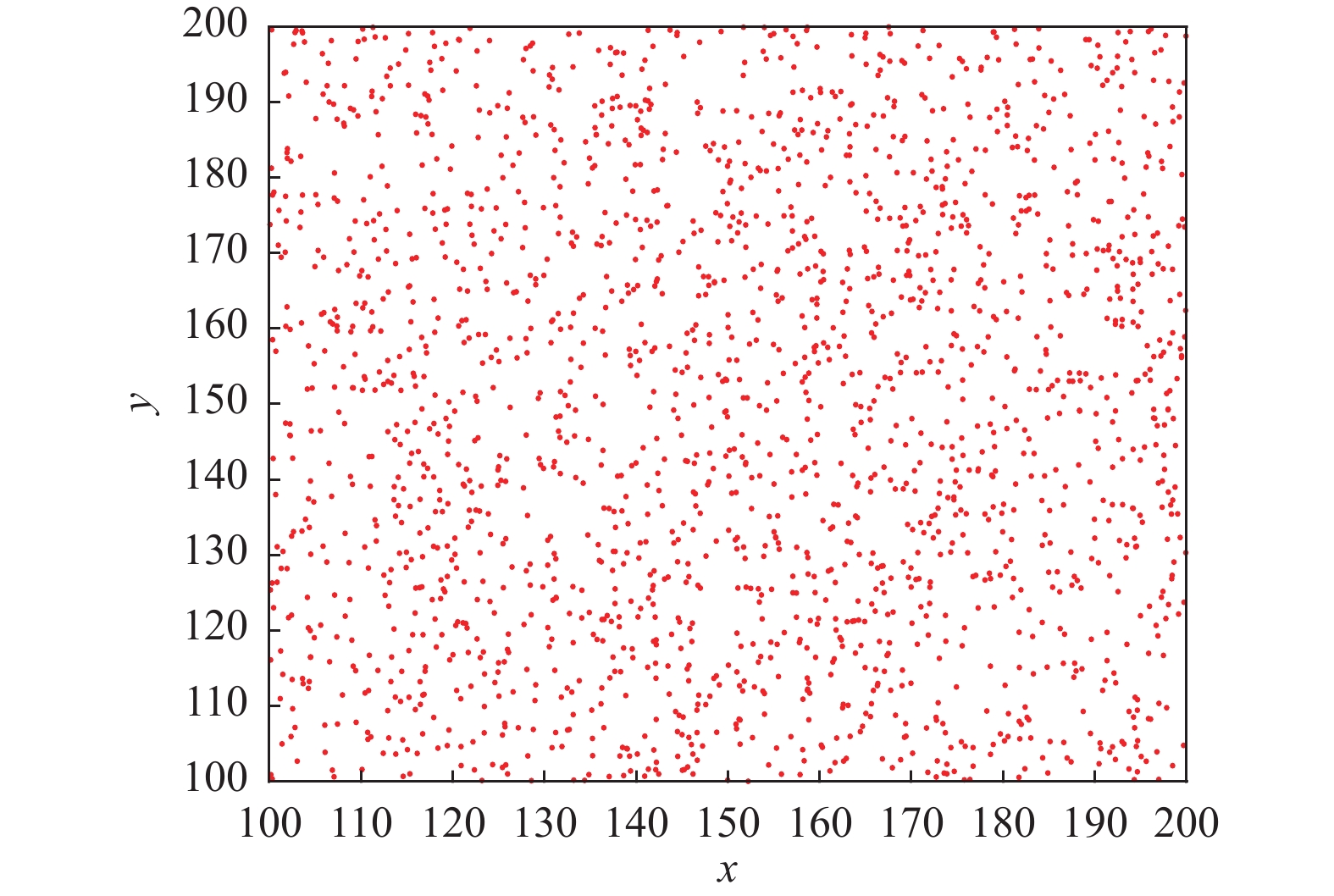
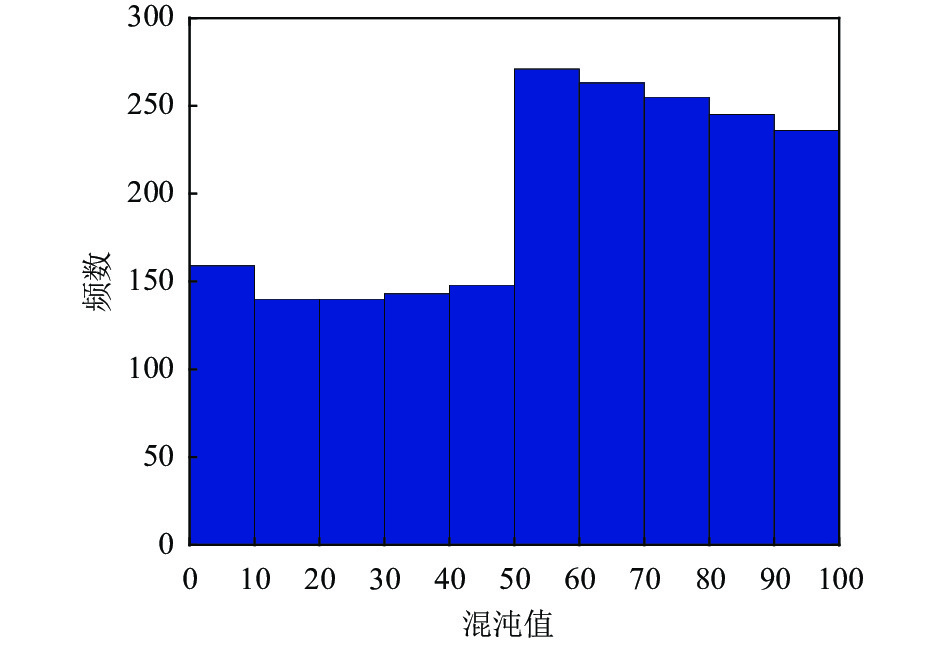
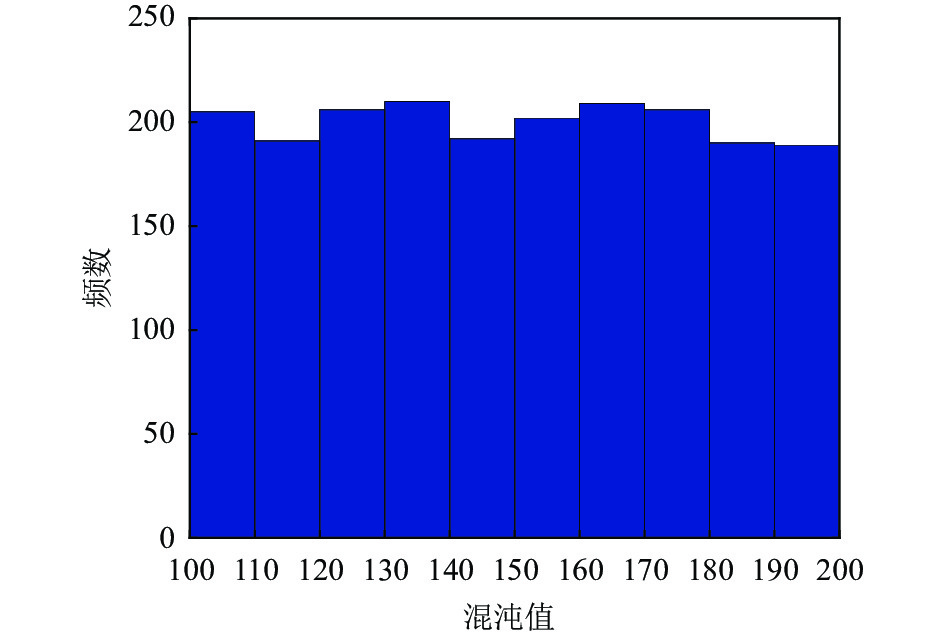
本测试设置的种群数是2000, 维数为2, 上界为100, 下界为0. 改进前后效果如图2–图5所示.

|
图 2 Tent分布情况 |
|
图 3 改进后的Tent分布情况 |
|
图 4 Tent混沌值分布情况 |
|
图 5 改进后的Tent混沌值分布情况 |
通过图2和图3对比发现改进后的Tent产生的混沌序列均匀性更好, 进而能保证算法在迭代前期具有良好的种群多样性; 对比图4与图5发现在 [0, 50]与 [50, 100]两个范围的原始Tent混沌映射取值概率差距较大, 而改进后的Tent混沌映射取值概率则相对均匀, 能有效提高算法的寻优精度与速度.
3.2.2 自适应权重结合随机差分变异策略基础WOA在迭代后期, 由于不能很好地寻找到最优解. 所以在算法中加入自适应权重可以有效提高算法的寻优能力. 当权重较大时, 有利于算法进行全局搜索; 当权重较小时, 有利于算法进行局部寻优. 因此本文引入自适应权重, 避免算法陷入局部最优. 自适应权重公式如下:
| \omega = \frac{{3{{\rm{e}}^{ - \left( {\frac{{k {\text{π}} t}}{{{t_{\max }}}}} \right)}}}}{{10}} | (16) |
其中, k为控制因子, 控制
根据
通过对式(16)中的k分别取0.5、1、1.5、1.8、2.5、3进行仿真, 得出如图6所示的变化曲线. 结合自适应权重的收敛要求及算法迭代后期权值的取值要求, 选取k=1.8的函数曲线. 不仅符合自适应权重收敛速率前快后慢的曲线变化要求, 还提升了算法后期寻优的精细程度, 在一定程度上提升了算法的寻优精度与收敛速度. 改进后的位置更新公式如下:
| X(t + 1) = \omega \cdot {X^*}(t) - A \cdot D{{ , \; p < 0}}{\text{.5}} | (17) |
| X(t + 1) = D' \cdot {{\rm{e}}^{bl}} \cdot \cos (2 {\text{π}} l) + \omega \cdot {X^*}(t){{ ,\; p }} \geqslant 0.5 | (18) |
在加入自适应权重的基础上引入随机差分变异策略对其鲸鱼个体位置再次进行更新, 来解决局部最优问题, 减少种群多样性的损失, 避免算法出现收敛早熟及精度低等问题. 公式如下:
| X(t + 1) = {r_1} \cdot \left( {{X^*}(t) - X(t)} \right) + {r_2} \cdot \left( {X'(t) - X(t)} \right) | (19) |
其中,
选取8个不同类型的基准测试函数对IWOA性能进行测试. 基准测试函数表达式、类型、搜索范围、理论最优值如表1所示, 其中, U表示单峰函数, M表示多峰函数.
改进的鲸鱼优化算法与灰狼优化算法 (gray wolf optimization, GWO)[20]、粒子群优化算法 (PSO)[21]、鲸鱼优化算法、麻雀搜索算法 (sparrow search algorithm, SSA)[22]和蝴蝶优化算法(butterfly optimization algorithm, BOA)[23]通过8个基准测试函数独立运行10次计算得出每个算法最优值的平均值和标准差, 对比结果如表2所示.

|
图 6 权重变化曲线 |
| 表 1 基准测试函数 |
| 表 2 IWOA算法与其他5种算法的比较 |
由表2可以看出, 与GWO、PSO、WOA、SSA、BOA算法相比, 不论是利用单峰函数还是多峰函数进行测试, IWOA不仅收敛精度更高、稳定性也更好.
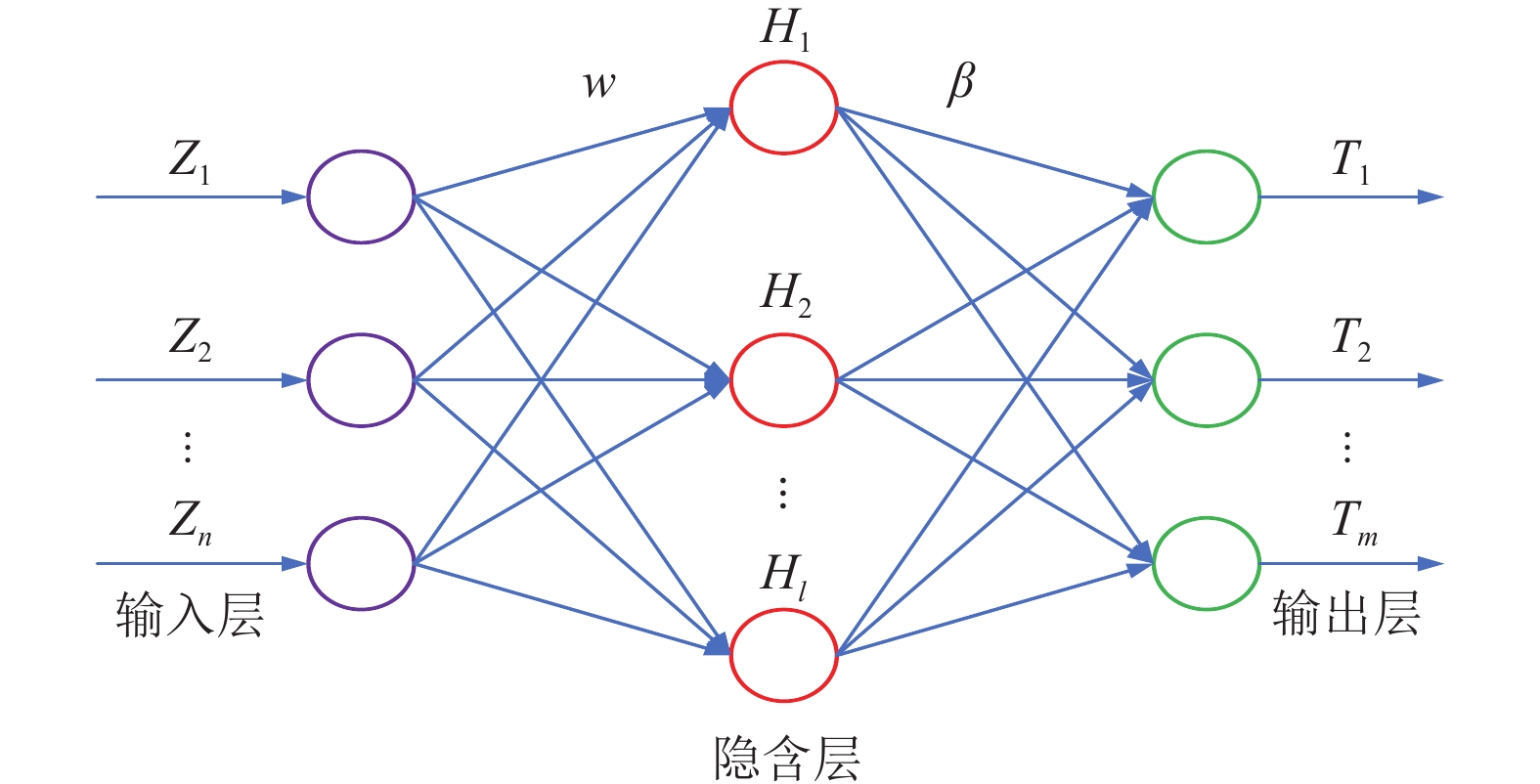
4 极限学习机极限学习机 (ELM) 是单隐层前馈神经网络. 由于ELM不使用梯度下降, 所以学习速度比 BP等传统前馈网络更快, 对于许多非线性样本也具有很好的适用性[24-26]. ELM网络结构如图7所示.
|
图 7 ELM网络结构 |
图7中, Z为模型的输入, w为输入层与隐含层之间的权重, H为隐含层输出, β为隐含层与输出层之间的权重, T为模型输出.
5 基于IWOA-ELM的航油闪点软测量建模利用 IWOA 优化 ELM 流程具体可分为以下4个步骤.
(1)数据归一化处理
选取初底油进料温度、塔底温度、常压炉出口温度、塔底出口温度、常三汽提塔液位、常一中流量作为输入变量, 共185组数据, 其中, 80%数据集当作训练集样本, 20%数据集当作测试集样本, 并对数据进行归一化. 归一化公式如下:
| y = \frac{{x - {x_{\min }}}}{{{x_{\max }} - {x_{\min }}}} | (20) |
其中, x为输入值, y为归一化后的数值, xmax与xmin为输入值中的最大与最小值.
(2)设置模型参数
1) ELM参数: ELM 的输入、输出层神经元个数分别为 6和1, 根据优选法[27]可以确定隐含层的节点数为7. 计算公式如下:
| {n_l} = \sqrt {{n_{\textit{z}}} + {n_u}} + m{\text{ , }}m \in [1, 10] | (21) |
| \frac{{{n_{\textit{z}}} + {n_u}}}{2} \leqslant {n_l} \leqslant ({n_{\textit{z}}} + {n_u}) + 10 | (22) |
其中,
已知, ELM的输入神经元个数为6, 输出层神经元个数为1, 代入式(22)可以计算出隐含层节点数最优取值范围为[4, 12], 再逐一计算所有可能构成的网络在相同的数据集和相同的迭代次数下的预测值总误差, 并择优选择其节点数. 计算公式如下:
| E = \frac{1}{2}\sum\limits_{j = 1}^{{n_u}} {{{(y(t) - \hat y(t))}^2}} | (23) |
其中,
各隐含层节点数的网络预测值的总误差如表3所示.
2) WOA参数: 算法的最大迭代次数设置为50, 鲸鱼个数设置为 30, 下界、上界为 [−1, 1], 并初始化每个鲸鱼的位置, 计算适应度值.
(3)迭代寻优
首先计算所有鲸鱼个体的适应度值并选取最优个体, 然后根据最小适应度值更新最优个体的位置. 在没有达到设定的迭代次数或误差率低于设定值时不断地进行寻优.
| 表 3 各隐含层节点数的网络预测值总误差 |
(4)常一线航空煤油闪点值预测
通过IWOA的寻优能力找到ELM的最优权重和最优阈值, 建立ELM预测模型, 应用于常一线航空煤油闪点值预测. 模型流程如图8所示.
6 实验验证 6.1 预测模型误差评价指标本文选用3种评价标准作为常一线航空煤油闪点预测的评价指标. 公式如下:

|
图 8 基于IWOA优化ELM模型流程图 |
1)均方根误差 (RMSE)
| {\textit{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{t = 1}^n {{{\left| {y(t) - \hat y(t)} \right|}^2}} } | (24) |
2)平均绝对误差 (MAE)
| MAE = \frac{1}{n}\sum\limits_{t = 1}^n {\left| {y(t) - \hat y(t)} \right|} | (25) |
3)平均绝对百分比误差 (MAPE)
| MAPE = \frac{1}{n}\sum\limits_{t = 1}^n {\left| {\frac{{\left| {y(t) - \hat y(t)} \right|}}{{y(t)}}} \right|} | (26) |
其中, n为预测样本数量,
本文用BP、ELM、WOA-ELM和IWOA-ELM 等4种常一线航空煤油闪点预测模型进行分析比较, 其训练相对误差、绝对误差和预测结果如图9–图11所示.
由图9与图10发现, 与BP、ELM、WOA-ELM相比IWOA-ELM模型的相对误差、绝对误差更趋近于零且变化相对更平缓, 由图11发现, IWOA-ELM模型预测的闪点值与实际值更贴近, 说明IWOA-ELM模型的预测精度更高, 从而验证了其模型的有效性.
各模型的测试误差如表4所示.
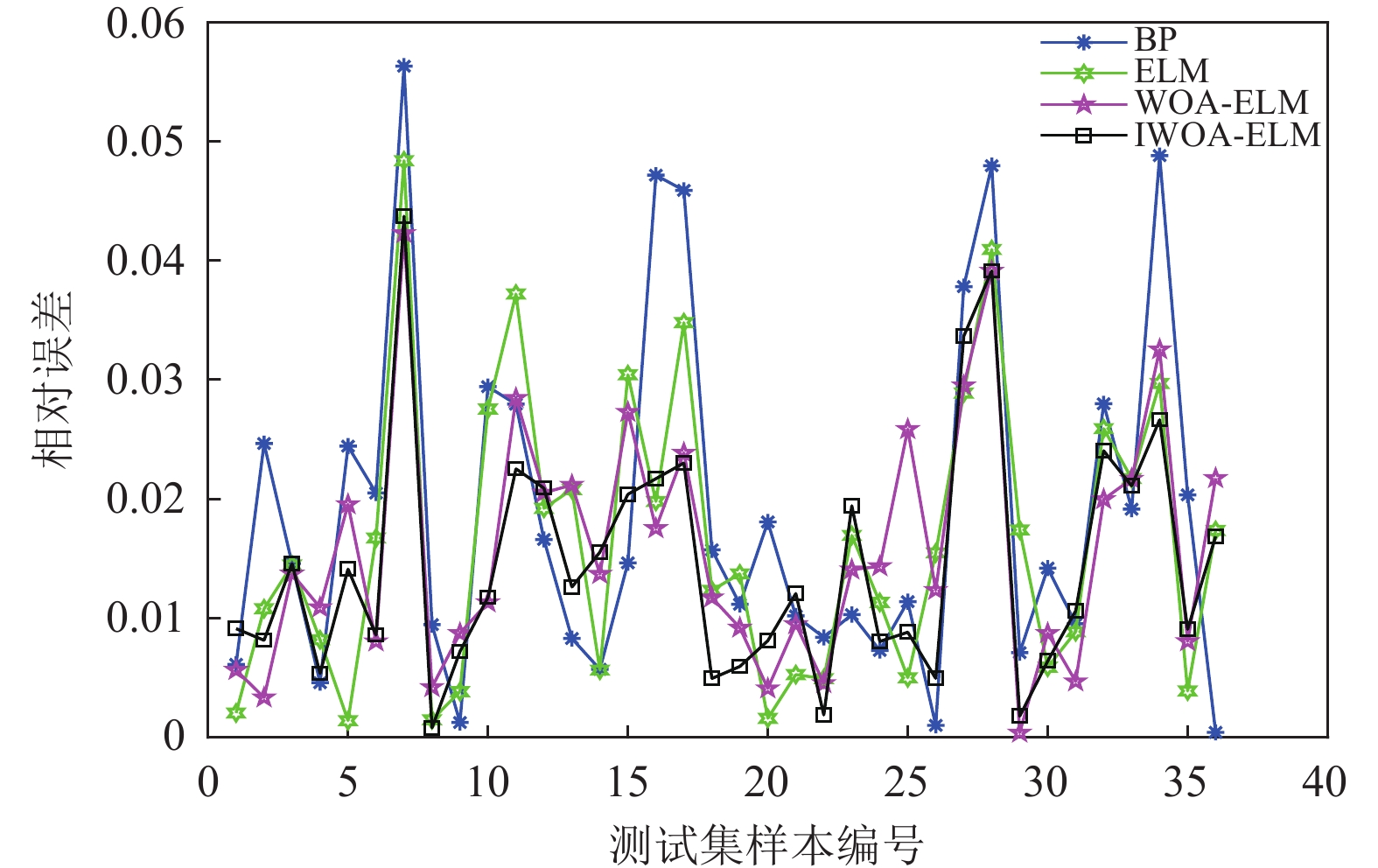
|
图 9 相对误差对比 |

|
图 10 绝对误差对比 |

|
图 11 预测结果对比 |
| 表 4 各模型的测试误差 |
由表4计算可知, IWOA-ELM模型与BP、ELM、WOA-ELM模型相比, 测试误差有明显的下降, 误差下降百分比如图12所示.
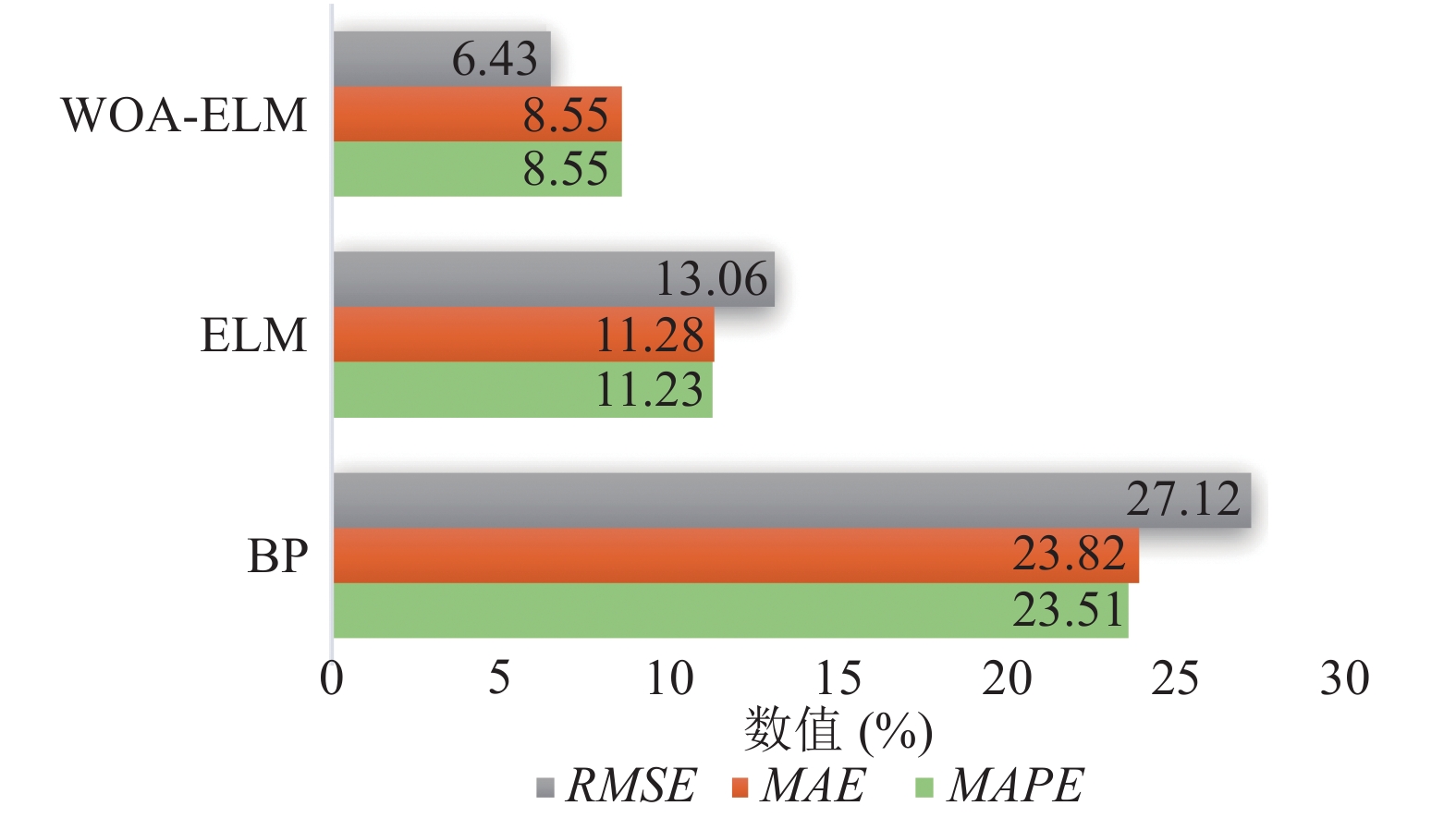
|
图 12 IWOA-ELM模型误差下降百分比 |
实验结果表明IWOA-ELM模型相比于BP模型、ELM模型与WOA-ELM模型, 在预测精度上得到了进一步的提升, 为航空煤油闪点在线预测提供了更好的预测模型.
7 结 论本文提出一种基于GRA-IWOA-ELM的常一线航空煤油闪点值预测的软测量建模方法, 利用GRA进行输入变量的筛选, 利用IWOA对 ELM 的权阈值进行优化, 有效提高了该模型的预测精度. 仿真结果表明, IWOA-ELM 模型相比 BP、ELM和WOA-ELM 模型的预测性能更好, 能更准确地预测出航空煤油闪点值, 是一种更有效的软测量建模方法.
| [1] |
曹鹏飞, 罗雄麟. 化工过程软测量建模方法研究进展. 化工学报, 2013, 64(3): 788-800. DOI:10.3969/j.issn.0438-1157.2013.03.003 |
| [2] |
黄道平, 刘乙奇, 李艳. 软测量在污水处理过程中的研究与应用. 化工学报, 2011, 62(1): 1-9. |
| [3] |
任超. 基于高阶特征模态识别的多工况软测量建模[硕士学位论文]. 太原: 太原理工大学, 2020.
|
| [4] |
Yu SW, Zhu KJ, Diao FQ. A dynamic all parameters adaptive BP neural networks model and its application on oil reservoir prediction. Applied Mathematics and Computation, 2008, 195(1): 66-75. DOI:10.1016/j.amc.2007.04.088 |
| [5] |
Roffel B, Betlem BHL, de Blouw RM. A comparison of the performance of profile position and composition estimators for quality control in binary distillation. Computers & Chemical Engineering, 2003, 27(2): 199-210. |
| [6] |
Yan WW, Shao HH, Wang XF. Soft sensing modeling based on support vector machine and Bayesian model selection. Computers & Chemical Engineering, 2004, 28(8): 1489-1498. |
| [7] |
谭均权, 涂永善, 刘子媛. 人工神经网络法预测轻质油品的闪点. 石化技术与应用, 2016, 34(1): 24-28. DOI:10.3969/j.issn.1009-0045.2016.01.006 |
| [8] |
王焕维, 俞英, 景冬莲, 等. 原油闪点预测模型的研究. 天然气化工-C1化学与化工, 2020, 45(2): 113-120. |
| [9] |
李郁. 应用人工神经网络方法预测柴油闪点研究. 炼油与化工, 2017, 28(3): 10-13. DOI:10.3969/j.issn.1671-4962.2017.03.004 |
| [10] |
李方方, 赵英凯, 姜志兵. 基于支持向量机的油品质量预测. 计算机工程, 2007, 33(2): 200-202. DOI:10.3969/j.issn.1000-3428.2007.02.070 |
| [11] |
赵超, 王贵评, 戴坤成, 等. 基于KPLS-LSSVM的航煤闪点和干点软测量应用研究. 计算机与应用化学, 2016, 33(2): 157-162. DOI:10.16866/j.com.app.chem201602006 |
| [12] |
Li JL. The analysis on regional differences of urbanization level in Shaanxi province based on grey correlative analysis. Physics Procedia, 2012, 33: 1510-1517. DOI:10.1016/j.phpro.2012.05.246 |
| [13] |
吴慧英, 杨日剑, 张颖, 等. 基于PCA-SVR的池塘DO预测模型. 安徽大学学报(自然科学版), 2016, 40(6): 103-108. |
| [14] |
Gu WG, Wang K, Huang YQ, et al. Energy optimization for a multistage crude oil distillation process. Chemical Engineering & Technology, 2015, 38(7): 1243-1253. |
| [15] |
王玮. 砾石充填防砂井堵塞及排砂解堵机理模拟研究[硕士学位论文]. 青岛: 中国石油大学(华东), 2019.
|
| [16] |
Mirjalili S, Lewis A. The whale optimization algorithm. Advances in Engineering Software, 2016, 95: 51-67. DOI:10.1016/j.advengsoft.2016.01.008 |
| [17] |
王梓辰, 窦震海, 董军, 等. 多策略改进的自适应动态鲸鱼优化算法. 计算机工程与设计, 2022, 43(9): 2638-2645. DOI:10.16208/j.issn1000-7024.2022.09.031 |
| [18] |
徐航, 张达敏, 王依柔, 等. 混合策略改进鲸鱼优化算法. 计算机工程与设计, 2020, 41(12): 3397-3404. DOI:10.16208/j.issn1000-7024.2020.12.15 |
| [19] |
毛清华, 杨林, 王艳亮. 融合改进Tent混沌和模拟退火的灰狼算法. 数学的实践与认识, 2021, 51(5): 147-161. |
| [20] |
Rajammal RR, Mirjalili S, Ekambaram G, et al. Binary grey wolf optimizer with mutation and adaptive K-nearest neighbour for feature selection in Parkinson’s disease diagnosis. Knowledge-based Systems, 2022, 246: 108701. DOI:10.1016/j.knosys.2022.108701 |
| [21] |
Shi YH, Eberhart R. Monitoring of particle swarm optimization. Frontiers of Computer Science in China, 2009, 3(1): 31-37. DOI:10.1007/s11704-009-0008-4 |
| [22] |
Xue JK, Shen B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Systems Science & Control Engineering, 2020, 8(1): 22-34. |
| [23] |
Arora S, Singh S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Computing, 2019, 23(3): 715-734. DOI:10.1007/s00500-018-3102-4 |
| [24] |
Huang GB, Wang DH, Lan Y. Extreme learning machines: A survey. International Journal of Machine Learning and Cybernetics, 2011, 2(2): 107-122. DOI:10.1007/s13042-011-0019-y |
| [25] |
褚鼎立, 陈红, 王旭光. 基于自适应权重和模拟退火的鲸鱼优化算法. 电子学报, 2019, 47(5): 992-999. DOI:10.3969/j.issn.0372-2112.2019.05.003 |
| [26] |
Huang GB, Zhou HM, Ding XJ, et al. Extreme learning machine for regression and multiclass classification. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2012, 42(2): 513-529. DOI:10.1109/TSMCB.2011.2168604 |
| [27] |
夏克文, 李昌彪, 沈钧毅. 前向神经网络隐含层节点数的一种优化算法. 计算机科学, 2005, 32(10): 143-145. |
 2023, Vol. 32
2023, Vol. 32



