路径规划是移动机器人领域的一个研究热点, 是移动机器人实现自主导航的关键技术之一. 目的是在已知或者未知的障碍物环境中搜索出一条从起始位置到目标位置的最优安全无碰撞路径, 评估标准一般为距离最短、耗时最短等. 路径规划算法大致可分为4类: 传统路径规划算法、图形学方法、智能仿生学算法和其他算法, 其中强化学习算法当前较为热门^[1-4].

关于强化学习在智能机器人路径规划和避障^{[5, 6]}中的应用, Q学习算法是较为常用的强化学习方法^[7]. 但是基本的强化学习方法也有一些缺点. 首先, 当机器人处于较为复杂的环境中时, 容易出现“维数诅咒”. 此外, 容易反复探索次优路径, 造成算法收敛速度缓慢, 陷入局部最优. 训练机器人时一般需要花费很长时间, 而启发式知识可为机器人的动作选择提供指导^[8], 帮助其更快地收敛.

Low等人^[9]引入了部分引导Q学习的概念, 利用花授粉算法来改进Q学习的初始化, 可以加速其收敛速度, 但该方法在复杂度较高的环境难以保证收敛到最优路径. 毛国君等人^[10]引入了动态探索因子的策略, 根据运行过程中环境的反馈, 调整贪婪因子的大小, 减少了寻优耗时, 但在运行初期仍需要花费大量时间随机探索未知环境. 徐晓苏等人^[11]利用人工势场法初始化Q表, 为机器人提供关于环境的先验知识, 大幅减少了前期的随机探索, 但该方法在迭代后期作用较小, 且适用范围较为局限. Pei等人^[12]基于机器人与目标点之间的距离提出了一种启发式搜索策略和距离度量标准, 在算法迭代过程中能够指引移动机器人向目标靠近, 但是该策略与实际环境的相关度较高, 不同的环境要设计不同的启发式函数, 且需要不断修正Q函数. Hao等人^[13]提出了一种潜在的动态Q学习方法, 将Q学习与人工势场法和动态奖励函数相结合来生成可行路径, 在路径长度和转弯角度两个指标上表现优异, 但与经典算法相比, 在计算时间和收敛速度方面没有明显提高. Chang等人^[14]将动态窗口法与Q学习相结合, 增加了新的评价功能, 提高了全局导航性能, 但其全局搜索能力较小, 且依赖于参考路径. 可见, 在考虑Q学习的改进时需要考虑动作选择的指导作用以及探索与利用的关系对收敛性和寻优耗时上的影响.

蚁群算法是一种分布式的智能仿生算法, 模拟了自然界中蚂蚁觅食的特征^[15], 具有正反馈、分布式计算及鲁棒性强等优势^[16], 其候选解构建过程与路径规划过程相似. 因此, 选用蚁群算法作为优化Q学习算法的对象. 田晓航等人^[17]引入蚁群算法的信息素机制, 提出了一种寻优范围优化方法, 减少智能体的无效探索次数, 但没有充分考虑到智能体探索的目的性. 石立培的方法^[18]中蚂蚁移动一次, 就对路径上的信息素进行一次局部的更新, 选择动作时同时考虑信息素浓度与Q值, 虽然可以实现指导后续搜索的效果, 但频繁的局部更新增加了耗时, 且与柯逸^[19]类似, 未考虑改进搜索策略对算法收敛性的影响, 复杂环境下性能提升较小.

因此, 针对基本Q学习在算法运行前期出现的搜索效率低, 寻优时间较长的问题, 利用改进后的自适应蚁群算法先探索未知环境, 通过产生的信息素矩阵实现Q表的不均匀初始化, 对机器人的寻优范围进行优化, 指导机器人在初期的探索和寻优过程. 另外, 设计了一个动态搜索策略, 通过环境的变化动态地改变搜索因子的大小, 提高机器人的探索效率.

1 本文基础算法思想及策略 1.1 蚁群算法

蚂蚁在寻找最优路径的过程中, 会根据可选路径上信息素浓度的大小选择动作, 同时会在其走过的路径上留下信息素. 在时刻 $ t $ , 蚂蚁 $ k $ 由第 $ i $ 个节点选择下一节点 $ j $ 是根据信息素和启发式信息的大小来判定的. 蚁群算法的转移概率如式(1)和式(2)所示.

$ P_{ij}^k = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{{\left[ {{\tau _{ij}}\left( t \right)} \right]}^\alpha }{{\left[ {{\eta _{ij}}\left( t \right)} \right]}^\beta }}}{{\displaystyle\sum\limits_{j \in allowe{d_k}} {{{\left[ {{\tau _{ij}}\left( t \right)} \right]}^\alpha }{{\left[ {{\eta _{ij}}\left( t \right)} \right]}^\beta }} }},\;j \in allowe{d_k}} \\ {\begin{array}{*{20}{c}} {0,\;}\qquad\qquad\qquad\qquad\quad\;\text{otherwise} \end{array}} \end{array}} \right. $

(1)

$ {\eta _{ij}} = \frac{1}{{{d_{ij}}}} $

(2)

其中, $ \alpha $ 为信息素启发因子, 表示路径选择时信息素浓度的重要性; $\; \beta $ 为期望启发因子, 表示启发式信息在路径选择时的重要性; $ allowe{d_k} $ 表示蚂蚁 $ k $ 在当前节点 $ i $ 可到达的下一节点 $ j $ 的集合, $ {\tau _{ij}}\left( t \right) $ 为路径 $ ij $ 上的信息素浓度, $ {\eta _{ij}}\left( t \right) $ 表示路径 $ ij $ 上的启发信息, $ {d_{ij}} $ 表示路径 $ ij $ 之间的欧式距离.

信息素更新策略为在一次循环中所有蚂蚁都完成迭代之后, 进行一次全局信息素更新, 经过多次循环后, 信息素呈现出不均匀的分布, 最优路径附近的信息素浓度高于其他区域. 全局信息素更新如式(3)–式(5)所示:

$ {\tau _{ij}}\left( {t + 1} \right) = \left( {1 - \rho } \right){\tau _{ij}}\left( t \right) + \rho \Delta {\tau _{ij}}\left( t \right) $

(3)

$ \Delta {\tau _{ij}}\left( t \right) = \sum\limits_{k = 1}^m {\Delta \tau _{ij}^k\left( t \right)} $

(4)

$ \Delta {\tau }_{ij}^{k}\left(t\right)=\left\{\begin{array}{l} \dfrac{Q}{{L}_{k}},\;\;\;\;k经过路径ij\\ 0,\;\quad\;\;\text{otherwise}\end{array}\right. $

(5)

其中, $\; \rho $ 为全局信息素挥发系数, $ \;\rho \in \left[ {0, 1} \right] $ , $ \Delta {\tau _{ij}}\left( t \right) $ 为一次迭代后所有蚂蚁留下的信息素, $ m $ 为蚂蚁总数. $ Q $ 为信息素强度, $ {L_k} $ 表示第 $ k $ 只蚂蚁在本次迭代中走过的路径总长度.

1.2 Q学习算法

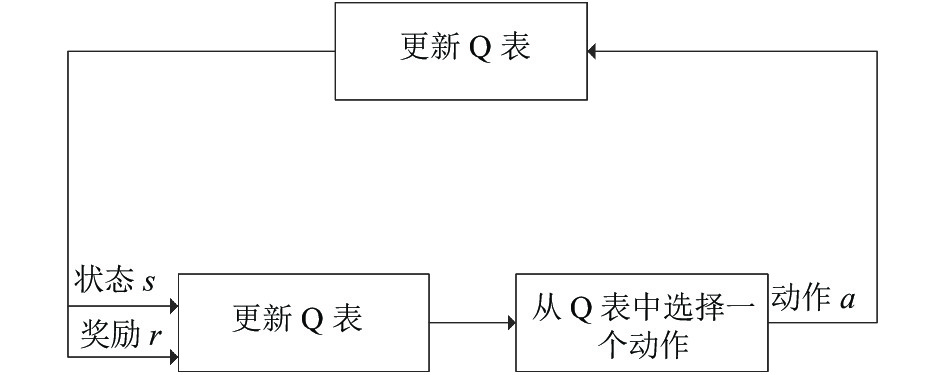
Q学习是强化学习中的一种无模型算法^[20], 是一种近似于动态规划的技术. Q值表示机器人在执行一个动作后, 由当前状态转向下一个有效状态的奖励值. 强化学习的框架如图1所示, 代理根据Q表选择一个动作 $ a $ 并执行它, 然后环境返回给机器人的一个状态 $ s $ 和执行动作 $ a $ 的奖励 $ r $ , 以更新Q表, 强化学习框架见图1.

在Q学习中, Q表是一个最优策略动作值函数, 按式(6)所示规律更新.

$ Q(s, a) \leftarrow Q(s, a) + \alpha \left[ {r + \gamma \mathop {\max }\limits_{a'} Q(s', a') - Q(s, a)} \right] $

(6)

其中, $ \alpha $ 为学习率, $ \gamma $ 为折扣因子, $ r $ 为即时奖励, $ s $ 为机器人当前的状态, $ a $ 为机器人选择的动作, $ s' $ 为执行动作 $ a $ 后的下一个状态, $ a' $ 为对应的下一个动作, $ \max Q(s', a') $ 为状态 $ s' $ 对应的最大累积奖励值.

2 本文算法 2.1 改进蚁群算法信息素增量的更新机制

基于精英蚂蚁模型和排序蚂蚁模型, 对基于自适应机制的蚁群算法中信息素增量的更新规则进行改进, 提出一种梯度更新机制来更新信息素增量, 以提高算法的收敛速度. 在所有蚂蚁完成一次迭代之后, 记录所有成功到达目标节点的蚂蚁信息, 统计其节点信息和路径长度, 然后计算当代最短路径长度和所有到达目标节点的平均路径长度.

一代寻优结束后, 先对当前最短路径和小于等于平均路径长度的路径按照梯度更新公式进行一次局部信息素更新, 大于平均路径长度的路径则不再进行信息素的加强. 通过给予不同等级的信息素浓度奖励, 可以加强较优的解对后续寻优过程的指导作用, 同时减少较差解的误导. 随后, 再进行一次全局信息素更新. 最短路径和小于等于平均寻优路径长度的路径上的信息素增量更新公式按照式进行计算, 局部信息素按式(7)–式(9)更新.

$ {\tau _{ij}}\left( {t + 1} \right) = \left( {1 - {\rho _{\rm{l}}}} \right){\tau _{ij}}\left( t \right) + {\rho _{\rm{l}}}\Delta {\tau _{ij}}\left( t \right) $

(7)

$ \Delta {\tau _{ij}}\left( t \right) = \sum\limits_{k = 1}^m {\Delta \tau _{ij}^k\left( t \right)} $

(8)

$ \Delta {\tau }_{ij}^{k}\left(t\right)=\left\{ \begin{array}{l} \begin{array}{ll}\dfrac{{Q}_{\phi }}{{L}_{k}}-\dfrac{{Q}_{\phi }}{{L}_{{{a}}}},\;k经过路径ij\end{array}\\ \begin{array}{ll}0,\;\qquad\quad\;\; \text{otherwise}\end{array}\end{array} \right.$

(9)

其中, $ {L_{a}} $ 表示平均寻优路径长度, $\;{\rho _\text{l}}$ 表示局部信息素挥发系数, $\;{\rho _\text{l}} \in \left[ {0, 1} \right]$ .

局部信息素加强时对信息素量 $ {Q_\phi } $ 进行改进, 改进公式如下.

$ {Q_\phi }\left( {t + 1} \right) = {Q_\phi }\left( t \right) + \eta \left( {{L_{b}} - {L_k}} \right) $

(10)

其中, ${L_{b}}$ 表示当前最短路径长度, $ \eta $ 表示距离因子.

2.2 动态Q学习中Q表的初始化

在基本Q学习中, Q表通常被初始化为某一固定的数值, 通常情况下设置为0. 基本的Q学习算法没有充分利用已知的条件, 算法运行初期随机性较高, 导致收敛速度较慢, 且效率低下. 但Q表的值存在一定的规律性, 一般情况下越靠近最优路径的位置, Q值应越大.

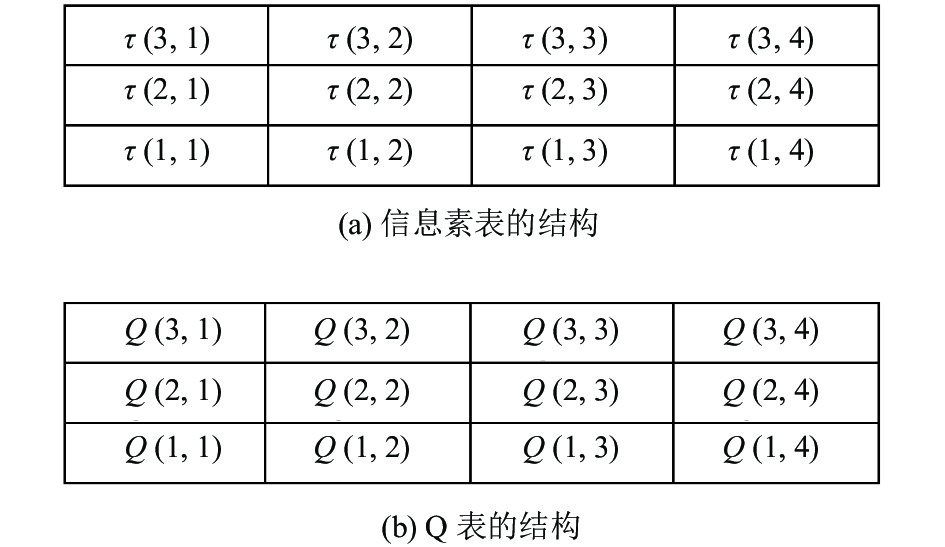
蚁群算法是一种在路径规划领域很有效的启发式算法, 其信息素表的结构与Q学习中Q表的结构类似, 二者更新方式也类似, 这是2种算法结合的关键. 本文规定机器人的移动方向为上、下、左、右的四叉树搜索策略, 信息素表和Q值表的部分结构见图2.

算法融合的规则为: 先用改进信息素更新策略的自适应蚁群算法进行路径预规划, 得到该环境下的次优路径, 不同的位置根据走过的蚂蚁数量、是否处于较优的路径以及周围是否有障碍物有着不同的信息素浓度. 将栅格地图上不同位置的信息素与其可选择的行动的个数相乘, 得到一个不均匀分布的信息素矩阵; 再用信息素矩阵对Q表赋初值, 完成Q表的初始化, 以指导后续搜索.

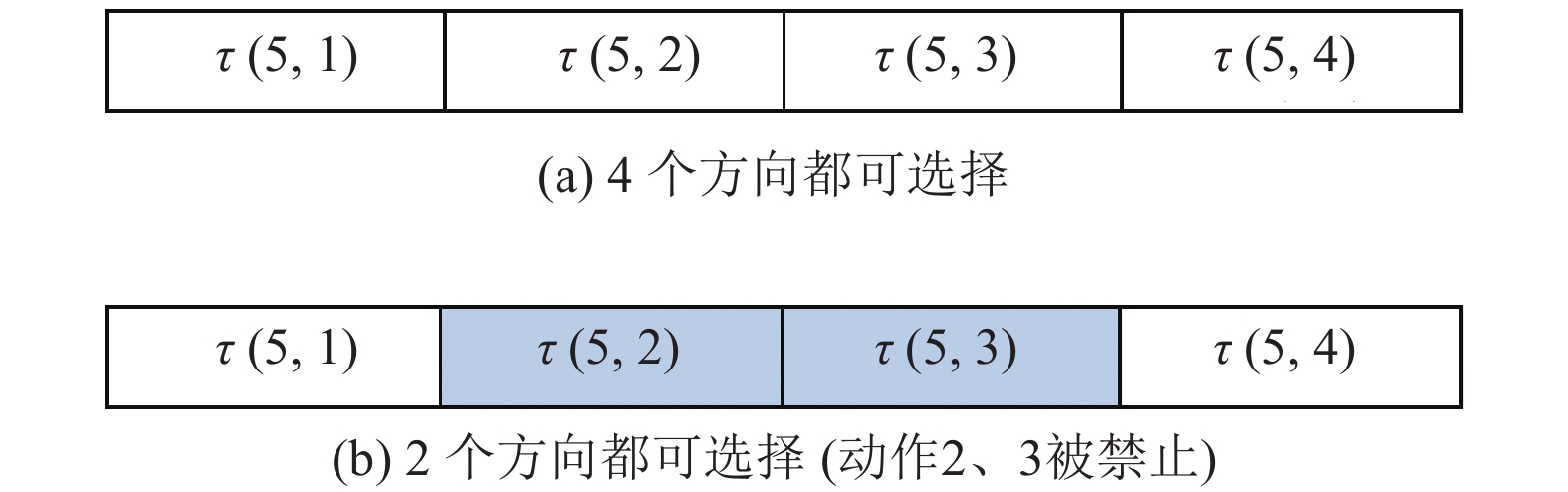
假设某一位置处于边界, 则只有2个方向可选择, 另2个方向信息素浓度低于阈值, 被标记为无效状态; 假设该位置既不处于边界, 周围也没有障碍物, 则4个方向的动作都可选择, 可选择动作部分结构见图3.

由于不同算法之间存在差异, 蚁群信息素 $ \tau $ 与Q值之间存在数量级上的差异, 因此按式(11)赋值.

$ Q\left( {s, a} \right) = \lambda \mu {\tau _{ij}}\left( t \right) $

(11)

其中, $ Q\left( {s, a} \right) $ 表示未赋初值的Q值, $ {\tau _{ij}}\left( t \right) $ 为对应位置的信息素浓度, $ \lambda $ 是一个大于0的常数, $\; \mu $ 为所处位置的可选移动方向的个数. 融合算法中Q表初始化的伪码描述见算法1.

算法1. Q表初始化

输入: $\scriptstyle \alpha $ 、 $\scriptstyle \;\beta $ 、 $\scriptstyle \;\rho $ 、 $\scriptstyle \;{\rho _l} $ 、 $\scriptstyle \lambda $ 、 $\scriptstyle Q $ 、迭代次数iter_number、蚂蚁数ant_number、起始节点start、目标节点goal

输出: $ \scriptstyle Q $ 值表

1. for NC=1:iter_number do

2.　 for ant=1:ant_number do

3. 　　初始化禁忌表, start加入禁忌表

4. 　　找到可行节点, 以供循环

5. 　　通过式(1)选择下一个节点

6. 　　 while(蚂蚁 $\scriptstyle k $ 没有到达终点) do

7. 　　　重新计算可行节点

8.　　　 $\scriptstyle allowe{d_k} $ $\scriptstyle \leftarrow $ 可行节点

9. 　　 end

10. 　　记录蚂蚁 $\scriptstyle k $ 走过的节点信息、路径长度

11. 　　通过式(7)局部信息素加强

12. 　　通过式(3)全局信息素更新

13. 　 end

14. end

15. 生成信息素矩阵

16. 通过式(11)的融合规则给Q表赋值

本文算法的奖励函数设置如式(12)所示.

$ r(s, a)=\left\{\begin{array}{l} -5\text{,\;}\quad 遇到障碍物\\ 1\text{,\;}\quad\;\;\; 正常通行\\ 5\text{,\;}\quad\;\;\; 目标位置\end{array} \right.$

(12)

2.3 动态搜索策略

基本Q学习的动作选择策略通常采用 $ \varepsilon $ -贪心策略, $ \varepsilon $ 值越大, 机器人在选择动作时, 进行随机探索的概率就越大; 反之, 寻优过程的目的性较强. 基于贪婪搜索策略改进的动态策略能够有效地解决容易陷入局部最优的缺点.

为使算法在运行的前、中、后期都有合适的探索概率, 结合迭代过程中的标准差, 设计了动态调整探索因子的方法, 以实现 $ \varepsilon $ 值的动态变化过程.

首先计算迭代过程的标准差, 并进行归一化处理; 由于运行初期机器人要充分探索未知环境, 因此标准差的值较大, $ \varepsilon $ 可保持在最大值 ${\varepsilon _\text{Max}}$ , 以提高探索的随机性, 机器人选择随机动作的概率较大, 避免陷入局部最优; 随着迭代次数的增加, 算法逐渐收敛, 标准差降低, $ \varepsilon $ 值随着标准差的降低逐渐减小; 最后稳定在最小值 ${\varepsilon _\text{Min}}$ , 机器人探索的目的性不断增强, 使算法快速收敛. 改进后的动态搜索策略伪码描述见算法2.

算法2. 动态搜索策略

输入: 迭代步数iter、标准差std_n、 $\scriptstyle {\varepsilon _\text{Max}}$ 、 $\scriptstyle {\varepsilon _\text{Min}}$

输出: 执行的动作 $\scriptstyle a $

1. 计算迭代过程的标准差std_n

2. 对std_n进行归一化处理, 使std_n $\scriptstyle \in $ (0, 1)

3. if std_n> $\scriptstyle {\varepsilon _\text{Max}}$ then

4. 　 $\scriptstyle \varepsilon $ $\scriptstyle \leftarrow $ $\scriptstyle {\varepsilon _\text{Max}}$

5. else if std_n< $\scriptstyle {\varepsilon _\text{Min}}$ then

6.　　　 $\scriptstyle \varepsilon $ $ \scriptstyle \leftarrow $ $\scriptstyle {\varepsilon _\text{Min}}$

7. 　　 else

8. 　　　 $\scriptstyle \varepsilon $ $ \scriptstyle \leftarrow $ std_n

9. 　　 end

10. end

11. for (each action a $\scriptstyle \in $ $\scriptstyle A\left( s \right) $ ) do

12. 　 if rand()< $\scriptstyle \varepsilon $ then

13. 　　 $ \scriptstyle a' $ $ \scriptstyle \leftarrow $ $ \scriptstyle a $ random action from $\scriptstyle s $

14.　 else

15.　　 $\scriptstyle a' $ $ \scriptstyle \leftarrow $ $\scriptstyle \varepsilon $ -greedy get $\scriptstyle a $

16.　　 执行动作 $ \scriptstyle a $

17.　 end

18. end

3 实验分析

为了验证本文所提算法的可行性和有效性, 基于Matlab设计了3种不同规格障碍物的环境地图进行仿真实验, 包括20×20的随机障碍物地图、30×30的特殊障碍物地图、40×40的随机障碍物地图. 在3类不同的地图上综合对比了基本Q学习算法 (basic Q-learning, BAS-Q)、文献[10]提出的算法 (DSS-Q)、利用自适应蚁群算法与Q学习融合的算法 (ant colony optimization Q-learning, ACO-Q)和改进蚁群与动态Q学习融合的算法 (DSSACO-Q), ACO-Q与DSSACO-Q的区别在于是否使用了本文所提出的动态搜索策略.

设定每次运行尝试的最大迭代次数为5000, 每次运行最大的探索步数为600, 每种算法分别重复执行10次. 统计平均路径长度、平均迭代次数和平均寻优耗时, 取其中一次迭代结果绘制路径规划图和迭代曲线对比图. 本文方法中蚁群信息素参数见表1, Q-learning参数见表2.

3.1 20×20障碍物环境

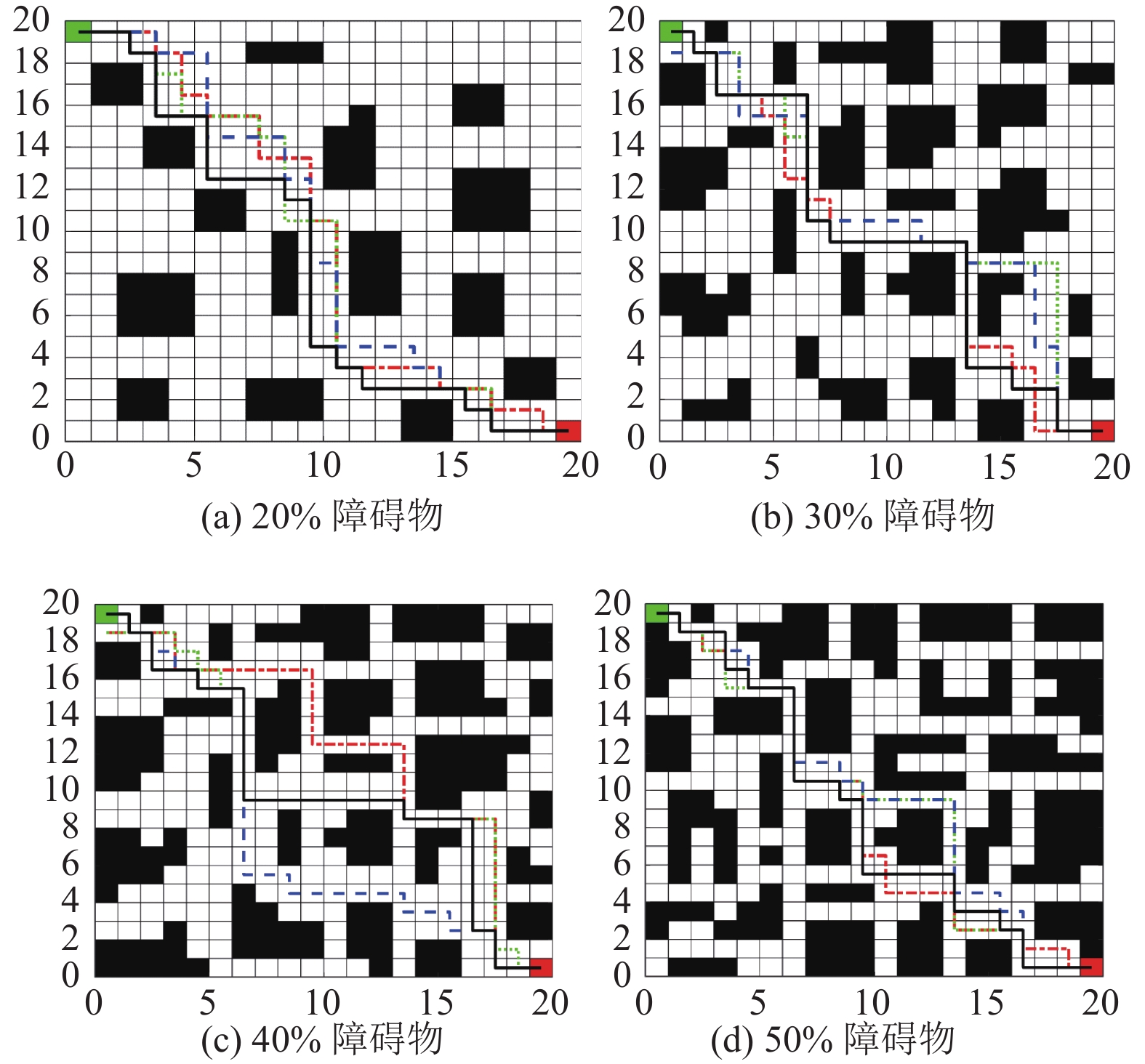
在Matlab中分别生成障碍物占比为20%、30%、40%和50% (不考虑障碍物重叠)的4张20×20栅格地图, 作为仿真验证环境.

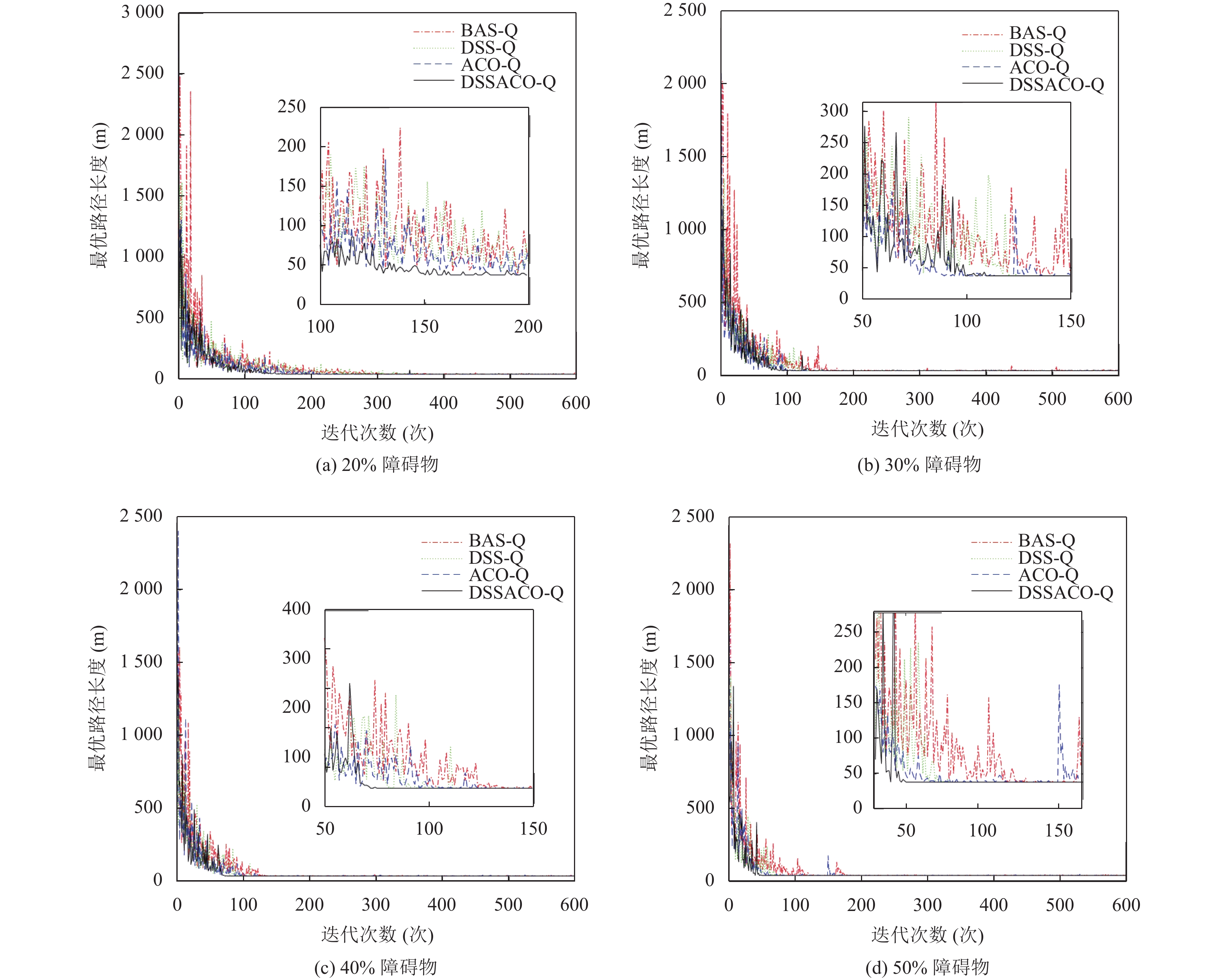
图4展示了4种算法运行中的一次路径规划结果, 图4(a)–(d)分别为20%–50%障碍物占比的路径规划结果. 如图所示, 4种算法在不同难度等级的障碍物环境下都找到了目标点. 图5展示了4种算法运行中一次的迭代曲线, 图5(a)–(d)分别为20%–50%障碍物占比的4种算法迭代曲线. 可以看出本文提出的方法能在算法前期迅速找到最优解, 且在迭代后期保持稳定, 波动较小, 明显优于其他3种算法.

表3展示了4种算法在不同难度等级障碍物下的平均寻优耗时对比和平均迭代次数对比. 不难发现, 在使用本文方法寻找到最优路径的前提下, 较BAS-Q算法的平均耗时约有49%的提升; 较DSS-Q算法的平均耗时约有15%的提升. ACO-Q算法的平均寻优时间高于DSS-Q算法的原因是, 该算法在运行初期先利用改进后的蚁群算法探索未知的障碍物环境, 然后再进行Q表的初始化过程, 增加了耗时. 但在加入本文提出的动态搜索策略后, 寻优耗时明显减少, 验证了动态搜索策略减少平均寻优耗时的有效性.

随着障碍物占比的不断提高, 算法的平均迭代次数呈下降趋势, 原因是在障碍物占比较少的环境中机器人有着更大的搜索空间, 需要更多的步骤去探索未知的环境, 增加了算法迭代次数. 与BAS-Q相比, DSSACO-Q能够更快收敛于最优路径, 平均迭代次数减少约28%; 与DSS-Q相比, DSSACO-Q的平均迭代次数约为DSS-Q的90%; 与ACO-Q相比, DSSACO-Q因为加入了动态搜索策略, 使得算法在寻优过程中的目的性增强, 随着障碍物占比的增加, 迭代次数下降更快, 且更快达到平稳, 验证了本文所提出的改进方法的有效性.

3.2 30×30障碍物环境

在30×30的栅格环境下, 障碍物的设置参照了文献[17]中的地图, 相较于随机的障碍物环境, 该地图中存在一定数量的凹形障碍物, 且该地图中障碍物体积较大, 机器人在寻优过程中更加容易陷入局部最优, 容易给算法造成额外的负担.

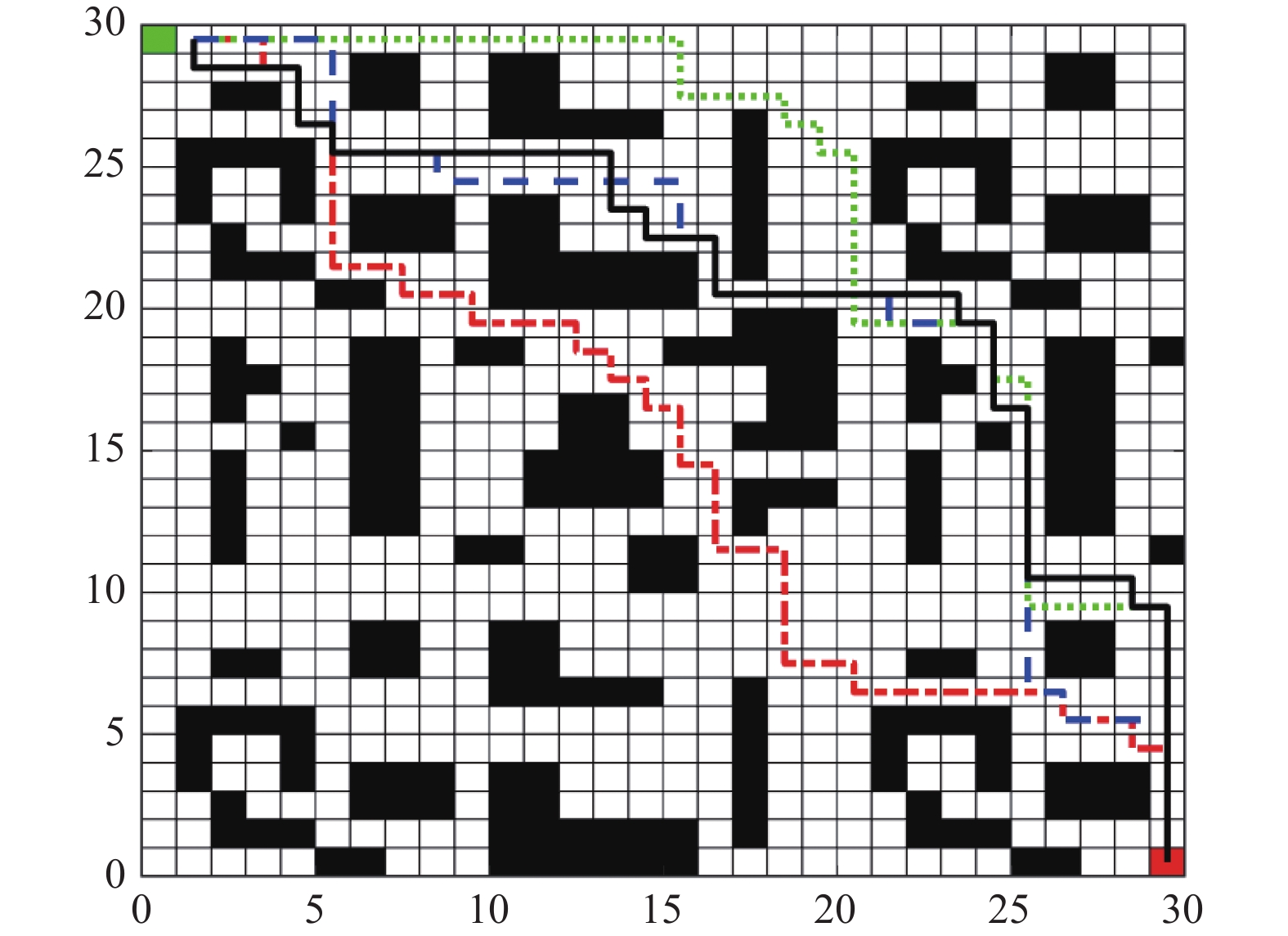
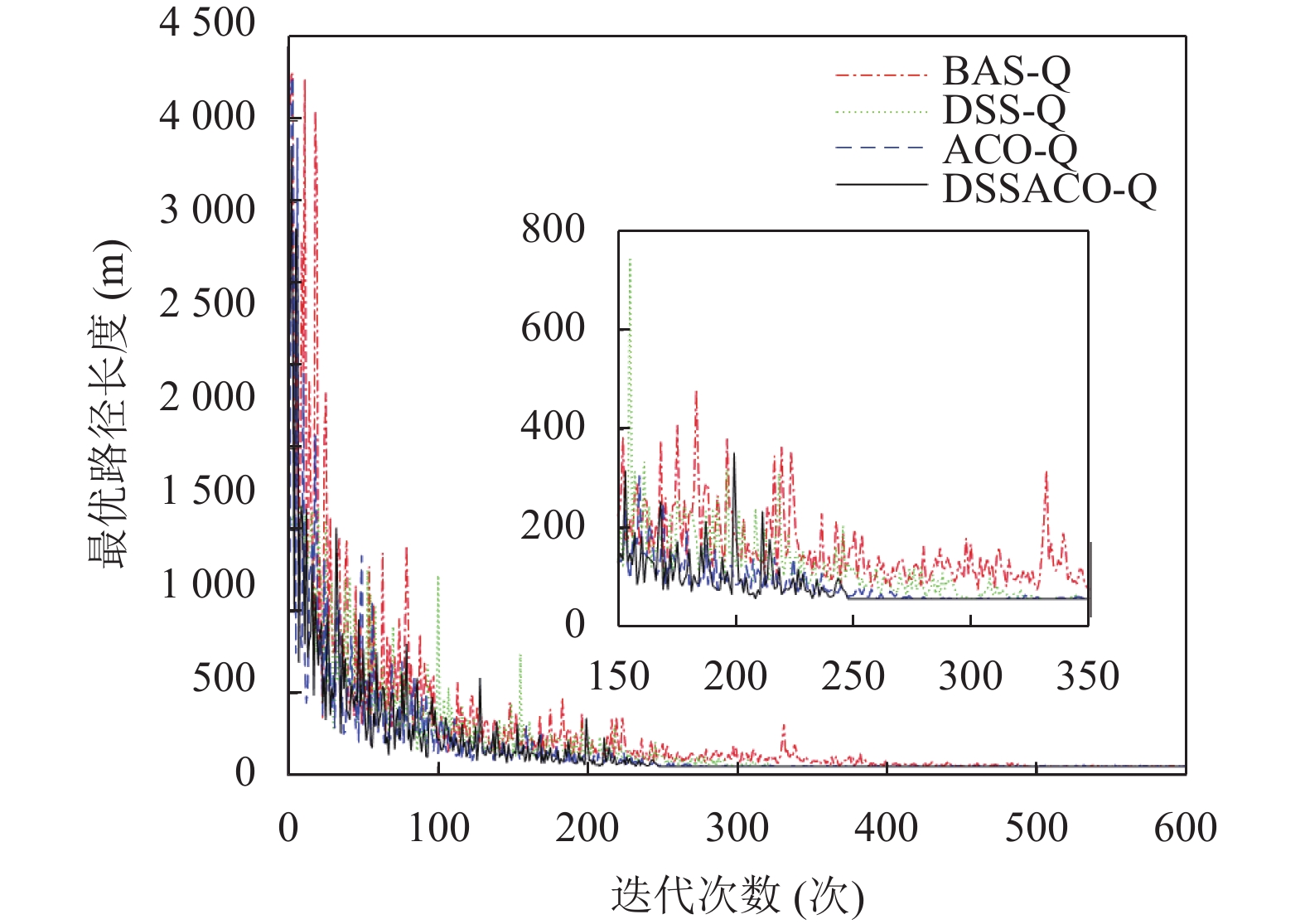
从表4中的数据可以看出4种算法找到的最优路径在长度上相等, 都找到了最优解. 图6展示了4种算法的一次路径规划结果, 图7展示了4种算法运行中一次的迭代曲线. 可以看出DSSACO-Q最先达到收敛, 且在迭代后期保持稳定, 优于其他3种算法. BAS-Q和DSS-Q一直到迭代后期才趋于平稳, ACO-Q同样较快达到了稳定, 但差于DSSACO-Q. 本文算法在平均迭代次数上相较于BAS-Q减少了41.7%, 较DSS-Q减少了15.2%; 平均寻优耗时上相较于BAS-Q减少了43.4%, 相较于DSS-Q减少了16.7%; 与未使用动态搜索策略的ACO-Q相比, DSSACO-Q平均迭代次数减少了7.3%, 平均寻优耗时减少了40.5%, 验证了本文提出的2个改进点的有效性.

3.3 40×40障碍物环境

为了进一步验证本文算法的有效性和可行性, 在40×40的栅格环境下, 设置了障碍物占比分别为20%和30% (不考虑障碍物重叠)的未知环境, 相较于其他两种障碍物环境, 该地图难度进一步加大.

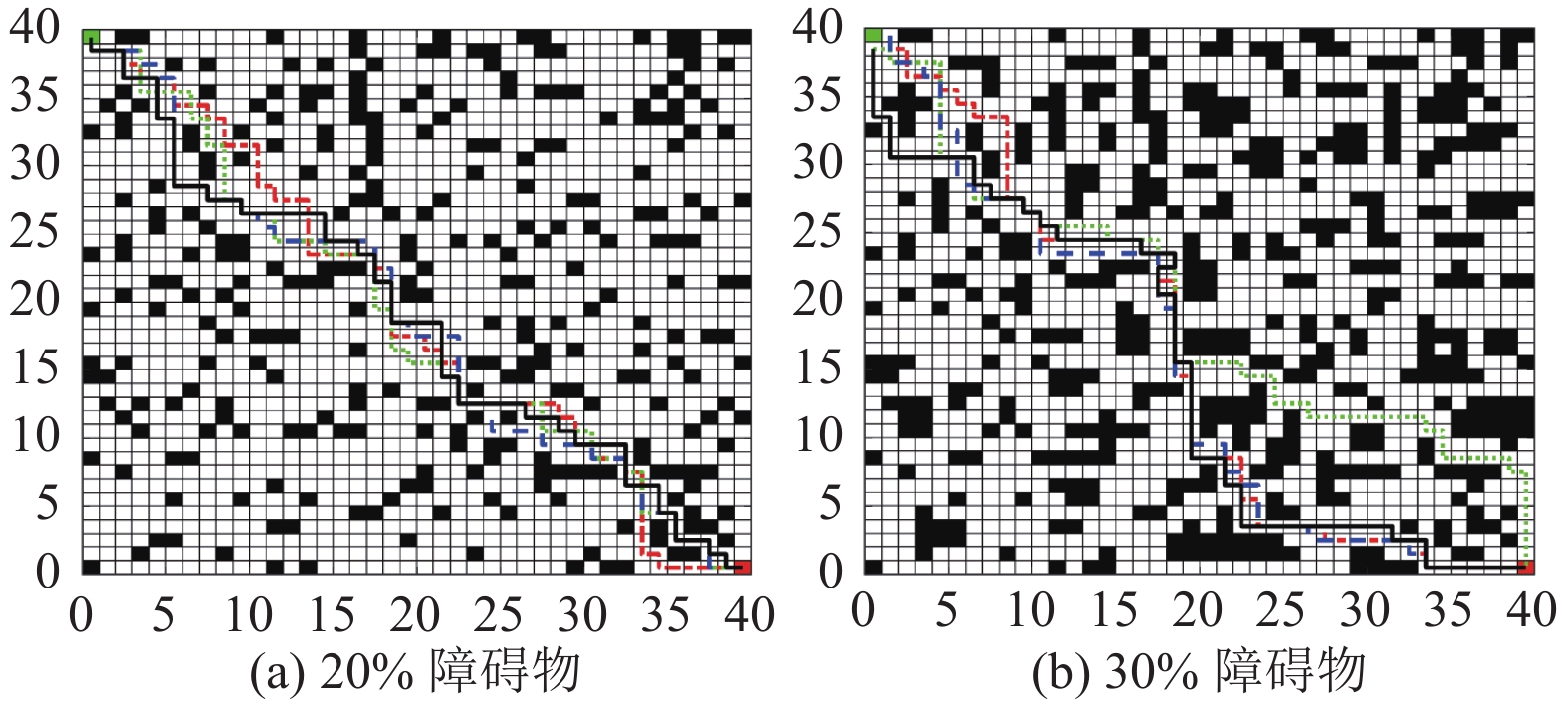
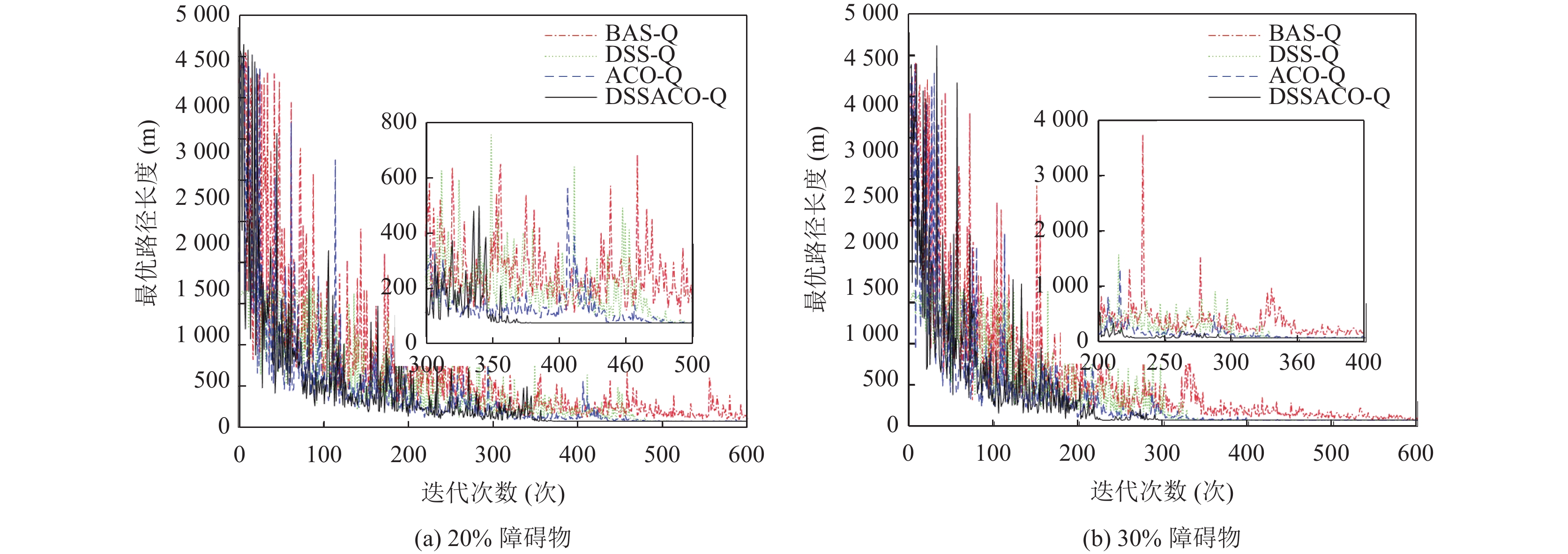
在40×40的障碍物环境下进行了2组不同难度等级的实验, 图8展示了4种算法在2种不同障碍物占比下的路径图, 图8(a)和图8(b)分别为20%和30%障碍物占比的路径规划结果. 图9展示了4种算法的迭代曲线对比, 图9(a)和图9(b)分别为20%和30%障碍物占比的4种算法迭代曲线. 从整体实验结果来看, 本文算法在收敛速度、全局搜索能力和寻优耗时上相比基本Q学习和文献[10]提出的方法都有一定的提升.

如表5所示, 在平均寻优耗时方面, 本文方法与BAS-Q相比, 约减少45%; 与DSS-Q相比, 约减少28%; 与ACO-Q相比, 约减少44%. ACO-Q的寻优时间高于DSS-Q, 同样是因为该算法在运行初期先利用改进蚁群算法探索出次优路径, 然后进行Q表的初始化, 增加了耗时. 但在加入本文提出的动态搜索策略后, 寻优耗时大幅下降.

平均迭代次数方面, 20%障碍物地图下的迭代次数更高, 是由于在障碍物占比较少的环境中机器人有着更大的搜索空间, 需要更多的步骤去探索未知的环境. 与BAS-Q相比, 本文算法的平均迭代次数在20%障碍物情况下减少48.9%, 30%情况下减少50.6%; 与DSS-Q相比, 在20%障碍物情况下减少16.2%, 30%情况下减少15.4%; 与ACO-Q相比, 在20%障碍物情况下减少11.8%; 在30%情况下减少13.1%, 验证了本文所提的算法融合方法和动态搜索策略的有效性.

4 结论与展望

本文在二维静态环境下, 为了解决基本Q学习算法应用于移动机器人路径规划时存在的收敛速度缓慢、容易陷入局部最优等问题, 提出一种改进蚁群算法与动态Q学习算法融合的路径规划方法, 用于移动机器人在不同形状、大小和布局的静态障碍物环境中进行路径规划. 通过仿真实验验证了本文所提出的路径规划算法可以避免陷入局部最优, 且能有效提高收敛速度. 通过本文的研究得出了以下结论.

(1)在自适应蚁群算法的基础上, 结合了精英蚂蚁模型和排序蚂蚁模型, 设计了一种新的信息素增量更新机制, 增强了较优路径对后续过程的指导作用, 以提高算法的收敛速度.

(2)将改进后的蚁群算法获得的先验知识整合到基本Q学习的路径规划过程中, 指导了机器人的搜索过程, 避免了不必要的探索.

(3)设计了一种动态搜索策略, 根据环境的反馈动态地调整 $ \varepsilon $ 值, 更好地平衡了探索与利用的关系.

在多种不同障碍物难度等级的环境中进行的仿真实验表明, 本文方法相较于基本Q学习算法、其他算法在收敛性和寻优耗时上都有一定的提高, 但仍存在以下不足.

(1)本文算法在融合启发式搜索策略时引入了多个参数, 在进行仿真实验时, 需要同时调节多个参数, 在一定程度上, 增加了敏感性.

(2)后续将研究本文方法在动态障碍物环境下的路径规划以及求解多目标路径规划的问题.