目标检测任务是目前计算机视觉领域研究的核心课题之一, 基本任务是找到感兴趣的目标确定其位置和其所属类别. 传统的目标检测算法主要通过手动设计准确的特征和建立准确的数学模型来实现对各种物体的检测, 如基于滑动窗口的VJ Det算法[1]和基于行人特征的HOG Det算法[2]等. 随着深度学习算法和相关硬件的发展, 目标检测开始进入深度学习的时代. 深度学习下的目标检测主要分为以YOLO系列为代表的单阶段(one-stage)和以RCNN系列为代表的两阶段(two-stage)方法[3]. 基于深度学习的目标检测算法由于其能够对目标特征自动提取而无需手动设计特征, 且算法适应性高, 能够进行迁移学习, 因此被广泛运用于人脸识别、车辆检测、医学影像等领域中. 虽然深度学习技术给目标检测带来了突破性的进展, 但是在实际任务中, 往往需要对小目标进行检测. 由于小目标在整幅图像中面积占比小、分辨率低和特征不显著等原因, 现有的各种目标检测框架都不能够很好地对小目标物体进行检测[4]. 许多科研工作者基于已有的各种目标检测框架提出了诸多优化改进方法, 以期提高现有检测框架的小目标检测能力. 徐思源等人主要通过对小目标数据集进行聚类分析以及改进YOLOv3特征提取结构的方法来提高检测网络对小目标物体的检测能力[5]. 刘竣文等人将YOLOv3特征提取网络替换为基于ResNet和DenseNet的特征提取网络RD-Net, 并引入混合空洞卷积, 提高检测框架对小目标的敏感程度[6]. 王建军等人根据不同尺度特征的重要性对YOLOv3的主干网络进行重构, 并引入RFB感受野模块增大特征图的感受野, 提高检测框架对小目标的检测效果[7].
本文针对小目标检测任务, 对经典YOLOv3检测框架进行改进优化. 首先, 调整YOLOv3特征提取网络的残差模块数量, 在保证不同尺度下网络特征提取能力不变的前提下扩充特征金字塔(feature pyramid networks, FPN)层数, 增大输出特征图的感受野, 引入全局信息注意力机制(global context, GC), 提高上下文特征捕获能力, 增强模型对小目标的识别精确度. 其次, 基于Retinex理论对训练集小目标进行随机数量的单尺度Retinex (single-scale Retinex, SSR)特征融合增强, 提高数据集中小目标的特征信息量. 最后, 结合bounding box在数据集上的分布特性, 使用自适应锚框优化算法, 对anchors尺度和长宽比例进行优化, 提高模型对小目标的匹配程度.
1 YOLOv3算法简介YOLOv3算法是单阶段目标检测算法的核心代表之一. YOLOv3模型由特征提取网络Darknet-53和特征金字塔FPN组成. 其中特征提取网络结构如图1所示[8]. 假设输入图片尺寸大小为416×416, Darknet-53将会对图片进行8倍、16倍和32倍的下采样, 分别得到大小为52×52、26×26和13×13的3层特征图.
将得到的3张特征图经过特征融合模块FPN的处理, 每个特征图都充分融合了自身特征信息和前面位置的特征信息, 输出大小为: (13, 13, 512)、(26, 26, 256)、(52, 52, 128)三张特征图, 每个特征图经过YOLO探测头, 最终得到大小为: (13, 13, 3×(num_classes)、(26, 26, 3×(num_classes+5)和(52, 52, 3×(num_classes+5))的3张预测图. 其中3表示每个特征图中一个特征点对应于3个anchor, num_classes表示数据集要预测的目标种类数量, 5表示预测框的置信程度和4个参数(预测框中心坐标x, y和宽高w, h).
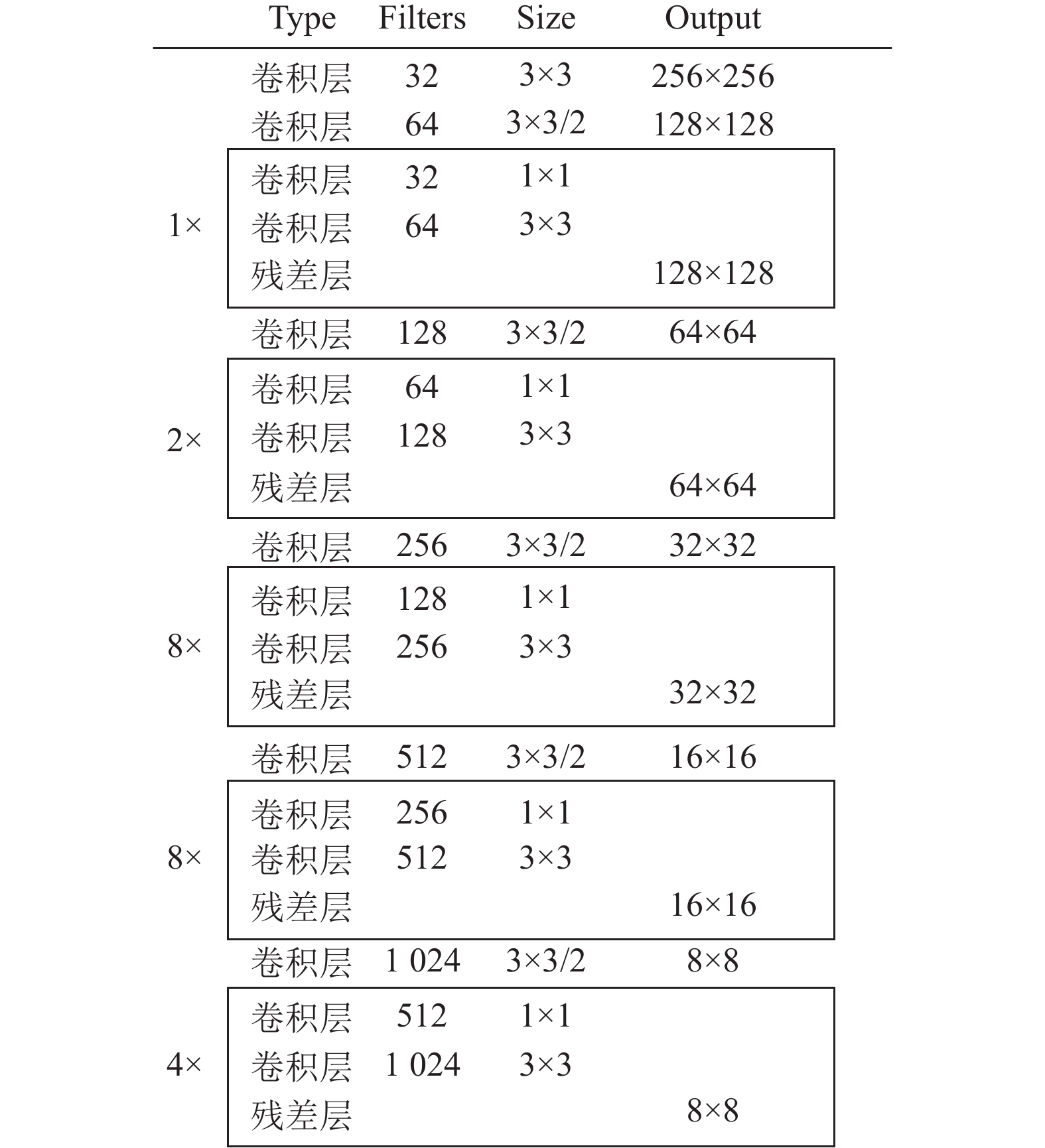
|
图 1 YOLOv3特征提取网络Darknet-53 |
YOLOv3的损失函数由预测边界框回归损失项、预测置信度损失项和预测类别损失项组成. 如式(1)所示:
| loss=λcoordS×S∑i=0M∑j=0Iobjij(2−wi×hi)[(xi−x∗)2+(yi−y∗)2]+λcoordS×S∑i=0M∑j=0Iobjij(2−wi×hi)[(wi−w∗)2+(hi−h∗)2]−S×S∑i=0M∑j=0Iobjij[C∗ilog(Ci)+(1−C∗)log(1−Ci)]−λnoobjS×S∑i=0M∑j=0Inoobjij[C∗ilog(Ci)+(1−C∗)log(1−Ci)]−S×S∑i=0Iobjij∑c∈class[p∗i(c)log(pi(c))+(1−p∗i(c))log(1−pi(c))] | (1) |
利用深度学习技术进行小目标检测的一大难点是: 小目标(将物体标注框的长宽乘积除以整个图像的长宽乘积, 再开根号, 如果结果小于3%, 则定义为小目标)本身分辨率较低, 其像素特征在经过以卷积操作为主的神经网络特征提取器后, 基本已经出现较大损失. 如果仅仅考虑局部小目标图像的特征提取不难得出, 在经过多次卷积后, 其特征权重随着卷积次数的增加呈指数下降. 特征提取器中越靠后的卷积操作得到的特征图基本已经丧失小目标特征信息, 因此无论后续经过多少次网络学习, 算法模型都无法对小目标检测达到一个较好的效果.
基于上述分析, 本文对YOLOv3网络结构作出如图2所示的改进. 本文延续Darknet-53整体结构特点, 首先对残差模块数量和排列作出调整, 将Darknet-53中最开始的两个残差模块数量分别扩大两倍, 得到Res2、Res4, 并将Res4的输出作为第1个特征图输出, 参与后续的特征融合. 这样的设计在第1次特征引出时, 减少了一次残差操作, 网络对浅层信息的提取保留水平得到提高, 然后将Res6模块修改为Res8模块, 保证模型对中大型目标特征提取的完善程度.
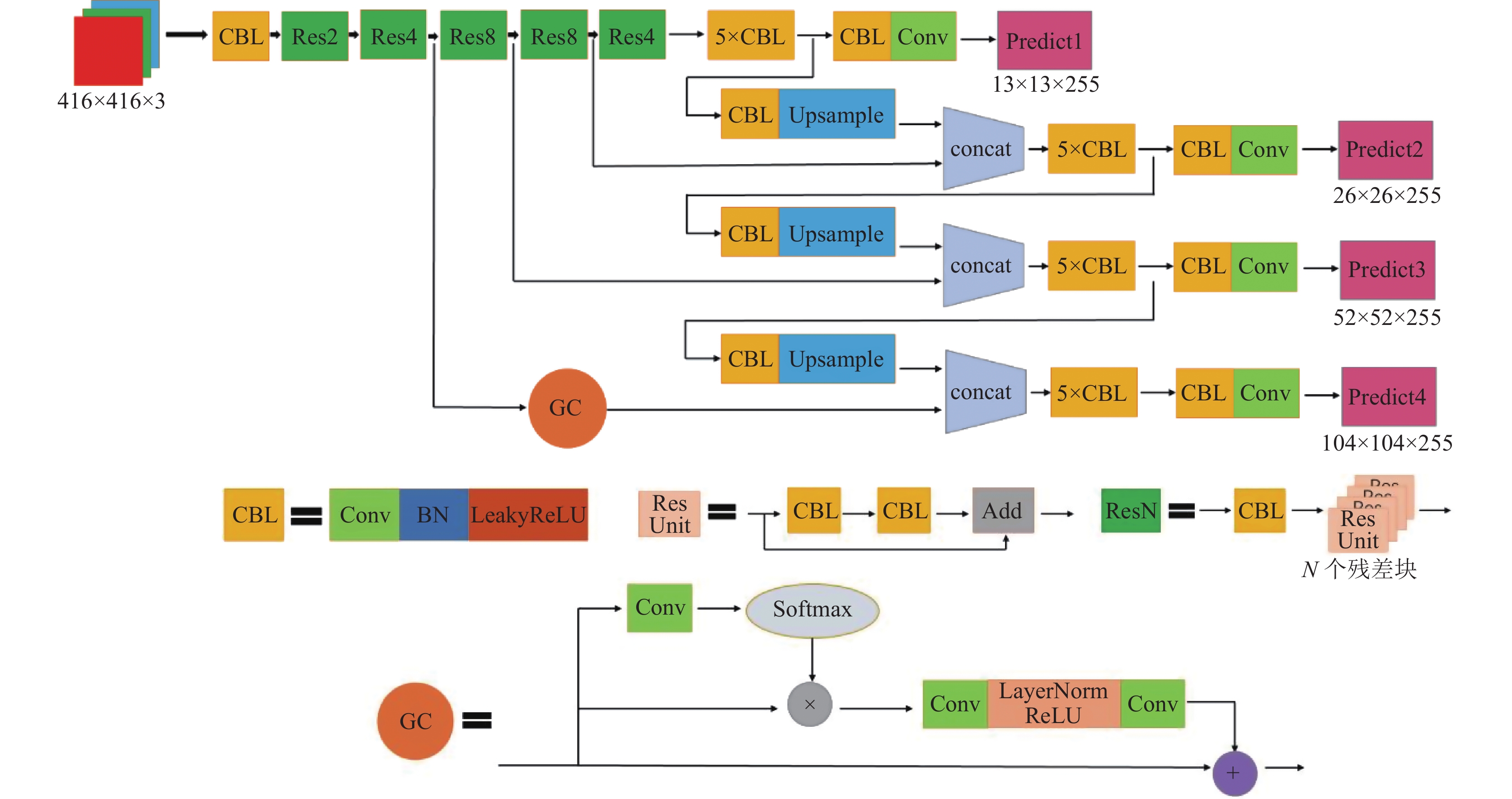
|
图 2 改进的YOLOv3算法模型结构 |
GC注意力机制融合SENet和NLNet两大经典注意力机制的优点, 能够充分挖掘上下文信息[9], 同时相对于其他注意力机制轻量化程度高, 对于模型速度的影响较低. 本文算法在第1个特征图进行融合操作之前引入GC注意力机制, 挖掘小目标与背景的差异性特征, 提高模型对于小目标检测的识别准确率和定位准确程度.
使用YOLOv3模型进行目标检测的输出结果是FPN结合YOLO-head得到的3张尺寸大小分别是13×13, 26×26和52×52的预测张量. 以13×13预测张量为例, 本质是将原始输入的416×416尺寸大小的图像用13×13的网格覆盖, 每个网格负责预测某个目标. 预测张量的尺寸决定了目标检测框架的精细化程度, 如果预测张量图越大, 那么小目标就更容易被检测出.
因此本文算法提前进行骨干网络特征图输出, 得到4张特征图, 构建4层FPN结构, 模型新输出的104×104大小的预测张量能够提高检测网络的精细化程度, 进一步提升算法对小目标的检测能力.
2.2 小目标数据SSR融合特征增强Retinex模型[10]中的照度分量可以视为无噪声干扰的原始图像在经过周围环境变化、拍摄失真等噪声干扰产生的一种非线性变换. 这种非线性变换作用于原始图像就得到了最终的实际图像. 因此只需要利用小目标图像所在区域的照度分量, 便能够反解出该区域的反射分量, 即得到小目标的原始图像, 增强数据集中小目标的本质特征信息量.
本文针对小目标检测, 随机对10%的训练集图像标注区域进行SSR操作 [11]. 在包含小目标的图像区域内建立Retinex模型如下:
| S(m,n)=R(m,n)×L(m,n) | (2) |
对式(2)两边取对数得到如下公式:
| log(S(m,n))=log(R(m,n))+log(L(m,n)) | (3) |
使用高斯环绕函数对光照分量进行估计, 代入式(3)得到:
| r(m,n)=log(S(m,n)L(m,n))=log(S(m,n))−log(S(m,n)×G(x,y)) | (4) |
其中, 高斯环绕函数是一个含有超参数
| G(x,y)i=12πσi2e(−x2+y22σi2) | (5) |
本算法中取
根据Retinex理论, 一幅图像可以视为反射图像和照度图像的合成, 反射图像中包含图像中物体自身的大量特征信息. 照度图像中则包含大量的外界噪声信息. 所以只需要对照度图像进行估计, 就可以得到反射图像, 即得到物体自身的特征信息[12]. 最初的Retinex算法主要是基于路径比较的算法, 缺点是无法对照射分量进行准确的估计, 得到的反射图像特征损失较大.
SSR利用高斯环绕函数式(5)对照度图像进行估计, 本质是在图像的每个通道用一个符合二维高斯分布的模板去代表照度图像,
通过上述算法得到局部新图像, 能够充分反映目标的本质特征如轮廓信息等. 结合原始局部图像构建局部图像SSR融合特征增强线性加权模型如式(6).
| R∗(m,n)=αE(m,n)+(1−α)R(m,n),α∈[0,1] | (6) |
其中,

|
图 3 不同细节突出因子下的飞机图像效果 |
可以发现, 随着
在经典YOLOv3算法中, 使用K-means算法得到锚框. 然而文献[13]经过实验指出: K-means算法得到的锚框不够理想并且锚框选取的提升空间是足够大的. 因此, 通过优化改进锚框计算方法进而提高模型表现效果是可行的.
Anchor box的选取可以用一组超参数来描述, 设共有K组锚框, 每个锚框有尺度
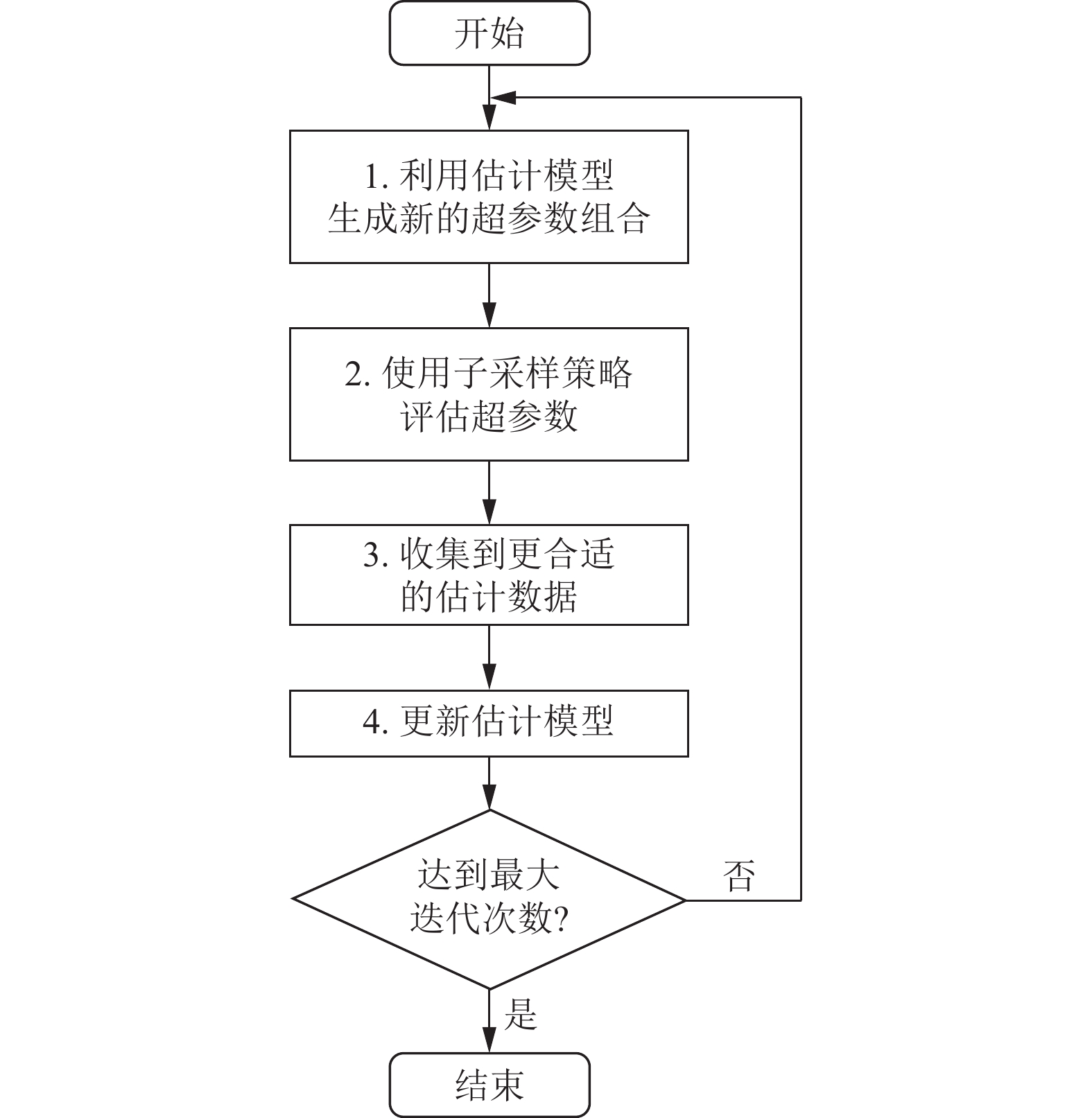
|
图 4 AABO算法流程图 |
图4中, 估计模型使用核密度估计函数(tree Parzen estimator, TPE)进行建模, TPE包含两个概率密度函数, 分别是
子采样策略用于评估一组超参数组合, 其算法步骤见算法1. 相比基于预算的超参搜索算法HyperBand[15], 该策略对缓慢收敛的小目标检测有更高的评估准确性.
算法1. 子采样策略
Input: 超参数组合集合
Output: 预算分配结果
1. r=1, 分别以预算
2. for
3. 当前获得最大预算的超参数组合记为
4. for
5. 若第k个超参数组合“优于”领先者, 则给予它额外
6. end for
7. 若没有找到“优于”领先者的超参数组合, 则给予领先者额外
8. end for
基于式(7)和式(8)两个条件[13]来评估一个超参数组合是否“优于”领先者, 阈值
| nk<nkcentandnk<cn | (7) |
| {cn⩽nk<nk′andˉY(k)1:nk⩾ˉY(k′)j:(j+nk−1)forsome1⩽j⩽nk′−nk+1whereˉY(k)l:u=u∑v=lY(k)v/(u−l+1) | (8) |
考虑到对一个锚框超参数组合评估的极高时间成本, 设计一个足够紧致但同时不过度损失探索性的搜索空间非常重要. 本文首先对RSOD数据集中所有标注框的尺度和高宽比进行统计, 剔除极端分布后作为基础搜索空间. 由于锚框参数的微调对检测效果影响微小, 对尺度和长宽比分别以0.1和0.01的采样间隔进行离散化, 从而在搜索过程中维持较高的探索性.
目标函数
| f(→x,epoch)=val_loss(→x,epoch)−e−(epochmax_budget)×mAPaircraft(→x,epoch) | (9) |
式(9)中,
锚框优化效果如图5所示, 红色框是真实值, 绿色框是第3层FPN对应的锚框, 即图2中Predict3. 图5(a)采用了YOLOv3中使用的K-means算法, 图5(b)采用了AABO算法, 迭代次数为27. 可以看到图5(a)中的3个锚框都与真实值有较大误差, 而经过优化后的图5(b)对小目标的预测具有更高的自适应性.

|
图 5 Anchor优化效果 |
3 算法实验
本文实验在Windows 10操作系统下进行, 使用TensorFlow 2.3.0搭建模型, GPU使用NVIDIA Tesla P100-PCIE. 总训练轮次设置为400, 优化器使用Adam. 使用余弦退火算法作为学习率的更新方式.
3.1 评价指标目标检测的效果由预测框的分类精度和定位精度共同决定, 因此目标检测问题既是分类问题, 又是回归问题. 本文采用全类平均精度(mean average precision, mAP)和F1分数来评价模型效果.
某个类别的分类准确度用平均准确率(average precision, AP)衡量, AP计算公式如下:
| AP=∫10P(R)dt | (10) |
其几何含义是PR曲线与坐标轴所围成的图形面积. 对于M分类的问题, 常使用mAP值作为分类效果评价指标, 计算公式如下:
| mAP=M∑i=1APiM | (11) |
F1分数是精确率P和召回率R的调和均值, 更能客观评价模型的全方位性能, F1计算公式如下:
| F1=2×P×RP+R | (12) |
理想情况下, 在模型训练过程中, 学习率应由大变小. 但在实际情况下, 由于模型较大且参数初始化是随机的, 梯度下降方向并不稳定, 因此需要在一段时间内设置较小的学习率[16], 然后再调高学习率, 最后逐渐调小学习率, 以便能够得到更加好的训练效果.
利用余弦退火算法[16]对学习率进行更新, 学习率更新公式如下:
| LRi=(LRmax−LRmin)×(iT1)2+LRmin | (13) |
式(13)是训练开始时的学习率变化公式,
| LRi=LRmin+0.5×(LRmax−LRmin)×(1+cos(iπT−T1)) | (14) |
式(14)是训练到
将训练过程中的学习率变化可视化如图6所示.

|
图 6 学习率变化曲线 |
分析学习率变化曲线可以知道, 在训练开始后的一段epoch内, 学习率从0.001快速增加至0.01. 此后学习率由0.01下降至0.001, 下降速度由慢变快再变慢.
3.3 不同α取值情况下的飞机AP值对比由图3可知, 取不同的

|
图 7 不同
|
分析图7可知, 随着
本文使用大部分检测物体为小目标的RSOD数据集进行模型消融实验. 共设置5种消融实验, 分别是经典YOLOv3算法、仅改进网络结构的YOLOv3算法、改进网络结构并且使用SSR增强的YOLOv3算法、改进网络结构并且使用anchors优化的YOLOv3算法和改进网络结构, 同时进行SSR增强和anchors优化的完整YOLOv3改进算法.
将验证集mAP@0.5作为评价指标, 记录400次训练过程中每10次结果中的最大mAP值, 绘制如图5所示的mAP变化曲线.
图8表明, 相比于经典YOLOv3模型, 经过任意一种文中的优化方法均能够较大幅度提高YOLOv3模型的效果.
对比分析经过结构改进的YOLOv3模型和经典YOLOv3模型的mAP变化曲线可知: 由于本文重新设置Darknet-53的残差模块数量及排列方式同时引入GC注意力机制, 提高了模型骨干网络对于RSOD数据集中大量小目标图像数据的特征提取能力, 同时能够保证对于中大型目标仍然良好的特征提取能力, 因此模型的学习效果明显得到提高. 在检测识别过程中, 扩充的FPN机制使得模型的感受野得到扩大, 能够对于目标区域物体进行更加精准的识别.

|
图 8 5次消融实验的mAP@0.5变化曲线 |
对比分析经过结构改进但未进行SSR数据增强的模型和经过SSR数据增强的模型可知: 经过SSR融合增强的数据集能够更好地体现目标物体的特征, 使得模型在训练过程中能够学习到目标物体更多的有效信息. 因此在检测过程中, 相比于仅改变网络结构的模型, 能够得到更好的mAP值.
对比分析经过结构改进但未进行anchors优化的模型和经过anchors优化的模型可知: 经过anchors优化的YOLOv3模型能够更好地对目标检测框进行匹配, 总体上获得更大的mAP值, 同时模型的收敛速率得到一定提高.
总体来说, 经过本文对YOLOv3算法进行的网络结构改进、训练集SSR特征融合增强学习和anchors优化后, 算法对于小目标的检测效果相比经典YOLOv3算法得到明显提高, 最优mAP值提高12%左右.
3.5 不同算法对比与检测效果可视化将本文算法与应用广泛的经典YOLOv3算法、YOLOv4算法、Efficientdet算法的相关性能指标进行对比, 如表1所示, 可以发现本文算法效果明显优于其他常用算法, 在RSOD数据集的大部分飞机(小目标)检测上具有0.915的AP值明显高于其他算法.
在不同情况下, 将本文算法与经典YOLOv3算法的检测效果进行如下可视化对比分析.
如图9所示为复杂背景下经典YOLOv3算法与本文算法的检测效果对比. 图9(a)为经典YOLOv3算法检测效果, 图9(b)为本文算法检测效果. 经典YOLOv3算法检测到9个目标, 本文算法检测到12个目标.
| 表 1 不同算法的性能对比表 |

|
图 9 复杂背景下检测效果对比 |
如图10所示为雾霾环境下经典YOLOv3算法与本文算法的检测效果对比. 图10(a)为经典YOLOv3算法检测效果, 图10(b)为本文算法检测效果. 经典YOLOv3算法检测到11个目标, 本文算法检测到24个目标.

|
图 10 雾霾环境下检测效果对比 |
如图11所示为多个小目标检测任务下经典YOLOv3算法与本文算法的检测效果对比. 图11(a)为经典YOLOv3算法检测效果, 图11(b)为本文算法检测效果. 经典YOLOv3算法检测到23个目标, 本文算法检测到32个目标. 可以看出, 经过本文优化的YOLOv3算法对于小目标的检测效果得到明显提升.
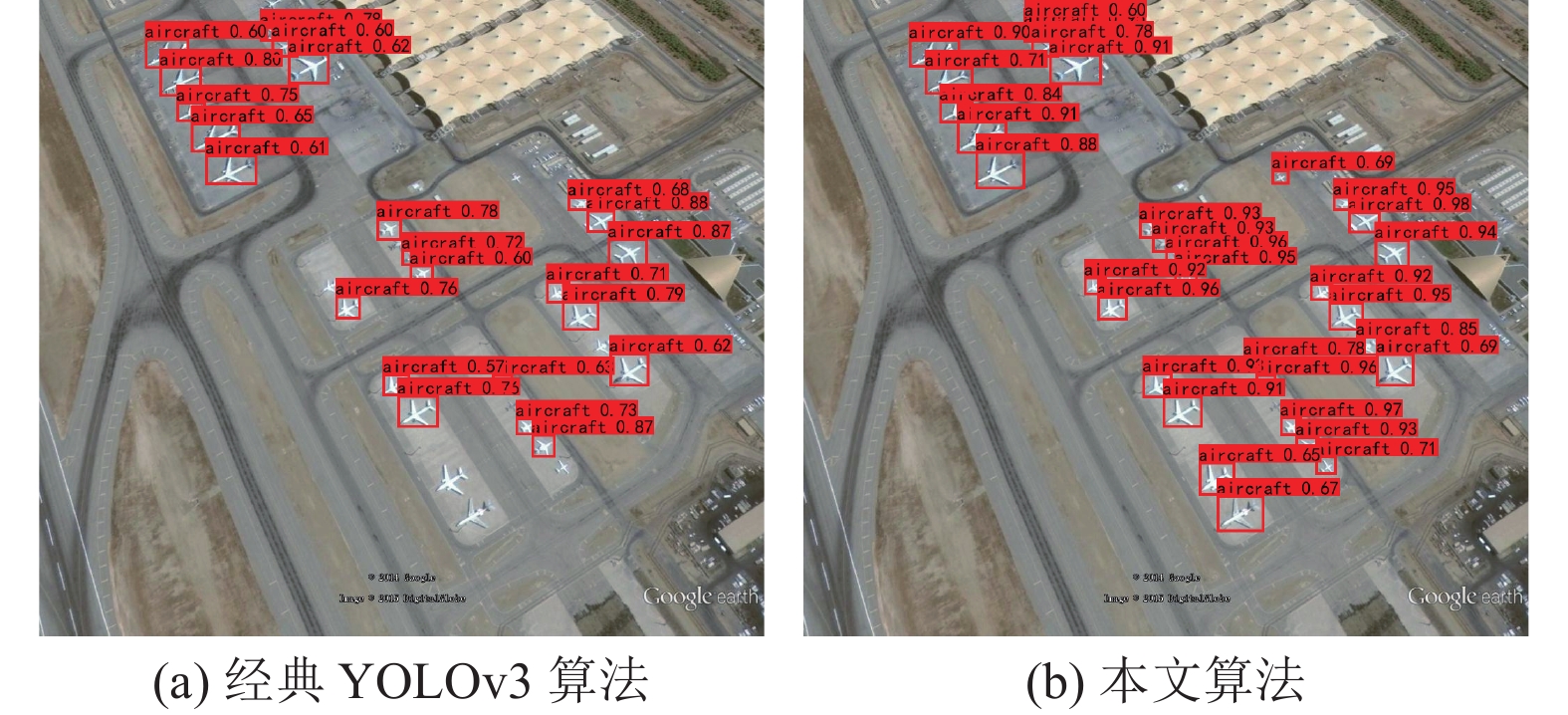
|
图 11 多个小目标任务检测效果对比 |
如图12所示为集群小目标检测任务下经典YOLOv3算法与本文算法的检测效果对比. 图12(a)为经典YOLOv3算法检测效果, 图12(b)为本文算法检测效果. 经典YOLOv3算法检测到10个目标, 本文算法检测到16个目标. 待检测的图片左上部分为集群小目标存在处, 可以发现经过本文优化的YOLOv3算法对于集群小目标检测效果得到明显提升.

|
图 12 集群小目标任务检测效果对比 |
4 总结与展望
本文基于经典YOLOv3算法, 首先对主干网络Darknet-53进行残差模块数量调整和重新排列组合, 保证不同尺度下网络特征提取能力不变, 扩充FPN层数, 扩大输出特征图的感受野, 并引入GC注意力机制, 提高模型上下文特征捕获能力, 增强了模型对小目标的特征学习和识别能力. 其次, 基于Retinex理论, 建立SSR融合特征增强线性加权模型, 取细节突出因子等于0.5, 随机对10%训练集目标进行特征增强, 提高了训练集小目标特征信息含量, 增强了模型训练效果. 最后结合bounding box在RSOD数据集上的分布特性, 使用AABO算法, 对anchors尺度和长宽比例进行优化, 提高了模型对小目标的匹配程度.
实验阶段, 针对遥感数据集RSOD, 首先, 设置5种消融实验, 对比分析了本文不同优化措施对经典YOLOv3算法效果的影响, 最终发现本文算法相比于经典YOLOv3算法, 在RSOD数据集上mAP@0.5值提高10.1%. 然后, 将本文算法在RSOD数据集上的表现效果与其他文献中的算法效果进行对比, 发现本文算法效果优于其他文献算法效果. 最后, 针对复杂背景下目标检测、雾霾环境下目标检测、多个小目标检测、集群小目标检测等实际场景下4种典型遥感目标检测任务, 将本文算法与经典YOLOv3算法进行效果对比, 发现本文算法在4种典型任务中的表现效果均明显优于经典YOLOv3算法.
本文采用不同措施提高YOLOv3算法对于遥感小目标的检测效果, 毫无疑问将一定程度提高模型的复杂程度, 降低模型的实时检测速度. 后续研究将考虑对模型进行剪枝操作, 得到轻量化模型, 以便结合实际硬件对遥感小目标进行实时检测.
| [1] |
Viola P, Jones MJ. Robust real-time face detection. International Journal of Computer Vision, 2004, 57(2): 137-154. DOI:10.1023/B:VISI.0000013087.49260.fb |
| [2] |
Dalal N, Triggs B. Histograms of oriented gradients for human detection. Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego: IEEE, 2005. 886–893.
|
| [3] |
方路平, 何杭江, 周国民. 目标检测算法研究综述. 计算机工程与应用, 2018, 54(13): 11-18, 33. DOI:10.3778/j.issn.1002-8331.1804-0167 |
| [4] |
刘洪江, 王懋, 刘丽华, 等. 基于深度学习的小目标检测综述. 计算机工程与科学, 2021, 43(8): 1429-1442. DOI:10.3969/j.issn.1007-130X.2021.08.012 |
| [5] |
徐思源, 储开斌, 张继, 等. 面向小目标检测的改进YOLOv3算法. 电光与控制, 2022, 29(8): 35-39. DOI:10.3969/j.issn.1671-637X.2022.08.007 |
| [6] |
刘竣文, 张永军, 李智, 等. 基于RDM-YOLOv3的头部检测. 激光与光电子学进展, 2022, 59(8): 0815011. |
| [7] |
王建军, 魏江, 梅少辉, 等. 面向遥感图像小目标检测的改进YOLOv3算法. 计算机工程与应用, 2021, 57(20): 133-141. |
| [8] |
Redmon J, Farhadi A. YOLOv3: An incremental improvement. arXiv:1804.02767, 2018.
|
| [9] |
Cao Y, Xu JR, Lin S, et al. GCNet: Non-local networks meet squeeze-excitation networks and beyond. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision Workshop. Seoul: IEEE, 2019. 1971–1980.
|
| [10] |
谢凤英, 汤萌, 张蕊. 基于Retinex的图像增强方法综述. 数据采集与处理, 2019, 34(1): 1-11. |
| [11] |
何艳, 方帅. 一种局部多尺度Retinex算法在雾天图像中的应用. 合肥工业大学学报(自然科学版), 2015, 38(10): 1333-1338. |
| [12] |
王利娟, 常霞, 张君. 基于Retinex的彩色图像增强方法综述. 计算机系统应用, 2020, 29(6): 13-21. DOI:10.15888/j.cnki.csa.007430 |
| [13] |
Ma WS, Tian TZ, Xu H, et al. AABO: Adaptive anchor box optimization for object detection via Bayesian sub-sampling. Proceedings of the 16th European Conference on Computer Vision. Glasgow: Springer, 2020. 560–575.
|
| [14] |
Falkner S, Klein A, Hutter F. BOHB: Robust and efficient hyperparameter optimization at scale. Proceedings of the 35th International Conference on Machine Learning. Stockholm: PMLR, 2018. 1437–1446.
|
| [15] |
Li LS, Jamieson K, DeSalvo G, et al. Hyperband: A novel bandit-based approach to hyperparameter optimization. The Journal of Machine Learning Research, 2017, 18(1): 6765-6816. |
| [16] |
He T, Zhang Z, Zhang H, et al. Bag of tricks for image classification with convolutional neural networks. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 558–567.
|
| [17] |
冯号, 黄朝兵, 文元桥. 基于改进YOLOv3的遥感图像小目标检测. 计算机应用, 2022, 42(12): 3723-3732. |
 2023, Vol. 32
2023, Vol. 32



