近年来人工智能技术不断发展, 从人工神经网络到卷积神经网络再到Transformer架构, 深度学习模型在生活中有着越来越广泛的运用. 但是, 研究者发现深度神经网络非常容易受到对抗样本的威胁^{[1, 2]}, 大量研究表明, 通过给良性样本添加特定的微小扰动制作成对抗样本在不引起人警觉的情况下可以轻易地欺骗模型, 从而产生大相径庭的预测结果. 攻击者可以通过伪造人脸图片来欺骗人脸识别模型从而非法入侵个人账户, 通过发射激光就可以攻击基于AI视觉的自动驾驶汽车^[3]. 制作攻击性更强、隐蔽性更高的对抗样本是对抗学习研究的一个重要方向, 有利于评估网络模型的鲁棒性和安全性, 并促进更加强大的防御方法的开发.

根据攻击过程中掌握目标模型知识的程度可以将现有的对抗攻击方法分为白盒攻击和黑盒攻击^[4]. 在白盒攻击方式中, 攻击者具有目标模型的完整知识, 可以分为基于梯度的攻击, 如FGSM^[2]、PGD^[5], 基于优化的方法C&W^[6]和基于生成对抗网络的攻击. 而黑盒攻击有很大限制, 攻击者无法访问模型细节, 只能查询访问的结果, 攻击难度更高, 在现实中更普遍. 黑盒攻击的一种实现方式是基于对抗样本迁移性实现迁移攻击, 以白盒攻击方法攻击代理模型生成对抗样本来获得对黑盒模型的欺骗. 提高模型的迁移性的优化方向主要有3类, 包括优化标准目标(FGSM、PGD)、修改注意力 (AOA^[7]、ATA^[8])和平滑梯度(DI^[9]、TI^[10]).

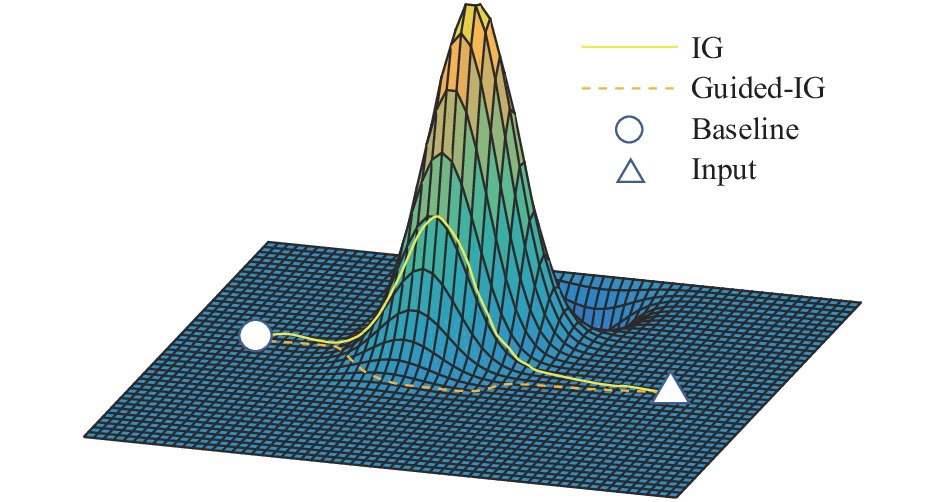
现有算法迁移攻击效果普遍不佳, Huang等人^[11]将积分梯度(integrated gradient, IG)^[12]引入对抗攻击, 提出了目前最先进的TAIG算法, 证明其可以从以上3个方面同时进行攻击, 在黑盒模式下具有较强的迁移攻击成功率. TAIG-S是TAIG算法的一个标准版本, 计算从基线到目标对象直线路径上的梯度的累积, 可以有效解决梯度饱和问题, 将注意力图作为反向更新方向来生成对抗样本. 但是其采用的直线路径未经过优化, 易进入与预测结果不相关的像素从而导致误差累积, 产生无效噪声干扰, 在一定程度上损失了迁移攻击的成功率. 为了解决上诉问题, 本文将引导积分梯度(Guided-IG)^[13]引入对抗攻击, 提出了Guided-TAIG方法. 具体的, 如图1所示, 在 TAIG-S算法基础上, 计算积分梯度时摒弃简单的直线计算, 沿着输入、基线和模型确定的自适应方向, 将计算生成的引导积分梯度作为对抗攻击过程中梯度的更新方向. 该算法可以过滤不相关像素的梯度误差累积, 更精细准确地找到模型最关注的特征区域, 进而生成攻击性和迁移性更强的对抗样本.

本文贡献主要有: (1) Guided-TAIG将积分梯度的直线路径优化为自适应路径, 修正攻击过程的扰动方向, 精确攻击模型关注的区域; (2)通过大量实验验证了所提算法在白盒和黑盒两种模式下都具有明显优越性.

1 相关工作 1.1 对抗攻击

对抗样本的概念最早由Szegedy等人^[1]于2013年提出, 发现在输入图片中添加微小的扰动成为对抗样本, 可以使图片以高置信度被误分为其他类别. 对抗样本的生成数学描述如下.

设图像分类器为函数 $F:{\mathbb{R}^n} \to {\mathbb{R}^k}$ , 其中, $ x \in {\mathbb{R}^n} $ 为输入图像, $y \in {\mathbb{R}^k}$ 为分类得分向量, $n$ 表示输入图片的维度, $k$ 为分类器的类别数. 通过 ${\textit{Softmax}}$ 函数将输出归一化为: $ {\displaystyle \sum _{i=1}^{k}{y}_{i}=1且0\leqslant {y}_{i}\leqslant \text{1}} $ , 其中 ${y_i}$ 是 $y$ 的第 $i$ 个分量. 则图像预测结果为:

$ pred(x) = \mathop {\arg \max }\limits_i {\textit{Softmax}}(F{(x)_i}),\quad i = 1, \cdots, k $

(1)

假设图像的真实标签为 ${y_{{\rm{true}}}}$ , 对抗攻击给原图添加微小噪声 $\delta $ , 其中 ${\left\| \delta \right\|_p} \leqslant \varepsilon $ , $\varepsilon $ 为扰动约束, $ {\Vert \cdot\Vert }_{p} $ 为 ${L_p}$ 范数, 制作成可以使分类器分类错误的对抗样本 ${x_{{\rm{adv}}}}$ , 使得:

$ pred({x_{{\rm{adv}}}}) \ne {y_{{\rm{true}}}},\quad {\rm{s.t.}}\quad {x_{{\rm{adv}}}} = x + \delta $

(2)

1.2 TAIG-S攻击算法

人类在做判断时往往选择性的关注信息的一部分, 忽略不重要的特征, 归因技术可以用来显示输入图片每个像素对最终结果的影响程度, TAIG-S首次将积分梯度用于生成对抗样本, 积分梯度是神经网络归因分析的工具, 结合了直接梯度DeepLift^[14]和基于反向传播的归因技术LRP^[15], 满足敏感性和不变性, 可以表明每个像素对网络输出的重要性, 从而可以作为网络的注意力. 积分梯度是从参考图像 $r \in {\mathbb{R}^n}$ 作为基线, 到输入图像 $x$ 的直线路径梯度积分, 对输入图像的第 $i$ 个像素的积分梯度的一个形式定义为:

$ {{I}}{{{G}}_i}(f, x, r) = ({x_i} - {r_i}) \times \int_{\eta = 0}^1 {\frac{{\partial f(r + \eta \times (x - r))}}{{\partial {x_i}}}d\eta } $

(3)

其中, ${r_i}$ 是 $r$ 的第 $i$ 个像素. 基线 $r$ 可以选取纯黑色、纯白色图片等. 完备性公理指出, $f(x)$ 与 $f(r)$ 之间的差值等于 ${{I}}{{{G}}_i}(f, x, r)$ 的和. TAIG-S将计算生成的积分梯度结果作为对抗攻击反向更新的方向, 来擦除与预测结果最相关的特征.

1.3 引导积分梯度

积分梯度采用简单的直线路径, 生成的结果具有大量无效像素产生的非零梯度积分累计噪声, 这由于网络模型的曲面映射形状, 沿直线很容易穿过非均匀梯度区域. 引导积分梯度是一种自适应路径的方法, 如图1所示, 在积分梯度基础上, 舍弃固定的积分方向, 不是所有像素的增量都相等, 而是在每一步都进行选择, 选择一个像素子集, 这些像素具有不等于输入的最小绝对值, 然后下一步只移动子集中那些更接近输入图像强度的部分, 当所有像素的强度与输入一致时, 则路径更新结束.

2 基于Guided-IG的对抗样本生成方法

本文提出了一种基于引导积分梯度的对抗样本生成方法Guided-TAIG, 下面详细介绍该方法的具体实现过程.

首先, 如第1.1节所描述, 定义一个映射函数 $ F:{\mathbb{R}^n} \to {\mathbb{R}^k} $ , 其表示分类网络, 输入 $n$ 维向量 $X$ , 并映射到含有 $k$ 维的输出 $Y$ . 积分梯度的一个重要概念是基线值, 表示不含任何信息的量, 用 ${X^B}$ 表示, 另一个概念是积分路径, 指连接基线值和输入值的参数曲线, 设 $\gamma :\alpha \to {\mathbb{R}^n}, \alpha \in [0, 1]$ , 其中, $\gamma (\alpha = 0) = {X^B}$ , $\gamma (\alpha = 1) = {X^I}$ , 则对于输入 ${X^I}$ 的每一维的积分梯度表示如下:

$ {{IG}}_i^{}({X^I}) = \int_{\alpha = 0}^1 {\frac{{\partial F(\gamma (\alpha ))}}{{\partial {\gamma _i}(\alpha )}}\frac{{\partial {\gamma _i}(\alpha )}}{{\partial \alpha }}} d\alpha $

(4)

积分梯度用路径上每一点的梯度累积来代替单独输入一点的梯度, 可以避免进入模型饱和区梯度为0的情况. 简单的, 当积分路径是直线, 即 $\gamma $ 为一次函数, 那么 $ \partial {\gamma _i}(\alpha )/\partial \alpha $ 退变为常数, 实际计算时将[0, 1]区间分成 $m$ 段, 每一段的路径为 ${\alpha _j} \to {\alpha _{j + 1}}$ , 则其离散形式为:

$ {{IG}}({X^I}) = \sum\limits_{j = 1}^m {\sum\limits_{i = 1}^n {\frac{{\partial F(\gamma ({\alpha _j})}}{{\partial {\gamma _i}({\alpha _j})}}} ({\gamma _i}({\alpha _j}) - {\gamma _i}({\alpha _{j - 1}}))} $

(5)

原始的积分路径穿过非均匀的梯度区域, 路径上可能会存在着与输入无关的非零梯度方向, 随着积分的累积, 与预测结果不相关区域的梯度值不会相互抵消而会成为噪声, 由此在对抗攻击任务的过程中, 计算后的不准确的更新方向会降低生成的对抗样本的攻击性与迁移性. 而理想的积分路径 ${\gamma ^ * }$ , 文献[13]用式(6)–式(8)来衡量:

$ {\gamma ^ * } = \arg \min \;{l_{{\rm{noise}}}} + {l_{{\rm{distance}}}} $

(6)

$ {l_{{\rm{noise}}}} = \sum\limits_{i = 1}^n {\int_{\alpha = 0}^1 {\left| {\frac{{\partial F(\gamma (\alpha ))}}{{\partial {\gamma _i}(\alpha )}}\frac{{\partial {\gamma _i}(\alpha )}}{{\partial \alpha }}} \right|} } {\kern 1pt} d\alpha $

(7)

$ {l_{{\rm{distance}}}} = \int_{\alpha = 0}^1 {\left\| {\gamma (\alpha ) - {\gamma ^{{\rm{cal}}}}(\alpha )} \right\|} {\kern 1pt} d\alpha $

(8)

其中, ${l_{{\rm{noise}}}}$ 是需要优化的噪声, 取值范围是无限的, 为了限制路径的取值, 引入有界限制 ${l_{{\rm{distance}}}}$ , ${\gamma ^{{\rm{cal}}}}(\alpha )$ 是实际计算时的路径点.

在实际计算中, 采用离散化的思想进行近似, 将从基线 ${X^B}$ 到输入 ${X^I}$ 路径划分为 $m$ 段, 每一段从起始点到目标点方向纠正的处理采用自适应的方法. 每一步中, 在每一点的梯度结果中找到一个特征子集 $S$ , 其是所有不等于输入 ${X^I}$ 的像素中绝对值最小的一部分的集合, 选取比例为 $p$ . 具体的, 先得到集合 ${S_{{\rm{tmp}}}}$ :

$ {S}_{{\rm{tmp}}}=\left\{\right|\partial F(x)/\partial {x}_{i}\left|\right\}\text{, }\;其中,\;i\in \left\{j\right|{x}_{j}\ne {x}_{j}^{I}\} $

(9)

将 ${S_{{\rm{tmp}}}}$ 从小到大排序, 选择前 $p$ 部分的像素下标组成集合 $S$ , 则更新之后的路径方向修改为:

$ {\left(\frac{\partial {\gamma }_{i}(\alpha )}{\partial \alpha }\right)}^{{\rm{new}}}= \left\{\begin{array}{l}{x}_{i}^{I}-{x}_{i}^{B}, \;\text{if}\;i\in S\\ 0,\; 其他\end{array}\right. $

(10)

令每一段的引导积分梯度为 ${{{{Guided}} {\textit{-}} {{I}}}}{{{{{G}}}}_{j, j + 1}}$ , 从而类比式(5), 得到优化之后的积分梯度:

$ \begin{split} & {{Guided {\textit{-}} IG}}({X^I}) = \sum\limits_{j = 1}^m {\sum\limits_{i = 1}^n {{{Guided {\textit{-}} I}}{{{G}}_{j - 1, j}}} } \\ & = \sum\limits_{j = 1}^m {\sum\limits_{i = 1}^n {\frac{{\partial F(\gamma ({\alpha _j})}}{{\partial {\gamma _i}({\alpha _j})}}} {{\left( {\frac{{\partial {\gamma _i}({\alpha _j})}}{{\partial {\alpha _j}}}} \right)}^{{\rm{new}}}}({\alpha _j} - {\alpha _{j - 1}})} \end{split} $

(11)

图2展示了积分梯度与引导积分梯度生成的归因图, 可以看出引导积分梯度过滤了原始梯度大量的无关噪声, 模型关注的区域更加集中. 引导积分梯度更能提取直接与网络模型预测结果相关的像素的强度, 反向更改这些像素点的值可以更改输入中包含的具体某一类别的信息, 这是对抗攻击可以进行的内部原因, 并可以直接应用于高质量对抗样本的生成过程. 类比FGSM和I-FGSM^[16]类型的攻击方法, 可以有以下单步攻击和多步攻击形式.

对于输入图像 $X$ , 单步攻击定义如下:

$ {X^*} = X + \varepsilon \times sign({{Guided {\textit{-}} IG}}(X)) $

(12)

其中, $\varepsilon $ 为扰动系数, 因为计算出的 ${\text{Guided-IG}}$ 矩阵元素大小不均, 为了限制其无穷范数, 用 $sign( \cdot )$ 函数提取积分梯度方向, 一步更新可以快速地生成对抗样本. 同时, 因为单步攻击只沿积分梯度方向更新一次, 跨越距离较大, 可以将一步扰动 $\varepsilon $ 均分为多步小扰动形式, 设划分步数为 $T$ 次, 则每次的扰动距离为 $\varepsilon /T$ . 在实际攻击过程中, 判断每一小步是否攻击成功, 如果不成功则再重新计算积分梯度进行下一小步的更新. 则所提出的Guided-TAIG多步攻击算法定义如下:

$\left\{ \begin{split} & X_0^* = X_{}^I \\ & X_{i + 1}^* = Clip\left\{ {\left. {X_i^* + \frac{\varepsilon }{T} \times sign({{Guided {\textit{-}} IG}}(X_i^*))} \right\}} \right. \end{split} \right.$

(13)

其中, $Clip\left( {\left. \cdot \right)} \right.$ 为裁剪函数, 将第 $i$ 步的更新结果限制在一定范围内. 算法伪代码如算法1所示.

3 实验分析

本节设计实验来验证和分析Guided-TAIG算法生成对抗样本的效果以及该方法的参数设计和对比研究. 分别介绍实验选用的数据集、白盒模式下的攻击效果、黑盒迁移的攻击性能以及算法参数分析.

3.1 实验设计

为了公正合理地评判不同攻击方法的优劣, 被测模型选择深度学习史上各阶段的经典模型VGG-16^[17], ResNet-50^[18] , InceptionV3 (Inc-V3)^[19], EfficentNet B3 (Effi-B3)^[20]. 随着深度学习的发展, 近几年Transformer架构的模型逐步展现出比传统CNN架构模型更具优势, 所以也选择了最先进的基于Transformer架构的分类模型Swin Transformer (Swin)^[21]和MViTv2^[22]. 并且对比了引入卷积的Transformer架构, convolutional Transformers (CvT)^[23], 分别选取各种模型的版本为Swin-B, MViTv2-B和CvT-13, 所有模型均在ImageNet数据集上进行训练.

本文使用的数据集为从ImageNet^[24]挑选的1 000张图片, 并且保证所有分类模型都可以正确预测结果, 这样可以忽略不同模型分类准确度的差异, 只关注对抗样本生成算法本身在不同结构模型上的攻击效果.

算法1. Guided-TAIG流程

输入: 分类模型 $\scriptstyle f$ , 图片 $\scriptstyle {x^I}$ , 基线 $\scriptstyle {x^B}$ , 标签 $\scriptstyle {y_{{\rm{true}}}}$ , 扰动距离 $\scriptstyle \varepsilon $ , 更新步数T, 离散路径分段 $\scriptstyle m$ , 像素更新比例 $\scriptstyle p$ .

输出: 对抗样本 $\scriptstyle {x_{{\rm{adv}}}}$ .

1. $\scriptstyle {x_{{\rm{adv}}}} \leftarrow {x^I}$

2. $\scriptstyle map \leftarrow {\textit{z}}ero({x^I})$ //shape与 $\scriptstyle {x^I}$ 一致

3. for $\scriptstyle t \leftarrow 1$ to $\scriptstyle T$ do

4. 　 $\scriptstyle x \leftarrow {x_{{\rm{adv}}}}$

5.　 $\scriptstyle grad \leftarrow \nabla f(x, {y_{{\rm{true}}}})$ //输入模型计算梯度

6.　 for $\scriptstyle \mu \leftarrow 1$ to $\scriptstyle m$ do

7.　　 $\scriptstyle \theta \leftarrow \infty $ //临时变量

8. 　　while $\scriptstyle \theta > 1$

9.　　　 $\scriptstyle tmp \leftarrow x$

10. 　　　 $\scriptstyle {d_t} \leftarrow {\left\| {{x^B} - {x^I}} \right\|_1}(1 - \mu /m)$

11.　　　 $\scriptstyle {d_c} \leftarrow {\left\| {x - {x^I}} \right\|_1}$

12.　　　 寻找 $\scriptstyle grad$ 中所有不等于 $\scriptstyle {X^I}$ 的像素中升序排列前 $\scriptstyle p$ 范围的集合 $\scriptstyle S$

13.　　　 $\scriptstyle {d_s} \leftarrow \sum\nolimits_{i \in S} {\left\| {{x_i} - X_i^I} \right\|} $

14. 　　　 $\scriptstyle \theta \leftarrow ({d_c} - {d_t})/{d_s}$

15. 　　　 $\scriptstyle {x_i} \leftarrow X_i^I, \, \forall i \in S$

16. 　　　 $\scriptstyle gra{d_i} \leftarrow {x_i} - x_i^B,\;\forall i \in S$

17. 　　　 $\scriptstyle gra{d_i} \leftarrow 0, \;\forall i \notin S$

18. 　　　 $\scriptstyle ma{p_i} \leftarrow ma{p_i} + ({x_i} - tm{p_i}) \times gra{d_i}$

19.　　　 end while

20. 　end for

21. $\scriptstyle {x_{{\rm{adv}}}} \leftarrow {x_{{\rm{adv}}}} + (\varepsilon /T) \times sign(map)$

22. $\scriptstyle {x_{{\rm{adv}}}} \leftarrow Clip({x_{{\rm{adv}}}})$ //裁剪到有效区间

23. end for

24. return $\scriptstyle {x_{{\rm{adv}}}}$

比较算法选择白盒攻击算法FGSM, C&W, 以及黑盒迁移性较强的攻击算法TAIG-S. 在白盒攻击中限制最大扰动像素大小 $\varepsilon $ , TAIG-S与Guided-TAIG都设置相同的 $m$ 值, 并固定Guided-TAIG的 $p$ 值.

评测指标包括: (1)攻击成功率: 攻击成功样本数/总样本数量; (2)平均攻击耗时: 每个样本的平均生成时间; (3)平均噪声和: 单样本平均添加的扰动在RGB三通道绝对值的和.

实验代码采用PyTorch框架编写, 硬件平台采用两块NVIDIA GeForce RTX 3090.

3.2 白盒单步攻击

首先将Guided-TAIG与流行的攻击方法进行比较, 实验限制为白盒单步攻击, 即直接攻击模型本身, 并且对原图只进行一轮扰动更新, 限定相同的最大扰动距离 $\varepsilon $ , 这样可以比较不同算法计算的更新方向的优劣. 而如果采用多步攻击, 则大多数算法都可以很容易的取得接近100%的攻击成功率. C&W是一种优化攻击, 其损失函数为对抗样本的预测输出和其one-hot编码差值的二范数, 实验采用迭代的方式优化噪声矩阵来扩大其损失函数. FGSM、TAIG-S和Guided-TAIG的损失函数都为交叉熵函数. TAIG-S和Guided-TAIG的分段值 $m$ 设置为30. 在 $\varepsilon $ 分别为8, 16, 25时, 比较不同算法分别单步攻击VGG-16、ResNet-50、Inc-V3、Effi-B3、Swin、MViTv2-B和CvT-13, 即设置攻击步数T= 1, 令p = 20%, 攻击成功率见表1. 从表中可以得出, 在白盒模式下, Guided-TAIG也可以取得很好的攻击成功率, 比TAIG-S平均成功率高出2%–3%, 超过了FGSM和C&W算法. 基于Transformer架构的模型相比CNN架构更难攻击. 同时也注意到FGSM在扰动距离增大的时候部分模型的攻击成功率不升反降, 这说明其优化方向并不精确, 给图像添加范围更大的错误扰动在一定程度上会降低对抗样本的攻击性. 而TAIG-S和Guided-TAIG计算的扰动反向更新方向更为准确, 随着扰动距离的增加, 对抗样本的攻击力显著增强.

给图片添加绝对值更小的扰动可以使攻击更加隐蔽, 表2比较了不同算法平均生成的每张对抗样本中修改像素3个颜色通道绝对值的和, 记为 $ \widetilde {\left| {noise} \right|} $ , 并且比较了不同算法在所有模型生成样本的平均耗时. 设置同样的扰动距离 $\varepsilon = 16$ , 迭代步数 $T = 1$ , Guided-TAIG攻击所有模型得到的 $ \widetilde {\left| {noise} \right|} $ 都是最小的, 因为像素的更新大小都是相同的, 在扰动的像素数量最少的情况下, 却得到了更优的攻击性能. 但是在耗时上Guided-TAIG处于劣势, 平均要花1 s多时间生成一张对抗样本, 并且分段数越多耗时显然会增加. 图3展示了攻击CvT-13模型的部分对抗样本. 第1列为原图, 第2–5列分别为不同算法生成的对抗样本示例, 从中可以看出Guided-TAIG制作的对抗样本噪声更加柔和, 在现实生活更有隐蔽性.

3.3 黑盒迁移攻击

迁移攻击是黑盒攻击常用的攻击方式, 主要利用了对抗样本具有迁移性, 通过攻击代理模型来生成对未知模型的攻击, 不同模型都偏向于利用图片的相似特征. 固定 $\varepsilon = 16$ , $m = 30$ , $T = 1$ , 分别用FGSM, C&W, TAIG-S和Guided-TAIG算法对每个代理模型进行攻击, 然后将生成的对抗样本作为数据集来攻击其他模型, 得到的迁移攻击成功率见表3. 表中每一行用同一种代理模型来迁移攻击其余黑盒模型, 相比TAIG-S, 所提算法迁移攻击成功率提升了0.4%–10%.

3.4 参数分析

这部分具体检验Guided-TAIG算法中不同参数对算法性能的影响.

首先固定Guided-TAIG积分梯度划分段 $m = 30$ , 扰动距离 $\varepsilon = 16$ , $p = 20{\text{%}} $ , 比较在不同的迭代步数 $T$ 下白盒攻击目标模型的成功率, 见图4. 横坐标为迭代的轮数, 纵坐标为攻击成功率, 随着 $T$ 的增加, 攻击效果明显增强, 在经过4–5轮的迭代攻击后, 所有模型都达到了95%及以上的攻击成功率. 纯CNN架构的模型最容易攻击, 纯Transformer的模型攻击成功率最低, 而结合两种架构为一体的CvT-13的被攻击难度介于两者之间. 当然, 这并不能直接说明Transformer架构就比CNN更鲁棒, 因为模型具有更多的参数量, 训练过程中采用了更优秀的损失函数和更大的数据集, 额外需要更多的实验来验证.

Guided-TAIG采用离散自适应的方式来计算积分梯度, 固定 $\varepsilon = 16$ , T = 1, $p = 20{\text{%}} $ , 下面比较不同分段数 $m$ 下白盒攻击的成功率, 见图5. 横坐标为 $m$ , 纵坐标为攻击成功率, 分别计算了 $m$ 等于5、10、20、30、40下的攻击效果. 随着分段数划分的越多, 需要的计算量更高, 攻击成功率逐渐趋近于饱和, $m = 20$ 时已经达到了可接受的结果.

在更新路径时, 选择的最小部分比例 $p$ 对结果也有影响, 不同取值的攻击成功率见图6. 固定 $\varepsilon = 16$ , $T = 1$ , $m = 20$ , $p$ 取值范围为10%–60%, 攻击成功率大致先上升再下降, 在20%–30%之间取得最大值.

4 结论与展望

本文改进了TAIG-S算法, 引入引导积分梯度到对抗攻击, 提出了一种Guided-TAIG算法, 限制了更新路径不相关的梯度累积并分别给出了Guided-TAIG单步攻击和多步攻击的形式. 实验表明该方法对不同架构的模型都具有较强的白盒攻击成功率, 生成的对抗样本噪声更小, 更具隐蔽性. 在黑盒迁移攻击实验中取得了最好的效果, 在实际攻击中相比TAIG-S提升了0.4%–10%的成功率. 随着迭代步数的增加对实验模型较容易的达到95%以上的攻击成功率. 劣势是该算法精确计算每一小段方向, 耗时较多. 后续计划将对积分路径进行更加细致化的改进, 增强对抗样本的攻击性能.