产品研发是企业战略计划的首要任务, 国家和企业都非常重视产品研发. 例如, 2021年, 国家研发经费支出达27864亿元, 潍柴动力的研发投入为85.69亿元. 研发项目投资大、结构复杂、周期长、不确定性大, 市场需求快速变化与研发周期长的矛盾日益突出. 企业单独依靠自身资源难以快速、高质量完成研发项目, 许多企业选择与其他企业合作进行协同研发. 协同研发能够有效消除参研团队的地域限制, 可合作的研发团队更多, 有效实现企业间的资源互补. 但协同研发过程中, 项目组织工作更复杂、不确定性更大, 进而加大了研发任务分配的难度. 任务分配不合理, 会导致研发项目执行过程中资源占用冲突频繁, 某些子项目(活动)需要长时间排队等待才能开始执行, 在很大程度上影响研发效率, 进而导致研发工期延长、研发成本增大. 因此, 如何把研发任务合理分配给各参研团队, 是研发项目管理的关键问题, 也是企业迫切需要解决的重要问题.

研发项目参研团队多、不确定性大、复杂性强, 传统网络计划技术难以准确描述其运行过程^[1]. 基于设计结构矩阵(design structure matrix, DSM)仿真建模是描述研发项目运行过程的一种重要方法^[2]. 通过仿真模型可分析资源约束、返工迭代、变更传播、并行策略等因素对研发项目运行效果的影响^[3]. 也有学者基于GERT、系统动力学等方法对研发项目进行仿真建模^{[4, 5]}. 决策者在评价研发任务分配方案时, 对各个指标的重视程度不同, 而且各个指标的效用价值不是线性的^[6]. 前景理论是在期望值理论和期望效用理论基础上提出的, 广泛应用于不确定性决策^[7]. 前景理论能够有效考虑研发项目运行效果指标效用的非线性, 是研发项目运行效果评价的一种理想方法^[8].

鉴于研发项目规模庞大, 通常把其分解为相对独立又相互依赖的多个子项目, 再把子项目分配给参研团队^[9]. 在研发项目执行过程中, 由于资源(参研团队)是有限的, 往往会发生一定程度的资源冲突^[10]. 研发任务分配是按照一定的规则把各个子项目(活动)合理分配给各个参研团队, 使得整个研发项目的运行效果最优^[11]. 研发任务分配问题通常是多目标优化问题, 可通过多目标进化算法求解^[12]. 在研发任务分配问题数学模型构建过程中, 通常把资源(参研团队)限制、依赖关系、逻辑顺序等作为约束条件, 以工期最短、成本最小、风险最低、鲁棒性最高等作为目标函数^{[13, 14]}. 基于NSGA-II、MOEA/D、粒子群算法、蚁群算法等多目标进化算法进行优化求解^[15-18].

综上, 多位学者围绕研发任务分配方案评价与优化进行了深入研究. 但是, 鲜有文献考虑参研团队能力的不确定性、研发项目运行效果指标的效用的非线性等问题. 本文综合考虑研发项目的多重不确定性因素, 构建研发项目运行过程仿真模型; 考虑决策者的心理因素, 结合仿真模型和前景理论评价研发任务分配方案; 在此基础上, 以前景价值作为适应度评价指标, 基于NSGA-III构建研发任务分配优化算法.

本文有效结合仿真、前景理论、智能进化算法, 系统构建研发任务分配方案评价与优化方法. 该方法能够准确估计不同任务分配方案下研发项目的运行效果; 在评价过程中考虑决策者的心理因素, 更符合决策者的实际决策过程; 集成多种理论方法构建优化算法, 能够搜寻到更满意的研发任务分配方案. 通过优化研发任务分配方案, 把各个子任务合理分配给各个参研团队, 减少研发项目运行过程中的返工迭代和团队占用冲突, 缩短研发工期、降低研发成本.

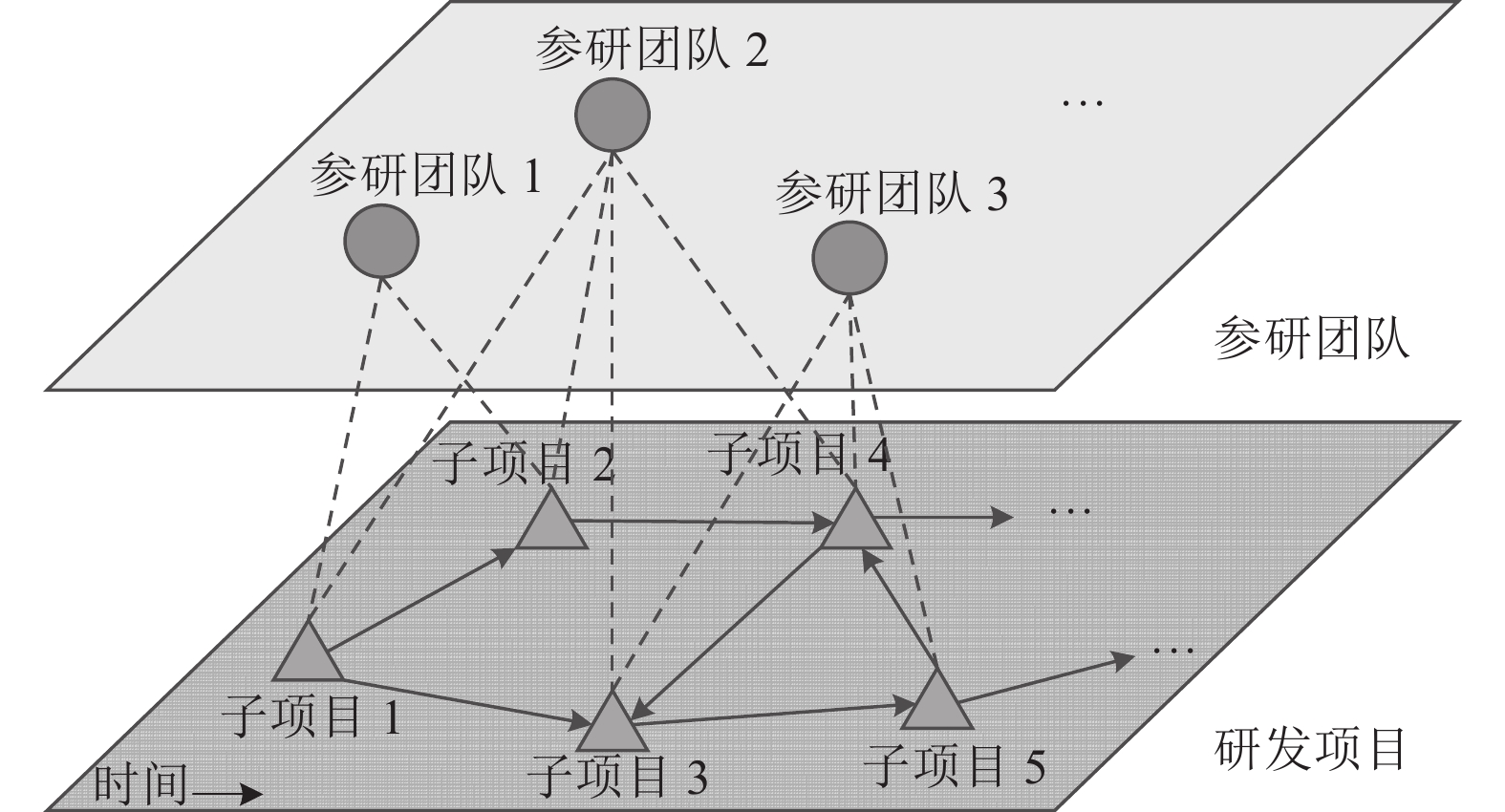
1 问题描述

随着产品越来越复杂, 产品研发项目规模越来越大, 通常把整个研发项目分解为若干个子项目, 再把研发任务分配给多个参研团队, 由多个参研团队协同研发. 研发项目与参研团队之间的关系如图1所示.

多个参研团队有能力完成某个子项目, 某个参研团队可以完成多个子项目, 但一个子项目只能由一个参研团队承担. 受多种因素的影响, 不同团队完成同一子项目所需的工期、成本不同, 同一团队完成同一子项目所需的工期、成本具有随机性. 本文主要研究在考虑多种不确定性因素的情形下, 如何把研发任务合理分配给各个参研团队, 使得研发项目工期最短、成本最小.

本文研究问题满足以下几个假设.

1) 不同团队完成同一子项目所需的时间、成本等不同.

2) 同一团队完成同一子项目所需的时间、成本等存在一定的随机性.

3) 可能会有多个团队都有能力完成某个子项目, 但一个子项目只能分配给一个团队.

4) 一个团队可以承担多个子项目, 但同一时刻只能执行一个子项目.

5) 研发项目执行过程会存在随机返工、随机重叠等不确定性因素.

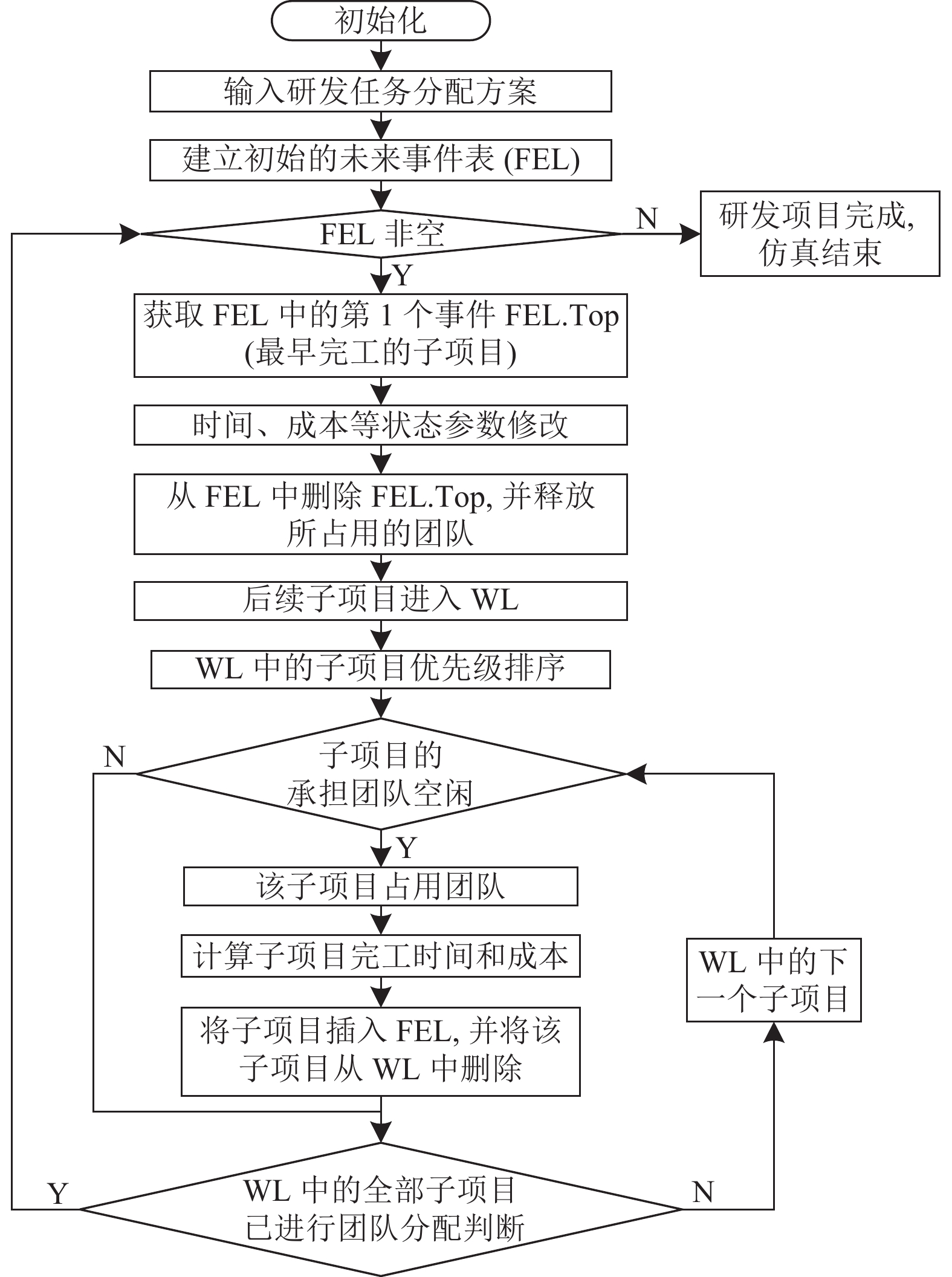
2 研发任务分配方案评价 2.1 研发项目运行过程仿真模型构建

研发项目运行过程具有不确定性, 可通过仿真估计其运行效果. 基于离散事件扫描法构建研发项目运行过程仿真模型, 仿真流程如图2所示.

仿真输入为研发任务分配方案, 输出为研发项目的工期、成本等运行效果指标. 初始化参数包括: 各参研团队有能力完成的子项目、参研团队完成子项目所需的工期和成本等指标、研发项目DSM、返工参数、重叠参数等. 子项目的状态包括前序子项目未完工导致的不能执行、排队等待、初次执行、返工执行、完工等, 参研团队的状态包括空闲、被占用等, 子项目完工触发研发项目和参研团队状态的转变. 由于一个参研团队可承担多个子项目, 在研发项目执行过程中, 子项目之间可能会存在团队占用冲突, 导致有些子项目需要排队等待. 在仿真模型中, 设置两个列表用于存储等待执行、正在执行的子项目: 等待列表(wait list, WL)表示正在排队等待执行的子项目清单; 未来事件表(future event list, FEL)表示正在执行的子项目清单.

在仿真过程中, 首先, 把最早开始执行的子项目列入FEL, 构建初始FEL. 然后, 判断FEL是否为空: 当FEL非空时, 表明存在未完成的子项目, 扫描FEL确定下一个完工的子项目, 在子项目完工的同时, 修改FEL、子项目状态、团队状态等参数. 某个子项目完工时, 判断其后续子项目哪些可以执行, 把可以执行的子项目放入WL排队等待. 当WL中的子项目的承担团队状态为空闲时, 该子项目可以进入FEL开始执行, 该子项目的承担团队状态变为被占用, 直至该子项目完工才能释放所占用团队. 当FEL为空时, 所有子项目已完工, 整个研发项目完成.

由于研发项目运行过程具有不确定性, 仿真输出的工期、成本均会在一定范围内波动, 采用多次仿真输出的平均值作为研发项目的运行效果评估指标值.

2.2 基于前景理论的研发项目运行效果评价

决策者通常会根据研发项目完成所需的工期、成本等指标评价任务分配方案. 对于决策者来说, 研发工期、研发成本大小与其效用之间的关系是非线性的. 为更好地描述研发工期、研发成本的效用, 本文基于前景理论计算研发工期、研发成本的前景价值, 通过前景价值评价研发任务分配方案.

2.2.1 变量和集合的表示

本文所构建的前景理论模型的参数主要包括:

$ DTP = \left\{ {DT{P_1}, DT{P_2}, \cdots , DT{P_m}} \right\} $ : 研发任务分配方案集合. 其中, $ DT{P_i} $ 为第i个研发任务分配方案, $ i \in M, M = \left\{ {1, 2, \cdots , m} \right\} $ .

$ C = \left\{ {{C_1}, {C_2}, \cdots , {C_n}} \right\} $ : 研发任务分配方案评价指标集合. 其中, $ {C_j} $ 为第j个评价指标, $j \in N,\; N = \left\{ {1, 2, \cdots , n} \right\}$ . 评价指标分为两类: 效益型指标 $ {N_1} $ , 该类指标取值越大, 分配方案越优; 成本型指标 $ {N_2} $ , 该类指标取值越小, 分配方案越优. 本文所构建模型中用到的工期、成本等指标均为成本型指标.

$ \omega = \left\{ {{\omega _1}, {\omega _2}, \cdots , {\omega _n}} \right\} $ : 评价指标权重向量. 其中, $ {\omega _j} $ 为任务分配方案评价指标 $ {C_j} $ 的权重, $ j \in N $ , 且满足 $ {\omega _j} \geqslant 0 $ , $\displaystyle \sum\nolimits_{j = 1}^n {{\omega _j}} = 1 $ .

$ D = {\left[ {{d_{ij}}} \right]_{m \times n}} $ : 研发任务分配方案效果评价矩阵. 其中, $ {d_{ij}} $ 为第i个任务分配方案的第j个评价指标值.

$ R = \left\{ {{r_1}, {r_2}, \cdots , {r_n}} \right\} $ : 研发任务分配方案评价指标的期望水平向量, $ j \in N $ . $ {r_j} $ 为评价指标j的期望水平.

2.2.2 任务分配方案评价

将任务分配方案评价指标期望水平 $ {r_j} $ 作为参照点, 分别计算各个方案的各个评价指标的损益值 $ \varphi \left( {{d_{ij}}} \right) $ , 计算公式为:

$ \varphi \left( {{d_{ij}}} \right) = \left\{ {\begin{array}{*{20}{l}} {{d_{ij}} - {r_j}},&{i \in M, j \in {N_1}} \\ {{r_j} - {d_{ij}}},&{i \in M, j \in {N_2}} \end{array}} \right. $

(1)

根据各任务分配方案的各个指标的损益值计算对应的前景价值 $ {V_{ij}} $ , 计算公式为:

$ {V_{ij}} = \left\{ {\begin{array}{*{20}{l}} {{{\left( {\varphi \left( {{d_{ij}}} \right)} \right)}^\alpha }},&{\varphi \left( {{d_{ij}}} \right) \geqslant 0} \\ { - \theta {{\left( { - \varphi \left( {{d_{ij}}} \right)} \right)}^\beta }},&{\varphi \left( {{d_{ij}}} \right) < 0} \end{array}} \right. $

(2)

其中, $ \alpha $ 和 $ \;\beta $ 分别为面对“收益”和“损失”时的风险态度系数, $ \alpha , \beta \in \left( {0, 1} \right) $ ; $ \theta $ 为损失规避系数, $ \theta $ 越大, 表明决策者对“损失”越敏感.

为消除前景价值为不同量纲的影响, 对前景价值进行归一化, 归一化公式为:

$ \begin{array}{*{20}{c}} {{Z_{ij}} = \dfrac{{{V_{ij}}}}{{{V_{\max j}}}}, }&{i \in M, j \in N} \end{array} $

(3)

其中,

$ \begin{array}{*{20}{c}} {{V_{\max j}}{\text{ = }}\mathop {\max }\limits_{i \in M} \left\{ {\left| {{V_{ij}}} \right|} \right\}, }&{j \in N} \end{array} $

(4)

最后, 计算各任务分配方案的综合前景值 $ {U_i} $ , 计算公式为:

$ \begin{array}{*{20}{c}} {{U_i} = \displaystyle\sum\limits_{j = 1}^n {{\omega _j}{Z_{ij}}} , }&{i \in M, j \in N} \end{array} $

(5)

3 研发任务分配优化算法构建 3.1 研发任务分配优化算法框架

研发任务分配方案优化为多目标优化问题, 搜寻最优解的难度大. NSGA-III把种群个体关联各个均匀分布的参考点, 进一步筛选子代、产生子代种群, 保证种群个体的多样性, 能够较好地解决多目标优化问题. 结合优化问题的特点和算法的适用情形, 本文基于NSGA-III构建研发任务分配优化算法, 如算法1所示.

算法1. 基于NSGA-III的研发任务分配优化算法

输入: 迭代次数、种群规模、交叉和变异概率等参数.

输出: 研发任务分配方案.

生成研发任务分配初始方案, 种群初始化

通过仿真获得各任务分配方案的项目运行效果指标

计算各个任务分配方案的前景价值

for $\scriptstyle t = 1 $ to $\scriptstyle MaxIt $ do

　　通过交叉产生子代: $\scriptstyle {P_c} $

　　通过变异产生子代: $\scriptstyle {P_m} $

　　当前种群 $\scriptstyle {P_t} $ 与子代种群合并: $\scriptstyle {R_t} = {P_t} \cup {P_c} \cup {P_m} $

　　通过仿真输出任务分配方案的运行效果指标

　　计算各个任务分配方案的前景价值

　　对任务分配方案集合进行非支配排序

　　选择任务分配方案构建新种群

end for

3.2 算法的关键问题实现

基于NSGA-III的任务分配优化算法的实现过程中, 主要解决编码规则、初始种群的生成、交叉和变异操作、适应度评价等关键问题.

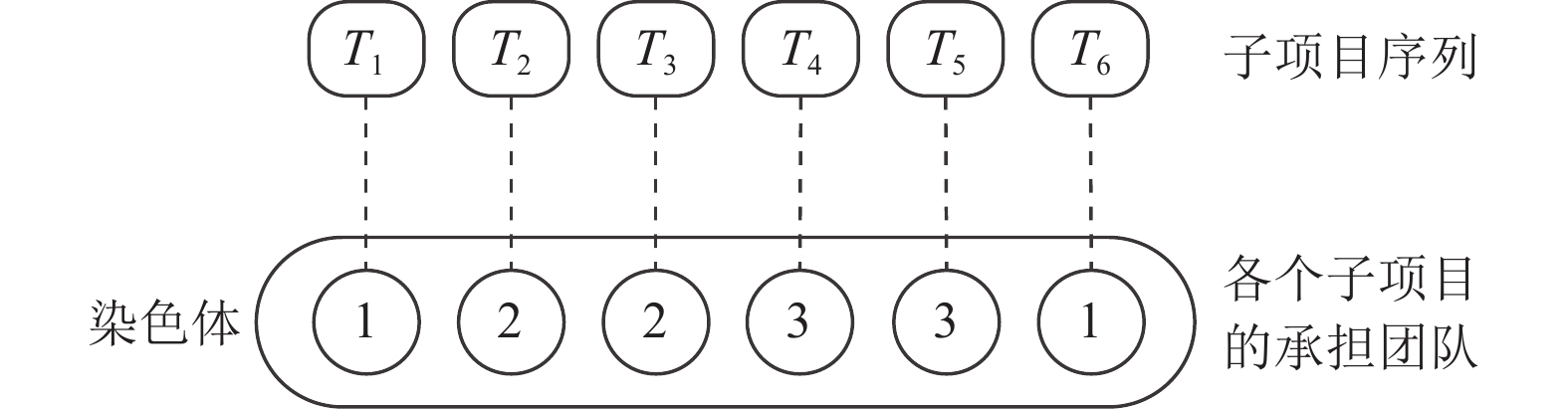
3.2.1 编码规则

研发任务分配方案编码由各个子项目的承担团队编号组成, 按照子项目编号顺序依次排列. 假设研发项目包含6个子项目、由3个参研团队协同完成, 染色体编码规则示意图如图3所示.

3.2.2 初始种群的生成

假设研发项目包括n个子项目, 由m个参研团队协同完成, 种群规模为PN. 初始种群生成方法为: 生成PN个长度为n、取值为 $ \left[ {1, m} \right] $ 之间的随机整数序列, 每个序列为一条染色体, 对应一个任务分配方案, 序列中的数字表示对应位置子项目的承担团队编号.

3.2.3 交叉和变异操作

通过交叉和变异操作, 改变染色体上的基因顺序, 形成新的染色体.

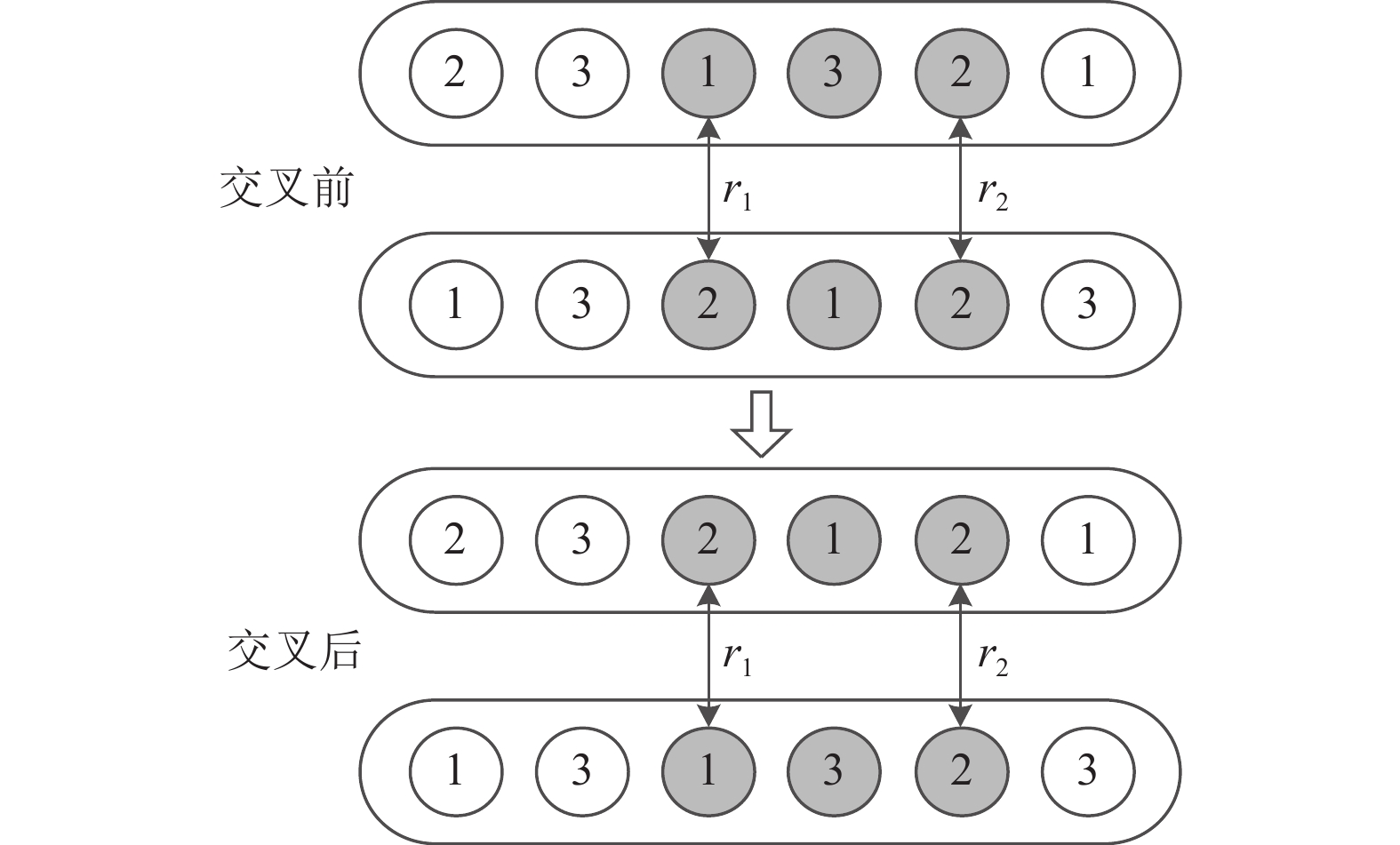
染色体交叉操作过程如图4所示: 首先, 从父代种群中随机选择两个个体作为父代染色体. 然后, 在 $ \left[ {1, n} \right] $ 区间内随机生成两个正整数 $ {r_1} $ 、 $ {r_2} $ , 表示父代染色体上的两个基因位置, 把 $ {r_1} $ 与 $ {r_2} $ 之间的基因作为交叉基因段. 最后, 交换选中的两个父代染色体的交叉基因段, 得到两个新染色体.

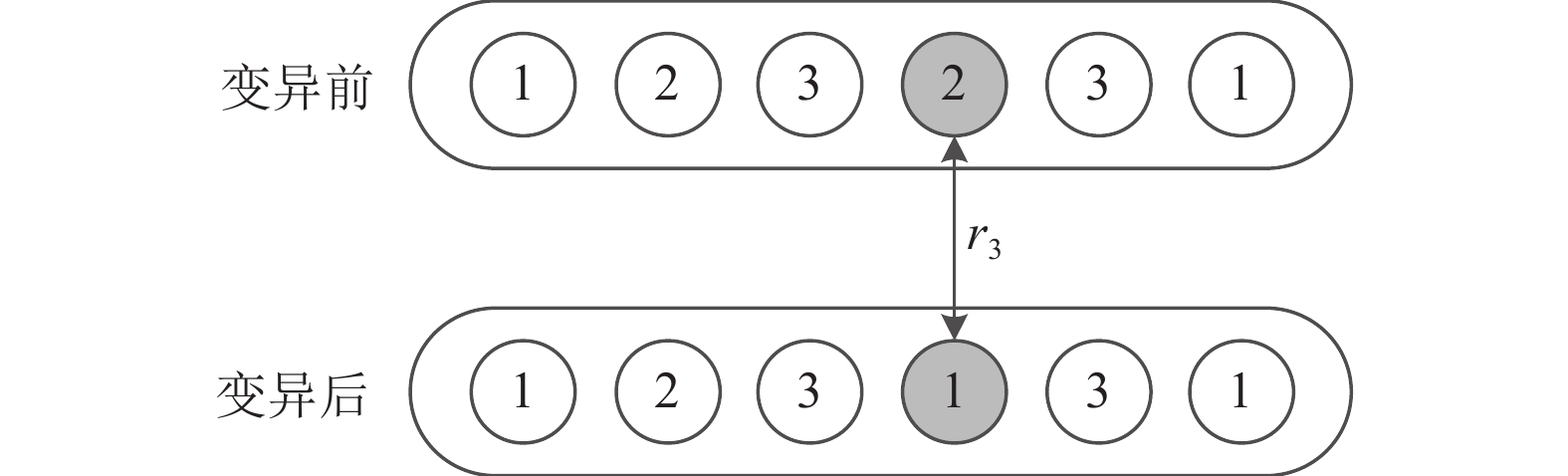
染色体变异操作过程如图5所示: 首先, 在 $ \left[ {1, n} \right] $ 区间内随机生成一个正整数 $ {r_3} $ , 表示父代染色体上的一个基因位置, 令其对应的承担团队编号为 $ {C_{{r_3}}} $ . 然后, 在集合 $ \left\{ {1, 2, \cdots , m} \right\} $ 中生成一个不等于 $ {C_{{r_3}}} $ 的整数 $ C{N_{{r_3}}} $ , 把 $ C{N_{{r_3}}} $ 作为染色体 $ {r_3} $ 位置变异后的基因.

3.2.4 适应度评价

以研发工期和研发成本的前景价值最大作为研发任务分配问题的目标函数, 即: $ \max \left( {{Z_{i1}}, {Z_{i2}}} \right) $ . 其中: $ {Z_{i1}} $ 为研发任务分配方案i情形下研发工期的前景价值, $ {Z_{i2}} $ 为研发任务分配方案i情形下研发成本的前景价值. 结合仿真输出和前景理论对各个任务分配方案进行适应度评价: 首先, 基于仿真输出某种任务分配方案下研发项目完成所需的工期和成本; 然后, 基于前景理论计算研发工期、研发成本的前景价值, 以前景价值作为研发任务分配方案的适应度评价指标.

4 算例研究 4.1 算例介绍

为验证本文模型和算法的有效性, 以某无人机研发任务分配问题为例进行算例研究. 该无人机研发项目共包含14个子项目, 由A、B、C三个参研团队协同完成, 各个团队的人员组织结构、技术结构、研发经验等不同, 完成子项目所需的工期、成本不同. 结合相关历史数据和专家经验, 估计得到参研团队完成各个子项目所需的工期、成本如表1所示, “—”表示所在格行对应的子项目不能由列对应的参研团队完成. 参研团队完成子项目所需的工期、成本均服从三角分布, 其中D_o、D_m、D_p分别表示最乐观工期、最可能工期、最悲观工期; C_o、C_m、C_p分别表示最乐观成本、最可能成本、最悲观成本.

4.2 优化结果分析

使用Matlab编程实现研发项目仿真模型、前景价值计算和NSGA-III算法. 优化算法的主要参数设置: 每种任务分配方案下的研发项目运行过程仿真次数为200次; 种群规模为100; 交叉概率为0.8; 变异概率为0.2; 迭代次数为200次. 运行优化算法得到满意的Pareto前沿, 把对应的任务分配方案下研发项目运行过程仿真次数增加至5 000次, 取新的Pareto解集与凸集的交集作为优化结果.

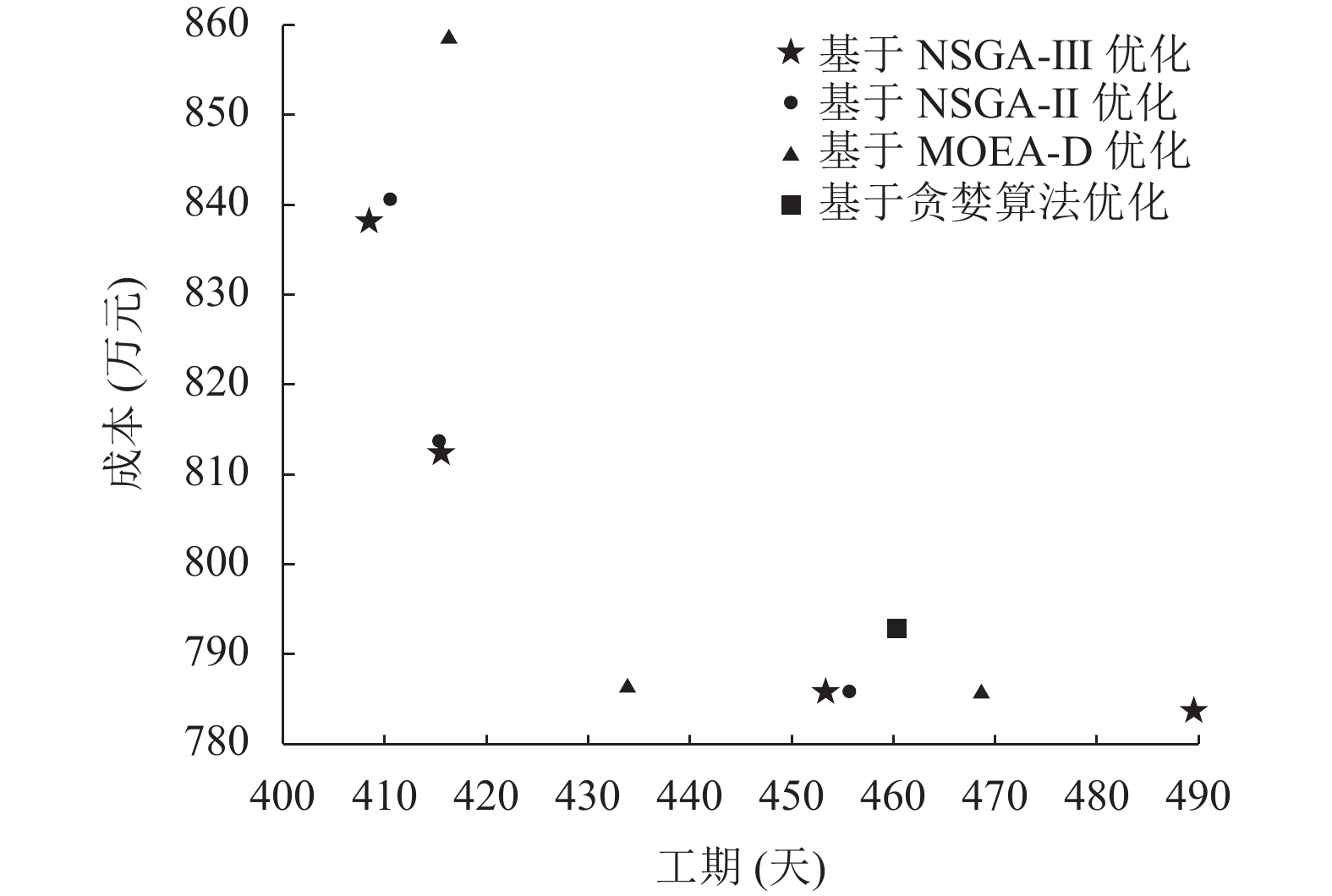
为对比算法的优化效果, 构建基于NSGA-II的研发任务分配优化算法、基于MOEA-D的研发任务分配优化算法、基于贪婪算法的研发任务分配优化算法. 4种算法优化得到的研发任务分配方案(数据代表按照顺序排列的给各个子项目分配的研发团队编号)及其对应的工期、成本如表2所示. 优化得到的任务分配方案情形下完成研发项目所需的工期、成本如图6所示. 图中, 五角星、圆形、三角形和正方形分别表示基于NSGA-III、NSGA-II、MOEA-D和贪婪算法优化得到的任务分配方案下完成研发项目所需的工期和成本.

比较不同算法优化得到的研发任务分配方案: 基于NSGA-III、基于NSGA-II和基于MOEA-D算法优化得到的研发任务分配方案中, 均存在可支配基于贪婪算法优化得到的研发任务分配方案. 可见, 在进行研发任务分配优化时, NSGA-III、NSGA-II和MOEA-D算法的优化效果均优于贪婪算法. 从优化后到的研发工期、研发成本等指标来看, 基于NSGA-III优化得到的任务分配方案明显优于基于NSGA-II优化得到的任务分配方案, 略优于基于MOEA-D优化得到的任务分配方案; 从算法的全局搜索能力来看, 基于NSGA-III能够优化得到对应工期、成本更大范围的任务分配方案, 明显优于基于NSGA-II和基于MOEA-D算法优化得到的任务分配方案. 可见, 通过本文所构建方法能够有效优化研发任务分配方案.

5 结论

本文考虑研发项目的多种不确定性因素, 基于仿真估计不同任务分配方案下的研发项目运行效果指标; 基于前景理论评价研发任务分配方案; 基于NSGA-III构建研发任务分配优化算法. 有机结合仿真模型、前景理论、智能进化算法构建研发任务分配方案评价与优化的系统方法. 本文主要做了以下工作.

1) 构建基于仿真模型和前景理论相结合的研发任务分配方案评价方法. 综合考虑参研团队能力的不确定性、研发项目运行过程的不确定性等多种不确定性因素, 构建研发项目运行过程仿真模型. 在此基础上, 根据仿真输出的研发项目运行效果指标, 考虑决策者的心理因素, 基于前景理论评价研发任务分配方案. 该评价方法能够更准确反映不同任务分配方案下研发项目的实际运行效果, 更契合决策者的实际评价、决策过程.

2) 构建研发任务分配优化算法. 根据研发任务分配问题的特点和算法的适用性, 基于NSGA-III构建研发任务分配优化算法. 通过与基于NSGA-II、基于MOEA-D、基于贪婪算法的研发任务分配优化算法比较表明, 基于NSGA-III构建的优化算法的全局搜索能力更强, 能够搜寻到更满意的研发任务分配方案.