伴随着工业互联网的发展, 工业互联网终端设备的数量以及这些设备产生的数据量都在激增^[1]. 但由于边缘终端设备的计算能力和存储能力有限^[2], 这些与日俱增的设备数据在边缘终端设备中的处理效率并不理想^[3], 同时在传统云计算处理模式下, 海量的数据传输会对网络带宽造成极大的压力^[4], 并且工业设备的许多数据都有非常短的时效性^[5], 对处理时间也有极高要求, 一旦处理延迟或断网, 就会失去决策的意义, 甚至造成重大生产事故^[6]. 工业互联网的发展要求边缘计算(mobile edge computing, MEC)来实现可靠的低延时实时响应和实时处理数据^[7], 工业生产的特殊性对边缘计算提出了新的要求: 由于工业设备的种类繁多, 产生应对异构边缘计算资源的分配等方面的艰巨挑战. 其次是工业生产要求实时、可靠的计算能力. 工业控制的部分场景要求计算处理的时延极低, 因此任务之间存在优先级关系, 边缘计算要先处理优先级高的任务满足工业生产实时性要求, 这对低优先级任务的处理带来很大挑战^[8-10].

边缘计算作为解决上述问题的一种有效技术, 通过合理的任务调度与资源分配, 能够缓解计算资源的紧张问题^[11]. 本文提出一种基于深度学习的动态优先级任务调度算法(dynamic priority task scheduling algorithm based on deep learning, DPTSA). 考虑到工业设备任务的实时性特征, 本方法通过动态更新任务优先级, 降低系统任务的等待时间, 有效提高系统任务完成率.

1 系统模型与优化问题

本节首先描述工业互联网场景下边缘计算的系统模型, 具体场景图如图1所示, 然后对该系统场景建立数学模型, 最后提出本文的优化问题.

1.1 系统场景

本文考虑工业互联网结合MEC服务器的应用场景, 主要架构分为3部分: 边缘服务器、边缘网关和设备终端.

边缘网关作为MEC系统调度中心, 其感知终端设备的请求服务和边缘侧所有边缘服务器的资源并负责处理终端设备的请求与任务的调度^[12]. 边缘网关与终端设备通过无线信道进行数据传输, 其中为每个设备分配无线信道带宽为w.

设定n台边缘服务器, 其具有不同的计算能力. 为终端设备提供任务卸载服务, 根据边缘网关任务调度处理来自终端设备的任务.

在该模型中, 任务集合定义为: $ O = ({O_1}, {O_2}, \cdots, {O_N}) $ , 其中, 每个任务都由它的任务数据量、任务优先级以及任务截止日期来表示.

设定m个终端设备, 其任务信息表示为 ${s_i} = \{ {o_j}|j \in {{O\} }}$ , 任务可以在本地处理或卸载至边缘服务器处理.

1.2 计算模型

终端设备通过无线信道与边缘网关进行通信, 我们假设在稳定的环境中进行数据传输, 每个设备的信道带宽为w, 根据香农公式可以得到数据的传输速率为:

$ r = w{\log _2}\left(1 + \frac{{Ph}}{{{N_0}}}\;\right)\;\; $

(1)

其中, P表示信号的发射功率, h表示信道增益, $ {N_0} $ 表示高斯白噪声功率.

用 $ {x_i} $ ={0, 1} 表示任务卸载决策, 当 $ {x_i} $ =0时任务在本地执行, $ {x_i} $ =1时任务卸载至边缘服务器执行.

当任务卸载处理( $ {x_i} = 1 $ )时, 首先需要通过无线信道, 将任务数据传输到边缘服务器, $ {n_0} $ 表示通信开销, 任务传输所需要的时延可以表示为:

$ t_i^{{\rm{trans}}} = \frac{{{n_0}{B_i}}}{r} $

(2)

当任务传输到边缘服务器后, 对任务进行处理, 任务处理所需要的时延可以表示为:

$ t_i^{e, {\rm{proc}}} = \frac{{\phi {B_i}}}{{{f_i}{f^e}}} $

(3)

其中, $ \phi $ 表示处理单位数据所需要的CPU周期数, $ {f_i} $ 表示任务所分配到的计算资源, $ {f^e} $ 表示边缘服务器能够提供的CPU频率. 因此任务卸载处理所需要的时延可以表示为:

$ t_i^e = t_i^{{\rm{trans}}} + t_i^{e, {\rm{proc}}} $

(4)

任务卸载处理所需要的成本包括传输成本和计算成本, 即:

$ c_i^e = {k_e}t_i^{e, {\rm{proc}}}{({f_i}{f^e})^3} + t_i^{{\rm{trans}}}p $

(5)

其中, $ {k_e} $ 表示边缘服务器的能效系数, p表示传输数据单位时间消耗的成本.

当任务在本地处理( $ {x_i} = 0 $ )时, 则:

$ t_i^{l, {\rm{proc}}} = \frac{{\phi {B_i}}}{{{f_i}{f^l}}} $

(6)

任务本地处理所需要的时延可以表示为:

$ t_i^l = t_i^{l, {\rm{proc}}} $

(7)

任务本地处理所需要的成本可以表示为:

$ c_i^l = {k_l}t_i^{l, {\rm{proc}}}{({f_i}{f^l})^3} $

(8)

对于本地计算, 其成本仅由处理数据产生, $ {k_l} $ 表示本地处理的能效系数.

综上, 任务i处理所需要的时延可以表示为:

$ {t_i} = t_i^{{\rm{wait}}} + {x_i}t_i^e + (1 - {x_i})t_i^l $

(9)

任务i处理所需要的成本可以表示为:

$ {{{c}}_i} = {x_i}{{c}}_i^e + (1 - {x_i})c_i^l $

(10)

我们定义第i个任务优先级为:

$ p_i^{{\rm{new}}} = \gamma {p_i} + \varepsilon \frac{1}{{({{\rm{e}}^{({t^{{\rm{dead}}}} - {t^{{\rm{wait}}}})}} - 1)}} + \lambda ({{\rm{e}}^{{t^{{\rm{wait}}}}}} - 1) $

(11)

任务的优先级受到任务初始优先级、任务截止时间、任务等待时间的影响^[13]. 我们定义第2项描述任务的迫切度, 任务等待时间保证任务不会长时间等待, 任务的优先级与任务初始优先级和任务等待时间成正比, 与任务的截止时间成反比; 在任务优先级约束下, 初始任务优先级高的任务的任务优先于其他任务, 当任务在时刻t进入任务队列时其任务优先级权重值最小, 在到达截止期时任务优先级达到最高.

1.3 优化问题

基于上述计算模型, 本文建立系统成本和任务处理时延最小化问题, 通过优化该问题解决任务卸载决策与资源分配问题. 优化问题可以表述为:

$\left\{ \begin{split} &\mathop {\min }\limits_{\{ {x_i}, {f_i}\} } \sum\limits_{i = 1}^M {[\alpha } {({x_i}{{c}}_i^e + (1 - {x_i})c_i^l)} + \beta {(t_i^{{\rm{wait}}} + {x_i}t_i^e + (1 - {x_i})t_i^l)}]\\ &{\rm{s.t.}}\; {x_i} \in \{ 0, 1\}, 0 \lt {f_i} \leqslant 1 \end{split}\right. $

(12)

在优化问题约束中, $\alpha 、\beta$ 分别表示成本和时延在优化问题中的权重, 任务卸载决策 $ {x_i} $ 为二元决策, 当任务i卸载决策为1时, 由于边缘服务器的数量为n, 我们在第2节中详细讨论任务卸载到哪一边缘服务器, 任务分配计算资源 $ {f_i} $ 满足大于0小于等于1, 即任务处理设备CPU频率的百分比, 其既影响任务计算时间, 又影响系统成本, 接下来, 我们对优化问题进行求解.

2 基于深度学习的动态优先级任务调度算法

针对问题式(12), 我们提出了一个基于深度学习的算法框架, 通过基于强化学习的思想, 对任务卸载与资源分配问题求解, 我们还提出动态优先级调度算法, 来缓解任务等待时间过长的问题.

如图2所示, DPTSA算法由5个模块组成: 生成模块接收任务信息S, 并输出一组决策, 变异模块根据生成模块输出的决策, 通过交叉、变异操作, 生成k个候选决策, 评价模块评估并选择一个最好的决策, 存储到经验缓冲区中, 并交由执行模块去执行, 训练模块从经验缓冲区中选择数据对生成模块网络参数进行优化.

2.1 生成模块

生成模块是一个多层全连接网络, 在开始时, 我们通过标准正态分布随机初始化该网络的参数, 生成模块以当前的任务信息 ${S_t} = \{ {s_i}|i \in {{D\} }}$ 为输入, 任务信息S包含m个设备待决策的任务信息, 输出为 $ \hat y $ , 即:

$ {\Pi _\theta }:{S_t} \mapsto {\hat y_t} = {{\{ x}}', f'\} $

(13)

其中, $ x' $ 为数量m×2的一个序列, 我们可以将 $ x' $ 前m个序列和后m个序列表示为 ${{\{ }}{{{x}}^a}, {x^e}\}$ , 那么 ${{{x}}^a} = [x_1^a, \cdots, x_m^a]$ 表示为m个设备的任务卸载决策, 由于卸载决策约束 $ {x_i} \in \{ 0, 1\} $ , 因此对于 ${{{x}}^a}$ 中的m个元素, 按以下规则量化:

$ {{x}}_i^a = \left\{ \begin{gathered} 0, \;{{x}}_i^a \leqslant 0.5 \\ 1 , \;{{x}}_i^a \gt 0.5 \\ \end{gathered} \right. $

(14)

即对于 ${{{x}}^a}$ , 神经网络输出大于0.5设置为1, 其他则为0.

$ {x^e} = [x_1^e, \cdots, x_m^e] $ 表示任务卸载边缘服务器序号, 其量化规则为:

$ {{x}}_i^e = \left\lfloor {{{x}}_i^e \times n} \right\rfloor $

(15)

其中, n表示边缘服务器的数量, 即对于 ${{{x}}^e}$ , 将其输出乘以n再向下取整. ${{f}}'$ 为数量m的一个序列, 表示为每个设备任务处理分配的计算资源.

2.2 变异模块

在神经网络做出决策的基础上, 对已编码的可行解进行交叉、变异操作^[14], 生成k个候选解.

首先根据生成模块的输出, 复制k个候选决策, 对于每个候选决策按照概率 $ {P_m} $ 对 ${{{x}}^a}$ 进行位点变异, 即若当前候选决策 ${{{x}}^a}$ 某位为0, 则通过变异操作变成了1. 对 ${{{x}}^e}$ 和 ${{f}}'$ 进行均匀性变异, 即对于 ${{{x}}^e}$ 和 ${{f}}'$ 的某位, 在其最小值与最大值之间以均匀概率随机选择一个数替代该位.

其次对所有候选决策进行均匀交叉, 即按照均匀概率抽取一些位, 每一位是否被选取是随机的, 且独立于其他位, 然后将两个候选决策被抽取位互换组成2个新候选决策.

通过变异模块产生多个候选解, 能够搜索到一些神经网络无法搜索到的解, 提高算法的运行效率.

2.3 评价模块与执行模块

对于变异模块所产生的k个候选解, 通过评价模块选择最优解. 即:

$ y = \min Critic({x_i}', {f_i}') $

(16)

对于每一个候选解, 其目标函数都可以表示为:

$ value = \mu {p_i}t_i^{{\rm{wait}}} + \alpha {c_i} + \beta {t_i} $

(17)

其中, ${p_i}t_i^{{\rm{wait}}}$ 表示任务优先级和任务等待时间的乘积, 最小化该值, 即任务优先级高的任务, 其等待时间应尽可能低, 保证高优先级任务能够尽快响应, $ \alpha {c_i} + \beta {t_i} $ 表示本文的优化目标最小化成本与时延. 因此y即所有候选解中值最小的一个解.

得到最佳候选决策后, 将该决策存入经验缓冲区中, 用于生成模块的训练, 然后利用该决策尽行任务信息更新, 首先根据式(11)更新所有任务的优先级, 然后对各个任务队列按照优先级大小进行排序, 然后按照y进行任务卸载与资源分配决策, 具体步骤如算法1所示.

算法1. 动态优先级更新算法

输入: m, n, 待决策队列wait, 传输队列trans, 处理队列proc.

输出: 任务信息 $\scriptstyle {S_t} $ .

1) i $\scriptstyle \leftarrow $ 0

2) WHILE i<m+n:

3)　 根据式(11)计算设备i所有任务优先级

4) 　对待决策队列wait[i], trans[i], proc[i]按优先级大小递减排序

5) 　IF 设备i未处理数据:

6) 　　　处理proc[i][0]

7) 　IF i<m:

8)　　 $\scriptstyle {S_i} \leftarrow {\rm{wait}}[i][0]$

9) 　　IF 设备i未传输数据:

10) 　　　传输trans[i][0]

11)　 i $\scriptstyle \leftarrow $ i+1

12) $\scriptstyle {S_t} = \{ {S_i}|0 \lt i \lt m\} $

2.4 训练模块

训练模块通过随机选取u个经验组成一个样本, 记为U, 通过U对生成模块进行训练, 其中每一个经验可以表示为 ${{\{ }}{S_i}, {y_i}\}$ , 我们使用经验做为标签, 对生成模块进行更新, 为了能获得更好的训练结果, 我们设定周期性训练生成模块, 设置经验缓冲区上限为128, 当经验数量超过64时, 随机选取数据样本训练生成模块, 然后使用Adam算法在数据样本上最小化其平均交叉熵损失函数, 即:

$ L(\theta ) = - \frac{1}{u}\sum\nolimits_{i \in U} {[{y_i}{{\log }_2}{S_i} + (1 - {y_i}){{\log }_2}} (1 - {S_i})] $

(18)

当经验缓冲区超过128时, 清空经验缓冲区, 重新收集数据样本, 以此减少训练初期积累的一些因为随机初始化网络的可行解的干扰, 提高训练效率, 训练流程如算法2所示.

算法2. DPTSA

输入:t, m, n, k, times, 经验缓冲区Memory.

输出: 策略 $ \scriptstyle {\Pi _\theta } $ .

1) 随机初始化生成模块网络参数 $\scriptstyle \theta $

2) t $\scriptstyle \leftarrow $ 0

3) WHILEt<times:

4) 　根据算法1得到当前任务信息 $ \scriptstyle {S_t} $

5) 　生成模块输出 $\scriptstyle {\Pi _\theta }:\;{S_t} \mapsto {\hat y_t}$

6) 　根据 $\scriptstyle {\hat y_t} $ 交叉、变异生成k个候选决策

7)　 $\scriptstyle y = \min Critic({x_i}', {f_i}') $

8)　 IF $\scriptstyle {\rm{Memory}} $ size>64&&t%10==0:

9) 　　 添加 $\scriptstyle ({S_t}, y) $ 到 $\scriptstyle {\rm{Memory}} $

10) 　　随机取样 $\scriptstyle \{ ({S_i}, {y_i})|i \in {\rm{Memory}}\}$ , 使用Adam算法更新 $\scriptstyle \theta $

11)　 IF Memory size>128:

12) 　　清空Memory

13)　 t $\scriptstyle \leftarrow $ t+1

2.5 任务调度算法

在本文所提深度学习框架中, 状态S是指终端设备的任务, 动作指任务调度. 设备任务包含优先级、截止时间等需求, 在训练阶段, 根据图2算法流程图, 生成模块负责根据状态S产生任务调度信息, 变异模块产生k个候选解, 评价模块选择最优解并存储, 训练模块根据规则训练生成模块; 在调度阶段, 首先根据当前状态S, 由生成模块产生任务调度信息, 然后根据算法1更新任务优先级, 最后根据任务调度信息分配任务与资源, 以得到新的状态 $ S' $ .

3 实验结果与分析

本节将对仿真实验的数据集以及实验环境和实验结果进行说明.

3.1 实验数据集

实验数据集采集于Google的Brog集群管理系统, 包含来自8个不同的Google计算集群的详细任务调度信息, 采集时间从2019年5月1日至2019年5月31日, 我们随机选择30个机器的任务调度信息组成了我们算法的实验数据集.

3.2 实验环境设置

在本实验使用的硬件设备中, CPU使用Intel Xeon Gold 6226R处理器, 其包含32个逻辑处理器. GPU使用NVIDIA Tesla V100 32 GB. 实验环境使用Python 3.7.0和PyTorch 1.8.1. 本文考虑一个多设备多边缘服务器场景, 其中设备数量为10, 边缘服务器数量为3, 网络带宽为100 MHz, 设备的CPU频率为1 GHz, 边缘服务器的CPU频率为3 GHz, $ \phi $ 设置为100, k设置为8, 训练时间设置为500, 变异概率 $ {P_m} $ 设置为0.1. 神经网络使用PyTorch构建, 采用多层全连接网络, 1个输入层、2个隐藏层和1个输出层, 隐藏层分别有256和128个神经元^[15].

为了与本实验方法进行比较, 我们选择4个算法作为基准算法.

(1) PTSA (priority task schedule algorithm): 按照固定优先级的任务调度算法.

(2) GA (greedy algorithm): 按照任务优先级高低, 以任务成本和任务处理时延最小为目标进行调度.

(3) OCO (offloading computing only): 设备任务卸载到边缘服务器处理.

(4) LCO (local computing only): 设备任务全部进行本地计算.

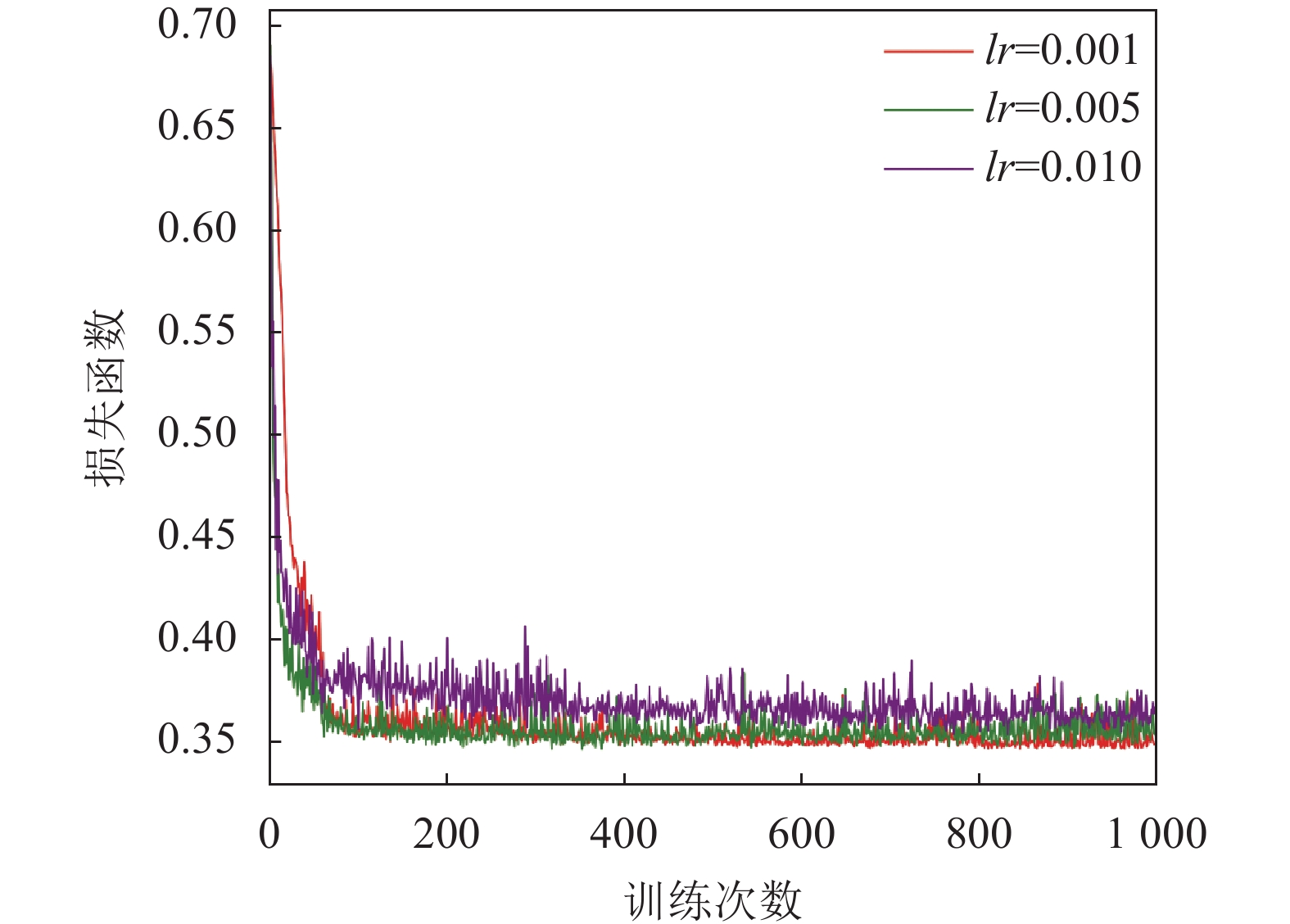
3.3 实验结果分析

首先, 我们通过实验检验DPTSA算法的收敛性, 通过分别设置神经网络学习率0.001, 0.005和0.01, 如图3所示, 不同学习率下损失函数的收敛情况.

当学习率为0.001时, 由于学习率较小, 因此损失函数下降的缓慢, 但是最终收敛到损失函数的极小值点, 在所有学习率中表现最好. 学习率为0.01时, 由于学习率较大, 训练初期波动较大, 损失函数下降速度很快, 但最后损失函数收敛到一个较高的值, 说明得到了一个次优解, 由于搜索范围较大, 最终没有收敛到全局最优. 学习率为0.005时, 由于学习率比0.001高, 收敛速度在所有学习率中最快, 并且最终收敛的损失函数最小值与学习率0.001时相差不大, 收敛到了一个较小值, 比较均衡, 以上数据表明, DPTSA算法有较好的收敛性.

然后, 如图4所示, 我们比较了不同算法下的系统成本, 实验结果表明, DPTSA和PTSA算法的系统成本远远低于另外3个基准算法, 并且OCO算法产生的系统成本是所有算法中最高的, 得益于深度学习强大的搜索能力和跳出局部最优解的能力, DPTSA算法的系统成本与PTSA算法成本基本相同, 并且略低于GA算法. 由于任务本地处理的能效系数与卸载到边缘服务器的能效系数差别大, 因此卸载到边缘服务器将产生更高的成本, 并且任务在本地处理耗费的时间远大于在边缘服务器处理的时间, 因此任务在本地处理也会有较高的成本. 动态优先级的调度方法影响了任务的执行先后顺序, 不会对任务资源分配产生影响, 因此与固定优先级的调度算法相比并不会降低成本. 以上结果验证本文所提的算法能够显著降低因为卸载策略不同而产生的系统成本.

本文所提算法通过优先级调度, 可以保证更多的任务在截止时间前完成. 图5展示了不同算法下超过截止时间的任务数量, 结果表明, PTSA算法能够长时间保证任务在截止时间前完成, 而4个基准算法随着时间增加, 超时任务的数量逐渐增加, 且LCO算法超时的任务增长速度最快. 随着时间增加, 任务的堆积, LCO算法因为本地计算资源有限的原因, 越来越多的任务因为等待而超时, 而OCO算法因为计算资源相对充足, 超时的任务明显比全部本地计算的少. 本文所提的算法根据优先级合理的调度和合理的卸载策略, 降低了任务的等待时间, 减少了任务超过截止时间的情况, 并且动态优先级保证了一些大型的任务不会因为过长的等待时间而超过截止时间, 因此DPSTA算法在保证任务在截止时间前完成方面比GA算法有更好的表现.

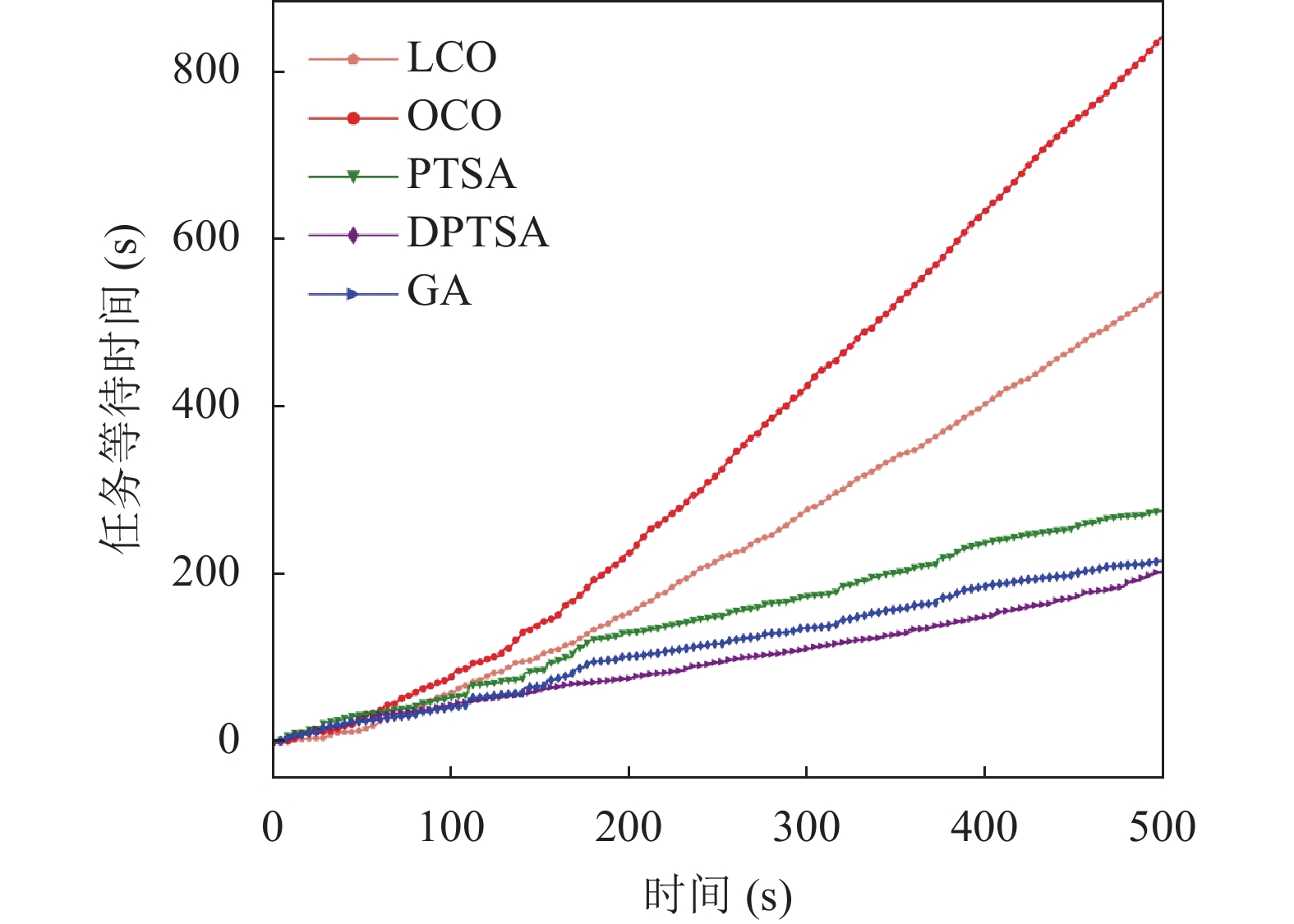
为了进一步比较所提算法在保证任务调度方面的性能, 如图6所示, 我们统计了所有任务的等待时间, 在实验的初始阶段, 任务等待时间相近似, 随着时间推移, 差距变大, 其中LCO算法任务等待时间增长速度最快, DPTSA算法增速最慢. 结果表明, 在任务等待时间方面, 本文所提算法远小于其他基准算法. DPTSA算法保证高优先级任务优先响应, 减少高优先级任务的等待时间, 并对长等待时间的任务动态提高优先级, 避免因等待时间长而超出任务截止时间, 因此其比PTSA算法和GA算法的任务等待时间要短.

综上所述, 本文所提出的DPTSA算法, 在系统成本、任务等待时间、超时任务数量等方面, 相比于其他4种对比方法, 均有一定优势, 因此该方法能够在保证系统成本前提下, 有效降低任务响应时间, 提高任务完成率.

4 结论与展望

为了提高工业互联网中设备任务的响应性能, 本文设计了一种基于深度学习的动态优先级任务调度算法DPTSA. 通过动态改变任务的优先级, 在保证系统成本的前提下, 提高任务的响应速度, 降低任务的等待时延, 平衡低优先级任务的处理减少了超时任务的数量. 本文还引入了交叉变异的思想, 通过交叉变异生成k个可行解能够扩大搜索空间, 提高深度学习的学习效率. 最后本文基于Google的Brog数据集进行了仿真实验, 验证本文算法的有效性, 并与基准算法进行比较. 实验结果表明, DPTSA能够有效降低任务的等待时延, 提高任务的完成率. 未来, 我们将会考虑更多的边缘计算环境因素, 研究异构环境下如何进行资源分配与任务调度, 在保证负载均衡的前提下, 提高边缘计算系统的资源利用率.