2. 中国科学院大学 电子电气与通信工程学院, 北京 100049
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
光学遥感图像在测绘、地球资源调查、地质灾害调查与救治、生态环境监测等领域发挥着十分重要的作用[1]. 高分辨率光学遥感图像包含了更为丰富的地物信息, 对后续目标检测、识别、解译等遥感图像高级视觉任务的分析处理精度与效率的提升具有十分重要的意义. 超分辨率 (super-resolution, SR)重建技术通过软件方式提升图像的分辨率, 能够在一定程度上规避硬件系统升级的弊端, 如成本高、研制周期长等[2], 使图像的解译能力和应用效能得到进一步增强, 具有极高的研究意义与实用价值.
Dong等[3]将卷积神经网络 (convolutional neural network, CNN)首次应用于自然图像的超分辨率重建, 提出了SRCNN (super-resolution CNN), 使用卷积神经网络进行超分辨率重建. 但是由于SRCNN中使用双三次插值的方法来放大图像, 重建效果不够理想. 因此, 在SRCNN的基础上Dong等[4]提出了改进的模型FSRCNN (fast SRCNN), 引入了反卷积层对图像进行放大, 并引入了更小卷积核和更多的卷积层, 取得了更好的效果和更快的收敛速度. Shi等[5]随后提出了ESPCN(efficient sub-pixel convolutional neural network), 采用亚像素卷积层代替反卷积层, 获得了更好的重建效果. Kim等[6]设计了包含20个卷积层的VDSR (very deep super-resolution)以获得更深层次的特征信息, 并首次将残差网络 (residual networks, ResNet)[7]引入了超分辨率重建领域, 有效解决了深度网络的梯度消失问题. Lim等[8]针对超深网络结构进一步改进, 提出了增强深度残差网络 (enhanced deep residual networks, EDSR). EDSR使用更多的卷积层提取特征, 去掉批规范化 (batch normalization, BN)层以提升效率, 采用L1范数作为损失函数, 获得了比VDSR更好的重建效果.
光学遥感图像相比自然图像, 除具有目标场景多、结构复杂、小目标密集分布的特点, 还因其远距离俯视成像的特点, 图像中的目标与背景耦合度高, 难以区分. 因此, 应用于自然图像的超分辨率重建模型需要结合光学遥感图像的上述特点进行针对性优化与验证, 才能获得适用于光学遥感图像的超分辨率重建模型, 有效提升图像的重建效果与信息提取能力. Lei等[9]基于SRCNN提出LGCNet (local-global combined network), 将网络提取的局部与全局特征联合起来进行超分辨率重建, 获得了明显优于传统浅层机器学习方法的重建效果. 李欣等[10]构建了包含4个卷积层的CNN模型, 在前3层中添加参数修正线性单元, 对局部响应归一化层进行优化, 模型在Pleiades卫星影像及AID遥感数据集上的抗过拟合能力和训练效率均有所提高. 李强等[11]基于生成对抗网络, 针对遥感图像的特点, 使用多尺度卷积级联增强全局特征, 并利用多尺度感受野模块与密集残差模块为生成网络的细节特征提取获取了更多纹理信息. 潘梦迪[12]针对重建图像缺乏细节信息的问题, 提出了一种基于密集剩余残差网络的机载遥感图像超分辨率重建模型, 密集和残差连接的引入使得信息能够在深度网络中更好的流动. 印珏泽等[13]结合对偶回归约束映射空间和通道注意力机制, 提出了基于对偶回归和残差注意力机制的图像超分辨率重建网络, 实现了较好的超分辨率重建效果. 上述研究从不同角度出发, 将视觉领域深度学习及自然图像超分辨率重建的先进技术引入光学遥感图像超分辨率重建领域, 进行了诸多有益的尝试, 使光学遥感图像超分辨率重建的研究不断深入, 取得了很大进展. 但是, 坐标注意力机制在遥感图像超分辨率领域中的应用尚不广泛, 现有模型多使用通道注意力机制, 对感受野尺度和通道内的信息关注有限.
本文针对现有光学遥感图像超分辨率重建模型对感受野尺度关注不足和对特征通道信息提取不充分的问题, 提出了一种基于多尺度特征提取和坐标注意力的光学遥感图像超分辨率重建模型. 该重建模型基于深度残差网络结构, 在网络的高频分支中设计了用于提取多尺度特征与坐标注意力的残差模块——MFCAB, 利用更深的网络层次、融合多尺度空间特征与坐标注意特征的多级残差模块, 对输入的低分辨率光学遥感图像的高频信息从空间、通道、位置等角度提取其显著性特征, 对图像的高频结构与特征进行充分发掘; 最后, 对各残差模块提取的特征进行多路径融合, 实现不同深度的MFCAB模块提取信息的有效融合.
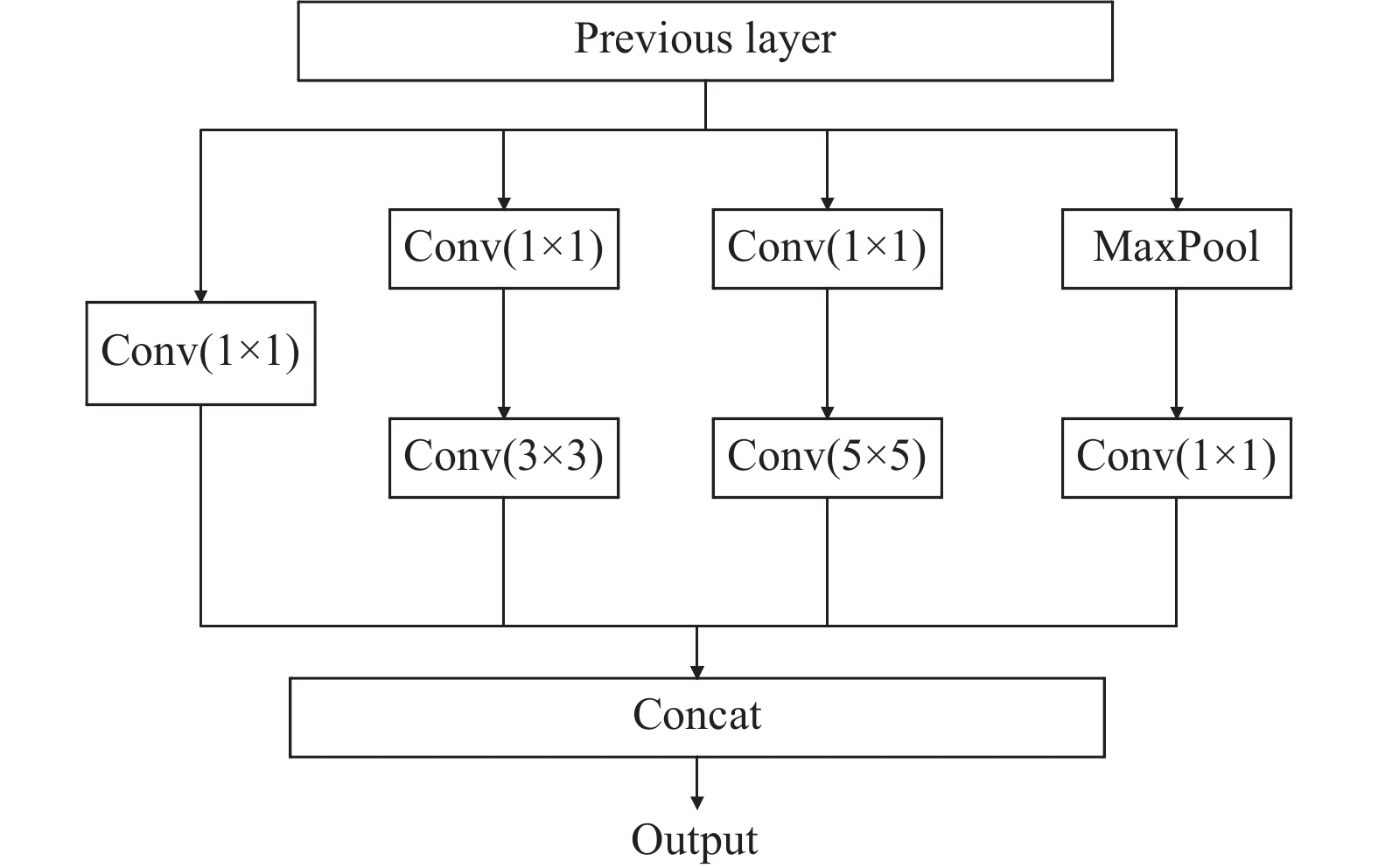
2 深度学习图像超分辨率重建特征提取 2.1 多尺度特征提取光学遥感图像具有目标尺度差异大、细节丰富、结构复杂、主体与背景区分不明显等特点, 传统超分辨率重建模型采用单一尺度的卷积核提取图像目标空间分布特征, 对图像高频结构与空间特征的发掘并不充分. 针对这一问题, 本文在残差网络设计中引入Inception结构[14], 如图1所示. Inception结构采用3个不同大小的卷积核和1个最大池化并联, 能够获得不同尺度感受野下的空间特征; 在并行的分支中, 首先通过1×1卷积进行维度调整, 然后经过不同尺度的卷积核和池化操作, 最后将提取的多尺度空间特征通过Concat操作特征融合, 有利于网络在不同深度层次中获取更完整的目标空间结构特征描述.
|
图 1 Inception结构描述 |
2.2 坐标注意力机制
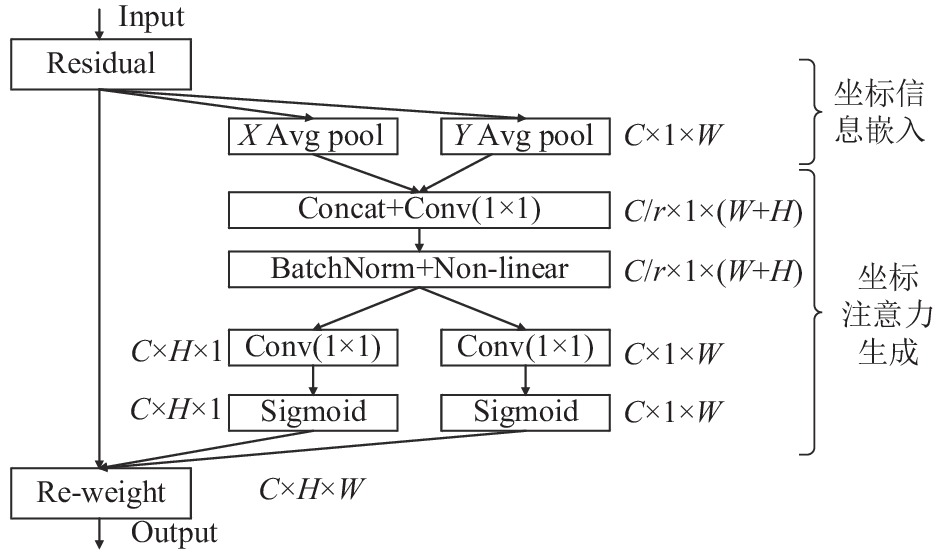
2017年, Hu等[15]将通道注意力机制加入深度残差网络中, 提出了SENet (squeeze-and-excitation networks), 通过挤压-激励 (squeeze-and-excitation, SE)操作, 把每一通道特征图通过全局池化计算为一个标量作为该特征图的权重; 而后通过全连接-Sigmoid激活-全连接层, 融合各个通道的特征信息, 根据生成的通道权重张量赋予每个通道不同的权重. SENet对每一通道特征图进行全局池化, 将其全局空间信息压缩成一个标量, 但没有考虑通道特征图内部特征之间的位置关系和方向关系, 这些信息的丢失可能会导致权重信息不准确、特征提取不充分. Hou等[16]在移动网络设计中提出了坐标注意力 (coordinate attention, CA)机制, 将同一通道特征图的位置信息嵌入到通道注意力提取过程中, 能够保留特征的方向敏感和坐标敏感信息. CA机制网络结构如图2所示, 主要分为两部分: 坐标信息嵌入和坐标注意力生成.
|
图 2 CA模块网络结构图 |
在坐标信息嵌入部分, 对于H行×W列×C通道的输入特征, CA机制对其每一通道的特征图分别在水平和垂直方向并行使用1维平均池化核进行编码操作, 可以表示为式(1). 其中, xc(h, i)和xc(j, w)分别表示第c通道特征图xc在高度为h处的水平方向特征和宽度为w处的垂直方向的特征;
| {zhc(h)=1W∑0⩽i<Wxc(h,i)zwc(w)=1H∑0⩽j<Hxc(j,w) | (1) |
在坐标注意力生成部分, CA机制首先将坐标信息嵌入输出的聚合特征图进行Concat连接, 并使用1×1卷积、BatchNorm (BN)层和非线性激活 (non-linear)层, 这一过程表示为式(2):
| f=δ(Conv1×1([Zh,Zw])) | (2) |
其中, Zh和Zw分别表示聚合的水平和垂直方向特征图, δ(·)
将中间特征f分割为两个独立的特征张量f h∈RC/r×H和f w∈RC/r×W. 然后将f h和f w分别经过1×1卷积调整维度, 从C/r个通道恢复到C个通道, 再经过Sigmoid激活函数得到水平方向和垂直方向的注意力权重gh和gw, 表示为式(3):
| {gh=σ(Conv1×1(fh))gw=σ(Conv1×1(fw)) | (3) |
其中,
最后将权重gh和gw第c通道的特征张量
| yc(i,j)=xc(i,j)×ghc(i)×gwc(j) | (4) |
本文在残差模块中引入以上坐标注意力机制, 在获取特征图通道间权重信息的同时, 还考虑特征图内与方向相关的位置信息的影响, 从而可以更准确表达特征与通道注意力, 提取更准确的高频信息.
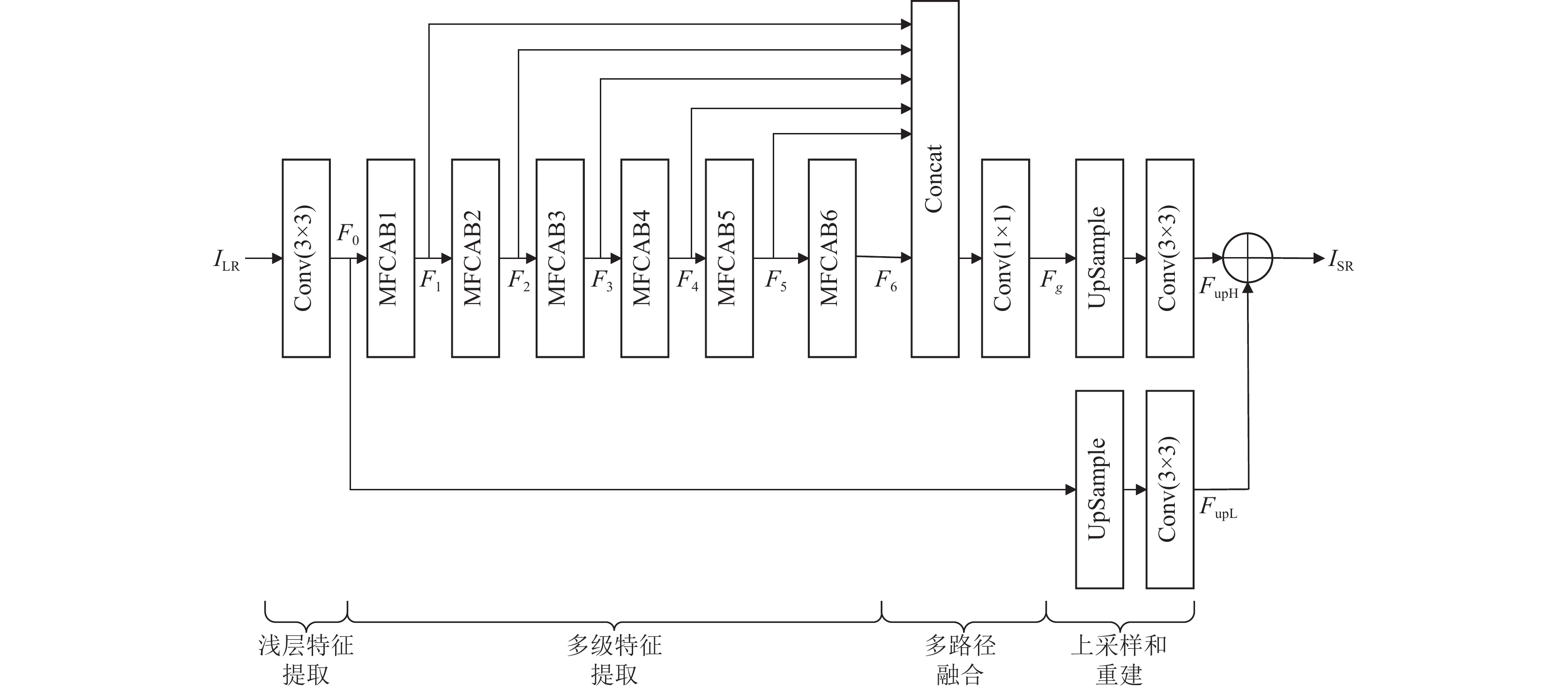
3 模型设计 3.1 网络框架本文设计的基于多尺度特征提取与坐标注意力机制的光学遥感图像超分辨率重建模型结构如图3所示. 该模型采用深度残差网络架构, 分为低频和高频两个分支, 分别对输入的低分辨率光学遥感图像ILR的低频信息与高频结构特征进行发掘与重构, 最后联合两路分支输出高分辨率重建图像ISR. 其中, 低频分支包含2个部分: 浅层特征提取、上采样与重建; 高频分支包含4个部分: 浅层特征提取、多级特征提取、多路径融合、上采样与重建.
|
图 3 基于多尺度特征提取与坐标注意力机制的光学遥感图像超分辨率重建模型框架 |
3.2 浅层特征提取
浅层特征提取将输入图像ILR经过一个卷积层, 通过卷积生成特征图F0. 该过程可以表示为式(5). 其中, Conv3×3(·)代表一个3×3的卷积层.
| F0=Conv3×3(ILR) | (5) |
光学遥感图像内容复杂且细节多, 为了更好地提取图像中的细节和高频特征信息, 本文基于EDSR的残差模块设计, 在模型高频分支设计了6个级联的多尺度特征提取和坐标注意力模块MFCAB, 用于对高频特征信息进行多级特征提取.
设模型中第x (x=1, 2, …, 6)个MFCAB的输出为Fx, 表示为:
| Fx=MFCABx(⋯MFCAB1(F0)⋯) | (6) |
其中, MFCABx(·)代表第x个MFCAB模块的提取操作.
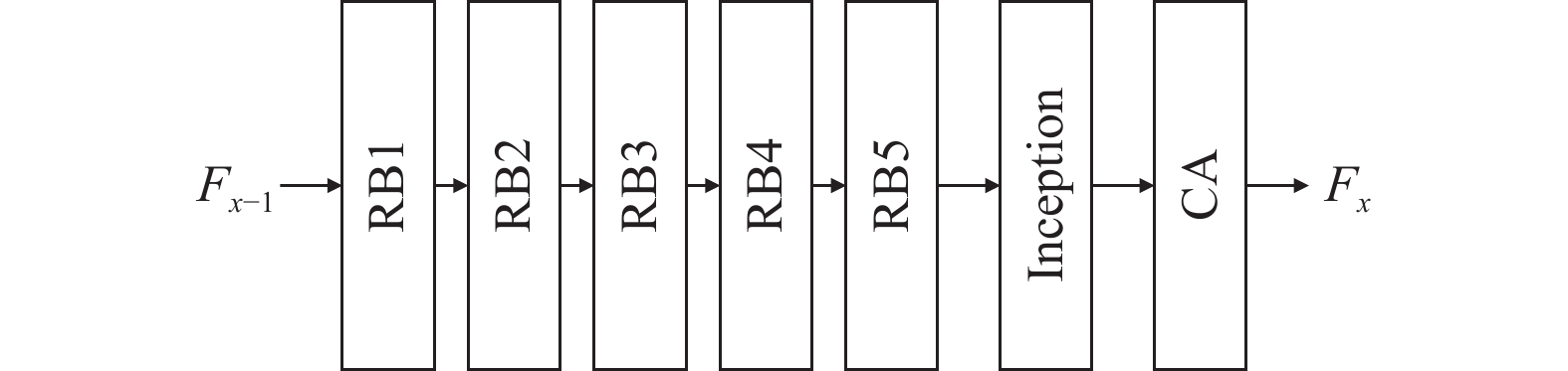
MFCAB模块包含5个残差子模块 (residual block, RB)、1个Inception子模块和1个CA子模块, 结构如图4所示.
|
图 4 MFCAB模块结构图 |
对于进入主网络高频分支的MFCAB模块的高频特征, 首先经过5个RB子模块进行特征提取, 然后经过Inception子模块进行多尺度空间特征提取与整合, 最后进入CA子模块, 获取包含特征位置信息的通道权重. 该部分的操作表示为:
| Fx=MFCABx(Fx−1)=A(RB5(⋯RB1(Fx−1)⋯)) | (7) |
其中, RBi(·)代表经过第i (i=1, 2, …, 5)个RB子模块, Fx–1和Fx分别代表第x个MFCAB模块的输入和输出, A(·)代表经过Inception和CA子模块操作.
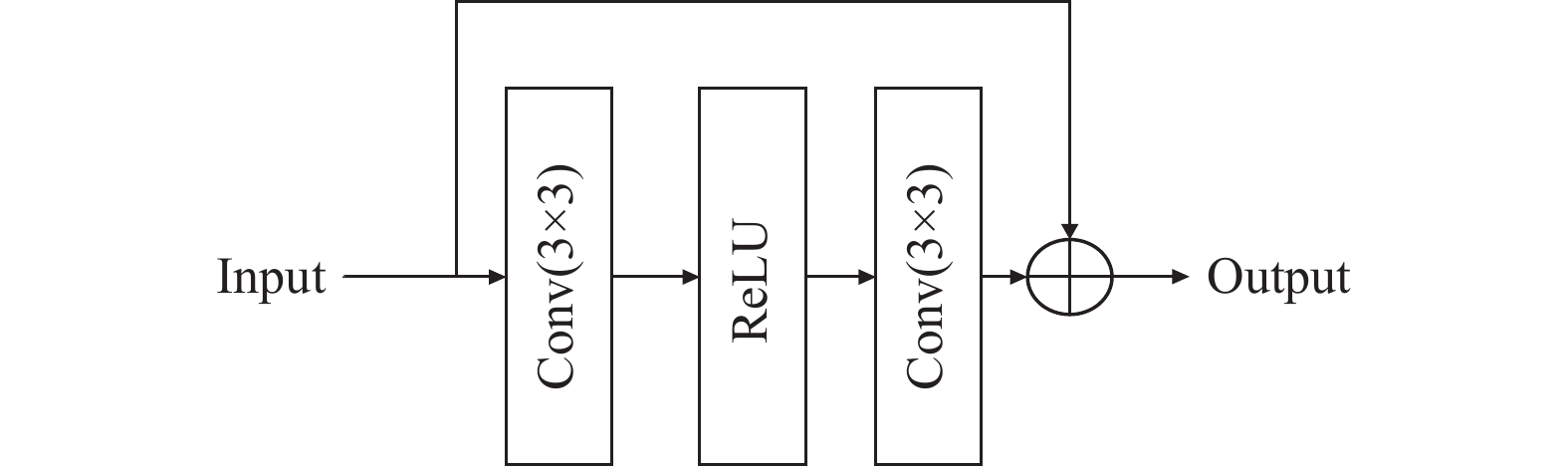
MFCAB中的RB子模块由1个卷积层、1个非线性激活层、1个卷积层组成, 输入和输出有一条残差连接, RB子模块结构如图5所示.
|
图 5 RB模块结构图 |
在Inception子模块中(如图1), 特征图在并行的分支中经过不同尺度的卷积核或池化操作提取多尺度空间特征, 最后通过Concat操作进行特征融合. 在CA子模块中, 首先进行坐标信息嵌入, 使用1维平均池化核分别沿垂直和水平方向将输入特征聚合为两个单独的方向感知特征张量; 然后进行坐标注意力生成, 将提取出的两个张量进行Concat连接, 再经过BN层和非线性激活层, 最后将生成的张量分割为横纵方向的张量并展开, 为输入特征图的对应位置添加注意力权重.
本文CA模块核心伪代码如算法1.
算法1. CA模块模型构建和前传函数
模型构建def __init__():
输入: 输入特征通道数inC, 输出特征通道数outC, 缩减因子r
输出: CA模块结构
1. #分别添加横纵两个方向平均池化层
self.pool_h = nn.AdaptiveAvgPool2d((None, 1))
self.pool_w = nn.AdaptiveAvgPool2d((1, None))
2. #根据缩减因子r计算压缩后的通道数tempC, 添加卷积层conv1
3. #添加BN层和非线性激活层, 激活函数为h_swish
4. #分别添加处理横纵两个分割后张量的卷积层conv_h和 conv_w
self.conv_h= nn.Conv2d(tempC, outC, kernel_size=1, stride=1, padding=0)
self.conv_w=nn.Conv2d(tempC, outC, kernel_size=1, stride=1, padding=0)
前传函数def forward(self, x):
输入: 待计算的特征矩阵x
输出: 计算后的特征矩阵out
1. #获取输入特征矩阵维度n, c, H, W
n, c, H, W = x.shape
2. #分别沿横纵两个方向进行池化, 获得张量x_h和x_w
x_h = self.pool_h(x)
x_w= self.pool_w(x)
3. #调整x_w中的H和W的顺序, 方便后续进行Concat操作
x_w = x_w.permute(0, 1, 3, 2)
4. #对x
x_cat = torch.cat([x_h, x_w], dim=2)
5. #x_cat通过conv1调整通道数, 再通过BN层和非线性激活层
x_cat = self.act1(self.bn1(self.conv1(x_cat)))
6. #对x_cat进行split操作, 分割为两个张量, 并将分割后的两个张量分别通过conv_h和conv_w恢复为原通道数, 而后再分别通过Sigmoid函数, 获得out_h和out_w
x_h, x_w = torch.split(x_cat, [H, W], dim=2)
x_w = x_w.permute(0, 1, 3, 2)
out_h = torch.Sigmoid(self.conv_h(x_h))
out_w = torch.Sigmoid(self.conv_w(x_w))
7. #将原始输入的特征张量x和out_w、out_h相乘, 对原始输入的特征张量x的不同坐标位置赋权重
out = x × out_w × out_h
8. #返回结果
return out
3.4 多路径融合多路径融合将高频分支中各个MFCAB模块输出的特征进行Concat合并与1×1卷积降维, 在反向传播的过程中实现特征自适应融合学习, 提高特征注意力, 适应不同复杂程度的重建任务. 这部分的操作可以表示为:
| Fg=Conv1×1(Concat(F1,F2,⋯,F6)) | (8) |
其中, Concat(·)表示多路径特征合并操作, Conv1×1(·)表示1×1卷积操作, Fg表示最终的全局特征融合后的输出. F1–F6分别表示子MFCAB模块的输出.
3.5 上采样与重建上采样是将低分辨率小尺寸的特征图重排为高分辨率大尺寸的特征图. 本文采用文献[5]提出的亚像素卷积方式进行上采样. 这个操作可以描述为:
| FupH=Cup1(Fg) | (9) |
| FupL=Cup2(F0) | (10) |
其中, FupH和FupL分别表示上采样后输出的高频特征图和低频特征图; Cup1(·)和Cup2(·)分别表示高频分支与低频分支的上采样操作.
重建部分通过一个3×3的卷积层将多通道特征图生成3通道SR图像, 最终的重建图像ISR由低频重建图和高频重建图相加后获得, 如式(11):
| ISR=Conv3×3(FupH)+Conv3×3(FupL) | (11) |
本模型使用平均绝对误差 (mean absolute error, MAE)作为损失函数, 也被称为L1范数损失. 该损失函数计算重建图像的预测值f(xi)和真实图像的yi之间距离的均值. 损失函数在模型训练中不断减小, 从而获得更好的重建效果. MAE损失函数如式(12):
| MAE=1nn∑i=1|yi−f(xi)| | (12) |
图6为在NWPU4500数据集上训练过程中的损失函数收敛图, 放大因子scale=2. 从图中可以看出, 随着训练的进行, 损失函数不断降低, 在300个epoch处损失函数达到收敛.
4.2 实验环境和数据集为分析和验证本文提出模型对于光学遥感图像超分辨率重建任务的适用性与有效性, 选用通用的NWPU-RESISC45、AID光学遥感图像数据集进行了消融实验和重建效果对比实验.
实验环境配置: GPU为Quadro RTX 8000 (48 GB), 软件环境为Ubuntu 18.04, PyTorch 1.9.0, CUDA 11.1.

|
图 6 L1损失函数收敛图 |
模型选择L1范数作为损失函数, 采用ADAM优化器, 参数为beta1=0.9, beta2=0.999, epsilon=1E–8, batch=16, 初始学习率1E–4, 经过200个epoch学习率下降一半, 一共训练300个epoch.
数据集方面, 选择通用的NWPU-RESISC45和AID数据集进行模型训练优化与测试. 在NWPU-RESISC45数据集的45个场景中分别各自随机选取100幅、4幅、4幅图像构成训练集 (4500幅)、验证集 (180幅)和测试集 (180幅); AID数据集采用相同方式构成训练集 (1600幅)、测试集 (200幅)、验证集 (200幅). 下文分别以NWPU4500和AID1600代指这两个数据集. 在训练时, 对训练集图像进行随机的90°旋转、水平翻转、垂直翻转来获得更多的训练数据, 训练时输入样本尺寸为48 pixel×48 pixel.
超分辨率重建图像的客观评价指标采用通用的峰值信噪比 (peak signal to noise ratio, PSNR)和结构相似度(structural similarity, SSIM).
4.3 消融实验为了验证本文模型的有效性, 在NWPU4500数据集上进行了消融实验 (放大因子scale=2), 测试添加Inception子模块和CA子模块对超分辨率重建的有效性. 消融实验结果如表1所示.
从表1可知, 单独添加Inception或CA子模块时, PSNR和SSIM均有所提高, 表明采用多尺度特征提取或坐标注意力机制对提升重建图像质量是有效的. 当同时使用Inception和CA子模块时, PSNR和SSIM均较不添加或单独添加时提升更为明显, 表明多尺度空间特征提取与坐标注意力机制结合使用, 对于高频特征提取能起到相互促进的效果, 将使光学遥感图像的超分辨率重建效果最优.
| 表 1 消融实验 |
4.4 超分辨率重建效果对比
表2给出了本文模型与Bicubic、FSRCNN、VDSR、EDSR等主流的超分辨率重建模型在NWPU4500和AID1600遥感图像数据集上的超分辨率重建效果 (放大因子scale分别为2、3、4)对比.
| 表 2 超分辨率重建效果对比 |
从表中可以看出, 深度学习模型的超分辨率重建效果均显著优于传统的双三次插值模型Bicubic, 显示出深度学习模型在光学遥感图像超分辨率重建方面的巨大潜力. 而EDSR与本文模型由于采用了更深和更宽的网络结构, 超分辨率重建图像的质量较VDSR、SRCNN提升更为明显. 由于在网络的高频分支使用了多尺度特征提取和坐标注意力机制, 除了在NWPU4500数据集中的4倍放大因子下指标略低, 本文模型在2个数据集上3种放大因子下的超分辨率重建质量均优于EDSR, 显示出本文模型对于光学遥感图像超分辨率重建具有更好的适用性. 由于NWPU4500数据集的图像初始尺寸为256×256, 在scale=4时下采样后图像尺寸仅为64×64, 而所需训练样本尺寸为48×48, 产生的样本变化有限, 可能限制了重建效果的提升.
4.5 视觉效果对比除通过客观量化评价指标分析本文模型的重建效果, 图7列出了本文模型与其他典型模型重建图像的视觉效果对比. 因篇幅所限, 仅列举出各模型对NWPU4500数据集中一幅图像, 放大因子scale=4时的重建效果.

|
图 7 视觉效果对比 |
5 结论与展望
本文提出了一种基于多尺度特征提取和坐标注意力的光学遥感图像超分辨率重建模型, 在深度残差网络的高频分支引入多尺度特征提取和通道注意力机制构建了MFCAB模块, 实现对通道特征图进行不同尺度的空间域信息提取, 并通过对通道中坐标的权重关系进行自适应学习, 能够更好地适应遥感图像物体跨度大、细节信息多的特点, 更好地提取高频信息, 对更重要的特征进行关注; 最后将多个MFCAB提取的特征进行多路径融合, 加强了各个网络块之间的联系, 充分利用特征信息.
本文模型在NWPU4500和AID1600两个光学遥感图像数据集上进行了测试与验证, 实验结果显示出模型的重建效果优于主流的图像超分辨率重建模型. 后续将重点针对大放大因子 (scale=4)下的模型优化、模型参量优化、模型泛化验证等方面开展进一步研究和测试.
| [1] |
王润生, 熊盛青, 聂洪峰, 等. 遥感地质勘查技术与应用研究. 地质学报, 2011, 85(11): 1699-1743. |
| [2] |
李胜楠. 基于深度学习的图像超分辨率算法研究[硕士学位论文]. 秦皇岛: 燕山大学, 2021.
|
| [3] |
Dong C, Loy CC, He KM, et al. Learning a deep convolutional network for image super-resolution. Proceedings of the 13th European Conference on Computer Vision. Zurich: Springer, 2014. 184–199.
|
| [4] |
Dong C, Loy CC, Tang XO. Accelerating the super-resolution convolutional neural network. Proceedings of the 14th European Conference on Computer Vision. Amsterdam: Springer, 2016. 391–407.
|
| [5] |
Shi WZ, Caballero J, Huszár F, et al. Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 1874–1883.
|
| [6] |
Kim J, Lee JK, Lee KM. Accurate image super-resolution using very deep convolutional networks. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 1646–1654.
|
| [7] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 770–778.
|
| [8] |
Lim B, Son S, Kim H, et al. Enhanced deep residual networks for single image super-resolution. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops. Honolulu: IEEE, 2017. 1132–1140.
|
| [9] |
Lei S, Shi ZW, Zou ZX. Super-resolution for remote sensing images via local-global combined network. IEEE Geoscience and Remote Sensing Letters, 2017, 14(8): 1243-1247. DOI:10.1109/LGRS.2017.2704122 |
| [10] |
李欣. 基于深度学习的单幅遥感图像超分辨重建[硕士学位论文]. 北京: 中国科学院大学(中国科学院遥感与数字地球研究所), 2018.
|
| [11] |
李强, 汪西原, 何佳玮. 基于生成对抗网络的遥感图像超分辨率重建改进算法. 激光与光电子学进展, 2023, 60(10): 432–439.
|
| [12] |
潘梦迪. 基于深度学习的机载遥感图像超分辨率重建[硕士学位论文]. 哈尔滨: 哈尔滨工程大学, 2020.
|
| [13] |
印珏泽, 周宁宁. 基于对偶回归和注意力机制的图像超分辨率重建网络. 计算机系统应用, 2023, 32(2): 111-118. DOI:10.15888/j.cnki.csa.008939 |
| [14] |
Szegedy C, Liu W, Jia YQ, et al. Going deeper with convolutions. Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015. 1–9.
|
| [15] |
Hu J, Shen L, Sun G. Squeeze-and-excitation networks. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Salt Lake City: IEEE, 2018. 7132–7141.
|
| [16] |
Hou QB, Zhou DQ, Feng JS. Coordinate attention for efficient mobile network design. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021. 13708–13717.
|
 2023, Vol. 32
2023, Vol. 32



