计算机系统应用  2023, Vol. 32 Issue (7): 276-283   PDF    
引用本文
李凝书, 关东海, 袁伟伟. 基于梯度结构的图神经网络对抗攻击. 计算机系统应用, 2023, 32(7): 276-283.http://www.c-s-a.org.cn/1003-3254/9166.html   
Li NS, Guan DH, Yuan WW. Gradient-structure-based Adversarial Attacks on Graph Neural Network. Computer Systems and Applications, 2023, 32(7): 276-283(in Chinese).http://www.c-s-a.org.cn/1003-3254/9166.html   
基于梯度结构的图神经网络对抗攻击
李凝书, 关东海, 袁伟伟     
南京航空航天大学 计算机科学与技术学院, 南京 211106
收稿日期：2022-12-17; 修改日期：2023-02-03; 采用时间：2023-02-20; csa 在线出版时间：2023-04-23
基金项目：国防基础科研计划(JCKY2020204C009)
通讯作者：关东海, E-mail: dhguan@nuaa.edu.cn.
摘要：图神经网络在半监督节点分类任务中取得了显著的性能. 研究表明, 图神经网络容易受到干扰, 因此目前已有研究涉及图神经网络的对抗鲁棒性. 然而, 基于梯度的攻击不能保证最优的扰动. 提出了一种基于梯度和结构的对抗性攻击方法, 增强了基于梯度的扰动. 该方法首先利用训练损失的一阶优化生成候选扰动集, 然后对候选集进行相似性评估, 根据评估结果排序并选择固定预算的修改以实现攻击. 通过在5个数据集上进行半监督节点分类任务来评估所提出的攻击方法. 实验结果表明, 在仅执行少量扰动的情况下, 节点分类精度显著下降, 明显优于现有攻击方法.
关键词: 图神经网络    节点分类    对抗性攻击    梯度攻击    
Gradient-structure-based Adversarial Attacks on Graph Neural Network
LI Ning-Shu, GUAN Dong-Hai, YUAN Wei-Wei     
College of Computer Science and Technology, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China
Abstract: Graph neural networks have achieved remarkable performance in semi-supervised node classification tasks. Relevant research has shown that graph neural networks are susceptible to perturbations, and there is research studying the adversarial robustness of graph neural networks. However, gradient-based attacks cannot guarantee optimal perturbation. Therefore, an adversarial attack method based on gradient and structure is proposed to enhance the gradient-based perturbation. The method first generates candidate perturbation sets by using first-order optimization of training losses, and then it evaluates the similarity of the candidate sets. Finally, it ranks them according to the evaluation results and selects a fixed-budget modification to achieve the attack. The proposed attack method is evaluated by performing a semi-supervised node classification task on five datasets. Experimental results show that the node classification accuracy decreases significantly when only a small number of perturbations are performed, which indicates that the proposed method significantly outperforms the existing attack methods.
Key words: graph neural network (GNN)     node classification     adversarial attacks     gradient attacks    

图结构数据在很多领域中表现出显著的作用, 如社交网络[1, 2]、药物发现[3]、知识图[4]、推荐系统[5]、生物网络[6]等. 图神经网络(graph neural network, GNN)涵盖图的节点特征与拓扑结构, 且有着强大的表示学习能力, 因此作为图学习任务需求的常用模型, 如节点分类[7, 8]、链路预测[9]等, 都显示出优良的效果. 然而现有研究表明, GNN易受到扰动而导致性能下降, 仅通过修改图结构或节点特征便可产生错误的结果. 例如, 在社交网络或电子商务网络上, 攻击者可以通过伪造账户添加链接, 或者修改受控账户的个人资料, 或撰写虚假评论来实现对抗性攻击. 因此, 研究各种图学习模型的鲁棒性并开发对对抗性攻击具有鲁棒性的模型非常重要.

目前已有大量研究人员探索了图神经网络的鲁棒性, Zügner等人[7]提出了一种利用增量计算的高效算法Nettack, 明确区分了攻击者和目标节点, 以贪婪方式操纵图结构和节点特征. Dai等人[10]提出了RL-S2V, 该方法将强化学习引入图对抗攻击, 并把攻击过程抽象为马尔可夫决策过程. Zügner等人[11]利用元学习Metattack将图作为优化目标产生用于攻击的图数据. Chang等人[12]提出GF-Attack方法, 利用图过滤器和特征矩阵构造了一种广义的黑盒对抗性攻击. Xu等人[13]提出了投影梯度下降(projected gradient descent, PGD)拓扑攻击和最小-最大(MinMax)拓扑攻击, 旨在从一阶优化的角度进行梯度攻击.

现有方法主要可以分为基于梯度的攻击与基于非梯度的攻击[14]. 尽管这些方法取得了一定的效果, 但仍存在局限性. 基于梯度的攻击中, 直接利用模型梯度信息的攻击算法易陷入局部最优解, 且部分存在计算量较大的问题. 而基于非梯度的攻击, 攻击算法较复杂, 难以扩展到复杂图数据上, 且攻击性能较差. 现有攻击方法存在以下问题[15]: 1) 在只进行少量扰动时, 攻击效果不够明显; 2) 元梯度的计算和存储都比较昂贵; 3) 需要访问模型的图滤波器.

针对上述攻击方法存在的诸多问题, 本文结合了基于梯度与非梯度的攻击, 提出一种基于梯度和结构的全局对抗攻击GSAtk (GradStructAtk), 该方法继承了基于梯度攻击的高性能优势, 综合权衡了攻击性能和效率. GSAtk的攻击策略包括生成候选集、相似性评分两部分. 首先, 基于训练损失的一阶优化方法, 产生候选扰动集. 然后, 根据相似性度量方法来评估候选集中的元素. 最后在5个数据集上进行实验, 实验结果表明, GSAtk攻击明显优于其他攻击方法. 工作贡献总结如下:

1) 提出一种攻击方法GSAtk, 通过操纵图结构, 增强了基于梯度的攻击, 且保证攻击不可察觉.

2) 对比了不同相似性度量方法的攻击效果, 并选出最优的, 保证了我们方法的可靠性.

3) 通过对多个数据集的实验表明, GSAtk优于攻击基线, 且只需要对图进行少量修改, 便可显著恶化节点分类结果.

1 相关理论

在本节中, 首先介绍本文中使用的符号和图卷积网络(graph convolutional network, GCN)的预备知识. $ G = (V, E) $ 表示一个无定向非加权图, 其中, $V$ 表示基数为 $N$ 的节点集, $E$ 表示基数为 $M$ 的边集. 设 $A \in {\{ 0, 1\} ^{N \times N}}$ 代表一个二元邻接矩阵, 且如果 $(i, j) \in E$ , ${A_{_{ij}}} = 1$ . $X \in {\{ 0, 1\} ^{N \times F}}$ 表示 $F$ 维二进制节点特征. 假定 $C = \{ {c_i}\} $ 表示一组类标签, 其中, ${c_i}$ 表示节点 $i$ 的基本真值标签, 将 $C$ 定义为标签集的大小. 标记节点集表示为 ${V_L}$ , 且 ${C_L} \in {\{ 0, 1\} ^{|{V_L}| \times C}}$ 表示标记节点集 ${V_L}$ 的一个热标记矩阵.

GNN是直接作用于图形结构数据的多层机器学习模型, 通过网络中节点间信息传递的方式来获取图中的依存关系, 并通过邻居来更新节点状态. 在这项工作中, 重点关注了GCN, 它遵循以下传播规则来聚合相邻特征:

$ {H^{(l + 1)}} = \sigma \left( {{{\tilde D}^{ - \frac{1}{2}}}\tilde A{{\tilde D}^{ - \frac{1}{2}}}{H^{(l)}}{W^{(l)}}} \right) $ (1)

其中, $\tilde A = A + I$ 是带有自循环的图 $G$ 的邻接矩阵, ${\tilde D_{ii}} = \displaystyle\sum\nolimits_j {{{\tilde A}_{ij}}} $ 是对角度矩阵. ${W^{(l)}}$ 是第 $l$ 层的可训练权重矩阵, 且 ${H^{(l)}}$ 是隐藏表示的矩阵. $\sigma ( \cdot )$ 表示一个非线性激活函数, 通常定义为ReLU.

对于节点分类任务, GCN的前向预测可以被认为是:

$ Z = {f_w}(A, X) = {{\textit{Softmax}}} \left( {\hat A{ReLU} \left( {\hat AX{W^{(0)}}} \right){W^{(1)}}} \right) $ (2)

其中, $\hat A = {\tilde D^{ - \frac{1}{2}}}\tilde A{\tilde D^{ - \frac{1}{2}}}$ , $w = \left\{ {{W^{(0)}}, {W^{(1)}}} \right\}$ 是旨在优化的模型权重参数集. 输出 ${Z_{u, c}}$ 表示一个节点 $u$ 属于标签 $c$ 的概率.

接下来, 为了帮助研究人员理解图对抗攻击的定义, 介绍了一个可以涵盖所有现有工作的统一问题公式:

$ \begin{split} & \mathop {\max }\limits_{_{G' \in \Phi (G)}} \sum\limits_i^{} {\mathcal{L}\left( {{f_{{w^*}}}({{G'}_i}), {y_i}} \right)} {\text{ }} \\ & {\text{s}}{\text{.t}}{\text{. }}{w^*} = \mathop {\arg \min }\limits_w \sum\limits_j^{} {\mathcal{L}\left( {{f_w}(\hat G_j^{}), {y_j}} \right)} \end{split} $ (3)

其中, $y$ 表示模型预测值或真值标签, $\Phi (G)$ 表示原始图 $G$ 上的扰动空间, $\mathcal{L}\left( { \cdot , \cdot } \right)$ 是旨在优化的损失函数. 当 $ \hat G = G' $ 时表示中毒攻击, 当 $ \hat G = G $ 时表示逃逸攻击.

$ G' \in \Phi (G) $ 可以表示节点操纵、拓扑修改和特征扰动等, 为了专注于攻击图的结构信息, 本文只通过翻转边来实现扰动. 在大多数实际场景中, 为了满足干扰不明显的要求, 攻击者必须限制他们可以执行的修改. 因此, 假设攻击者一共有固定的 $b$ 个翻转的预算. 每次翻转都会改变 $A$ , 上述攻击预算将导致 ${\left\| {{A^{(b)}} - A} \right\|_0} \leqslant 2b$ .

2 GSAtk方法

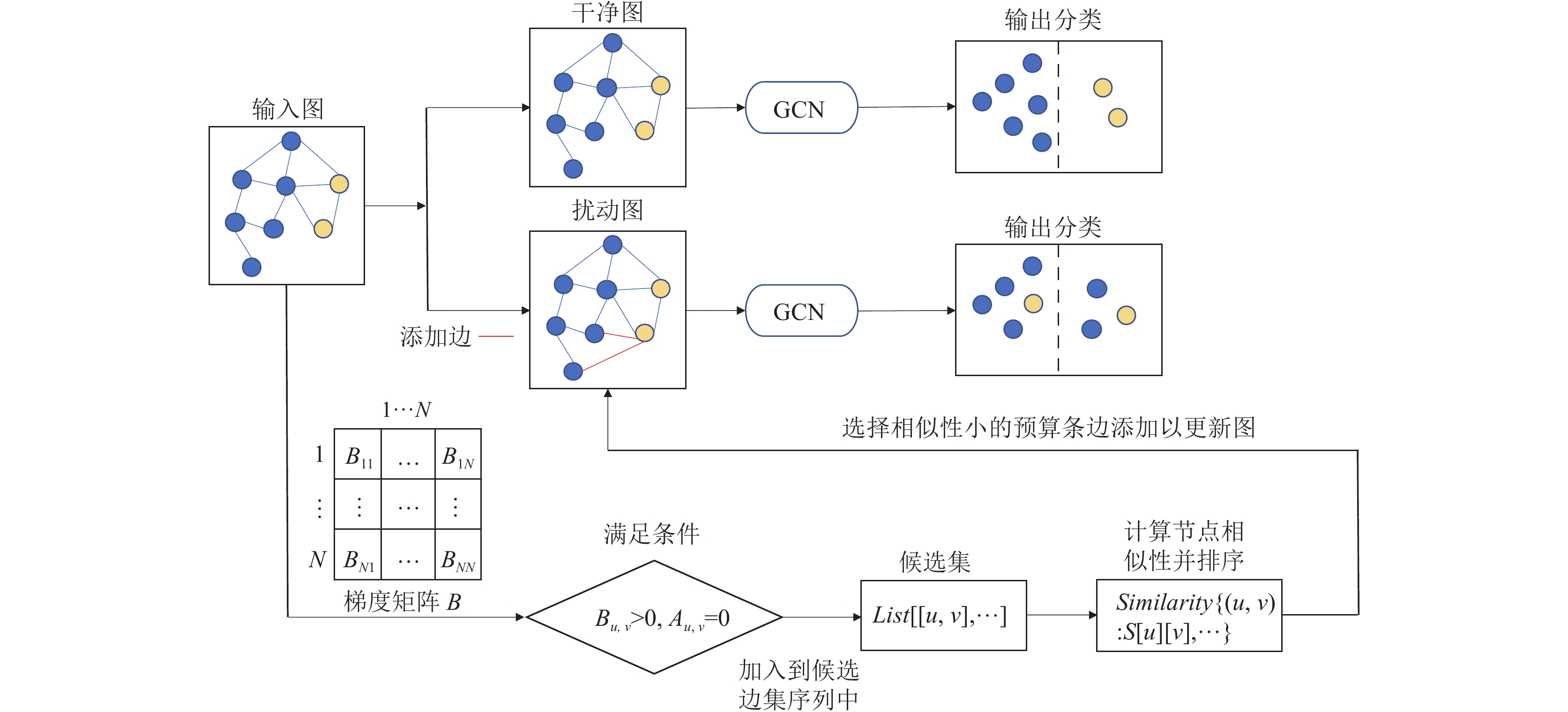
GSAtk攻击方法包括生成候选集与相似性评分两个阶段. 在第1个阶段, 基于梯度生成候选扰动边集. 在第2个阶段, 计算候选集中每条边对应的节点相似性并排序, 然后选择固定预算的边集进行修改. 此外, 对比并选择了3种不同的相似性评分方法. GSAtk的算法框架图如图1所示. 每个阶段的详细信息描述如下.

图 1 GSAtk算法框架图

2.1 生成候选集

该阶段的目标是生成一个候选集, 以便后续阶段从中选择进行翻转的边. 虽然在图结构攻击中添加或删除边都是可能的, 但据研究, 攻击方法倾向于添加伪边而不是删除现有边. 直观地说, 创建假边将从新链接的邻居中注入新信息, 而删除边只会影响消息传递过程中现有邻居的权重. 因此, 与以往不同的是, 本文只考虑添加边, 且一次性生成.

给定图 $G$ 、邻接矩阵 $A$ 、特征矩阵 $X$ 和一个热标签矩阵 ${C_L}$ , 训练损失 ${L_{{\rm{tra}}}}$ 定义为:

$ {L_{{\rm{tra}}}} = Loss({C_L}, {f_{{w^ * }}}(A, X)) $ (4)

其中, $Loss( \cdot , \cdot )$ 通常可以选择交叉熵或基于边缘的损失, $ {f_{{w^ * }}} $ 是第2节提到的前向预测, 且最优参数: ${w^*} = \mathop {{{\rm{argmin}}} }\limits_w {Loss} \left( {{C_L}, {f_w}(A, X)} \right)$ .

通过将邻接矩阵 $A$ 视为可微输入, 其中, 每个元素的一阶梯度可以精确计算, 引入了梯度矩阵 $B \in {R^{N \times N}}$ , 两个节点 ${{u}}$ 、 $v$ 之间的梯度定义为:

$ {B_{u, v}} = {\left. {\frac{{\partial {L_{{\rm{tra}}}}\left( A \right)}}{{\partial {A_{u, v}}}}} \right|_A} $ (5)

不同于只关注最大梯度的方法, 本文在 $V \times V$ 中选择最有可能构造候选集的 $\Delta $ 项, 且只考虑添加边. 生成开始于从 $B$ 的上三角部分中 $|{B_{ \cdot , \cdot }}|$ 最大的那个条目, 记为 $(u, v)$ . 如果满足以下条件,

$ {B_{u, v}} > 0, {A_{u, v}} = 0 $ (6)

则接受 $(u, v)$ , 否则将其拒绝. 然后, 移动到 $B$ 的上三角部分中具有第二大 $|{B_{ \cdot , \cdot }}|$ 的条目, 并检查其是否满足上述类似条件. 若满足, 则将其加入候选集. 类似的过程继续进行, 直到候选集的大小达到 $\Delta $ .

2.2 相似性评分

研究发现, 不同的节点更有可能通过攻击算法连接. Zügner等人[7]报告称, 来自不同类别的节点更有可能被连接. 文献[16]表明, 节点距离会有效的影响图对抗攻击, 且链接远程节点比链接附近节点会导致更有效的攻击. 同时, 节点距离较大时, 节点类别更加趋于不同.

距离表示一种形式的节点不相似性, 因此将距离推广到相似性度量. 在得到候选集后, 计算候选集中所有条目的相似性得分, 然后按照相似性度量的大小对候选边集进行排序. 最后从排序后的候选集中选取顶部 $ b $ 条边以获得最终的扰动图.

本文使用了3种不同的相似性度量方法Community、Jaccard和Katz相似性进行对比.

Katz指标[17]能够识别不同邻居节点的影响力, 它考虑所有路径数, 并对邻居节点设置不同的权重, 即路径越短赋予的权重越大. 2个节点之间的相似度定义为:

$ s(u, v) = \sum\limits_{l = 1}^\infty {{\beta ^l}} \left| {paths_{u, v}^l} \right| = \sum\limits_{l = 1}^\infty {{\beta ^l}} {\left( {{A^l}} \right)_{u, v}} $ (7)

其中, $ paths_{u, v}^l $ 表示节点 $u$ 到节点 $v$ 长度为 $l$ 的路径个数, $A$ 是邻接矩阵. 矩阵 $A$ 的第 $l$ 次幂的每个项与相应节点对之间长度为 $l$ 的路径个数相等. $\;\beta $ 为权重衰减因子, 且 $\;\beta $ 的取值须小于邻接矩阵 $A$ 最大特征值的倒数, 以保证数列的收敛性. 矩阵形式的表达式为:

$ S = \beta A + {\beta ^2}{A^2} + {\beta ^3}{A^3} + \cdots = {(I - \beta A)^{ - 1}} - I $ (8)

其中, $I$ 是单位矩阵.

对于基于社区Community的相似性, 本文使用Louvain方法[18]执行社区检测. Louvain算法是一种基于模块度的无监督启发式算法. 其基本思想包括模块度最大化和节点合并, 重复执行这两个步骤直到模块度不再增大. 然后, 将两个节点之间的相似度设定为它们对应社区的相似度.

Jaccard相似系数用于比较有限样本集之间的相似性和差异性. 定义为:

$ J(P, Q) = \frac{{|P \cap Q|}}{{|P \cup Q|}} = \frac{{|P \cap Q|}}{{|P| + |Q| - |P \cap Q|}} $ (9)

其中, 定义 $P$ 、 $Q$ 分别表示两个节点的特征.

GSAtk算法的基本思想是基于相似性分数贪婪地选择攻击, 直到超过攻击预算. 在算法1中总结了GSAtk攻击.

算法1. GSAtk攻击

输入: 图 $\scriptstyle G = (V, E) $ , 邻接矩阵 $\scriptstyle A$ , 特征矩阵 $\scriptstyle X$ , 基本真值标签 $\scriptstyle C$ , 候选集 $\scriptstyle \Delta $ , 攻击预算 $\scriptstyle b$ .

输出: 修改后的图 $\scriptstyle G' $ .

1. for $\scriptstyle t$ = 1, 2, …, $\scriptstyle \Delta $ do

2. 　 if $\scriptstyle {B_{u, v}} > 0$ and $\scriptstyle {A_{u, v}} = 0$

3. 　　Candidate_edges.append( $\scriptstyle [u, v]$ )

4. similarity[( $\scriptstyle u, v$ )] = similarity score

5. 根据得分进行排序sorted(similarity.items())

6. 选择相似性最小的 $\scriptstyle b$ 个边集进行添加

7. 更新邻接矩阵 $\scriptstyle A$ .

3 实验 3.1 实验设置

(1) 数据集. 实验采用了4种常用的引文网络: Cora[19]、Cora_ML[20]、Citeseer[19]、PubMed[21]以及一个政治博客图PolBlogs[22]. 对于这些引文网络, 节点表示文档, 边表示引用关系. 此外, 每个节点都与一组单词特征(属性)相关联. 数据集概述如表1所示.

表 1 数据集统计

由于PubMed数据集规模较大, 对其取样后进行实验. 此外, 遵循Nettack[7]的设置, 对于存在单节点的数据集, 只考虑图的最大连通分量. 本文将每个数据集随机分成10%的标记节点和90%的未标记节点.

(2) 基线. 为了评估方法的有效性, 将GSAtk与以下5种基线方法进行对比, 包括EpoAtk[23]、Structack[16]、PGD[13]、MinMax[13]和DICE[24].

EpoAtk: 该方法引入了一个重组过程, 以避免从长期角度来看训练损失的局部最大值, 增强了基于梯度的图扰动.

Structack: 选择中心性最低的节点并链接这些节点, 以使链接节点之间的相似性最小化. 表明基于结构的非信息攻击可以接近信息攻击的性能.

PGD和MinMax: 根据GNN是否可再训练分为两种新的拓扑攻击, 都应用投影梯度下降来解决凸松弛后的优化问题. MinMax试图通过攻击可重新训练的GNN来构建更强大的攻击. 这两种攻击需要访问模型参数.

DICE: 一种简单的启发式算法, 边缘仅在同一类的节点之间删除, 并且仅在不同类的节点之间插入.

(3) 参数设置. 综合遵循现有攻击方法的基本设置, 将候选集 $\Delta $ 的大小设置为4000. 攻击预算即攻击者可以干扰的边缘百分比, 设置为1%, 2%, 3%, 5%, 10%, 15%, 20%, 使用Adam优化器并将学习率设置为0.01. 使用两层GCN作为目标模型, 即想要误导的威胁模型, 虽然可以获得威胁模型的所有信息, 但实际上没有利用它们的权重. 在扰动过程中, 训练损失的梯度是从重新训练的模型而不是原始威胁模型中学习的. 为了使验证结果更具统计学意义, 对每个实验结果重复50次, 并在评估中删除了5个最高和最低精度, 计算了半监督节点分类精度的平均值.

3.2 攻击性能

对于方法GSAtk, 表2显示了各个数据集上不同相似性评分在不同扰动率下的误分类率.

表 2 方法GSAtk在不同相似性评分下的误分类率 (%)

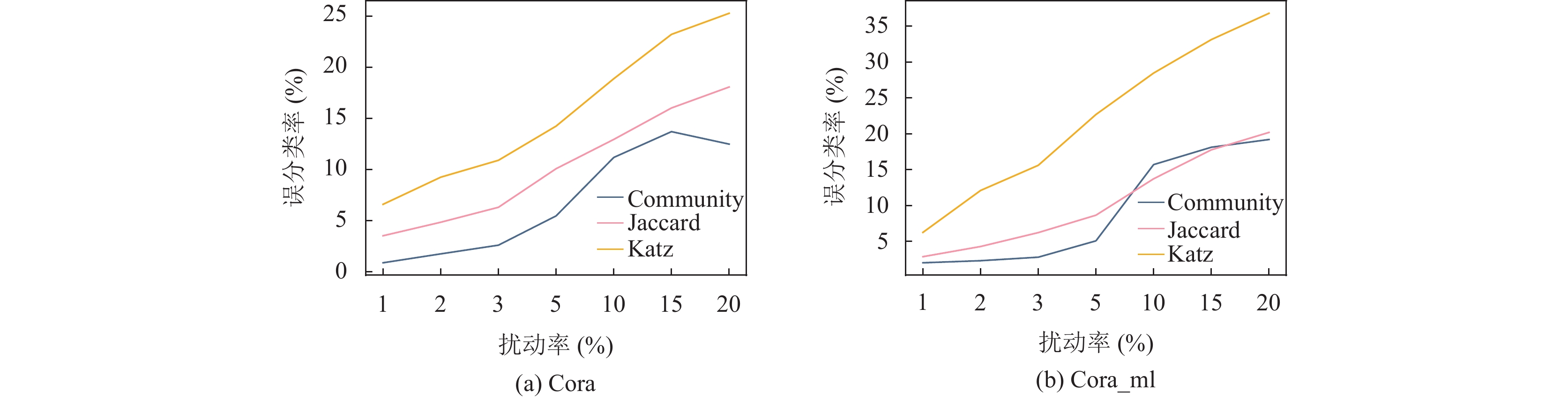
首先, 攻击者的目标是使原始模型达到低分类精度, 即模型性能越低, 误分类率越高, 攻击者越强大. 根据表2, Katz相似性评分方法相较于其他方法明显有更好的攻击性能, 且在各个数据集上都有较好的表现. 随着扰动率的增加, 误分类率也逐步提升. 图2中更加直观地展示了实验结果. 另外, 其他两个相似性方法表现不佳, 主要归因于: 基于Community的方法会导致社区过大, 不能及时收敛. 它所采用的贪婪思想容易使得社区划分出现过拟合的情况以及局部最优的问题. 而Jaccard相似系数, 本文使用节点特征作为样本集来计算相似性, 可见, 并非特征共有元素越多, 节点越相似, 即二者不具备强相关性. Katz相似性是基于网络全域的节点相似性指标, 它考虑到了全部网络的信息来计算网络中节点的相对影响, 适用于不同网络. 本文采用的数据集是逐渐生长的科学网络, 其中, 每个节点和边的信息都尤为重要, 因此, Katz相似性评分更适用于本文模型. 后文将采用Katz相似性评分方法.

表3给出了不同数据集针对不同攻击方法的分类精度. 为了比较, 还显示了未扰动的自然模型的分类精度(用“Clean”表示).

根据表3, 模型在干净图上都达到了较高的分类精度, 这表明攻击定会降低模型的性能. 与基线方法相比, GSAtk产生了实质性的精度下降, 实现了更好的攻击效果. 对于所有数据集, 该方法可以在1%的攻击预算下实现竞争性或更好的攻击性能. 这存在以下原因.

1) 首先, 基线方法无法在其策略设置中找到最有影响力的边, 其中, EpoAtk攻击虽然引入重组阶段来优化局部最大值问题, 但其扩展的搜索空间并不完善, 只考虑了两种变体.

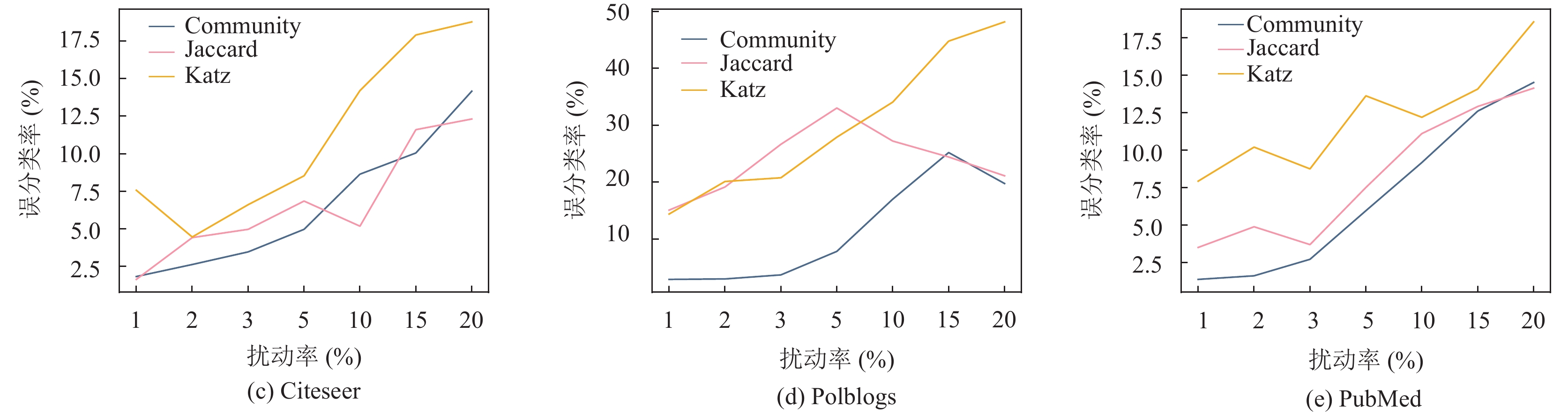
图 2 5个数据集上不同相似性评分在不同扰动率下的误分类率

图 2 5个数据集上不同相似性评分在不同扰动率下的误分类率(续)

表 3 不同攻击方法的分类精度

2) Structack攻击仅考虑了节点中心性和相似性对模型带来的影响, 并未考虑到对抗样本对目标模型梯度的影响.

3) 相反, PGD与MinMax攻击是基于梯度的优化攻击, 缺乏对图结构自身的关系分析.

4) DICE攻击虽相比其他方法具有更多的信息, 包括所有可用的真实类标签, 但既没有考虑模型梯度, 也没有引入图结构属性.

5) 其次, 本文提出的方法同时考虑了以上两个因素以实现扰动生成, 双重约束使得添加的边对模型性能极具影响力, 增强了基于单因素的扰动. GSAtk通过生成候选集与相似性评分两个阶段, 结合考虑了模型梯度与图结构属性, 解决了基线方法存在的缺陷.

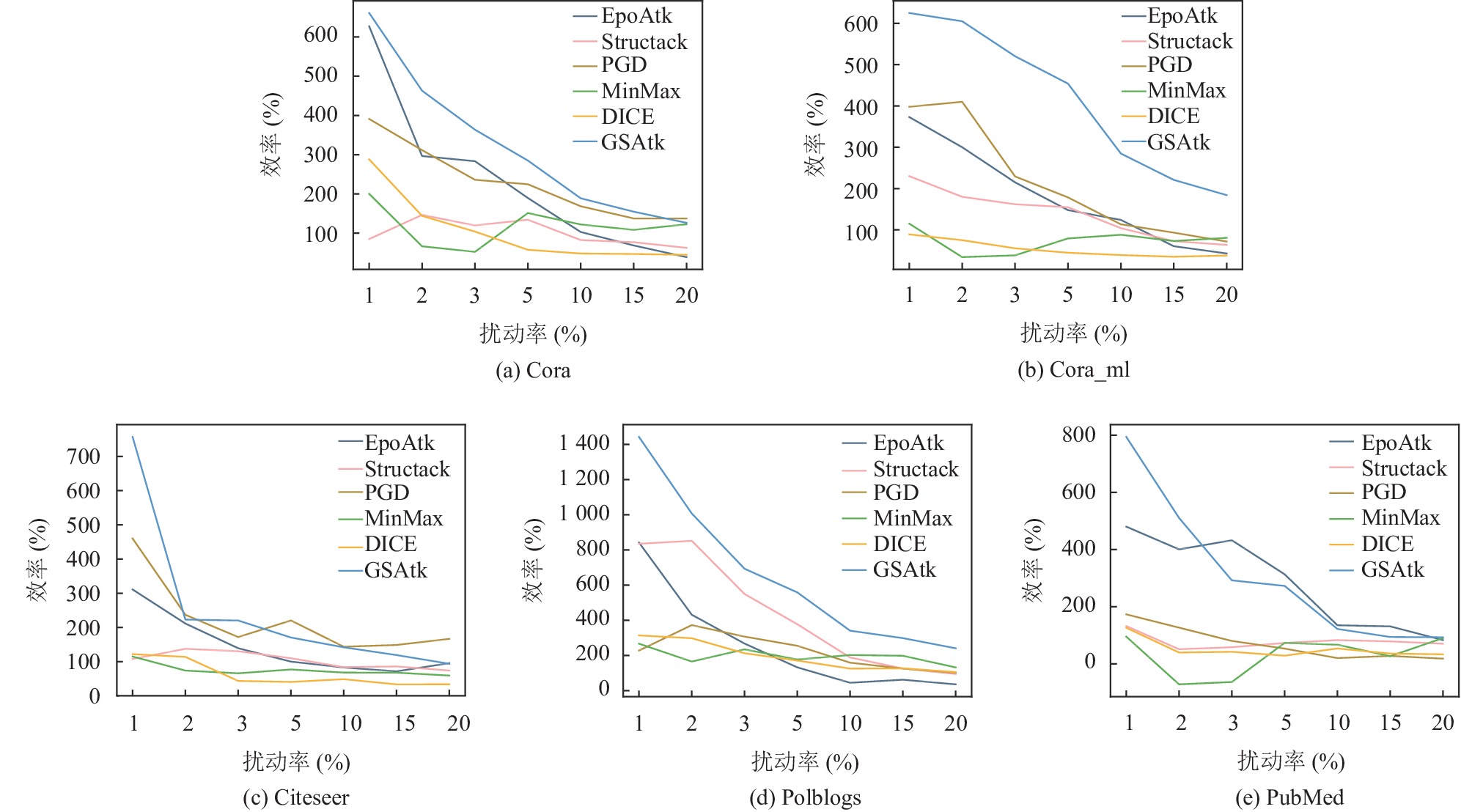
为了更直观地展示GSAtk的高效率, 计算了不同数据集在不同方法下的误分类率与效率, 效率公式表示为误分类率/扰动率, 具体如图3所示.

图 3 5个数据集上各方法在不同扰动率下的攻击效率

根据图3, 虽然GSAtk在部分数据集上存在波动, 但整体上都优于基线方法, 且在扰动率低的情况下有显著的攻击性能. 仅考虑了添加边, GSAtk就会导致性能的明显下降, 特别是Cora、Cora_ml与Polblogs数据集. 值得注意的是, Epoatk和PGD方法通常优于DICE和MinMax攻击. 可见相比可再训练的模型, 预定义的模型更容易受到攻击, 而DICE方法随机性很强, 导致攻击不具有针对性. 将GSAtk应用于图对抗攻击与防御任务[25], 解决了传统攻击方法中性能与效率的平衡问题. 采用的相似性评分引入图结构属性, 有效增强了基于梯度的攻击, 降低了分类精度, 二者的结合有效保证了在极少量扰动时达到很好的攻击效果.

4 结论

本文研究了图神经网络的对抗性攻击, 并提出了一种针对节点分类任务的攻击框架GSAtk, 该框架基于梯度与结构. 攻击方法包含生成候选集与相似性评分两个阶段, 克服了攻击离散图结构数据的困难. 在5个图形数据集上的实验中, GSAtk能够以最小的扰动代价取得最大的攻击效果, 实现了具有不可察觉性的高效攻击, 明显优于现有攻击方法.

此外, 本文的工作主要集中在节点分类任务和全局攻击场景. 未来还需将该方法进行扩展, 以更大的灵活性将其推广到其他图形分析任务.

参考文献
[1]
Fan WQ, Ma Y, Li Q, et al. Graph neural networks for social recommendation. Proceedings of the 2019 World Wide Web Conference. San Francisco: ACM, 2019. 417–426.
[2]
Zhang SX, Chen HX, Ming X, et al. Where are we in embedding spaces? A comprehensive analysis on network embedding approaches for recommender systems. arXiv:2105.08908, 2021.
[3]
Shi CC, Xu MK, Zhu ZC, et al. GraphAF: A flow-based autoregressive model for molecular graph generation. Proceedings of the 8th International Conference on Learning Representations. Addis Ababa: ICLR, 2020. 1–18.
[4]
Lin XX, Yang H, Wu J, et al. Guiding cross-lingual entity alignment via adversarial knowledge embedding. Proceedings of the 2019 IEEE International Conference on Data Mining (ICDM). Beijing: IEEE, 2019. 429–438.
[5]
Ying R, He RN, Chen KF, et al. Graph convolutional neural networks for Web-scale recommender systems. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. London: ACM, 2018. 974–983.
[6]
Zitnik M, Leskovec J. Predicting multicellular function through multi-layer tissue networks. Bioinformatics, 2017, 33(14): i190-i198. DOI:10.1093/bioinformatics/btx252
[7]
Zügner D, Akbarnejad A, Günnemann S. Adversarial attacks on neural networks for graph data. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. London: ACM, 2018. 2847–2856.
[8]
Bojchevski A, Günnemann S. Adversarial attacks on node embeddings via graph poisoning. Proceedings of the 36th International Conference on Machine Learning. Long Beach: PMLR, 2019. 695–704.
[9]
Zhang MH, Chen YX. Link prediction based on graph neural networks. Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montréal: Curran Associates Inc., 2018. 5171–5181.
[10]
Dai HJ, Li H, Tian T, et al. Adversarial attack on graph structured data. Proceedings of the 35th International Conference on Machine Learning. Stockholm: PMLR, 2018. 1123–1132.
[11]
Zügner D, Günnemann S. Adversarial attacks on graph neural networks via meta learning. Proceedings of the 7th International Conference on Learning Representations. New Orleans: ICLR, 2019. 1–15.
[12]
Chang H, Rong Y, Xu TY, et al. A restricted black-box adversarial framework towards attacking graph embedding models. Proceedings of the AAAI Conference on Artificial Intelligence, 2020, 34(4): 3389-3396. DOI:10.1609/aaai.v34i04.5741
[13]
Xu KD, Chen HG, Liu SJ, et al. Topology attack and defense for graph neural networks: An optimization perspective. Proceedings of the 28th International Joint Conference on Artificial Intelligence. Macao: IJCAI, 2019. 3961–3967.
[14]
任一支, 李泽龙, 袁理锋, 等. 图深度学习攻击模型综述. 信息安全学报, 2022, 7(1): 66-83. DOI:10.19363/J.cnki.cn10-1380/tn.2022.01.05
[15]
翟正利, 李鹏辉, 冯舒. 图对抗攻击研究综述. 计算机工程与应用, 2021, 57(7): 14-21. DOI:10.3778/j.issn.1002-8331.2012-0367
[16]
Hussain H, Duricic T, Lex E, et al. Structack: Structure-based adversarial attacks on graph neural networks. Proceedings of the 32nd ACM Conference on Hypertext and Social Media. ACM, 2021. 111–120.
[17]
Newman M. Networks. 2nd ed. Oxford: Oxford University Press, 2018.
[18]
Blondel VD, Guillaume JL, Lambiotte R, et al. Fast unfolding of communities in large networks. Journal of Statistical Mechanics: Theory and Experiment, 2008, 2008: P10008. DOI:10.1088/1742-5468/2008/10/P10008
[19]
Yang ZL, Cohen WW, Salakhutdinov R. Revisiting semi-supervised learning with graph embeddings. Proceedings of the 33rd International Conference on International Conference on Machine Learning. New York: JMLR.org, 2016. 40–48.
[20]
Bojchevski A, Günnemann S. Deep Gaussian embedding of graphs: Unsupervised inductive learning via ranking. Proceedings of the 6th International Conference on Learning Representations. Vancouver: ICLR, 2018. 1–13.
[21]
Sen P, Namata G, Bilgic M, et al. Collective classification in network data. AI Magazine, 2008, 29(3): 93. DOI:10.1609/aimag.v29i3.2157
[22]
Adamic LA, Glance N. The political blogosphere and the 2004 U.S. election: Divided they blog. Proceedings of the 3rd International Workshop on Link Discovery. Chicago: ACM, 2005. 36–43.
[23]
Lin XX, Zhou C, Yang H, et al. Exploratory adversarial attacks on graph neural networks. Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM). Sorrento: IEEE, 2020. 1136–1141.
[24]
Waniek M, Michalak TP, Wooldridge MJ, et al. Hiding individuals and communities in a social network. Nature Human Behaviour, 2018, 2(2): 139-147. DOI:10.1038/s41562-017-0290-3
[25]
陈晋音, 张敦杰, 黄国瀚, 等. 面向图神经网络的对抗攻击与防御综述. 网络与信息安全学报, 2021, 7(3): 1-28. DOI:10.11959/j.issn.2096-109x.2021051