2. 工业安全与应急技术安徽省重点实验室, 合肥 230009;
3. 合肥工业大学 科学技术研究院, 合肥 230009
2. Anhui Province Key Laboratory of Industry Safety and Emergency Technology, Hefei 230009, China;
3. Academy of Science and Technology, Hefei University of Technology, Hefei 230009, China
拉索是斜拉桥以及一些常用建筑的重要组成部分, 是桥梁以及建筑物的主要承重结构, 拉索张力的测量在桥梁施工过程和投入使用时都是必不可少的环节, 索力是否处于正常值范围内可作为判定桥梁健康状态的标准[1]. 因此, 定期检测拉索的张力大小可以避免发生桥梁发生剧烈晃动、倒塌等安全事故.
目前, 桥梁拉索的现场张力检测方法, 包括油压表法、磁通量法、压力传感器法以及振动频率法. 其中, 油压表测量法和压力传感器法通常在桥梁建造阶段使用; 磁通量法适用于长期监测和非接触式测量, 但初始成本较大, 安装方便性有待提高. 故振动频率法广泛地应用在桥梁拉索张力监测过程中, 即先测量出拉索振动频率, 再通过频率到索力的计算公式计算出拉索张力[2]. 振动频率法广泛应用于桥梁结构监测中, 常常通过安装加速度传感器来完成拉索振动频率的测量. 这意味着需要繁琐的工具安装和数据采集才可以实现数据传输的要求, 同时也面临着传感器的维护和管理等诸多问题.
随着计算机视觉的发展, 基于视觉的振动频率测量法得到国内外研究人员的关注. 2008年, Ji等[3]利用两台相机来获取线状物体的动态响应, 采用长度匹配算法在无标定的情况下获取振动物体的频率和幅值. 2011年, Kim等[4]提出了一种利用数字图像处理技术测量多点位移响应的方法, 测量了悬索桥的振动频率. 2012年, Chen等[5]利用拉索的直线特性确定其中点, 把中点当作目标点来提取拉索振动的位移. 2014年, 晏班夫等[6]将计算机视觉运用到拉索振动频率测量中, 利用目标检测算法以及卡尔曼滤波法对目标点进行跟踪, 从而获取拉索振动频率. 2017年, Feng等[7]提出使用亚像素方向匹配算法进行振动频率计算, 视频第1帧作为参考帧, 与之后的每一帧做差值得到相对位移, 通过FFT计算出振动频率. 然而在日常生活中, 拉索的振动幅度较为微弱, 并且在拍摄视频时会受到光照等因素的影响, 导致算法对拉索振动检测不准确.
近年来, 一种基于欧拉相位的振动检测算法的提出, 可有效得解决测量物体振动时其振动幅度过小的问题, 并减轻光照变化对振动测量的影响. 2013年Wadhwa等[8]提出了基于相位的欧拉视角视频放大技术 (phase-based video magnification, PVM), 利用空间相位信息提取视频中的微小运动信号. 近年来该算法的快速发展为振动检测提供了新思路. 2014年, Wadhwa等[9]利用Riesz金字塔代替复数可控金字塔, 提升了算法计算速度. 2017年Chen等[10]将PVM与基于相位的光流[11, 12]相结合, 在多个实验室环境中测量简单结构的共振频率和模态形状. 2017年, Davis等[13]通过基于相位的振动提取方法获得了金属棒和玻璃材料的模态频率. 2018年Choi等[14]利用PVM技术设计了一套视觉检测系统用于测量结构的固有频率, 进而检测悬臂梁的结构损伤, 将悬臂梁损伤位置和损伤程度的识别问题转化为目标函数最小化问题, 并用遗传算法进行求解. 2020年, Peng等[15]提出了一种改进的基于相位的运动提取方法 (phase-based vibration extraction, PVE), 直接将相位变化转换为位移变化, 用来测量物体的振动. 然而上述研究都是在实验室理想环境下对被测物展开实验, 通常都是使用拍摄设备找到最理想角度进行视频拍摄, 在实验过程中未考虑外界环境因素如车辆、风激励以及拉索与地面的角度等对振动信号造成的影响并且在实际斜拉桥路面展开拍摄时, 复杂的路况导致无法随时选取理想的拍摄角度, 拉索振动方向及拍摄示意图如图1所示(拉索的主振方向总是垂直与拉索本身的[16]), 经实验证明现有算法在真实场景下对拉索振动频率测量的鲁棒性较差, 因此以上研究不适用于实际场景下的拉索振动频率检测.

|
图 1 拉索拍摄视角示意图 |
本文将基于相位的运动提取方法运用到拉索振动测量中, 提出了一种基于方向自适应复可控滤波器的新型拉索振动检测方法. 针对实际场景下拉索振动的方向特征, 对上述研究中[8-15]的空间滤波和相位提取方式进行了改进. 根据拉索的形态特征提取出边缘区域, 并确定拉索主振方向; 基于主振方向设计方向模板, 构造方向自适应复数可控滤波器组, 提取出不同尺度同一方向的空间相位信息, 并对边缘区域的拉索相位进行增强; 在此基础上, 将每一帧图像处理得到的不同尺度的空间相位进行平均, 按时间顺序排列生成相位序列; 最后, 计算相位序列的幅度频谱函数, 求解其峰值点所对应频率, 即为拉索主振频率.
1 本文方法本文提出了基于方向自适应复数可控滤波器的拉索振动检测方法. 该方法主要实现步骤如下: 1)采集拉索振动视频, 利用拉索的直线特性检测拉索位置[17], 并确定拉索主振方向; 2)根据拉索的振动方向特性, 设计方向自适应复可控滤波器组, 对视频的每一帧图像进行分解处理, 得到不同尺度同一方向的相位谱和幅度谱, 并对拉索边缘区域相位进行增强; 3)将每一帧图像处理得到的不同尺度的空间相位进行平均, 按时间顺序排列生成相位序列; 4)对提取到的相位序列进行傅里叶变换得到拉索振动主频频率. 整体流程框图如图2所示.

|
图 2 本文算法框架图 |
视频的每帧图像中都蕴含丰富的相位信息, 基于相位的欧拉振动检测算法可以有效地提取出图像的相位信息, 在对图像处理的精确度上做出了很大的贡献. 基于相位的振动检测算法利用傅里叶变换的时移特性对图像中蕴含的相位信息进行提取, 将运动信号转换为相位信号, 更加直观地将运动信号表示出来.
本文使用一维图像的像素分布
| $ f(x) = \sum\limits_{\omega = - \infty }^\infty {{A_\omega }{{\rm{e}}^{j\omega x}}} $ | (1) |
其中,
令每个频率对应的傅里叶级数展开式为:
| $ {S_\omega }(x) = {A_\omega }{{\rm{e}}^{j\omega x}} $ | (2) |
| $ f(x + \delta (t)) = \sum\limits_{\omega = - \infty }^\infty {{A_\omega }} {{\rm{e}}^{j\omega (x + \delta (t))}} $ | (3) |
此时, 每个频率对应的傅里叶级数展开式为:
| $ {S_\omega }(x, t) = {A_\omega }{{\rm{e}}^{j\omega (x + \delta (t))}} $ | (4) |
由此可以观察到图像每个像素点在
| $ {Y_\omega }(x, t) = \omega \delta (t) $ | (5) |
因此,
拉索的主振方向垂直于拉索边缘, 若要提取出主振方向, 先利用直线检测算法确定拉索边缘的位置. 张宇航等[18]使用基于Canny算子的边缘识别算法获取边缘图像序列, 但传统的图像边缘检测算法只使用如sobel算子、Canny算子等对图像进行处理, 无法去除干扰直线, 即会提取出每帧图片中的大部分直线, 但不能精确针对拉索边缘直线进行检测. 一般情况下, 拉索两边缘的长度在所拍摄的视频中会大于干扰线段, 基于霍夫变换改进的最大长度线段检测算法可以有效地解决这一问题.
霍夫变换进行直线检测的原理[19]是利用点与线的对偶性, 即二维图像中的直线的坐标与极坐标中的点是一一对应的, 极坐标中的点与二维图像中的直线也是一一对应的. 因此霍夫直线检测算法就是把寻找图像中直线的问题转换为寻找极坐标中的峰值来完成的. 每帧图像中构成直线的像素坐标值在
通常情况下, 傅里叶变换只能用来处理所拍摄视频的全局运动, 但当振动信号并非存在于整个视频中, 而是只出现在其中的部分区域时, 使用全局傅里叶变换对视频进行处理会造成较大的误差. 因此, Wadhwa等[8]提出了基于空间局部相位的运动提取这一概念, 使用复可控金字塔将图像中的正弦曲线分解为局部的正弦信号, 进而表示局部的运动.
由于拉索的主振方向总是垂直于拉索边缘, 为了能够增大所提取振动信号的信噪比, 提高拉索振动检测精度, 本文设计了方向自适应复可控金字塔, 实现拉索主振方向的自动选取, 在减少其他方向运动干扰的同时也减少了计算量.
复可控金字塔的本质是对图像进行频域多分辨率处理, 视频的每帧图像经不同尺度、不同方向的滤波器进行处理后得到不同尺度、不同方向的频率信息, 对该信息进行处理即得到图像空间域的局部相位信息[22]. 基于拉索的振动方向特性, 本文对原始复可控滤波器进行改进, 设计了方向自适应复可控滤波器. 传统的复可控滤波器的本质是基于“尺度-方向”的带通滤波器, 其中, “尺度”指的是金字塔分解的层数, 而“方向”则是对二维图像滤波时选取的方向. 针对拉索来说, 需要设计不同尺度同一方向的复可控滤波器, 对拉索的主振方向进行自动选取并且进行多尺度滤波.
首先获取图像中运动信号的局部相位.
| $ {{T}_{i, j}} = \arg (IDFT({{H}_{i, j}} \odot DFT(I)) $ | (6) |
其中, IDFT、DFT分别代表离散傅里叶逆变换和离散傅里叶变换, arg表示对复数求幅角,
(1) 设计极坐标系. 将一维图像的平面直角坐标系转化为极坐标系. 将图像矩阵进行归一化到 [−1, 1]内, 将其转化为极坐标, 即极径的最大值为
(2) 设计不同尺度的高通和低通模板. 高通模板 (HM): 在(1)中的极坐标中, 针对任一尺度的极径
高通模板设计过程如下:
| $ HM = \left\{ \begin{gathered} 1,\qquad\qquad\qquad\qquad\quad\;{\textit{r}} \geqslant {{\textit{r}}_i} \\ \left| {\cos \left[ {\frac{{\text{π}} }{{2\tau }}\left( {{{\log }_2}\left( {\frac{{{r_{\max }}}}{r}} \right)} \right)} \right]} \right|,\;{{\textit{r}}_i} \times {2^{ - \tau }} \lt r \lt {r_i} \\ 0,\qquad\qquad\qquad\qquad\quad\;{\textit{r}} \leqslant {{\textit{r}}_i} \times {2^{ - \tau }} \\ \end{gathered} \right. $ | (7) |
其中, r为极径, 当r大于并等于
低通滤波器设计过程如下:
| $ LM = 1 - H{M^2} $ | (8) |
可以观察到, 低通滤波器是由高通滤波器模板转化而来. 图3为所得到的高通模板和低通模板的示意图.

|
图 3 高通滤波器模板和低通滤波器模板示意图 |
在设计滤波器时需要保证极径大小在图像大小的范围内, 所以
| $ H = \left\lfloor {{{\log }_2}\left( {\min \left( {a, b} \right)} \right)} \right\rfloor - 2 $ | (9) |
其中, 图像宽度为a, 长度为b, H为方向自适应复可控金字塔分解的总层数.
(3) 生成每一尺度下的带通模板BM. 每个尺度的带通模板都是由该尺度的低通模板与下一尺度的高通模板相乘所得, 即:
| $ BM = HM \odot LM $ | (10) |
式(10)表示将高通模板中的矩阵与低通模板中的矩阵的对应元素相乘, 生成新的带通模板, 如图4所示.

|
图 4 带通滤波器模板 |
(4) 设计方向模板. 针对拉索的针对特性, 设计全方向的模板, 可以自动选取拉索的主振方向, 将图像分成T个方向 (一般取T=4), 方向模板设计如下.
| $ \Theta {\text{ = }}\left\{ {\begin{array}{*{20}{l}} {2\sqrt {\dfrac{{{2^{2\left( {T - 1} \right)}} \cdot \left( {T - 1} \right)!}}{{T \cdot \left( {2\left( {T - 1} \right)} \right)!}}} \cdot {{\left[ {\cos \left( {\theta - {\theta _0}} \right)} \right]}^{T - 1}}, {\text{ }}\left| {\theta - {\theta _0}} \right| \lt \dfrac{{\text{π}} }{2}} \\ 0 , \qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad {\rm{others}} \end{array}} \right. $ | (11) |
其中,
拉索的主振方向即为垂直于拉索的边缘的方向[16], 传统的复可控金字塔中的方向滤波器固定选取0、45°、90°、135°等4个方向, 由于拉索的主振方向并不一定落在这些特殊角度, 因此, 当拉索倾斜角度与原始方向滤波器选取角度不匹配时, 无法匹配拉索的主振方向, 提取到的拉索振动信号微弱, 此时对拉索振动信号会出现较大误差. 传统的方向滤波器如图5(a)所示, 本文改进的自适应方向滤波器 (两根任意拉索主振方向对比)如图5(b)所示.

|
图 5 传统方向滤波器和方向自适应滤波器 |
(5) 生成方向自适应复可控滤波器组. 将每个尺度的带通滤波器模板与方向模板相乘, 就可得到不同尺度同一方向的自适应滤波器, 即:
| $ {\Lambda _i} = B{M_i} \odot \Theta $ | (12) |
其中,
通过方向自适应复可控金字塔的处理可以得到图像的相位信息, 上述步骤只获取二维图像的离散信息, 因此, 图像的局部相位可通过式(13)获取.
| $ {\Phi _i} = \arg \left( {IDFT\left( {{\Lambda _i} \odot DFT(I)} \right)} \right) $ | (13) |
其中,
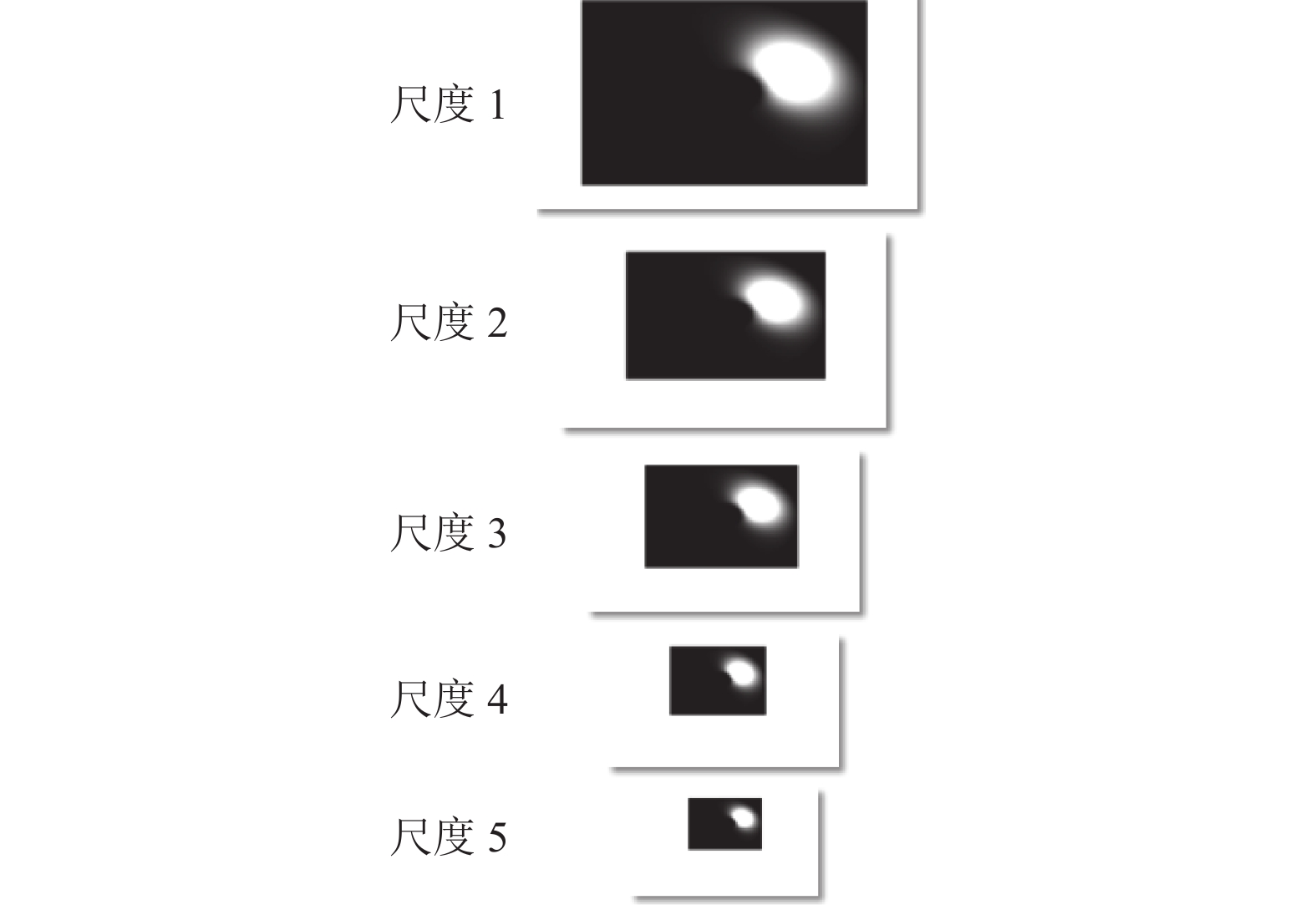
|
图 6 方向自适应复可控滤波器组 |
方向自适应金字塔通过对拉索主振方向的选取, 将视频中每一帧图像中的亮度信号分解为不同尺度同一方向的局部相位, 从而提取出目标拉索的振动信号. 因一段视频由若干帧图片组成, 将式(13)转化为以下形式.
| $ {\Phi _{i, m}} = \arg \left( {IDFT\left( {{\Lambda _i} \odot DFT({I_m})} \right)} \right) $ | (14) |
其中,
为了获取不同空间尺度下拉索的振动信息, 增强拉索振动信号的信噪比, 对获取到的不同尺度的相位矩阵取平均值, 即:
| $ {\Phi ' _m} = \frac{1}{H}\sum\limits_{i = 1}^H {{\Phi _{i, m}}} $ | (15) |
其中, H为相位矩阵,
| $ \phi \left( m \right) = \frac{1}{{A \cdot B}}{\sum\limits_x {\sum\limits_y {{\Phi ' _m}} } } $ | (16) |
其中,
相位序列
| $ \hat \phi \left( k \right) = \sum\limits_{m = 0}^{M - 1} {\phi \left( m \right)} \cdot {{\rm{e}}^{ - i\frac{{2{\text{π}} }}{M}mk}},\;k = 0, 1, \cdots , M - 1 $ | (17) |
其中
| $ {k_{\max }} = \max \left\| {\hat \phi \left( k \right)} \right\| $ | (18) |
通过式(19)将
| $ f = \frac{{\left( {{k_{\max }} - 1} \right) \cdot {\textit{Fs}}}}{M} $ | (19) |
其中, Fs表示视频的采样率,
本文实验拍摄场景如下: 场景1为合肥工业大学东风广场, 场景2为合肥市南淝河大桥. 实验所选取拉索L1–L3位于合肥工业大学东风广场, 如图7(a1)所示. 拉索一端连接广场遮阳棚, 一端连接地面, 起到固定遮阳棚的作用. 拉索长度约10 m, 与地面夹角范围为30°–55°; 由于遮阳棚重量较轻, 拉索受力较小, 因此在橡胶锤激励下东风广场拉索所产生振动趋向于低频. 实验所选取拉索D1–D6位于南淝河大桥. 拉索一端连接桥面, 一端连接桥体顶端, 承受桥面重力. 拉索长约30 m, 与地面夹角范围为45°–60°, 由于桥上斜拉索所受拉力较大, 其在激励下更容易产生较高频率的振动[24].
本实验使用佳能相机拍摄拉索振动的视频, 相机分辨率为1280×720, 帧率为50 fps, 拍摄视频时间为10 s. 同时使用YX 1207加速度传感器获取拉索振动数据作为真值, 采样率为51.2 Hz. 分别使用本文算法、文献[15]的PVE算法以及文献[7]的Thornton2017模板匹配算法对采集数据进行处理, 获取所拍摄视频中拉索的振动峰值频率以及频谱图进行对比试验.
使用橡胶锤手动对拉索进行激励, 三脚架和相机在距离拉索4 m的位置进行视频拍摄, 选取东风广场拉索和南淝河大桥拉索进行实验, 使用相机对各拉索拍摄视频对拉索振动频率进行测量, 同时将加速度计粘贴到对应拉索上进行真值采集. 实验场景图如图7所示, 其中, (a2)从左到右分别为L1–L3所拍摄视频截图, (b2)从左到右分别为D1–D5所拍摄视频截图.
以下3个统计量构成了本文频率测量性能的评价指标.
1) 所得峰值频率:
| $ {P_{AS}} = ({\text{argmax}}(AS) - 1) \cdot \frac{{{F_S}}}{N}\sqrt {{a^2} + {b^2}} $ | (20) |
其中, PAS为测量的幅度频谱, N为数据点个数,

|
图 7 本文实验场景图以及各拉索视频截图 |
2) 所得频谱与真值的均方误差, 记为RMSE, 用来反映多次测量结果中, 所测频率偏离真实频率的程度.
| $ {{\textit{RMSE}}_{AS}} = \sqrt {\frac{1}{N}\sum\limits_{k = 1}^N {(A{S_k} - GA{S_k}} {)^2}} $ | (21) |
其中, GAS为加速度传感器的幅度频谱真值, N是数据点个数, k是频谱的采样点序号.
3) 所得频谱与真值频谱间的相关系数:
| $ PC{C_{AS}} = \frac{{\displaystyle\sum\nolimits_{{{k}} = 1}^N {(A{S_k} - \overline {AS} )(GA{S_k} - \overline {GAS} )} }}{{\sqrt {\displaystyle\sum\nolimits_{k = 1}^N {{{(A{S_k} - \overline {AS} )}^2}} \sqrt {\displaystyle\sum\nolimits_{k = 1}^N {{{(GA{S_k} - \overline {GAS} )}^2}} } } }} $ | (22) |
其中,
为了进一步分析本文方法对拉索频率的检测效果, 以L1拉索为例, 给出本文算法、PVE、Thornton2017等3种方法检测得到的幅度频谱, 如图8所示. 此外, 为了便于直观对比各算法性能, 每种方法所测得的频谱与加速度传感器所测真值频谱放在同一坐标系中, 并进行相关系数计算. 表1所示为各方法测量结果的评价指标.
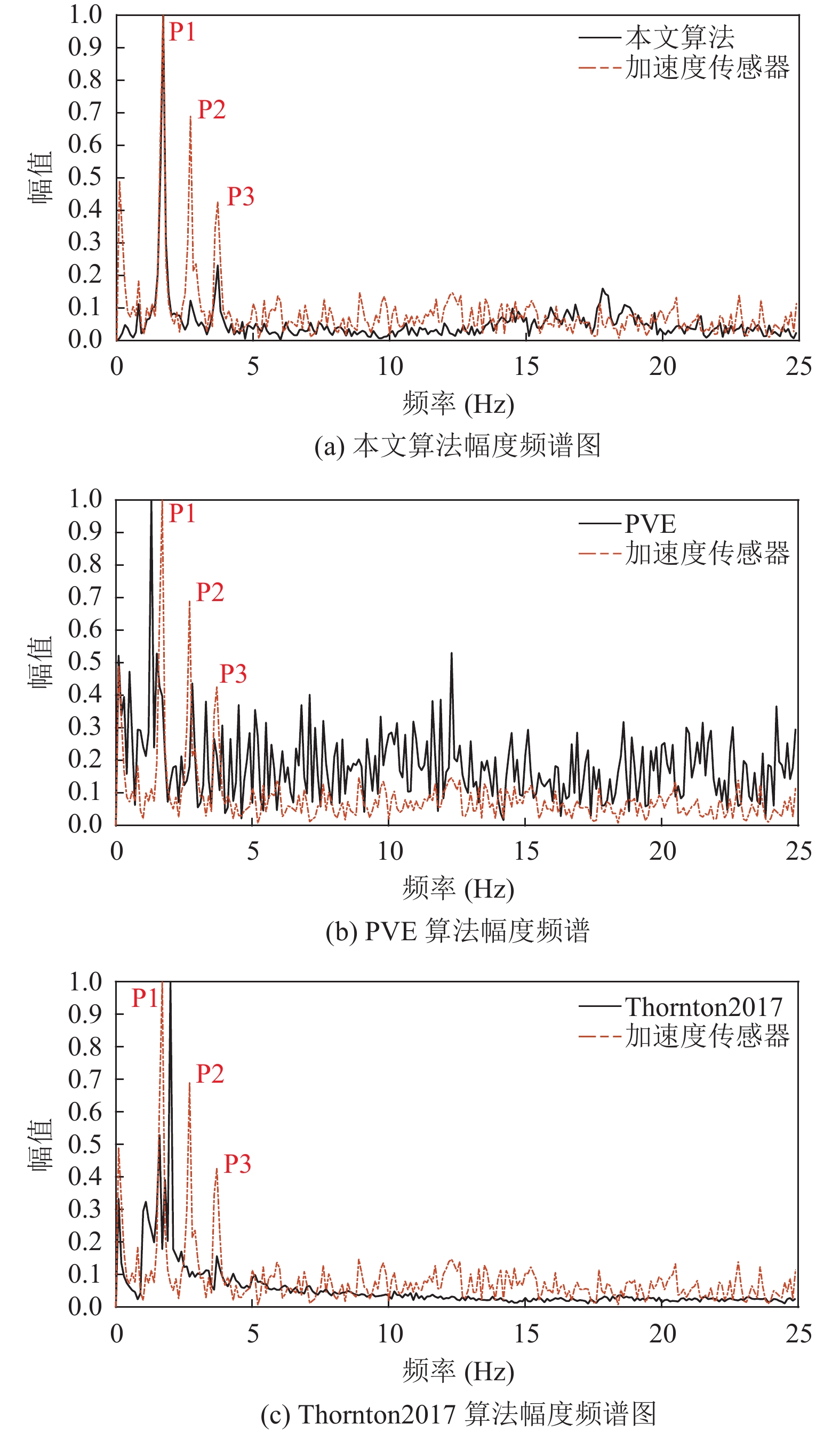
|
图 8 L1拉索检测所得幅度频谱图 |
从结果可知, 本文算法取得了最佳测量效果. 本文算法所测峰值频率与加速度传感器真值一致, 并且与加速度传感器的频谱相关系数 (PCCAS)达到了最高的0.7119. Thornton2017所测峰值频率与真值频率产生了0.3 Hz的误差, 均方误差 (RMSE)明显高于本文算法, 与真值频谱的相关性明显低于本文算法. PVE的峰值频率与真值偏差最大, 测量效果在3种方法中最不理想.
此外, 加速度传感器所测频谱存在3个峰值 (分别在频谱图中以P1, P2, P3标注). 图9从细节上展示了本文算法在峰值P1, P2, P3所处频段内 (1.0–4.3 Hz)的检测效果. 由本节结果可知, 本文算法在全部3个谱峰处均正确检测出峰值频率, 并且在谱峰相关频段内与真值频谱的相关系数达到了0.8347, 如表2所示.
| 表 1 L1拉索检测所得结果评价指标 |

|
图 9 L1谱峰幅度频谱图 |
| 表 2 L1谱峰频率对比 |
为了进一步验证本文方法对拉索频率检测的有效性, 使用本文算法、PVE、Thornton2017对L2、L3拉索的振动视频再次进行处理, 最终得到的全部3根拉索的检测结果如表3所示.
从结果可以看出, 对于L2、L3两根拉索, 本文方法相比较于对比算法仍旧具备较高的鲁棒性, 峰值频率的误差最小, 与真值频谱的相关性也最高. 因此, 本文方法能够实现准确的拉索频率测量.
2.2.2 南淝河桥拉索南淝河大桥拉索较东风广场拉索更长、与地面夹角也更大. 使用橡胶锤对拉索进行激励, 同时使用加速度传感器测量拉索的振动频率. 以D1拍摄的视频处理结果为例, 同上节对L1处理步骤对D1进行数据处理, 将本文算法以及两种对比算法所测得的频谱与加速度传感器所测真值频谱分别放在同一坐标系中, 并进行相关系数计算. 在本文算法、PVE、Thornton2017等3种方法下所得的幅度频谱如图10所示, 表4所示为各方法测量结果的评价指标.
| 表 3 东风广场拉索检测所得结果汇总及评价指标 |
通过分析本节实验可得出结论: 本文算法对D1测量得到的频谱与加速度传感器的频谱相关系数(PCCAS)为0.8199, 远高于PVE算法与Thornton2017算法PCCAS数值. Thornton2017所测峰值频率与真实峰值频率产生了0.4 Hz的误差, 均方误差值一致, 且本文算法对D1测量得到的频谱与加速度传感器的频谱相关系数 (RMSE)明显高于本文算法, 与真值频谱的相关性明显低于本文算法. PVE的峰值频率与真实峰值偏差最大, 并且均方误差 (RMSE)和频谱相关系数 (PCCAS)在3种方法中最不理想.
此外, 加速度传感器所测频谱存在4个峰值(分别在频谱图中以P1, P2, P3, P4标注). 图11从细节上展示了本文算法在峰值P1, P2, P3, P4所处频段内 (1.7–6.7 Hz)的检测效果. 针对D1拉索振动频率, 加速度传感器得出4个峰值频率, 而本文算法只测到了3个. 通过分析D1振动的多个峰值的测量结果, 可以看出本文算法对高频谐振分量的测量结果准确度略低于L1测量结果, D1谱峰频率对比结果如表5所示.
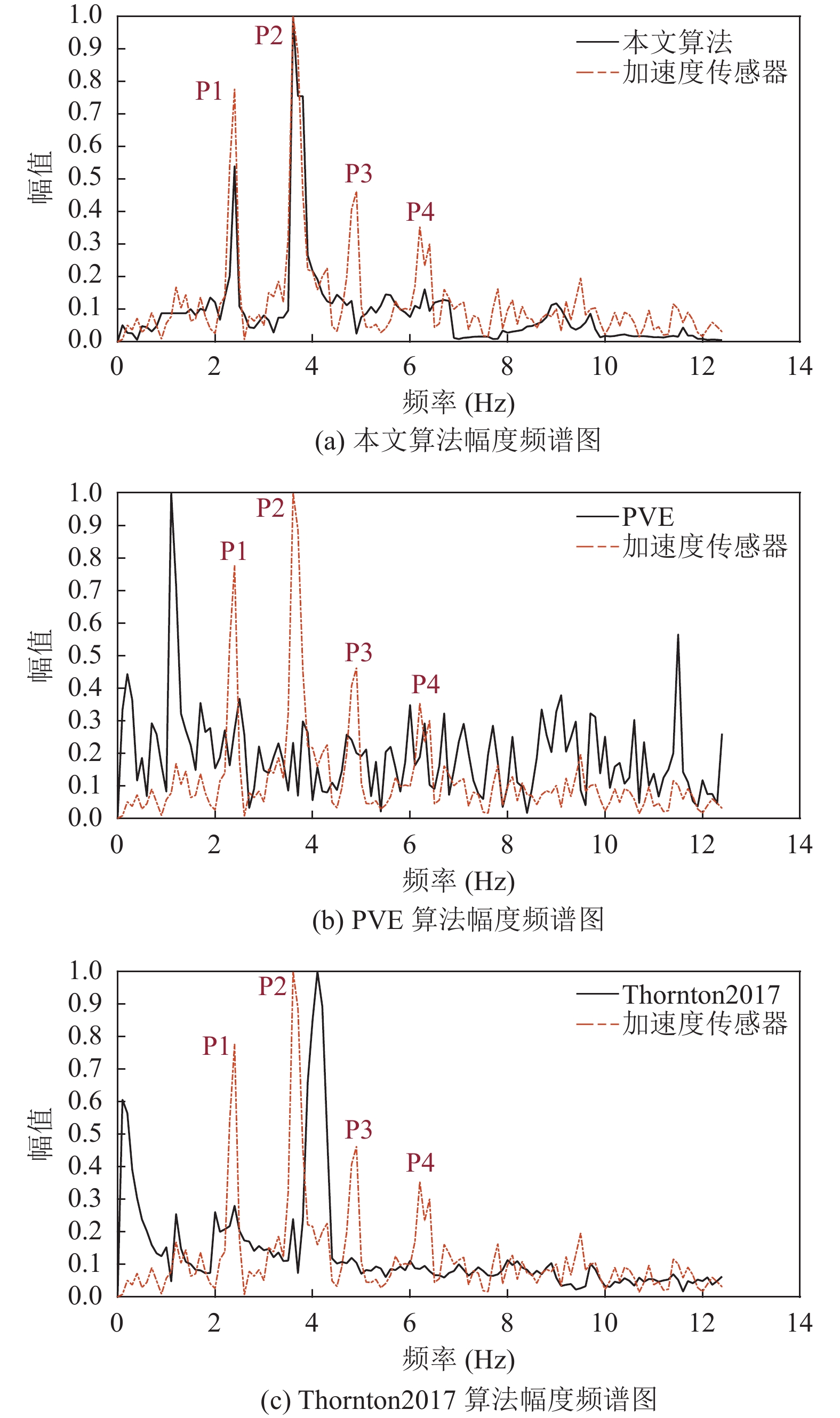
|
图 10 D1幅度频谱图 |
| 表 4 D1结果评价指标 |
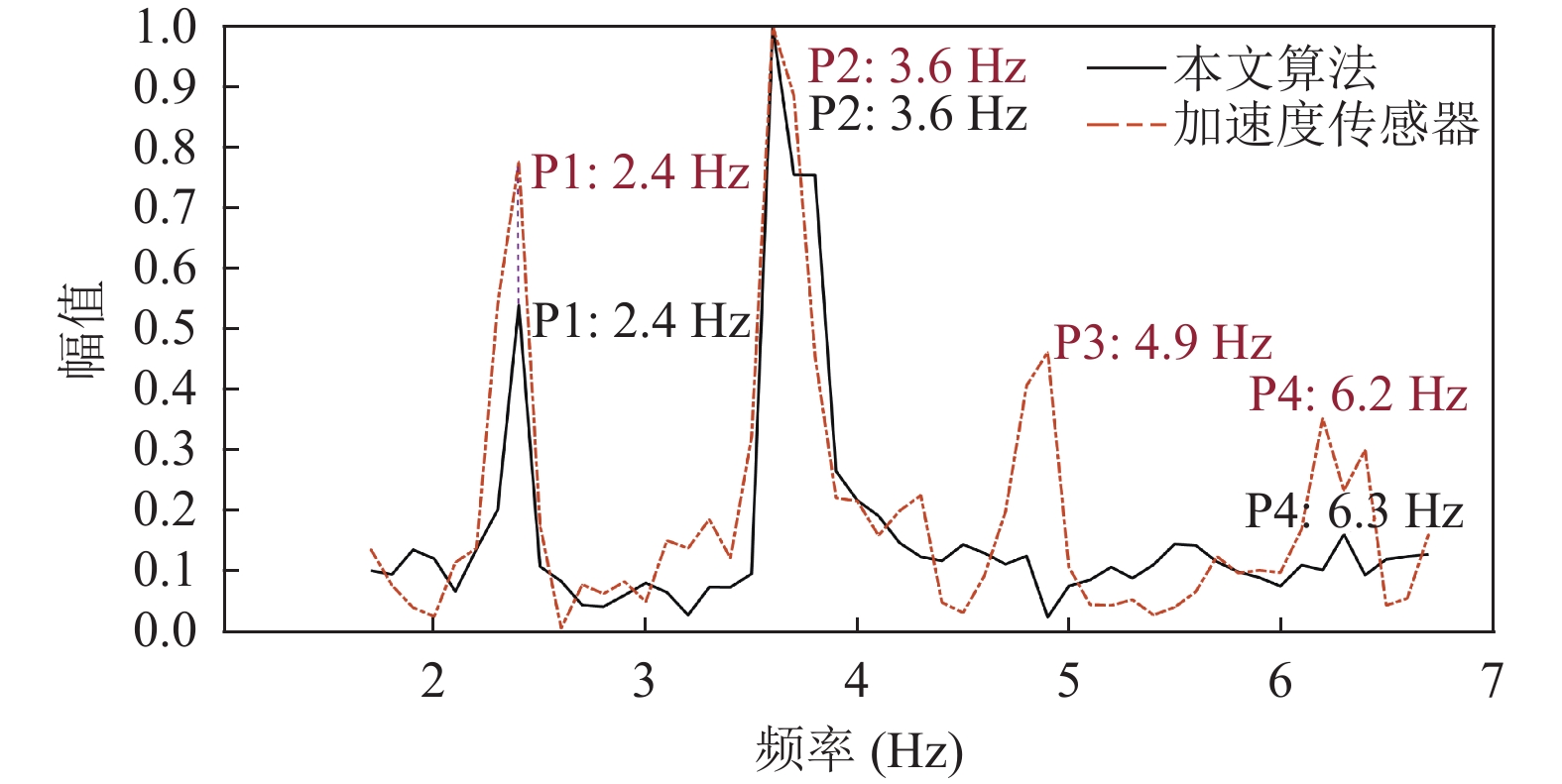
|
图 11 D1谱峰幅度频谱图 |
| 表 5 D1谱峰频率对比 |
相较于本文算法, 两种对比算法在真实场景下对拉索振动频率进行测量时都存在较大误差.
为了进一步验证本文方法对拉索频率检测的有效性, 使用本文算法、PVE、Thornton2017对D2–D5拉索的振动视频再次进行处理, 最终得到的全部5根拉索的检测结果如表6所示.
| 表 6 南淝河大桥拉索结果汇总及评价指标 |
由实验可以看出, 本文算法能够有效地解决真实场景下的振动频率测量问题, 能够准确地从拍摄视频中提取出拉索的振动信号, 相较于其他方法, 本文的误差更小, 鲁棒性更强.
2.2.3 补充实验本文算法基于空间相位的振动提取框架, 对光照变化和图像噪点具备较高的鲁棒性, 在夜晚光照微弱的环境下对东风广场拉索L1进行视频拍摄, 拍摄设备参数同实验设置, 拍摄场景图如图12所示.
本文算法在光照微弱环境下对L1拍摄视频进行处理, 将本文算法所测得的频谱与加速度传感器所测真值频谱分别放在同一坐标系中, 并进行相关系数计算, 频谱图如图13所示. 通过分析夜晚场景下L1振动的多个峰值的测量结果, 可以看出本文算法在光照不佳的情况下仍具有较高的准确性.

|
图 12 夜晚实验场景图 |

|
图 13 L1夜晚场景下谱峰幅度频谱图 |
表7所示为本文算法在夜晚场景下测量结果的评价指标. 本文算法所测峰值频率与加速度传感器真值一致, 并且与加速度传感器的频谱相关系数 (PCCAS)达到0.6681. 由表7可出结论, 本文算法在光照不足情况下对拉索振动频率检测效果较好, 验证了本文算法框架对光照变化具有较高的鲁棒性.
| 表 7 L1夜晚场景下结果评价指标 |
2.3 实验分析
实验结果表明, 在3种对比方法中, 本文算法达到了最高的测量准确率, 其次是Thornton2017采用的模板匹配方法, 测量效果最差的是经典PVE. 对于经典PVE算法, 一方面由于使用固定方向的复数可控滤波器, 难以准确匹配到拉索的主振方向, 因而无法精确提取拉索的微小振动信号; 另一方面, 未对拉索边缘区域的相位信号进行增强, 导致振动信号湮没于相位噪声中. 因此, 经典的PVE算法若直接用于拉索振动测量, 提取到的振动信号可能包含大量噪声. 对于Thornton2017采用的模板匹配方法, 其运动信号提取方式是基于图像亮度的, 受图像噪声和环境光照变化影响较大, 影响到对目标振动信号的提取. 此外, 拉索结构的自相似性和背景的细微变化容易导致模板匹配错误, 进而引入高频噪声, 导致振动频谱向高频方向偏移(Thornton2017检测东风广场拉索的主振频率比真值高了0.3 Hz). 本文算法采用方向自适应复可控滤波器精确匹配拉索的主振方向, 并通过相位谱加权增强了边缘振动信号; 同时, 基于空间相位的振动提取框架也保证了算法对光照变化和图像噪点具备较高的鲁棒性. 因而本文算法能够准确实现拉索振动信号的提取和频率测量.
通过分析两个场景中拉索振动的多个峰值的测量结果, 可以看出本文算法对高频谐振分量的测量结果较差. 场景2中加速度传感器测出了4个峰值, 而本文算法只测到了3个, 原因在于相位谱加权的过程, 可能会将部分高频振动信号产生的相位变化当作噪声消除掉. 因此, 在最后获取到的幅度频谱函数中, 不存在这些振动分量所对应的谱峰. 然而, 对于强度较大的主振频率, 本文算法始终能够保持良好的检测效果.
3 结论与展望本文提出了基于方向自适应复数可控滤波器的拉索振动检测方法, 针对实际环境下拉索的振动特性, 设计了方向自适应复可控金字塔, 对真实场景下所拍摄的拉索视频进行有效处理, 实现了拉索振动频率的精确测量. 本文算法相较于传统视觉相位振动检测算法, 具有更高的鲁棒性. 实验表明, 本文算法与基于加速度传感器测量的拉索振动频率具有同等的测试精度.
在斜拉桥开通使用后, 其拉索振动可能会出现多阶频率, 本文算法现阶段对拉索振动的高阶频率检测具有一定程度的局限性. 在未来的研究中, 将针对拉索振动的高阶频率开展研究, 提高算法对拉索振动频率检测的鲁棒性.
| [1] |
Li H, Ou JP. The state of the art in structural health monitoring of cable-stayed bridges. Journal of Civil Structural Health Monitoring, 2016, 6(1): 43-67. DOI:10.1007/s13349-015-0115-x |
| [2] |
陈泽贤. 基于数字图像处理技术的索力测试应用研究[硕士学位论文]. 广州: 广州大学, 2017.
|
| [3] |
Ji YF, Chang CC. Nontarget stereo vision technique for spatiotemporal response measurement of line-like structures. Journal of Engineering Mechanics, 2008, 134(6): 466-474. DOI:10.1061/(ASCE)0733-9399(2008)134:6(466) |
| [4] |
Kim SW, Kim NS. Multi-point displacement response measurement of civil infrastructures using digital image processing. Procedia Engineering, 2011, 14: 195-203. DOI:10.1016/j.proeng.2011.07.023 |
| [5] |
Chen CC, Tseng HZ, Wu WH, et al. Modal frequency identification of stay cables with ambient vibration measurements based on nontarget image processing techniques. Advances in Structural Engineering, 2012, 15(6): 929-942. DOI:10.1260/1369-4332.15.6.929 |
| [6] |
晏班夫, 陈泽楚, 朱子纲. 基于非接触摄影测量的拉索索力测试. 湖南大学学报(自然科学版), 2015, 42(11): 105-110. DOI:10.16339/j.cnki.hdxbzkb.2015.11.035 |
| [7] |
Feng DM, Scarangello T, Feng MQ, et al. Cable tension force estimate using novel noncontact vision-based sensor. Measurement, 2017, 99: 44-52. |
| [8] |
Wadhwa N, Rubinstein M, Durand F, et al. Phase-based video motion processing. ACM Transactions on Graphics, 2013, 32(4): 80. |
| [9] |
Wadhwa N, Rubinstein M, Durand F, et al. Riesz pyramids for fast phase-based video magnification. Proceedings of the 2014 IEEE International Conference on Computational Photography. Santa Clara: IEEE, 2014. 1–10.
|
| [10] |
Chen JG, Wadhwa N, Cha YJ, et al. Modal identification of simple structures with high-speed video using motion magnification. Journal of Sound and Vibration, 2015, 345: 58-71. DOI:10.1016/j.jsv.2015.01.024 |
| [11] |
Gautama T, van Hulle MA. A phase-based approach to the estimation of the optical flow field using spatial filtering. IEEE Transactions on Neural Networks, 2002, 13(5): 1127-1136. DOI:10.1109/TNN.2002.1031944 |
| [12] |
Fleet DJ, Jepson AD. Computation of component image velocity from local phase information. International Journal of Computer Vision, 1990, 5(1): 77-104. DOI:10.1007/BF00056772 |
| [13] |
Davis A, Bouman KL, Chen JG, et al. Visual vibrometry: Estimating material properties from small motions in video. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(4): 732-745. DOI:10.1109/TPAMI.2016.2622271 |
| [14] |
Choi AJ, Han JH. Frequency-based damage detection in cantilever beam using vision-based monitoring system with motion magnification technique. Journal of Intelligent Material Systems and Structures, 2018, 29(20): 3923-3936. DOI:10.1177/1045389X18799961 |
| [15] |
Peng C, Zeng C, Wang YG. Camera-based micro-vibration measurement for lightweight structure using an improved phase-based motion extraction. IEEE Sensors Journal, 2020, 20(5): 2590-2599. DOI:10.1109/JSEN.2019.2951128 |
| [16] |
汪峰, 向泓嘉, 刘章军. 随机激励下斜拉索-梁参数振动模型及响应分析. 应用力学学报. http://kns.cnki.net/kcms/detail/61.1112.O3.20220617.1857.002.html. (2022-01-10).
|
| [17] |
张倩, 陈其浩, 杨硕. 基于改进概率霍夫变换的表格字符定位算法. 软件导刊, 2021, 20(11): 204-209. DOI:10.11907/rjdk.211928 |
| [18] |
张宇航, 苏成, 邓逸川. 基于欧拉运动放大算法的桥梁索力测试方法研究. 图学学报, 2021, 42(6): 941-947. |
| [19] |
Yang G, Hu JP, Hou ZC, et al. A new Hough transform operated in a bounded Cartesian coordinate parameter space. IET Image Processing, 2022, 16(8): 2282-2295. DOI:10.1049/ipr2.12489 |
| [20] |
李长有, 陈国玺, 丁云晋. 改进Canny算子的边缘检测算法. 小型微型计算机系统, 2020, 41(8): 1758-1762. DOI:10.3969/j.issn.1000-1220.2020.08.031 |
| [21] |
赵子润, 高保禄, 郭云云, 等. 基于改进Canny算法的噪声图像边缘检测. 计算机测量与控制, 2020, 28(12): 202-206, 212. DOI:10.16526/j.cnki.11-4762/tp.2020.12.042 |
| [22] |
宋正伟, 陈鲸, 杨学志, 等. 基于振动相位信号分解的非接触式心率检测. 计算机系统应用, 2021, 30(10): 171-179. DOI:10.15888/j.cnki.csa.008125 |
| [23] |
Zang ZD, Yang XZ, Zhang G, et al. Phase-based vibration frequency measurement from videos recorded by unstable cameras. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 5018714. |
| [24] |
傅理文, 吴书正, 夏庆云. 拉索振动的参数分析及测试系统研究. 城市道桥与防洪, 2017(12): 171-176. DOI:10.16799/j.cnki.csdqyfh.2017.12.048 |
 2023, Vol. 32
2023, Vol. 32


