随着现代医学影像技术的发展, 医学图像被广泛应用在临床的诊断和治疗中^[1]. 常见的医学图像应用于临床治疗的例子有图像融合、影像导航手术等, 而其中的关键技术为医学图像配准技术. 医学图像配准是指将两张医学图像在空间坐标以及内部结构上进行对齐, 以达到定位病灶的效果. 从数学模型上来说, 医学图像配准的实质即为通过优化算法迭代寻找某个空间变换, 使得在这个空间变换下, 两张图像的相似程度达到最高^[2]. 在骨科手术、放射治疗等治疗方法中, 2D/3D医学图像配准技术是一种稳定、常用的辅助手段, 它可以有效降低手术的复杂程度, 被广泛应用于手术的术前规划和术中实践等环节^[3].

为了完成医学图像配准的任务, 需要使用某种优化算法进行迭代, 以找到某种最优的空间参数^{[4, 5]}. 近些年来, 元启发式优化算法(meta-heuristics optimization algorithms)具有简单性、独立性、灵活性以及无梯度性等优点^[6], 已被广泛应用于各种领域. Faramarzi等人^[7]在2020年提出平衡优化器(equilibrium optimizer, EO)的新型优化算法, 这是一种基于群体智能的全局优化算法, 其灵感来源于控制体积上的混合动态质量平衡, 通过对控制体积中进入、离开和生成的质量进行浓度更新, 达到最终的动态平衡状态. 相比于其他优化算法, EO求精确解的能力更高, 且全局搜索能力更强, 但EO存在初始化种群多样性较低、收敛速度慢和易陷入局部最优解的问题^[8]. 针对上述问题, 已经有相关文献对此进行改进. Fu等人^[9]提出并行平衡优化器的框架, 采用多组结构, 组间采用两种策略来加快算法的收敛速度并促进算法寻找更优解, 并改进了 $ {a_2} $ 的公式来提高算法搜索能力. Gupta等人^[10]在平衡优化器中引入高斯变异的策略, 还有基于种群分割和重建概念的额外探索性搜索机制. 引入的新概念能保持解的多样性, 并提高收敛速度以获得更精确的解. Tang等人^[11]首先将种群分成3个子种群, 并执行不同的策略来指导种群进化; 其次引入高斯分布估计策略, 提高算法性能. 以上改进策略虽然在性能上有所改善, 但仍存在陷入局部极值、求解精度低的问题, 且对医学图像配准算法的适用性较低.

针对上述存在的问题, 本文提出一种基于改进平衡优化器的医学2D/3D图像快速配准算法: 首先, 引入Logistic-Tent混沌映射初始化种群, 保证初始种群的离散度和多样性; 其次, 对迭代函数进行公式更新, 让其全局搜索能力进一步提高; 之后针对算法陷入局部极值而搜索停滞的问题, 引入Levy飞行策略对粒子进行扰动, 从而逃离局部极值, 重新进入搜索; 最后, 将改进后的平衡优化器应用于医学图像配准, 并对配准的流程进行优化, 将Host端和Device端的数据传输进行并行处理, 以提高配准速度.

1 平衡优化器

平衡优化器是一种基于物理的元启发式算法, 其中式(1)表示通用质量平衡方程的一阶常微分方程, 通过对控制体积中进入、离开和生成的质量进行浓度更新, 达到最终的动态平衡状态.

$ V\frac{{dC}}{{dt}} = Q{C_{{\rm{eq}}}} - QC + G $

(1)

其中, $V$ 为容器的容积, $V\dfrac{{dC}}{{dt}}$ 表示容器内的质量变化率, $C$ 为溶液密度, $Q$ 为流进或流出控制容积的容量流率, ${C_{{\rm{eq}}}}$ 表示平衡状态下的浓度, $G$ 为容器内的质量生成速率.

将式(1)中控制体积的浓度 $C$ 作为时间 $t$ 的函数并做积分, 得到式(2):

$ C = {C_{{\rm{eq}}}} + ({C_0} - {C_{{\rm{eq}}}})F + \frac{G}{{\lambda V}}(1 - F) $

(2)

其中, ${C_{{\rm{eq}}}}$ 代表平衡状态下的浓度, $F$ 是一个指数项, 定义如式(3)所示. $G$ 代表质量的生成速率.

$ F = {{\rm{e}}^{ - \lambda (t - {t_0})}} $

(3)

其中, $\lambda $ 表示流动率, ${t_0}$ 和 ${C_0}$ 代表初始时间和浓度.

1.1 种群初始化

和大多数元启发式算法类似, EO使用初始种群来启动优化过程. 初始浓度基于粒子数和维度, 在设定的搜索范围内, 随机定义初始种群. 如式(4)所示.

$ \vec C_{d, i}^{{\rm{initial}}} = {C_{\min }} + ran{d_i}({C_{\max }} - {C_{\min }}) $

(4)

其中, $\vec C_{d, i}^{{\rm{initial}}}$ 表示第 $i$ 个粒子的初始位置向量, 且 $d \in [1, D]$ , $D$ 表示待优化问题的维度; $i \in [1, N]$ , $N$ 表示粒子个数. ${C_{\max }}$ 和 ${C_{\min }}$ 分别代表搜索空间的上界和下界, $rand$ 代表0–1范围内的随机数.

1.2 平衡池

为了确定全局平衡状态, 搜索过程中, 算法会找到迄今为止最佳的4个粒子 ${C_{{\rm{eq}}(1)}}$ – ${C_{{\rm{eq}}(4)}}$ , 以及4个最佳粒子的算术平均值 ${C_{{\rm{eq}}({\rm{ave}})}}$ , 这5个粒子共同组成平衡状态池 ${C_{{\rm{eq}}, {\rm{pool}}}}$ .

$ {\vec C_{{\rm{eq}}, {\rm{pool}}}} = \left\{ {\vec C_{{\rm{eq}}(1)}}, {\vec C_{{\rm{eq}}(2)}}, {\vec C_{{\rm{eq}}(3)}}, {\vec C_{{\rm{eq}}(4)}}, {\vec C_{{\rm{eq}}({\rm{ave}})}}\right\} $

(5)

每次迭代中的每个粒子都有相同的概率被随机选中, 并继续引导其他粒子的更新.

1.3 指数项

指数项 $F$ 在浓度更新过程中影响探索和开发之间的平衡. 探索代表算法的全局搜索能力, 而开发代表算法的局部寻优能力. 由于实际容器中流动率 $\lambda $ 可能随时间变化, 因此假设 $\lambda $ 取[0, 1]之间的随机向量. 重新定义的指数项如下所示:

$ \vec F = {{\rm{e}}^{ - \vec \lambda (I - {I_0})}} $

(6)

其中, 变量 $I$ 被定义为迭代函数, 随着迭代次数增加而降低:

$ I = {\left(1 - \frac{{Iter}}{{Max\_iter}}\right)^{\left({a_2}\frac{{Iter}}{{Max\_iter}}\right)}} $

(7)

其中, $Iter$ 和 $Max\_iter$ 分别代表当前迭代次数和最大迭代次数, ${a_2}$ 用于控制算法的开发能力. 为了确保函数收敛, 同时提高算法的平衡性控制, 其中:

$ {I_0} = \frac{1}{{\vec \lambda }}\ln ( - {a_1}sign(\vec r - 0.5)[1 - {{\rm{e}}^{ - \vec \lambda I}}]) + I $

(8)

其中, ${a_1}$ 用于控制算法的探索能力, $\vec r$ 、 $\vec \lambda $ 表示 $[0, 1]$ 区间内的随机向量, $sign(\vec r - 0.5)$ 负责探索和开发的方向.

将式(8)代入式(6), 可以得到:

$ \vec{F}={a}_{1}sign(\vec{r}-0.5)[{{\rm{e}}}^{-\vec{\lambda }I}-1] $

(9)

1.4 生成速率

EO算法中的生成速率 $\vec G$ 通过改进开发阶段来提供精确解. 一般形式的生成率一阶指数衰减过程可以定义为:

$ \vec G = {\vec G_0}{{\rm{e}}^{ - \vec k(t - {t_0})}} $

(10)

在EO算法中, 定义 $\vec k = \vec \lambda $ , 并代入指数项, 则生成速率方程可以定义为:

$ \vec G = {\vec G_0}{{\rm{e}}^{ - \vec \lambda (I - {I_0})}} = {\vec G_0}\vec F $

(11)

其中, ${\vec G_0}$ 可以由式(12)计算得出:

$ {\vec G_0} = \overrightarrow {GCP} ({\vec C_{{\rm{eq}}}} - \vec \lambda \vec C) $

(12)

$ \overrightarrow {GCP} = \left\{ \begin{array}{l} 0.5{r_1} , \quad {r_2} \geqslant GP \\ \, \;{\kern 1pt} 0, \quad \;\;\;\;\; {r_2} \lt GP \\ \end{array} \right. $

(13)

其中, $ {r_1}, r_2^{} $ 代表区间[0, 1]中的两个随机数, $\overrightarrow {GCP} $ 用于控制生成速率. 综上, 最终浓度更新的方程可以表示为:

$ \vec C = {\vec C_{{\rm{eq}}}} + (\vec C - {\vec C_{{\rm{eq}}}})\vec F + \frac{{\vec G}}{{\vec \lambda V}}(1 - \vec F) $

(14)

方程包括3项: 第1项是平衡浓度, 第2项用于控制全局搜索, 第3项用于控制局部搜索, 以获得更加精准的解.

2 基于Logistic-Tent混沌映射及Levy飞行策略的平衡优化器算法 2.1 Logistic-Tent 混沌映射

混沌映射具有非线性复杂的动力学系统, 由于初始值敏感性、伪随机行为和参数敏感性等重要的特征^[12], 经常被应用于产生初始化种群. 平衡优化器使用随机数生成初始种群, 存在聚集度高、降低种群多样性的风险. 经混沌映射产生的初始种群由于其产生的随机性可以人为控制, 可用于优化算法中增加种群多样性, 扩大前期搜索范围和速度^[13].

Logistic混沌映射由式(15)可以表示:

$ {x_{m + 1}} = f(x) = a \cdot {x_m} \cdot (1 - {x_m}) $

(15)

其中, $a \in (0, 4)$ 并且 ${x_m} \in (0, 1)$ . 当 $a \in (3.5699, 4)$ 时, 映射呈现出混沌行为. Logistic混沌映射的主要特点是对初始值敏感, 结构简单.

Tent混沌映射可以由式(16)表示:

$ {x_{m + 1}} = f(x) = \left\{ \begin{array}{l} a \cdot \dfrac{{{x_m}}}{2},\quad\;\;\;\; {x_m} \lt 0.5 \\ a \cdot \dfrac{{1 - {x_m}}}{2}, \;\;{x_m} \geqslant 0.5 \\ \end{array} \right. $

(16)

其中, $a \in (0, 4)$ 并且 ${x_m} \in (0, 1)$ .

Gupta等人^[14]提出将简单的一维Logistic、Tent混沌映射进行交叉组合为混合的Logistic-Tent混沌映射模型, 该模型与简单一维混沌映射相比, 拥有更高性能以及更快速度. Logistic-Tent映射的数学表达式如下:

$ {x_{m + 1}} = f(x) = \left\{ \begin{array}{l} \left(a \cdot {x_m} \cdot (1 - {x_m}) + (4 - a) \cdot \dfrac{{{x_m}}}{2}\right)\bmod 1,\\ {x_m} \lt 0.5 \\ \left(a \cdot {x_m} \cdot (1 - {x_m}) + (4 - a) \cdot \dfrac{{1 - {x_m}}}{2}\right)\bmod 1,\\ {x_m} \geqslant 0.5 \\ \end{array} \right. $

(17)

其中, $a \in (0, 4)$ 并且 ${x_m} \in (0, 1)$ .

由于Logistic-Tent产生相对均匀的伪随机点, 为避免迭代中陷入周期循环点, 初始值种子点随机选取, 即:

$ {x_i} = f(x) = \left\{ \begin{array}{l} \left(a \cdot {r_i} \cdot (1 - {r_i}) + (4 - a) \cdot \dfrac{{{r_i}}}{2}\right)\bmod 1,\quad\;\; {r_i} \lt 0.5 \\ \left(a \cdot {r_i} \cdot (1 - {r_i}) + (4 - a) \cdot \dfrac{{1 - {r_i}}}{2}\right)\bmod 1, {r_i} \geqslant 0.5 \\ \end{array} \right. $

(18)

其中, $x$ 为Logistic-Tent映射产生的点, ${r_i} = rand(0, 1)$ , $i$ 为粒子维数.

Logistic-Tent映射在[0, 1]的分岔图如图1所示, 可以看出映射效果十分均匀.

通过式(18)产生混沌映射的值后, 代入式(4)可得到改进的基于Logistic-Tent映射的初始化种群, 即:

$ \vec C_{d, i}^{{\rm{initial}}} = {C_{\min }} + {x_i}({C_{\max }} - {C_{\min }}) $

(19)

由Logistic-Tent产生的初始随机种群相对全随机初始种群更为分散, 均匀地分布于搜索空间内.

2.2 迭代函数的更新

平衡优化器中, 通过迭代函数I来控制粒子的前进步长. 通过式(9)可以得到, I的取值直接影响指数项, 进而影响粒子步长. 标准平衡优化器中, 迭代函数随着迭代次数增加呈现非线性递减的趋势, 在粒子寻优过程中表现为前期拥有较大步长而后期步长逐渐减小. 即, 通过迭代函数I, 来调节算法的全局搜索能力和局部搜索能力. 图2表示迭代函数对于步长的影响, 可以看出, 随着迭代次数增加, 粒子步长大体呈现减小的趋势.

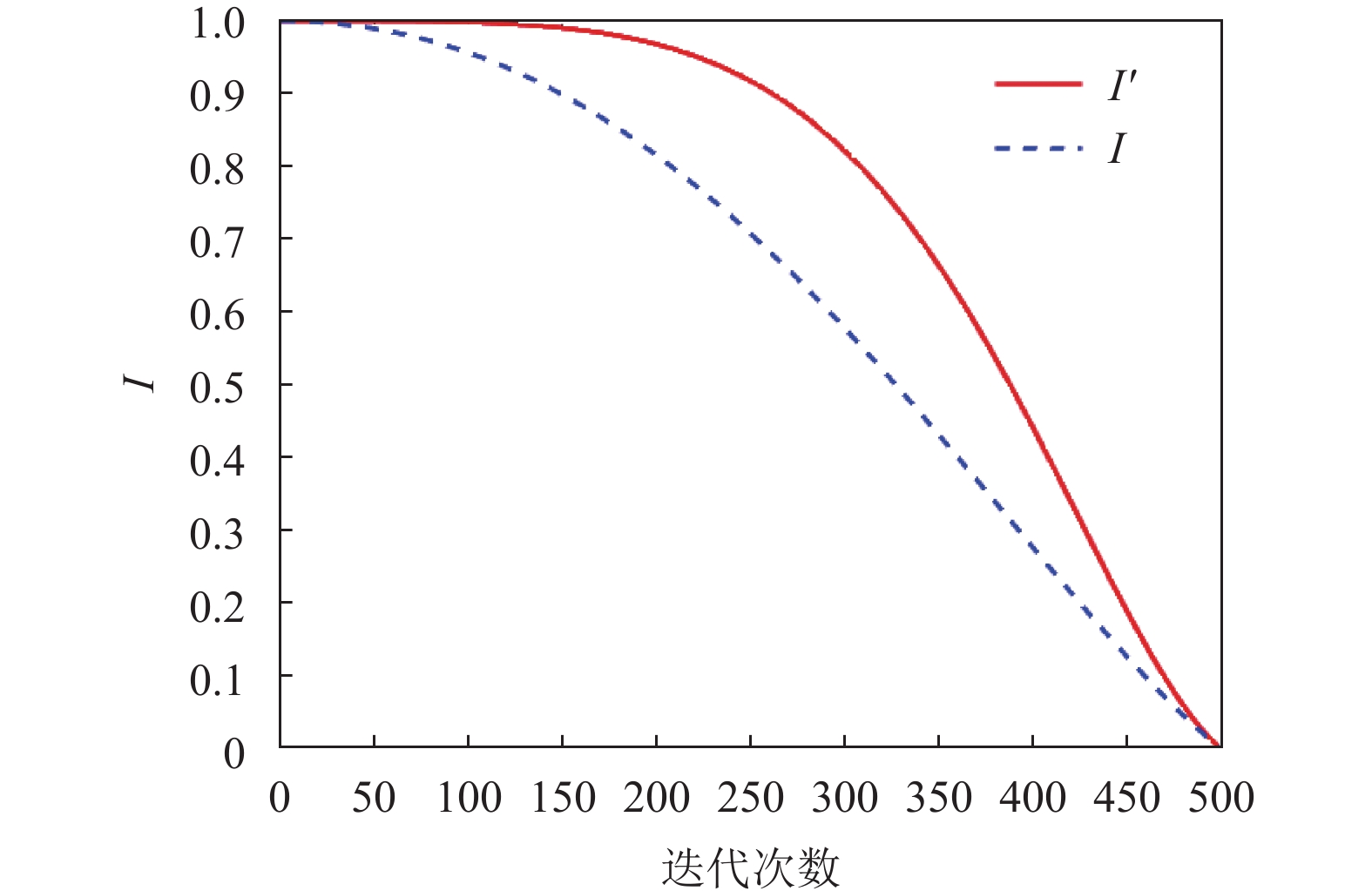
本文对迭代函数进行更新, 以提高算法的收敛速度以及搜索能力. 更新后的迭代函数 $I'$ 被定义为:

$ I' = {\left(1 - \frac{{Iter}}{{Max\_iter}}\right)^{\left({a_2}{{(\frac{{Iter}}{{Max\_iter}})}^3}\right)}} $

(20)

更新后的迭代函数使优化算法在前期有更强的全局搜索能力, 能够发现更多可能存在的全局最优解. 随着迭代次数增多, 这种能力逐渐下降, 更新后迭代函数曲线如图3.

2.3 Levy飞行策略

从式(5)可以得出, 平衡优化器根据迄今为止的5个最优粒子共同组成平衡池, 引导其余粒子的更新. 复杂求解问题往往存在多个局部最优值, 当迭代后期随着5个最优粒子的聚集度升高, 当平衡池中所有粒子搜索至某一极值附近时, 算法就会陷入停滞, 这会增加陷入局部最优的风险. 为了使粒子脱离局部极值, 需要对粒子进行某种扰动策略. 丁瑞成等人^[15]、梁田等人^[16]已经证明在灰狼优化器(grey wolf optimizer, GWO)以及粒子群优化算法(particle swarm optimization, PSO)^[17]中引入Levy飞行策略让算法有效逃离局部极值状态, 避免算法早熟收敛.

Levy飞行是一种重要的非高斯随机游动, 这种游动最主要的特点是能够在不确定的环境中最大限度地探索空间^[18]. 粒子根据Levy飞行进行更新的模型如下:

$ L = \frac{\mu }{{{{\left| \nu \right|}^{\frac{1}{\beta }}}}} $

(21)

其中, $\;\mu $ 、 $\nu $ 满足正态分布, $\mu \sim N(0, \sigma _\mu ^2)$ , $\nu \sim N(0, \sigma _\nu ^2)$ .

其中 ${\sigma _\mu }$ 、 ${\sigma _\nu }$ 满足:

$ {\sigma _\mu } = {\left\{ {\frac{{\Gamma (1 + \beta )\sin \left(\dfrac{{{\text π} \beta }}{2}\right)}}{{\Gamma \left(\dfrac{{1 + \beta }}{2}\right){2^{\frac{{\beta - 1}}{2}}}\beta }}} \right\}^{\frac{1}{\beta }}} $

(22)

$ {\sigma _\nu } = 1 $

(23)

其中, $\Gamma (x)$ 称为伽马函数. $\;\beta \in [0, 2]$ , 通常取1.5.

当连续两次迭代中, 适应度的平均值没有发生变化, 或大于前一代适应度平均值, 判定算法已经进入停滞状态, 并使用Levy飞行策略对粒子进行扰动. 粒子进行扰动的模型如下:

$ C_i^{t + 1} = C_i^t + {S_L} $

(24)

$ {S_L} = L \otimes ({C_{{\rm{eq}}}} - L \otimes {C_i}) $

(25)

其中, $C_i^t$ 表示第 $i$ 个粒子在第 $t$ 次迭代时的位置, ${S_L}$ 表示服从Levy飞行策略的步长, $L$ 由式(21)计算得出.

2.4 算法步骤

步骤1. 设置算法初始化输入参数, 包括迭代次数N、最大粒子个数P、权重系数a₁和a₂、生成概率GP.

步骤2. 使用Logistic-Tent混沌映射初始化N个粒子的种群.

步骤3. 计算种群适应度.

步骤4. 判断算法是否停滞, 若是, 则根据式(24)更新粒子, 并重新计算它们的适应度.

步骤5. 根据适应度筛选出全局最优的4个候选粒子 ${C_{{\rm{eq}}(1)}}$ – ${C_{{\rm{eq}}(4)}}$ .

步骤6. 根据4个最佳候选粒子以及它们的平均值构建平衡池 ${C_{{\rm{eq}},{\rm{pool}}}}$ , 并从中随机选出一个粒子作为平衡粒子 ${C_{{\rm{eq}}}}$ 以引导种群更新.

步骤7. 根据式(20)计算迭代函数的值.

步骤8. 根据式(11)更新生成速率的值, 并根据式(14)指导粒子完成更新.

步骤9. 判断是否达到最大迭代次数, 若否, 则执行步骤3–步骤9; 若是, 则算法终止, 并输出最优的位置以及适应度值.

3 算法评估 3.1 测试数据以及测试环境

为了验证算法的有效性, 从标准测试函数中选取10个基准测试函数, 其中F1–F5为单峰函数, 主要测试算法的收敛速度和寻优精度; F6–F9为多峰函数, 主要测试算法跳出局部最优的能力. F10为固定维多峰函数. 10个基准函数详细信息如表1所示.

实验环境为Windows 11家庭中文版, 处理器为AMD Ryzen 7 4800U @1.80 GHz, 内存大小16 GB, 编程环境为Matlab R2020a.

3.2 基准函数测试

为了验证算法的有效性, 实验设置了同为元启发式算法的粒子群优化算法(PSO)、灰狼优化算法(GWO)、遗传算法(genetic algorithm, GA)^[19]以及标准平衡优化器(EO)算法作为参照组进行对比. 实验中, 将粒子个数统一设置为30个, 迭代次数设置为最大500次. 每个优化算法独立运行30次, 并取30次结果的平均值和标准差, 平均值和标准差分别反映算法的准确性和稳定性. 其中F1–F9为非固定维度函数, 将它们的维度统一设置为30. 不同优化算法对基准函数的运行结果如表2所示, 函数收敛曲线如图4所示. 表2中AVE和STD分别表示结果的平均值和标准差.

由表2和图4得到的结果可以得出, 对于单峰函数F1, F2, F3, F4, F5, PSO和GA均表现欠佳, 算法收敛速度、寻优精度较差, GWO、LTEO、EO在单峰函数上能收敛与最优值较为接近的结果, 其中LTEO在F1、F2的收敛速度与标准EO较为接近, 但寻优精度优于标准EO, 在F3、F4的收敛速度和寻优精度都要优于标准EO, 在F5的收敛速度略低于EO, 但迭代后期取得了更优解. 对于多峰函数F6、F7、F8、F9, GA综合表现最差, 往往在前中期早熟, 算法进入停滞, PSO具备一定的跳出局部极值能力, 但收敛速度过慢. 相比之下GWO、LTEO和EO均具备跳出局部极值的能力, 其中LTEO由于具备良好的全局搜索能力和局部寻优性能, 在多数函数中均收敛至更接近全局最优的解. 综合来说, LTEO在大部分测试函数的收敛速度、寻优精度以及跳出局部极值能力都要优于其他优化函数.

3.3 3种改进策略效果分析

为了验证3种改进策略对于算法结果的影响, 设计了消融实验来分别验证. 实验设计采用Logistic-Tent混沌映射的EO算法(L-EO)、采用新迭代函数公式的EO算法(I-EO)以及采用Levy飞行策略的EO算法(LV-EO)进行对比, 实验结果见表3.

从表3的结果可以得出, 对于引进Logistic-Tent混沌映射初始化种群的L-EO算法相较于EO算法, 在多数函数测试中可以提高算法寻优结果, 但提升并不明显. 原因是因为引入混沌映射提高了初始种群离散度, 但对算法后续迭代并无明显帮助, 对于多峰函数F9, L-EO取得了最佳成绩, 这是因为在某些特定函数中混沌映射的初始种群能更易发现全局最优. 对于引入更新迭代函数公式的I-EO, 在大部分单峰函数以及部分多峰函数中都能取得最优解. 可见对于更新的迭代函数公式, 能有效提高前期搜索的迭代步长, 使算法前期能有更快的迭代速度, 算法后期则逐步减小步长, 使得算法更专注于发掘局部最优解. 引入Levy飞行策略的LV-EO相较于EO, 在多数测试函数中都能取得更优解, 但对于单峰和多峰函数来说提升并不明显, 而对于固定维多峰函数来说提升较大. 综合来说, 引入更新迭代函数的I-EO在单峰函数有更大优势, 而L-EO和LV-EO在某些多峰函数上更有优势.

3.4 Wilcoxon秩和检验

为了避免算法的偶然性, 需要对算法进行显著性分析, 以验证算法在统计学上的显著性. 在表1所示的10个基准函数中对比PSO、GWO、GA、EO与LTEO的Wilcoxon秩和检验p值, 结果如表4所示. 当p值小于0.05时, 认为两种算法具有显著性差异. 符号“+”“–”以及“=”分别表示LTEO的差异性检验结果优于、差于和相当于当前算法, “NA”表示两种算法性能相当. 实验参数设置与第3.2节保持一致.

通过表4的实验结果可见, LTEO在大部分基准函数测试中都表现出显著差异性. 从统计学上来说, LTEO寻优能力要优于PSO、GWO、GA和EO, 是一种具有良好性能和鲁棒性的优化算法.

4 基于改进平衡优化器的医学图像配准算法 4.1 配准基本原理

2D/3D医学图像配准的实质即为寻找一种最优的空间变换, 在这个空间变换下, CT数据根据投影算法生成的浮动图像与参考图像之间的相似度达到最高^{[20, 21]}. 其中浮动图像一般指数字放射重建(digitally reconstructed radiograph, DRR)^[22]图像, 参考图像一般指X光图像. 其数学模型可以解释如下:

$ S(T) = S(x, DRR(T(y))) $

(26)

其中, $ S $ 代表相似度函数, $ T $ 代表空间变换, $ x $ 代表X光图像, $ y $ 代表CT数据, $ DRR $ 代表对应空间变换矩阵下的DRR图像, 配准过程即为寻找空间变换矩阵 $ T $ 使得 $ S $ 达到最大值, 即:

$ {T^*} = \arg \mathop {\max }\limits_T S(T) $

(27)

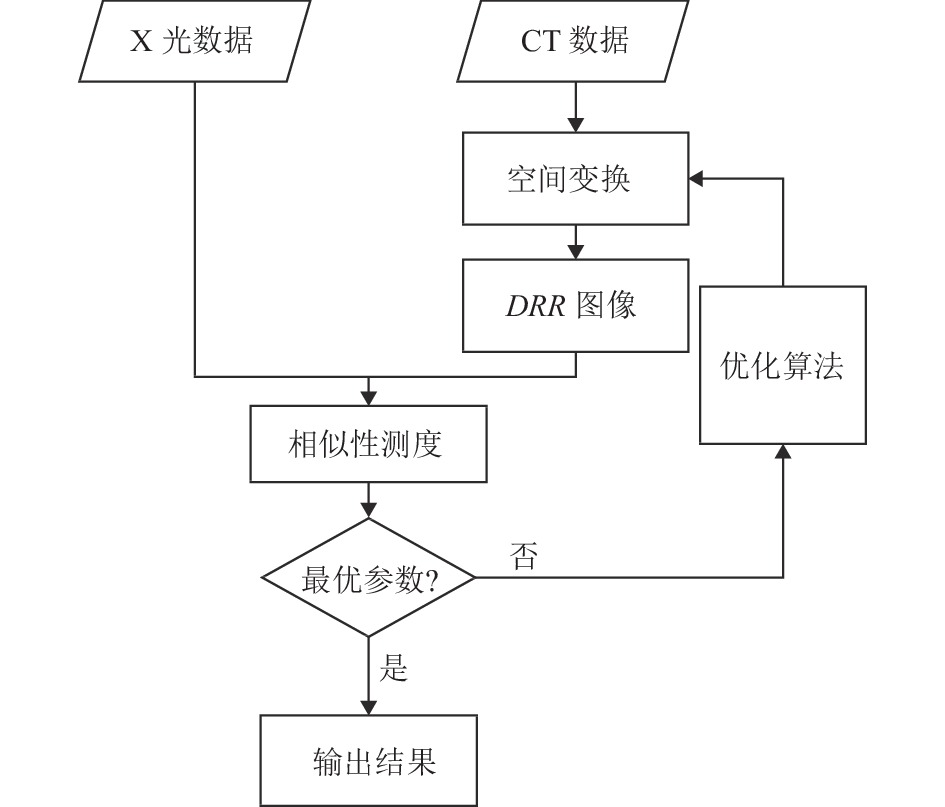
由于T一般包含6个自由度, 分别为X、Y、Z轴方向上的位移和旋转, 所以这是一个多参数寻优的问题, 一般通过多次迭代找到最优的参数^[23]. 2D/3D医学图像配准流程如图5所示.

4.2 图像配准中的适应度函数

2D/3D医学图像配准的适应度函数定义为浮动图像和参考图像之间的相似度测度^[24], 用以衡量两张图像间的相似程度, 通常以归一化互相关系数 (normalized cross correlation, NCC)^[25]来定义两张图像的相似度测度, 归一化互相关通过计算两幅图像之间的相关系数来衡量匹配关系, 其公式可以表示为:

$ \begin{split} & NCC =\\ & \frac{{\displaystyle\sum\limits_{i = 1}^N {\displaystyle\sum\limits_{j = 1}^M {[{I_X}(i, j) - {{\overline I }_X}][{I_{DRR}}(i, j) - {{\overline I }_{{{DRR}}}}]} } }}{{\sqrt {\left[\displaystyle\sum\limits_{i = 1}^N \displaystyle\sum\limits_{j = 1}^M {({I_X}(i, j) - {{\overline I }_X})}^2\right]\left[\displaystyle\sum\limits_{i = 1}^N \displaystyle\sum\limits_{j = 1}^M {{({I_{{{DRR}}}}(i, j) - {{\overline I }_{DRR}})}^2}\right] } }} \end{split} $

(28)

其中, $ {\overline I _X} $ 表示X光图像灰度均值, $ {\overline I _{DRR}} $ 表示DRR图像灰度均值. NCC取值范围为[−1, 1], 若为1表示两幅图像完全相关, 0表示不相关, −1表示两幅图像负相关.

4.3 针对CUDA的流程优化

DRR属于投影图像, 一般由优化算法计算出所需的参数, 之后将参数传输至显卡(Device)端进行绘制. 绘制后的DRR图像需要传输回主机(Host)进行后续计算. 在这个过程中, Host和Device之间数据传输容易受到PCIe总线带宽的限制, 其传输速度远远低于Device内部存储空间的数据交换^[26]. 所以其中一种性能调优的方式即尽量减少主机和设备之间的数据传输次数.

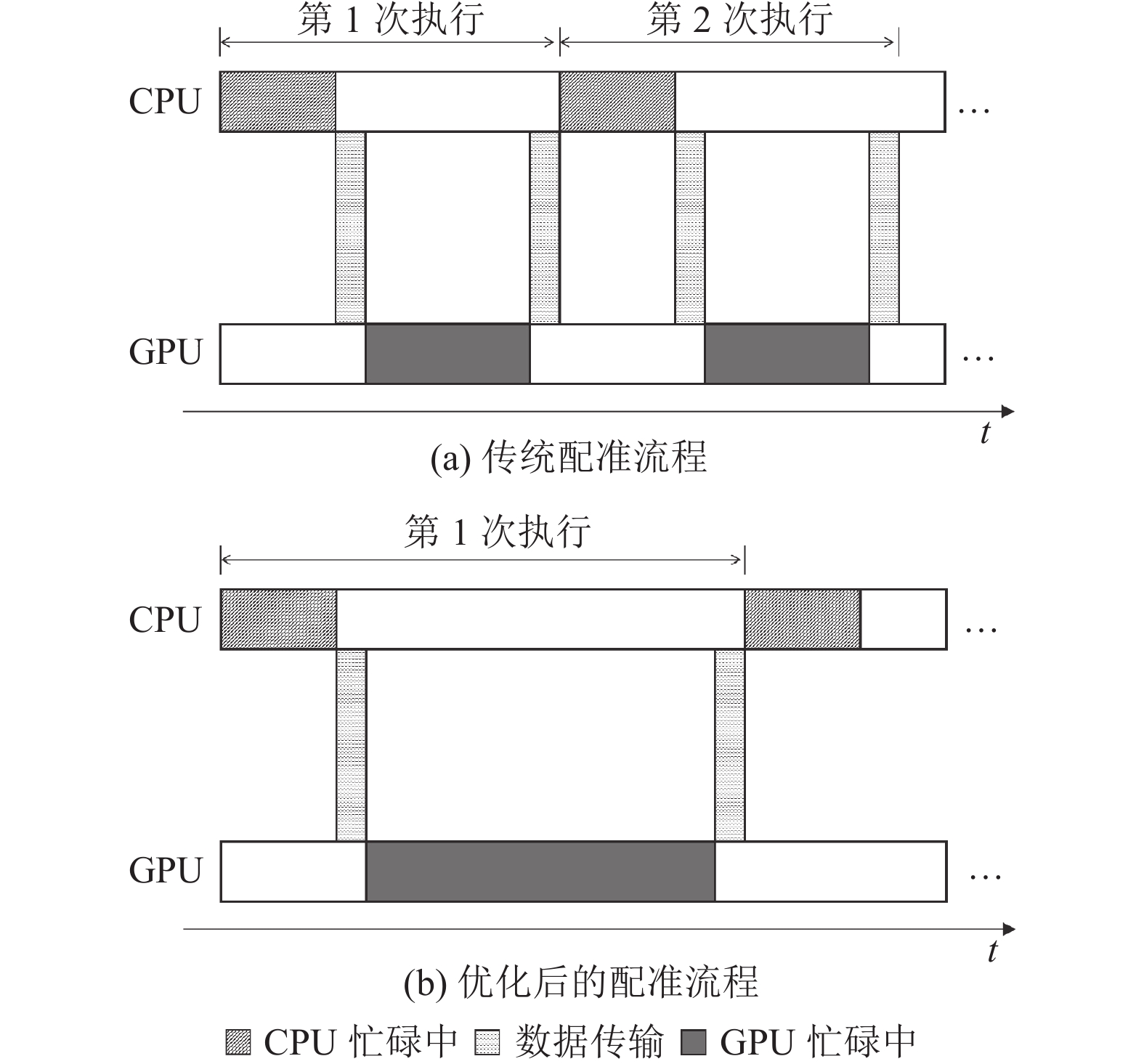
基于这种思想, 本文重新设计了DRR绘制和进行相似性测度的方式. 标准流程过程中, Host端每次向Device端发送一组数据, 请求生成单张DRR, 之后在Device端计算相似度测度值后返回Host端. 改进的流程改为Host端将发送多组数据, 请求生成DRR数据组, 在Device端计算出DRR数据组的相似度值后, 一并返回Host端. 在数据总量不变的情况下, 改进后的方案大幅减少了Host端和Device端的数据传输次数. 流程优化效果图如图6所示.

如图6所示, 流程图中以2个粒子为例, 将两张DRR图像合并为DRR图像组后共同传输到CUDA进行Device端的计算, 之后将返回图像组的结果. 相比于优化前执行流程, 本方案能有效减少数据传输次数, 从而减少配准耗时. 其中, 方案中使用到的数据结构如图7所示.

具体实现流程为:

(1)根据设定的搜索范围和粒子数N, EO算法随机定义初始种群.

(2)算法进入迭代, 将N个粒子的值发送至Device端, 由CUDA架构生成这些粒子的DRR图像组, 拼接为DRR图像组, 设单张DRR宽度为width, 高度为height, 则DRR图像组的大小为width×(height×N).

(3)同样在Device端, 由核函数并行的计算出所有DRR与参考图像的相似度测度.

(4)将结果返回Host端, 交由优化算法进行后续计算.

4.4 医学图像配准实验

实验数据来源于临床采集的人体脊柱CT数据, 数据共5组, 数据参数和概况如表5所示. 本实验硬件环境为CPU: Inter Core i5-4590@3.30 GHz, 内存为16 GB, 显卡型号为NVIDIA GeForce GTX 1060, 编程环境为Microsoft Visual Studio 2022.

由于临床提供的真实X光图像存在各种噪声干扰, 术中临床配准中需要对X光进行预处理或图像分割. 为了排除噪声对实验结果产生的不利影响, 更好地验证基于改进的平衡优化器的配准效果, 本文设计模拟配准实验进行验证. 模拟实验采用“黄金标准法”^[27]进行配准, “黄金标准法”即为在配准过程中, 用已知的参数生成DRR图像作为“黄金标准”, 代替真实X光数据进行配准. 最终将配准得到的结果与“黄金标准”进行误差分析, 即可评判系统的优劣. 首先实验采用CT图像在固定位姿生成的DRR图像作为参考图像, 令参考图像在每个自由度+10个单位生成DRR图像, 作为起始配准图像.

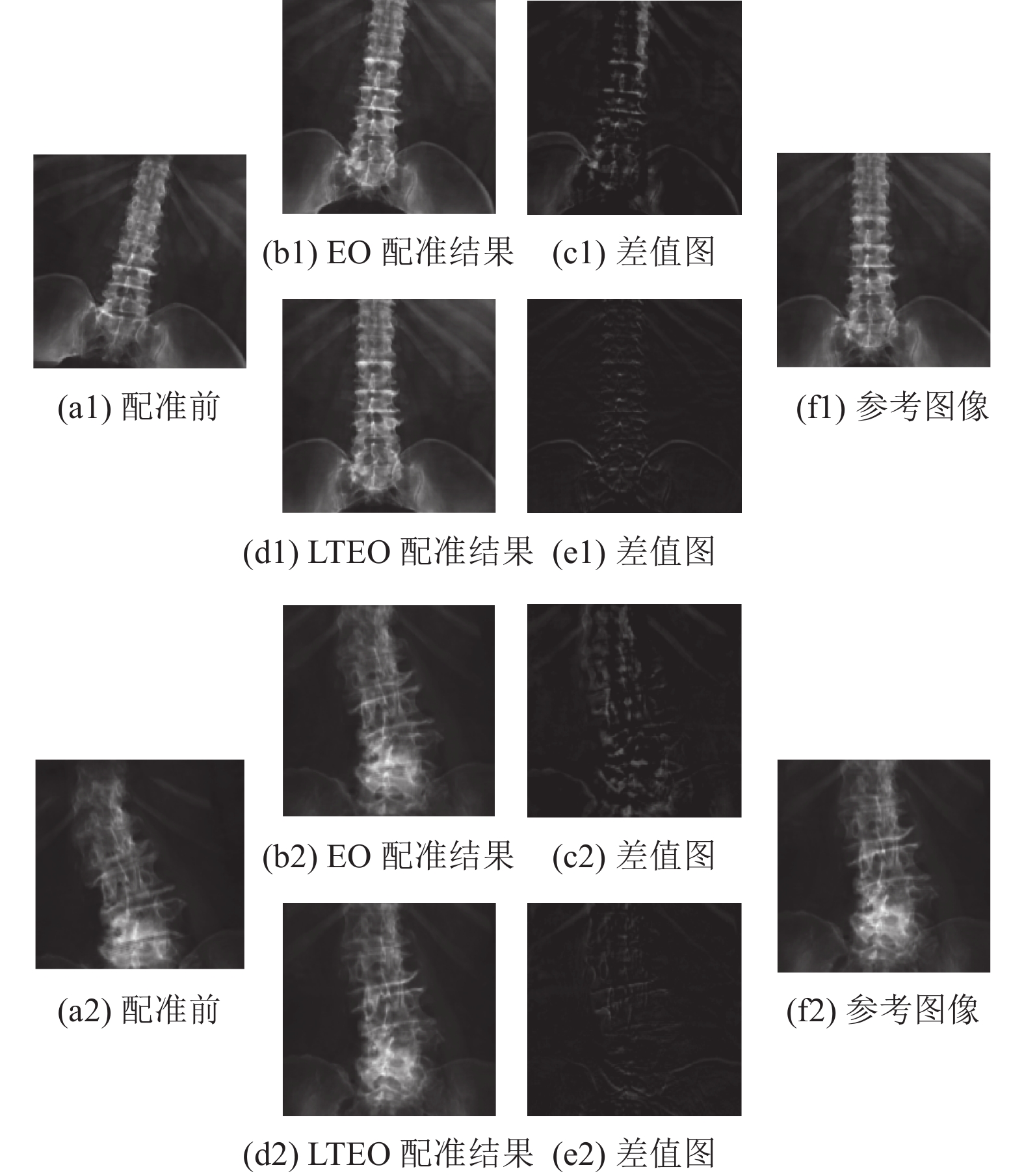
本文模拟配准实验分为配准精度实验和配准时间实验两个部分, 其中配准精度实验使用LTEO以及EO作为优化算法对图像进行配准, 对比两者的配准精度; 配准时间实验分别使用改进的配准流程和标准配准流程进行配准, 以验证改进的配准流程速度的提升. 两组测试中均采用控制变量法对除优化算法以外的其他环节进行限定. 以上两组对比试验种群数量均设置为10个, 迭代次数设置为100次, 在5组脊柱CT数据上运行10次, 并统计5组数据最终的误差均值. 图8是配准结果可视化展示, LTEO和EO共用图8(a1)和图8(a2)中的浮动图像作为起始配准图像, 比较配准结束后于参考图像的差异. 为了便于观察, 绘制出配准结果于参考图像之间的差值图, 其计算方式为配准结果图像与参考图像做减法运算. 图9中展示了配准结果的旋转误差和平移误差. 表6展示了配准时间实验结果. 表7则统计EO配准结果以及LTEO配准结果与参考图像之间的结构相似性测度(structural similarity, SSIM)以及峰值信噪比(peak signal-to-noise ratio, PSNR).

在配准过程中, 由于物体绕X轴旋转产生俯仰角, 在以CT中心为坐标轴原点的俯仰角旋转中DRR变化并不明显, 所以X轴配准误差会大于Y、Z轴; 在平移配准过程中Z轴控制物体距离远近, 假设使物体沿X、Y、Z这3个轴移动同样距离, X、Y轴上的移动比Z轴的更容易观测, 也就是说, 在DRR渲染过程中, 距离带来的差异并不明显, 所以Z轴配准误差会显著大于X、Y轴.

在配准精度实验, 即图8、图9以及表7的结果中, 展示了LTEO和EO的配准精度差异. 从图9可见, 两组测试中X轴旋转和Z轴误差值范围都较大, 其中EO对照组数据在Z轴平移误差均值大于6 mm以上, 在临床上结果较差. LTEO组在6个自由度上的结果都要优于EO组的结果, 都在临床可接受范围内. 由图8的配准结果以及差值图比较可见, 在相同的起始配准图像条件下, 使用LTEO作为优化算法进行配准, 得到的配准结果要优于EO配准结果. 表7的相似度评估中, LTEO配准结果的SSIM、PSNR值都要优于EO配准结果, 表明了改进配准算法的有效性.

在表6的结果中, 改进的配准流程相比于标准流程, 平均达到34%的速度提升, 至多达到38%以上的速度提升, 改进的配准流程可显著降低临床手术中医生的等待时间.

综上, 基于LTEO的2D/3D快速医学图像配准系统的配准速度和精度与标准医学图像配准系统相比, 都具有较强的竞争性.

5 结语

针对平衡优化器存在初始种群多样性较低、收敛速度慢以及易陷入局部极值的问题, 提出了一种改进的平衡优化器算法: 引入了Logistic-Tent混沌映射来对种群进行初始化, 以提高种群多样性; 其次修改迭代函数的公式, 让算法更注重全局范围的搜索, 提高收敛速度并利于找到全局最优解; 之后引入Levy飞行策略对粒子进行扰动, 使其逃脱局部极值, 避免算法过度早熟. 针对医学图像配准任务中时间较长的问题, 提出一种优化流程, 将单张数据处理为数据组, 从而减少数据传输次数, 进而减少配准耗时. 对于本文提出的算法, 设计了基准函数实验和仿真配准实验两种实验进行验证, 结果表明, 本文提出的改进平衡优化器算法具有较好的寻优精度和速度; 基于改进平衡优化器的医学2D/3D图像快速配准系统同样拥有较好的配准速度和精度. 未来研究方向可考虑将改进的LTEO应用于医学双平面配准, 以进一步提高配准精度.