随着社会的发展进步, 现代科技的迅速崛起, 智慧化建设及信息化发展战略建设应运而生, 要想在各行业中具有一定的核心竞争力, 具有智能化、系统化的大型系统是必不可少的, 因此系统安全性的评估越来越重要. 安全风险评估作为大型系统安全保障功能的重要内容之一, 是从风险管理角度出发, 运用科学的手段和方法, 系统地分析安全业务存在的潜在威胁以及脆弱性. 因此, 对于指标体系的构建、指标权重的确定以及指标权重的融合便是众多决策专家学者关注的焦点. 通过查阅文献概括出国内外对于构建安全风险评估研究常用的方法有, 模糊层次分析法[1]、事件树和故障树[2]、灰色关联分析法[3]和贝叶斯网络[4]等. 上述方法构建的安全风险评估模型, 推进了评估方法的研究进展, 但这些方法都各有利弊, 许多研究在方案评价指标权重的确定方面, 未能给出科学合理的处理. 例如在构建安全指标重要性时, 仅利用专家的经验去给出该指标的重要程度, 主观因素影响过大, 单纯地采用主观赋权法, 可能会忽视客观对象的信息特征; 而客观赋权法虽然依靠数据的真实性, 具有较强的说服力, 但是缺少专家经验的积累, 往往可能与实际相悖论, 缺乏对安全态势因素的全面考虑; 以及主、客观权重具有不同的权威性或可靠度, 若只简单地进行线性组合或者人为定义去确定权重系数, 往往会使得评估结果不太准确. 因此, 本文在充分分析各风险指标影响因素的基础上, 采用权值分配和矩阵分析的D-S证据合成算法将多位专家的对于安全风险的差异性进行融合, 使得求出的安全风险指标主观权重更加科学合理; 通过改进D-S证据理论算法将主、客观权重进行组合的方式, 克服了单一赋权方法所带来的评估结果片面性, 而且组合的方式不仅减少了AHP法专家经验赋权的主观性, 也减小了数据变化导致权重值的波动; 经过每一次的证据合成, 即主观权重确定过程以及组合权重合成过程, 指标权重的不确定度逐渐降低, 有效地减少了评估结论的不确定度; 最后结合TOPSIS评价方法对整个模型中的风险值进行量化分析, 提出了融合权集的安全风险评估模型. 该模型通过识别影响系统安全的关键因素, 可以直接将评估对象的安全性进行以数据形式可视化, 为风险的控制和管理提供合理有效的依据.
1 基于D-S证据的多源证据权重融合算法 1.1 D-S证据理论基础D-S证据理论是解决不确定性信息的强有力决策工具, 可以很好地处理可靠性信息中的不确定性, 有效融合不同来源信息[5]. 该理论主要通过引入基本信任函数(mass函数), 通过将mass函数推广至识别框架下的全部子集, 然后利用Dempster组合规则对不同证据产生的概率进行融合, 该理论的核心是提供了一种融合多源数据的合成算法, 从而减少因为不确定信息产生的误差, 降低某一侧的输入带来的指向性误差, 可以很好地解决证据加权以及模型支持度问题, 提高某命题置信程度的证据组合规则. 目前已成为不确定性信息可靠性处理的重要工具[6]之一, 被广泛应用于信息融合[7]、软件需求融合[8]、金融安全[9]等领域.
(1) 识别框架
假设识别框架为
| $ \left\{ \begin{gathered} m(\phi ) = 0 \\ \sum\limits_{{{A}} \subseteq \Omega } {m(A) = 1} \\ \end{gathered} \right. $ | (1) |
(2) Dempster合成原则
D-S证据理论的核心就是对证据的合成, 综合所有证据对问题的支持程度, 得到综合概率. 但是传统D-S证据合成规则, 在安全风险评价的过程中, 若出现证据之间的冲突较大时, 直接利用合成规则进行数据融合, 可能得到的结果不太符合实际情况. 因此, 本文通过采用权值分配和矩阵分析的算法改进D-S合成算法, 进行证据之间的融合[10], 从而降低传统算法中存在的“证据冲突”问题.
对于信度的合成规则可总结为:
| $ m(A)=\left\{\begin{array}{l} 0,\; A=\varnothing \\ \displaystyle\sum_{\cap H_i=A, 1 \leqslant i \leqslant n} \prod m_i\left(H_n\right)+f(A),\; A \neq \varnothing \end{array}\right. $ | (2) |
其中, Hn表示不同证据源,
组合权重是指通过两种及两种以上传统算法计算得出的指标权重, 通过特定的方式进行结合, 得到综合权重, 是一个更全面的、可靠的权重确定方法. 经过实验对比, 本文采取改进层次分析法和熵权法进行对模型体系中的指标进行主、客观赋权. 层次分析法 (AHP)通常是依靠专家打分法或者问卷调查, 具有一定的主观性和偶然性. 而熵权法是将指标通过数据具象化表示, 更侧重于数据的客观性, 以及纵向能力的体现, 但缺乏横向能力的比较. 因此, 通过综合考虑选取上述两种传统计算权重的算法, 能够更好地在各自领域上发挥赋权计算的优势. 利用改进的D-S证据融合算法将主、客观权重进行融合, 得到组合权重.
1.2.1 改进AHP法确定主观权重层次分析法是一种对定性问题进行定量分析的多准则决策方法, 该方法通常是将一个复杂系统的若干要素分类形成多层次体系. 具体步骤如下: (1)构建层次结构模型包括目标层、准则层(决策准则)和指标层(决策对象); (2)采用3标度法比较各指标间的安全性程度, 构造判断矩阵; (3)计算最大特征根
信息熵是对系统的不确定性的量度, 根据指标数据的差异化程度, 来确定其包含信息量的多少, 通常指标值的变异程度越大, 该评价指标的信息熵越小, 反之, 亦然. 通过对评估矩阵计算, 从而得出各指标的权重, 具体步骤如下.
(1)构建初始矩阵
设安全风险评价对象的个数为m, 安全风险评价体系中指标层的评价指标个数为n, 由此构成m×n阶初始决策矩阵.
| $ X = {[{x_{ij}}]_{m \times n}} $ |
(2)指标归一化处理
考虑到每个指标的计量单位不同, 在计算综合资源指标前, 需要对其进行标准化处理, 即将所有的安全指标的绝对值转化为相对值.
正向型资源指标归一化, 用于处理效益型决策参数, 这类决策参数的特点是值越大效果越好, 其计算公式如下:
| $ x'_{ij} = \frac{{{x_{ij}} - \sqrt {\displaystyle\sum\limits_{j = 1}^n {x_j^2} } }}{{\sqrt {\displaystyle\sum\limits_{j = 1}^n {x_j^2} } }} $ | (3) |
负向型资源指标归一化, 用于处理成本型决策参数, 这类决策参数的特点是值越小效果越好, 其计算公式如下:
| $ x'_{ij} = \frac{{\sqrt {\displaystyle\sum\limits_{j = 1}^n {x_j^2} } - {x_{ij}}}}{{\sqrt {\displaystyle\sum\limits_{j = 1}^n {x_j^2} } }} $ | (4) |
(3)计算第j个指标的信息熵
| $ {e_j} = - {({\rm{ln}}m)^{ - 1}}\sum\limits_{i = 1}^n {{P_{ij}}{\rm{ln}}({P_{ij}})} $ | (5) |
其中,
| $ {P}_{ij}=\frac{x'_{ij}}{{\displaystyle \sum _{i=1}^{n}x'_{ij}}}, i \subseteq (1, 2, \cdots, m), j \subseteq (1, 2, \cdots, n) $ |
且当
(4)计算各指标的客观权重
| $ w'_e = \frac{{1 - {e_j}}}{{m - \displaystyle\sum\limits_{j = 1}^m {{e_j}_{}} }}, j = 1, 2, \cdots , m $ | (6) |
传统的D-S组合规则具有证据冲突等问题, 为减小证据间的冲突, 本文将不同来源的证据即主、客观权重进行折扣权重计算; 再将折扣权重进行加权平均证据计算, 从而获得证据的相似度, 即调整权重; 最后将折扣权重和调整权重通过线性组合计算出证据的综合权重. 以下是一些重要定义[12].
(1)识别框架(评判集)建立
证据源数据的获取包括评估指标体系的建立以及评估指标权重的确定. 指标体系由目标层、准则层和指标层组成. 识别框架是指标体系中各指标层中的各个指标因素组成的集合, 设
(2)构造概率分配函数
折扣权重作为先验知识信息体现了不同的证据源对识别框架中各真子集的识别具有不同可靠信度, 从而为了求解折扣权重, 引入距离函数定义[13].
距离函数
| $ d(w'_a, w'_e) = {\left[ {\frac{1}{2}\sum\limits_{j = 1}^n {{{(w'_a - w'_e)}^2}} } \right]^{\tfrac{1}{2}}} $ | (7) |
| $ D = |{w_1} - {w_2}| $ | (8) |
根据上文构建如下方程组求解折扣权重配置系数
| $ \left\{ \begin{gathered} d{(w'_a, w'_e)^2} = {D^2} \\ {w_1} + {w_2} = 1 \\ \end{gathered} \right. $ | (9) |
根据距离函数求解证据源折扣权重系数
| $ {s_i} = 1 - \sqrt {\sum\limits_{j = 1}^n {{{\left(m_{ij}^{{w_i}} - \sum\limits_{i = 1}^L {m_{ij}^{{w_i}}} \right)}^2}} } $ | (10) |
对
计算各证据
| $ m_{ij}^{{\alpha _i}} = {\alpha _i}{\beta _{ij}} $ | (11) |
融合各证据源数据后, 即每个命题子集
| $ w = \sum\limits_{i = 1}^L {{\alpha _i}{\beta _{ij}}} $ | (12) |
TOPSIS亦称“优劣解距离方法”, 是一种有效的多属性多目标决策方案[14]. 首先构建初始化决策矩阵, 通过归一化的加权数据矩阵构造出决策问题的正负理想解, 计算方案与正负理想解的距离, 得出贴合度, 作为评价方案的优劣依据. 其中, TOPSIS综合决策评价算法的关键是如何合理的确定指标权重, 上述通过基于D-S证据的多源证据权重融合算法, 已给出指标权重的确定过程. TOPSIS决策算法的具体步骤如下.
(1)构造决策矩阵
根据指标体系, 通过从智慧工地平台上获取数据, 选取n个评价对象, m个指标. 构造决策矩阵
(2)归一化决策矩阵
采用标准化方法对决策矩阵进行归一化处理, 消除决策参数之间不同量纲之间的影响, 其计算为:
| $ x'_{ij} = \frac{{\max ({x_j}) - {x_{ij}}}}{{\max ({x_j}) - \min ({x_j})}} $ | (13) |
其中,
(3)构造加权决策矩阵
本文通过上述基于改进D-S证据理论的融合权集计算组合权重, 并应用到决策矩阵中, 构造加权决策矩阵如下:
| $\left\{ \begin{split} & Z = {({{\textit{z}}_{ij}})_{m \times n}} ,\; i = 1, 2, \cdots, m,\; j = 1, 2, \cdots, n\\ & {{\textit{z}}_{ij}} = \frac{{x'_{ij}}}{{\sqrt {\displaystyle\sum\limits_{i = 1}^n {x{_{ij}^{'2}} }} }}.{w_j} \end{split} \right.$ | (14) |
其中,
(4)计算正负理想解
| $ \left\{ \begin{gathered} {Z^ + } = (Z_1^ + , Z_2^ + , \cdots , Z_n^ + ) = (\max \{ {{\textit{z}}_{1n}}, {{\textit{z}}_{2n}}, \cdots, {{\textit{z}}_{mn}}\} ) \\ {Z^ - } = (Z_1^ - , Z_2^ - , \cdots , Z_n^ - ) = (\min \{ {{\textit{z}}_{1n}}, {{\textit{z}}_{2n}}, \cdots, {{\textit{z}}_{mn}}\} ) \\ \end{gathered} \right. $ | (15) |
(5)计算每个评价对象到正、负理想解距离:
| $ D_i^ + = \sqrt {\sum\limits_{j = 1}^{{m}} {{{(Z_j^ + - {{\textit{z}}_{ij}})}^2}} } $ | (16) |
| $ D_i^ - = \sqrt {\sum\limits_{j = 1}^{{m}} {{{(Z_j^ - - {{\textit{z}}_{ij}})}^2}} } $ | (17) |
其中,
(6)计算相对贴合度:
| $ {S_i} = \frac{{D_i^ + }}{{D_i^ - + D_i^ + }} $ | (18) |
其中, 相对贴合度
通过构建安全风险评估模型来评价建筑工地安全风险系数及其安全性问题, 具体的建模过程如图1所示. 首先, 通过多方面的综合考虑、调查以及研究选取对于安全有所影响的指标, 建立安全评价指标体系; 其次, 通过本文中提出的基于D-S证据合成算法改进AHP法, 求出指标体系中的各级指标所占的主观权重. 同时, 为避免主观赋权带来的主观性和偏差性影响, 通过熵权法求出各级指标所占的客观权重; 然后, 将求出的二级指标主、客观权重, 作为不同的证据源, 通过采用改进D-S证据理论进行证据融合, 得到融合权重(组合权重), 使得指标权重更具客观性和稳定性; 最后, 将上述求出的二级指标组合权重以及建筑工地智慧平台原始数据, 作为TOPSIS决策算法的输入进行计算, 通过构造加权决策矩阵, 最终得到多个建筑工地的相对安全风险系数, 从而判断该建筑工地的安全性.

|
图 1 安全风险评估方法流程 |
3 模型应用
本文以江苏省某地的智慧工地平台后台数据作为实验数据, 利用上述建立的基于改进D-S证据理论-融合权集的安全风险模型对该地多处施工现场进行安全评价, 从而验证模型可信度.
3.1 构建建筑工地安全评价体系建立完整的评价体系需要以大量科学的研究分析为基础, 并且遵循科学性、系统性和全面性的原则. 因此, 为正确识别施工现场安全的影响因素, 通过综合研究比较各影响因子, 最终构建出建筑工地安全评价体系, 包括5个准则层(U1、U2、U3、U4、U5), 18个指标层(U11、U12、U13、U21、U22、U31、U32、U33、U34、U35、U36、U37、U41、U42、U43、U51、U52、U53), 如图2所示.

|
图 2 建筑工地安全评价体系 |
3.2 计算评估指标权重 3.2.1 主观权重计算
在构建的建筑工地安全评价体系中, 其顶层是建筑工地施工现场风险总目标层, 中间层为准则层(一级指标), 底层为指标层(二级指标). 本文因篇幅的限制, 只列出准则层中一级指标的权重计算过程. 通过专家问卷调查, 确定各一级指标关于建筑工地安全风险的相对重要性, 构建判断矩阵, 并验证矩阵是否满足一致性要求. 表1列出3位专家评判准则层相对重要性判断矩阵A1、A2和A3, 分别计算后, 得到各自的矩阵的特征向量即主观权重, 再将求解出的不同专家经验值主观权重, 通过改进D-S证据融合算法进行融合. 最终, 得到融合后的主观权重.
| 表 1 准则层相对重要性判断矩阵 |
由此可得:
将
同理, 求得各二级指标相对于建筑工地安全风险评价准则层一级指标的权重, 以及相对于目标层的综合权重.最终, 得到所有二级指标的综合主观权重
通过智慧工地平台数据库获取该地多处施工现场各项指标数据, 构建评估矩阵. 由于工程项目安全问题, 只对外开放归一化数据, 如表2所示, 其中, 教育培训U11和机械设备监测数U22为正向型资源指标, 其余, 均为负向型资源指标.
利用式(3)–式(6)计算指标层中评价指标客观权重
| 表 2 各施工现场原始数据正则化 |
3.2.3 权重融合
将上述求出的主观权重和客观权重进行融合代入式(7)–式(9)中, 求出折扣权重配置系数
根据得到的二级指标主、客观权重和基于距离函数求解的折扣权重系数, 采用改进D-S证据理论的组合规则进行权重融合, 由式(10)得到调整权重
由于不同的证据具有不同的权威性或可靠度, 应用传统D-S证据理论做决策时, 对于低冲突证据的处理较合理, 但是当遇到高度冲突的时候会具有一票否决的缺点. 比如, Zadeh悖论问题[15]. 为此, 本文中所提出的模型考虑到证据的可信度问题, 引入折扣权重的求解方法, 关联证据源之间的联系, 从而获取折扣权重
|
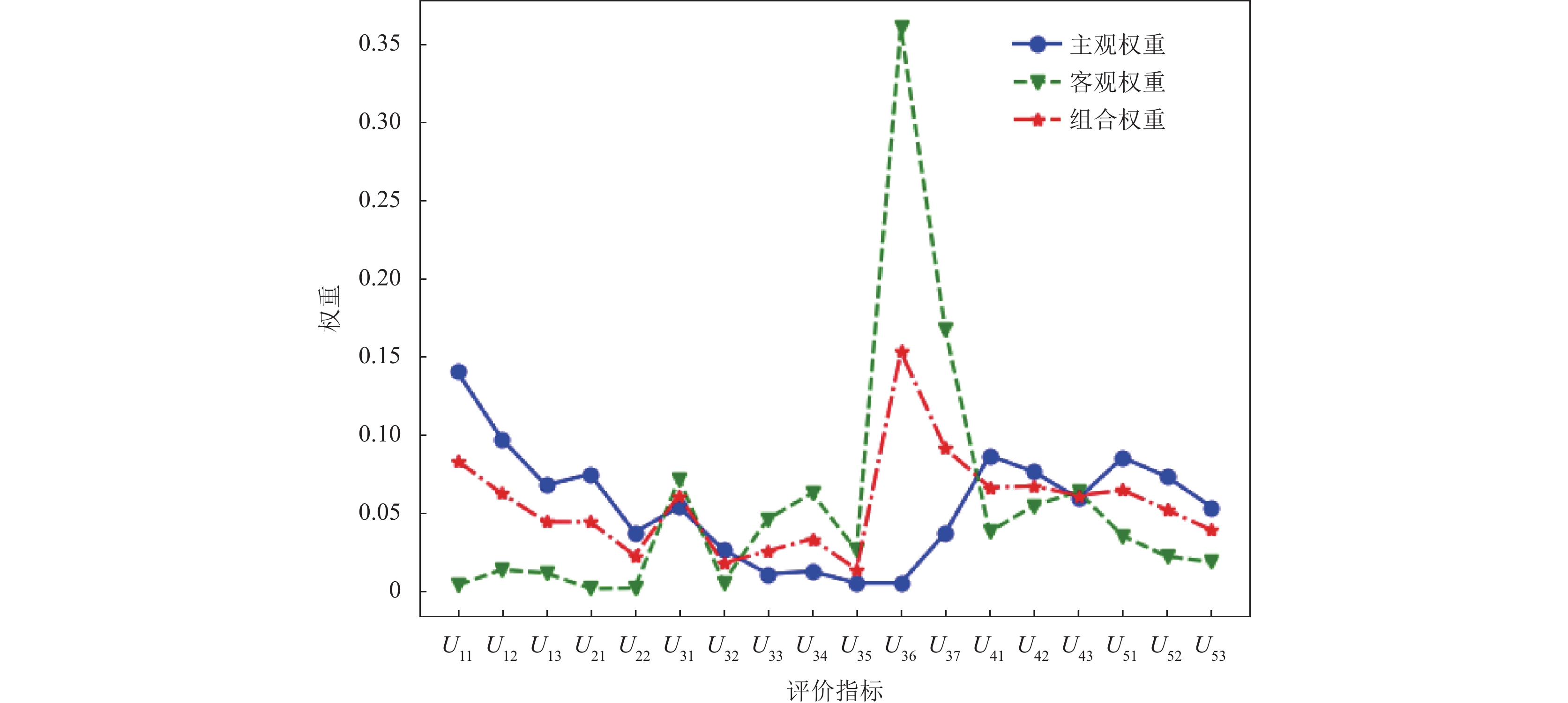
图 3 评价指标权重对比 |
图3为主观权重、客观权重以及组合权重对比曲线. 由图3可见, 根据改进AHP法和熵权法计算得到主、客观权重对于某些指标具有较大的差异. 比如, 指标U36(模板工程检查), 该指标的主观权重和客观权重分别为0.004 9和0.360 2, 具有较大的差值, 在建筑工地现场, 该项指标权重应该理论上低于高处作业检查U34、文明施工检查U32等指标. 由此可见, AHP (层次分析法)在计算权重时, 只聚焦了专家主观意见, 缺乏对实际施工现场运行时所反映真实现状的衡量, 将两种方法得到的权重, 通过设计的模型进行融合, 不仅能够体现不同专家对不同指标的经验, 也能充分利用真实数据提供的信息特征, 得到一个更加符合实际运行的指标权重值.
建筑施工现场中, 有关影响事故发生的研究中表明, 对于人的不安全行为, 往往是导致事故发生的重要原因. 但是, 一旦因为机械设备、危大工程等模块指标出现问题, 在施工现场往往会发生更大的问题. 因此, 对于危大工程模块与机械设备安全模块, 都是各施工现场安全性保障中关注的核心指标. 由图3可见, 这两个模块所占权重比例较大, 与目前施工现场实际运行安全风险性相符合, 进一步说明本文提出的融合权集模型的有效性.
3.3 TOPSIS算法综合评判根据表2中各施工现场的数据以及上述求解出的组合权重构建出加权判断矩阵, 并运用式(16)–式(18)计算出“正理想解”和“负理想解”的欧式空间距离和相对接近度. 相对接近度越接近1, 表明其越接近最优等级, 施工现场安全性越高.
各施工现场的相对贴进度
| 表 3 各施工现场相对接近度计算结果 |
4 总结
本文从建筑工地现场实际出发, 针对建筑工地安全风险评估过程中施工现场风险因素的重要性难以赋权的问题, 建立了基于改进D-S证据理论-融合权集的安全风险综合评价模型. 该模型首先利用江苏省智慧工地数据和住建局专家的经验问卷数据, 通过改进的层次分析法和熵权法计算求出主、客观权重; 其次, 采用改进D-S证据理论确定折扣权重和调整权重, 将主、客观权重进行融合; 最后, 综合计算得到组合权重. 两者的结合, 在降低专家们主观性影响的同时, 解决了由于数据变化所带来的权重波动性变化大的问题, 提高综合评价结果的准确性.
基于改进D-S证据理论-融合权集的TOPSIS安全风险评估方法是一种新的信息化系统安全风险的评价方法. 从新的角度将客观数据和经验知识更切合实际的融入到安全风险综合评价当中. 由于整个安全系统是一个复杂的系统, 系统指标的选取可以进一步的空间完善, 一些权重计算还可以进一步研究.
| [1] |
武阳, 李雪巍. 基于三角直觉模糊层次分析法的国产CPU产品成熟度评价软件开发. 计算机应用与软件, 2019, 36(8): 8-12, 35. |
| [2] |
徐英卓. 张倩. 基于故障树的钻井井塌事故分析方法研究. 智能计算机与应用, 2020, 10(9): 53-54, 60. |
| [3] |
王虎军. 基于灰色关联分析法的绿色施工评价研究[硕士学位论文]. 邯郸: 河北工程大学, 2019.
|
| [4] |
毛子骏. 梅宏. 肖一鸣, 等. 基于贝叶斯网络的智慧城市信息安全风险评估研究. 现代情报, 2020, 40(5): 19–26, 40.
|
| [5] |
游昊, 石恒初, 杨远航, 等. 基于改进D-S证据理论的电网故障多源信息智能融合诊断方法. 广东电力, 2020, 33(11): 16-25. |
| [6] |
韩德强, 杨艺, 韩崇昭. D-S证据理论研究进展及相关问题探讨. 控制与决策, 2014, 29(1): 1-11. |
| [7] |
Li YZ, Yao SJ, Zhang RY, et al. Analyzing host security using D-S evidence theory and multisource information fusion. International Journal of Intelligent Systems, 2021, 36(2): 1053-1068. DOI:10.1002/int.22330 |
| [8] |
梅莹, 丁晓明. 证据理论在软件需求工程中的应用研究. 计算机科学, 2012, 39(S3): 237-239. |
| [9] |
Xiao Z, Yang XL, Pang Y, et al. The prediction for listed companies’ financial distress by using multiple prediction methods with rough set and Dempster-Shafer evidence theory. Knowledge-based Systems, 2012, 26: 196-206. DOI:10.1016/j.knosys.2011.08.001 |
| [10] |
王姣, 范科峰, 莫玮. 基于改进D-S证据理论和BN的信息安全风险评估. 电视技术, 2017, 41(6): 24-30. |
| [11] |
邓雪, 李家铭, 曾浩健, 等. 层次分析法权重计算方法分析及其应用研究. 数学的实践与认识, 2012, 42(7): 93-100. |
| [12] |
付艳华. 一种基于证据综合权重折扣的加权平均法. 东北大学学报(自然科学版), 2010, 31(7): 917-920. |
| [13] |
董增寿, 邓丽君, 曾建潮. 一种新的基于证据权重的D-S改进算法. 计算机技术与发展, 2013, 23(5): 58-62. |
| [14] |
孙然然, 陈家旭, 李晓璐, 等. 面向运营安全的城市轨道交通线网性能综合评价. 科学技术与工程, 2020, 20(36): 15067-15073. |
| [15] |
Zadeh LA. Review of books: A mathematical theory of evidence. AI Magazine, 1984, 5(3): 81-83. |
 2023, Vol. 32
2023, Vol. 32


