目标跟踪一直以来都是一项具有挑战性的工作[1], 也是计算机视觉领域的热点之一, 受到了学者的广泛关注. 目前, 目标跟踪广泛应用于视频图像、智能交通、行为分析等领域[2]. 尽管近年来跟踪技术取得了长足的进步, 许多高效算法陆续被提出, 但目标跟踪任务仍面临着目标尺度形变大、相互遮挡和相似背景干扰等诸多挑战, 使其仍然成为当前研究热点[3].
孪生网络目标跟踪算法作为当前主流算法之一, 该算法将目标跟踪任务建模为一种相似性度量的问题, 其通过目标模板帧与搜索帧进行相似度计算, 得到一张响应图, 然后根据响应图的得分判断目标的位置信息. 这种算法的优点是网络结构简单, 算法速度较高[4]. 然而, 由于孪生网络目标跟踪算法仅使用第1帧的特征信息与搜索帧进行相似度匹配, 因此当目标面对复杂场景时, 目标跟踪就会受到严重影响, 从而降低模型的跟踪性能[5].
针对上述问题, 本文提出了一种基于多支路的孪生网络目标跟踪算法(Siamese network tracker based on multiple branches, SiamMB), 其贡献如下.
1)增加邻近帧支路, 提取与搜索帧更加接近的目标信息, 提高了跟踪器对目标的判别能力, 降低了目标在遭受到遮挡、形变等挑战时跟踪失败的风险.
2)融合了空间注意力机制, 对不同空间位置的特征施加不同的权重, 从而获得更具有判别能力的特征.
1 相关工作目前, 目标跟踪算法主要分为基于相关滤波的跟踪算法和基于深度学习的跟踪算法[6].
早期的单目标跟踪算法以相关滤波为主. 2010年, Bolme等人首次将相关滤波应用于目标跟踪领域, 并提出最小输出误差平方和跟踪算法MOSSE[7], 该算法采用灰度特征训练目标区域的外观模型, 并利用离散傅里叶变换将目标与所有候选区域之间的相似度计算转换为频域, 大大提高了目标跟踪速度. 2012年, Heriques等人[8]提出了基于MOSSE的循环跟踪核检测结构CSK, 该算法通过训练样本循环矩阵, 大大增加了训练样本的数量. 在此基础上, KCF算法[9]采用了多通道的HOG特征取代了CSK的灰度特征, 提高了算法的鲁棒性. 此外具有代表性的相关滤波算法还有HCFT[10]等. 虽然上述算法在目标跟踪方面取得了良好的效果, 但缺乏对目标尺寸变化的考虑, 在面对遮挡、形变等复杂场景时容易受到外界环境的干扰, 导致跟踪的精度与成功率偏低[3].
与基于相关滤波的目标跟踪方法相比, 基于深度学习的目标跟踪算法在性能上有很大的提高, 已成为当前主流方法[11]. Wang等人[12]于2013年提出了首个将深度学习成功应用于目标跟踪领域的算法DLT (deep learning tracker), 该算法使用堆叠去噪自动编码器来学习大图像数据集中的通用图像特征作为辅助数据, 然后将学到的特征传输到在线跟踪任务, 并且DLT利用了多个非线性变换, 优化了跟踪的性能. 随着深度学习的发展, 基于孪生网络的目标跟踪算法因其强大的性能成为目标跟踪领域的主流算法. SINT[13]是第1个将孪生网络用于目标跟踪领域的算法, 其简单地将跟踪过程视为一个相似度学习问题, 寻找目标在每个搜索帧中的最优匹配响应, 为目标跟踪开辟了新的研究方向. 2016年, Bertinetto等人提出了全卷积孪生跟踪算法SiamFC[14], 其将AlexNet作为特征提取网络, 简化了相似度计算过程, 跟踪实时性也得到了提高. SiamRPN[15]将区域建议网络应用于孪生网络, 通过分类和回归分支来提高跟踪精度. 2019年, SiamRPN++算法[16]在SiamRPN的基础上, 利用ResNet进行特征提取, 提出了一种空间感知采样策略, 实现了多层融合, 进一步提高了跟踪精度. SiamGAT[17]利用图注意力机制将目标信息从模板特征传播到搜索特征, 同时提出了一种目标感知区域选择机制, 以适应不同对象的长宽比变化.
2 基于多支路的孪生网络目标跟踪 2.1 网络结构本文提出的目标跟踪算法SiamMB是在SiamRPN的基础上改进的, 如图1所示, 图中SAM为空间注意力模块,
1)特征提取网络, 其中模板帧图像Z和搜索帧图像X利用ResNet50网络进行特征提取, 邻近帧图像P由大小为5×5的卷积核进行卷积.
2)空间注意力网络, 输入来自特征提取网络的特征图, 对目标特征进行聚焦, 增强特征之间的判别性.
3)分类和回归网络, 这一部分由区域提议网络(RPN网络)实现. 其中分类网络用于区分目标是前景或背景, 回归网络用于确定目标的大小.
2.2 增加邻近帧支路的网络鲁棒性增强方法在目标跟踪中, SiamRPN网络仅使用模板帧图像的目标信息, 在面对遮挡和形变等复杂场景时鲁棒性不足, 从而增加了目标丢失的风险[3], 但是目标在前后两帧中的尺寸和空间位置通常不会发生巨大的变化[18], 受此启发, 本文在SiamRPN网络的基础上, 对邻近帧跟踪得到的结果图进行裁剪, 提取目标所在区域, 再进行缩放, 这时我们已经得到与搜索帧目标相似的邻近帧图像P, 将其作为我们网络的邻近帧支路, 提取更加接近搜索帧目标的特征信息, 以增强网络在复杂场景下的鲁棒性.

|
图 1 SiamMB的网络结构图 |
首先, 利用ResNet50网络对模板帧和搜索帧图像进行特征提取, 分别得到特征图
| FZ = φ(Z),FZ∈R16×16×256 | (1) |
| FX = φ(X),FX∈R32×32×256 | (2) |
其中,
| FP=Conv5×5(P), FP∈R16×16×256 | (3) |
其中, Conv表示卷积操作, 卷积核大小为5×5. 然后将
| HclsZ = Conv3×3(SZ) | (4) |
| HclsP = Conv3×3(SP) | (5) |
| HclsX = Conv3×3(SX) | (6) |
其中,
| OclsZ = HclsZ∗HclsX | (7) |
| OclsP = HclsP∗HclsX | (8) |
| Rcls = λOclsZ + (1−λ)OclsP | (9) |
其中,
为了能从复杂的背景下区分出跟踪目标, 需要对目标中的特征进行聚焦, 增加特征之间的判别性[19]. 因此, 本文引入空间注意力机制网络, 突出特征图中重要的目标区域, 抑制无用的背景信息. 空间注意力网络如图2所示.
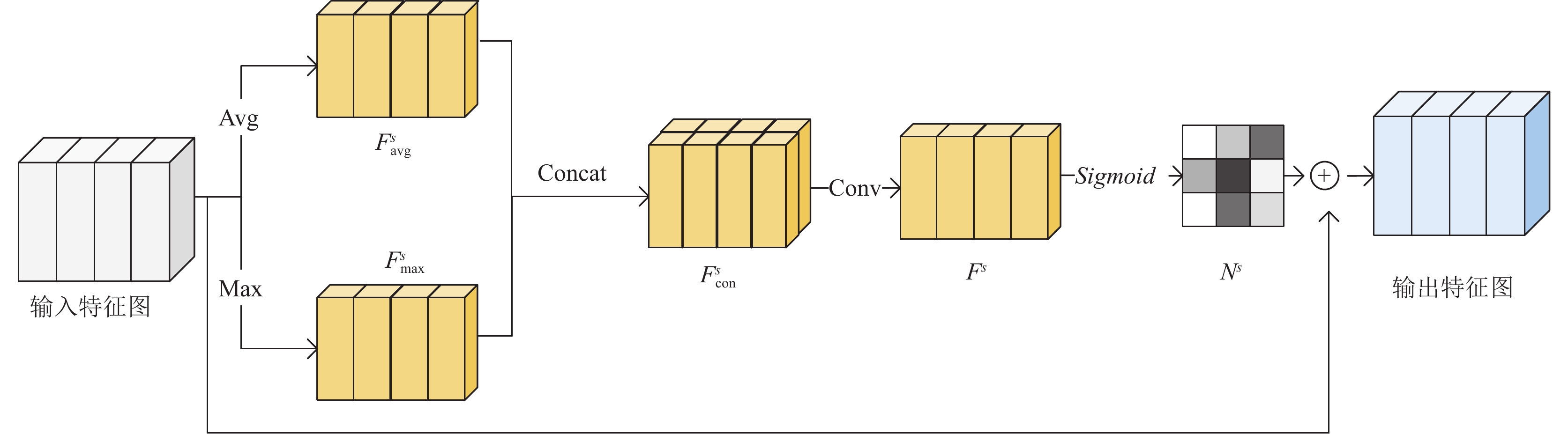
|
图 2 空间注意力网络结构图 |
在模板帧支路中, 将
| Fscon=[Fsavg;Fsmax],Fscon∈R16×16×2 | (10) |
接下来使用大小为7×7的卷积核进行卷积, 生成空间注意力图
| Fs=Conv7×7(Fscon),Fs∈R16×16×1 | (11) |
再通过Sigmoid函数进行归一化, 得到
| Ns=Sigmoid(Fs) | (12) |
| SZ=Ns⊗FZ | (13) |
同样, 邻近帧支路和搜索帧支路分别将
本文提出的算法训练过程中, 总损失计算公式为:
| L = Lcls+αLreg | (14) |
其中,
| L(yi,pi) = −(yi⋅log(pi)+(1−yi)⋅(1−pi)) | (15) |
其中,
若样本总数为
| Lcls=1Ncls∑Nclsi=1L(yi,pi) | (16) |
| {δ[0]=Tx−OxOw,δ[1]=Ty−OyOhδ[2]=lnTwOw,δ[3]=lnThOh | (17) |
其中,
| SmoothL1(x,σ)={0.5σ2x2,|x|<1σ2|x|−12σ2,|x|⩾1σ2 | (18) |
| Lreg=∑3i=0SmoothL1(δ[i],σ) | (19) |
其中,
实验环境: 本文算法是使用Python 版本为3.6.5和PyTorch 1.8.1框架实现的. 在CentOS 7操作系统上, 使用CPU型号为Intel(R) Xeon(R) Bronze 3204 CPU @ 1.90 GHz, GPU为GeForce RTX 3080 Ti进行实验.
训练数据集: 首先将ResNet50在ImageNet数据集上进行预训练, 然后将预训练后的ResNet50在ImageNet VID和GOT-10k数据集上进行迭代训练. 其中ImageNet VID共有3 862个视频片段用于训练, GOT-10k包含了560类常见目标和87类运动模式.
参数设置: 本文训练周期为300个epoch, 每批次训练图片数量(batch size)为10张, 其中前130个epoch学习率为0. 001, 后170个epoch的学习率衰减至0.000 01. 使用随机梯度下降法(stochastic gradient descent, SGD)优化网络, 动量设置为0.9. 为了更好地应对目标尺度变化, anchor设置为 0. 33、0. 5、1、2、3共5种长宽比.
3.2 数据集介绍 3.2.1 OTB2015数据集OTB2015[20]是单目标跟踪领域最常用的基准之一, 包含了目标跟踪中常见的难点, 包括光照变化、尺度变化、遮挡、形变、运动模糊等11个视频属性, 共100个跟踪视频序列, 评价指标如下.
1)跟踪精度: 计算模型跟踪预测的中心点和目标真实位置的中心点之间的欧氏距离:
| ε=√(xp−xg)2+(yp−yg)2 | (20) |
其中,
| Precision=PNF | (21) |
其中, P代表
2)成功率: 计算模型跟踪预测的目标边界框与真实边界框间的重叠率, 也称为交并比, 计算公式为:
| IoU=|Rp∩Rg||Rp∪Rg| | (22) |
其中,
| Success=SNF×100% | (23) |
其中, S代表成功的帧数,
VOT2018数据集[21]由VOT (visual object tracking)挑战赛于2018年提出, 包含60个不同类别的序列, 评价指标包括: 跟踪准确率(Accuracy), 鲁棒性(Robustness)和期望平均重叠率(EAO).
1)跟踪准确率: 用来评价跟踪器跟踪目标的准确度, 数值越大, 准确度越高, 由真实框与预测框的IoU来定义, 第t帧的准确率定义为:
| ϕt=|At∩Agt||At∪Agt| | (24) |
其中,
| Accuracy=1Nvalid∑Nvalidt=1ϕt | (25) |
其中,
2)鲁棒性: 表示跟踪过程中的错误率, 重叠率为0即为跟踪失败, 数值越小, 表面鲁棒性越强, 具体定义为:
| Robustness=FNF | (26) |
其中, F表示跟踪失败帧数;
3)期望平均重叠率: 是准确率和鲁棒性的综合评估指标, 将所有序列按长度分类, 相同长度的序列测得的准确率取平均. 计算公式为:
| ˆϕ(Ns)=1M∑Mt=1(1Ns∑Nsi=1ϕi) | (27) |
其中,
| EAO=1Nhi−Nlo∑NhiNs−Nloˆϕ(Ns) | (28) |
为了验证本文算法的性能, 在OTB2015和VOT2018数据集上对SiamMB进行了评估, 并与近年来的一些主流跟踪算法进行了比较.
3.3.1 OTB2015数据集实验分析式(9)中权重参数
| 表 1 λ取不同值时的跟踪结果 |
在确定λ取值后, 为了验证SiamMB的性能, 本文选取了6个主流算法在OTB2015数据集上进行了对比. 对比算法分别是: SiamFC, SiamRPN, DaSiamRPN, SiamFC++, SiamCAR, SiamGAT. 实验结果如表2所示, 本文提出的SiamMB在对比主流跟踪器中取得了良好的竞争力, 与SiamGAT算法相比, 跟踪精度和成功率分别提高了0.4%和0.8%, 与SiamRPN相比, 提升效果明显, 跟踪精度和成功率分别提高了7.1%和7.9%, 证明本文算法的改进能有效地提高跟踪的鲁棒性, 提升跟踪的性能.
| 表 2 不同算法在OTB2015数据集上的Precision和Success |
3.3.2 VOT2018数据集实验分析
我们将提出的SiamMB算法在VOT2018数据集上进行实验, 并与SiamFC, SiamRPN, DSiam, SiamVGG, SiamMask, SiamGAT这6种跟踪算法进行比较. 同时我们比较了不同跟踪算法的3个评价指标: Accuracy、Robustness和EAO, 细节如表3所示, 我们可直观地看出, SiamMB在Accuracy、EAO值上分别比SiamRPN提高了0.3%、2.2%, Robustness值降低了4.7%. 在Accuracy值与SiamMask相差不大的同时, Robustness和EAO都优于其他算法, 表现出了良好的竞争力, 说明本文的改进大大提高了跟踪的准确性, 验证了SiamMB在面对复杂场景时, 能够展现出较好的尺度适应能力, 保证算法的鲁棒性.
为了验证模型的通用性, 本文与相关滤波类目标跟踪中具有代表性的算法KCF、SRDCF、C-COT、ECO、ASRCF、UPDT在OTB2015与VOT2018数据集上进行了对比实验. 并分别用Precision、Success和Accuracy、Robustness、EAO评价指标进行分析. 具体实验结果如表4所示.
| 表 3 算法在VOT2018上的跟踪准确率、鲁棒性和期望平均重叠率 |
由表4可以直观看出, 本文算法在OTB2015数据集上成功率达到了最高值, 相比UPDT算法提高了1.7%, 跟踪精度仅次于UPDT算法, 相比ECO算法提高了1.5%. 在VOT2018数据集上, 本文算法鲁棒性与ECO算法不相上下, 其余评价指标均达到了最高值, Accuracy与EAO值相比UPDT算法分别提高了0.8%, 验证了本文算法有效提高了跟踪鲁棒性, 改善了跟踪的性能, 证明本文算法在目标跟踪领域具有良好的竞争力.
| 表 4 本文算法与相关滤波类目标跟踪算法对比 |
3.4 定性分析实验
为了更加直观地展现出本文算法的优越性, 将SiamMB与SiamGAT、SiamRPN进行对比. 从OBT2015中选取Basketball、Bolt、Girl2和Human2这4组具有代表性场景的视频序列. 包含目标快速运动、尺寸变化、目标与背景相似和遮挡等多种复杂场景, 其中, Basketball和Bolt视频序列主要针对快速运动和相似背景干扰情况下的实验验证, Human2视频序列主要针对大尺度形变情况下的实验验证, Girl2视频序列主要针对遮挡情况下的实验验证. 几种对比算法的跟踪效果如图3所示.
Basketball和Bolt: 目标快速移动以及相似背景干扰, 导致模型的判别性不足, SiamGAT跟踪出现漂移, SiamRPN跟踪丢失, 而本文算法利用空间注意力机制, 提高了模型的抗干扰能力和提取特征的能力, 表现出了良好的跟踪效果.

|
图 3 SiamMB、SiamGAT和SiamRPN算法的跟踪结果 |

|
图 3 SiamMB、SiamGAT和SiamRPN算法的跟踪结果(续) |
Human2: 目标发生大尺度变化, 其他算法都发生了不同程度上的跟踪漂移, 特别是在第244帧的时候, SiamRPN跟踪丢失, 只有本文算法准确定位跟踪目标.
Girl2: 目标发生了完全遮挡或部分遮挡, 其中SiamGAT可以跟踪到目标, 但是跟踪过程中出现了漂移, 目标框与目标重叠率较低, SiamRPN则在第260帧完全跟踪丢失, 而本文算法增加邻近帧支路, 提高了算法跟踪的鲁棒性, 所以跟踪效果最好.
通过以上定性实验分析, SimaRPN在面对复杂场景时出现跟踪漂移甚至完全丢失, 无法完整的跟踪目标. SiamGAT在跟踪丢失之后能够再次定位目标, 但是目标边界框与目标的重叠率较低, 整体性能较差. 而本文算法在面对以上复杂情况也能够保持良好的跟踪性能, 实现目标的准确定位.
3.5 消融实验为了验证SiamMB改进模块的有效性, 本文在OTB2015数据集上进行了消融实验. 表5展示了不同模块组合对算法性能的影响.
表5中, 基线(Baseline)为SiamRPN模型, Model1和Model2分别在SiamRPN的模板帧支路和搜索帧支路融合了空间注意力机制, Model3则在SiamRPN的基础上增加了邻近帧支路, Model4在Model3的邻近帧支路融合了空间注意力机制, Model5在SiamRPN的基础上增加了邻近帧支路, 并且在3个支路中都融合了空间注意力机制.
| 表 5 OTB2015数据集上的消融实验结果 |
Model1成功率和跟踪精度在基线模型的基础上分别提高了0.03和0.07, Model2成功率和跟踪精度在基线模型的基础上分别提高了0.013和0.02, 证明了空间注意力机制能够增强特征之间的判别性, 为目标跟踪提供更加鲁棒的特征信息, 进一步证明了空间注意力机制对模型改进的有效性.
相比基线模型, Model3的成功率和跟踪精度分别提高了0.044和0.059, 反映了在跟踪过程中, 邻近帧支路能够提供更加具有判别性的特征信息, 增强算法在复杂场景下的鲁棒性, 证明了这种模型改进的有效性.
Model4在Model3的基础上, 成功率和跟踪精度分别提高了0.006和0.003, 证明本文两个改进能够有效结合起来.
Model5则为SiamMB网络, 成功率在Model4的基础上提高了0.029, 跟踪精度提高了0.009, 与目前主流算法相比, 有较强的竞争力, 尤其在应对复杂环境时, 本文模型体现出了更强的鲁棒性.
经消融实验对比, Model5的跟踪精度和成功率都达了最高值, 能达到最好的跟踪效果.
4 结论与展望针对目标形变、遮挡及相似背景干扰等复杂场景下跟踪出现漂移甚至丢失的问题, 本文提出一种基于多支路的孪生网络目标跟踪算法SiamMB, 增加邻近帧支路以增强网络的鲁棒性, 同时融合空间注意力机制, 有效地抑制无用的背景信息, 突出目标区域. 在OTB2015和VOT2018数据集上与主流的算法进行了对比, 本文算法相对于其他算法跟踪性能更加稳定.
该算法在跟踪精度与成功率上都有较大的提升, 但仍有进一步提升的空间, 后续我们将从以下两个方面提升算法的性能.
1)将该算法改进模块与性能更好的孪生网络跟踪模型相结合来提升算法的整体性能.
2) SiamMB模型在跟踪精度与区分相似干扰物、抗遮挡的能力大大提升, 但是跟踪过程中参考的目标信息仅有模板帧和邻近帧, 未来将加入更多的中间帧来提高对目标变化的适应能力.
| [1] |
孟琭, 杨旭. 目标跟踪算法综述. 自动化学报, 2019, 15(7): 1244-1260. DOI:10.16383/j.aas.c180277 |
| [2] |
Zhao JG, Cao XY. Research on target tracking algorithm in occlusion scene. Journal of Physics: Conference Series, 2021, 1748(3): 032048. DOI:10.1088/1742-6596/1748/3/032048 |
| [3] |
程旭, 崔一平, 宋晨, 等. 基于时空注意力机制的目标跟踪算法. 计算机科学, 2021, 48(4): 123-129. DOI:10.11896/jsjkx.200800164 |
| [4] |
韩瑞泽, 冯伟, 郭青, 等. 视频单目标跟踪研究进展综述. 计算机学报, 2022, 45(9): 1877-1907. DOI:10.11897/SP.J.1016.2022.01877 |
| [5] |
章泉源, 王昱程, 陈曦, 等. 基于全卷积孪生网络的模糊目标跟踪. 武汉大学学报(理学版), 2021, 67(5): 411-421. DOI:10.14188/j.1671-8836.2021.0042 |
| [6] |
陈志良, 石繁槐. 结合双模板融合与孪生网络的鲁棒视觉目标跟踪. 中国图象图形学报, 2022, 27(4): 1191-1203. DOI:10.11834/jig.200660 |
| [7] |
Bolme DS, Beveridge JR, Draper BA, et al. Visual object tracking using adaptive correlation filters. Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010. 2544–2550.
|
| [8] |
Henriques JF, Caseiro R, Martins P, et al. Exploiting the circulant structure of tracking-by-detection with kernels. Proceedings of the 12th European Conference on Computer Vision. Florence: Springer, 2012. 702–715.
|
| [9] |
Henriques JF, Caseiro R, Martins P, et al. High-speed tracking with kernelized correlation filters. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596. DOI:10.1109/TPAMI.2014.2345390 |
| [10] |
Ma C, Huang JB, Yang XK, et al. Robust visual tracking via hierarchical convolutional features. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2019, 41(11): 2709-2723. DOI:10.1109/TPAMI.2018.2865311 |
| [11] |
陈旭, 孟朝晖. 基于深度学习的目标视频跟踪算法综述. 计算机系统应用, 2019, 28(1): 1-9. DOI:10.15888/j.cnki.csa.006720 |
| [12] |
Wang NY, Yeung DY. Learning a deep compact image representation for visual tracking. Proceedings of the 26th International Conference on Neural Information Processing Systems. Lake Tahoe: Curran Associates Inc., 2013. 809–817.
|
| [13] |
Tao R, Gavves E, Smeulders AWM. Siamese instance search for tracking. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 1420–1429.
|
| [14] |
Bertinetto L, Valmadre J, Henriques JF, et al. Fully-convolutional Siamese networks for object tracking. Proceedings of the 2016 European Conference on Computer Vision. Amsterdam: Springer, 2016. 850–865.
|
| [15] |
Li B, Yan JJ, Wu W, et al. High performance visual tracking with Siamese region proposal network. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 8971–8980.
|
| [16] |
Li B, Wu W, Wang Q, et al. SiamRPN++: Evolution of Siamese visual tracking with very deep networks. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 4277–4286.
|
| [17] |
Guo DY, Shao YY, Cui Y, et al. Graph attention tracking. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021. 9538–9547.
|
| [18] |
Wang NY, Shi JP, Yeung DY, et al. Understanding and diagnosing visual tracking systems. Proceedings of the 2015 IEEE International Conference on Computer Vision. Santiago: IEEE, 2015. 3101–3109.
|
| [19] |
刘嘉敏, 谢文杰, 黄鸿, 等. 基于空间和通道注意力机制的目标跟踪方法. 电子与信息学报, 2021, 43(9): 2569-2576. DOI:10.11999/JEIT200687 |
| [20] |
Wu Y, Lim J, Yang MH. Object tracking benchmark. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1834-1848. DOI:10.1109/TPAMI.2014.2388226 |
| [21] |
Kristan M, Leonardis A, Matas J, et al. The sixth visual object tracking VOT2018 challenge results. Proceedings of the 2018 European Conference on Computer Vision (ECCV) Workshops. Munich: Springer, 2018. 3–53.
|
 2023, Vol. 32
2023, Vol. 32



