2. 广东石油化工学院 自动化学院, 茂名 525000
2. School of Automation, Guangdong University of Petrochemical Technology, Maoming 525000, China
安全帽是各行各业安全生产工作者和高空作业人员必不可少的一种安全用具, 在施工现场的安全管理中, 施工作业人员佩戴安全防护器具可以提高作业过程中的安全性. 安全帽呈半球形且表面较为光滑, 当有物体砸落在安全帽上时, 砸落物体的力不会集中在一点而是会向帽壳周围传递形成一个受力面, 这样可以将一个点受到的力缓冲至一个面来承受, 避免了冲击过程中的应力集中, 从而降低了伤亡事故发生的概率. 由于施工作业人员在作业时时常不佩戴安全帽, 轻视佩戴安全帽的重要性, 导致一些受伤事件. 因此可以设计一种安全帽佩戴检测的方法去检测施工现场中人员是否佩戴安全帽, 提高作业人员的安全性. 传统的人工检查安全帽佩戴情况具有局限性, 不能时时刻刻地关注到所有施工作业人员, 易造成安全事件的发生. 为了解决现有施工场地存在的这一安全管理局限性问题, 出现许多安全帽自动监测的方法, 对施工人员是否佩戴安全帽的实时检测具有重大的研究意义.
目前目标检测方法主要可以分为传统检测方法以及基于深度学习的检测方法. 传统目标检测方法需要先手工提取对象特征然后再对提取到的特征进行分类处理, 传统检测方法主要有V-J检测算法[1]、HOG+SVM检测算法[2]、DPM算法[3]等, 但是传统目标检测方法存在着时间复杂度高、窗口冗余以及手工设计的特征对于多样性的特征变换没有体现出很好的鲁棒性. 为了解决以往检测方法存在着的问题, 学者们尝试将深度学习的方法运用在目标检测上. 基于深度学习的目标检测算法主要分为两类: 一类是基于候选区域的两阶段目标检测算法, 如R-CNN[4]、SPPNet[5]、Fast R-CNN[6]、Faster R-CNN算法[7]等; 一类是基于回归的单阶段目标检测算法, 如SSD[8]、YOLO系列[9-12]、RetinaNet算法[13]等. 在基于深度学习的安全帽检测算法中, 文献[14]中孙勇等人提出一种基于YOLOv3的安全帽检测方法, 采用密集卷积网络(DenseNet)的方法处理低分辨率的特征层, 在保持特征提取充足的情况下降低了计算复杂度. 文献[15]中宋晓凤等人针对YOLOv5s原主干网对特征融合不充分的问题, 将主干特征提取网络中的残差块替换成ResNetBlock结构中的残差块, 以此提升 YOLOv5s 在细粒度上的融合能力. 文献[16]中施辉等人采用图像金字塔结构获取不同尺度大小的特征图, 用于位置和类别预测; 在模型训练过程中改变输入图像的尺寸大小, 提升模型对尺度大小的鲁棒性, 提高了安全帽检测准确率. 以上学者通过将原主干特征提取网络替换为更适合当前目标检测任务的特征提取网络、对主干特征提取网络特征提取模块的加强以及在训练过程中的多尺度训练方法, 均在一定程度上提升了模型检测性能. 本文以密集小目标的检测为总体设计思路, 针对在安全帽检测中的密集小目标样本总体存在的缺检、漏检现象提出一种基于改进YOLOX-s的安全帽检测方法.
新一代目标检测算法YOLOX[17]有着较好检测性能, 其算法有着模型大小不同的发行版本如YOLOX-x、YOLOX-l、YOLOX-m以及YOLOX-s. 考虑到在施工环境下进行实时检测时需要兼顾检测精度与检测速度, 因此本文使用轻量级网络结构的 YOLOX-s 作为基准模型对安全帽进行检测. 针对网络对于密集小目标的检测效果不佳的情况, 将特征提取网络中含有大量位置信息的浅层特征层经过送入加强特征提取网络与含有大量语义信息的深层特征层进行融合, 并增加一个解耦头(decouple head)进行密集小目标检测; 对定位损失函数和置信度损失函数进行改进, 提升了模型对于密集小目标的检测性能. 实验结果表明: 本文改进后的算法对安全帽佩戴检测具有较高的检测精度, 同时在检测速度上符合实时检测要求.
1 YOLOX算法原理YOLOX算法[17]是旷视科技在2021年提出的新一代YOLO系列目标检测算法, 相较于在它之前发布的YOLOv3、YOLOv4、YOLOv5目标检测算法在性能方面有着显著提升. YOLOX算法是基于YOLOv3进行改进的, YOLOX算法原作者在对YOLOv3算法的检测头进行改进时发现YOLOv3原来的耦合检测头在网络结构设置上可能还可以再优化改进, 于是进而采用了解耦头来替换原YOLOv3中的耦合检测头, 改进后发现精度和速度均有所提升. YOLOX同YOLOv5一样, 在网络结构上设计了多个深度与宽度不同的版本, 用户可根据自身对精度以及检测速度的要求来选择不同版本. 本文综合精度以及检测速度两方面的考虑, 选择YOLOX-s作为本文改进的基准算法, YOLOX-s算法的深度和宽度分别为YOLOX算法的0.33和0.5倍. YOLOX-s检测算法同YOLOX算法其他版本一样, 算法结构由CSPDarknet主干特征提取网络、PANet加强特征提取网络以及解耦头检测模块共同组成, 原理图如图1所示.

|
图 1 YOLOX-s算法原理图 Fig. 1 Schematic diagram of YOLOX-s algorithm |
1.1 YOLOX-s算法主要流程
检测图片输入网络后, 首先通过图像预处理统一调整为640×640的大小, 之后输入CSPDarknet主干特征提取网络进行特征提取, 得到3个有效特征层, 有效特征层的大小分别为80×80×128、40×40×256以及20×20×512. 有效特征层在特征加强网络中依次进行卷积调整通道数、上采样、特征拼接融合, 3个特征层特征依次叠加融合后进行下采样再次进行特征融合, 加强特征提取能力. 加强特征提取层输出3层特征加强融合后的加强特征层, 将3层加强特征层分别送入检测小目标、中目标以及大目标的解耦头检测模块进行检测.
1.2 无锚框机制(anchor-free)YOLOX-s虽是由YOLOv3改进而来的, 但是在锚框机制上却不同于YOLOv3以及由YOLOv3改进而来的YOLOv4、YOLOv5目标检测算法. YOLOX-s考虑到有锚框机制(anchor-based)需要通过先验知识去手动设计并调整锚框数量及大小, 并且在检测过程中会在特征图上生成大量的锚框, 而这些生成的锚框大多数会在下一阶段通过非极大值抑制(NMS)被消除, 这样会造成大量的不必要的计算导致计算资源的浪费, 同时生成大量的锚框中只有少部分置信度大于IoU阈值的锚框内的样本会判定为正样本, 而其他置信度低于IoU阈值的锚框则会被判定为负样本, 这样可能会导致网络在训练过程中形成正负样本不均衡的问题, 使得网络收敛性能变差. 采用无锚框机制(anchor-free)可以降低不必要的计算开销, 并且减少正负样本不均衡问题的出现, 无锚框机制并不代表是完全取消了锚框, 而是将原来对每个大、中、小网格的3个预测框减少为1个预先设置好的预测范围(如3×3的网格范围)如果样本中心点落在了该预测范围内并且置信度大于IoU阈值, 则判断该样本为正样本. 无锚框机制(anchor-free)减少了其余两个框的计算量以及负样本的数量, 有效地提高了网络在训练过程中的收敛性能.
1.3 解耦头不同任务的评价体系大多数是不完全相同的, 正如YOLO系列目标检测中的分类任务以及定位任务一样, 这两种不同的任务的评价体系一般来说也是不完全相同的. 以往的YOLO系列目标检测算法同时也包括近些年的YOLOv4、YOLOv5目标检测算法, 采用的都是将分类任务和定位任务融合在一起的耦合头, 这样可能会导致两种不同的任务以及评价体系产生冲突, 从而有可能使得网络的收敛性能达不到最优. 采用解耦头可以使得网络在训练过程中的分类任务与定位任务分别按照各自的评价体系进行损失值计算, 有效地缓解了任务之间发生冲突的可能性, 但是很显然将分类与定位任务进行解耦后不可避免地会增加计算量. YOLOX-s在权衡检测精度与检测速度后, 最终选取了轻量级解耦头的方案(如图1中右下角的YOLOHead模块所示), 即特征图由Neck层进入检测层时先经过1×1卷积统一调整通道数, 而后依据任务的不同, 分别设置分类任务通道以及定位任务通道, 每个通道按顺序通过两层3×3卷积层提取特征后再经1×1卷积层调整通道数执行分类及定位任务. YOLOX-s将耦合头替换成解耦头使得分类及定位两大任务依据各自的评价体系进行评价, 使得任务之间发生冲突的可能性降低, 提高了网络收敛性能.
2 YOLOX算法改进通过对原YOLOX-s算法网络训练完之后得出的模型进行数据分析, 发现模型对于本文所选取的数据集的误检及漏检主要是集中在数据集的小目标正样本上, 为了提升模型对于数据集中小目标样本的检测效果, 本文对YOLOX-s算法改进主要为以下3个方面.
(1)改进原网络结构, 将包含众多位置信息的浅层特征层从主干特征提取网络中提取出来, 并在加强特征提取网络中进行特征融合, 从而加强网络模型对位置信息的特征提取; 将检测层中将原来3个解耦头提升至4个解耦头, 提升图像中的小目标样本检测性能.
(2)改进IoU损失函数, 将原IoU损失函数改为SIoU损失函数, SIoU损失函数[18]考虑到了角度因素并重新定义了相关损失函数, 提升了目标定位精度.
(3)改进置信度损失函数, 引入了varifocal loss函数[19]均衡了正样本与困难样本之间的关系, 使网络更加注重困难样本, 提升了网络训练效果.
(4)引入CA (coordinate attention)注意力机制[20]至Neck层的特征图上采样操作之后, 改善原特征层经过上采样后对特征的噪声放大和模糊等影响, 增强了网络的特征表达能力, 使得网络训练出的模型性能更佳.
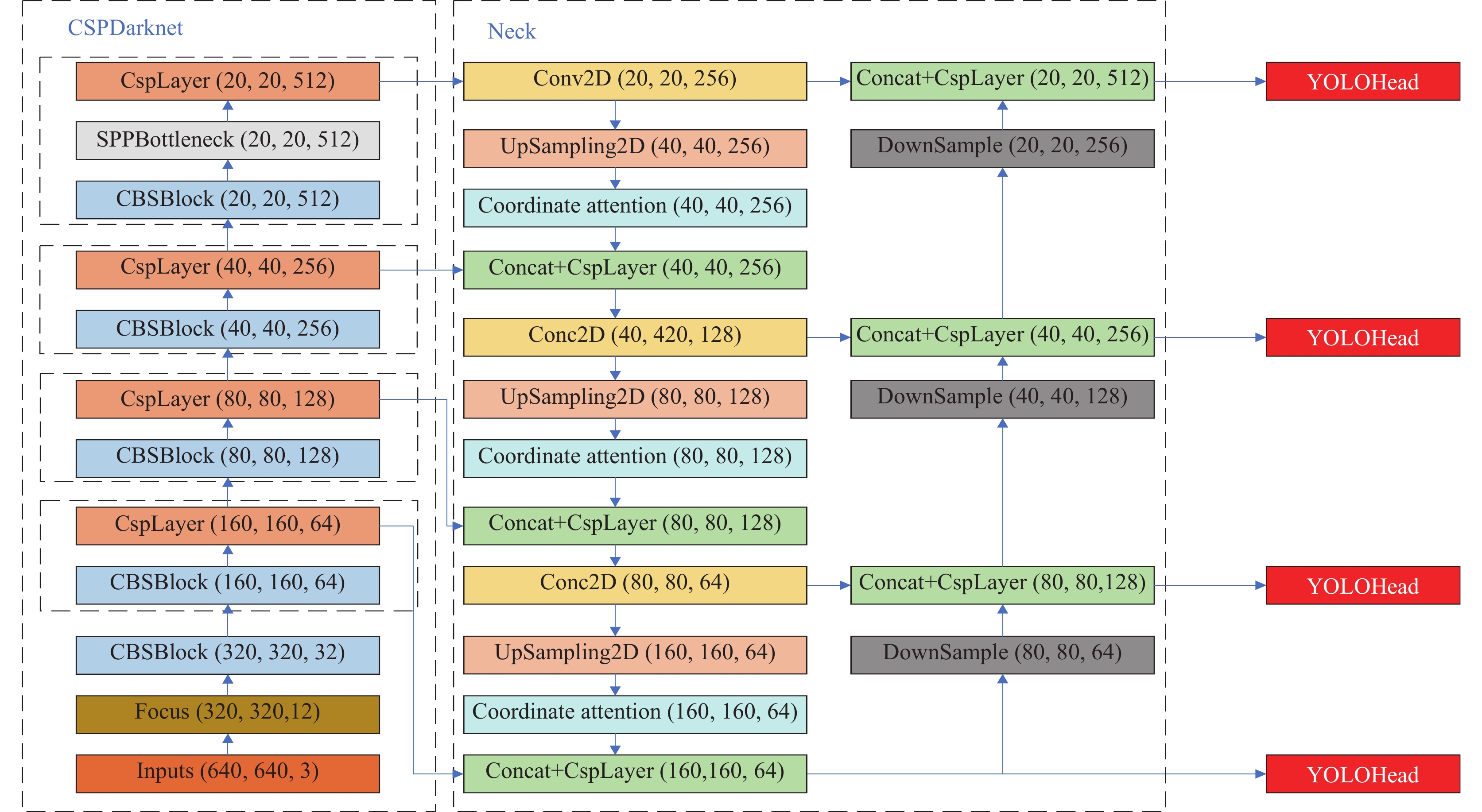
2.1 网络结构改进对原YOLOX-s算法网络训练完之后得出的模型进行推理检测, 发现模型对于本文所选取的数据集的误检及漏检主要是集中在数据集的小目标正样本上, 为了提升模型对于数据集中的小目标样本的检测效果, 将包含众多位置信息的160×160浅层特征层从主干特征提取网络中提取出来, 将160×160浅层特征层在加强特征提取网络中进行特征融合, 从而加强网络模型对位置信息的特征提取. 由于本文所采取的数据集中包含有大量微小目标, 于是在检测层中将原来3个解耦头提升至4个解耦头, 新增加的解耦头输入特征层大小为160×160, 该解耦头的感受野可以更好地匹配上数据集中的小目标样本, 使得图像中的小目标样本在检测时能够被注意到, 而不会因为感受野过大而导致小目标在检测时被忽略, 可以让模型对于图像中的小目标有着更好的检测性能. 改进后的YOLOX-s原理图如图2所示.
2.2 损失函数改进 2.2.1 SIoU损失函数改进针对原定位损失函数在收敛速度上较慢, 并且本文数据集中存在着众多小目标样本, 在进行定位损失函数计算时, 预测框与真实框常是包含与被包含的关系. 如果采用原IoU损失函数作为边界框回归损失, 那么在出现重叠时, 原IoU损失函数并没有考虑到预测框与真实框之间的方向因素, 没有能为边界框提供方向上的判断. 因此将原IoU损失函数改为SIoU损失函数, SIoU损失函数考虑到了角度因素, 重新定义了相关损失函数. 损失函数组成包含以下4个部分.
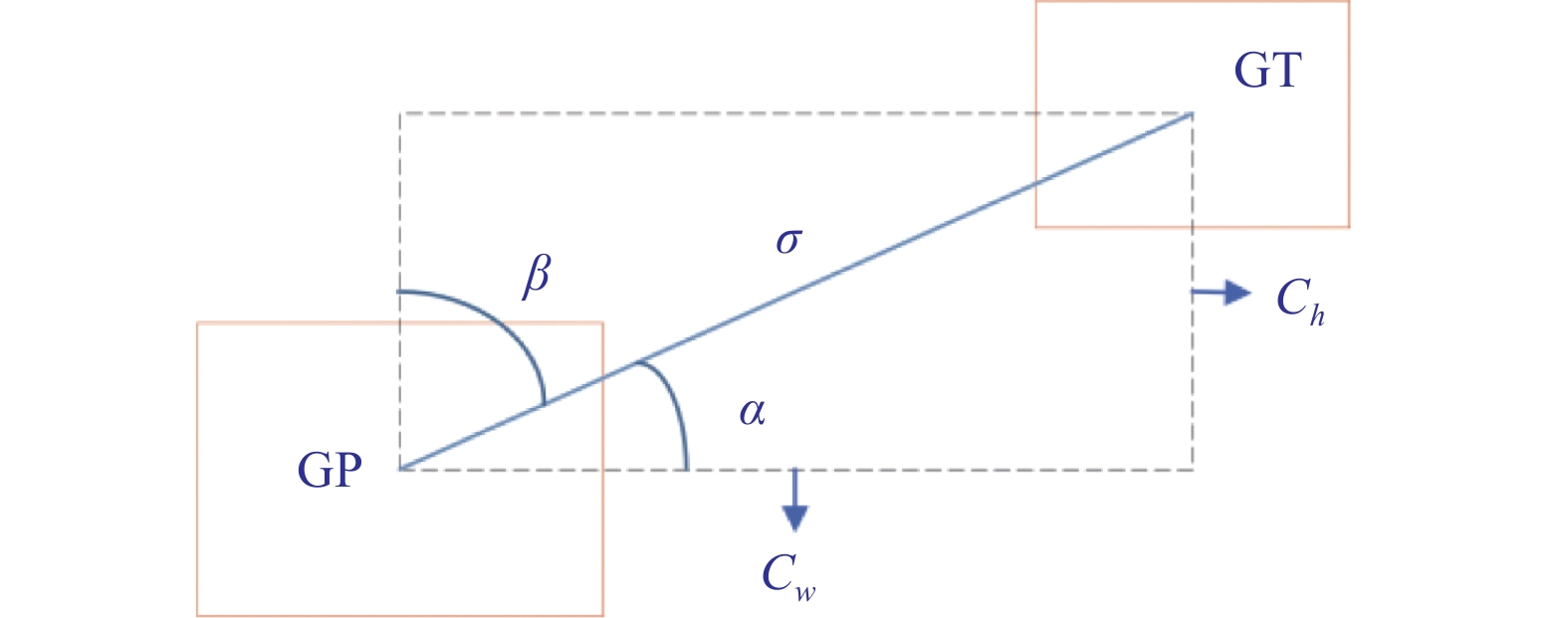
(1)角度损失, 其定义如下:
| $ \Lambda = \cos \left(2 \times \left(\arcsin \left(\frac{{{C_h}}}{\sigma }\right) - \frac{\text π }{4}\right)\right) $ | (1) |
其中,
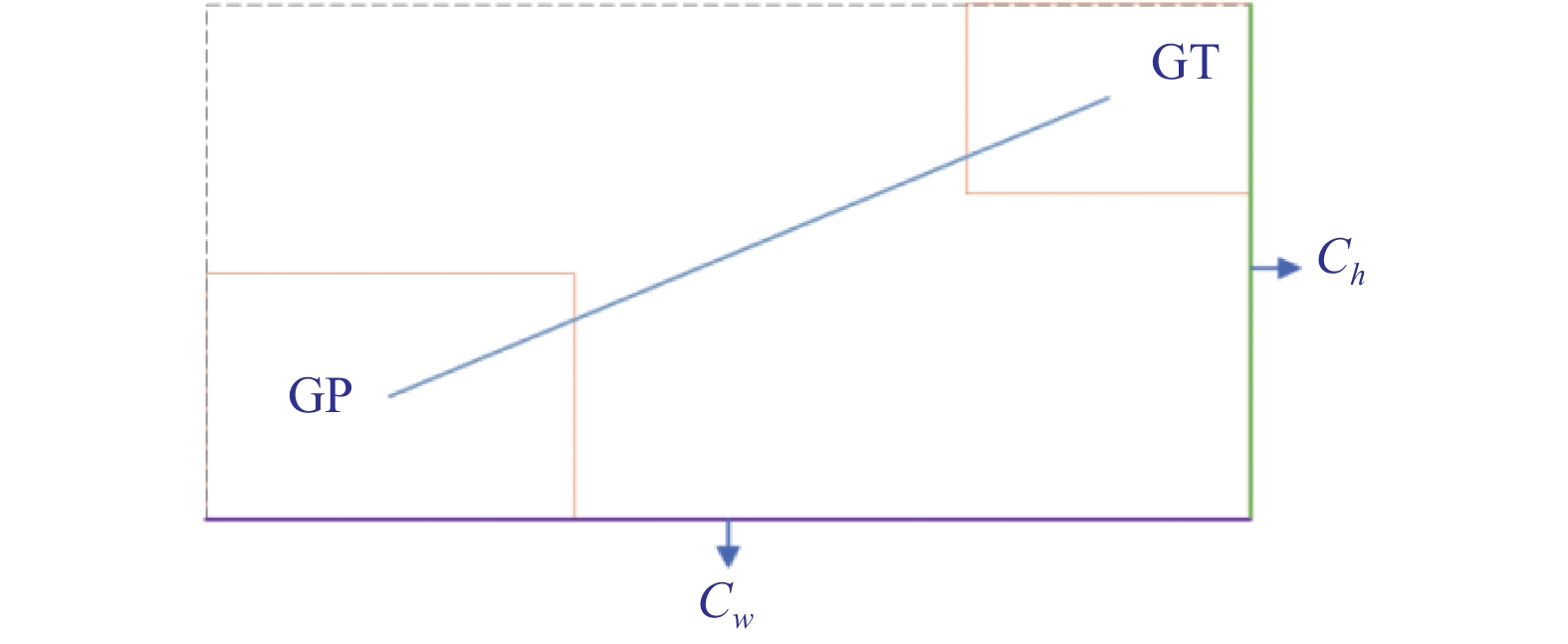
(2)距离损失, 如图4, 其定义如下:
| $ \Delta = \sum\limits_{t = x, y} {(1 - {{\rm{e}}^{ - \gamma {\rho _t}}})} = 2 - {{\rm{e}}^{ - \gamma {\rho _x}}} - {{\rm{e}}^{ - \gamma {\rho _y}}} $ | (2) |
其中,
| $ {\rho _x} = {\left(\frac{{b_{{c_{{x}}}}^{gt} - {b_{{c_{{x}}}}}}}{{{c_w}}}\right)^2} $ | (3) |
| $ {\rho _{\text{y}}} = {\left(\frac{{b_{{c_y}}^{gt} - {b_{{c_y}}}}}{{{c_h}}}\right)^2} $ | (4) |
| $ \gamma = 2 - \Lambda $ | (5) |
其中,
|
图 2 改进后的YOLOX-s原理图 Fig. 2 Improved YOLOX-s schematic diagram |
|
图 3 角度损失图 Fig. 3 Angular loss diagram |
|
图 4 距离损失图 Fig. 4 Distance loss diagram |
(3)形状损失, 如图5, 其定义如下:
| $ \Omega = {\sum\limits_{t = w, h} {(1 - {{\rm{e}}^{ - {\omega _t}}})} ^\theta } = {(1 - {{\rm{e}}^{ - {\omega _w}}})^\theta } + {(1 - {{\rm{e}}^{ - {\omega _h}}})^\theta } $ | (6) |
其中,
| $ {\omega _w} = \frac{{|w - {w^{gt}}|}}{{\max (w, {w^{gt}})}} $ | (7) |
| $ {\omega _h} = \frac{{|h - {h^{gt}}|}}{{\max (h, {h^{gt}})}} $ | (8) |
其中,

|
图 5 形状损失图 Fig. 5 Shape loss diagram |
(4) IoU损失:
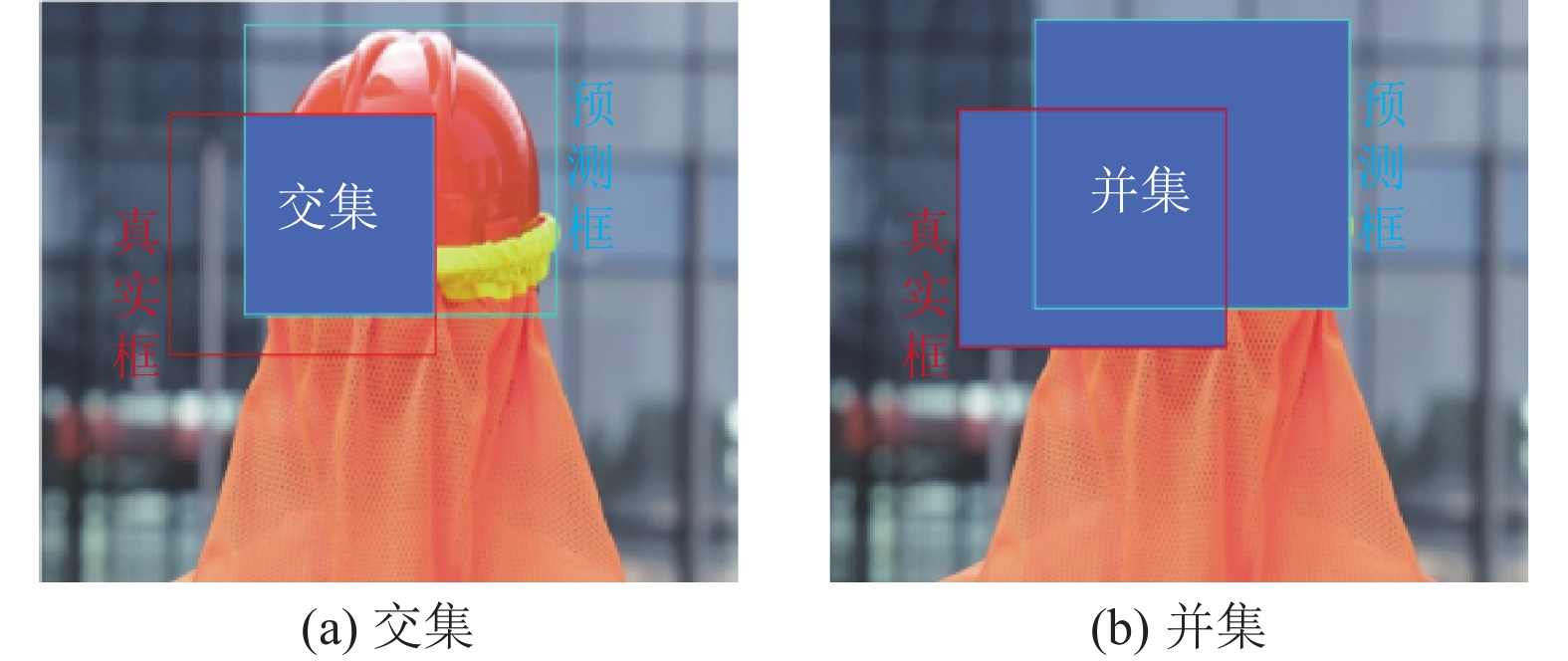
| $ IoU=\frac{交集}{并集} $ | (9) |
其中, 交集为图6(a)中蓝色区域, 并集为图6(b)中蓝色区域.
最终SIoU损失函数由以上4部分构成, 公式为:
| $ Los{s_{{\rm{SIoU}}}} = 1 - IoU + \frac{{\Omega + \Delta }}{2} $ | (10) |
|
图 6 IoU损失图 Fig. 6 IoU loss graph |
2.2.2 Varifocal loss置信度损失函数改进
因为本文数据集存在着目标密集且正负样本不均匀的问题, 于是引入了varifocal loss函数对置信度损失函数进行改进, 平等的对待正负样本, 防止在训练过程中出现类别不均衡的问题, 其定义如下:
| $ VFL(p, q) = \left\{ {\begin{array}{*{20}{l}} { - q(q\log (p) + (1 - q)\log (1 - p))}, \\ { - a{p^\gamma }\log (1 - p)}, \end{array}} \right.\begin{array}{*{20}{c}} {q \gt 0} \\ {q = 0} \end{array} $ | (11) |
其中,
Varifocal loss函数通过参数
本文设计的改进后的损失函数中的定位损失函数为SIoU损失函数, 置信度损失函数为varifocal loss函数, 分类损失函数采用Bce loss函数. 改进后各类损失函数以及总损失函数表达式为:
| $ Los{s_{{\rm{IoU}}}} = \sum\limits_{i = 1}^N {\left(1 - IoU + \frac{{\Omega + \Delta }}{2}\right)} $ | (12) |
| $ Los{s_{{\rm{obj}}}} = \left\{ {\begin{array}{*{20}{l}} { - \displaystyle\sum\limits_{i = 1}^N {(q(q\log (p) + (1 - q)\log (1 - p)))}, }\quad {q \gt 0} \\ { - \displaystyle\sum\limits_{i = 1}^N {(a{p^\gamma }\log (1 - p))} }, \qquad\qquad\qquad\quad\; {q = 0} \end{array}} \right. $ | (13) |
| $ Los{s_{{\rm{cls}}}} = - \sum\limits_{i = 1}^N {({t_i}\log ({p_i}) + (1 - {t_i})\log (1 - {p_i}))} $ | (14) |
| $ Los{s}_{总}=\frac{1}{N}(Los{s}_{{\rm{IoU}}}+Los{s}_{{\rm{obj}}}+Los{s}_{{\rm{cls}}}) $ | (15) |
其中, N为一个Batchsize的设置的样本数量,
CA注意力机制不同于通道注意力机制将输入通过空间全局池化将转化为C×1×1的特征层, CA是将通道注意力按照空间域的空间分布分解为两个分别沿着垂直方向与水平方向的方向聚合特征的C×H×1和C×1×W特征层. 通过对空间域两个方向分别关注, 使其可以沿着一个空间方向获取长距离依赖, 并且保留另一个空间方向精确的位置信息. 然后, 将生成的特征图分别进行特征编码, 形成一对方向感知和位置敏感的注意力特征图. 最后, 将它们乘以输入特征图, 以此来增强感兴趣区域的表达. CA注意力机制结构示意图如图7所示.

|
图 7 CA注意力机制结构示意图 Fig. 7 Schematic diagram of the structure of the Coordinate attention mechanism |
CA注意力机制作用的具体流程如下.
(1)在空间域的垂直方向与水平方向上分别采用1×W、H×1大小的池化核进行平均池化, 将位置信息聚集到各空间方向上. 计算公式如式(16)、式(17)所示:
| $ {\textit{z}}_c^h(h) = \frac{1}{W}\sum\limits_{0 \leqslant i \lt W} {{x_c}(h, i)} $ | (16) |
| $ {\textit{z}}_c^w(w) = \frac{1}{H}\sum\limits_{0 \leqslant j \lt H} {{x_c}(j, w)} $ | (17) |
其中,
(2)在空间位置信息聚合得到输出值后, 将其中一空间方向张量的维度进行维度转换, 使其能与另一空间方向张量进行维度层面的拼接. 将拼接后的张量通过1×1卷积核大小的标准卷积模块(2D卷积层+Batch-Norm层+非线性激活函数层)进行特征提取. 计算公式如式(18)所示:
| $ f = \delta ({F_1}[{{\textit{z}}^h}, {{\textit{z}}^w}]) $ | (18) |
其中,
(3)将经过1×1标准卷积模块特征提取后的特征层进行垂直方向和水平方向上的注意力权重重新分配. 计算公式如式(19)、式(20)所示:
| $ g^h = \sigma(F_h(f^h)) $ | (19) |
| $ g^w = \sigma(F_w(f^w)) $ | (20) |
其中,
(4)将水平方向与垂直方向的注意力权重矩阵分别作用于原特征层, 加强原特征层对语义位置信息的表达能力. 计算公式如式(21)所示:
| $ y_c(i,j)=x_c(i,j)\times g_c^h(i)\times g_c^w(j) $ | (21) |
其中,
本文将CA注意力机制引入至Neck层的每个上采样操作之后, 将上采样之后的特征层执行CA注意力机制, 可以进一步减小上采样过程中可能造成的噪声放大和模糊等影响. 本文考虑到计算开销成本, 以及原网络的下采样操作采用的是卷积核为3×3, 步长为2的标准卷积模块, 原下采样操作对于特征的提取整合能力相较于上采样操作对于特征更具鲁棒性, 故只将CA注意力机制应用于每个下采样操作之后, 在不增加较多计算开销的前提下, 有效增强了网络的特征表达能力.
3 实验 3.1 实验数据集本文实验所采用的数据集是从开源的SHWD数据集选取的4 290张图片, 该数据集涵盖了工地以及其他多种场合下佩戴安全帽的情况, 并将该数据集的类别分为hat (佩戴安全帽)类以及person (未佩戴安全帽)类, 数据集格式为Pascal VOC格式, 标注文件为XML格式文件, 在正式开始训练前将数据集按照8:1:1的比例划分为训练集、验证集与测试集.
3.2 实验环境本文所采用的实验环境为: Windows 11 系统, 显卡采用NVIDIA GeForce RTX 3060 Laptop GPU, 深度学习框架选取PyTorch. 在网络训练过程中使用GPU进行加速, 使得网络训练过程中效率提高, 实验所采用的环境如表1所示.
| 表 1 实验运行环境 Table 1 Experimental operating environment |
3.3 模型训练
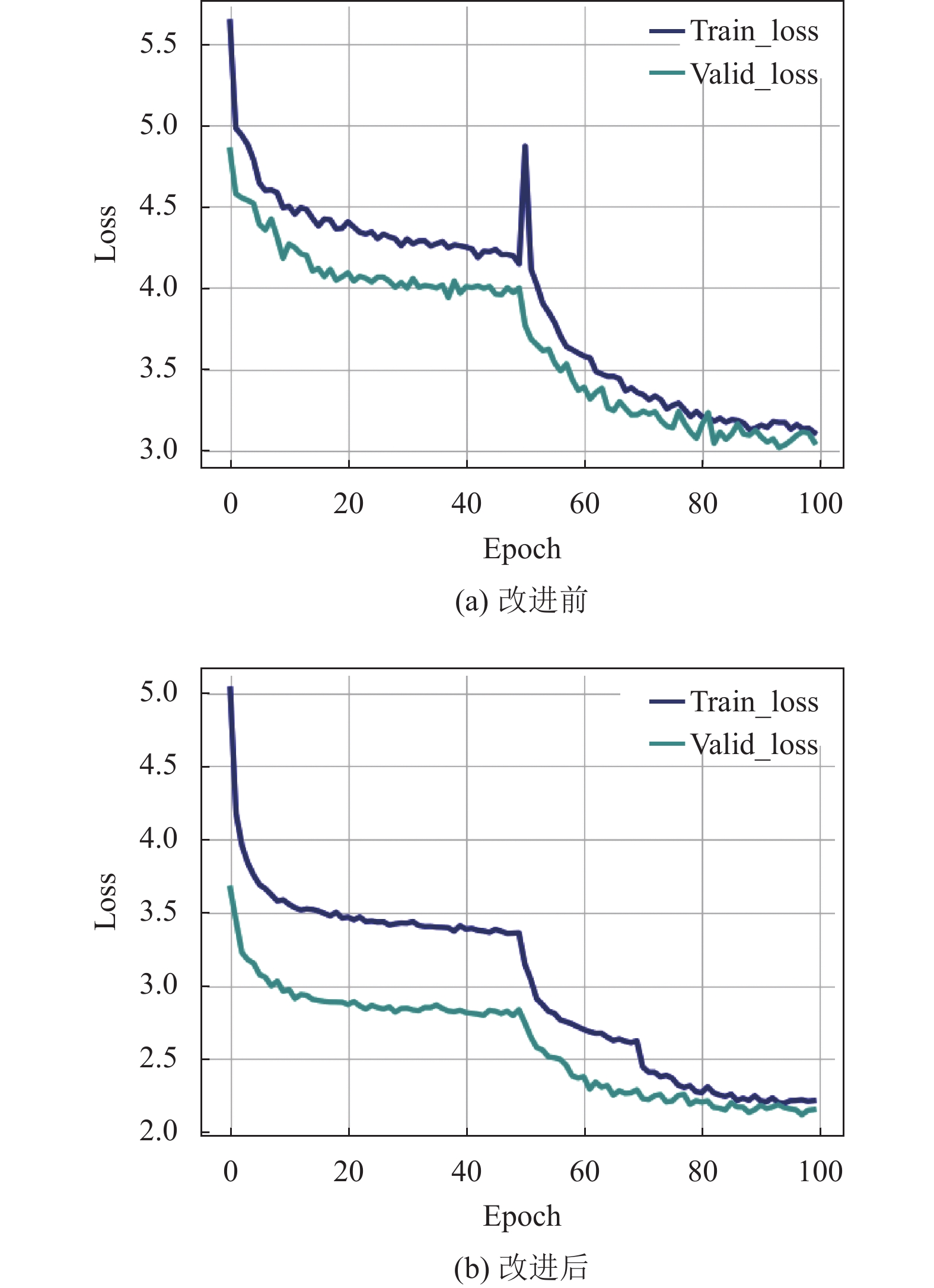
本文使用的训练集的类别与主流开源数据集如COCO数据集、VOC2007数据集以及VOC2012数据集在类别上具有一定的相似性, 故采用迁移学习的方式来训练模型, 模型总共训练100个epoch, 总迭代次数为43 400次. 网络在开始训练时加载预训练模型并在前50个epoch阶段进行冻结训练(此时模型主干特征提取网络参数不发生改变), 在50到100个epoch阶段解冻恢复正常训练. 根据实验环境及数据集情况将网络参数设置为: 冻结训练阶段批次大小为8, 解冻训练阶段批次大小为4, 网络训练学习动量为0.93, 训练时采用的优化器为SGD优化器, 网络训练过程如图8所示, 相较于改进前整体稳步收敛, 没有发生损失值突变以及过拟合现象.
3.4 评价指标本实验采用的检测精度评价指标为精确率(precision, P)、召回率(recall, R)、平均精度(average precision, AP)以及评价精度均值(mean average precision, mAP); 采用的检测速度评价指标为每秒传输帧数(frame per second, FPS); 采用网络模型参数量(Parameter)来评价网络模型的大小.
3.4.1 查全率(R)与查准率(P)查全率与查准率的公式分别为式(22)与式(23):
| $ R = \frac{{TP}}{{TP + FN}} \times 100{\text{%}} $ | (22) |
| $ P = \frac{{TP}}{{TP + FP}} \times 100{\text{%}} $ | (23) |
其中, TP表示正确预测的正样本数量, FN表示错误预测的负样本数量, FP表示错误预测的正样本数量, (TP+FN)表示所有正样本的数量, (TP+FP)表示所有预测为正确的样本数量(包含负样本).
|
图 8 损失值图 Fig. 8 Loss value diagram |
3.4.2 平均精度(AP)与平均精度均值(mAP)
平均精度与平均精度均值的公式分别为式(24)与式(25):
| $ AP = \int_0^1 {P(R){{d}}R} $ | (24) |
| $ mAP=\frac{1}{N}{\displaystyle \sum _{{k}=1}^{N}AP({k})} $ | (25) |
其中, AP表示单个类别的平均检测精度, 而mAP表示的是全局的平均精度均值(用来评价整体模型的检测精度), 模型检测时可以用mAP来衡量检测性能, 其mAP越高, 表示模型的检测效果更好.
3.5 实验结果及分析 3.5.1 对比试验通过对本文改进后的算法进行验证, 并与其他主流检测算法进行性能比较, 对比试验如表2所示. 从表2中可以看到Fast R-CNN、RetinaNet、SSD-VGG算法的mAP值均小于60%且person (未佩戴安全帽)的检测AP值均较低不符合检测精度要求, 其中SSD-VGG的检测速度(FPS)较快, Fast R-CNN的精度相对较高但检测速度最慢且参数量高达136.71M. YOLOv3、YOLOv4的检测精度均小于80%且参数量均较大, 不适合在硬件方面部署, 轻量级YOLOv5-s、原YOLOX-s算法的参数量较小且在检测精度与检测速度上均有着良好的表现. 本文改进后的算法相较于主流算法在参数量上较小且检测精度较高, 且相较于原算法改进后的YOLOX-s算法mAP值提升了3.59%, 其中hat (佩戴安全帽)类别的AP值提升了1.87%, person (未佩戴安全帽)类别的AP值提升了5.31%, 检测速度为54.73帧/s, 能够在大多数情况下及时有效地检测出安全帽佩戴情况. 尽管在检测速度上有所降低, 但符合场景实时检测要求, 能够完成安全帽实时检测任务且适合在硬件方面落地部署.
| 表 2 对比试验 Table 2 Comparison test |
3.5.2 消融实验
为了验证本文所采用的各个改进策略的有效性, 将各个改进策略分别加入原模型, 进行消融实验, 如表3所示. 可以看到加入Neck改进策略、SIoU损失函数改进策略、varifocal loss函数改进策略以及CA注意力机制改进策略后, mAP值总体稳步提升, 验证了每一步改进策略的有效性.
| 表 3 消融实验 Table 3 Ablation experiments |
3.5.3 检测结果可视化
从检测结果图片可以很清晰地看到, 改进后的算法较改进前检测性能更好. 原算法以往对于小目标的漏检以及误检问题在改进后有了很好地改善, 如图9、图10所示, 改进后的算法相较于原算法检测到的目标更多更准, 检测性能更佳.

|
图 9 改进前后检测效果对比图 Fig. 9 Comparison of detection effect before and after improvement |

|
图 10 改进前后检测效果对比图 Fig. 10 Comparison of detection effect before and after improvement |
4 结论与展望
本文提出一种基于YOLOX-s的改进算法, 算法参考多尺度检测的思想针对小目标在实际环境下难以检测的问题, 提出增加一个针对小目标的160×160的小目标检测头来提升小目标检测的效果, 并且通过优化损失函数以及引入CA注意力机制, 使得训练过程中网络收敛与回归性能更佳. 通过实验可知, 本文改进后的算法在满足现场实时检测速度要求的情况下具有较高的准确性, 且参数量较小, 在今后的研究中将继续尝试对模型剪枝、量化后移植进硬件后进行现场部署, 实现现场终端实时检测.
| [1] |
Viola P, Jones M. Rapid object detection using a boosted cascade of simple features. Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Kauai: IEEE, 2001.
|
| [2] |
Dalal N, Triggs B. Histograms of oriented gradients for human detection. Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego: IEEE, 2005. 886–893.
|
| [3] |
Felzenszwalb P, McAllester DA, Ramanan D. A discriminatively trained, multiscale, deformable part model. Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition. Anchorage: IEEE, 2008. 1–8.
|
| [4] |
Girshick R, Donahue J, Darrell T, et al. Rich feature hierarchies for accurate object detection and semantic segmentation. Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition. Columbus: IEEE, 2014. 580–587.
|
| [5] |
He KM, Zhang XY, Ren SQ, et al. Spatial pyramid pooling in deep convolutional networks for visual recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1904-1916. DOI:10.1109/TPAMI.2015.2389824 |
| [6] |
Girshick R. Fast R-CNN. Proceedings of the IEEE International Conference on Computer Vision. Santiago: IEEE, 2015. 1440–1448.
|
| [7] |
Ren SQ, He KM, Girshick R, et al. Faster R-CNN: Towards real-time object detection with region proposal networks. Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal: MIT Press, 2015. 91–99.
|
| [8] |
Liu W, Anguelov D, Erhan D, et al. SSD: Single shot multibox detector. Proceedings of the 14th European Conference on Computer Vision. Amsterdam: Springer, 2016. 21–37.
|
| [9] |
Redmon J, Divvala S, Girshick R, et al. You only look once: Unified, real-time object detection. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 779–788.
|
| [10] |
Redmon J, Farhadi A. YOLO9000: Better, faster, stronger. Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 6517–6525.
|
| [11] |
Redmon J, Farhadi A. YOLOv3: An incremental improvement. arXiv:1804.02767, 2018.
|
| [12] |
Bochkovskiy A, Wang CY, Liao HYM. YOLOv4: Optimal speed and accuracy of object detection. Computer Vision and Pattern Recognition. arXiv:2004.10934, 2020.
|
| [13] |
Lin TY, Goyal P, Girshick R, et al. Focal loss for dense object detection. Proceedings of the IEEE International Conference on Computer Vision. Venice: IEEE, 2017. 2999–3007.
|
| [14] |
张勇, 吴孔平, 高凯, 等. 基于改进型YOLOv3安全帽检测方法的研究. 计算机仿真, 2021, 38(5): 413-417. DOI:10.3969/j.issn.1006-9348.2021.05.085 |
| [15] |
宋晓凤, 吴云军, 刘冰冰, 等. 改进YOLOv5s算法的安全帽佩戴检测. 计算机工程与应用, 2023, 59(2): 194-201. DOI:10.3778/j.issn.1002-8331.2206-0468 |
| [16] |
施辉, 陈先桥, 杨英. 改进YOLOv3的安全帽佩戴检测方法. 计算机工程与应用, 2019, 55(11): 213-220. DOI:10.3778/j.issn.1002-8331.1811-0389 |
| [17] |
Ge Z, Liu ST, Wang F, et al. YOLOX: Exceeding YOLO series in 2021. arXiv:2107.08430, 2021.
|
| [18] |
Gevorgyan Z. SIoU loss: More powerful learning for bounding box regression. arXiv:2202.12740, 2022.
|
| [19] |
Zhang HY, Wang Y, Dayoub F, et al. VarifocalNet: An IoU-aware dense object detector. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021. 8510–8519.
|
| [20] |
Hou QB, Zhou DQ, Feng JS. Coordinate attention for efficient mobile network design. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). Nashville: IEEE, 2021. 13708–13717.
|
 2023, Vol. 32
2023, Vol. 32


