2. 中国科学院大学, 北京 100049;
3. 辽宁省生态环境监测中心, 沈阳 110161;
4. 沈阳市第二十二中学, 沈阳 110075
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Liaoning Ecological and Environmental Monitoring Center, Shenyang 110161, China;
4. Shenyang No.22 Middle School, Shenyang 110075, China
随着经济和社会的快速发展, 大量空气污染物排放在大气中, 造成严重的大气污染, 对人体造成严重的危害. 近些年来, 我国政府加大了生态文明建设的投资, 加强了生态环境保护的力度, 在全国各个地区搭建空气质量监测站, 用来监控空气污染物(PM2.5, PM10, NO2等)质量数据. PM2.5作为衡量空气污染物浓度的重要指标, 对其浓度进行准确的监控预测, 能够减少对人们身健健康的侵害, 进一步推进大气污染物监控治理工作, 能够有效地保护大气环境[1, 2].
当前PM2.5浓度预测的方法主要有传统机器学习和深度学习. 传统机器学习方法主要包括移动平均自回归(autoregressive integrated moving average model, ARIMA)、支持向量机(support vector machine, SVM)、随机森林(RF)、集成学习、智能优化算法等. 严宙宁等[3]利用ARMIA模型对深圳日平均PM2.5浓度进行预测, 得到较好的预测结果. 石峰等[4]提出群智能灰狼最优化算法, 模型具有较好的泛化能力、预测能力和鲁棒性. 尹建光等[5]采用小波分解与最小二乘支持向量回归相结合的方法对PM2.5进行建模预测, 提高预测精度, 特别是对于浓度变化较大的点预测精度较高. 然而, 上述传统方法都采用PM2.5日均浓度作为输入, 现实监测站是以小时为单位检测记录PM2.5浓度, 经过加工的日均浓度数据损失了原有的数据信息, 得到的预测结果准确度较低[6]. 此外, ARIMA、SVM、智能优化算法等受到算法本身的限制, 只能对PM2.5浓度进行短期预测, 缺乏了对时间序列数据周期性、趋势性等长期特征的捕获, 预测效果也会受到影响[7].
近些年来, 随着数据量的激增、计算机算力的大幅提升, 深度学习在处理复杂时间序列的问题上取得较大的进步[8]. 深度学习主要的网络模型有卷积神经网络(convolutional neural network, CNN)、循环神经网络(recurrent neural network, RNN)、对抗生成网络(generative adversarial network, GAN)等. 在解决长时依赖的问题上, 许多研究者都使用RNN的变体结构LSTM. 例如, 刘旭林等[9]考虑PM2.5浓度与气象要素的时空相关性, 建立CNN-Seq2Seq预测模型, 有效提高PM2.5浓度未来一小时预测精度. 邓丽等[10]考虑时间因素、空间因素、气象因素和空气污染物因素等多种因素, 提出了SSAE深度特征学习和LSTM网络的模型. 黄伟建等[11]考虑到PM2.5多元数据间的时空相关性, 通过构建本地记忆组件和邻域组件对时间和空间依赖关系, 提出一种TSMN预测模型. 由此可见, LSTM因其能够捕捉中长期时间依赖的信息在空气质量预测领域的应用取得了不错的效果. 2017年, Google机器翻译团队采用attention机制来进行机器翻译任务, 取得显著成效[12]. 此后, 注意力机制在语音、自然语言处理、计算机视觉等领域取得重大突破. 已有文献将注意力机制应用到PM2.5浓度预测的研究较少.
综上所述, 本文提出一种基于高斯概率估计和注意力机制的高斯-注意力预测模型, 将历史PM2.5数据和其他空气质量数据的分层时间戳信息对齐作为输入[13], 通过多头注意力机制捕捉影响PM2.5空气质量浓度关键的信息, 再经过高斯似然估计得到预测结果, 并对预测结果进行比较和评价.
2 高斯-注意力模型预测PM2.5浓度 2.1 问题分析PM2.5浓度预测的问题本质上是时间序列的问题, 利用历史N个时间段的数据, 去预测未来M个时间间隔的数据[14]. 即利用历史数据Xhis=[Xt–N+1, …, Xt]去预测未来数据Xfu=[Xt+1, … , Xt+M], PM2.5浓度预测示意图如图1所示.

|
图 1 PM2.5浓度预测 |
PM2.5浓度不仅受到历史PM2.5数据的影响, 同时也受到大气污染物和气象要素等因素影响[15]. 因此, 应当将同一时间点的空气质量监测站的其他监测数据如NO2、SO2等作为输入, 即第t个时间点的Xt =[PM2.5, NO2, …, SO2], 通过对多种历史数据特征进行建模处理, 实现对PM2.5浓度预测. 我们的目标是建模得到如式(1)所示的条件分布:
| P(Yt+1:t+τ|X1:t;θ)=∏t+τt+1P(Yt|X1:t−1;θ) | (1) |
其中, θ表示模型中所有可学习的参数, X1:t 表示1–t时刻历史的监测数据, Yt 表示模型预测得到的PM2.5浓度数据.
2.2 高斯概率模型在本文中, 由于空气监测站的检测数据都是实值数据, 这些长期、大量的观测数据受到多种因素的影响使得观测数据的分布呈现为高斯分布. 因此, 本文通过构建高斯概率密度函数直接预测下一个时间点的概率分布的所有参数θ (均值和方差) , 通过采样得到下一个时间节点的PM2.5预测值. 高斯概率密度函数如式(2)所示:
| lG(y|μ,σ)=(2πσ2)−12exp(−(y−μ)22σ2) | (2) |
其中, μ表示数学期望,
注意力机制的本质来自人类的视觉感知机制, 人们在进行视觉感知的时候, 会根据需求将注意力放在特定的一部分. 注意力机制通过对输入权重分配的关注, 可以快速提取稀疏数据的重要特征. 注意力函数是将一个查询(query)和键值对(key-value)映射到输出的方法[16]. 计算注意力得分如图2所示.
计算注意力得分主要分为3步: 第1步是将q
| f(Q,Ki)={QTKidotQTWαKigeneralWα[Q;Ki]concat | (3) |
其中, Q表示query矩阵, Ki表示第i个key, Wα表示权重矩阵, f(Q, Ki)表示query跟第i个Key的相似度, dot表示QT与K的点积, general表示QT与K的加权点积, concat表示QT与K的拼接.
第2步是使用一个Softmax函数对权重进行归一化处理.
| ai=Softmax(f(Q,Ki))=exp(f(Q,Ki))∑jexp(f(Q,Kj)) | (4) |
其中, ai表示第i个权重归一化的值.
最后一步是将权重和相应的键值value进行加权求和得到最后的注意力得分.
| Attention(Q,K,V)=∑iaiVi | (5) |
其中, Vi表示第i个value的值, Attention(Q, K, V)表示最后的注意力得分.

|
图 2 计算注意力得分图 |
2.4 高斯-注意力预测模型
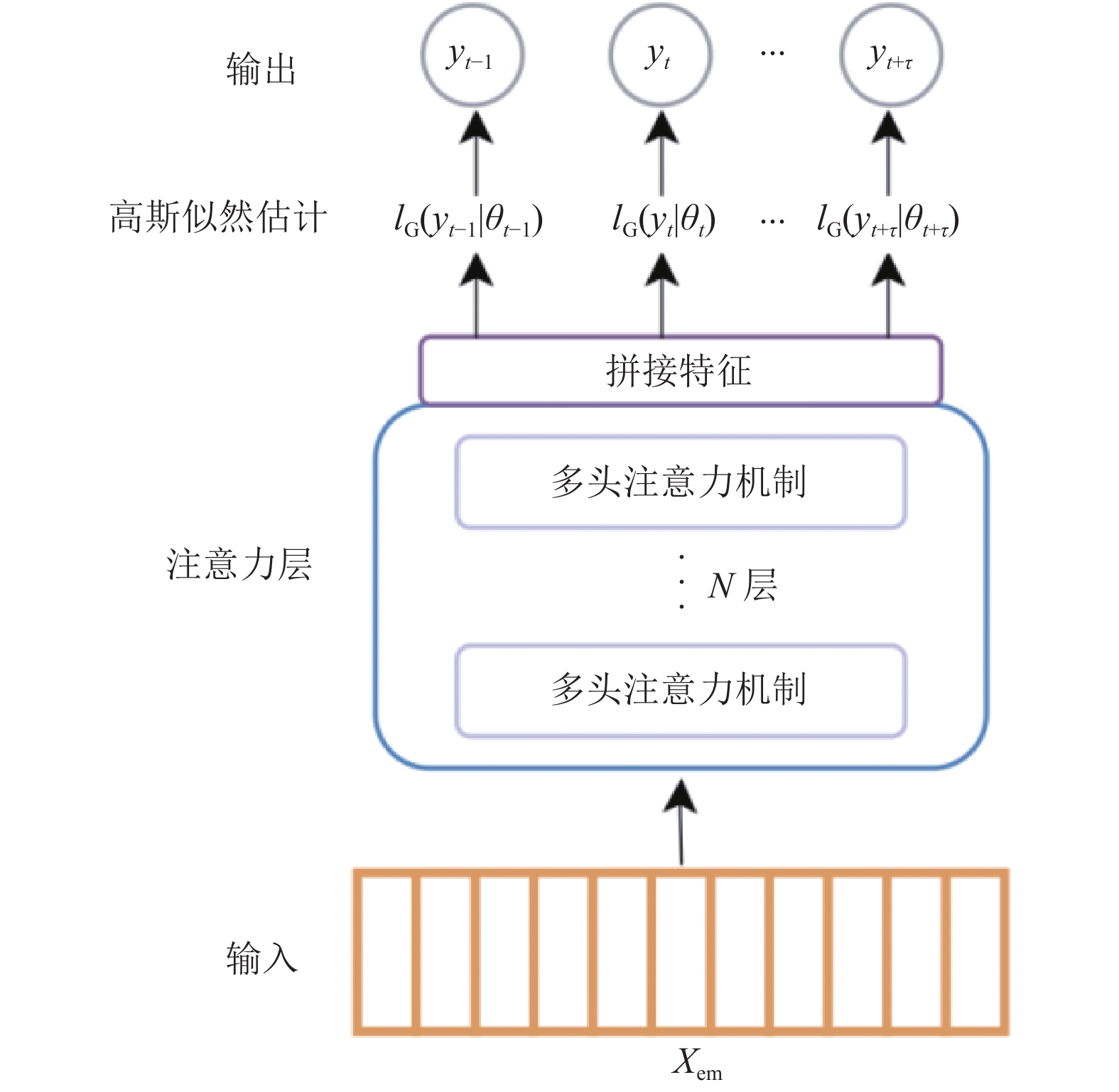
本文通过注意力机制和高斯概率估计相结合实现. 高斯-注意力预测模型由输入、注意力层、高斯概率估计、输出构成. 高斯-注意力预测模型根据历史空气质量观测数据来预测未来PM2.5浓度值. 高斯-注意力预测模型如图3所示.
高斯-注意力预测模型的核心模块是多头注意力机制和高斯似然估计, 能够对长序列的空气质量数据进行建模, 捕获其复杂的数据特征从而进行预测. 其中多头注意力机制能够关注不同子空间的不同的部分的信息, 能够将关联化的空气质量数据特征进行深层次挖掘, 得到更加有效特征. 高斯似然估计通过对拼接后的数据特征建模, 能够得到准确PM2.5浓度值的概率分布, 减低模型过拟合的风险. 本文使用的多头注意力机制如图4所示.
如图4所示,h表示多头注意力机制中的头数. 注意力集中机制中的Q、K、V通过不同的线性变换得到新的一组Q、K、V. h组不同的Q、K、V通过计算注意力得分得到h组不同的注意力得分. 将h组的注意力得分拼接, 经过线性变换得到最后的输出.
|
图 3 高斯-注意力预测模型 |

|
图 4 多头注意力机制 |
为了捕获空气质量数据间的长期依赖和全局信息, 我们考虑空气质量数据的分层时间戳的信息(周, 日, 小时). 如图5所示, 本文提出一个统一、对齐的输入表示来解决这个问题.
模型的输入Xem包括原始信息、局部信息、全局信息3个部分, 长度为d. 局部信息是一个固定的位置嵌入如式(6), 式(7)所示:
| PE(pos,2i)=sin(pos/(2Lx)(2i/d)) | (6) |
| PE(pos,2i+1)=cos(pos/(2Lx)(2i/d)) | (7) |
其中, i=[1, …, [d/2]]. 全局信息由两个可学习的日嵌入和周嵌入组成. 为了对齐输入的维度, 本文用一个一维的卷积滤波器对原始小时数据进行卷积处理得到原始信息.
模型在训练阶段中, 多头注意力机制能到看到全局的信息, 能够一次性的更新t长度的所有参数θ. 模型预测阶段中, 由于只能看到当前的时间步的信息, 因此在计算注意力得分的时候需要将未来的信息进行掩码处理. 模型的训练阶段采用均方误差MSE作为模型的损失函数, 具体计算过程如式(8)所示.
| loss=1/N∑N1(yp−xt)2 | (8) |
其中, N表示样本总数, yp表示模型预测的t时刻PM2.5浓度值, yt表示t时刻真实的PM2.5浓度值.

|
图 5 输入对齐表示 |
3 实验结果与分析 3.1 数据来源及分析
本文数据集选择2019年6月1日到2021年3月11日沈阳市某监测站点的6种空气质量监测数据(PM2.5、PM10、SO2、NO2、NO、CO)作为实验数据, 单位为μg/m3. 原始数据周平均浓度如图6所示, 基本统计特征如表1所示.
由图6可知, 6种空气质量监测数据浓度变化有相同的趋势, PM2.5, PM10, CO具有相同的数据特征变化较为剧烈. NO2, NO, SO2变化相对平缓.
由表1可知, CO的量级较大, NO和SO2量级较小, PM2.5、PM10 、NO2属于同一量级. 综上所述, 6种空气质量监测数据具有密不可分的相似性, 同时不同数据特征间有高度的复杂性.

|
图 6 2019-06-01至2021-03-11 原始数据周平均浓度 |
| 表 1 6种空气质量监测数据统计特征(μg/m3) |
由于一些不可控的因素例如网络信号丢失, 采集器突然宕机等导致部分原始数据会出现异常情况, 所以在此次研究中采用了24 小时均值法对异常和缺失的原始数据进行数据预处理, 使空气质量的监测数据尽可能地保存相应的特征. 实验选择历史一周的小时空气质量数据作为输入, 预测未来一天的PM2.5各小时浓度值.
3.2 实验参数本实验的环境主要参数, 平台: Google Colab, GPU显卡: Telsa P100, 显存为16 GB, 操作系统为Ubuntu 18.04. 本文提出高斯-注意力预测模型的超参数主要涉及多头注意力机制. 当高斯-注意力预测模型超参数设置如表2所示时, 模型预测性能最优.
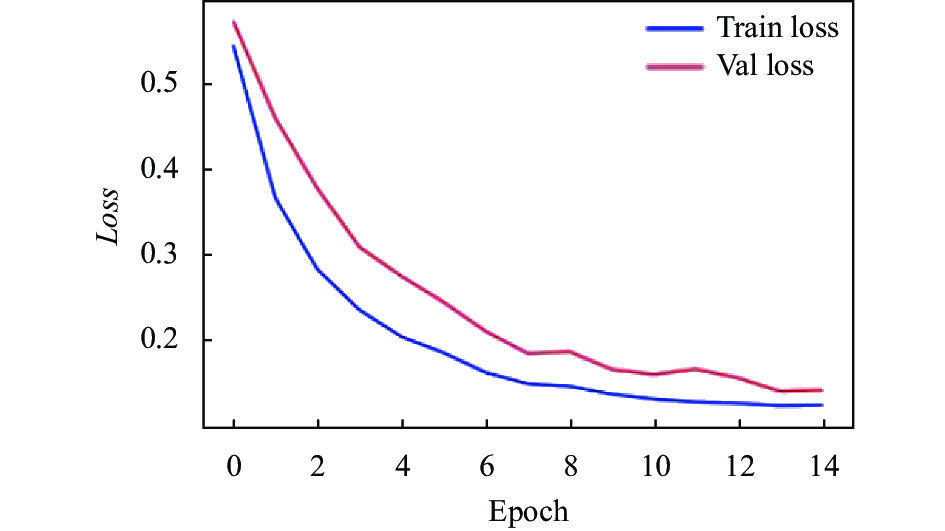
模型使用MSE作为损失函数, 按照表2超参数组合迭代完成15轮训练, 模型在训练集和验证集loss值变化曲线如图7所示.
由图7可知, 随着迭代次数的增加, 训练集和验证集的loss值在训练初期快速下降, 当迭代次数达到10次, 训练集的loss趋于平稳, 验证集的loss产生小幅度的波动. 表明模型已经能很好表示数据间的复杂特征. 为了避免模型发生过拟合现象, 模型选择在15轮停止训练.
| 表 2 最优超参数组合 |
|
图 7 模型loss变化曲线 |
3.3 实验结果
为了验证算法高斯-注意力预测模型的有效性, 本文选择与当前主流空气质量预测方法ARIMA、LSTM、DeepAR[17]进行比较. 对比实验在相同的实验环境中进行, 上述3种模型的超参数设置均为最优超参数组合, 本文模型与上述3种主流方法的部分预测值如表3.
| 表 3 不同模型部分预测值(μg/m3) |
由表3可知, 高斯-注意力模型预测值相较于传统方法ARIMA及深度学习方法LSTM、DeepAR模型更接近真实的PM2.5浓度值, 误差绝对值也有所降低. 为了更直观的体现各预测模型在测试集上的预测性能, 因此绘制4种模型在测试集上预测值和真实值的折线图, 如图8所示.

|
图 8 4种方法PM2.5浓度预测图 |
由图8可知, 高斯-注意力预测模型的整体预测结果好于3种基准模型ARIMA、LSTM、DeepAR. 由图8的红框可知, 传统模型ARIMA预测结果有明显的滞后性, 整体的数据趋势出现了向后的偏移, 这表明相较于深度学习方法, 传统模型ARIMA对多维时序数据的处理能力不足, 不能表达深层次的特征信息. LSTM模型能在一定程度上缓解这个问题, DeepAR和高斯-注意力模型通过高斯似然估计对PM2.5浓度进行采样预测, 解决了数据向后偏移的问题. 由图8的紫框可知, LSTM、DeepAR模型在变化剧烈的序列上预测结果较差, 高斯-注意力预测模型得到更好的拟合结果. 由于DeepAR模型中提取特征的部分是LSTM, 这表明相较于LSTM, 本文提出的高斯-注意力预测模型中的多头注意力机制能够关注到全局信息, 通过不同子空间对高维空间的复杂特征进行抽取, 在变化剧烈的序列上有很好的预测性能.
由表4可知, 4种模型在MSE和MAE的评价指标下, 高斯-注意力预测模型均取得最好的结果. 相较于基准模型中性能较优的DeepAR, 高斯-注意力预测模型的MSE、MAE分别下降了21%、15%. 该实验验证本文提出的高斯-注意力预测模型对解决多维时序问题的优越性, 能得到准确性和鲁棒性较强的空气质量预测结果.
| 表 4 模型实验结果 |
不同的注意力层对输入数据有不同的注意力得分. 第1、4层注意力得分如图9所示, 注意力机制的第1层能够注意到每天的整体情况, 给予每天的输入数据相似的权重. 注意力机制的第4层进一步压缩了注意力机制的范围, 给予较长时间间隔的数据很少的关注, 反而更加在意最近48 h数据的影响.

|
图 9 第1、4层注意力得分 |
4 结束语
本文提出了一种基于高斯概率估计和注意力机制的高斯-注意力预测模型. 为了捕获空气质量数据间的长期依赖和全局信息, 将不同时间戳的信息对齐得到原始信息、局部信息、全局信息作为输入. 引入多头注意力机制, 通过不同子空间对输入序列的全局信息进行学习, 得到深层次的数据特征, 再经过高斯似然估计对PM2.5浓度质量数据进行概率估计. 最终通过与多种模型对比, 高斯-注意力预测模型在各个评价指标方面均取得最优结果. 另外, 当前模型只考虑了空气质量数据的时序特征, 未来将结合不同位置的空气质量监测站数据, 对空气质量数据的空间和时间特征进行挖掘, 得到更加有效的预测结果.
| [1] |
Pui DYH, Chen SC, Zuo ZL. PM2.5 in China: Measurements, sources, visibility and health effects, and mitigation
. Particuology, 2014, 13: 1-26. DOI:10.1016/j.partic.2013.11.001 |
| [2] |
Chen PF, Bi XH, Zhang JQ, et al. Assessment of heavy metal pollution characteristics and human health risk of exposure to ambient PM2.5 in Tianjin, China
. Particuology, 2015, 20: 104-109. DOI:10.1016/j.partic.2014.04.020 |
| [3] |
严宙宁, 牟敬锋, 赵星, 等. 基于ARIMA模型的深圳市大气PM2.5浓度时间序列预测分析
. 现代预防医学, 2018, 45(2): 220-223, 242. |
| [4] |
石峰, 楼文高, 张博. 基于灰狼群智能最优化的神经网络PM2.5浓度预测
. 计算机应用, 2017, 37(10): 2854-2860. DOI:10.11772/j.issn.1001-9081.2017.10.2854 |
| [5] |
尹建光, 彭飞, 谢连科, 等. 基于小波分解与自适应多级残差修正的最小二乘支持向量回归预测模型的PM2.5浓度预测
. 环境科学学报, 2018, 38(5): 2090-2098. |
| [6] |
蒋洪迅, 石晓文, 孙彩虹, 等. 基于DLENN模型的沈阳地区PM2.5浓度预测
. 系统工程, 2021, 39(2): 13-21. |
| [7] |
Mirzaei M, Amanollahi J, Tzanis CG. Evaluation of linear, nonlinear, and hybrid models for predicting PM2.5 based on a GTWR model and MODIS AOD data
. Air Quality, Atmosphere & Health, 2019, 12(10): 1215-1224. |
| [8] |
Lim B, Zohren S. Time-series forecasting with deep learning: A survey. Philosophical Transactions of the Royal Society A, 2021, 379(2194): 20200209. DOI:10.1098/rsta.2020.0209 |
| [9] |
刘旭林, 赵文芳, 唐伟. 应用CNN-Seq2seq的PM2.5未来一小时浓度预测模型
. 小型微型计算机系统, 2020, 41(5): 1000-1006. DOI:10.3969/j.issn.1000-1220.2020.05.017 |
| [10] |
邓丽, 邬群勇, 杨水荣. 融合SSAE深度特征学习和LSTM网络的PM2.5小时浓度预测
. 环境科学学报, 2020, 40(9): 3422-3434. |
| [11] |
黄伟建, 李丹阳, 黄远. 基于深度学习的PM2.5浓度长期预测
. 计算机应用研究, 2021, 38(6): 1809-1814. |
| [12] |
Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc., 2017. 6000–6010.
|
| [13] |
Zhou HY, Zhang SH, Peng JQ, et al. Informer: Beyond efficient transformer for long sequence time-series forecasting. Proceedings of the AAAI Conference on Artificial Intelligence, 2021, 35(12): 11106-11115. |
| [14] |
傅颖颖, 张丰, 杜震洪, 等. 融合图卷积神经网络和注意力机制的PM2.5小时浓度多步预测
. 浙江大学学报(理学版), 2021, 48(1): 74-83. |
| [15] |
张莹, 张婕, 王式功, 等. 成都市PM2.5浓度变化的影响因素交互作用研究
. 中国环境科学, 2021, 41(10): 4518-4528. DOI:10.3969/j.issn.1000-6923.2021.10.006 |
| [16] |
Bahdanau D, Cho K, Bengio Y. Neural machine translation by jointly learning to align and translate. arXiv:1409.0473, 2014.
|
| [17] |
Salinas D, Flunkert V, Gasthaus J, et al. DeepAR: Probabilistic forecasting with autoregressive recurrent networks. International Journal of Forecasting, 2020, 36(3): 1181-1191. DOI:10.1016/j.ijforecast.2019.07.001 |
 2023, Vol. 32
2023, Vol. 32



