2. 北京信息科技大学 商务智能研究所, 北京 100192;
3. 北京信息科技大学 信息管理学院, 北京 100192
2. Institute of Business Intelligence, Beijing Information Science & Technology University, Beijing 100192, China;
3. School of Information Management, Beijing Information Science & Technology University, Beijing 100192, China
价格预测对于大宗商品市场的稳定具有重要意义, 商品价格的剧烈波动可能会导致商品市场发生多种风险, 尤其是在农产品等领域, 对于价格的波动更为敏感, 一旦受到影响引发价格波动风险, 会对社会造成巨大的损失. 因此, 准确的预测商品价格可以提前发现大宗商农产品市场的变化趋势, 为商品生产者以及消费者提供参考, 降低损失, 稳定商品市场, 对其进行研究是十分必要的. 大宗农产品市场受到供求关系 、金融、政策及其他如品种联动等多种因素的影响, 具体包括供求、其他大宗商品、汇率、期货市场、国际形势及天气等因素[1]. 由于大宗农产品市场具有受上下游产业链、天气以及金融因素影响较大且相关关系复杂的特点, 因此准确预测大宗农产品价格仍然是十分困难的. 目前, 使用广泛的大宗农产品价格预测方法多使用深度学习模型, 虽然可以在一定程度上克服机器学习模型难以利用复杂相关关系的局限性, 但是存在依赖数据完整性及过拟合等问题. 针对以上问题, 本文提出通过集成深度学习模型与机器学习模型以减少模型对于数据的依赖性, 从而提升对价格进行预测的鲁棒性, 进而准确地预测大宗农产品价格.
1 价格预测相关研究深度学习因其可更充分地利用数据集中的大量特征, 在数据量充足且相关特征较多的情况下预测效果通常较传统机器学习好, 目前被很多学者用于农产品价格预测[2]. 深度学习方法使用多层神经网络如卷积神经网络(convolutional neural networks, CNN), 长短期记忆神经网络(long short-term memory neural network, LSTM)等进行预测, 如Jaiswal等人[3]使用长短期记忆神经网络, 时延神经网络(time delay neural network, TDNN)和自回归移动平均模型(autoregressive integrated moving average, ARIMA)模型对玉米和棕榈油的国际月价进行预测及模型对比分析, 发现LSTM有着比ARIMA和TDNN更小的误差; 江知航等人[4]使用LSTM与BILSTM模型对2016–2019年的棉花价格数据进行预测, 取得了更低的预测误差; Chuluunsaikhan等人[5]使用多层感知机 (multi-layer perceptron, MLP)、卷积神经网络、LSTM与机器学习模型岭回归(ridge)、随机森林(random forest, RF)、梯度提升(gradient boosting, GB)及统计学模型带额外输入的自回归移动平均模型(autoregressive integrated moving average with extra input, ARIMAX)分别对韩国猪肉价格进行预测, 发现深度学习模型LSTM的误差低于其他模型.
同时, 以CNN-LSTM模型为代表的基于深度学习的混合模型在价格预测领域逐渐受到关注[6-10], 如Nassar等人[11]使用CNN-LSTM等模型预测新鲜农产品价格, 发现在其上添加注意力机制的CNN-LSTM-Attention模型表现较好, 在价格预测的准确性方面优于机器学习模型和简单的深度模型. Lu等人[12]搭建CNN-BiLSTM-Attention模型预测股票价格并搭建LSTM, CNN-BiLSTM, BiLSTM-Attention等深度学习模型进行比较, 发现CNN-BiLSTM-Attention模型较其他模型决定系数(R2)最大且均方根误差(RMSE)和绝对误差(MAE)最小. 如曹超凡等人[13]构建了MDT-CNN-LSTM模型, 对4类股票指数数据使用多向延迟嵌入(MDT)进行数学变换并使用CNN-LSTM进行预测, 取得了比传统方法更低的误差. Yu等人[14]提出了一种相空间重建长短期记忆神经网络(PSR-LSTM)方法, 将金融产品价格数据利用时间序列相空间重建(PSR)方法进行重构并使用LSTM进行预测, 实验结果表明他们所提出的预测模型方法具有较低的误差.
由于混合深度学习模型仍然具有表现依赖完整时间序列及容易产生过拟合等问题[15], 而集成学习因其可以克服单一模型的这些局限性, 有可能比单一模型有着更好的效果[16]. 集成学习方法常见的有分解集成学习方法、堆叠式集成学习方法、增强式集成学习方法等. 其中分解集成学习方法考虑数据非平稳及非线性对数据进行分解与集成, 如Rezaei等人[17]使用经验模态分解(empirical mode decomposition, EMD)和完全集成经验模态分解(complete ensemble empirical mode decomposition , CEEMD)对股票数据进行分解后分别使用CNN-LSTM模型进行预测并集成, 实验结果表明混合模型误差较CNN-LSTM模型低且CEEMD-CNN-LSTM最低. 还有许多学者使用集合经验模态分解(ensemble empirical mode decomposition, EEMD)、变分模态分解(variational mode decomposition, VMD)等其他分解方法构建分解集成模型进行研究[18, 19], 但是, 由于分解集成方法需要分解出多类数据并分别使用多种模型训练及选择, 所以导致运算速度较慢. 因此, 目前主流的集成学习方法仍为易于搭建及运算速度较快的堆叠式集成学习方法, 如Silva等人[20]对巴西玉米和糖的价格使用ARIMA、季节性差分自回归滑动平均模型(seasonal autoregressive integrated moving average, SARIMA)、支持向量回归 (support vector regression, SVR)、AdaBoost和LSTM模型及它们的部分集成进行预测, 发现LSTM分别和SVR及ARIMA的集成模型有着更小的平均绝对误差(MAE), 均方误差(MSE)及更高的R2分数. Parida等人[21]通过基于CNN和堆叠自动编码器(stacked autoencoder, SAE)的深度学习集成模型对29 mm棉和一种农用商品瓜尔胶的收盘价进行预测, 在价格波动较大的价格预测中误差较传统方法小. 如Xiao等人[22]提出LSTM-EL方法, 该方法将数据先通过LSTM神经网络, 生成特征嵌入, 然后将它作为GBRT和RF模型的输入分别进行预测并集成. 最后将它们与普通的LSTM, GBRT, RF模型进行了比较, 发现最终的混合集成模型拥有比单一模型更低的误差. 增强式集成学习方法将误差较大的数据权重调高并再次搭建模型进行迭代, 如Ribeiro等人[23]使用基于随机森林的套袋式集成方法、梯度增压机(gradient boosting machine, GBM)、极端梯度增压机(extreme gradient boosting machine, XGB), 堆叠(stacking)以支持向量机回归(SVR)、多层感知器神经网络(MLP)和K-最近邻(KNN)作为参考模型, 发现使用增强式集成学习方法XGB、GBM综合MAPE及绝对百分比误差(APE)的性能最好.
综上所述, 基于混合深度学习模型的增强式集成学习模型由于可以在一定程度上减少对数据完整性的依赖性, 并且更加充分地利用数据特征, 在农产品价格领域有着比传统方法更低的误差. 为了更加准确地预测价格, 为价格波动风险的预警提供支持, 本文结合在深度学习模型中误差较低的CNN-BiLSTM-Attention模型与机器学习模型SVR和LightGBM进行增强式集成, 对不同品类的农产品进行预测与分析.
2 本文方法本文提出了一种CNN-BiLSTM-Attention与两种机器学习方法的增强式集成学习方法, 方法流程图如图1所示.
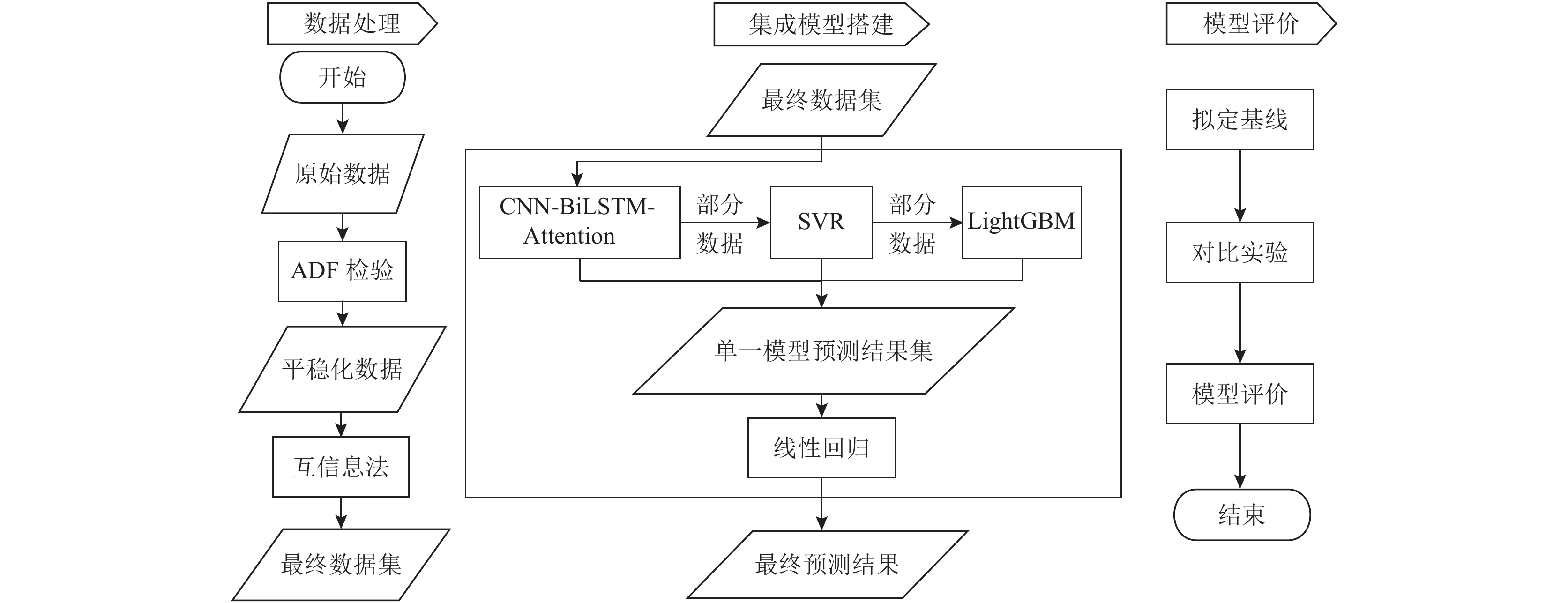
|
图 1 方法流程图 Fig. 1 flowchart of the method |
首先进行数据处理, 包括对数据进行缺失值填充, 时间对齐和线性相关分析去重的数据预处理; 基于互信息法的特征选择. 然后分别训练多种深度学习模型进行模型选择, 依据模型的RMSE, MAE, R2等评价结果选择可以生成时空特征并关注关键特征的CNN-BiLSTM-Attention与SVR, LightGBM使用增强式集成学习方法以线性回归为元学习模型进行集成. 最后使用RMSE, MAE, R2与单一模型进行比较与评价.
2.1 数据处理方法大宗农产品受到包括天气, 需求等众多因素的影响, 且不同大宗农产品的影响因素与程度不同. 由于无关变量在数据集中产生了额外的噪声, 会引发神经网络的预测精度下降的问题[24]. 因此对于收集到包含多种影响因素的特征数据, 需要通过互信息法进行特征选择, 找出影响程度较高的特征, 以提升模型的计算效率与预测精度.
对棉花与小麦的数据使用互信息法计算目标数据与各个特征数据的互信息值以筛选出影响较明显的特征. 一般而言, 两个时间序列的相关性越大, 其互信息值就会越大[25]. 在信息论中, 互信息的描述如下: 在信道的一端有着信息源X, 它向信道中发射信息x, 在另一端的接收端则会收到x经过信道影响后转变的y或f(x). 接收端通过y推断信息源X发射x的概率即后验概率p(x|y), 同时信息源X发射x的概率称为先验概率p(x). 定义p(x)与p(x|y)比值的对数为y对x的互信息值.
互信息值的计算方法如下.
1) 计算元素长度为n的随机变量X的熵H(X):
| $ {{H}}\left( X \right) = - \sum\limits_{i = 0}^n {{p} (x = {a_i})} {\ln }{p} (x = a\;) $ | (1) |
其中, p(x=ai)为变量X内第i个离散点ai的概率密度函数.
2)计算随机变量X和Y的联合熵H(X, Y)的方法如下:
| $ H\left( {{{X, Y}}} \right) = - \sum\limits_{i = 0}^n {{{p}}(x = {a_i}, y = {b_i})} {\ln}p(x = {a_i}, y = {b_i}) $ | (2) |
则有H(X|Y)=H(X)+H(Y|X)=H(Y)+H(X|Y), 可以推导出H(X)–H(X|Y)=H(Y)–H(Y|X), 而这个差就叫作X和Y的互信息, 记作I(X, Y).
3)可得I(X, Y)=H(X)–H(X|Y)=H(X)+H(Y)–H(X, Y), 计算互信息I(X, Y) 的方法如下:
| $ I\left({X, Y}\right)=-{\displaystyle \sum _{i=0}^{n}{p}(x={a}_{i}, y={b}_{i})}\cdot\mathrm{ln}\frac{p(x={a}_{i})p(y={b}_{i})}{p(x={a}_{i}, y={b}_{i})} $ | (3) |
最后使用不同阈值筛选去除互信息值过小的与价格变化关系较小特征, 留下互信息值较大的几个与价格变化相关度较高的特征.
2.2 集成模型搭建方法本文提出的预测模型方法首先训练多种深度学习模型进行模型选择. 将选择的基模型在训练集上误差大于MAE的数据作为训练集训练机器学习模型, 使用相同方式将机器学习模型预测效果较差的数据取出再训练下一个机器学习模型, 然后使用线性回归作为元学习模型对3个模型的结果进行集成, 最后在测试集上与单一模型进行评价与比较.
2.2.1 深度学习模型本文在卷积神经网络、双向长短期记忆神经网及它们的混合模型如带注意力机制的卷积双向长短期记忆神经网络模型等进行模型选择.
添加注意力机制的卷积双向长短期记忆神经网络模型(CNN-BiLSTM-Attention)由卷积神经网络层, 长短期记忆神经网络层以及注意力层组成, 其结构如图2所示. 输入的大宗农产品价格相关特征数据先经过卷积层进行卷积操作以提取数据空间特征. 由于卷积后提取的数据特征维度过高, 因此在其后加上池化层以降低特征维度. 然后再通过BiLSTM层, 将前面的输出分别输入给一个正向及一个逆向的LSTM层, 以获取正向及逆向的时间序列时间特征. 最后将提取的时间与空间特征输入到Attention层, 以关注影响输出目标及后一天农产品价格的特征, 提高模型预测的精度.

|
图 2 添加注意力机制的卷积双向长短期记忆神经网络 Fig. 2 CNN-BiLSTM-Attention |
本文使用1D-CNN处理价格时间序列数据, 以有效地提取数据的局部特征. 卷积神经网络(CNN)是深度学习中很常用的一种, 多使用于图片识别, 自然语言处理等领域. 其根据处理的数据不同又可分为一维卷积(1D-CNN), 二维卷积(2D-CNN)等, 其中1D-CNN主要用于序列建模与自然语言处理领域. CNN一般包括输入层, 卷积层, 池化层, 全连接层和输出层. 它的结构如图3所示, 其核心为卷积层, 池化层和全连接层. 由于农产品价格相关特征数据多为时序序列数据, 通过卷积层的可以提取数据在某一方向的平移特征, 在时间序列的表现为提取序列的空间特征, 因此使用一维卷积神经网络可以提取输入的时间序列数据的空间特征.
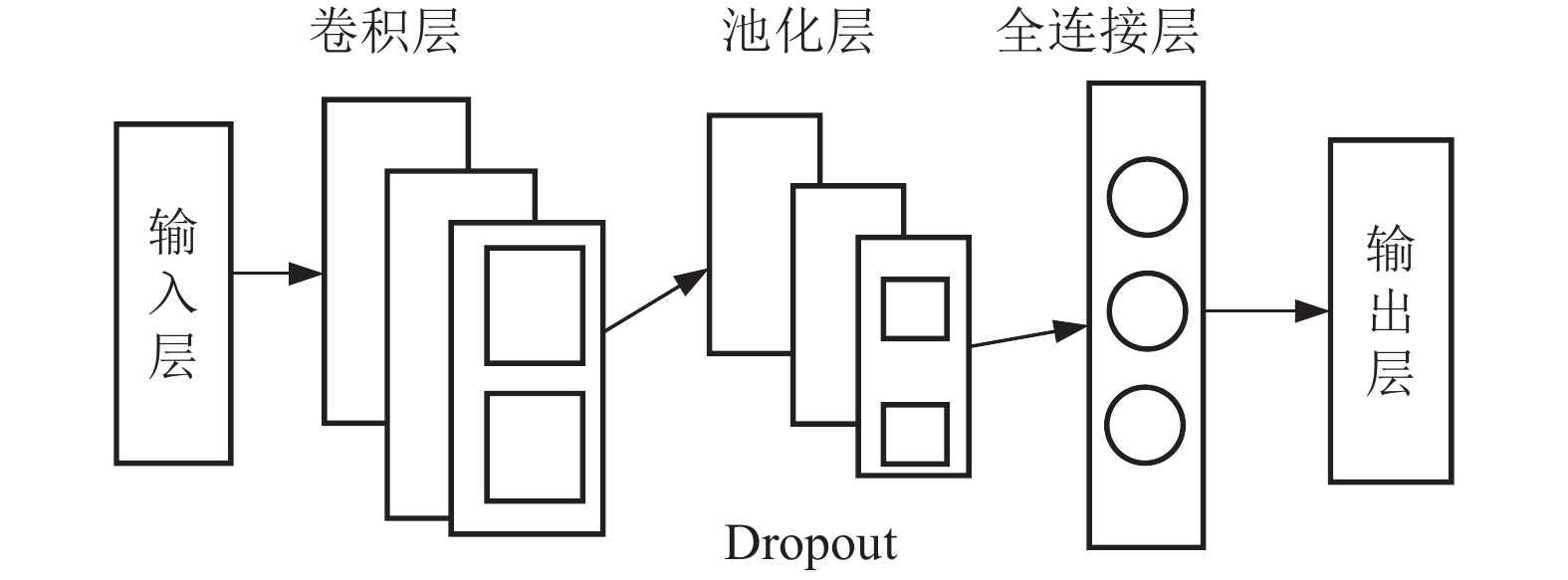
|
图 3 卷积神经网络 Fig. 3 Convolutional Neural Network |
本文使用双向长短期记忆神经网络提取序列时间特征. 双向长短期记忆神经网络(BiLSTM)是长短期记忆神经网络(LSTM)的一种改进, 堆叠了一个前向传播及一个后向传播的LSTM层, 分别重复训练输入的大宗农产品价格相关特征时间序列数据及其倒序后的时间序列数据以提取时间特征. LSTM单元结构如图4所示.

|
图 4 长短期记忆神经网络单元 Fig. 4 The unit of Long Short-Term Memory |
其计算过程如下:
| $ 遗忘门: {{{f}}_t} = \sigma ({{{W}}_f} \cdot \left[ {{{{h}}_{t - 1}}, {{{x}}_t}} \right] + {{{b}}_f}) $ | (4) |
| $ 输入门: {{{i}}_t} = \sigma ({{{W}}_i} \cdot \left[ {{{{h}}_{t - 1}}, {{{x}}_t}} \right] + {{{b}}_i}) $ | (5) |
| $ {\widetilde {{C}}_t} = \tanh ({{{W}}_C} \cdot \left[ {{{{h}}_{t - 1}}, {{{x}}_t}} \right] + {{{b}}_C}) $ | (6) |
| $ 输出门: {{{o}}_t} = \sigma ({{{W}}_o}\left[ {{{{h}}_{t - 1}},{{{x}}_t}} \right] + {{{b}}_o}) $ | (7) |
| $ 长期记忆: {{{C}}_t} = {{{f}}_t} \cdot {{{C}}_{t - 1}} + {{{i}}_t} \cdot {\widetilde C_t} $ | (8) |
| $ 短期记忆: {{{h}}_t} = {{{o}}_t} \cdot \tanh ({{{C}}_t}) $ | (9) |
其中,
由于提取的时间与空间特征数量较多, 本文通过注意力机制对模型进行优化. 注意力机制(Attention)通过计算注意力的概率分布, 从大量特征中选择关键的特征, 增加模型计算效率. 其计算分为3步.
1) 首先输入特征ht与Attention的权重Wh相乘再加上Attention的偏置bh通过tanh函数计算输出与输入特征的相关性量st. 如式(10)所示:
| $ {{{s}}_t} = \tanh ({{{h}}_t} \cdot {{{W}}_h} + {{{b}}_h}) $ | (10) |
2) 再将其归一化并经过Softmax函数得到注意力分数量at. 如式(11)所示:
| $ {{{a}}_t} = {\textit{Softmax}}\left( {\rm{exp}}({{{s}}_t})\Bigg/\sum {\rm{exp}}({{{{s}}_t}}) \right) $ | (11) |
3) 最后at与ht相乘以加权相加得到最终输出注意力值向量s. 如式(12)所示:
| $ {{s}} = \sum {{{{a}}_t}} {{{h}}_t} $ | (12) |
训练过程中深度学习模型使用的损失函数为MSE, 其计算方法如式(13)所示:
| $ {\textit{MSE}}=\frac{1}{n}{{\displaystyle \sum _{i=1}^{n}({y}_{i}-{\hat{y}}_{i})^{2}}} $ | (13) |
由于深度学习模型对数据数量及完整性等依赖性强, 因此选择机器学习模型SVR和LightGBM与深度学习模型进行增强式集成, 使用线性回归作为元学习模型, 通过增强式的集成学习方法改善深度学习模型的预测结果.
其中支持向量机回归(SVR)是支持向量机(SVM)在回归任务上的一个分支, 是一种经典的机器学习方法, 有着良好的预测性能. 它通过将输入的商品价格数据映射进高维特征空间并找到一个与样本点总偏差最小且线性可分的超平面, 再将超平面映射回原空间, 以实现回归预测. 与传统的回归模型不同, 它设置一个阈值, 只有误差程度超过阈值才计算损失, 并通过最大化间隔带的宽度与最小化总损失来优化模型. 可以有效地拟合特征及输出的非线性关系, 以准确得预测农产品价格.
LightGBM是微软提出的一个实现梯度提升决策树(gradient boosting decision tree, GBDT) 算法的增强式集成学习框架, 它在XGBoost方法的基础上进行优化, 通过迭代训练弱分类器以得到最优的模型, 且限定只能使用回归树模型作为弱分类器. 但是通过使用基于直方图的决策树算法避免过拟合且具有更好的推广性, 以及使用带有深度限制的节点展开方法(leaf-wise)来提升模型预测精度. 拥有更快的计算速度及更好的预测精度, 可以准确地预测农产品价格.
将深度学习模型预测结果较差的数据输入到SVR模型中, 再将SVR模型预测结果较差的数据输入到LightGBM模型中, 通过增强的集成学习方法弥补单一模型难以全面利用数据间复杂相关关系的缺陷, 减少预测结果对于数据完整性的依赖性, 提升预测价格的精度.
2.2.3 模型评价方法模型使用RMSE、MAE及R2进行评价, 它们的计算方式如式(14)–式(16)所示:
| $ {\textit{RMSE}}=\sqrt{\frac{1}{n}{{\displaystyle \sum _{i=1}^{n}({y}_{i}-{\hat{y}}_{i})}}^{2}} $ | (14) |
| $ {\textit{MAE}}=\frac{1}{n}{\displaystyle \sum _{i=1}^{n}\left|{y}_{i}-{\hat{y}}_{i}\right|} $ | (15) |
| $ {{R}}^{2}=1-\frac{{\displaystyle \sum _{i=1}^{n}{({y}_{i}-{\hat{y}}_{i})}^{2}}}{{\displaystyle \sum _{i=1}^{n}{({y}_{i}-{\overline{y}}_{i})}^{2}}} $ | (16) |
其中, yi表示真实值,
本节首先介绍实验过程中的数据分析与处理过程, 包括数据预处理, 特征选择等; 然后介绍集成模型的构建, 分别为基模型搭建以及模型集成, 最后对实验的结果进行分析.
3.1 数据分析与处理由于取得的棉花与小麦的数据来源不同, 所以需要先对其分别进行数据预处理, 经过时间对齐, 缺失值填充等操作后, 将目标数据差分后, 再对数据使用互信息法进行特征处理, 最后划分得到模型训练及验证使用的数据.
3.1.1 数据来源及数据预处理根据文献[1]中对大宗农产品市场影响因素的研究, 小麦及棉花市场受到相关商品如上下游大宗商品, 金融因素如能源、期货市场、汇率等以及主要产地天气因素的影响, 因此从Kaggle、万德数据、RP5地方天气数据、英伟财情等来源收集需要的数据. 其中小麦价格数据及其相关商品数据来源于Kaggle, 按日期对齐后共2339条, 数据特征及说明如表1所示. 棉花价格数据来源于万德数据, 按日期对齐后共2883条, 天气数据来源于RP5地方天气数据, 油价数据以及汇率数据来源于英伟财情数据, 数据特征及说明如表2所示.
| 表 1 小麦数据特征 Table 1 Description of wheat dataset characteristics |
| 表 2 棉花数据特征 Table 2 Description of cotton dataset characteristics |
对于取得的小麦价格数据、相关商品数据以及油价数据等, 先经过如下步骤.
1)时间对齐, 将时间跨度不同的数据修改时间跨度为天, 并取有交集的数据.
2) 缺失值填充, 对存在缺失值的小麦与棉花价格数据使用KNN方法进行填充, 对其他数据进行前向填充.
3) 对处理过后的商品价格数据进行滞后, 使其后一天的价格作为目标数据, 再加入前两天的价格作为新特征.
4) 之后对特征数据进行相关性分析, 去除线性相关较高的特征, 或通过差分以及作差等运算将其转换为新特征, 保留线性相关性较小的非重复特征.
5)对特征数据与目标数据使用互信息法计算互信息值进行特征选择, 对不同模型调整阈值选出合适的特征, 去除无关特征.
6) 最后将得到的数据按7:3划分为训练集及测试集.
经过预处理的数据即可分别供多种深度学习及机器学习的基模型进行训练, 以选出性能较好且可互补的模型使用线性回归进行集成, 分配权重, 生成最终的集成模型.
3.1.2 基于互信息法的特征选择通过对数据采用互信息法通过调整不同阈值, 以找出与目标相关度较低的几项特征进行去除, 使得更重要的特征可以被保留下来, 达到加快训练速度, 提高预测精度的目的. 将拆分为特征及目标的数据, 输入到互信息函数中, 生成各特征与目标数据的互信息值, 然后设置不同阈值, 通过保留互信息值超出阈值的特征以进行特征选择. 表3和表4分别为小麦与棉花互信息值阈值为0.01的特征选择结果说明.
通过表3和表4可以发现, 小麦价格波动受到相关商品、布伦特原油及通货膨胀率的影响较大, 而棉花价格波动受到天气, 商品价格波动, 纱线价格, 交易年份的影响较大.
| 表 3 小麦保留特征 Table 3 Description of wheat retention characteristics |
| 表 4 棉花保留特征 Table 4 Description of cotton retention characteristics |
3.2 模型构建及调参 3.2.1 基模型搭建及调参
使用贝叶斯调参方法重复训练以调整模型超参数, 调参过程中, 基础层包括输入层、中间层及输出层各一层, 同时混合模型每种神经网络层各一层, 调整的深度学习模型参数为神经网络隐藏层层数0–3, 神经网络细胞数32–256, dropout值0.0–0.5, 迭代次数epochs 5–50, 块大小batch_size 30–200, 学习率learn_rates 0.001–0.01; 机器学习模型中调整的SVR参数为3种核函数, 惩罚系数C 0.0001–1.0; LightGBM参数为学习率learning_rate 0.001–0.01, 树模型的最大深度3–7, subsample 0.5–1.0. 使用相同的训练集、测试集、时间步长、特征与相同的参数范围通过贝叶斯调参方法进行训练及调参, 最终获得的深度学习模型在性能上是有可比性的.
最后调整出的深度学习模型参数如表5所示.
对于训练出的深度学习模型, 使用测试集进行评价, 综合考虑R2等评价指标以选择合适的基模型, 分别训练CNN、LSTM、BiLSTM、CNN-BiLSTM、BiLSTM-Attention、CNN-BiLSTM-Attention等深度学习模型. 在时间序列模型中棉花采用15天的历史数据预测后一天的价格, 小麦采用10天的历史数据预测后一天的价格. 训练后使用测试集进行评价, 各深度学习模型评价结果如表6所示.
从表6可以发现3种混合深度学习模型BiLSTM-ATT、CNN-BiLSTM和CNN-BiLSTM-Attention在小麦及棉花价格预测上的预测结果准确性方面均优于传统的深度学习模型LSTM、BiLSTM及CNN, R2较大; 而混合深度学习模型中CNN-BiLSTM-Attention的预测结果R2最小, 因此在混合深度学习模型中选择CNN-BiLSTM-Attention作为基模型, 与SVR和LightGBM进行集成.
| 表 5 深度学习模型参数 Table 5 Parameter of Deep learning models |
| 表 6 深度学习模型结果 Table 6 Results of Deep learning models |
3.2.2 模型的集成
将CNN-BiLSTM-Attention模型在训练集上误差大于MAE的数据作为训练集训练SVR模型, 再将SVR模型在其训练集是预测结果误差大于MAE的数据取出训练LightGBM模型, 然后使用线性回归作为元学习模型对3个模型的结果进行集成, 最后在测试集上进行评价, 与单一模型进行比较.
4 结果及分析本实验各单一模型及集成模型评价结果如表7所示.
通过表5和表6的预测结果可以发现机器学习模型一般较深度学习模型误差更大, 而混合模型的集成模型预测结果误差比传统深度学习模型小. 同时也可以分析CNN-BiLSTM-Attention与SVR、LightGBM进行集成后可以有效地改善预测结果, 能够有效集合各自的优点, 克服单一模型的局限性, 有着比单一的机器学习及深度学习模型更低的RMSE及更高的R2. 同时因为是与机器学习模型进行集成, 计算速度较之单一的混合深度学习模型并没有明显下降.
| 表 7 集成模型结果 Table 7 Results of deep learning models |
最终集成模型对小麦价格部分预测结果如图5所示; 最终集成模型对棉花价格部分预测结果如图6所示.
图5和图6分别显示了最终模型的预测结果, 可以发现模型的预测值与真实值相差较小, 可认为该集成模型在农产品价格预测上有着较低的预测误差.

|
图 5 小麦价格预测结果 Fig. 5 Forecasting results of wheat price |
|
图 6 棉花价格预测结果 Fig. 6 Forecasting results of Cotton price |
通过表6、表7、图5、图6的结果可以发现, 本文提出的模型在性能上优于其他几种模型. 相对于单一的深度学习模型, 基于CNN-BiLSTM-Attention的集成学习模型对于数据完整性的依赖较小, 即使有部分数据存在大量缺失, 导致深度学习模型在这部分数据中效果较差, 也可以通过与其他机器学习模型集成减少误差; 同时, 通过对误差较大的数据进行增强式集成, 可以对深度学习模型预测结果中过拟合的部分进行改善, 因此, 提出的集成学习模型可以在原有深度学习混合模型基础上, 提升价格预测的准确性.
5 结束语本文针对价格预测问题提出了一种基于CNN-BiLSTM-Attention的集成学习方法, 旨在通过深度学习模型与机器学习模型进行集成, 改善深度学习模型的预测结果. 首先对棉花及小麦的价格数据使用各种深度学习模型进行建模, 最后选出了误差最低的CNN-BiLSTM-Attention作为基模型, 将其与SVR、LightGBM模型使用线性回归进行增强式集成. 最终的实验结果表明通过与机器学习模型进行增强式集成可以有效改善所选混合深度学习模型的预测结果, 所生成的集成学习模型有着比单一模型更好的预测精度.
| [1] |
孙玉奎, 高苗苗. 大宗商品价格影响因素及分类型比较研究. 价格理论与实践, 2018(9): 86-89, 102. DOI:10.19851/j.cnki.cn11-1010/f.2018.09.022 |
| [2] |
Sun Y, Guo J, Shan S, et al. Wheat futures prices prediction in China: A hybrid approach. Discrete Dynamics in Nature and Society, 2021, 2021: 5545802. DOI:10.1155/2021/5545802 |
| [3] |
Jaiswal R, Jha GK, Kumar RR, et al. Deep long short-term memory based model for agricultural price forecasting. Neural Computing and Applications, 2022, 34(6): 4661-4676. DOI:10.1007/s00521-021-06621-3 |
| [4] |
江知航, 王艳霞, 颜家均, 等. 基于BiLSTM的棉花价格预测建模与分析. 中国农机化学报, 2021, 42(8): 151-160. DOI:10.13733/j.jcam.issn.2095-5553.2021.08.21 |
| [5] |
Chuluunsaikhan T, Ryu GA, Yoo KH, et al. Incorporating deep learning and news topic modeling for forecasting pork prices: The case of South Korea. Agriculture, 2020, 10(11): 513. DOI:10.3390/agriculture10110513 |
| [6] |
Cai RC, Zhu BJ, Ji L, et al. An CNN-LSTM attention approach to understanding user query intent from online health communities. Proceedings of the 2017 IEEE International Conference on Data Mining Workshops (ICDMW). New Orleans: IEEE, 2017. 430–437.
|
| [7] |
Kim TY, Cho SB. Particle swarm optimization-based CNN-LSTM networks for forecasting energy consumption. Proceedings of the 2019 IEEE Congress on Evolutionary Computation (CEC). Wellington: IEEE, 2019. 1510–1516.
|
| [8] |
Kim TY, Cho SB. Predicting the household power consumption using CNN-LSTM hybrid networks. Proceedings of the 19th International Conference on Intelligent Data Engineering and Automated Learning. Madrid: Springer, 2018. 481–490.
|
| [9] |
Hasan MN, Toma RN, Nahid AA, et al. Electricity theft detection in smart grid systems: A CNN-LSTM based approach. Energies, 2019, 12(17): 3310. DOI:10.3390/en12173310 |
| [10] |
Zheng L, Xue WH, Chen F, et al. A fault prediction of equipment based on CNN-LSTM network. Proceedings of the 2019 IEEE International Conference on Energy Internet (ICEI). Nanjing: IEEE, 2019. 537–541.
|
| [11] |
Nassar L, Okwuchi IE, Saad M, et al. Deep learning based approach for fresh produce market price prediction. Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN). Glasgow: IEEE, 2020. 1–7.
|
| [12] |
Lu WJ, Li JZ, Wang JY, et al. A CNN-BiLSTM-AM method for stock price prediction. Neural Computing and Applications, 2021, 33(10): 4741-4753. DOI:10.1007/s00521-020-05532-z |
| [13] |
曹超凡, 罗泽南, 谢佳鑫, 等. MDT-CNN-LSTM模型的股价预测研究. 计算机工程与应用, 2022, 58(5): 280-286. DOI:10.3778/j.issn.1002-8331.2108-0104 |
| [14] |
Yu PF, Yan XS. Stock price prediction based on deep neural networks. Neural Computing and Applications, 2020, 32(6): 1609-1628. DOI:10.1007/s00521-019-04212-x |
| [15] |
Semwal VB, Gupta A, Lalwani P. An optimized hybrid deep learning model using ensemble learning approach for human walking activities recognition. The Journal of Supercomputing, 2021, 77(11): 12256-12279. DOI:10.1007/s11227-021-03768-7 |
| [16] |
Li Y, Pan Y. A novel ensemble deep learning model for stock prediction based on stock prices and news. International Journal of Data Science and Analytics, 2022, 13(2): 139-149. DOI:10.1007/s41060-021-00279-9 |
| [17] |
Rezaei H, Faaljou H, Mansourfar G. Stock price prediction using deep learning and frequency decomposition. Expert Systems with Applications, 2021, 169: 114332. DOI:10.1016/j.eswa.2020.114332 |
| [18] |
方雪清, 吴春胤, 俞守华, 等. 基于EEMD-LSTM的农产品价格短期预测模型研究. 中国管理科学, 2021, 29(11): 68-77. DOI:10.16381/j.cnki.issn1003-207x.2019.0765 |
| [19] |
Wang JJ, Chen Y, Zhu SZ, et al. Depth feature extraction-based deep ensemble learning framework for high frequency futures price forecasting. Digital Signal Processing, 2022, 127: 103567. DOI:10.1016/j.dsp.2022.103567 |
| [20] |
Silva RF, Barreira BL, Cugnasca CE. Prediction of corn and sugar prices using machine learning, econometrics, and ensemble models. Engineering Proceedings, 2021, 9(1): 31. DOI:10.3390/engproc2021009031 |
| [21] |
Parida N, Mishra D, Das K, et al. On deep ensemble CNN-SAE based novel agro-market price forecasting. Evolutionary Intelligence, 2021, 14(2): 851-862. DOI:10.1007/s12065-020-00466-w |
| [22] |
Xiao W, Xu C, Liu HL, et al. A hybrid LSTM-based ensemble learning approach for China coastal bulk coal freight index prediction. Journal of Advanced Transportation, 2021, 2021: 5573650. DOI:10.1155/2021/5573650 |
| [23] |
Ribeiro MHDM, dos Santos Coelho L. Ensemble approach based on bagging, boosting and stacking for short-term prediction in agribusiness time series. Applied Soft Computing, 2020, 86: 105837. DOI:10.1016/j.asoc.2019.105837 |
| [24] |
Li DF, Li ZR, Sun K. Development of a novel soft sensor with long short-term memory network and normalized mutual information feature selection. Mathematical Problems in Engineering, 2020, 2020: 7617010. DOI:10.1155/2020/7617010 |
| [25] |
Li CW, Zhan LW, Shen LQ. Friction signal denoising using complete ensemble EMD with adaptive noise and mutual information. Entropy, 2015, 17(9): 5965-5979. DOI:10.3390/e17095965 |
 2023, Vol. 32
2023, Vol. 32


