目标跟踪作为计算机视觉领域最具挑战的关键技术之一, 在机器人视觉导航, 无人驾驶, 医学诊断等多个领域有着广泛的应用[1]. 在实际跟踪中, 由于场景的多变性和复杂性, 实现高效目标跟踪仍具挑战性, 尤其是目标的跟踪定位问题. 目前国内外研究者为解决跟踪中的定位问题已做出了大量研究.
1975年在基于概率密度梯度函数的计算中, 首次定义了均值偏移(meanshift)概念[2], 1995年Cheng阐述了均值偏移的应用范畴[3], 部分学者在其之后也对均值偏问题运用在跟踪方法中. 2009年, 多实例目标跟踪算法通过分类的方式对目标实施追踪[4]. 2010年, 平均误差的最小输出和(minimum output sum of squared error, MOSSE)[5]作为跟踪界相关滤波器的开山之作, 该算法采用了最小化均方差方式去训练目标的位置滤波器, 并以此确定目标的位置. 此后, 一些基于MOSSE的追踪算法(循环结构内核(circulant structure kernel, CSK)[6]、核相关滤波(kernel correlation filter, KCF)[7]、判别尺度空间跟踪(discriminative scale space tracker, DSST)[8])等新算法也陆续诞生, 速率都能够超过每秒数百帧, 从而能够在实时的追踪系统中普遍地使用.
而部分性能更优良的改进追踪算法也随之提出. 其中较经典的算法有卡尔曼滤波(Kalman filter)算法[9], 粒子滤波(particle filter)算法[10]以及基于峰值旁瓣比的抗遮挡目标跟踪方法. 例如文献[11,12]通过卡尔曼滤波器来预测车辆在下一帧中的运动状态来解决车辆的定位问题, 但这种方法在复杂行车场景中具有局限性. 李军等[13]采用峰值旁瓣比并结合粒子滤波来进行状态估计以解决目标框丢失问题, 但这种方法只能处理短暂的完全遮挡, 无法解决目标精准定位的问题. 张红颜等[14]将目标的总体色彩特征划分为局部色彩特征进而提高算法的抗遮挡能力, 但这种方法在目标颜色相近的情况下容易跟错目标. 文献[15-17]通过卷积神经网络提取目标深度特征, 将深度特征融入相关滤波, 并采用高置信度更新的方式提高抗遮挡能力, 但这种方法局限于复杂的计算量. 宦若虹等[18]基于积分直方图进行特征提取, 对不同的遮挡情况采取不同跟踪机制, 但这种方法没有有效解决目标准确定位问题.
在相关滤波算法中, 判别尺度空间算法是将尺度和位置估计相结合的算法, 其引入快速傅里叶变换使跟踪速度有了很大提升, 并能准确评估目标的位置和尺度, 因此其在目标跟踪、智能监控方面应用广泛[19]. 但将其应用于行人跟踪时, 该算法对因行人形变、环境变化导致的定位不准确问题的处理能力较弱.
为解决行人形变、环境变化导致的定位不准确问题, 本文在DSST的基础结构下, 利用fhog特征[20]在行人跟踪上的优势, 以原算法所计算的行人位置为中心, 再次提取行人的fhog特征, 将其与位置滤波器模板做相关运算来纠正行人位置. 同时利用Kalman滤波算法对纠正后的行人位置进行预测和再次纠正. 整个算法的流程图如图1所示.

|
图 1 改进算法流程图 |
本文的主要贡献如下.
(1) 首次将位置纠正方法应用在行人跟踪上. 通过再次提取行人的fhog特征并进行相关运算, 能够扩大行人的检索范围并提取出较完整的行人特征描述子, 从而对行人的位置进行纠正. 同时, 也能够在不大幅度降低算法速度的前提下, 训练纠正位置的滤波器模板, 提高跟踪性能.
(2) 将Kalman滤波器的预测和纠正功能应用在行人跟踪中. Kalman滤波器的预测和纠正模型将行人纠正的位置再次进行了纠正, 实现了对行人位置的双重纠正, 从而再次提高跟踪算法的性能.
本文的其余部分组织如下: 第2节详细介绍了DSST算法, 第3节详细介绍了本文所提出的改进方法, 第4节展示了跟踪评价指标和对行人的跟踪实验结果, 最后对全文进行了总结.
2 判别尺度空间算法相关滤波[21-23]是当前研究的热点, 其源于信号处理领域. 在众多相关滤波算法中, 判别尺度空间跟踪算法(DSST)是将尺度和位置估计相结合的算法, 其可以对目标尺度进行精确估计. 首先其通过所训练的位置滤波器确定目标所在的位置, 在已确定的位置基础上, 再由不同尺度的样本所训练出的尺度滤波器对该目标尺度进行估计, 两种滤波器的设计思想相同.
以下分别介绍了判别尺度空间算法的位置滤波器和尺度滤波器模型的详细构建策略.
2.1 位置滤波器模型首先以跟踪目标为中心, 提取3倍于目标大小的图像块的fhog特征, 采用正则化最小二乘模型构造最小代价函数, 即每个通道的最优滤波器由式(1)构造:
| $ \varepsilon = {\left\| {\sum\limits_{l = 1}^d {{h^l} \otimes {f^l} - g} } \right\|^2} + \lambda {\sum\limits_{l = 1}^d {\left\| {{h^l}} \right\|} ^2} $ | (1) |
其中,
为提高运算速度, 将式(1)转换到频域计算, 根据极值点求导法则可得滤波器式(2):
| ${H^l} = \frac{{\overline G {F^l}}}{{\displaystyle\sum\limits_{k = 1}^d {\overline {{F^k}} {F^k}} + \lambda }} $ | (2) |
其中,
为将前后时刻的目标外观相联系, 需要利用式
| $ \left\{ \begin{gathered} A_t^l = (1 - \eta )A_{t - 1}^l + \eta \overline G F_t^l \\ {B_t} = (1 - \eta ){B_{t - 1}} + \eta \sum\limits_{k = 1}^d {\overline {F_t^k} F_t^k} \\ \end{gathered} \right. $ | (3) |
其中,
对于新的一帧, 在前一帧位置基础上提取3倍于目标大小的图像块特征, 经过离散傅里叶变换后得到
| $ {Y_t} = \frac{{\displaystyle\sum\limits_{l = 1}^d {\overline {A_{t - 1}^l} } Z_t^l}}{{{B_{t - 1}} + \lambda }} $ | (4) |
对式(4)进行反傅里叶变换, 其响应最大值所对应的区域
| $ {y_t} = {F^{ - 1}}({Y_t}) $ | (5) |
为确定跟踪目标更精确的尺度, 通过不同尺寸的目标样本特征加以训练构造出尺度滤波器, 最终将两个滤波器分别得到的位置和尺度作为跟踪结果.
以位置滤波器所获取的目标的位置为中心, 利用:
| $ {Y_{s, t}} = \frac{{\displaystyle\sum\limits_{l = 1}^d {\overline {A_{t - 1}^l} } Z_{s, t}^l}}{{{B_{t - 1}} + \lambda }} $ | (6) |
对式(6)进行反傅里叶转换, 响应最大值所对应的尺度即是当前目标尺寸.
DSST算法将跟踪任务看作目标定位和尺度估计两个独立的问题. 先使用跟踪物体的fhog特征训练位置滤波器, 从而判断目标中心位置, 接着利用目标的33个尺度样本特征训练另一个尺度滤波器, 来检测目标的尺度变化, 通过两个滤波器的相互作用, DSST算法能够解决目标定位和尺度自适应的问题, 其算法流程图如图2所示.

|
图 2 DSST算法流程图 |
判别尺度空间跟踪算法虽然可以较准确评估目标的位置和尺度, 不过该算法对行人行走过程中因形变和环境变化而导致的定位不准确的问题的处理能力较弱. 特别在行人快速行走过程中, 因滑动窗口提取的特征不完善, 易造成跟踪模型被污染、行人最终定位精度不高的问题.
3 改进方法 3.1 基于fhog特征对原跟踪算法的位置进行纠正在机器学习算法中, 特征工程是十分关键的. 相比于其他的特征描述方式, 原跟踪算法的fhog特征有许多优势. 因为fhog特征主要是对图像的局部区域通过处理得到的, 因此其在图像几何、光学变化方面都具有很好的不变性. 另外, 在精确的方向抽样和较强的局部光学归一化等条件下, 若人的姿态一直是直立的状态, 如果做了微小的身体动作, 那么这种微小的姿态差异就不会影响行人检测的效果, 所以fhog特征描述子在行人检测领域特别适用.
为解决行人在行走过程中因形变和环境变化而导致的跟踪定位不准确问题, 本文在不改变判别尺度空间算法特征的前提下, 充分利用fhog特征在行人检测中的优势, 以原跟踪算法的位置滤波器所计算的位置为中心, 再次提取出目标的fhog特征并将其与位置滤波器模板进行相关运算, 最终目标位置在原算法基础上得到了纠正, 位置滤波器的模板也再次得到了更新. 其中, 算法改进后流程图如图3所示.
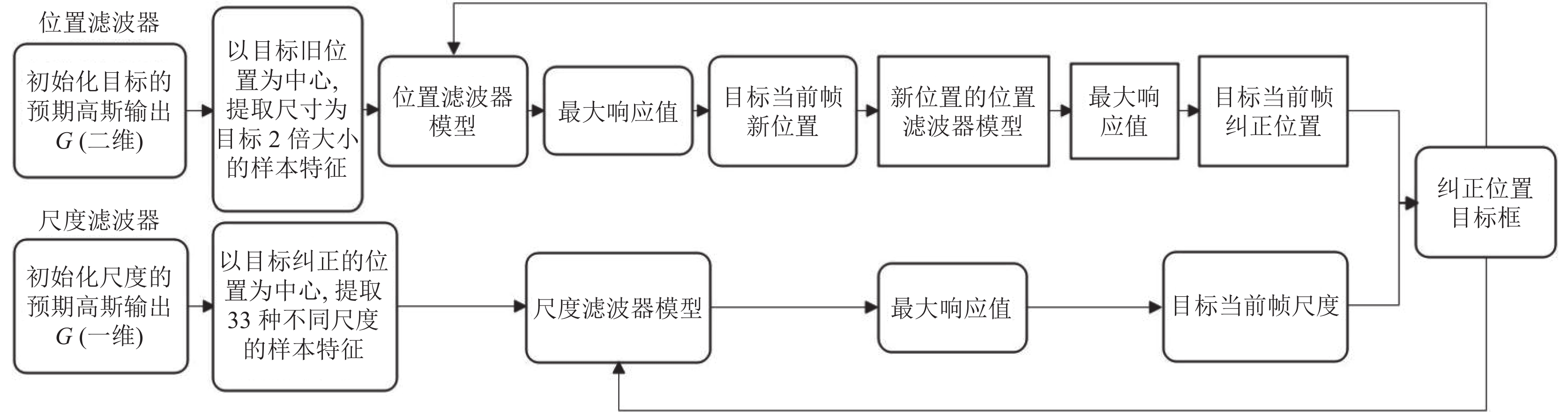
|
图 3 基于fhog特征改进算法流程图 |
3.2 基于纠正位置, Kalman滤波算法对其预测和再次纠正
现实世界具有不确定性, 而系统的不确定性主要体现在3个方面: 不存在完美的数学模型、系统的扰动是不可控的、测量传感器会存在误差. 在具有不明确信号的系统中, Kalman滤波对系统接下来的状态可以做出较有根据的估计, 即便系统伴随着各种干扰, Kalman滤波总能指出真实发生的情况.
Kalman滤波基本方程是时域内的递推形式, 运算流程包含预测和纠正两个阶段, 解决问题时不需要储存大量信息. 如果观察到新数据就可算新滤波值, 占用存储空间小且速度快, 满足实时性, 适用于嵌入式系统, 可处理平滑随机过程又能处理多维问题, 所以Kalman思想当前被广泛用于图像信息处理领域.
3.2.1 Kalman滤波简述Kalman filter假设:
1) 观测噪声和过程噪声都是满足高斯分布的.
2) 状态转移方程和观测方程都是线性的, 预测和更新都建立在线性计算基础上的.
3) 先验估计和后验估计误差都符合期望为0的高斯分布.
4) 观测噪声和模型噪声分布并不随系统状态改变而发生变化. 即过程噪声协方差矩阵
5) 初始状态下, 状态向量不受噪声影响.
定义1. 定义一个随机离散时间过程的状态向量, 该过程可用一个离散随机差分方程式表述:
| $ {x_k} = A{x_{k - 1}} + B{u_{k - 1}} + {w_{k - 1}} $ | (7) |
其中,
定义2. 定义一个观测变量:
| $ {Z_k} = H{x_k} + {V_k} $ | (8) |
其中,
根据前一刻后验估计值估计当前时刻的状态, 从而得到当前时刻的先验估计值:
| $ \left\{ \begin{gathered} \hat x _k^\_ = A{\hat x _{k - 1}} + B{u_{k - 1}} \\ P_k^ - = A{P_{k - 1}}{A^{\rm{T}}} + Q \\ \end{gathered} \right. $ | (9) |
其中,
通过当前时刻的观测值更正预测阶段的估计值, 即通过先验估计值得到当前的后验估计值, 其中卡尔曼滤波器状态的更新方程式如下所示:
| $ \left\{ \begin{gathered} {K_k} = P_k^ - {H^{\rm{T}}}{(HP_k^ - {H^{\rm{T}}} + R)^{ - 1}} \\ {\hat x _k} = \hat x _k^\_ + {K_k}({Z_k} - H\hat x _k^\_) \\ {P_k} = (I - {K_k}H)P_k^ - \\ \end{gathered} \right. $ | (10) |
其中,
本文将DSST算法作为行人的基础跟踪器, 除了将原算法的位置滤波器所计算的行人位置进行了纠正, 本文在纠正位置的基础上还引入Kalman滤波器. 基于纠正位置, 通过Kalman滤波器的预测功能, 使得纠正位置再次得到了纠正, 最终使得行人的定位更加准确.
首先, 将第1帧中行人的位置初始化为
| $ \left\{ \begin{gathered} {{{v}}_{{{{x}}_{{k}}}}} = {x_k} - {x_{k - 1}} \\ {{{v}}_{{{{y}}_{{k}}}}} = {y_k} - {y_{k - 1}} \\ \end{gathered} \right. $ | (11) |
| $ \left\{ \begin{gathered} {{{a}}_{{{{x}}_{{k}}}}} = {v_{{x_k}}} - {v_{{x_{k - 1}}}} \\ {{{a}}_{{{{y}}_{{k}}}}} = {v_{{y_k}}} - {v_{{y_{k - 1}}}} \\ \end{gathered} \right. $ | (12) |
| $ \left\{ \begin{gathered} {{{P}}_{{x_k}}} = {x_{k - 1}} + {v_{{x_{k - 1}}}} \cdot \Delta k + 0.5 \cdot {a_{{x_{k - 1}}}} \cdot \Delta {k^2} \\ {{{P}}_{{{{y}}_{{k}}}}} = {y_{k - 1}} + {v_{{y_{k - 1}}}} \cdot \Delta k + 0.5 \cdot {a_{{y_{k - 1}}}} \cdot \Delta {k^2} \\ \end{gathered} \right. $ | (13) |
其中,
卡尔曼滤波器作为目标状态的估计策略, 假设目标跟踪算法的运动模型为以上匀加速模型, 则运动目标和观测向量可以用如下线性方程进行描述:
| $ {x_k} = A{x_{k - 1}} + B{u_{k - 1}} + {w_{k - 1}} $ | (14) |
| $ {Z_k} = H{x_k} + {V_k} $ | (15) |
在以上两个方程中,
对于满足上述条件的系统, 卡尔曼滤波器是最优的信息融合处理器. 首先, 利用目标的运动模型, 预估目标在下一帧状态下的位置; 其次, 式
| $ { \hat x _k^\_} = A{\hat x _{k - 1}} + B{u_{k - 1}} $ | (16) |
| $ P_k^ - = A{P_{k - 1}}{A^{\rm{T}}} + Q $ | (17) |
其中,
以DSST的位置滤波器所检测到的目标位置作为测量值
| $ {K_k} = P_k^ - {H^{\rm{T}}}{(HP_k^ - {H^{\rm{T}}} + R)^{ - 1}} $ | (18) |
| ${\hat x _k} = {\hat x} _k^\_ + {K_k}({Z_k} - H\hat x_k^\_) $ | (19) |
| $ {P_k} = (I - {K_k}H)P_k^ - $ | (20) |
其中,
卡尔曼预测阶段负责目标位置预测和噪声协方差更新. 首先, 设定前一帧中所使用的目标运动状态向量为
本文采用DSST算法作为行人跟踪器, 将纠正位置方法和Kalman滤波器融合到其中, 融合之后的跟踪算法结构如前文图1所示. 其中除正则化项
在国际标准跟踪评测中, 跟踪器的性能通常由中心位置误差(center location error, CLE)和距离精确度(distance precision, DP)和重叠精确度(overlap precision, OP)这3个度量指标来评价[24].
4.1.1 中心位置误差(CLE)和距离精度(DP)对一个长度为
| $ CLE = \sqrt {{{(x_t^g - x_t^o)}^2} + {{(y_t^g - y_t^o)}^2}} $ | (21) |
CLE主要测量的是目标的跟踪框坐标与标记的真实坐标之间的像素差异, 能够在一定程度上反应跟踪算法的精确度. CLE值越小, 则表示跟踪算法对该帧目标的跟踪精度越高. 为获取算法在整个视频序列中的总体性能, 可统计其在整个视频序列中的中心位置误差, 然后再取平均值得到平均中心位置误差. 一般来说, 算法在视频序列上的平均中心位置误差越小, 跟踪算法的性能越好. 虽然CLE简单常用, 但它没有考虑目标的旋转和尺度变化, 因此当目标在跟踪过程中出现较大尺度或旋转变化时, 它并不能精确地评价跟踪算法的精度. 所以引入了距离精度DP, 其表示CLE低于某一个阈值范围的帧数占视频序列的总帧数的比例, 其中实验的阈值选为20 pixels.
4.1.2 重叠精度(OP)重叠精度OP是另一个被广泛使用的评价标准, 反映的是每一帧预测的目标区域
| $ OP = \frac{{Area(B_i^t \cap B_j^t)}}{{Area(B_i^t \cup B_j^t)}} $ | (22) |
其中,
由上图可知重叠精度的计算结果在越接近1, 说明跟踪算法预测的目标区域与实际的目标区域重合度越高, 算法的跟踪精度越高. 同样的, 可以计算跟踪算法在测试视频所有帧的重叠精度的平均值(即平均重叠精度)来评价其在视频序列上的整体表现, 平均重叠精度越大, 算法的性能越好. 重叠精度考虑了目标旋转、尺度变换等因素, 能够更好地反映跟踪结果的精确度, 所以综合以上3种评价方法可以更好地评价跟踪结果.
4.2 算法改进前后结果对比分析本文挑选OTB-100中的行人数据集在Matlab软件进行实验. 在这些视频序列中, 选择了8组数据集进行效果展示, 其中改进前后的跟踪效果如图5所示, 序列中绿色的跟踪框表示原算法的跟踪效果, 红色的跟踪框表示改进后的跟踪效果, 图片的左上角数字表示视频序列的帧数.
为了更精确验证本文所提出策略的有效性, 将标准DSST算法与位置经过双重纠正后的DSST算法通过距离精度DP, 重叠精度OP, 中心位置误差CLE这3个指标进行比较, 比较数据如图6和表1所示.
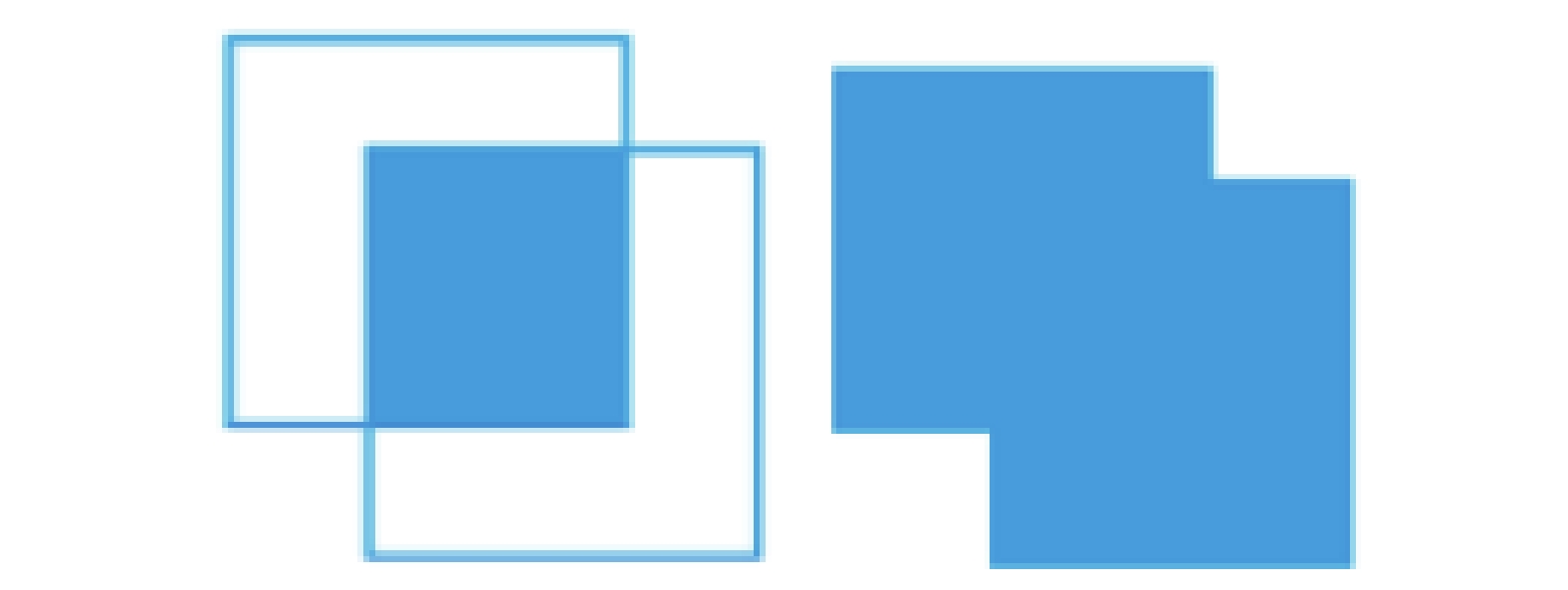
|
图 4 目标区域和真实标记区域的并集与交集 |

|
图 5 行人数据集 |

|
图 5 行人数据集(续) |

|
图 6 改进前后比较数据 |
| 表 1 改进前后比较数据 |
表1和图6表明, 与标准的DSST算法相比, 所提改进方案的跟踪性能得到了提升, 尤其在数据集Crossing, David3, Dancer, Crowds, Skater, Skater2, Woman, Human2和Human5中改进方案的跟踪性能显著提升. 由于行人快速移动和图像出现模糊时, 利用fhog特征在行人检测上的优势, 通过在原算法位置上再次提取fhog特征并进行相关运算, 能够使得跟踪目标的搜索范围再次扩大从而提取了更精确、更完整的行人特征描述子, 最后通过卡尔曼滤波对行人位置的预测和纠正功能, 使得位置在原算法的基础上得到了双重纠正, 最终所更新的位置滤波器模板也更大程度上使得跟踪性能得到提高.
5 总结本文针对判别尺度空间跟踪算法在目标跟踪中出现的问题, 对算法进行了以上方式的改进. 首先, 通过fhog特征适用于行人检测的优势[25], 在不改变该算法特征和不大幅度降低算法速度的前提下, 以位置滤波器计算的位置为中心, 使用滑动窗口再次提取行人的fhog特征, 并将其与位置滤波器模板进行相关运算后, 得到纠正后的行人位置, 然后以纠正位置为中心训练位置滤波器模型, 从而使得行人的定位精度在原算法基础上得到了提升. 其次, 针对行人行走过程中出现快速移动和环境变化的问题, 本文引入了具有数据融合功能的Kalman滤波算法, 通过其加入, 行人的定位再次得到了纠正, 最终跟踪精度也随之提升.
| [1] |
Collins RT, Lipton AJ, Kanade T, et al. A system for video surveillance and monitoring. Technical Report, Pittsburgh: Carnegie Mellon University, 2002.
|
| [2] |
Fukunaga K, Hostetler L. The estimation of the gradient of a density function, with applications in pattern recognition. IEEE Transactions on Information Theory, 1975, 21(1): 32-40. DOI:10.1109/TIT.1975.1055330 |
| [3] |
Cheng YZ. Mean shift, mode seeking, and clustering. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995, 17(8): 790-799. DOI:10.1109/34.400568 |
| [4] |
Babenko B, Yang MH, Belongie S. Robust object tracking with online multiple instance learning. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8): 1619-1632. DOI:10.1109/TPAMI.2010.226 |
| [5] |
Bolme DS, Beveridge JR, Draper BA, et al. Visual object tracking using adaptive correlation filters. Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco: IEEE, 2010. 2544–2550.
|
| [6] |
Henriques JF, Caseiro R, Martins P, et al. Exploiting the circulant structure of tracking-by-detection with kernels. Proceedings of the 12th European Conference on Computer Vision. Florence: Springer, 2012. 702–715.
|
| [7] |
Henriques JF, Caseiro R, Martins P, et al. High-speed tracking with kernelized correlation filters. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596. DOI:10.1109/TPAMI.2014.2345390 |
| [8] |
Danelljan M, Häger G, Kan FS, et al. Accurate scale estimation for robust visual tracking. Proceedings of the 2014 British Machine Vision Conference. BMVA Press, 2014.
|
| [9] |
Kalman RE. A new approach to linear filtering and prediction problems. Journal of Basic Engineering, 1960, 82(1): 35-45. DOI:10.1115/1.3662552 |
| [10] |
李由, 张恒, 李立春. 基于多测量融合的粒子滤波跟踪算法. 国防科技大学学报, 2007, 29(5): 26-30. DOI:10.3969/j.issn.1001-2486.2007.05.007 |
| [11] |
李文姣, 秦勃. 基于卡尔曼滤波器的抗遮挡车辆跟踪算法. 计算机应用, 2012, 32(S2): 174-176, 179. |
| [12] |
Ettlinger A, Neuner H, Burgess T. Development of a Kalman filter in the Gauss-Helmert model for reliability analysis in orientation determination with smartphone sensors. Sensors, 2018, 18(2): 414. DOI:10.3390/s18020414 |
| [13] |
李军, 曹梦婷. 基于置信图峰值旁瓣比优化的遮挡目标跟踪方法: 中国, 108986142A. 2018-12-11.
|
| [14] |
张红颖, 王赛男, 胡文博. 基于分块颜色直方图的MS跟踪算法. 中国民航大学学报, 2019, 37(1): 39-45. DOI:10.3969/j.issn.1674-5590.2019.01.008 |
| [15] |
火元莲, 李明, 曹鹏飞, 等. 基于深度特征与抗遮挡策略的运动目标跟踪. 西北师范大学学报(自然科学版), 2020, 56(4): 49-56. DOI:10.16783/j.cnki.nwnuz.2020.04.008 |
| [16] |
Ma C, Huang JB, Yang XK, et al. Hierarchical convolutional features for visual tracking. Proceedings of the 2015 IEEE International Conference on Computer Vision. Santiago: IEEE, 2015. 3074–3082.
|
| [17] |
Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. arXiv:1409.1556, 2015.
|
| [18] |
宦若虹, 王楚, 陶一凡, 等. 一种抗遮挡的基于积分直方图的粒子滤波目标跟踪方法: 中国, 107507222A. 2021-01-01.
|
| [19] |
Haritaoglu I, Harwood D, Davis LS. W4: Real-time surveillance of people and their activities
. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(8): 809-830. DOI:10.1109/34.868683 |
| [20] |
Dalal N, Triggs B. Histograms of oriented gradients for human detection. Proceedings of the 2015 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego: IEEE, 2005. 886–893.
|
| [21] |
张云洲, 郑瑞, 暴吉宁, 等人. 基于多个相关滤波器的行人跟踪尺度算法. 东北大学学报(自然科学版), 2019, 40(9): 1228–1233, 1239.
|
| [22] |
Zhang YH, Yang YJ, Zhou WN, et al. Motion-aware correlation filters for online visual tracking. Sensors, 2018, 18(11): 3937. DOI:10.3390/s18113937 |
| [23] |
Xu LY, Luo HB, Hui B, et al. Real-time robust tracking for motion blur and fast motion via correlation filters. Sensors, 2016, 16(9): 1443. DOI:10.3390/s16091443 |
| [24] |
Wu Y, Lim J, Yang MH. Object tracking benchmark. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1834-1848. DOI:10.1109/TPAMI.2014.2388226 |
| [25] |
Felzenszwalb PF, Girshick RB, McAllester D, et al. Object detection with discriminatively trained part-based models. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(9): 1627-1645. DOI:10.1109/TPAMI.2009.167 |
 2023, Vol. 32
2023, Vol. 32


