复杂网络中的许多应用通常能够用图来表示, 如: 万维网、社交网络、分子生物学等[1-3]. 这些网络图的规模随着时间的推移而增大. 在大规模的图中进行查询、计算等操作时, 难以保证时效性. 图摘要(graph summarization)的目的就是将原图转换为一个更紧凑的摘要图, 同时尽可能地保留原图的结构模式、查询答案或特定属性分布[4]. 随着摘要图的规模变小, 在其上进行的模式识别、社团挖掘、度或特征向量中心性查询等图操作方法耗时更小[5].
图摘要问题分为图有损摘要问题和图无损摘要问题两大类. 对于图无损摘要问题来说, 该问题要求找出的摘要图能够在使用校正信息的条件下重建为原图. 最小描述长度(minimum description length, MDL)[6]和空间复杂度[7]通常用于衡量所生成摘要图的质量. 同时, 图无损摘要问题通过将团、星、链等结构信息和校正信息一起存储在超点、超边中来辅助摘要图的重建[8-10].
图有损摘要则不保存校正信息, 因此空间复杂度更低. 其通过摘要图与原始图的邻接矩阵差异范数来衡量摘要图的质量. 常见的算法是采用节点分组和聚合的方法寻找差异范数最小的摘要图. LeFevre等人[11]提出的算法GraSS在每次迭代中贪心地选取导致当前l1-重构误差增量最小的节点对合并; 在此基础上, Beg等人提出了算法SAA[12], 其中新增了节点对的评分和计算策略, 用于优化算法的时间与效果; Riondato等人[13]则将每个顶点作为一个n维向量, 采用欧氏距离聚类方法(K-median和K-means)寻找摘要图, 目标是最小化l2-重构误差. 此外, Lee等人[14]通过结合MDL方法和图的稀疏化来寻找尽可能小的摘要图; Zhou等人[15]提出了保留度的邻接矩阵作为目标函数来摘要图, 从而使得摘要图的度查询误差更小; 而Fan等人[16]采用压缩的技术寻找摘要图.
针对不同类型的网络图也有一些启发式的图摘要算法, 例如, 基于社会背景和特征来摘要社交网络[17-19]; 基于时序动态图[20-22]和异构网络[23]等进行图摘要的系列算法[24]. 并且, 图摘要技术还时常被用作数据匹配、模式挖掘等其他问题[5, 25]的预处理过程.
本文研究图的有损摘要问题的有效算法. 现有的基于节点聚合思想的图有损摘要算法每次迭代中仅贪心地合并一个节点对, 导致迭代轮次过多, 时间上较慢; 而在节点对选取上则没有考虑节点之间的结构关系. 针对以上问题, 本文提出了一个两阶段算法TS_LGS, 在第一阶段批量合并对结果影响较小的节点对, 加快算法的迭代; 在第2阶段则结合节点的权重和相连性选择对结果影响更小的节点对合并, 从而更快地找到质量更好的摘要图.
本文组织和结构如下: 第1节是图有损摘要问题的数学表述, 第2节简要介绍了基于节点聚合的图有损摘要的主要算法, 第3节描述了我们的TS_LGS算法, 第4节给出了实验比较结果, 最后是本文的总结.
1 问题表述图有损摘要(lossy graph summarization, LGS)问题定义如下: 给定一个包含n个节点的原图G(V, E)和正整数k(k≤n), 找到具有k个超节点的摘要图S(VS, ES)来表示原图G, 满足摘要图与原图的重构误差(reconstruction error, RE)要最小[11]. 图有损摘要下文简称为图摘要. 图1中给出了一个图摘要示例.
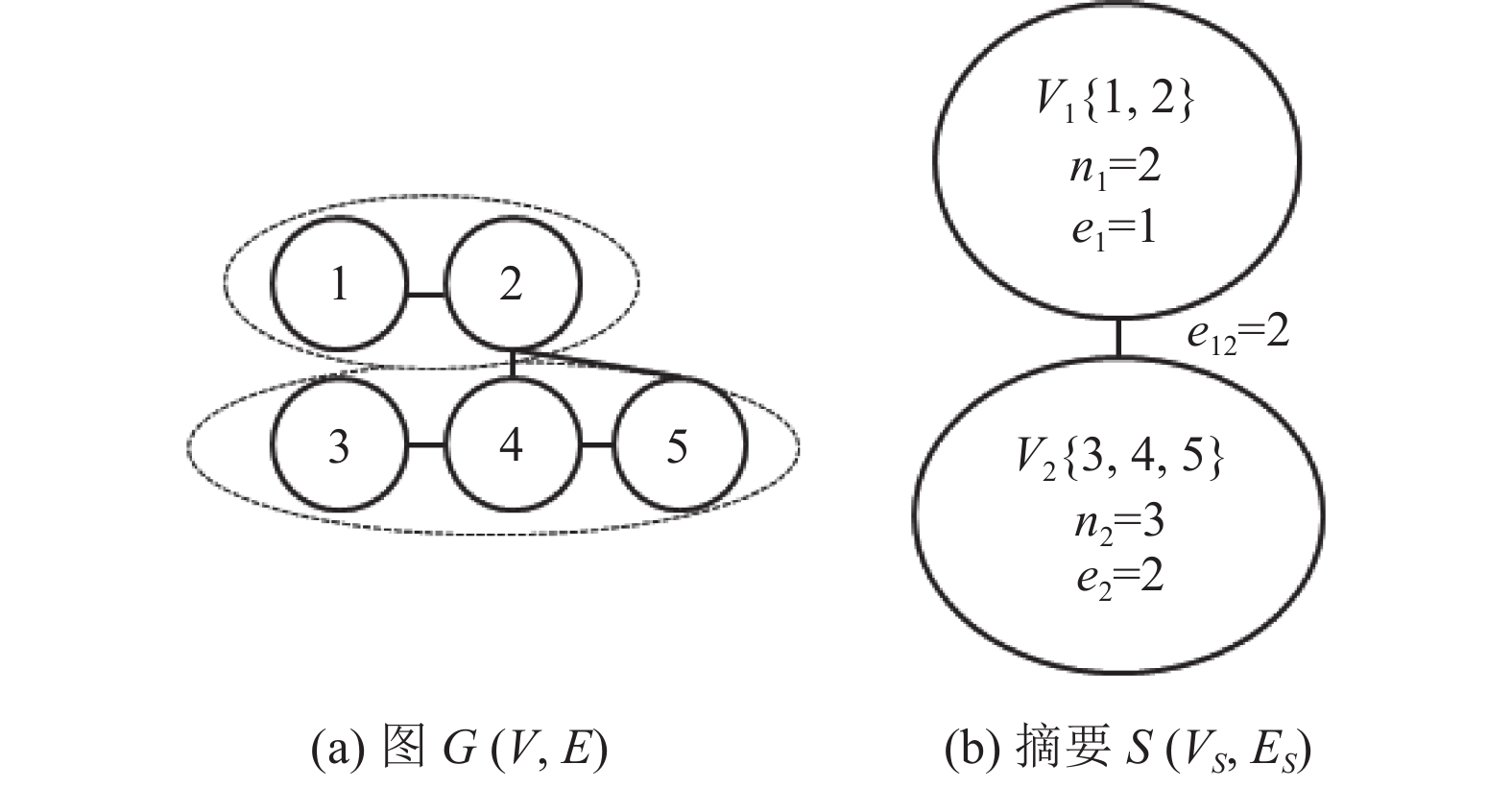
|
图 1 图摘要示例 |
摘要图S(VS, ES)是一个k点带权无向图, 其中VS={V1, …, Vk}是V的一个k划分, 每个Vi称作是摘要图的一个超节点, 有两个属性: 内部节点数目ni, 内部点之间的边数ei; 超节点对(Vi, Vj)之间的边权重eij为Vi与Vj点之间边数, 而ES为所有超节点之间带权边的集合.
给定一个摘要图S, 由S重建的图的期望邻接矩阵为n阶方阵
| $ \overline{A}(u, v)=\left\{ { \begin{array}{ll}\dfrac{{e}_{i}}{\left(\begin{array}{c}{n}_{i}\\ 2\end{array}\right)}, & u, v\in V\\ 0\text{, }& u=v\\ \dfrac{{e}_{ij}}{{n}_{i}{n}_{j}}, & u\in {V}_{i}, v\in {V}_{j}\end{array} } \right.$ | (1) |
摘要图S的质量可以用lp-重构误差来度量, 即
| $ R{E}_{p}(G|S)=\left({\displaystyle {\sum }_{i=1}^{\left|V\right|}{\displaystyle {\sum }_{j=1}^{\left|V\right|}|\overline{A}(i, j)-A(i, j){|}^{p}}}\right)^{1/p} $ | (2) |
其中, A(i, j)表示图G的邻接矩阵中i行j列的值,
Lefevre等提出的算法k_GS[11]的核心思想是以最小重构误差增量为目标, 在算法迭代过程中依次选取合并后重构误差增量最小的节点对合并. 其主要流程如下: 在每次迭代过程中, 首先需要随机选取P(t)个节点对, 然后分别计算节点对合并后的重构误差变化量, 其计算时间为O(P(t)×n); 再将重构误差增量最小的节点对删除并聚合为新的超节点, 其计算时间为O(n). 由于算法最多迭代n–k+1轮, 因此当P(t)=nt= O(n)时算法时间复杂度为O((n×n+n)×n)= O(n3).
为了降低算法的时间复杂度, 同时降低迭代过程中节点对随机选取对摘要图质量的影响, Beg等人在算法k_GS的基础上提出了算法SAA[12], 其主要优化策略包括: 简化了节点对合并后重构误差增量的计算, 并使用了加权采样选取增量更小的节点对的方法. 首先, SAA将式(2)中的l1-RE 计算过程拆分为式(3):
| $ RE\left( {G{\text{|}}S} \right) = \mathop \sum \limits_{i = 1}^k \left(4{e_i} - \frac{{4e_i^2}}{{\left( {\begin{array}{*{20}{c}} {{n_i}} \\ 2 \end{array}} \right)}}\right) + \mathop \sum \limits_{i = 1}^k \mathop \sum \limits_{j = 1, i \ne j}^k \left(2{e_{ij}} - \frac{{2e_{ij}^2}}{{{n_i}{n_j}}}\right) $ | (3) |
再将节点对合并后重构误差变化量定义为节点对的评估得分, 从而使得节点对合并后的影响可以形式化为评估得分的计算, 如式(4)所示:
| $ \begin{split} scor{e_t}(a, b) =& RE(G|{S_{t - 1}}) - RE(G|S_t^{a, b}) \\ = & - \frac{{4e_a^2}}{{\left( {\begin{array}{*{20}{c}} {{n_a}} \\ 2 \end{array}} \right)}} - \sum\limits_{i = 1, i \ne a}^{n(t)} {\frac{{4e_{ai}^2}}{{{n_a}{n_i}}}} + \frac{{4e_{ab}^2}}{{{n_a}{n_b}}} - \frac{{4e_b^2}}{{\left( {\begin{array}{*{20}{c}} {{n_b}} \\ 2 \end{array}} \right)}} \\ & - \sum\limits_{i = 1, i \ne a}^{n(t)} {\frac{{4e_{bi}^2}}{{{n_b}{n_i}}}} + \frac{{4{{({e_a} + {e_b} + {e_{ab}})}^2}}}{{\left( {\begin{array}{*{20}{c}} {{n_a} + {n_b}} \\ 2 \end{array}} \right)}} \\ & + \frac{4}{{{n_a} + {n_b}}}\sum\limits_{i = 1, i \ne a, b}^{n(t)} \left(\frac{{e_{ai}^2}}{{{n_i}}} + \frac{{e_{bi}^2}}{{{n_i}}} + \frac{{2{e_{ai}}{e_{bi}}}}{{{n_i}}}\right) \\ \end{split} $ | (4) |
其中, RE(G|St–1)是第t–1轮迭代时形成的摘要图的重构误差, RE(G|Sta.b)是第t轮迭代时合并节点对(a, b)后的摘要图的重构误差, scoret(a, b)则表示第t轮迭代时合并节点对(a, b)的评估得分. 从而将寻找合并后重构误差增量最小节点对转换为寻找得分最高的节点对. SAA通过将na, ea等结构信息存储在超节点中并采用count-min sketch[26]的方法近似计算
| $ f\left(a\right)=-\frac{4{e}_{a}^{2}}{\left(\begin{array}{c}{n}_{a}\\ 2\end{array}\right)}- \displaystyle\sum\limits_{i = 1\atop i \ne a}^{n\left( t \right)} \frac{4{e}_{ai}^{2}}{{n}_{a}{n}_{i}} $ | (5) |
| $ w\left( a \right) = \left\{ {\begin{array}{*{20}{c}} {\dfrac{{ - 1}}{{f\left( a \right)}}}, &{f\left( a \right) \ne 0} \\ 0, &{f(a) = 0} \end{array}} \right. $ | (6) |
SAA采用平衡二叉树的形式来辅助挑选节点对, 使得对摘要重构误差影响更小的节点对更容易被选中, 相较于k_GS中的随机采样更为合理. 当抽样节点数P(t)=logn时, SAA寻找的摘要图质量已经与抽取n对节点的k_GS类似. 虽然使用维持的平衡二叉树抽取节点仍需要logn的时间, 但整体时间复杂度已经降为了O(nlog2n) .
3 TS_LGS算法本文沿用了k_GS与SAA算法中迭代合并最小重构误差增量的节点对来寻找摘要图的基本模式. 并在SAA的加权抽样基础上进一步提出了TS_LGS算法, 通过批量合并节点对来加快算法的迭代, 并使用节点相连性来优化节点对的选取. 该算法将整个迭代过程分为了两个阶段(使用阶段阈
本文使用原图中度数大于平均度的节点数作为阶段阈值来划分算法的第1阶段和第2阶段, 在不同阶段使用不同的改进策略寻找摘要图. 阶段阈值的计算方法如式(7)所示:
| $ t{h_{\overline d}} = \left| {\left\{ {v|{\text{v}} \in V, d(v) > \overline d} \right\}} \right| $ | (7) |
其中,
(1)第1阶段: 批量合并策略
我们记录当前节点对合并得分的最佳值bestScoret, 在一定程度上它能反应出之前合并的节点对的得分情况. 假定t轮迭代中节点对最高得分为maxScoret, 则当前的节点对最佳合并得分bestScoret可由式(8)计算:
| $ {\textit{bestScore}}{}_{t}= \mathrm{min}\left({\textit{bestScore}}{}_{t-1}, {\textit{maxScore}}{}_{t}\right) $ | (8) |
实验中我们观察到如下情况: 在第1阶段, 图中有许多度小于图的平均度的节点, 在合并这些节点时, 重构误差的变化量较小. 针对其他图摘要凝聚算法每轮迭代仅合并一个节点对的情况, 本文提出一个基于当前最佳合批量合并的方法. 具体来说, 在第1阶段迭代过程中, 若当前抽样的节点对得分高于bestScoret, 就直接将其合并. 反之, 若当前抽样节点对最高得分maxScoret依旧低于bestScoret时, 则将bestScoret更新为maxScoret. 这样有效地减少了算法迭代的次数, 从而能减少了整体的运行时间.
(2)第2阶段: 相邻优先合并策略
节点权重只考虑了单个节点对得分的影响, 而忽略了节点对之间的关系. 在式(3)中, eab代表超节点对(a, b)之间边的数量. 如果节点对不相连, 则eab=0, 公式中
TS_LGS算法的过程可以简单描述为: 首先计算图的平均度
TS_LGS算法的具体描述如算法1所示.
算法1. TS_LGS
输入: 图G(V, E), 摘要图节点数k, 抽样节点数P(t)
输出: 摘要图S
1.
2.
3. 构建抽样节点树D
4. while nt > k do
5. if nt >
6. for i ∈ P(t) do
7. (node1, node2) = getSample(D)
8. score = getScore(node1, node2)
9. 保留最高得分maxScoret节点对maxPair
10. if score ≥ bestScoret–1
11. 合并节点对(node1, node2)
12. end for
13. if maxScoret < bestScoret–1
14. bestScoret = maxScoret
15. 合并得分最高节点对maxPair
16. else //第2阶段
17. for i ∈ P(t) do
18. for j ∈
19. (node1, node2) = getSample(D)
20. 如果node1, node2相连则退出循环
21. end for
22. 保留最高得分maxScoret节点对maxPair
23. end for
24. 合并得分最高节点对maxPair
25. end while
26. return S
3.3 复杂度分析TS_LGS算法分为了两个阶段, 第1阶段的时间复杂度为
本文实验所使用的对比算法包括k-GS、SAA、SAA(w=50)、SAA(w=100) (w为近似计算参数取值)、S2L, 在几个典型的测试数据集上比较了重构误差和查询误差.
实验均用Java实现, 部分算法存在随机性, 实验结果取运行100次后的均值, 耗时较长的实验结果为运行10次后均值. 运行环境为Windows 10操作系统, 内存8 GB, 处理器Intel(R) Core(TM) i7-7700 CPU @3.60 GHz.
4.1 数据集本文实验选用6个不同规模的真实网络数据集, 它们来自不同的应用场景[8,11,12,14], 网络的基本信息如表1所示.
| 表 1 数据集 |
4.2 实验设置与评价指标
(1)重构误差RE(G|S)
本文使用重构误差来衡量摘要图与原始图的差异情况. 重构误差越小, 表示摘要图与原始图的差距越小. 重构误差的具体表达式见式(2).
(2)节点度平均差与标准差
给定节点v∈V, 其在摘要图上的度计算方式如式(9)所示:
| $ \overline{ d}\left(v\right)={\displaystyle \sum }_{j=1}^{\left|V\right|}\overline{A}\left(v, j\right) $ | (9) |
在原始图与摘要图上对t个节d(v1)点进行度查询, 其度分别为d(v1), d(v2), …, d(vt)和
| $ {D}_{{\rm{avgError}}}=\frac{{{\displaystyle \sum }}_{i=1}^{t}\left|d\left({v}_{i}\right)-\overline{ d}\left({v}_{i}\right)\right|}{t} $ | (10) |
同理, 原始图与摘要图的节点度标准差DstdError可由式(11)表示.
| $ {D}_{{\rm{stdError}}}=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^{t}(\left|d\left({v}_{i}\right)-\overline{ d}\left({v}_{i}\right)\right|-{D}_{{\rm{avgError}}}{)}^{2}}{t}} $ | (11) |
(3)特征向量中心性平均差与标准差
给定点v∈V, 其在摘要图上的特征向量中心性计算方式如式(12)所示:
| $ \overline{ p}\left(v\right)=\frac{\overline{ d}\left(v\right)}{2\left|E\right|} $ | (12) |
在原始图与摘要图上对t个节点进行特征向量中心性查询, 其特征向量中心性分别为p(v1), p(v2), …, p(vt)和
| $ {P}_{{\rm{avgError}}}=\frac{{{\displaystyle \sum }}_{i=1}^{t}\left|p\left({v}_{i}\right)-\overline{ p}\left({v}_{i}\right)\right|}{t} $ | (13) |
同理, 原始图与摘要图的特征向量中心性误差标准差PstdError可由式(14)表示.
| $ {P}_{{\rm{stdError}}}=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^{t}(\left|p\left({v}_{i}\right)-\overline{ p}\left({v}_{i}\right)\right|-{P}_{{\rm{avgError}}}{)}^{2}}{t}} $ | (14) |
(4)三角形密度相对差
本文使用三角形密度相对差表示原始图与摘要图在三角形密度上的差异情况. 其可以用式(15)所表示.
| $ TD=\frac{\overline{ T}-T}{T} $ | (15) |
其中, T表示原始图的三角形个数,
本文使用节约轮次(理论迭代次数与实际迭代次数之差)与节约率(节约轮次与理论迭代次数之比)来形式化表示第一阶段加速合并时TS_LGS算法减少的迭代轮次. 本文在不同规模真实数据集上(见表1), 通过控制摘要图剩余节点数k和抽样节点数P(t)来比较TS_LGS与其他算法寻找摘要图的运行时间以及摘要图的重构误差、查询误差等评价指标. 具体结果及分析如下.
(1) 不同k与P(t)下重构误差与运行时间
在小规模网络上(如表2所示), TS_LGS在R1数据集上能够在与SAA差不多的时间内找到l1-RE更低的摘要图. 在R2数据集上TS_LGS则能够更快地形成摘要图. 而在中规模网络(如表3所示)和大规模网络(如表4所示)上, 相较于现有的k-GS、SAA以及SAA(w=50)、SAA(w=100)算法, TS_LGS算法提取的图摘要几乎都具有更小的l1-RE, 并且运行时间更少(迭代轮次节约率在60%左右). 同时, 在不同数据集下, TS_LGS找到的摘要图相比其他算法也具有较小的l2-RE (如表5所示). 而随着图的规模变大或者抽样节点数P(t)的增多, 可以看到, TS_LGS算法不管是寻找的摘要图的重构误差, 还是运行时间, 都优于其余同类算法. 这说明TS_LGS算法能够很好地扩展到更大规模的网络上.
| 表 2 小规模网络上算法对比 |
| 表 3 中规模网络上算法对比 |
| 表 4 大规模网络上算法对比 |
| 表 5 不同算法下l2-RE对比 |
(2)剩余节点数下重构误差与运行时间
图2和图3是在R3网络上, 当k=10000, P(t)=n时, 重构误差、运行时间与图的剩余节点数的关系. 可以看出, TS_LGS算法在第1阶段时, 生成的摘要图的重构误差略高于算法SAA生成的摘要图, 低于其余算法生成的摘要图, TS_LGS算法的运行时间则不超过其他算法的1/2. 而在第2阶段时, TS_LGS形成的摘要图重构误差增速开始变缓, 运行时间消耗开始增加. 当剩余节点数达到k时, TS_LGS的运行时间依旧比其余算法少, 同时找到的摘要图重构误差也是最低的. 这说明了TS_LGS算法分为两个阶段是合理且有效的.
(3)查询结果对比
在R1与R4数据集上, 本文分别在不同k下, 对原始图和摘要图进行了度、特征向量中心性、三角形密度等相关指标的查询结果对比. 从表6可以看出, 在小规模网络上, TS_LGS算法在度和特征向量中心性的平均差与标准差上与SAA可以达到类似的效果, 在三角形密度相对差上则更接近0. 而从表7可以看出, 随着图的规模增大, k的取值越来越小. TS_LGS算法在各项查询指标上的结果都优于其余算法.
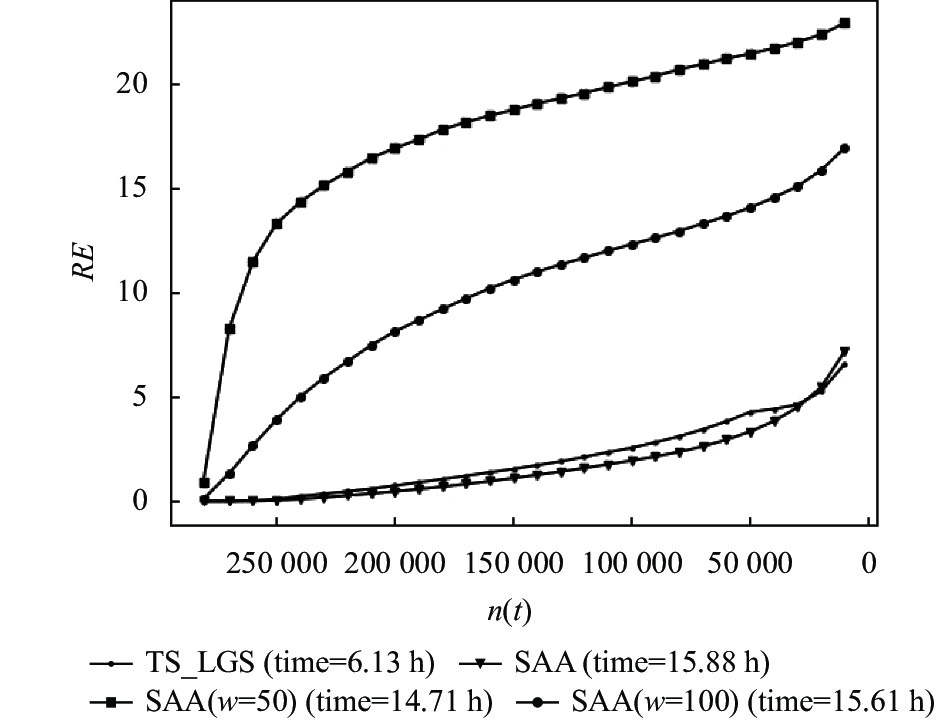
|
图 2 剩余节点数与重构误差 |

|
图 3 剩余节点数与运行时间 |
| 表 6 R1上各算法查询结果对比 |
| 表 7 R4上各算法查询结果对比 |
5 总结
对于图有损摘要问题, 本文提出了一种两阶段算法TS_LGS. 首先, TS_LGS计算了度大于平均度的节点数作为算法的阶段阈值. 在当前节点数大于阶段阈值的第1阶段, TS_LGS提出了一种节点对合并的计算方法, 用于加速合并对摘要图质量影响较小的节点对; 当第2阶段, TS_LGS基于图的平均度和结构信息提出了另一种节点对的挑选合并方法, 使得合并后的摘要图重构误差变化更小. 本文在6个不同规模的真实网络上进行了实验, 结果表明本算法与其他同类算法相比, 能够更快的寻找到质量更好的摘要图. 并且, TS_LGS算法具有良好的扩展性, 能够适用于更大规模的网络.
| [1] |
Tian YY, Hankins RA, Patel JM. Efficient aggregation for graph summarization. Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data. Vancouver: ACM, 2008. 567–580.
|
| [2] |
Maserrat H, Pei J. Community preserving lossy compression of social networks. Proceedings of the 12th IEEE International Conference on Data Mining. Brussels: IEEE, 2012. 509–518.
|
| [3] |
Shin K, Ghoting A, Kim M, et al. SWeG: Lossless and lossy summarization of Web-scale graphs. Proceedings of the World Wide Web Conference. San Francisco: ACM, 2019. 1679–1690.
|
| [4] |
Bonifati A, Dumbrava S, Kondylakis H. Graph summarization. arXiv. 2004.14794, 2020.
|
| [5] |
王鹤. 基于图摘要的图模式挖掘研究与实现[硕士学位论文]. 南京: 东南大学, 2018.
|
| [6] |
Rissanen J. Modeling by shortest data description. Automatica, 1978, 14(5): 465-471. DOI:10.1016/0005-1098(78)90005-5 |
| [7] |
Lelewer DA, Hirschberg DS. Data compression. ACM Computing Surveys, 1987, 19(3): 261-296. DOI:10.1145/45072.45074 |
| [8] |
Navlakha S, Rastogi R, Shrivastava N. Graph summarization with bounded error. Proceedings of the 2008 ACM SIGMOD International Conference on Management of Data. Vancouver: ACM, 2008. 419–432.
|
| [9] |
Ko J, Kook Y, Shin K. Incremental lossless graph summarization. Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: ACM, 2020. 317–327.
|
| [10] |
Koutra D, Kang U, Vreeken J, et al. VOG: Summarizing and understanding large graphs. Proceedings of the 2014 SIAM International Conference on Data Mining. Philadelphia: Society for Industrial and Applied Mathematics, 2014. 91–99.
|
| [11] |
LeFevre K, Terzi E. GraSS: Graph structure summarization. Proceedings of the 2010 SIAM International Conference on Data Mining. Columbus: Society for Industrial and Applied Mathematics. 2010. 454–465.
|
| [12] |
Beg MA, Ahmad M, Zaman A, et al. Scalable approximation algorithm for graph summarization. Proceedings of the 22nd Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. Melbourne: Springer, 2018. 502–514.
|
| [13] |
Riondato M, García-Soriano D, Bonchi F. Graph summarization with quality guarantees. Data Mining and Knowledge Discovery, 2017, 31(2): 314-349. DOI:10.1007/s10618-016-0468-8 |
| [14] |
Lee K, Jo H, Ko J, et al. SSumM: Sparse summarization of massive graphs. Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: ACM, 2020. 144–154.
|
| [15] |
Zhou HQ, Liu SH, Lee K, et al. DPGS: Degree-preserving graph summarization. Proceedings of the 2021 SIAM International Conference on Data Mining (SDM). Society for Industrial and Applied Mathematics. Waltham, 2021. 280–288.
|
| [16] |
Fan WF, Li JZ, Wang X, et al. Query preserving graph compression. Proceedings of the 2012 ACM SIGMOD International Conference on Management of Data. Scottsdale: ACM, 2012. 157–168.
|
| [17] |
Zhuang H, Rahman R, Hu X, et al. Data summarization with social contexts. Proceedings of the 25th ACM International Conference on Information and Knowledge Management. Indianapolis: ACM, 2016. 397–406.
|
| [18] |
Chierichetti F, Kumar R, Lattanzi S, et al. On compressing social networks. Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Paris: ACM, 2009. 219–228.
|
| [19] |
Safavi T, Belth C, Faber L, et al. Personalized knowledge graph summarization: From the cloud to your pocket. Proceedings of the 2019 IEEE International Conference on Data Mining. Beijing: IEEE, 2019. 528–537.
|
| [20] |
王健. 基于张量分解的高效图摘要算法研究[硕士学位论文]. 武汉: 华中科技大学, 2021.
|
| [21] |
McNeil M, Ma BY, Bogdanov P. SAGA: Signal-aware graph aggregation. Proceedings of the 2022 SIAM International Conference on Data Mining. Alexandria: Society for Industrial and Applied Mathematics. 2022. 136–144.
|
| [22] |
Shin K. Mining large dynamic graphs and tensors [Ph.D. Thesis]. Pittsburgh: Carnegie Mellon University, 2019.
|
| [23] |
徐正祥, 王英, 汪洪吉, 等. 基于特征加强的异构网络潜在摘要模型. 计算机科学与探索, 2022, 16(11): 2537-2546. DOI:10.3778/j.issn.1673-9418.2104081 |
| [24] |
Liu YK, Safavi T, Dighe A, et al. Graph summarization methods and applications: A survey. ACM Computing Surveys, 2019, 51(3): 62. |
| [25] |
Ahmadi N, Sand H, Papotti P. Unsupervised matching of data and text. Proceedings of the 38th IEEE International Conference on Data Engineering. Kuala Lumpur: IEEE, 2022. 1058–1070.
|
| [26] |
Cormode G, Muthukrishnan S. An improved data stream summary: The count-min sketch and its applications. Journal of Algorithms, 2005, 55(1): 58-75. DOI:10.1016/j.jalgor.2003.12.001 |
 2023, Vol. 32
2023, Vol. 32


