米波雷达因优良的远距离探测、抗反辐射导弹、反隐身等性能而得到快速发展[1]. 在低仰角目标测高过程中, 强多径效应使米波雷达无法辨别直达波与多径回波. 在复杂阵地环境下, 经复杂阵地反射的回波在幅度与相位上均会发生无规律扰动并伴随多路径现象, 这也是低仰角测高在雷达界引起广泛关注并难以解决的原因[2].
米波雷达低仰角测高一直被研究. 初期的研究成果有单脉冲测角法、复角法和双零点法等方法. 随着阵列超分辨的发展, 出现了特征子空间类算法和最大似然类算法. 但是当直达波与反射回波的入射夹角低于波束宽度的1/4时, 超分辨算法失效[3]. 同时超分辨算法还有使用前提, 一般需要阵地相对平坦, 目标多径回波单个存在且其抵达每个阵元的入射角须认为一致, 目标的直达波与多径回波均需认为来自远场且相关. 若阵地比较复杂, 例如起伏的山川, 复杂阵地会使多径回波产生无规律扰动, 使经典多径模型失配.
近年来, 压缩感知技术[4-7]与稀疏学习[8-12]被进一步研究, 相关知识均被普遍引入到雷达测高中. 因考虑了空域中信号存在的稀疏特性, 不要求提前知晓信号的数目, 稀疏恢复类算法比子空间类算法的测角精度更优. 基于
当阵地复杂时, 合成导向矢量最大似然(synthesized vector maximum likelihood, SVML)算法适用的前提无法得到满足, 出现模型失配问题, 算法测角性能受到影响. 为了解决这个问题, 本文把基于稀疏贝叶斯学习的扰动多径(perturbational multipath sparse Bayesian learning, PSBL)算法[13]高精度估计出的扰动参数引入到SVML算法中, 研究基于扰动模型的SVML算法在复杂阵地的测角性能, 最后给出一系列仿真分析和实测数据分析.
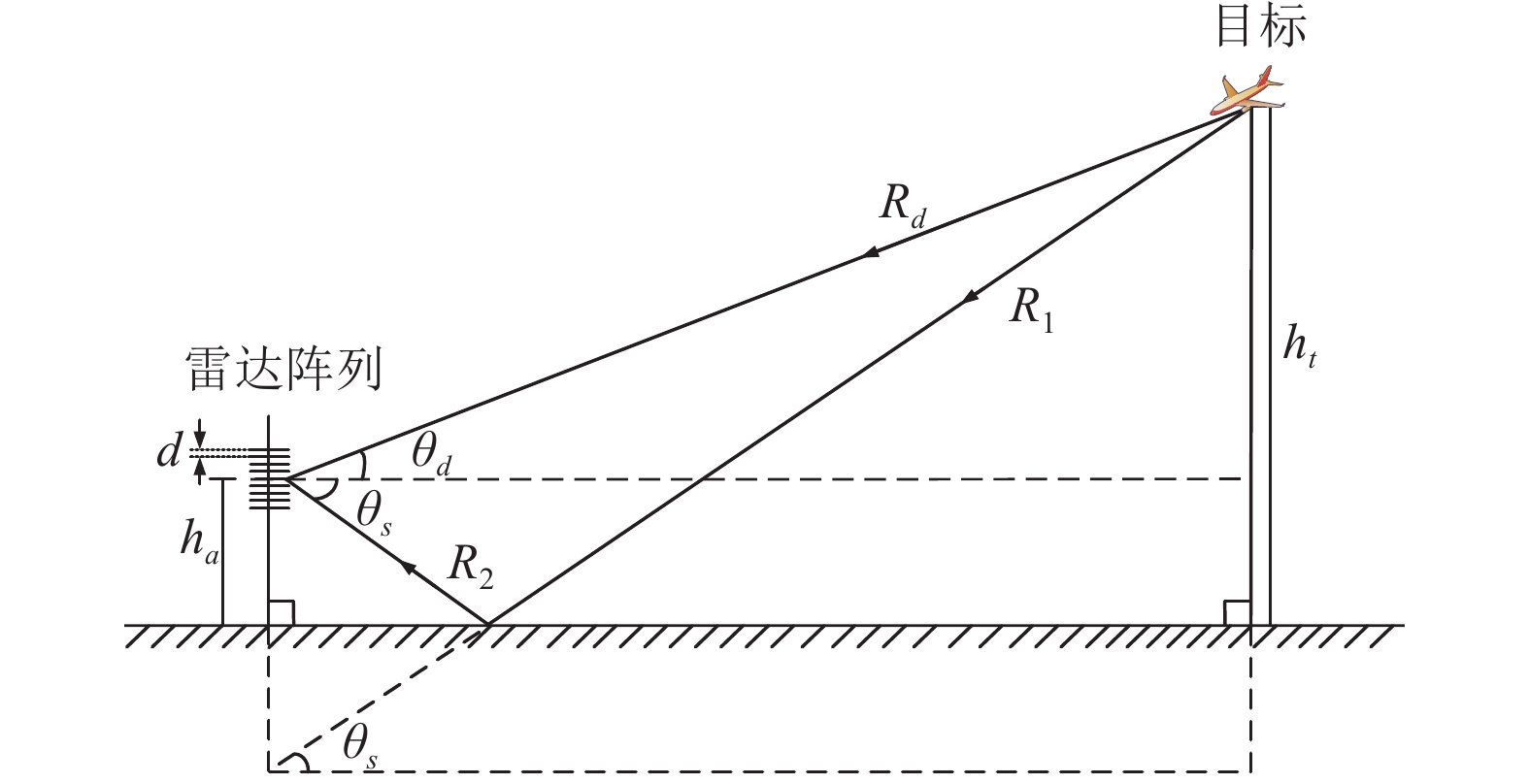
1 扰动多径模型经典多径模型是建立在地面平坦的前提下, 某个目标的回波包括直达波与镜面多径回波, 如图1所示[14]. 假设
阵列接收信号满足:
| X(t)=Xd(t)+Xs(t)+N(t)=[a(θd)+ρe−jκΔRa(θs)]s(t)+N(t) | (1) |
其中,
|
图 1 经典多径模型 |
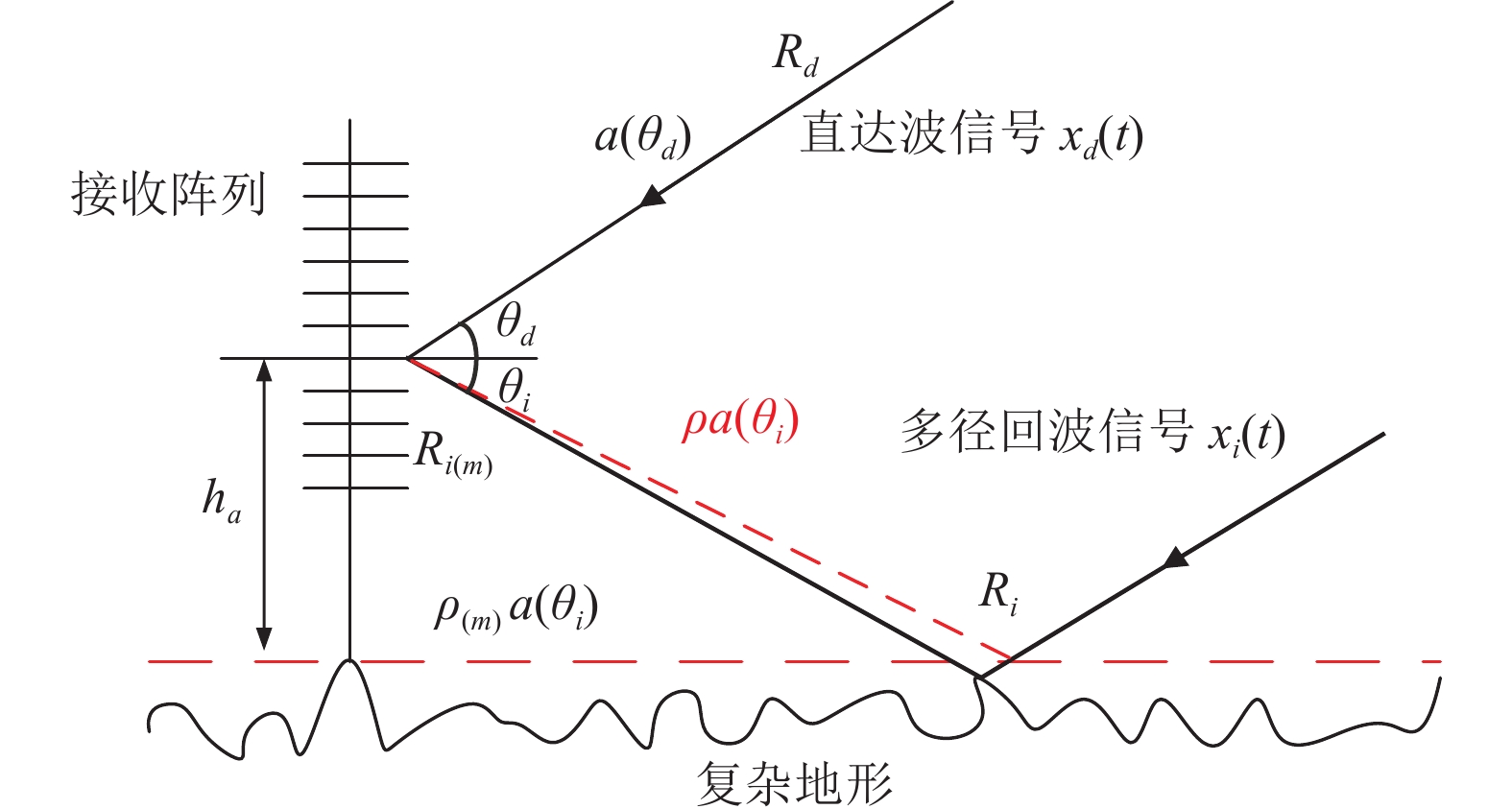
复杂阵地是不平坦的反射面, 会使回波发生不规则反射, 把阵地对多径的扰动用扰动参数表示, 构建的扰动多径模型[13]如图2所示.
|
图 2 扰动多径模型 |
在扰动多径模型中, 每根天线对应的反射区域不同, 可采用复反射系数表示相应反射区域的复杂度. 针对第
| γm=ρ(m)e−j2πΔRm/2πΔRmλλρe−j2πΔR/2πΔRλλ | (2) |
扰动参数是复杂的, 具备时变特点, 其本质为某个未知的变量, 不能仅仅用一个恒定的值表示.
假设线阵获得
| X=(A(θd)+ρe−j2πΔR/−j2πΔRλλΓA(θi))S+N | (3) |
其中,
| Γ=[γ1⋱γM]∈CM×M | (4) |
对于扰动参数
| γm=(1+Δγa)exp(jπ(180∘+Δγp)180∘),m=1,⋯,M | (5) |
其中,
| Δγa∼U(−fγ0,fγ0) | (6) |
| Δγp∼U(−gγ0,gγ0) | (7) |
其中,
SVML算法[15]高精度估计的前提是阵地平坦, 结合雷达、反射面与目标存在的几何关系, 直达波导向矢量
合成导向矢量可表示如下:
| Asyn(θ)=A(θd)+ρe−j2πΔRλA(θs)=A(θ)+ρe−j4πhasin(θ)λA(−θ) | (8) |
合成导向矢量的投影矩阵为:
| PAsyn=Asyn(θ)[AHsyn(θ)Asyn(θ)]−1AHsyn(θ) | (9) |
目标波达方向的最大似然估计值[11]:
| ˆθd=max | (10) |
其中,
稀疏贝叶斯学习[16-18]涉及经验贝叶斯原理与信号稀疏性, 具备熟练求解特殊结构的能力. 在复杂阵地环境下, PSBL算法的构建思想是稀疏贝叶斯学习与先验信息共同建立信号模型, 再结合期望最大化算法(expectation maximization, EM)[19]迭代更新未知参数, 实现目标仰角和高度的高精度估计.
SVML算法适合的是比较平坦的阵地, 而实际阵地大部分是错综复杂的, 会使多径回波发生无规律反射. 当环境是复杂阵地时, SVML算法出现模型失配问题, SVML算法估计出的目标仰角往往与真实目标仰角存在偏差, 无法高精度完成角度估计. 为了解决这个问题, 研究基于扰动模型的SVML算法, 复杂阵地对多径回波造成的扰动程度用扰动参数体现.
针对复杂阵地, SVML算法结合PSBL算法的优势, 实现基于扰动模型的SVML算法研究, 以实现测角性能的提高. 基于扰动模型的SVML算法主要思想是引入反映阵地复杂度的扰动参数来修正复杂阵地对SVML算法造成的影响. 所以, 把PSBL算法高精度估计出的扰动参数引入到SVML算法是基于扰动模型的SVML算法能否应用于复杂阵地的关键.
把PSBL算法估计出的扰动参数引入到SVML算法中, 新的合成导向矢量可写作:
| \begin{split} {A_{{\rm{syn}}}}(\theta ) &= A({\theta _d}) + \rho {{\rm{e}}^{\frac{{ - j2 {\text{π}} \Delta R}}{\lambda }}}\varGamma A({\theta _s}) \\ & = A(\theta ) + \rho {{\rm{e}}^{\frac{{ - j4 {\text{π}} {h_a}\sin (\theta )}}{\lambda }}}\varGamma A( - \theta ) \\ \end{split} | (11) |
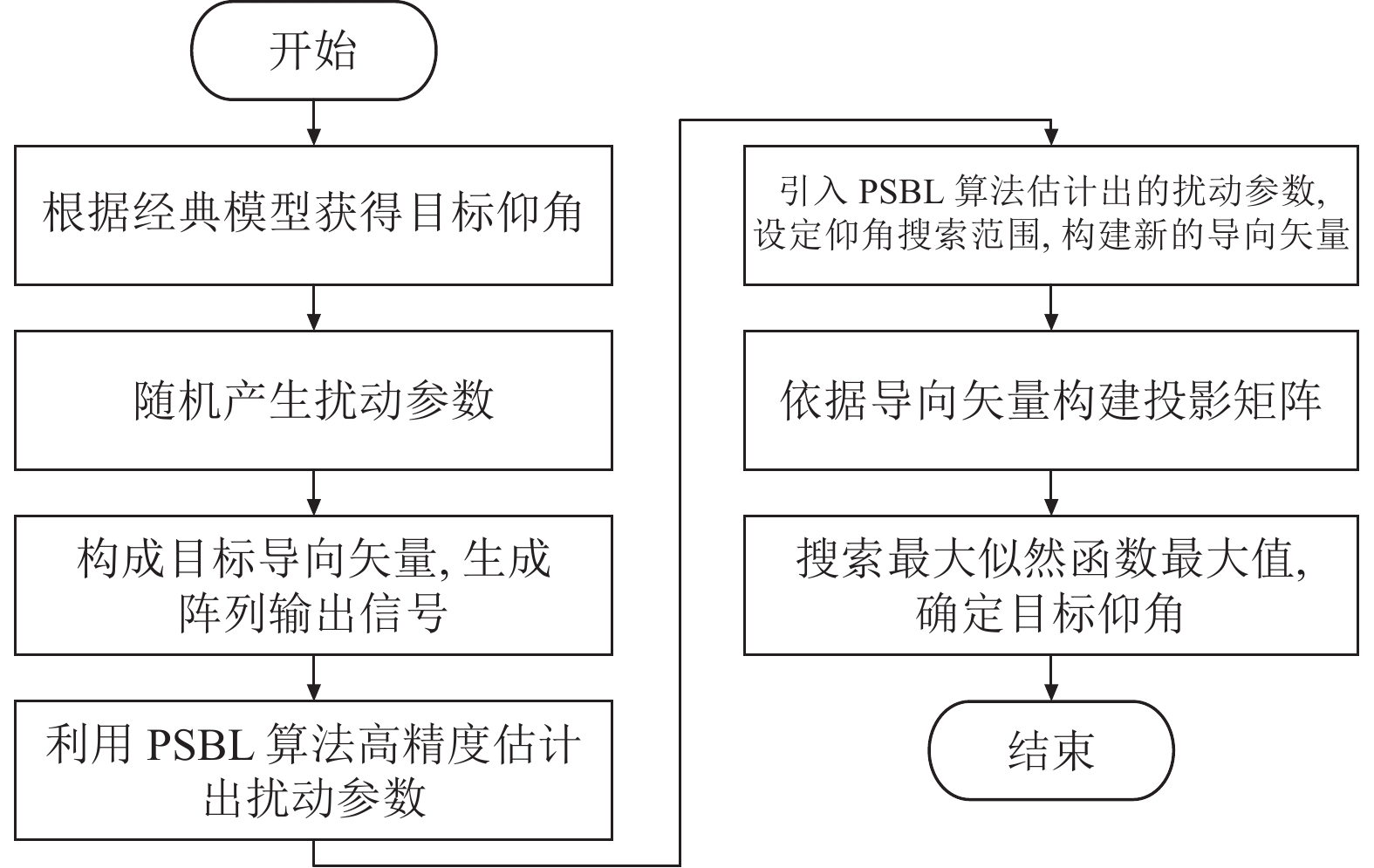
基于扰动模型的SVML算法进行角度估计的具体流程如图3所示. 首先给定目标仰角或目标高度, 目标高度结合经典多径模型的几何关系即可获得目标仰角; 然后借用计算机随机产生扰动参数, 用扰动参数反映多径回波经过复杂阵地受到的扰动. 扰动参数再同目标仰角、反射角等参数共同构建目标导向矢量; 引入PSBL算法高精度估计出的扰动参数, 设定一个目标仰角搜索范围, 重新构建新的导向矢量; 最后利用新的导向矢量构建投影矩阵, 同阵列协方差矩阵共同构成最大似然函数, 再搜索其最大值, 得到目标仰角.
|
图 3 基于扰动模型的SVML算法流程图 |
当SVML算法考虑了反射回波在幅度与相位上的畸变后, 采用扰动多径模型更贴合复杂阵地的情况, 针对基于扰动模型的SVML算法可进行仿真验证.
3 仿真分析 3.1 算法初始值设置PSBL算法迭代过程中的目标函数会逐渐变小, 该现象是EM算法的性质导致的, 同时也表明此算法可以获得目标函数的极值解, 但收敛时输出的解不一定是全局最优. 初始值的设置很关键, 对收敛能否达到全局最优起决定性作用. 若选取不适, 收敛结果会出现局部极值点, 使算法无法实现高精度参数估计. 米波雷达的天线是水平极化时, 相匹配的地面反射系数往往比−1略大, 本文的地面反射系数设定为
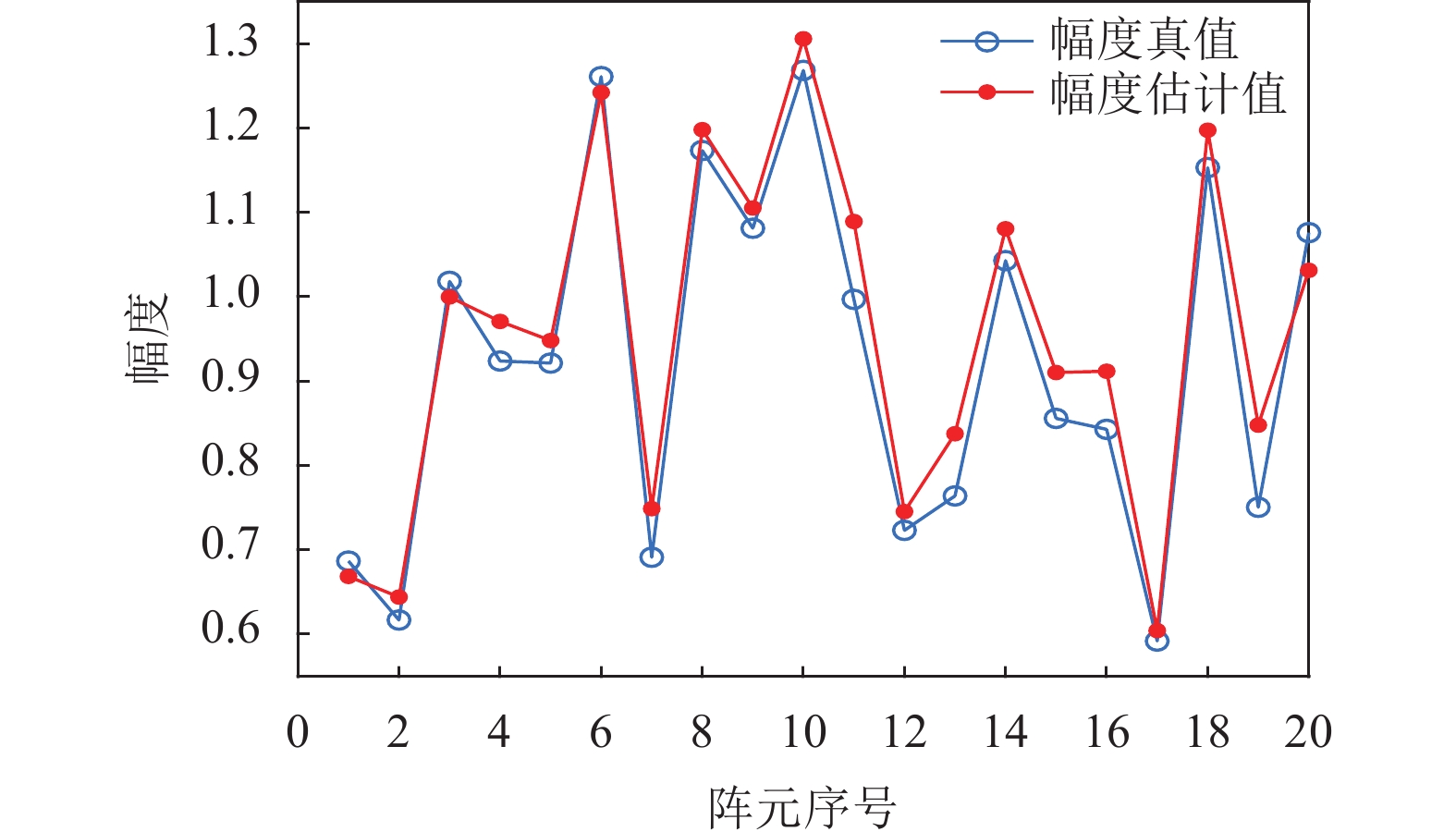
基于扰动多径模型的PSBL算法对复杂阵地情况下的目标参数高精度估计取决于扰动参数的高精度估计. 本文借用计算机仿真分析此算法估计扰动参数的精确程度. 扰动参数的幅度扰动服从
|
图 4 PSBL算法对扰动参数的幅度估计 |
|
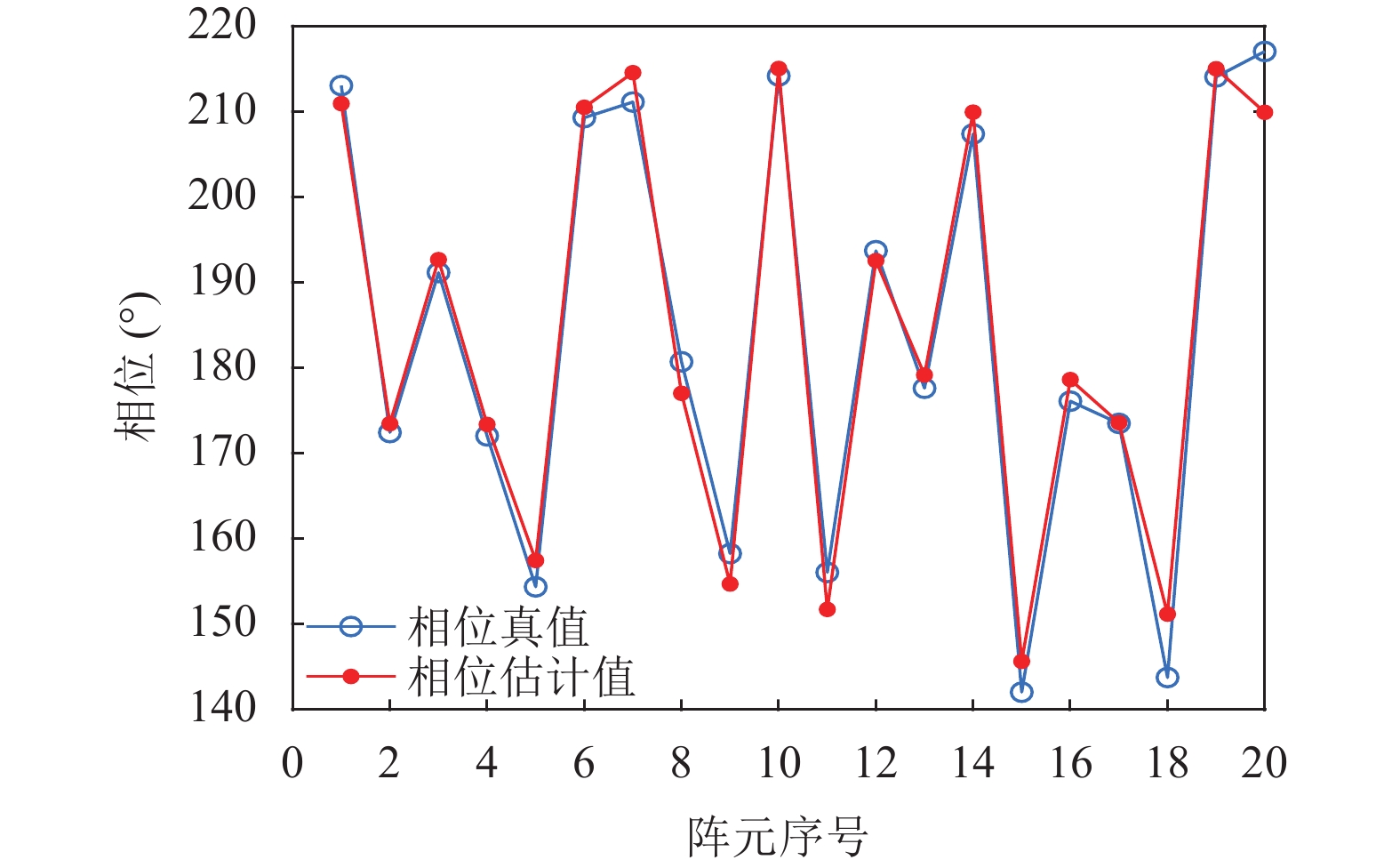
图 5 PSBL算法对扰动参数的相位估计 |
图4是PSBL算法对扰动参数的幅度估计, 图5是PSBL算法对扰动参数的相位估计. 两幅结果图均体现了算法估计值与真值的高度拟合, 关于扰动参数的幅度估计误差不超过0.1, 相位估计误差不超过6°. 对扰动参数幅度与相位上的估计均表明PSBL算法可以估计出体现阵地复杂程度的扰动参数, PSBL算法对其估计的准确性是基于扰动模型的SVML算法准确估计目标波达方向的前提.
3.3 算法估计性能受扰动大小的影响扰动参数
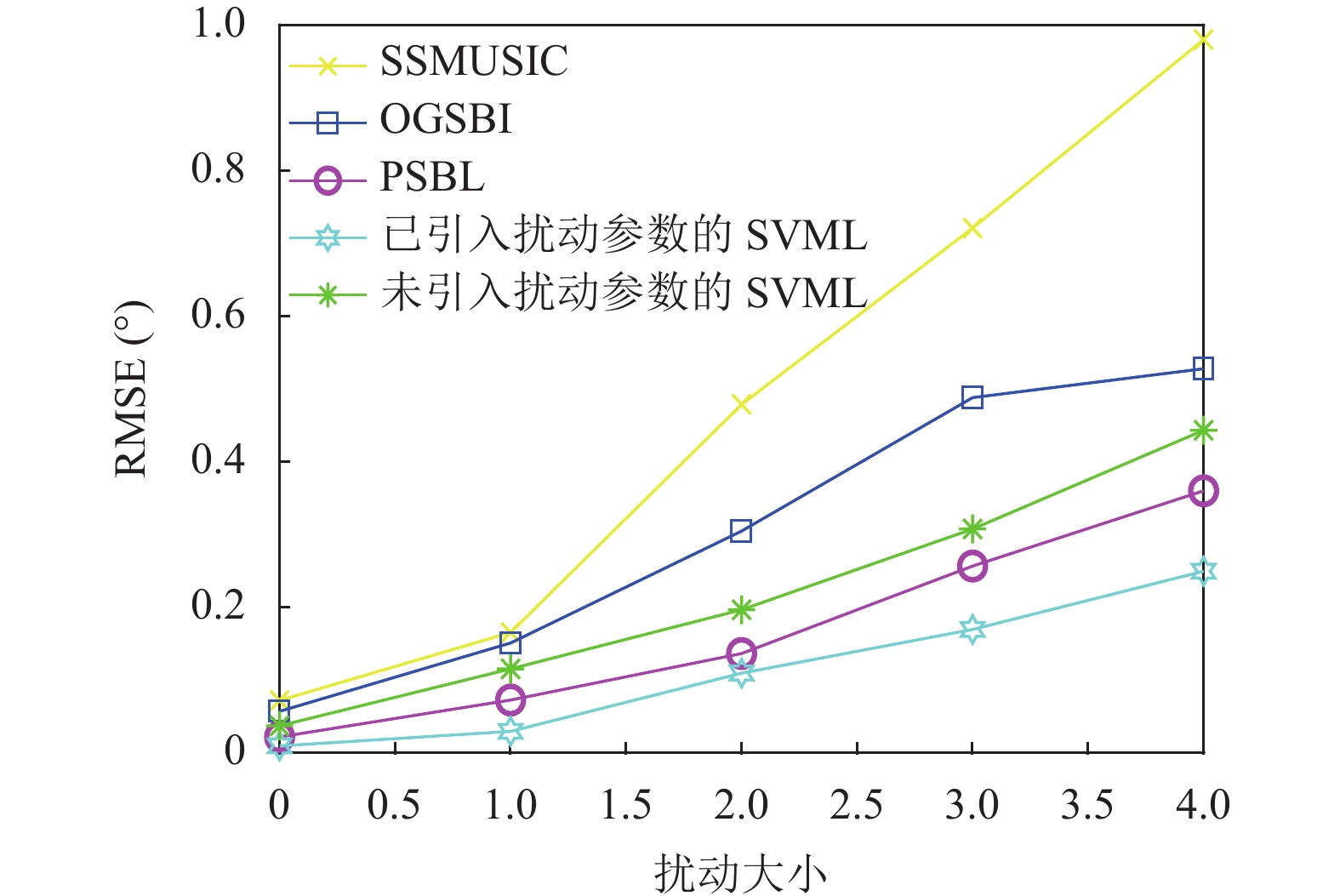
|
图 6 测角精度随扰动大小的变化 |
该组实验仿真了不同算法的RMSE随扰动大小逐渐增加时的变化, 结果表明各算法均随扰动大小的变大而呈现测角估计性能变差的趋势. 图6中已引入扰动参数的SVML算法是基于扰动多径模型, 未引入扰动参数的SVML算法是基于经典多径模型, 结果表明扰动多径模型更加贴合复杂阵地实际反射情况, 扰动参数的引入使SVML算法的测角性能得到了改善.
3.4 算法估计性能受信噪比的影响仿真分析不同算法随信噪比增加时的性能. 设定扰动参数的幅度扰动为
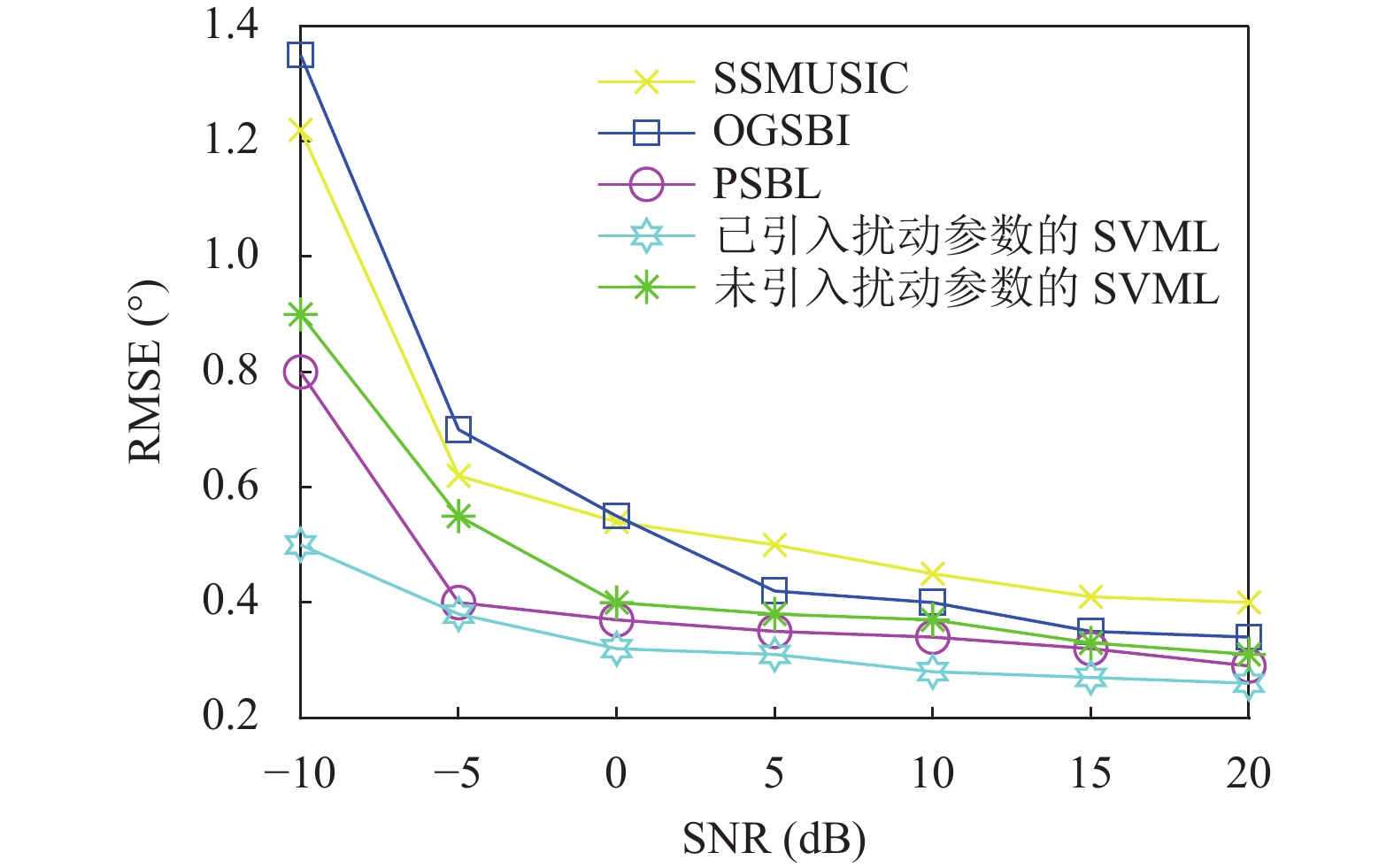
|
图 7 测角精度随信噪比的变化 |
由图7可知各算法均随SNR的变大而呈现测角估计性能变好的趋势. 在相同SNR情况下, 基于扰动模型的SVML算法的测角性能比基于经典多径模型的SVML算法测角性能好, 同时优于其他算法. 当信噪比较低时, 引入扰动参数的SVML算法的测角性能同样很好. 仿真结果表明扰动参数的引入可以改善SVML算法在复杂阵地的测角性能.
3.5 目标角度估计仿真模拟设计一个目标向远离雷达的方向飞去, 同时保持目标与地面的垂直距离恒定不变, 选定目标在距离地面12 km的高空. 整个过程中, 雷达与目标的直线距离从60 km变化到280 km. 同时模拟一个复杂阵地, 扰动大小是4, 扰动参数的幅度扰动为
从目标角度估计结果图8可以看出, 以上各算法在高仰角范围内的目标角度估计性能均比在低仰角范围内的目标角度估计性能好. 当对低仰角目标进行估计时, 从图8(a)、图8(b)两种经典测高算法的结果图可知两算法对角度的估计均明显偏离真实值, 误差非常大. 基于经典多径模型的SVML算法因为复杂阵地对多径回波的影响, 也无法完成高精度测角. PSBL算法和基于扰动模型的SVML算法考虑了体现阵地复杂性的扰动参数, 角度估计的曲线与目标真实角度曲线的拟合度很高, 误差较小. 仿真结果表明, 扰动参数的引入使SVML算法得到了改进, 改善了目标低仰角估计性能, 改进后的算法更适合于复杂阵地的低仰角测高.
4 实测数据分析使用某型号米波雷达的实测数据研究本文提出的算法. 24阵元等距形成此雷达阵列, 且雷达处于复杂阵地, 会使多径回波产生不规则反射, 符合本文算法的研究设定. 对回波数据作一系列处理后可知一条航线的航迹图, 如图9所示.
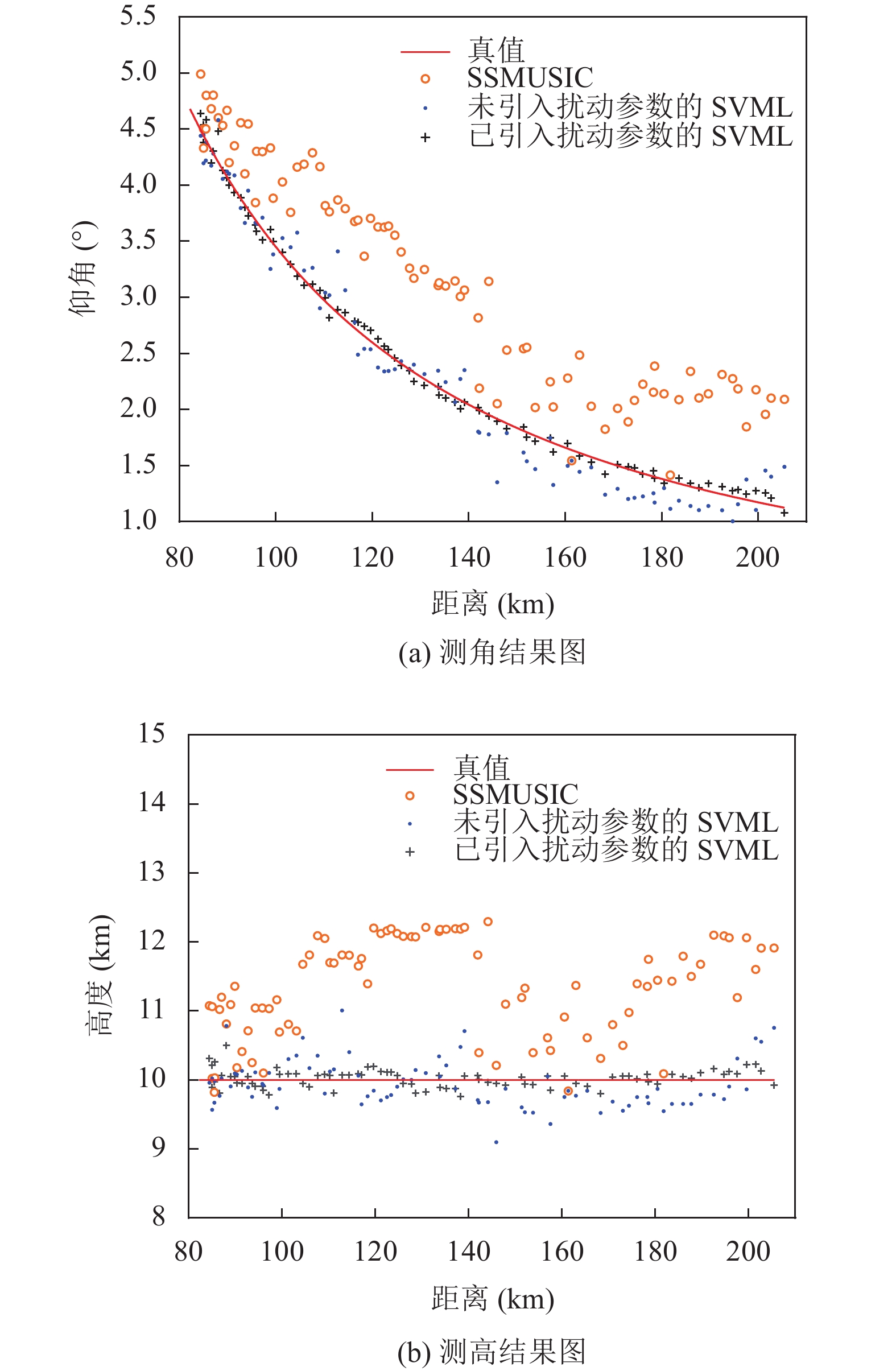
分别用SSMUSIC算法, 未引入扰动参数的SVML算法和本文提出的算法作参数估计, 结果如图10所示.
图10(a)为对实测数据进行测角处理的结果图, 图10(b)为对实测数据进行测高处理的结果图. 两张结果图可明显看出各个算法对角度和高度进行估计时与真值的误差程度, 其中经过基于扰动模型的SVML算法处理后的结果误差更小, 更稳定. 由此可知, 基于扰动模型的SVML算法相比未加入扰动参数的SVML算法明显改进了性能, 更适合复杂阵地的测角和测高.

|
图 8 目标角度估计结果图 |
5 结论
本文依次对经典多径模型、扰动多径模型和SVML算法的原理作简单介绍, 然后提出了基于扰动模型的SVML算法, 并进行了一系列仿真分析和实测数据分析. PSBL算法把多径回波经过复杂阵地在幅度和相位上的畸变建模为扰动参数, 用扰动参数体现阵地的复杂度. 通过仿真表明PSBL算法可以高精度的估计出扰动参数. SVML算法在低仰角完成高精度估计的前提是阵地比较平缓, 在复杂阵地情况下会出现模型失配. 针对复杂阵地, 把PSBL算法高精度估计出的扰动参数引入到SVML算法中, 研究基于扰动模型的SVML算法的测角性能, 将该算法与一些经典的测角算法和未做改进前的SVML算法做比较. 通过设计的几组实验仿真结果和实测数据分析可知, 基于扰动模型的SVML算法比未引入扰动参数的SVML算法的测角性能更好, 更适合复杂阵地的测角.
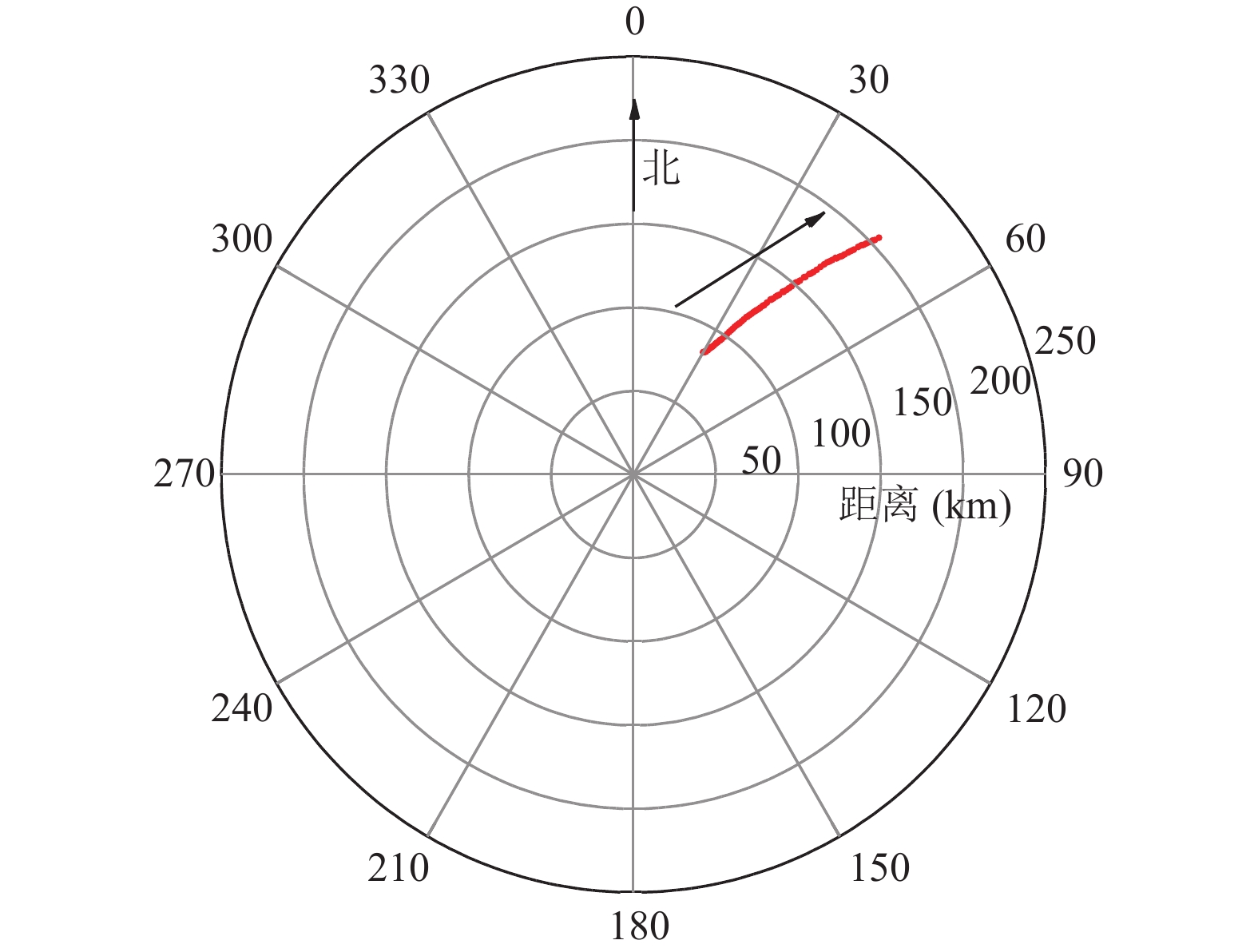
|
图 9 航迹图 |
|
图 10 实测数据处理结果图 |
| [1] |
Kuschel H. VHF/UHF radar. Part 1: Characteristics. Electronics & Communication Engineering Journal, 2002, 14(2): 61-72. DOI:10.1049/ecej:20020203 |
| [2] |
Zheng YS, Chen BX. Altitude measurement of low-angle target in complex terrain for very high-frequency radar. IET Radar, Sonar & Navigation, 2015, 9(8): 967-973. DOI:10.1049/iet-rsn.2014.0544 |
| [3] |
Lo T, Litva J. Low-angle tracking using a multifrequency sampled aperture radar. IEEE Transactions on Aerospace and Electronic Systems, 1991, 27(5): 797-805. DOI:10.1109/7.97325 |
| [4] |
窦慧晶, 梁霄, 张文倩. 基于压缩感知理论的二维DOA估计. 北京工业大学学报, 2021, 47(3): 231-238. DOI:10.11936/bjutxb2019100002 |
| [5] |
Wang GB, Zhao PY, Wang LM, et al. A two-dimensional DOA estimation method based on virtual extension of sparse array. Journal of Electrical and Computer Engineering, 2021, 2021: 1654836. DOI:10.1155/2021/1654836 |
| [6] |
Liu F. DOA estimation of underwater acoustic targets based on Bayesian compressed sensing. Journal of Physics: Conference Series, 2022, 2173: 012047. DOI:10.1088/1742-6596/2173/1/012047 |
| [7] |
Goto K, Maruta K, Ahn CJ. Compressed sensing based low complexity 2D-DOA estimation by separation and pair-matching approach. IEICE Communications Express, 2020, 9(6): 224-229. DOI:10.1587/comex.2020XBL0015 |
| [8] |
章涛, 张亚娟, 孙刚, 等. 稀疏贝叶斯字典学习空时机动目标参数估计算法. 电子与信息学报, 2022, 44(8): 2884-2892. DOI:10.11999/JEIT210567 |
| [9] |
王琦森, 余华, 李杰, 等. 基于稀疏贝叶斯学习的空间紧邻信号DOA估计算法. 电子与信息学报, 2021, 43(3): 708-716. DOI:10.11999/JEIT200656 |
| [10] |
郭英, 东润泽, 张坤峰, 等. 基于稀疏贝叶斯学习的多跳频信号DOA估计方法. 电子与信息学报, 2019, 41(3): 516-522. DOI:10.11999/JEIT180435 |
| [11] |
Chen P, Cao ZX, Chen ZM, et al. Off-grid DOA estimation using sparse Bayesian learning in MIMO radar with unknown mutual coupling. IEEE Transactions on Signal Processing, 2019, 67(1): 208-220. DOI:10.1109/TSP.2018.2881663 |
| [12] |
Yu DK, Wang X, Fang WW, et al. DOA estimation based on root sparse Bayesian learning under gain and phase error. Journal of Communications and Information Networks, 2022, 7(2): 202-213. DOI:10.23919/JCIN.2022.9815203 |
| [13] |
郑轶松. 米波阵列雷达低仰角测高若干问题研究[博士学位论文]. 西安: 西安电子科技大学, 2017.
|
| [14] |
杨雪亚. 米波雷达阵列超分辨和测高方法研究[博士学位论文]. 西安: 西安电子科技大学, 2011.
|
| [15] |
Zhu W, Chen BX. Altitude measurement based on terrain matching in VHF array radar. Circuits, Systems, and Signal Processing, 2013, 32(2): 647-662. DOI:10.1007/s00034-012-9472-4 |
| [16] |
Gerstoft P, Mecklenbräuker CF, Nannuru S, et al. DOA estimation in heteroscedastic noise with sparse Bayesian learning. Proceedings of the 2020 International Applied Computational Electromagnetics Society Symposium. Monterey: IEEE, 2020. 1–2.
|
| [17] |
Liu Q, Wang XP, Huang MX, et al. DOA and range estimation for FDA-MIMO radar with sparse Bayesian learning. Remote Sensing, 2021, 13(13): 2553. DOI:10.3390/rs13132553 |
| [18] |
Liu Q, Wang XP, Wan LT, et al. An accurate sparse recovery algorithm for range-angle localization of targets via double-pulse FDA-MIMO radar. Wireless Communications and Mobile Computing, 2020, 2020: 6698446. DOI:10.1155/2020/6698446 |
| [19] |
Moon TK. The expectation-maximization algorithm. IEEE Signal Processing Magazine, 1996, 13(6): 47-60. DOI:10.1109/79.543975 |
 2023, Vol. 32
2023, Vol. 32



