随着数字化信息技术在军事中的广泛应用, 电子战成为一种新型作战方式. 其中通过采用各种探测设备实现对通信目标的识别与定位是电子战中的重要一环. 常见的通信辐射源无源定位方式有采用到达时间差(time difference of arrival, TDOA)^[1]、到达时间(time of arrival, TOA)、到达角度(angle of arrival, AOA)^[2]、到达频率差(frequence difference of arrival, FDOA)^[3]等模型. 其中到达时间差定位误差较小, 且不需要和目标通信辐射源建立协作关系, 同时联合不同体制的测量方式在一定程度上增加了定位信息的可靠性, 因而受到了学者们的格外关注. 本文就时频差模型联合定位进行讨论.

时频差模型的测量参数关于通信辐射源具有高度非线性^{[4, 5]}. 对于时频差模型的解算方法主要分解析法、搜索法以及迭代法3种. 解析法中, 文献[6]针对运动目标的定位, 提出基于时频差模型的两步加权最小二乘方法(two-stage weighted least squares, TSWLS), 当测量噪声较小时, 该闭式解方法的定位误差较小且靠近克拉美罗下限(Cramer-Rao lower bound, CRLB). 文献[7]利用时频差方程的伪线性特性, 将定位方程转变成约束加权最小二乘问题, 再采用拉格朗日乘子法求解完成定位. 定位结果优于两步加权最小二乘法定位方法. 解析法的计算复杂度低且具有显式解, 但当测量噪声较高时定位误差较大, 同时该类方法需要推导伪线性方程, 普适性不高. 搜索法中, 文献[8]针对迭代法定位需要初始解且复杂度高的不足, 提出一种混合优化算法, 将加权最小二乘与萤火虫算法结合起来, 其算法提高了定位精度同时减少了计算量. 但该文仅讨论二维的情况. 搜索法在解空间中寻优性能较强, 可以精确地完成对目标模型参数的优化和估计, 但有陷入局部最优的风险. 迭代法中, 文献[9]针对两阶段加权最小二乘法适应噪声能力较弱的问题, 提出一种利用泰勒级数展开的误差修正方法, 以此减少两步法中第2步将误差进行平方运算带来的影响. 文献[10]针对常规算法适应测量噪声能力弱的问题, 先将无源定位问题处理成二次规划问题, 然后应用拉格朗日乘子法进行解算完成初步定位, 基于位置估计应用泰勒级数展开再进一步完成参数优化. 迭代法的抗噪声性能较好, 但对初始值的选择较为敏感, 初始值误差较大时迭代结果不容易收敛.

综合上述文献可知, 针对复杂环境下运动通信辐射源的无源定位, 闭式解算法计算复杂度较低, 同时考虑遗传算法内部逻辑清晰, 搜索效率高、优化非线性参数能力强. 本文提出解析法与智能优化算法相结合的时频差混合定位方法. 同时联合多组时频差数据进行递推, 保证定位结果的可靠性. 仿真实验表明, 当观测数据中包含的噪声较大时, 本文所提的混合时频差定位方法的定位均方根误差更小.

1 多站TDOA/FDOA定位模型

本文考虑在三维空间中利用M个静态接收站对运动的通信辐射源完成定位. 本文假设目标通信辐射源真实的位置坐标和速度分别为 $ {u^o} = {[{x^o}, {y^o}, {{\textit{z}}^o}]^{\rm{T}}} $ 、 $\mathop {{\dot u^o}} = {[\mathop {{\dot x^o}} , \mathop {{\dot y^o}} , \mathop {{{\dot {\textit{z}}}^o}} ]^{\rm{T}}}$ . 接收站的位置 $ {s_i} = {[{x_i}, {y_i}, {{\textit{z}}_i}]^{\rm{T}}} $ 已知, 其中 $ i = 1, 2, \cdots, M $ . 设第1个接收站 $ {s_1} $ 为主站, 其余接收站为辅站. 在TDOA和FDOA测量噪声的扰动下, 本文估计得到的目标辐射源的位置和速度为 $ u = {[x, y, {\textit{z}}]^{\rm{T}}} $ 、 $\mathop {\dot u} = {[\mathop {\dot x} , \mathop {\dot y} , \mathop {\dot {\textit{z}}} ]^{\rm{T}}}$ . 本算法主要讨论接收站数量大于4的超定情形^{[11, 12]}. 第i个接收站到目标辐射源的距离可以表示为:

$ r_i^o = \left\| {{u^o} - {s_i}} \right\| = \sqrt {{{\left( {{u^o} - {s_i}} \right)}^{\rm{T}}}\left( {{u^o} - {s_i}} \right)} $

(1)

目标辐射源到主辅站的真实时差为 $ t_{i1}^o $ 、信号的传播速度为c, 则接收站间关于目标辐射源的时差方程为:

$ r_{i1}^o = ct_{i1}^o = r_i^o - r_1^o $

(2)

其中, $ r_{i1}^o $ 是站点间真实距离差, $ i = 2, 3, \cdots, M $ . 将式(2)变形为 $ r_{i1}^o + r_1^o = r_i^o $ 同时联立式(1)进行平方处理, 得到具体的TDOA方程组. 不失一般性地, M个接收站得到M–1个时差方程:

$ r{_{i1}^{o2}} - {s_i}^{\rm{T}}{s_i} + {s_1}^{\rm{T}}{s_1} = 2r_{i1}^or_1^o - 2{\left( {{s_i} - {s_1}} \right)^{\rm{T}}}{u^o} $

(3)

其中, 多条曲线相交且交点处就是目标位置.

时差方程只能用于估计辐射源的位置, 对于速度的估计需要依赖于频差方程^[13]. 因此本文对式(1)求时间的导数得到接收站与目标通信辐射源之间真实距离变化率和目标辐射源位置参数的关系:

$ \mathop {\dot r_i^o} = \frac{{{{(\mathop {{\dot u^o}} - \mathop {{\dot s_i}} )}^{\rm{T}}}({u^o} - {s_i})}}{{r_i^o}} $

(4)

则接收站间关于目标辐射源的频差方程为:

$ \mathop {\dot r_{i1}^o} = c\mathop {\dot t_{i1}^o} = \mathop {\dot r_i^o} - \mathop {\dot r_1^o} $

(5)

为了完成对目标辐射源速度估计, 对式(3)求时间的导数得到对应的FDOA方程组^[14]:

$ \begin{split} & 2(\mathop {\dot r_{i1}^o} r_{i1}^o + \mathop {\dot r_{i1}^o} r_1^o + r_{i1}^o\mathop {\dot r_1^o} ) = \\ &\qquad 2(\mathop {\dot s_i^{\rm{T}}} - \mathop {\dot s_1^{\rm{T}}} {s_1} - {(\mathop {{\dot s_i}} - \mathop {{\dot s_1}} )^{\rm{T}}}{u^o} - {({s_i} - {s_1})^{\rm{T}}}\mathop {{\dot u^o}} ) \end{split}$

(6)

其中, $\mathop {\dot r_{i1}^o}$ 是站点间的真实的距离差变化率, $ i = 2, 3, \cdots, M $ . 基于方程组的高度非线性, 从时频差模型中求解目标辐射源位置、速度估计并非易事^[15].

实际中仅能获取到时频差数据的观测值, 考虑TDOA和FDOA的观测值采用加性噪声方式进行表述. 距离差向量 $r = {[{r_{21}}, {r_{31}}, \cdots, {r_{M1}}]^{\rm{T}}}$ 、距离差变化率向量 $\mathop {\dot r} = {[\mathop {{\dot r_{21}}} , \mathop {{\dot r_{31}}} , \cdots, \mathop {{\dot r_{M1}}} ]^{\rm{T}}}$ 的测量值可以表示为: $ r = {r^o} + c\Delta t = {r^o} + {n_t} $ 、 $\mathop {\dot r} = \mathop {{\dot r^o}} + c\Delta \mathop {\dot t} = \mathop {{\dot r^o}} + {n_f}$ . 其中 $ c\Delta t $ 和 $ c\Delta \mathop t\limits^. $ 是时频差的测量噪声, 它们服从0均值, 且方差为 $ \sigma _s^2 $ 的高斯分布^{[16, 17]}, 协方差矩阵分别为 $ {Q_t} $ 和 $ {Q_f} $ .

2 观测数据的分析和预处理

非合作的通信辐射源进入到目标区域进行无源定位时, 多径时延以及设备时延等产生的观测误差会对通信辐射源的定位精度产生严重干扰. 本节先对噪声进行分析建模, 同时考虑如何有效利用已知的时频差数据去分析后续观测数据, 从而对未知辐射源定位过程中的测量噪声进行预处理校正.

2.1 测量噪声的分析建模

本文假定测量噪声为均值为0、方差在某一个有界集合的高斯噪声. 时频差噪声分别记为 $ {n_t} $ 和 $ {n_f} $ , 则时频差的测量值可以表示为: $ r = {r^o} + {n_t} $ 、 $\mathop {\dot r} = \mathop {{\dot r^o}} + {n_f}$ . 在保持接收站布局形式不变的情况下, 用已知的通信辐射源进行不同位置的运动来获取大量观测数据. $ r $ 、 $\mathop {\dot r}$ 是接收站的观测数据, $ {r^o} $ 、 $\mathop {{\dot r^o}}$ 已知, $ {n_t} = r - {r^o} $ 、 ${n_f} = \mathop {\dot r} - \mathop {{\dot r^o}}$ , 通过已知的大量观测数据就可以预先分离出噪声数据, 并对噪声模型进行估计分析. 本文使用最大似然(ML)对噪声的参数进行估计来构建出具体噪声分布模型. 设有N组噪声数据已采集, 建立似然方程:

$ L\left( {\mu , {\sigma ^2}} \right) = \prod\nolimits_{i = 1}^N {\frac{N}{{\sqrt {2{\text{π}} } \sigma }}} {{\rm{e}}^{ - \frac{{{{\left( {{n_i} - \mu } \right)}^2}}}{{2{\sigma ^2}}}}} $

(7)

方程求解估计出高斯噪声模型的均值和方差分别为:

$ \left\{ \begin{gathered} \mu = \overline x = \frac{1}{N}\sum\nolimits_{i = 1}^N {{n_i}} \\ {\sigma ^2} = \frac{1}{N}\sum\nolimits_{i = 1}^N {{{\left( {{n_i} - \overline x } \right)}^2}} \\ \end{gathered} \right. $

(8)

2.2 时频差序列的筛选

分析噪声分布的本身特性建立先验数据与实测数据的关系, 当对未知的通信辐射源进行定位时对采集的时频差序列进行校正, 保证实测数据的可靠性. 简单的表示为:

$ {r_{{\rm{Fin}}}} = {r^o} + {r_n} - \Delta {r_n} $

(9)

其中, $ \Delta {r_n} $ 通过噪声模型得到. $ {r_n} $ 为实测加性噪声, ${r_{{\rm{Fin}}}}$ 为筛选后的时频差数据. 为保证无源定位过程中时频差数据的稳定性, 本文采集多组时频差序列进行处理. 已知估计的测量噪声服从均值为 $\; \mu $ 、标准差为 $ \sigma $ 的高斯分布. 本文考虑将包含噪声的时频差测量值进行筛选, 尽可能地保证时频差数据准确、有效.

基于噪声的概率密度函数对时频差进行处理. 鉴于时频差噪声 $ {n_t} $ 和 $ {n_f} $ 位于区间 $ [\mu - 2\sigma , \mu + 2\sigma ] $ 的概率为95.4%. 本文则假定无源定位过程中时频差测量噪声全部位于这个区间, 通过小概率的偏差换取观测值的可靠性, 因此在多组观测值的基础上尽可能剔除含有大噪声的观测数据. 最终选取地J组时频差有效序列可以表示为:

$ {r_i} = {[{r_{i, 21}}, {r_{i, 31}}, \cdots, {r_{i, M1}}]^{\rm{T}}}, \; i = 1, 2, \cdots, J $

(10)

$ \dot {{r_i}} = {[{\dot r _{i, 21}}, {\dot r _{i, 31}}, \cdots, {\dot r _{i, M1}}]^{\rm{T}}}, \; i = 1, 2, \cdots, J $

(11)

从噪声的统计特性出发进行数据分析是把相互独立的先验数据与实测数据结合起来的一种思路.

3 加权最小二乘联合遗传算法的滑动递推定位方法 3.1 加权最小二乘参数估计

首先定义待测变量 ${\theta ^o} = {[{u^o}^{\rm{T}}, r_1^o, \mathop {{\dot u^{o{\rm{T}}}}} , \mathop {\dot r_1^o} ]^{\rm{T}}}$ , 它包含未知通信辐射源的位置 ${u^o}^{\rm{T}}$ 、速度 $\mathop {{\dot u^{o{\rm{T}}}}}$ 、到主站距离 $ r_1^o $ 以及到主站的距离变化率 $\mathop {\dot r_1^o}$ 这4个参数. 假设 ${u^o}^{\rm{T}}$ 、 $ r_1^o $ 、 $\mathop {{\dot u^{o{\rm{T}}}}}$ 、 $\mathop {\dot r_1^o}$ 是不相关的, 这样就可以将式(3)和式(5)的非线性方程伪线性化^[18]. 把式(3)和式(5)中的真实值用观测值代替后联立得到定位模型的误差向量:

$ {\lambda _t} = h - G\theta $

(12)

其中,

$ h = \left[ {\begin{array}{*{20}{c}} {r_{21}^2 - s_2^{\rm {T}}{s_2} + s_1^{\rm {T}}{s_1}}\\ {r_{31}^2 - s_3^{\rm {T}}{s_3} + s_1^{\rm {T}}{s_1}}\\ \vdots \\ {r_{M1}^2 - s_M^{\rm {T}}{s_M} + s_1^{\rm {T}}{s_1}}\\ {2( {{\dot r_{21}}} {r_{21}} - {\dot s_2^{\rm {T}}} {s_2} + {\dot s_1^{\rm {T}}} {s_1})}\\ {2( {{\dot r_{31}}} {r_{31}} - {\dot s_3^{\rm {T}}} {s_3} + {\dot s_1^{\rm {T}}} {s_1})}\\ { \vdots }\\ {2( {{\dot r_{M1}}} {r_{M1}} - {\dot s_M^{\rm {T}}} {s_M} + {\dot s_1^{\rm {T}}} {s_1})} \end{array}} \right] $

(13)

$ G = \left[ {\begin{array}{*{20}{c}} {{{({s_2} - {s_1})}^{\rm {T}}}}&{{r_{21}}}&{{0^{\rm {T}}}}&{{0^{}}} \\ {{{({s_3} - {s_1})}^{\rm {T}}}}&{{r_{31}}}&{{0^{\rm {T}}}}&{{0^{}}} \\ \vdots & \vdots & \vdots & \vdots \\ {{{({s_M} - {s_1})}^{\rm {T}}}}&{{r_{M1}}}&{{0^{\rm {T}}}}&{{0^{}}} \\ {{{( {{\dot s_2}} - {{\dot s_1}} )}^{\rm {T}}}}&{ {{\dot r_{21}}} }&{{{({s_2} - {s_1})}^{\rm {T}}}}&{ {{r_{21}}} } \\ {{{( {{\dot s_3}} - {{\dot s_1}} )}^{\rm {T}}}}&{ {{\dot r_{31}}} }&{{{({s_3} {} - {s_1})}^{\rm {T}}}}&{ {{r_{31}}} } \\ { \vdots }&{ \vdots }&{ \vdots }&{ \vdots } \\ {{{( {{\dot s_M}} - {{\dot s_1}} )}^{\rm {T}}}}&{ {{\dot r_{M1}}} }&{{{({s_M} - {s_1})}^{\rm {T}}}}&{ {{r_{M1}}} } \end{array}} \right] $

(14)

其中, ${0^{\rm{T}}}$ 是 $ 1 \times 3 $ 的行向量. 综合由式(12)得到 $ {\theta ^o} $ 的最小二乘估计为:

$ \theta = {[{u^{\rm {T}}}, {r_1}, \mathop {{\dot u^{\rm {T}}}} , \mathop {{\dot r_1}} ]^{\rm {T}}} = {({G^{\rm {T}}}WG)^{ - 1}}G^{\rm{T}}Wh $

(15)

其中, 加权矩阵定义为:

$ W = {B^{ - {\rm{T}}}}{Q^{ - 1}}{B^{ - 1}} $

(16)

其中, $ B = \left[ {\begin{array}{*{20}{c}} {{B_t}}&O \\ {{B_f}}&{{B_t}} \end{array}} \right] $ , ${B_t} = 2dia{{g}}\{ r_2^o, r_3^o, \cdots, r_M^o\}$ 是关于接收站间距离的对角矩阵, ${B_f} = 2diag\{ \mathop {\dot r_2^o}, \mathop {\dot r_3^o} , \cdots, \mathop {\dot r_M^o} \}$ 是距离变化率的对角矩阵, $ Q = \left[ {\begin{array}{*{20}{c}} {{Q_t}}&{{O_{(M - 1)(M - 1)}}} \\ {{O_{(M - 1)(M - 1)}}}&{{Q_f}} \end{array}} \right] $ 是关于时频差数据的协方差矩阵. 在采用加权最小二乘法处理过程中, 鉴于加权矩阵 $ W $ 与通信辐射源到各接收站的距离和距离变化率有直接关系^[19], 但 $ {r_i} $ 和 $\mathop {{\dot r_i}}$ 是未知的, 因此本文先使用其协方差矩阵的逆矩阵 $ {Q^{ - 1}} $ 代替 $ W $ 进行式(15)预先的求解, 如式(17)、式(18)所示:

$ W = {Q^{ - 1}} $

(17)

$ \theta = {({G^{\rm {T}}}{Q^{ - 1}}G)^{ - 1}}G^{\rm{T}}{Q^{ - 1}}h $

(18)

求解得到目标通信辐射源的位置和速度, 利用此次估计的解更新式(16)中加权矩阵 $ W $ 的参数, 再次对式(15)方程进行求解, 完成对通信辐射源位置估计. 本文考虑通信辐射源的速度估计与位置参数密切相关, 在加权最小二乘估计求解过程中, 联立时差、频差模型可以利用更多的测量参数, 在一定程度上提高了初始解的可靠性.

3.2 遗传算法的参数优化

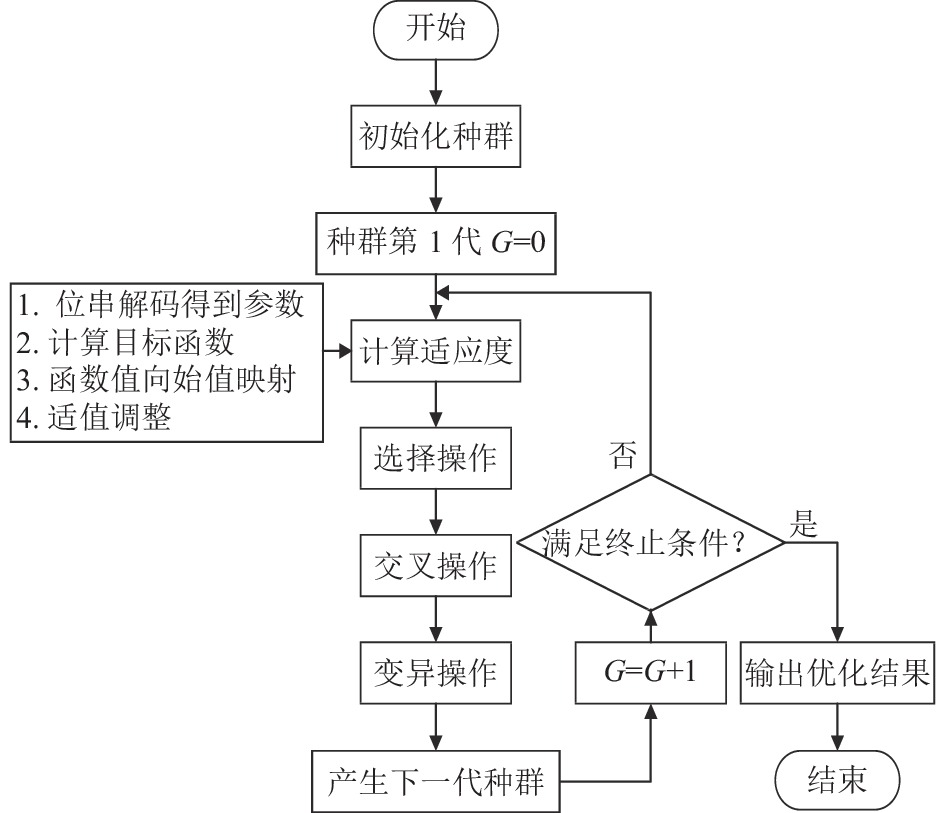
遗传算法是一种全局寻优的智能算法, 本质是模拟自然进化来实现对最优解的寻找. 如图1所示为算法流程框图, 其核心思想就是通过对种群进行初始化、编码、选择、交叉、变异等操作, 让适应度函数有向优化. 在种群进化的过程中, 所有个体逐步向最优的个体靠近并逐渐达到统一, 即找到最优解. 遗传算法内部能够自我迭代, 从而优胜劣汰保留最优解.

本文在第1步中基于时频差参数利用加权最小二乘法完成了通信辐射源的粗定位, 其结果可提供遗传算法有限的搜索区域完成参数优化, 实现更高的定位精度. 针对种群的初始化, 选择以通信辐射源位置的初步估计 $ {u^{\rm{T}}} $ 为中心随机生成. 假设种群大小为 $ n $ , 解空间的搜索半径为 $ R $ . 个体的初始化位置可以表示为:

$ P = {u^{\rm{T}}} + rand(1, 3)(R) $

(19)

其中, ${u^{\rm{T}}}$ 表示遗传算法的搜索中心, 让初始种群P的个体尽可能地靠近搜索中心. 针对解空间的编码, 本文采用二进制编码. 假设变量 $ X $ 的定义域为 $ [a, b] $ , 每一个区间都可以用一个二进制串 $ \langle {s_{l - 1}}, {s_{l - 2}}, \cdots, {s_0}\rangle $ 进行表示, 且直接映射到解空间. 其中 $ l $ 代表可以映射到解空间的二进制串的长度, 实际精度为 $ \dfrac{{b - a}}{{{2^l} - 1}} $ . 假设个体的编码为 $ {s_k}{s_{k - 1}}{s_{k - 2}}\cdots{s_2}{s_1} $ 解码的过程可以表示为:

$ X = a + \left( {\sum\nolimits_{i = 1}^k {{b_i} \times {2^{i - 1}}} } \right) \cdot \frac{{b - a}}{{{2^k} - 1}} $

(20)

针对适应度函数的设定, 本文考虑将最小均方误差准则和时频差方程相结合, 选择将目标通信辐射源位置到主、副站间的距离差的和作为适应度函数进行优化, 如式(21):

$ - f(x) = \sum\nolimits_{i = 2}^M {{{(r_i^o - r_1^o - {r_{i1}})}^2}} $

(21)

其中, 适应度函数 $ f(x) $ 越大, 目标函数的误差越小. 另一方面针对传统遗传算法后期迭代效率低, 优化效果不明显的不足, 本文设置阈值 $ \delta $ 作为衡量遗传算法终止的条件, 如式(22):

$ \delta = {f_{{\rm{Max}}}} - \overline {{f_m}} $

(22)

其中, ${f_{{\rm{Max}}}}$ 是每一代中最优的适应度, $ \overline {{f_m}} $ 表示第m代种群整体的平均适应度. $ \delta $ 作为宏观上反映进化程度的一个数值. 随着算法内部的解的迭代, $ \delta $ 会越来越小. 在选择的过程中, 个体被遗传的概率 $ {p_i} $ 为: $ {p_i} = \dfrac{{{f_i}}}{{\displaystyle\sum\nolimits_j^n {{f_i}} }} $ , $ {f_i} $ 为第i个个体适应度. 用 $ \displaystyle\sum\nolimits_j^n {{f_i}} $ 表示所有个体的适应度值, 且累计概率为 $ {q_i} = \displaystyle\sum\nolimits_{j = 1}^i {{p_i}} $ . 即随机产生 $ (0, 1) $ 的随机数x, 当且仅当 $ {q_i} \leqslant x \leqslant {q_{i + 1}} $ , 选择个体i.

交叉和变异是种群进化的核心, 在传统遗传算法中, 这两个概率在整个算法过程中始终是定值. 对此本文进行优化, 根据种群迭代次数的增加, 个体的适应度不断提高, 此时通过阈值 $ \delta $ 大小来衡量种群进化的程度, 降低交叉和突变的可能使其不容易进行. 从而减小优化解被破坏的可能.

3.3 多组数据递推求解

考虑通信辐射源移动速度相对于信号传播速度c很慢, 相邻两次获取时间差序列时, 通信辐射源移动速度相对信号传输速度视为静止, 因此采用一种滑动递推的处理方式完成目标通信辐射源的定位. 本文对筛选后的J组时频差观测数据进行递推. 如式(23):

$ {P_{i + 1}} = u_i^{\rm{T}} + rand(1, 3)(R), \; i = 1, 2, \cdots, J $

(23)

前一次的优化结果 $u_i^{\rm{T}}$ , 作为后一次遗传算法的搜索中心去初始化种群 $ {P_{i + 1}} $ 并采用后一组时频差序列完成求解, 即将式(23)、式(21)联立递推. 在完成位置估计后更新通信辐射源的位置参数 $ u $ . 鉴于式(6)频差模型与时差模型的关系, 基于最优的位置参数对目标通信辐射源速度 $ \mathop u\limits^. $ 进行估计, 最终完成对目标通信辐射源的定位.

4 实验仿真及分析

本节对所提出的递推式混合TDOA/FDOA定位方法进行计算机仿真实验, 并采用多次蒙特卡洛实验对不同定位方法进行仿真得到位置估计、速度估计. 不失一般性地, 分别为时差和频差添加均值、方差为常数的高斯噪声作为误差项. 其中协方差矩阵记为:

$ {Q_f} = {Q_t} = \left[ {\begin{array}{*{20}{c}} {\sigma _S^2}&{0.5\sigma _S^2}& \ldots &{0.5\sigma _S^2} \\ {0.5\sigma _S^2}&{\sigma _S^2}& \ldots &{0.5\sigma _S^2} \\ \vdots & \vdots & \ddots & \vdots \\ {0.5\sigma _S^2}&{0.5\sigma _S^2}& \ldots &{\sigma _S^2} \end{array}} \right] $

(24)

定位性能利用均方根误差(RMSE)进行评估分析. 仿真实验的次数设置为l=2000, 均方根误差定义为:

$ {{\textit{RMSE}}}(\theta ) = \sqrt {{{\sum\nolimits_{i = 1}^l {\left\| {{\theta _i} - {\theta ^o}} \right\|} }^2}/l} $

(25)

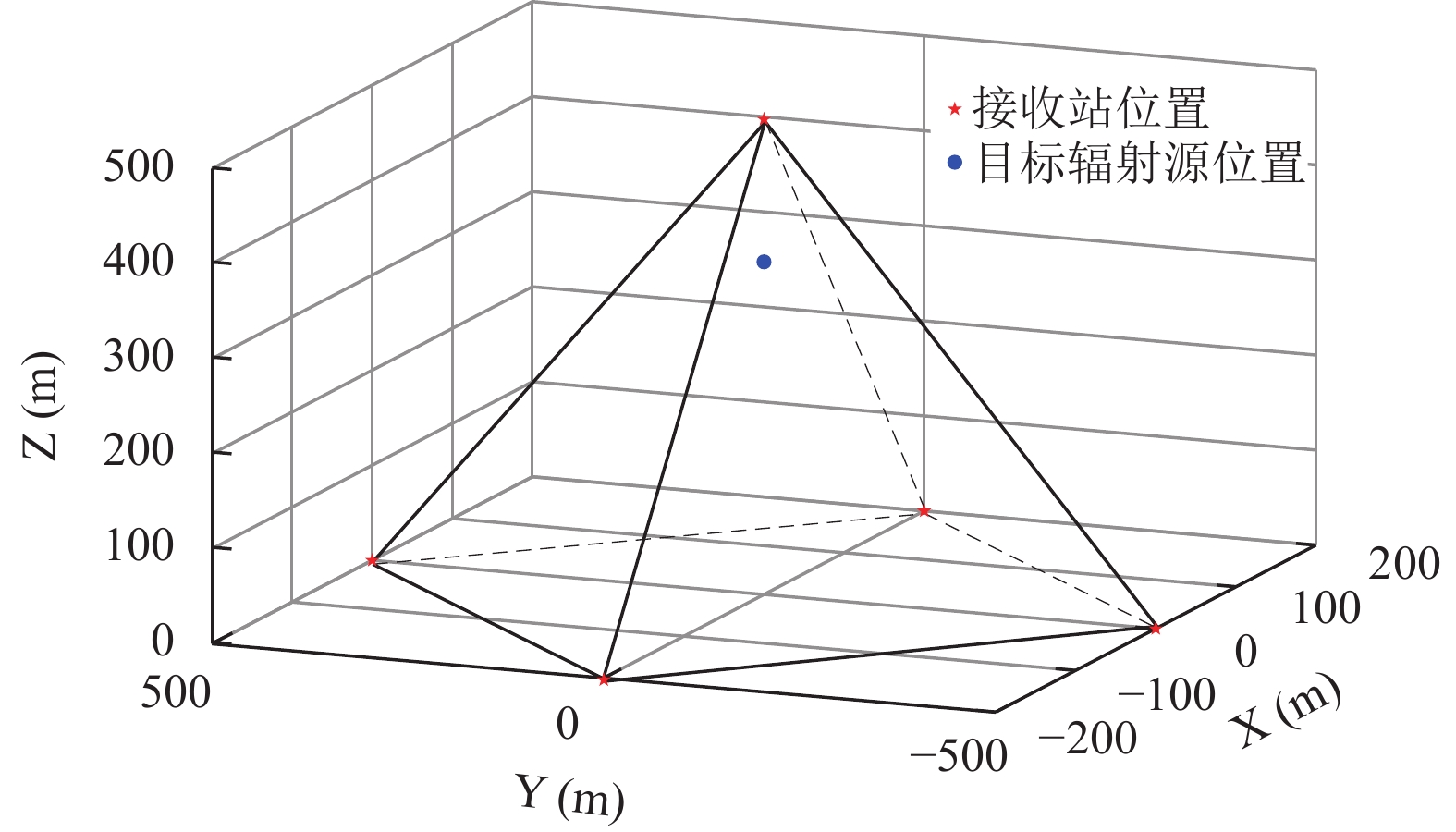
本文仿真采用M=5个接收站对远场、近场情形下的目标通信辐射源完成定位, 以及部分算法间的对比. 情形1近场的定位场景中, 通信辐射源的位置和速度分别为 ${u^o} = {[200, 300, 400]^{\rm{T}}}$ m和 $\mathop {{\dot u^o}} = {[ - 10, 15, 30]^{\rm{T}}}$ m/s. 情形2远场的定位场景中, 通信辐射源的位置和速度分别为 ${u^o} = {[1500, 2000, 2500]^{\rm{T}}}$ m和 $\mathop {{\dot u^o}} = {[ - 10, 15, 30]^{\rm{T}}}$ m/s. 情形1、情形2均采用CRLB、TSWLS、约束整体最小二乘(constrained total least squares, CTLS)作为对比的方法进行仿真并讨论. 如表1是接收站的布站坐标、图2是空间中接收站的分布位置.

图3、图4是在情形1下对近场通信辐射源的定位误差变化曲线. 其中横坐标表示的是噪声的大小, 用对数的形式进行表述, 单位是dB; 纵坐标表示的是位置或速度估计的均方根误差, 单位是m. 如图3所示, 对于位置估计, 当测量噪声低于0 dB时, 3种方法均可达到CRLB, 算法间的定位精度没有明显差别, 都在可控的范围内. 当噪声方差高于5 dB且随着噪声水平的增大, 不同方法的位置误差均明显增大, 同时开始偏离CRLB, TWLS算法的定位精度明显下降. 本文算法的定位精度在噪声为7.5 dB时开始偏离CRLB, 且位置估计的均方根误差均低于另外两种算法. 当噪声方差为20 dB时, 相比于经典两步加权最小二乘法的定位均方根误差, 本文算法的位置精度大约提高30 m、速度精度大约提高100 m.

图5、图6是在情形2下对远场通信辐射源的定位误差变化曲线. 相较于情形1, 远场定位的误差普遍较大. 分析算法间的异同, 在利用加权最小二乘处理的过程中, 目标通信辐射源到各接收站的距离基数大, 在误差项的影响下系数矩阵出现严重病态问题, 对后续算法产生较大影响. 如图5所示对于远场目标通信辐射源定位, 在测量噪声较小时3种方法都可以达到CRLB. 当测量噪声方差为−20 dB时3种定位方法均开始偏离CRLB. TWLS、CTLS算法基于加权最小二乘采用矩阵处理非线性参数的过程中忽略 $ r_1^o $ 的非线性特性, 而本文算法在初值的基础上, 利用改进的遗传算法联合时频差序列不断迭代修正参数估计. 本文的递推式混合定位算法在同等噪声水平下, 对于远场目标通信辐射源位置估计、速度估计的精度更高, 更加贴近CRLB.

对于情形1、情形2下, 位置估计的精度高于速度估计精度. 从本文算法本身进行分析, 本文考虑式(3)是式(6)的基础, 频差是基于时差推导出的, 加权最小二乘联合遗传算法对位置估计后再进行速度估计. 频差模型中的误差项包括位置估计误差、测量噪声, 因此对于速度估计的影响较大.

图7是不同智能寻优算法对于时频差参数优化的对比曲线, 横坐标表示算法自身的迭代次数, 纵坐标表示位置估计的均方根误差, 单位是m. 设置噪声方差为15 dB, 对情形1下的近场目标通信辐射源多次位置估计, 同参数下比较传统遗传算法、局部搜索算法以及本文改进的遗传算法的参数优化性能. 如图7所示本文改进的遗传算法相较于传统遗传算法、局部搜索算法具有更快的收敛速度. 多次仿真结果表明, 传统遗传算法内部平均需要进行124次迭代、局部搜索算法内部平均需要进行117次迭代、本文的遗传算法内部平均需要进行96次迭代. 改进的遗传算法相比其他智能寻优算法迭代次数更少, 提高了算法的寻优效率. 仿真实验表明, 根据阈值调整交叉算子、变异算子的概率可以有效地跳出局部最优解, 加快算法前期的搜索效率和算法后期的稳定性.

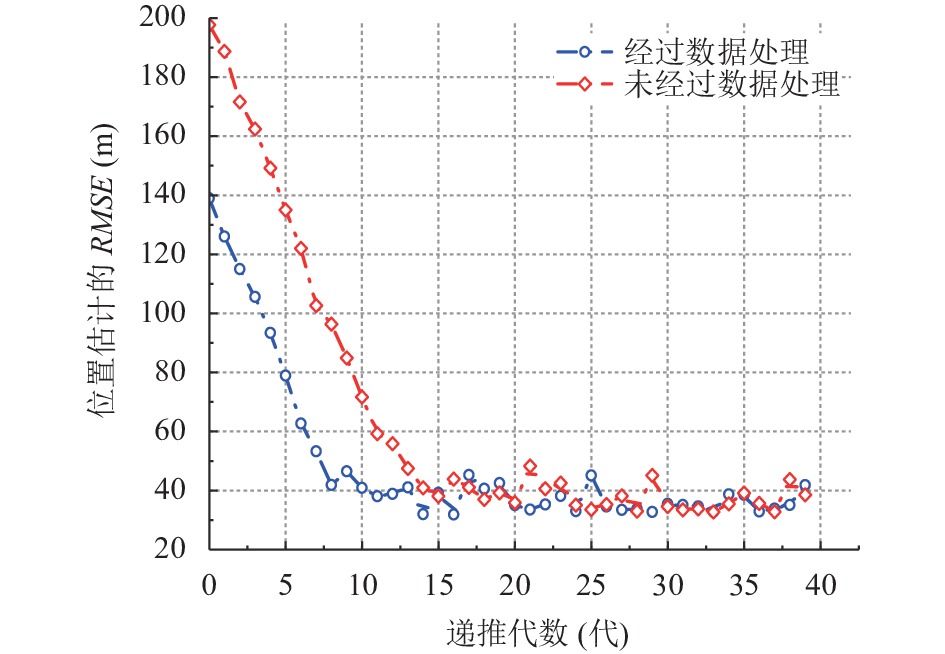
图8是目标通信辐射源滑动递推求解过程中定位误差的变化曲线. 横坐标是递推的次数, 单位是代、纵坐标是位置估计的均方根误差, 单位是m. 如图8所示, 在滑动递推的过程中位置估计的误差逐次降低直至稳定. 设置噪声方差为15 dB、递推次数40, 对情形1下的近场目标通信辐射源进行多次估计. 对比是否对时频差数据进行预处理的两种情况下的迭代次数与误差的关系. 仿真结果表明, 对时频差数据进行预先筛选校正, 可以保证遗传算法的种群围绕可靠的初值进行初始化, 递推过程中的误差很快就能收敛到一个下限. 如图8所示利用处理后的时频差数据进行递推, 平均9次就可以达到最优, 而直接使用原始观测数据进行递推, 平均需要14次才能趋于稳定. 充分利用了多组时频差序列的有效信息, 提高定位结果的可靠性及精度. 但多次迭代是以时间为代价, 迭代次数的增加导致时间开销变大、影响实时性.

5 结论与展望

基于TDOA/FDOA联合定位中, 针对闭式解算法对于测量噪声敏感且在大的测量噪声下定位精度不高的问题. 本文讨论了一种基于滑动递推的时频差联合定位思路. 首先利用已知时频差数据分析误差模型对观测值进行预处理, 其次采用加权最小二乘法与遗传算法相结合的递推方法完成对通信辐射源的位置及速度估计. 仿真结果显示, 在大噪声环境下本文算法相比TSWLS、CTLS算法定位精度更高, 且噪声功率较大时, 定位优势明显且更加贴近CRLB. 本文算法是一种解析法与智能寻优算法相结合的方法. 下一步研究工作主要是完成对于运动目标的轨迹监测, 以及对不同测量噪声的分析和预处理.