小样本学习下的特征中心对齐域适应算法

引用本文

韦柳幸, 陈春霞, 余志斌. 小样本学习下的特征中心对齐域适应算法. 计算机系统应用, 2023, 32(6): 166-172.http://www.c-s-a.org.cn/1003-3254/9126.html

Wei LX, Chen CX, Yu ZB. Domain Adaptation Algorithm with Feature Center Alignment for Few-shot Learning. Computer Systems and Applications, 2023, 32(6): 166-172(in Chinese).http://www.c-s-a.org.cn/1003-3254/9126.html

小样本学习下的特征中心对齐域适应算法

韦柳幸¹, 陈春霞², 余志斌¹

1. 西南交通大学电气工程学院, 成都 611756;
2. 成都工业学院经济与管理学院, 成都 610031

收稿日期：2022-11-22; 修改日期：2022-12-23; 采用时间：2023-01-16; csa 在线出版时间：2023-04-14

通讯作者：余志斌, E-mail: zbinyu@126.com.

摘要：域适应是一种在训练集和测试集不满足独立同分布条件时使用的迁移学习算法. 当两个领域间的分布差异较大时, 会降低域内可迁移性, 并且现有域适应算法需要获取大量的目标域数据, 这在一些实际应用中无法实现. 针对现有域适应方法的不足, 基于卷积神经网络提出小样本学习下的基于特征中心对齐的域适应算法, 寻找域不变特征的同时, 提高目标域特征的可区分度, 提高分类效果. 面向小样本条件下的office-31公共数据集识别和雷达工作模式识别的仿真实验结果表明, 所提方法对office-31数据集的平均识别精度比最大均值差异方法提升12.9%, 而对雷达工作模式识别精度达到91%, 比最大均值差异方法性能提升10%.

关键词: 域适应迁移学习特征对齐卷积神经网络(CNN) 深度学习

Domain Adaptation Algorithm with Feature Center Alignment for Few-shot Learning

WEI Liu-Xing¹, CHEN Chun-Xia², YU Zhi-Bin¹

1. School of Electrical Engineering, Southwest Jiaotong University, Chengdu 611756, China;
2. School of Economics and Management, Chengdu Technological University, Chengdu 610031, China

Abstract: Domain adaptation is a transfer learning algorithm used when the training and test sets do not satisfy the independent homogeneous distribution condition. When the distribution difference between two domains is large, the intra-domain transferability will be reduced, and the existing domain adaptation algorithms need to obtain a large amount of target domain data, which cannot be achieved in some practical applications. In view of the shortcomings of existing domain adaptation methods, the convolutional neural network model is used, and a domain adaptation algorithm based on feature center alignment for few-shot learning is proposed to find domain invariant features, improve the distinguishability of target domain features, and strengthen the classification accuracy. Simulation and experimental results for office-31 public dataset recognition and radar working pattern recognition under small sample conditions show that the proposed method improves the average recognition accuracy of the office-31 dataset by 12.9% compared with the maximum mean discrepancy method, and the radar working pattern recognition accuracy reaches 91%, which is 10% better than the maximum mean discrepancy method.

Key words: domain adaptation transfer learning feature alignment convolutional neural network (CNN) deep learning

传统的机器学习在面对新任务时, 需要重新构建针对新任务的模型, 并且需要大量的已标注数据进行训练, 这将花费大量的时间和人力. 然而, 在实际的工程应用中, 很难获取大量已标注数据, 但是任务之间通常存在一定的相关性, 而迁移学习的核心思想则是利用两个任务之间的相关性, 将某一领域或任务上学习获得的知识应用到另一相似的领域或任务中.

域适应方法作为广泛应用的一种迁移学习方法, 一般指源域和目标域特征空间和标签空间一致, 但是两个领域的边缘分布不一致时, 通过减小源域和目标域之间的分布差异, 使目标域获得良好的表现性能.

现有的域适应方法可以分为两大类: 基于领域对抗^[1-3]和基于分布差异^[4-6]. 基于领域对抗方法, 借鉴博弈思想, 通过一个域分类器混淆源域和目标域间的样本, 以此使特征提取器生成域不变特征. 基于领域分布差异的领域自适应方法将两个领域样本映射到域不变的特征空间, 减小源域和目标域之间的特征分布差异, 降低目标域的泛化误差. 基于领域分布差异的方法, 使用某种距离度量对齐源域和目标域.

域对抗网络(domain adversarial neural network, DANN)^[1]由特征提取器、分类器和一个域分类器组成. 在训练的过程中, 对来自源域的带标签数据, 网络不断最小化标签预测器的损失; 对来自源域和目标域的全部数据, 网络不断最大化域判别器的损失. 文献[2]提出对抗熵优化, 将分布不同的源域样本和目标域样本之间的熵最大化, 以便混淆域分类器, 并提高特征的可迁移性. 领域对抗的域适应方法通过域分类器和分类器之间的对抗博弈, 虽然能增强特征之间的可迁移性, 但是当目标域只有少量训练样本时, 领域间样本数量不均衡会导致模型鲁棒性变差, 使模型倾向于识别样本数量更多的源域数据.

深度适配网络(deep adaptation network, DAN)^[4]将源域特征和目标域特征之间的最大均值差异(maxi-mum mean discrepancy, MMD)作为领域分布差异, 通过最小化领域间的MMD值, 对齐源域和目标域之间的特征分布. Deep Coral^[5]针对目标域泛化效果不佳的问题, 使用二阶特征度量领域间的分布差异. ATM (adversa-rial tight match)^[6]则提出了最大密度差异(MDD)度量不同类别特征间的距离, 通过类间距离最大化实现领域自适应. 当领域间的分布差异较大时, 现有方法会导致两个领域间的不同类别特征出现错误适配现象, 无法缩减领域间的分布差异, 并且忽略了特征间的类内可区分性, 导致迁移效果不佳.

当前域适应算法集中于无监督或半监督域适应^[7–10], 无监督域适应指目标域拥有大量的无标签样本, 而半监督域适应则获取目标域的伪标签用于训练. 这类算法需要大量的目标域无标注样本, 而在一些实际应用中往往无法获取大量的目标域无标签样本, 或者样本标注代价较大, 例如在雷达电子对抗中通常难以获取大量的目标域数据. 因此, 提出了小样本域适应算法.

小样本域适应指目标域在少量已标注训练样本下的域适应训练, 这对目标域资源的需求更少, 更贴合实际应用, 适用范围更广泛. 然而, 小样本域适应算法引入目标域的小样本约束后, 极易使模型出现过拟合现象. 因此, 本文提出小样本条件下基于特征中心对齐的域适应算法.

本文提出小样本条件下基于特征中心对齐的域适应算法, 面向仿真雷达PAPI (脉冲幅值处理间隔雷达图谱)数据的小样本问题, 进行小样本下的雷达工作模式识别. 雷达PAPI数据根据不同工作模式下雷达信号幅值随时间变化呈现不同的特点这一特性, 构建不同的雷达工作模式图谱. 针对雷达信号截获不完整、信息收集不充分致使雷达侦察数据呈现小样本的条件下, 现有雷达常规五参数对雷达工作模式表征能力不足, 使用雷达PAPI作为一种新的雷达工作模式的表征形式, 用于小样本条件下基于域适应算法的雷达工作模式识别.

为验证本文所提算法的有效性, 使用视觉迁移学习中的主流公共数据集office-31进行试验. 首先, 使用已知的雷达工作模式数据作为源域, 训练卷积神经网络作为预训练模型; 然后, 以源域特征均值作为特征中心, 基于特征中心对齐进行域适应, 并引入目标域小样本约束; 最后, 通过对仿真生成的雷达PAPI数据进行实验验证, 本文提出的小样本下基于特征中心对齐的域适应算法具有较好的鲁棒性和泛化能力.

1 基于特征中心对齐的域适应

本文提出的基于特征中心对齐的域适应算法改进自传统的基于领域分布差异域适应算法, 对目标域小样本特征和所属类别特征中心进行对齐适配, 并在目标域小样本训练中加入小样本的标签信息, 防止目标域过拟合.

1.1 特征提取

基于特征对齐的域适应算法通过对目标域小样本特征和由源域计算得到的所属类别特征中心适配, 进行特征知识的迁移. 其中, 样本特征由卷积神经网络提取^[11–13]. 卷积神经网络属于端到端网络, 由两个模块组成, 卷积层叠加组成的特征提取器和分类器. 特征提取器具有表征数据的能力, 卷积层在表征图像特征时, 根据卷积核设置的参数对图像的局部像素学习, 然后在更高层将局部信息整合.

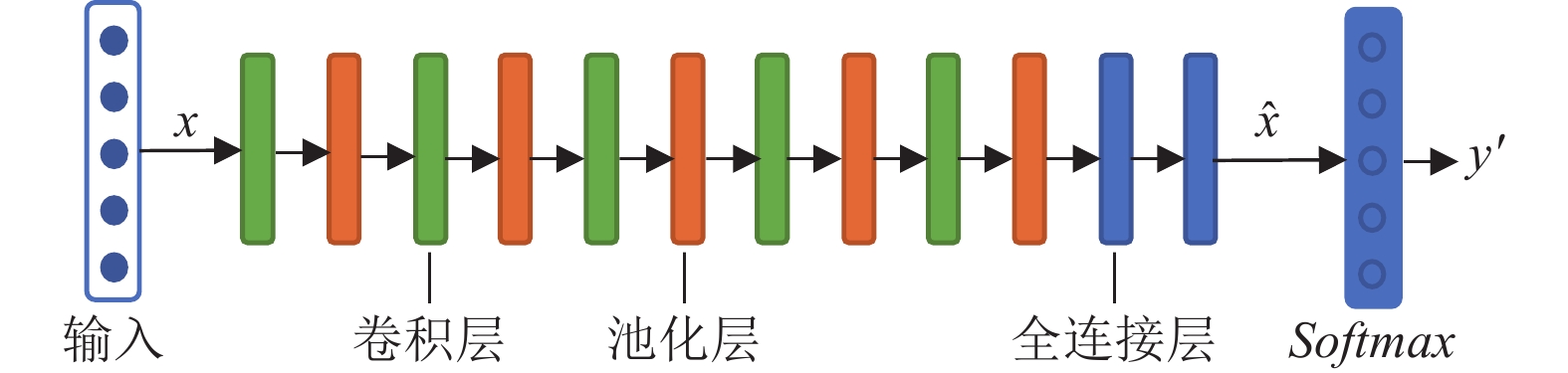
本文以卷积神经网络为主框架, 由特征提取器和分类器两部分组成, 其结构如图1所示. 特征提取器由5层卷积层、池化层以及2层全连接层逐级搭建组成, 用于提取输入数据 $x$ 的隐形特征 $\hat x$ ; Softmax分类器计算特征 $\hat x$ 隶属每一类别的概率值, 并把概率最大的类别作为预测输出 ${y{'}}$ .

图 1 卷积神经网络

1.2 特征中心对齐

源域定义为 $ {D_S} = {\{ x_i^s, y_i^s\} ^{{n_s}}} $ (其中, $x_i^s$ 为样本, $y_i^s \in (1, \cdots, m)$ 为标签, $m$ 为类别数量, ${n_s}$ 为源域样本数量), 目标域为 ${D_T} = {\{ x_j^t, y_j^t\} ^{{n_t}}}, {\{ x_k^t\} ^n}$ (其中, $x_j^t$ 为已知标签样本, $y_j^t \in (1, \cdots, m)$ 为标签, $m$ 为类别数量, ${n_t}$ 为目标域已知标签样本数量, $x_k^t$ 为未知标签样本, $n$ 为目标域未知标签样本数量).

两个领域的特征空间和标签空间相同, 即 ${y^s} = {y^t}$ , 条件分布相同 $p({y^s}|{x^s}) = p({y^t}|{x^t})$ , 但是边缘分布不同, 即 $p({x^s}) \ne p({x^t})$ . 因为两个领域的边缘分布不同, 直接使用由源域数据训练生成的模型识别目标域数据效果不佳. 基于领域距离的域适应算法则通过适配两个领域特征之间的边缘分布, 减小由分布差异造成的目标域泛化误差.

度量领域分布差异的常见方法为最大均值差异(MMD). MMD通过样本间的一阶矩度量两个领域的分布差异, 将数据映射到高维空间, 并对齐源域和目标域的样本均值. MMD定义如下:

$ mmd({X^s}, {X^t}) = \left| {\frac{1}{{{n_t}}}\sum\limits_{j = 1}^{{n_t}} {\phi (x_j^t)} - \frac{1}{{{n_s}}}\sum\limits_{i = 1}^{{n_s}} {\phi (x_i^s)} } \right|_H^2\;\;\;\; $

(1)

基于领域分布差异的域适应方法在训练模型时关注于两个领域的域不变特征, 当领域分布差异较小时, 目标域可以达到较好的识别效果. 但是, 当领域分布差异较大时, 直接对齐源域和目标域的样本均值会导致两个领域间不同类别特征出现错误适配, 无法有效减小两个领域之间的特征分布差异.

本文基于领域分布差异的域适应方法, 提出基于特征中心对齐(center-maximum mean discrepancy, C-MMD)的域适应方法. C-MMD定义如下:

$ c\_mmd({X^s}, {X^t}) = \left| {\frac{1}{{n_t^{{c_j}}}}\sum\limits_{{c_j}, j = 1}^{n_t^{{c_j}}} {[\phi (x_j^t)} - \frac{1}{{n_s^{{c_i}}}}\sum\limits_{{c_i} = {c_j}, i = 1}^{n_s^{{c_i}}} {\phi (x_i^s)} } \right|_H^2\;\;\;\; $

(2)

C-MMD在特征空间中计算目标域样本 $x_j^t$ 与其所属类别特征中心 ${c_j}$ 的距离, 其中特征中心 ${c_j}$ 为源域中相同类别样本在特征空间中的均值, 即式(2)右边第2项.

在基于领域分布差异的域适应算法中, 用领域内不同类别样本之间的距离描述领域的样本分布. 如图2基于领域分布差异的域适应过程, 图2(a)、图2(b)分别表示源域和目标域的样本分布, 其中S表示源域所有样本的中心, T表示目标域所有样本的中心. 图2(c)为MMD域适应算法, 通过减小源域样本中心S和目标域样本中心T的距离, 对齐源域和目标域的样本分布. 如图2(c)所示, 当两个领域间的样本分布差异较大时, MMD算法会导致目标域内不同类别的特征出现错误分类. 而C-MMD算法如图2(d)所示, 目标域A类别的样本向其特征中心C1 (C1为源域中A类别的特征中心)靠近, B类别的样本向其特征中心C2 (C2为源域中B类别的特征中心)靠近. C-MMD算法对齐目标域的样本 $x_j^t$ 与其特征中心 ${c_j}$ (源域中同一类别的特征中心), 即缩短两个领域之间同一类别特征的距离, 减小两个领域间的特征分布差异, 如图2(e)所示.

图 2 基于领域分布差异的域适应

C-MMD对齐目标域和源域中相同类别样本的特征中心, 通过缩短两个领域中同一类别特征之间的距离, 可以有效减小两个领域间的分布差异, 提高领域间的可迁移性. 在两个领域间分布差异较大时, 对齐两个领域间的相同类别特征, 提高域间相同类别特征的适配率, 确保目标域中不同类别特征之间的可区分度.

因为源域中的特征已经具有较强的可区分性, 所以将目标域特征对齐所属类别特征中心时, 目标域样本学习到源域的域内不变特征知识, 使得目标域具有类内距离小的表征特征, 并且更好的学习到源域中的可区分特征知识.

1.3 联合损失函数

在卷积神经网络中, 损失函数对于获取更好更抽象的特征表达具有重要作用. 本文提出联合损失函数进行目标域训练, 最小化目标域的分类损失和特征中心对齐, 联合损失函数如下:

$ L = {L_t} + \lambda \times c\_mmd\;\;\; $

(3)

$ {L_t} = \frac{1}{{{n_t}}}\sum\limits_i {\sum\limits_{c = 1}^m {{y_{ic}}\log ({p_{ic}})} } $

(4)

其中, L为联合损失值, ${L_t}$ 为目标域分类损失函数(交叉熵损失函数), $ {p_{ic}} $ 为样本 $x_j^t$ 属于标签 $ {y_{ic}} $ 的概率; $c\_mmd$ 为特征中心对齐值, $\lambda $ 为目标函数的平衡参数. 因为特征中心对齐值 $c\_mmd$ 很小, 而当损失值很小时会导致梯度消失的现象, 即该值无法更新网络参数, 因此 $\lambda $ 取经验值, 与分类损失 ${L_t}$ 在一个量级即可.

过少的训练样本无法反映整体数据的分布, 使模型对训练样本实现很高的分类率, 而对测试数据集的分类率很低. 因此在小样本条件下, 单独最小化目标域分类损失函数会导致模型过拟合. 而单独最小化 $c\_mmd$ 则会恶化特征, 网络将源域和目标域映射到特征空间中的同一点, 使 $c\_mmd$ 变为0, 这样的特征无法构建稳健的分类模型^[14].

联合损失函数则可以获取类内距离小、类间距离达的特征表达. 联合损失函数首先最小化特征中心对齐值, 即最小化源域和目标域中相同类别特征间的距离, 提升目标域特征的类内相似度, 通过减小两个领域间的分布差异, 提高域间的可迁移性. 然后最小化目标域小样本的分类损失, 加入目标域小样本的标签信息, 提高目标域域内不同类别间的可区分度.

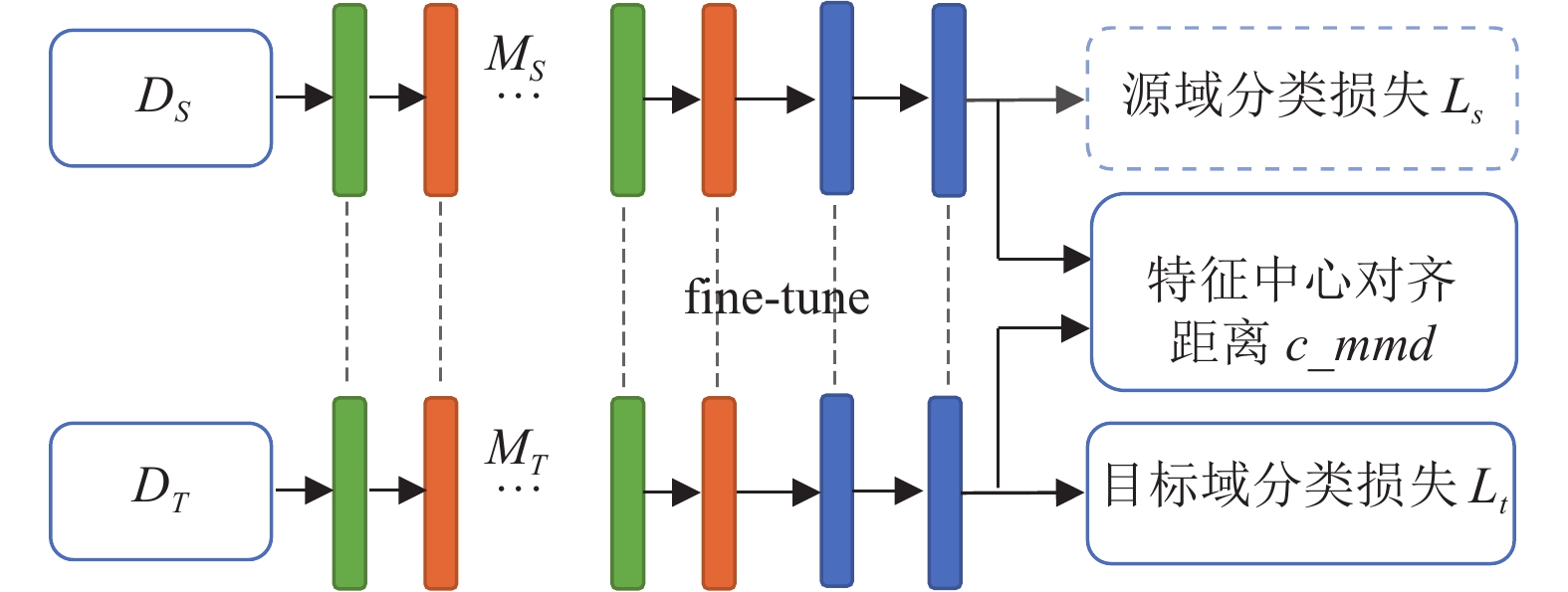
基于特征中心对齐的域适应过程如图3所示. 首先, 源域 $ {D_S} $ 训练过程中最小化源域分类损失 ${L_s}$ , 以训练好的源域模型作为预训练模型^[15,16], 然后预训练模型参数作为初始参数对目标域进行二次训练, 在目标域小样本 ${D_T} = {\{ x_j^t, y_j^t\} ^{{n_t}}}$ 二次训练时最小化联合损失L.

基于特征中心对齐的域适应过程, 设计算法1.

图 3 基于特征中心对齐的域适应过程

算法1. 基于特征中心对齐的域适应算法

1) 输入源域 $\scriptstyle {D_S} $ 的训练数据集 $\scriptstyle {\{ x_i^s, y_i^s\} ^{{n_s}}} $ , 模型训练过程中最小化源域分类损失函数 $\scriptstyle {L_S}$ (交叉熵损失函数), 迭代训练得到性能良好的预训练模型 $\scriptstyle {M_S}$ ;

2) 源域 $ \scriptstyle {D_S} $ 的数据集 $ \scriptstyle {\{ x_i^s, y_i^s\} ^{{n_s}}} $ 输入预训练模型 $\scriptstyle {M_S}$ 计算每个类别的特征中心 $\scriptstyle {C_j} = \frac{1}{n_s^{{c_j}}}\sum\limits_{j = 1}^{n^{{c_j}}_s} {\phi (x_j^s)} ,\; j = 1,\; \cdots,\; m$ ;

3) 目标域 $\scriptstyle {D_T}$ 的小样本训练数据集 $\scriptstyle {\{ x_j^t, y_j^t\} ^{{n_t}}}$ 输入预训练模型 $\scriptstyle {M_S}$ 中进行二次训练, 训练过程中最小化联合损失函数 $\scriptstyle L = {L_t} + \lambda \times c\_mmd$ , 迭代训练得到性能良好的目标域分类模型 $\scriptstyle {M_T}$ ;

4) 目标域 $\scriptstyle {D_T}$ 待测的未知样本 $\scriptstyle {\{ x_k^t\} ^n}$ 输入分类模型 $\scriptstyle {M_T}$ 获得分类结果.

2 实验 2.1 实验数据

实验首先使用视觉迁移学习中的主流公共数据集office-31^[17]进行测试. office-31数据集由3个子数据集组成, 分别为: Amazon (A)、Webcam (W)、DSLR (D), 3个子数据集分别有2817、498、795个样本, 分别为31类在生活办公中常见的物品, 在图像成像质量、成像环境和收集方式上均不同. 实验中所使用的雷达工作模式数据是由仿真雷达信号的幅值特性表征的PAPI (脉冲幅值处理间隔雷达图谱)数据, 分别仿真了STT、MTT、TAS、TWS这4种工作模式.

2.2 实验设置

模型采用Adam优化算法最小化联合损失函数, 学习速率为0.0001, 迭代步数为5 000. GPU为NVIDIA GTX2080Ti, 内存为64 GB, CPU为Intel Xeon Silver 4214, 软件环境采用cuda、Python 3、PyTorch.

实验采用总体分类精度(overall accuracy)以及各类别分类精度(category accuracy)对算法进行评估. 总体分类精度指正确分类样本数与总的样本数之比, 用于评估模型的整体性能; 各类别分类精度指该类别正确分类样本数与该类别总的样本数之比, 便于观察模型对每个类别的分类情况.

本文采用Deep Coral, MMD, C-MMD三个算法进行对比实验. 其中, C-MMD为本文提出的基于特征中心对齐算法, MMD为最大均值差异算法, 而Deep Coral则是将源域和目标域的二阶统计特征进行对齐. 在雷达电子对抗中, 当样本小于100时即可认定为小样本数据量, 所以本次实验在5、10、20、50四种不同小样本条件下进行实验.

2.3 实验结果分析 2.3.1 office-31数据集实验结果

使用office-31数据集验证本文算法有效性时, 设置目标域每个类别已标注样本量为10个样本, 其余样本作为测试集. 实验结果如表1所示, 总体分类精度取10次分类结果均值.

表 1 不同域适应算法在office-31数据集上的总体分类精度

在office-31数据集迁移任务中, C-MMD方法均取得了最高精度. 3种域适应算法在D域和W域的迁移任务中均取得了最高分类精度, 这是因为它们均为摄像头采集的图像, 较高相似度的数据分布使得两个领域之间能更好地进行迁移. C-MMD算法在6个迁移任务上的平均分类精度比Deep Coral算法提高了9.1%, 比MMD算法提高了12.9%. 在A域和D域的迁移任务中, C-MMD算法的分类精度显著提升, 因为C-MMD算法在两个领域分布差异较大时, 通过减小域间同类别特征间的距离, 促进源域和目标域特征分布的对齐, 提高了域间的可迁移性. 但是C-MMD算法在W-A迁移任务中分类精度提升得并不明显, 相比于Deep Coral算法精度只提升了1%.

2.3.2 增强特征性能

在面向雷达数据的实验中, 目标域每个类别已标注训练样本数量为50, 4个类别一共200个样本, 分别由Deep Coral, MMD, C-MMD三个算法训练得到目标域模型 ${M_{t\_{\rm{Coral}}}}$ 、 ${M_{t\_{\rm{MMD}}}}$ 、 ${M_{t\_{\rm{CMMD}}}}$ , 并对模型的输出特征进行t-SNE降维与三维可视化. 对特征进行可视化, 可直观地观察特征间的可区分性, 当同类特征之间的间隔小, 不同类特征之间的间隔大时, 该特征具有更强的可区分性. 神经网络的输出特征为高维数据, 因此需要高维数据降维到三维空间中.

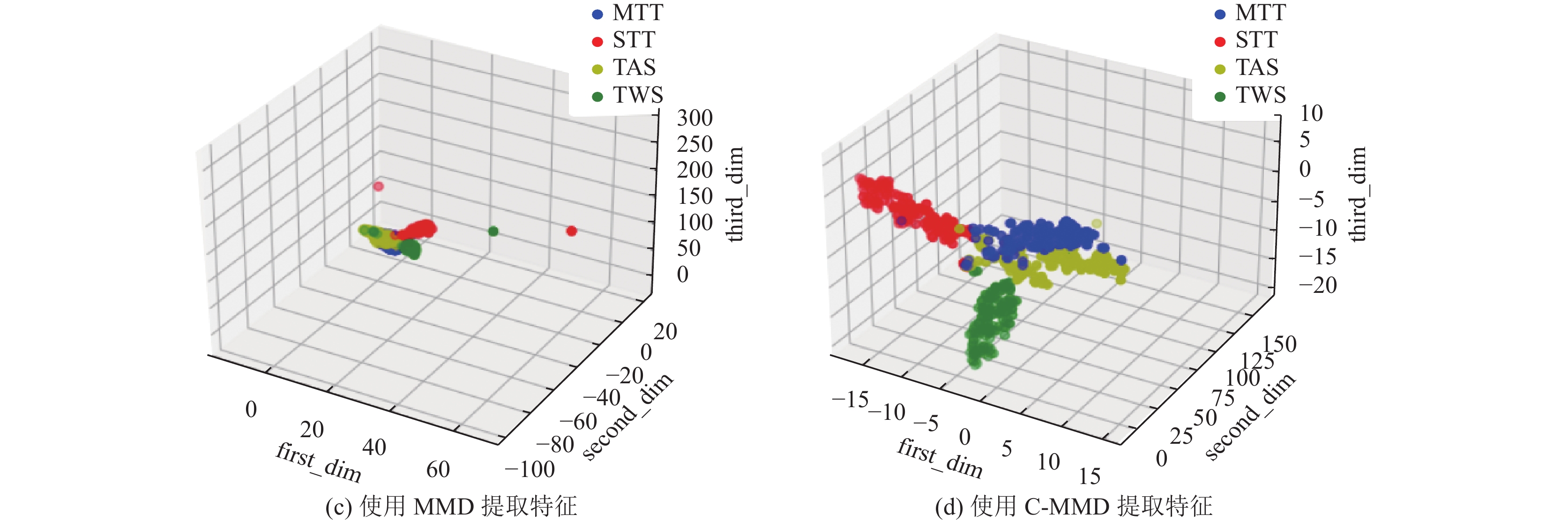
t-SNE属于非线性降维算法, 可以捕获高维数据的复杂流形结构, 与原始数据保持良好的相似性. 由图4雷达工作模式数据特征三维图可知, 当目标域待分类样本直接使用源域模型提取特征时, 呈现同类特征距离大且不同类特征距离小的特点, 特征不具备区分性. 当使用域适应算法进行迁移学习时, 不论是Deep Coral还是MMD算法, 虽然可以缩进同类特征之间的距离, 但是却忽略了不同类特征之间的可区分性. 而本文提出的C-MMD算法, 在减小同类特征距离时, 增加了不同类特征之间的距离, 使得域内不同类特征之间具有更强的区分性.

2.3.3 目标域训练样本数量对识别效果的影响

为验证小样本条件下面向雷达工作模式识别时C-MMD算法的有效性, 设置4组不同目标域训练样本数量的实验组, 目标域中每个类别训练样本数量分别为5、10、20、50, 即目标域4个雷达工作模式总体训练样本数量分别为20、40、80、200; 每组实验的测试样本数量均为16个/每类别, 一共64个样本. 每个实验组分别使用Deep Coral, MMD, C-MMD算法进行迁移学习, 总体分类精度取10次分类精度的平均值.

图 4 雷达工作模式数据特征三维可视图

图 4 雷达工作模式数据特征三维可视图(续)

如表2所示, 随着目标域雷达训练数据减少, 总体分类精度也在下降, 但是C-MMD算法的总体分类精度高于Deep Coral算法和MMD算法10%. 当目标域只有5个训练样本时, Deep Coral算法和MMD算法的总体分类精度分别下降到0.7114和0.6297, 而C-MMD算法的总体分类精度为0.8156, 充分验证C-MMD算法在小样本条件下, 提升雷达工作模式总体分类精度的可行性.

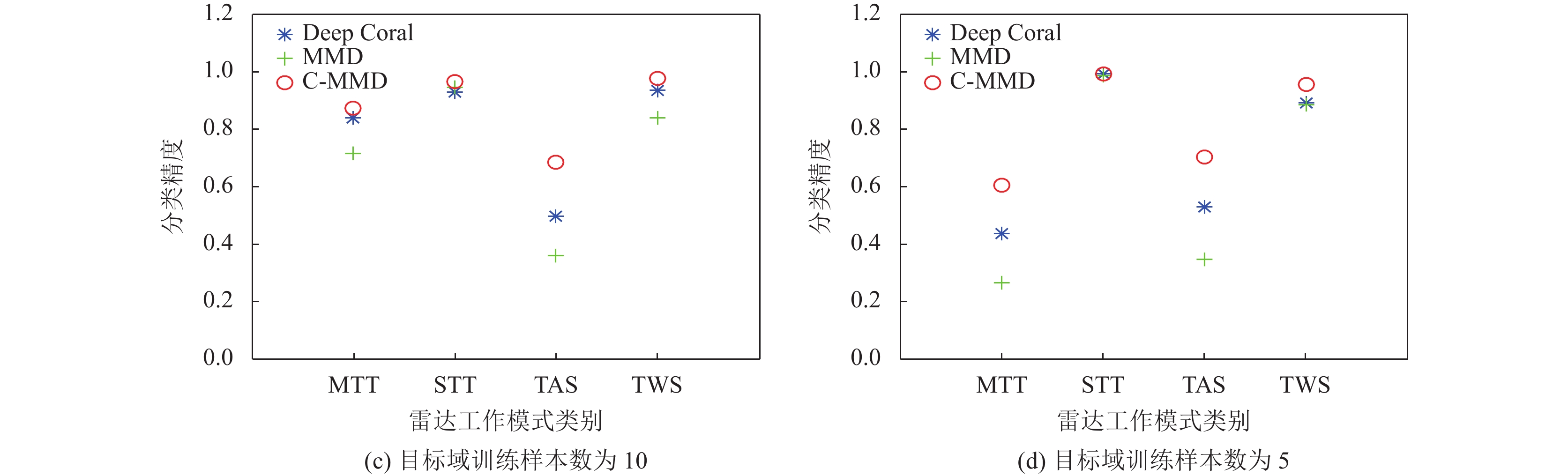
图5为目标域不同训练样本数量下每个雷达工作模式类别的分类精度对比图, 从各个类别的分类精度验证算法可行性. C-MMD算法对于每一个类别的分类精度领先其他算法, 并且每一类别之间的分类精度差异不大, 其中3种算法对STT、TWS类别的分类能力基本一致并且分类精度较高. 当目标域每个类别训练样本数量大于20个时, 尽管Deep Coral算法和MMD算法的总体分类精度较高, 但是对于MTT以及TAS的分类精度却很低; 当目标域每个类别训练样本数量下降为5个时, 3种算法对于MTT以及TAS的分类精度均下降.

表 2 不同域适应算法在雷达数据上的总体分类精度

3 结论与展望

针对领域间分布差异大、域内可区分性低导致域适应目标域泛化误差大的问题, 本文提出了基于特征中心对齐(C-MMD)的域适应算法. C-MMD算法在公共数据集office-31上表现良好, 验证了本文算法的适用性. 面向小样本条件下雷达工作模式的识别, 算法首先使用已知的雷达工作模式数据作为源域, 训练卷积神经网络作为预训练模型, 然后以源域特征均值作为特征中心, 使用目标域小样本雷达工作模式数据集基于特征中心对齐进行域适应训练, 提升了领域间的可迁移性. 仿真实验表明本文提出的C-MMD算法较Deep Coral算法和MMD算法, 在小样本条件下总体分类精度提高了10%左右.

图 5 目标域不同训练样本数量下每个类别的分类精度对比

图 5 目标域不同训练样本数量下每个类别的分类精度对比(续)

与此同时, 虽然随着目标域训练样本数量的减少, C-MMD算法总体分类精度保持在较高的水平, 但是MTT和TAS这两类模式的分类精度却急剧下降. 这也是之后的研究中需要进一步研究与改进的方向: 小样本条件下, 提升总体分类精度的同时也要确保每个类别的分类精度, 以及增强算法鲁棒性

参考文献

[1]	Ganin Y, Lempitsky V. Unsupervised domain adaptation by backpropagation. Proceedings of the 32nd International Conference on International Conference on Machine Learning. Lille: JMLR.org, 2015. 1180–1189.
[2]	Ma A, Li JJ, Lu K, et al. Adversarial entropy optimization for unsupervised domain adaptation. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(11): 6263-6274. DOI:10.1109/TNNLS.2021.3073119
[3]	Zhang Y, Wang NB, Cai SB, et al. Unsupervised domain adaptation by mapped correlation alignment. IEEE Access, 2001, 8, 6: 44698-44706.
[4]	Long MS, Cao Y, Wang JM, et al. Learning transferable features with deep adaptation networks. Proceedings of the 32nd International Conference on International Conference on Machine Learning. Lille: JMLR.org, 2015. 97–105.
[5]	Sun BC, Saenko K. Deep CORAL: Correlation alignment for deep domain adaptation. Proceedings of the 2016 ECCV Workshops. Cham: Springer, 2016. 443–450.
[6]	Li JJ, Chen EP, Ding ZM, et al. Maximum density divergence for domain adaptation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021, 43(11): 3918-3930. DOI:10.1109/TPAMI.2020.2991050
[7]	Kang GL, Jiang L, Wei YC, et al. Contrastive adaptation network for single- and multi-source domain adaptation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022, 44(4): 1793-1804. DOI:10.1109/TPAMI.2020.3029948
[8]	Luo YW, Liu P, Zheng L, et al. Category-level adversarial adaptation for semantic segmentation using purified features. IEEE Transactions on pattern Analysis and Machine Intelligence, 2022, 44(8): 3940-3956.
[9]	Luo YW, Ren CX. Conditional bures metric for domain adaptation. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021. 13984–13993.
[10]	Sharma A, Kalluri T, Chandraker M. Instance level affinity-based transfer for unsupervised domain adaptation. Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Nashville: IEEE, 2021. 5357–5367.
[11]	Zhang FH, Qi XJ, Yang RG, et al. Domain-invariant stereo matching networks. Proceedings of the 16th European Conference on Computer Vision. Glasgow: Springer, 2020. 420–439.
[12]	Ghifary M, Kleijn WB, Zhang MJ. Domain adaptive neural networks for object recognition. Proceedings of the 13th Pacific Rim International Conference on Artificial Intelligence. Gold Coast: Springer, 2014. 898–904.
[13]	Krizhevsky A, Sutskever I, Hinton GE. ImageNet classification with deep convolutional neural networks. Communications of the ACM, 2017, 60(6): 84-90. DOI:10.1145/3065386
[14]	Wen YD, Zhang KP, Li ZF, et al. A discriminative feature learning approach for deep face recognition. Proceedings of the 14th European Conference on Computer Vision. Amsterdam: Springer, 2016. 499–515.
[15]	Guo YH, Li YD, Wang LQ, et al. AdaFilter: Adaptive filter fine-tuning for deep transfer learning. Proceedings of the AAAI Conference on Artificial Intelligence, 2020, 34(4): 4060-4066. DOI:10.1609/aaai.v34i04.5824
[16]	Jang Y, Lee H, Hwang SJ, et al. Learning what and where to transfer. Proceedings of the 36th International Conference on Machine Learning. Long Beach: PMLR, 2019. 3030–3039.
[17]	Saenko K, Kulis B, Fritz M, et al. Adapting visual category models to new domains. Proceedings of the 11th European Conference on Computer Vision. Heraklion: Springer, 2010. 213–226.