2. 中国核动力研究设计院 核反应堆系统设计技术重点实验室, 成都 610213
2. Science and Technology on Reactor System Design Technology Laboratory, Nuclear Power Institute of China, Chengdu 610213, China
同步数据流语言目前在航空航天、轨道交通、核电能源等领域的安全关键系统(safe-critical system, SCS)[1]中得到广泛应用. 这些领域相关系统的任何一个小错误, 都将会给人类的生命财产、社会生产以及生活环境带来重大影响. 如何保证构造这些系统的基础软件(如编译器)的可靠性, 逐渐成为该领域的研究重点.
传统的保证编译器正确性的做法大多采用对生成代码进行大量测试或对生产过程采取严格的过程管理. 但随着软件规模的增大, 此类方法逐渐变得低效; 同时传统检测方法无法验证错误是否由编译器本身引入. 在安全关键领域中传统方法几乎已达到了其检测能力的极限. 因此需要更严苛的方法, 即形式化的方法来保证编译器的可靠.
形式化方法基于严格的数学和机械化理论, 能够对数学理论或系统设计进行建模、归约和验证, 辅助解决和改善数学以及软件安全性方面的种种问题. 何炎祥等人对编译器领域的可信软件构造理论和方法进行了深入研究, 将可信编译器的构造方式分为两类, 分别是对编译器自身进行正确性验证的“经验证的编译器(verified compiler)”和对编译后代码进行正确性验证的“验证编译器(verifying compiler)”[2]. 通过将编译器的执行语义抽象为数学断言, 并以定理证明的形式直接验证编译器的源语言和目标语言语义的一致性, 能够最大限度地减少“误编译”问题产生. 对编译器进行定理证明的研究中CompCert[3]为杰出代表, 该编译器完成了C语言的子集Clight到汇编语言的编译和证明工作. 其编译工作被划分为多个阶段, 使用辅助证明工具Coq[4]对每个阶段的语义保持性进行了证明, 保证编译过程的正确性. CompCert已达到了人们所期望的最高可信程度, 其生成代码可直接用于工业生产中, 为工业界后续制定高可靠的编译标准奠定了基础.
对编译器编译后的代码进行正确性验证的方式有携带证明PCC (proof carrying code)和在携带证明基础上更加通用的翻译确认(translation validation). 相较于翻译确认, 携带证明偏向于对编译后的结果进行安全性验证, 而不是对编译器本身进行证明[5]. 在携带证明的基础上, Pnueli等人[6]首先提出了翻译确认的机制, 该方法通过构建一种统一的语义框架来为源语言和目标语言进行建模, 并为两个语义模型构建出特定的语义等价关系, 然后设计出一种能够验证两个语义模型等价关系的确认程序. 该程序可以通过求解证明、符号计算、类型检查或静态分析等方式来确认语义模型是否等价, 如果等价则会给出证明脚本, 否则会给出反例. 基于翻译确认思想, Pnueli实现了两种同步数据流语言到C的编译器的翻译确认工作[7], 这两种编译器也包含了大约100条优化规则, 并且证明翻译确认同样可以保证优化后的编译器的正确性.
近年来Ngo等人[8]基于翻译确认的思想, 也开展了同步数据流语言Signal到C的编译器验证工作, 包括: 针对源代码和目标代码的统一语义框架PDS(polynomial dynamical systems), 并给出两种语义的抽象时钟等价关系, 并通过SMT求解器来验证等价关系的一致性, 从而保证了编译器的时钟语义一致性; 然后Ngo等人在一种一阶逻辑公式定义的时钟模型的基础上, 开展了保持时钟语义的翻译确认工作[9, 10]; 利用同步数据流语言的求值图(SDVGs)对翻译前后依赖关系的保持性进行了确认[10]; 并利用SDVGs对求值语义的保持性进行了确认[11]. 基于以上技术, 该团队提出了一种对大规模同步数据流语言编译器验证的拓展性良好的翻译确认方案, 该方案主要侧重于对同步数据流语言时钟、数据依赖以及变量求值等方面等价性的保持.
如果翻译前后两种语言的语义等价性易于构造, 或者两者的等价关于易于定义, 那么使用翻译确认是一种非常有效的验证方式. 其易于拓展的特性, 能够保证在不改动原有编译框架的基础上增加额外内容. 但是当源语言和目标语言差异较大时, 其定义工作相对较难, 同时证明过程也更加困难; 同时由于翻译确认只会关注部分性质的保持性, 其不可避免地会出现误报, 因而在工业级的开发中更多作为基于定理证明方式的补充证明.
Coq是目前流行的定理证明工具之一. 该工具的核心是一种名为归纳构造演算的基础理论. 通过该理论, Coq将多类型的函数式编程语言和高阶逻辑进行结合, 拥有强大的数学理论基础. 同时Coq在编程推理方面也有强大的表现能力, 允许用户通过构造简单项, 执行简单证明, 并在此基础上进行拓展, 直至完成完整的证明系统[4]. Coq还提供一体化的交互式证明、编译环境和程序抽取功能, 以便用户能够及时地编写、验证定义的定理, 并将完成验证的程序抽取为OCaml语言. 代码的成功抽取也意味着程序性质验证成功.
目前国内外也正逐步开展基于定理证明方法的算法与软件安全性验证工作, 文献[12]总结了矩阵的形式化方法并完成对矩阵的分块矩阵的运算方法进行形式化定义及验证工作; 文献[13]对操作系统的需求层进行形式化建模, 并提出模型需要满足的相关性质, 然后对模型进行验证; 文献[14]对分布式系统中常用的分布式共识算法Basic Paxos进行了形式化地建模验证, 证明了该算法满足共识性. 目前国外基于Lustre语言编译器的验证工作, 是法国Pouzet教授团队的Vélus编译器[15]. 该编译器以一种基于对象的中间语言作为桥梁, 实现了一个小型但具有Lustre语言全部特征的子集MiniLS中间语言, 并基于该语言实现了一个同步数据流语言可信编译器的原型系统. 随后基于该原型系统完成了基于对象的中间语言Obc到Clight的翻译与验证. 国内对可信的Lustre编译器的研究有清华大学的L2C编译器[16]. 相较于Vélus, 该编译器支持更多Lustre特性[17]. 该编译器在完全验证单一时钟的基础上, 实现了Lustre嵌套时钟特性的验证, 能够应用于工业开发中. 基于定理证明的形式化证明方式工作量较大, 整体逻辑较为复杂; 当翻译前后中间语言跨度较大时, 将翻译分为多个阶段进行, 能够最大程度地保证生成代码的可靠性和安全性, 同时也能提升编译器的可扩展性. 对于一个工业级的可信编译器来说, 良好的可扩展性也能提升工业生产的效率. 基于定理证明的形式化证明方式是目前安全关键领域相关系统最理想的证明方式.
目前多数基于模型的形式化研究往往对部分现实问题进行了简化, 如Vélus编译器不能完全支持Lustre中常用的时钟、时态算子[17]. 本文基于我国安全关键领域的实际需求, 针对工业生产中参数的转化问题进行研究. 在工业生产中不可避免地需要传递大量参数, 编译器直接生成的代码如果参数过多, 会出现代码可读性差, 难以维护的问题, 同时还可能因为参数的生成错误, 导致系统出错. 因此为了增加代码的可读性, 减少维护成本, 并为后期增加对状态机特性提供支持, 需要将相应的输入参数转化为易于维护和拓展的形式, 同时对生成的输入参数进行相应的检查. 为了保证翻译修改后代码的可靠性和正确性, 并确保生成的代码能正确应用在安全关键系统之中, 转化过程需要采用定理证明的方式进行实现. 在总体方法上, 本文采用与上述文献相同的基于模型的形式化验证思想, 以面向领域的类Lustre语言Lustre*为源语言, 完成与Clight对接; 通过交互式辅助证明工具Coq, 将同步数据流语言编译至嵌入式控制领域常用代码过程涉及的基础数据类型、数据结构以及翻译算法进行抽象, 并以数学断言的形式给出整个翻译阶段的形式化定义.
基于以上论述, 本文从同步数据流语言的特性出发, 总结同步数据流在输入结构体翻译阶段的问题. 同时对该翻译阶段的语法、语义以及语义环境进行形式化定义, 找出该阶段需要验证的性质. 然后结合现实应用, 定义翻译算法和验证算法正确性的思路, 最后完成翻译的证明. 整个实验过程将在Coq中完成, 文中将给出部分定义实例. 以上研究成果将为同步数据流语言编译器的验证工作提供理论依据.
1 同步数据流语言同步数据流语言源于工业生产中使用的响应式系统, 这些系统需要不断地与环境交互, 然后将从环境中采集的实时数据作为输入, 完成相应计算并做出对应的输出. 传统C语言在系统规模扩大后不再能胜任响应式系统的开发要求, 为此人们开展了同步泛型的相关研究, 并在30多年的研究成果, 研究出多个得到广泛应用的同步语言, 如Esterel[18], Lustre[19, 20], Signal[21, 22]. 其中Lustre与Signal侧重于描写语言的数据流特征, 因此也被称为同步数据流语言.
同步数据流语言重点在于同步与数据流特性, 其中同步指语言遵循的基本原则同步假设: 系统从当前周期的数据采集任务开始到下一周期的数据采集任务之前, 必须完整的完成一次数据采集, 数据逻辑运算并得出相应输出; 数据流特性指程序中所有变量都是一个无限长的流式数据对象, 该对象中包含了变量的取值和当前周期下的时钟, 每个时钟周期中变量能否取值将由变量的时钟决定, 除明确指定外, 每个变量的默认时钟为所属节点的时钟.
在Lustre语言中, 主节点将作为与外界进行数据交流的窗口, 执行同步假设中数据采集任务. 并且主节点承担着调用其他节点执行逻辑运算的任务, 并输出相应结果. 基于以上原因主节点的默认时钟恒为真, 即每个周期主节点都需要从外界得到相应输入. 但不同的系统为Lustre程序提供输入的方式不尽相同, 且Lustre语言的输入参数结构与嵌入式C语言有较大差异. 在实际工业生产中, 采用一种合理的翻译方式来解决数据流与输入结构是一个难点.
目前Lustre语言已被广泛应用于安全关键领域的嵌入式软件中, 此类软件使用图形编辑器来描述图形控制算法, 并将图形控制算法以Lustre语言的形式输出, 如SCADE Suit和核能高级工程师站NASPES (nuclear advanced software platform of engineer station software). 其中NASPES是由中国核动力研究设计院开发的基于模型的控制算法开发环境, 是核能高级仪控软件平台NASPIC (nuclear advanced software platform instrument and control)的重要组成部分, 主要应用于核电站嵌入式软件控制领域.
NASPES集成了图形化控制算法设计、可信代码生成、控制算法调试和仿真功能. 如图1仪控算法开发过程所示, 核电仪控工程师首先用图形化的方式在NASPES的组态绘图软件NASLAND中对核电站控制算法进行建模, 然后使用代码生成器将图形算法翻译为C程序. 在实施阶段, 生成的C程序会被上传到NASPES中编译为可执行代码, 最终在ARM48中运行. 为提升核仪控工程师的开发效率, NASLAND中包含了100多个核能领域仪控设备的基础算子模块, 除基础的与、或、非门外还包括集成多个算子的边沿脉冲发生器模块、报警模块等. 目前已设计10余个基于基础算子模块的核仪控算法组态.
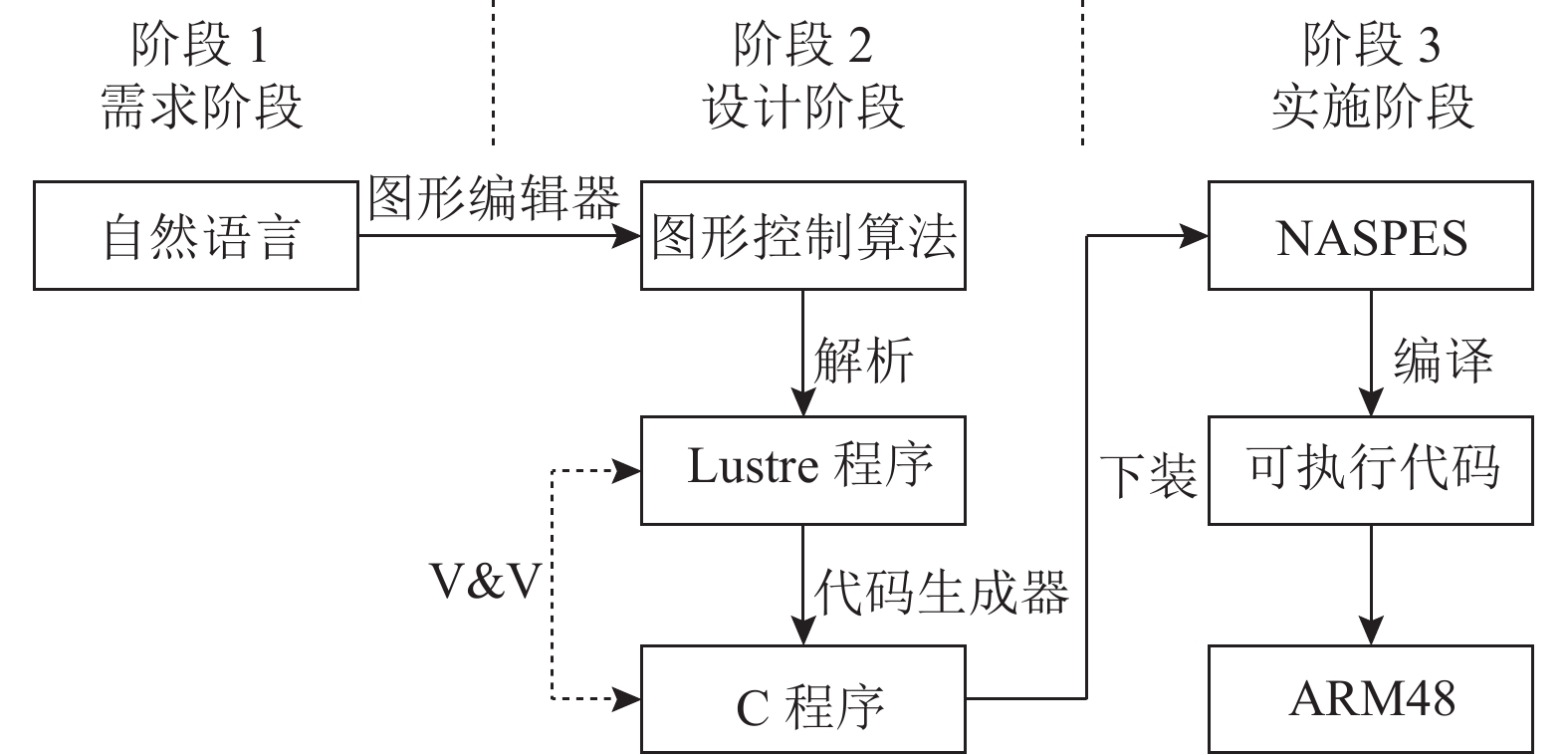
|
图 1 仪控算法开发过程 |
早期NASPES将图形控制算法翻译为C程序主要使用SCADE的安全代码生成器KCG, 该生成器采用了大规模测试并遵守了严格的验证和确认过程(V&V), 以消除错误来保证翻译的正确性, 但其依旧无法保证解决“误编译”问题. 为保证代码可靠, 有必要在代码生成器的开发过程中找到一种更严格的解决“误编译”的方法.
本文将给出一种Lustre语言主节点输入结构的翻译方式, 使其符合命令式语言特征, 并给出该翻译方式翻译前后语义保持性的证明方法, 保证翻译结果的可靠性, 避免“误编译”现象的发生.
2 形式化的语法和语义定义在翻译和证明工作中, 语法和语义的定义是基础, 也是重点. 由于Coq无法直接验证语法和语义的正确性, 当多个问题叠加在一起时, 证明需要考虑额外的内容. 因此, 本文参考CompCert的设计思路, 将翻译分为多个阶段进行, 保证每个阶段解决单一问题. 如图2所示, 本文将整个翻译过程划分为Lustre*、Lustre* AST、LustreR1、LustreR2等多个中间阶段. 每个阶段根据功能不同, 设计了独立的语法和语义, 不同阶段需要通过具体的翻译通道(如TransMainArgs)进行过渡. 如果翻译前后不同阶段的语法规则类似, 这些中间阶段可基于某一阶段的基础语法, 根据功能增加操作语义.

|
图 2 翻译过程 |
本文将主节点输入结构的翻译工作进行提取, 于TransMainArgs阶段执行. 翻译前后中间阶段LustreR1和LustreR2的语义以LustreR阶段语义作为基础, 并根据工作内容对语义适当调整.
2.1 抽象语法树的定义定义翻译函数前, 需要对翻译中间过程的抽象语法树进行定义. 在Coq语法树将以构造子和构造内容的形式进行定义. 基于该定义, Coq能够对源程序的语法结构进行静态检查, 保证语法结构的正确, 并将源码内容按定义方式进行提取.
在构造抽象语法树的过程中, 为保证语法树在各阶段中的通用性, 以及专注于对翻译问题的研究, 语法树的设计采用自顶而下的方式, 将其划分为4个层次, 分别是程序层, 节点层, 等式层以及表达式层. 各个翻译阶段程序层和节点层的定义框架大致相同, 只是语句层和表达式层定义会根据阶段做出相应调整.
程序层作为语法定义的最顶层, 主要用于在各个翻译阶段之间传递源程序携带的关键信息. Lustre程序被划分为类型定义块, 全局常量块以及节点块, 不同阶段程序体会携带额外的内容, 但框架整体变化不大. 其抽象语法如下所示:
| $ \begin{split} \langle program\rangle :: = & \langle decls\rangle \\ \langle decls\rangle :: = & \langle type\_decl\rangle \\ & |\langle const\_decl\rangle \\ & |\langle node\_decl\rangle \end{split} $ | (1) |
节点层用于确定程序具体逻辑. 节点层中包含该程序的节点块以及相关信息. 节点块中存放了一个由一系列节点组成的列表, 其中主节点作为程序最初的入口函数, 其他节点作为功能承担者被主节点或除自己以外的其他节点调用. 单个Lustre的节点由节点名输入参数, 输出参数, 局部变量定义, 语句块等主要部分和辅助证明的参数(如节点类型)等构成, 节点层的定义如下:
| $ \begin{split} \langle node\_decl\rangle \text{ }:: = & \text{ }\langle {\textit{funcType}}\rangle \text{ }IDENT\text{ }(\langle decls\rangle )\\&\text{ returns (}\langle decls\rangle )\text{ }\langle body\rangle \\ \langle {\textit{funcType}}\rangle \text{ }:: = & \text{ }node|function\\ \langle decls\rangle \text{ }:: =&\text{ }[\langle {var}\_decl\rangle \text{ };\text{ }\langle {var}\_decl\rangle ]\\ \langle {var}\_decl\rangle \text{ }:: =&\text{ }IDENT\text{ }\{, \text{ }IDENT\text{ }\}:\\& \langle kind\rangle \text{ [}when\text{ }\langle clock\_expr\rangle ]\text{ }\\ \langle clock\_expr\rangle \text{ }:: =&\text{ }IDENT\\& |not\text{ }IDENT\\& |not\text{ (}IDENT)\\& |IDENT\text{ (}IDENT)\\ \langle body\rangle \text{ }:: =&\text{ }[{var}\langle decls\rangle ]\text{ }let\text{ }\langle equations\rangle \text{ }tel\text{ }[\text{‘};\text{'}] \end{split} $ | (2) |
语句层的定义是对节点语句块的语句进行抽象得到, 根据阶段的不同, 语句结构也不尽相同, 但大多语句可以统一表示为: 右值表达式列表赋值给左值表达式列表的形式. 在TransMainArgs阶段, 语句的定义方式如下:
| $ \begin{split} \langle equations\rangle \text{ } :: =&\text{ }\langle equation\rangle \text{ }\langle equation\rangle \\ \langle equation\rangle \text{ }:: =&\text{ }\langle lhs\rangle \text{ }=\langle expr\rangle \text{ }\\ \langle lhs\rangle \text{ }:: =&\text{ }\langle lhs\_id\rangle \text{ }, \text{ }\{\langle lhs\_id\rangle \}\\ \langle lhs\_id\rangle \text{ }:: =&\text{ }IDENT \end{split}$ | (3) |
与语句层类似, 表达式层的内容也会根据翻译阶段的不同而有所差异. 在本文工作阶段, 表达式主要分为两类, 一类是无法继续细分的表达式如常量表达式, 变量表达式, 输入参数表达式等; 另一类是一些基本运算操作, 结构体求成员变量表达式等. 此处仅展示常用表达式定义方式:
| $\begin{split} \langle expr\rangle \text{ } :: =&\text{ }\langle atom\_expr\rangle \\& |\text{ }\langle expr\_list\rangle \\& |\text{ }\langle temp\_expr\rangle \\& |\text{ }\langle unop\rangle \text{ }\langle expr\rangle \\& |\text{ }\langle expr\rangle \text{ }\langle binop\rangle \text{ }\langle expr\rangle \\& |\text{ }\langle nary\rangle \text{ }\langle expr\rangle \\& |\text{ }{\rm{if}}\text{ }\langle expr\rangle \text{ }{\rm{then}}\text{ }\langle expr\rangle \text{ }{\rm{else}}\text{ }\langle expr\rangle \\& |\text{ }\langle struct\_expr\rangle \\ \langle expr\_list\rangle \text{ }:: =&\text{ (}\langle expr\rangle \text{ }\{\text{ }, \langle expr\rangle \text{ }\}) \end{split} $ | (4) |
由于Lustre语言的数据流特性, 其语义环境的定义需要考虑周期的相关操作. 在定义过程中, 语义环境被分为全局环境和局部环境两项. 全局环境用于保存整个程序的一些关键信息, 包括所有节点的信息以及全局常量相关信息. 局部环境用于存放节点的内容信息, 局部环境分为3部分, 分别是用于存储节点局部信息的本地环境le, 用于存放历史信息的时态环境te和用于统筹历史信息和节点调用信息的顶层环境e.
本地环境le存储了每个节点在每个周期的局部变量相关信息, 时态环境te将会存储每个节点自程序运行到当前周期所有的本地环境. 在Lustre中, 每个节点无论是否调用均会得到执行, 因此时态环境理论上是一个无限增加的流序列, 且周期相同的每个节点的序列长度相等, 每一项的序号对应了节点信息当时所处的周期. 由于节点调用的存在, 除主节点外节点之间可相互调用, 因此顶层环境e以树型结构的方式来存储节点调用的信息. 顶层环境有两层环境, 一个是当前节点的时态环境te, 一个是存储当前节点所调用的子节点内容的子环境e*.
图3中描述了一个包含A、B、C、D这4个节点的语义环境, 其中各个节点的历史环境te存放了节点在不同时刻的本地环境. A节点作为主节点调用了B节点和C节点, 其子环境e*中将存放B节点和C节点的局部环境. 同时D节点的局部环境也将作为C节点的子环境, 和B、C节点共同组成A节点的子环境.

|
图 3 语义环境定义 |
2.3 操作语义定义
操作语义是对程序执行步骤的抽象, 将输入参数涉及的节点的操作语义进行形式化描述, 作为后续翻译过程的正确性的证明的基础. 一段能完整地能执行功能的代码, 在执行初时需要为所有变量分配对应的内存空间, 使变量能保存数据并基于得到的数据执行计算逻辑. 此处使用第2.2节定义的语义环境来模拟实际分配的内存空间, 这样给变量分配内存将被转化为给变量分配环境空间.
基于以上思想, 节点的执行过程可以被形式化地定义为: 在节点执行初期, 为所有变量分配环境空间; 由于仅有输入参数能得到对应的值, 仅需要为输入参数对应的空间赋予对应的数值; 然后检查环境中的变量是否有重复. 完成以上步骤后, 执行节点定义的逻辑语句, 为所使用的变量以及返回值更新对应的数值. 最后检查是否存在类型不匹配问题和外部调用, 完成以上步骤即完成一次节点的执行过程.
| $ \begin{array}{c} {alloc} \_variables{{ }}\left( {empty\_locenv, {{ {\textit{allvarsof}}}}\left( {fd} \right)} \right) = te \\ {locenv} \_setvar{{ }}\left( {te, {\text{ }}fd.args, {\text{ }}vas} \right) = te1 \\ {{ids}}\_{{norepet}}\left( {fd} \right) \\ gc \vdash \left( {te1, {\text{ }}fd, {\text{ }}eh, {\text{ }}se, {\text{ }}{eval} \_stmt{{ }}\left( {fd.stmt} \right)} \right) \Rightarrow \\ \left( {te2, {\text{ }}eh1, {\text{ }}se'} \right) \\ {{locenv}}\_{{getvars }}\left( {te2, rets} \right) = vrs \\ {has} \_{\textit{types}}{{ }}\left( {vrs, {\text{ }}rets} \right) \\ {external} \_kind{{ }}\left( {fd.kind} \right) = false \\ \overline {{eval} \_node\left( {eh, se, fd, vas} \right) = eh1, {\text{ }}se', {\text{ }}vrs} \end{array} $ | (5) |
TransMainArgs阶段的工作重点在于如何将主节点复杂的输入参数以满足命令式语言规范的格式进行处理, 以及如何对节点中涉及到输入参数的变量进行更替. 在C语言中, 内容独立且可自定义的结构体能够很好地表达主节点复杂的输入参数, 其他程序也能以较为通用的方式获取并处理主节点的输入参数. 因此, 该阶段的翻译工作将着重于结构体的构造以及变量的替换方法.
在翻译前, 首先需要解决输入结构体类型定义问题. 在Coq中, 能被提取的内容需要符合抽象语法树定义的类型语法结构, 即必须为生成的输入参数结构体定义其标识符和结构体的成员变量类型. 为此, 如算法1所示, 首先对主节点的内容进行提取, 将主节点名作为结构体的类型名nid, 并将原输入参数列表经过整理变换作为结构体的成员变量ids, 然后根据Coq中的结构体语法定义, 生成
代码1.
Definition trans_body (fd: ident*node): node :=
let b := snd fd in
let nid := fst fd in
let ids := map fst (nd_args b) in
let sty := mkstruct fd in
let mkv := trans_v ids (Svar INSTRUCT sty) in
let s := trans_stmt mkv (nd_stmt b) in
(mknode Node ((INSTRUCT, sty)::nil) (nd_rets b) (nd_flags b) (nd_svars b) (nd_vars b) s b.(nd_sid) b.(nd_fld)).
然后需要构造新的结构体变量mkv, 通过更新算法将新生成的输入结构体变量用于对涉及输入参数的语句进行修改. trans_stmt函数将对主节点的语句块内容进行遍历, 当发现节点b中的节点语句块nd_stmb中有原输入参数变量时, 使用结构体变量mkv对原始变量进行修改.
3.2 语义等价的标准在操作语义中, 两条命令等价的公式如下:
| $ {c_1}\sim{c_2}, {\text{ }}{\rm{iff}}\;{\text{ }}\forall \sigma , {\text{ }}\sigma ' \in \Sigma .{\text{ }}\langle {c_1}, \sigma \rangle {\text{ }} \to \sigma ' \Leftrightarrow {\text{ }}\langle {c_2}, \sigma \rangle \to \sigma ' $ | (6) |
式(6)表示, 对于任意状态
从形式化的角度看, 证明系统真正需要检查的是编译后的代码是否满足了某些功能规范: 即我们需要将编译前后的行为以数学断言的方式定义, 并证明这些行为是一致的. 这样从程序外部看, 程序执行得到的结果并没有发生变化, 同时也保证了编译器的安全性, 从而保证了程序的等价. 翻译过程中任意两个阶段的中间语言定义为S和T (T由S经过一次或多次翻译得到), 语义保持性的公式可描述为:
| $ \forall P{\text{ }}prop(P) \Rightarrow prop(\tau (P)) \wedge {S_S}(P) \approx {S_T}(\tau (P)) $ | (7) |
其中,
基于上述过程中对整个翻译阶段内容的形式化描述, 可以通过Coq自带的定理证明策略, 对翻译过程的语义等价性进行证明. 语义等价性的描述本质上是对翻译可能引起的情况以性质的方式进行描述. 证明即是使用机械化的逻辑, 证明这些性质以消除由翻译引起的误解. 证明的实现则是对定义的性质进行归纳: 将较大而复杂的性质拆分为小且简单性质进行证明, 当复杂性质的所有子性质均得到证明时, 则复杂性质得到证明. 由于语义等价性标准的确立, 可以根据具体的翻译内容将语义等价命题拆分为多个部分进行证明, 此处将描述一些对等价性证明较为重要的命题证明内容.
3.3.1 翻译前后局部环境的匹配证明通过对执行语义的描述可以看到, 环境是对内存空间的模拟. 因此对输出结果一致性的保证在一定程度上可以通过对环境空间一致性的保证体现. 在TransMainArgs阶段翻译前后局部环境的差别主要源于输入参数的改变, 因此系统为所有变量分配的环境空间可能由此出现不同. 通过Coq对环境能否匹配的逻辑推论过程进行形式化描述, 并通过已知条件和证明策略对该过程进行证明, 从而保证环境的一致性.
从环境的角度来看翻译前后的程序的执行过程, 首先翻译前后的程序均需要为程序中所有变量基于其类型分配环境空间. 由于翻译生成了新的结构体变量, 在分配环境的过程中, 翻译后的程序本身需要检查结构体类型以及变量是否存在, 然后依据结构体变量中成员变量数量和类型分配内存空间. 此时新结构体类型由于是通过将输出参数列表组合而成, 根据C语言内存分配的定义, 结构体内容的内存分配还需要满足对齐规则且大小与原参数大小一致. 满足以上规则即可保证翻译前后分配的环境空间(内存空间)是一致的.
基于以上推论, 局部环境匹配的推理过程可以被形式化地描述为代码2所示的形式化引理: 对于任意翻译前的环境e1, 为程序的所有变量分配环境空间后得到新的环境空间, 此新空间中不能存在翻译后的结构体变量INSTRUCT, 同时需要保证每一个翻译前的输入参数变量类型大小均小于等于4 B. 那么如果存在一个环境空间e2, 为该空间所有变量分配环境空间后, 每个变量都能在e1 中找到对应的变量; 且环境e2中存在一个特殊的结构体变量, 该结构体变量被分配的空间大小和e1中所有输入参数的空间大小相等; 同时e1的每一个输入参数均能在结构体中找到对应的变量. 满足以上过程的推断即可保证编译前后的局部环境保持了一致性.
代码2.
Lemma alloc_variables_exists:
forall f e1, alloc_variables empty_locenv (allvarsof f) e1 ->
forall fid, ~ In INSTRUCT (allidsof f ++ predidof f) ->
ids_norepet f ->
sizeof_fld (fieldlist_of (nd_args f)) <= Int.max_signed ->
(forall id ty, In (id, ty) (nd_args f) -> 0 < sizeof ty) ->
exists e2, alloc_variables empty_locenv (allvarsof (trans_body (fid,f))) e2
/\ locenv_match (fid,f) e1 e2
/\ exists m, e2 ! INSTRUCT = Some (m,mkstruct (fid,f))
/\ Z.of_nat (length m) = sizeof (mkstruct (fid,f))
/\ (forall id ty, In (id, ty) (nd_args f) ->
exists mv : mvl, e1 ! id = Some (mv,ty)
/\ Z.of_nat (length mv) = sizeof ty).
该引理的证明过程则是不断地使用Coq提供的证明策略, 将推论拆分为多个子性质, 并构造为新的引理进行证明. 如证明翻译后的为所有变量分配空间得到的环境依旧为e2时, 需要先保证翻译前的所有变量能正确分配空间得到e2. 而所有变量的空间分配可以拆分为对输入变量、输出变量和局部变量各自的空间分配. 由于3种变量在翻译前未进行修改, 可以直接对三者通过内存和环境的匹配予以证明. 对于参与到翻译过程中的变量的相关推论也是相同思路. 在翻译后, 此时由于不能保证翻译后的输入结构体和输出、局部变量的隔离性, 不能简单地拆分. 因此需要通过引入新的引理, 将为输入变量和局部变量的环境分配转换到在总体环境下单独执行, 得到新的环境空间. 这样为所有翻译后的变量分配环境空间将转化为: 在已为输入变量和局部变量分配空间后的环境下, 为输入结构体分配空间, 以得到同样的环境e2, 通过此方法推论得以证明并将转化为的证明的前提条件.
基于以上思想, 复杂的推论将被逐步拆分为多个简单的, 基于翻译后输入结构体性质的假设, 最后对输入结构体在环境中的存在性进行证明, 从而保证了分配参数后的局部环境在翻译前后的一致性.
根据执行语义来看, 除了分配参数后环境的一致性以外, 环境的匹配还包括输入参数绑定后的环境一致性问题, 以及翻译前后执行语义的一致性问题. 除此之外包括程序初始化的一致性等, 此类性质在推论的定义思路上与本问题类似, 因此不做过多赘述.
3.3.2 程序结果的一致性证明通过对第3.3.1节提及的翻译过程中出现的不一致的语法的语义性质的定义与证明, 能够最终证明程序体在翻译前后语义的一致性, 即翻译前后输入、输入结果以及环境的变化的等价. 基于第3.3.1节推论的形式化思路, 对程序的执行过程和本阶段的工作内容进行抽象, 程序执行的推论形式化描述如代码3所示: 对翻译前的程序体prog1来说, 为主节点初始化后可得到对应的常量环境和自定义环境e. 其中翻译前的程序体, 在为其输入对应的输入数据流vass后, 执行程序的逻辑运算得到对应的输出数据流vrss. 由于该阶段的工作是输入参数结构的修改, 不涉及内容修改, 因此输入数据流对应的值与初始化后环境空间中存储的输入参数的值匹配. 而对于翻译后的程序体prog2来说, 在保证该程序体的主节点初始化后得到的环境与翻译前相同, 且两个程序的返回值列表相等的基础上, 如果为翻译后结构体提供与翻译前的程序相同的输入数据流, 在翻译后的程序执行逻辑运算后, 其得到的输出数据流与翻译前的程序经计算得到的输出数据流的结果一定是一致的, 即翻译行为并没有改变原程序体的语义, 从而保持了语义的一致性. 其形式化定义如代码3.
代码3.
Theorem trans_program_correct:
forall gc e main1 vass mass vrss maxn,
Lenv.initial_state prog1 gc init_node main1 e->
exec_prog prog1 gc (eval_node true) main1 e 1 maxn vass vrss ->
vargs_matchss (nd_args (snd main1)) vass mass ->
exists main2, Lenv.initial_state1 prog2 gc init_node main2 e
/\ nd_rets (snd main2) = nd_rets (snd main1)
/\ nd_kind (snd main2) = Node
/\ exec_prog1 prog2 gc (eval_node true) main2 e 1 maxn mass vrss.
对该过程的证明将通过Coq的证明策略, 以分类讨论的形式, 分解为多个覆盖范围更小的性质, 而这些性质推论多数已提前证明完毕, 如第3.3.1节介绍的局部环境匹配性质. 但在证明过程中可以发现, 该定理是一个整体性的推论, 需要全面考虑所有可能出现的情况, 因此还需要提出更多引理, 如当输入参数不存在时候的环境的匹配的证明. 然后将这些已证明的子定理应用于整个证明过程的假设中, 将待证明的假设逐步转化为前提, 应用于不同情况, 即可完成整个程序正确性定理的证明.
4 实验实验总共由3部分组成: 首先是构造主节点输入结构的翻译程序, 使用翻译程序对近300个Lustre源程序测试用例进行测试, 保证翻译过程的基本正确性; 然后再通过交互式定理证明器Coq对翻译过程的语义进行保持性证明, 保证翻译过程的语义一致性; 最后使用NASLAND的基础算子和组态算法对翻译程序进行验证. 在对翻译过程进行语义一致性证明时可能会修改翻译过程的代码, 因此前两个实验会不断交替进行, 直到所有语义证明完成.
在Coq中, 如果翻译过程符合Coq的编码规范, 并且证明过程没有发生错误, Coq可以通过自身的提取机制, 将翻译算法提取到Ocaml程序中, 最后将Ocaml编译为可执行的可信代码编译器.
在测试阶段, 首先将单个核仪控基础算子构造为独立的算法组态, 并利用可信代码编译器生成所有算法组态的C程序. 然后通过人工检查的方式, 检查代码的正确性, 并与KCG生成的C程序进行人工对比. 最后将由可信代码编译器以及KCG生成的C程序分别通过NASPES编译为可执行代码, 下装到核电站嵌入式设备中, 对比验证功能的正确性. 最终结果显示, 由可信代码编译器生成的C程序正确实现了NASLAND中100多个基础算子以及10余个核仪控算法组态的功能.
实验表明通过形式化的可信代码翻译程序能够生成与源代码行为一致的目标代码, 并保证目标代码可信.
5 结论为提升编译器的可靠性, 并保证可信编译器生成的可信代码能够应用于安全关键领域的核仪控系统中. 本文运用形式化的方法对同步数据流语言 Lustre*到 C的编译器的输入参数的翻译工作进行了形式化描述及验证. 该阶段的工作均借助辅助定理证明助手Coq完成.
(1) 通过对Lustre的语法解析, 定义了Lustre和中间语言LustreR的抽象语法树, 在Coq中形式化地描述的了该抽象语法树.
(2) 根据Lustre的特性, 定义出该语言的语义环境, 并基于语义环境形式化地演绎了节点的执行语义.
(3) 针对该阶段的主要工作内容, 形式化地定义主节点输入参数的翻译方法, 将复杂的输入参数以结构体的方式翻译, 以满足核电仪控系统的使用要求.
(4) 定义翻译前后语义等价的判断标准, 并基于该标准完成对翻译前后执行语义一致性的形式化验证.
(5) 本研究实现了Lustre语言的输入参数从同步数据流模式到命令式语言的翻译, 测试通过了100多个核能领域仪控设备基础算子以及10余个核仪控算法组态, 其生成的可信代码应用于核仪控设备上. 可以为后续其他同步特征的命令式语言翻译提供参考.
| [1] |
Knight JC. Safety critical systems: Challenges and directions. Proceedings of the 24th International Conference on Software Engineering. Orlando: Association for Computing Machinery, 2002. 547–550.
|
| [2] |
何炎祥, 吴伟, 刘陶, 等. 可信编译理论及其核心实现技术: 研究综述. 计算机科学与探索, 2011, 5(1): 1-22. DOI:10.3778/j.issn.1673-9418.2011.01.001 |
| [3] |
Leroy X. Formal verification of a realistic compiler. Communications of the ACM, 2009, 52(7): 107-115. DOI:10.1145/1538788.1538814 |
| [4] |
Bertot Y, Castéran P. Interactive theorem proving and program development: Coq’Art: The Calculus of Inductive Constructions. Springer Science & Business Media, 2013.
|
| [5] |
Necula GC, Lee P. The design and implementation of a certifying compiler. ACM SIGPLAN Notices, 1998, 39(4): 612–625,
|
| [6] |
Pnueli A, Siegel M, Singerman E. Translation validation. Proceedings of the 4th International Conference on Tools and Algorithms for the Construction and Analysis of Systems. Lisbon: Springer, 1998. 151–166,
|
| [7] |
Pnneli A, Shtriehman O, Siegel M. Translation validation for synchronous languages. Proceedings of the 25th International Colloquium on Automata, Languages, and Programming. Aalborg: Springer, 1998. 235–246.
|
| [8] |
Ngo VC, Talpin JP, Gautier T, et al. Formal verification of compiler transformations on polychronous equations. Proceedings of the 9th International Conference on Integrated Formal Methods. Pisa: Springer, 2012. 113–127,
|
| [9] |
Ngo VC, Talpin JP, Gautier T, et al. Translation validation for clock transformations in a synchronous compiler. Proceedings of the 18th International Conference on Fundamental Approaches to Software Engineering. London: Springer, 2015. 171–185.
|
| [10] |
Ngo VC, Talpin JP, Gautier T, et al. Formal verification of synchronous data-flow program transformations toward certified compilers. Frontiers of Computer Science, 2013, 7(5): 598-616. DOI:10.1007/s11704-013-3910-8 |
| [11] |
Ngo VC, Talpin JP, Gautier T. Translation validation for synchronous data-flow specification in the SIGNAL compiler. Proceedings of the 35th International Conference on Formal Techniques for Distributed Objects, Components, and Systems. Grenoble: Springer, 2015. 66–80,
|
| [12] |
麻莹莹, 马振威, 陈钢. 基于Coq的分块矩阵运算的形式化. 软件学报, 2021, 32(6): 1882-1909. DOI:10.13328/j.cnki.jos.006255 |
| [13] |
姜菁菁, 乔磊, 杨孟飞, 等. 基于Coq的操作系统任务管理需求层建模及验证. 软件学报, 2020, 31(8): 2375-2387. DOI:10.13328/j.cnki.jos.005961 |
| [14] |
李亚男, 邓玉欣, 刘静. 基于Coq的Paxos形式化建模与验证. 软件学报, 2020, 31(8): 2362-2374. DOI:10.13328/j.cnki.jos.005960 |
| [15] |
Bourke T, Brun L, Dagand PÉ, et al. A formally verified compiler for Lustre. Proceedings of the 38th ACM SIGPLAN Conference on Programming Language Design and Implementation. Orlando: Association for Computing Machinery, 2017. 586–601.
|
| [16] |
尚书, 甘元科, 石刚, 等. 可信编译器L2C的核心翻译步骤及其设计与实现. 软件学报, 2017, 28(5): 1233-1246. DOI:10.13328/j.cnki.jos.005213 |
| [17] |
康跃馨, 甘元科, 王生原. 同步数据流语言可信编译器Vélus与L2C的比较. 软件学报, 2019, 30(7): 2003-2017. DOI:10.13328/j.cnki.jos.005755 |
| [18] |
Berry G, Gonthier G. The ESTEREL synchronous programming language: Design, semantics, implementation. Science of Computer Programming, 1992, 19(2): 87-152. DOI:10.1016/0167-6423(92)90005-V |
| [19] |
Pilaud D, Halbwachs N, Plaice JA. LUSTRE: A declarative language for real-time programming. Proceedings of the 14th ACM SIGACT-SIGPLAN Symposium on Principles of Programming Languages. Munich: ACM, 1987. 178–188.
|
| [20] |
Halbwachs N, Caspi P, Raymond P, et al. The synchronous data flow programming language LUSTRE. Proceedings of the IEEE, 1991, 79(9): 1305-1320. DOI:10.1109/5.97300 |
| [21] |
LeGuernic P, Gautier T, Le Borgne M, et al. Programming real-time applications with SIGNAL. Proceedings of the IEEE, 1991, 79(9): 1321-1336. DOI:10.1109/5.97301 |
| [22] |
Le Guernic P, Talpin JP, Le Lann JC. Polychrony for system design. Journal of Circuits, Systems, and Computers, 2003, 12(3): 261-303. DOI:10.1142/s0218126603000763 |
 2023, Vol. 32
2023, Vol. 32


