图论问题在计算机科学领域具有重要地位, 作为运筹学领域的一个重要分支, 当今最大流算法已经被广泛运用于实际工程与技术中. 例如, 计算机网络中基于最大流的路由选择算法[1, 2], 分布式存储系统的查询[3], 除此之外, 最大流算法还大量运用于计算机视觉领域中对图形的分割、立体和重塑[4, 5], 以及机器学习领域[6, 7]. 因此, 为了提升对大数据量最大流模型的求解速度, 对最大流算法的优化是十分必要的, 最大流问题的研究具有较高的实用价值.
最大流问题是指在一张给定流网络上进行搜索、计算由源点s出发到汇点t的最大可行流量. 最大流算法大体上分为两大类: 第1类是由Ford等人在1956年提出的增广算法[8], 增广算法将网络中所能找到的任意一份流量称为可行流量, 当且仅当其符合容量限制与流守恒定律. 该类算法的思想是在流网络中不断地寻找增广路径与该路径的阻塞流, 直到网络中由源点s到汇点t的所有可行路径都被阻塞, 即网络中不存在任何一条增广路径时, 算法终止. 第2类最大流算法是由Karzanov在1974年提出的基于“预流”概念的预流推送算法[9].
对于基于增广路径的经典算法Ford-Fulkerson算法而言, Edmonds等人[10]和Dinitz[11]分别在1972年和1970年提出了运用层次网络来对搜索策略进行改进. 随着大数据时代的来临, 信息数据量爆炸式激增, 传统的增广路径最大流算法的搜索策略无法高效的应用于现今复杂多样的流网络结构. 因此, 许多学者已经对最大流算法提出了优化和改进, 其中包括对动态网络最大流算法的优化, 对包含交叉顶点的最大流算法优化以及通过构建反向有效网络来优化Dinic算法等[12-17].
在实际工程应用中, 传统基于深度优先策略的Ford-Fulkerson算法和基于宽度优先策略的Edmonds-Karp算法时常因为无法高效的应用于稠密网络而不受工程实践者的青睐, 而基于层次网络的Dinic算法有着简洁、易懂且高效的特点, 常受到实践者们的喜爱. 但Dinic算法在实际运用的过程中会反复搜索网络的“无效部分”, 且随着流网络规模及稠密程度的增大, Dinic算法的效率将变得十分低下. 针对这一问题, 本文对基于层次网络的原始Dinic算法在增广路径搜索策略上实现优化, 通过记录单次搜索的搜索状态来实现记忆化搜索, 能够有效地避免算法进行无效的搜索和增广, 最终提高算法效率. 除此之外, 在本文实验部分提出了搜索步数、增广步数以及有效搜索率等概念来衡量、量化和对比算法额外代价与搜索效率.
1 基本概念与定义 1.1 最大流的数学模型若带权有向网络G=(V,E, W)满足以下两个条件: 1) s、t均属于结点集合V且源点s入度为0, 汇点t出度为0; 2)设c(u,v)为边容量, 对任意的边满足:
| $ \forall \left( {{{u}}, {{v}}} \right) \in {{E}}, \;{{c}}\left( {{{u}}, {{v}}} \right) = W(u, v) $ | (1) |
则称G为流网络, 记作G=(V, E, C). 在流网络G=(V, E, C)中, 设实值函数f为G的流, 对任意的边满足容量限制:
| $ \forall \left( {{{u}}, {{v}}} \right) \in {{E}},\; 0 \leqslant {{f}}\left( {{{u}}, {{v}}} \right) \leqslant {{c}}\left( {{{u}}, {{v}}} \right) $ | (2) |
且同时满足流守衡定律:
| $ {\displaystyle \sum }_{v\in \text{ }V\backslash u}f\left(v, u\right)={\displaystyle \sum }_{v\in V\backslash u}f\left(u, v\right) $ | (3) |
则称流f为流网络G上的一个可行流量. 则由流f所诱导的残流网络为
| $ {c_f}\left( {u, v} \right) = \left\{ \begin{gathered} c(u, v) - f(u, v),\; (u, v)\in E \\ f(v, u),\;(v, u)\in E \\ \end{gathered} \right. $ | (4) |
其中, 对R中任意的边满足:
| $ {E_f} = \left\{ {\left( {{{u}}, {{v}}} \right) \in E{{|}}\forall {c_f}\left( {{{u}}, {{v}}} \right) \geqslant 0} \right\} $ | (5) |
最大流问题是求解当前流网络G中的最大可行流f的容量总和:
| $ {f}_{\mathrm{max}}=Max\left({\displaystyle \sum }_{v\in \text{ }V\backslash \left\{t\right\}}f\left(u, t\right)\right) $ | (6) |
层次网络
STACK表示在搜索过程中动态变化的堆栈, 按搜索次序依次存入流网络G中各待处理的结点. SEEN是一个无序的结点集合, 保存当前搜索已访问结点.
1.4 深度优先搜索树| $ TREE(s, t)=\{(t{\textit{-}}v)\text{, }(v{\textit{-}}\cdots {\textit{-}}u), (u{\textit{-}}s)\} $ | (7) |
将一条s-t路径P以结点n分为上、下两个部分, 即
原始Dinic算法的思想是先用宽度优先策略在残流网络R上生成层次网络D, 再对层次网络D采用深度优先策略搜索增广路径, 直至当前层次网络中无法找到任意一条s-t增广路径时, 对当前残流网络重新划分层次, 直至残流网络无法再生成层次网络时, 算法结束. Dinic算法描述如算法1.
算法1. Dinic算法
输入: G=(V, E, C), 源点s和汇点t
输出: 残流网络R和最大流fmax
1) 初始化:
2) 步骤1. 使用宽度优先搜索对残流网络R分层, 生成层次网络
3) 步骤2. 若汇点t属于层次网络
4) 步骤3. 在所得层次网络
5) 步骤4. 计算路径P的阻塞流:
| $\scriptstyle {c_f}\left( P \right) = \min \left( {R\left( {u, v} \right){\text{|}}\forall \left( {u, v} \right) \in P} \right) $ |
转步骤5;
6) 步骤5. 执行推流, 更新残流网络:
| $\scriptstyle {{R}}\left( {{{u}}, {{v}}} \right) = {{R}}\left( {{{u}}, {{v}}} \right) - {c_f}\left( P \right), \; \forall \left( {{{u}}, {{v}}} \right) \in {{P}} $ |
| $\scriptstyle {{R}}\left( {{{v}}, {{u}}} \right) = {{R}}\left( {{{v}}, {{u}}} \right) + {c_f}\left( P \right),\; \forall \left( {{{u}}, {{v}}} \right) \in {{P}} $ |
转步骤6;
7) 步骤6. 更新最大流
原始Dinic算法在层次网络中搜索增广路径时, 会随着搜索次数的增加逐渐减慢算法在单张层次网络上的收敛速度, 其原因是深度优先搜索策略总是从源点s起始, 每当成功找到s-t路径时, 其阻塞流几乎无可避免地会对后续若干次路径搜索产生影响. 在后续搜索中, 深度优先的搜索策略会继续反复的搜索残流网络中的“无效部分”, 这些“无效部分”是若干次搜索所阻塞的路径或流网络中本来就存在的仅具有上连通性而不具有下连通性的路径的集合. 最坏情况下, Dinic算法在单张层次网络上每次搜索一条s-t增广路径的代价随搜索次数依次递增.
如图1(a)所示层次网络为例, 当前层次为3. 图1–图3展示了深度优先策略的搜索步骤, 其中右侧所示STACK是搜索过程中动态堆栈. 表1汇总了搜索过程及搜索代价.
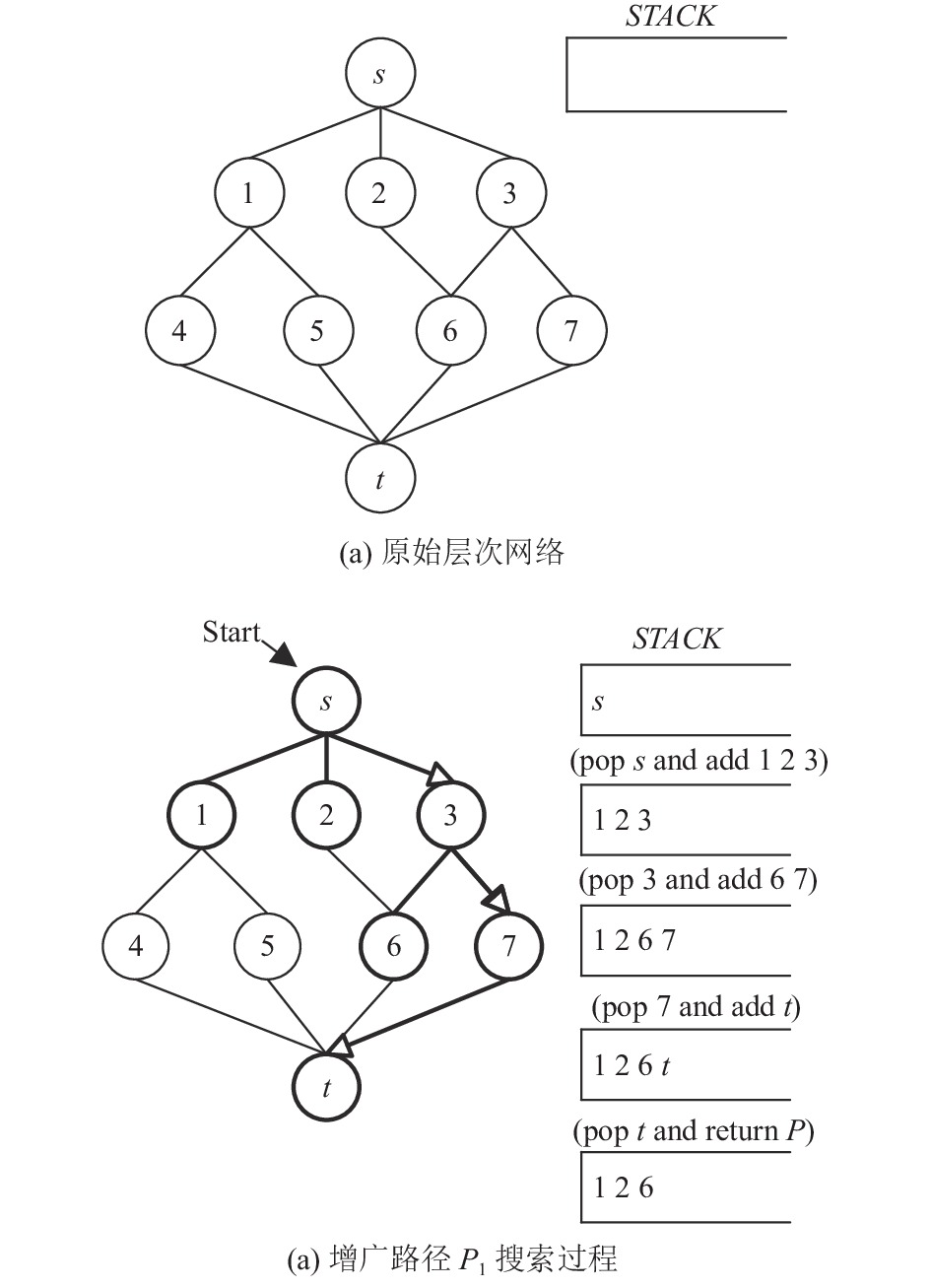
|
图 1 原始层次网络与搜索增广路径P1 |
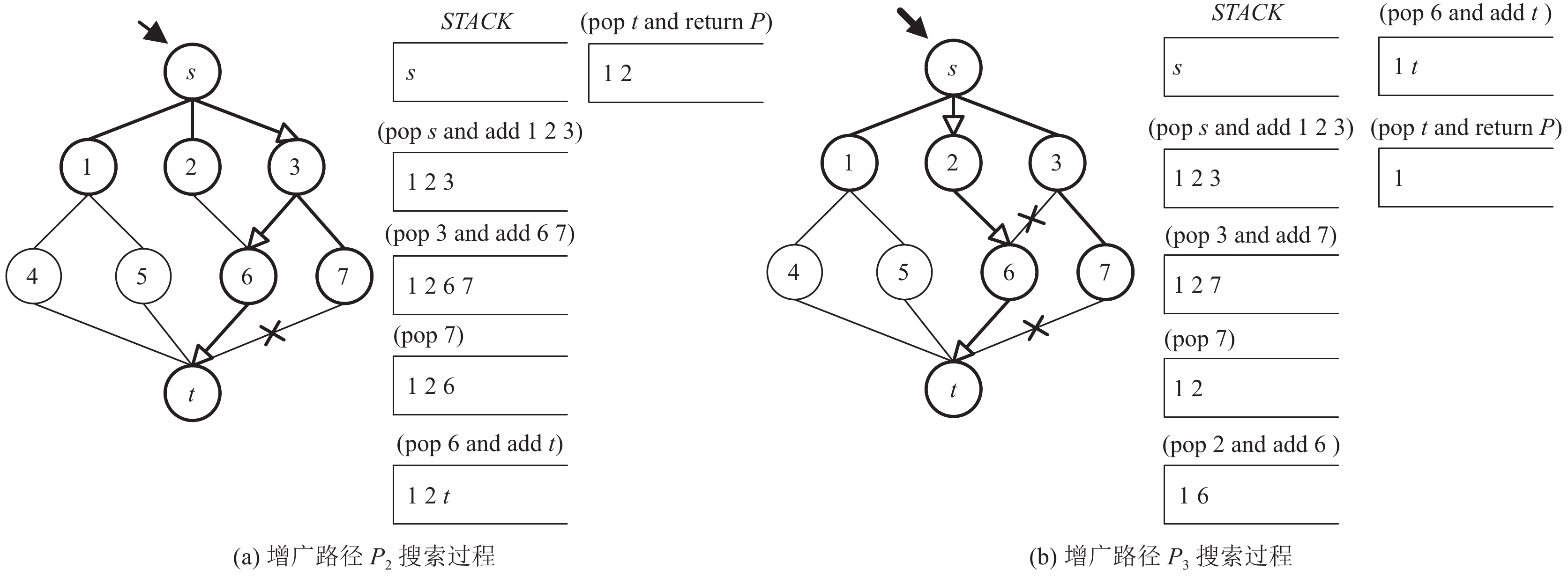
|
图 2 搜索增广路径P2、P3 |

|
图 3 搜索增广路径P4、P5 |
| 表 1 原始Dinic算法搜索过程 |
由上述例子可以得出, 深度优先的搜索策略能够成功地在层次网络中找到所有可能的增广路径P1、P2、P3、P4、P5, 但Dinic算法每次都从源点s起始, 额外增加了许多不必要的无效搜索步数, 增加额外开销. 例如, 在搜索增广路径P2时, (3, 7)是无效搜索步, 见图2(a); 在搜索增广路径P5时, (s, 3)、(3, 7)、(s, 2)、(2, 6)、(1, 5)是无效搜索步, 见图3(b). 由此可见, Dinic算法在层次网络中搜索增广路径的额外代价随搜索次数增加而递增.
3 记忆化搜索算法 3.1 算法思想由上述举例中不难发现, 相邻的两次路径搜索过程中至少存在前k步重合(
(1) 满足连通性限制.
(2) 满足最短路径限制.
深度优先搜索策略每次搜索从源点s起始, 仅当
记忆化搜索策略还需保证所得s-t路径满足最短路径限制. 假设层次网络
本文提出的记忆化搜索策略与常规深度优先搜索策略不同之处在于, 算法将上轮搜索结果和状态保存在STACK, SEEN, TREE中, 在此基础上进行下一次搜索并持续更新当前搜索状态, 来保证每次调用搜索时总能针对网络中未搜索过的部分, 避免了原始Dinic算法反复的搜索残流网络中的“无效部分”. 从宏观上看, 每轮执行的若干次记忆化搜索等效于在单张层次网络上进行一次完整的深度优先遍历, 得到若干条增广路径. 记忆化搜索算法描述如算法2.
算法2. 记忆化搜索算法
输入:
输出: STACK, SEEN, TREE
1) 步骤1. 若STACK非空则取栈顶元素u, 转步骤2; 反之, 算法结束;
2) 步骤2. 若所取得顶点u是源点s, 则转步骤4; 反之, 转步骤3;
3) 步骤3. 若结点u在搜索树TREE中上连通性校验通过, 则转步骤4; 反之, 将结点u设置成未访问态, 即
4) 步骤4. 获取结点u的邻接结点v, 转步骤5;
5) 步骤5. 若结点v是未访问态, 即
6) 步骤6. 若邻接结点v在结点u的下一层, 即
7) 步骤7. 将结点v加入动态堆栈STACK; 将结点v设置成已访问态; 将边
基于记忆化搜索策略的最大流算法首先会根据残流网络R来构建层次网络
算法3. 基于记忆化搜索策略的最大流算法
输入: G=(V, E, C), 源点s和汇点t
输出: 残流网络R和最大流fmax
1) 初始化:
2) 步骤1. 使用宽度优先搜索对残流网络R分层, 生成层次网络
3) 步骤2. 若汇点t属于层次网络D, 转步骤3; 反之, 返回当前最大流fmax, 算法结束;
4) 步骤3. 将源点s加入动态堆栈STACK中, 即
5) 步骤4. 在所得层次网络D上采用记忆化搜索策略搜索s-t增广路径P. 若路径P存在, 则转步骤5; 反之, 转步骤1;
6) 步骤5. 计算路径P的阻塞流:
| $\scriptstyle {c_f}\left( P \right) = \min \left( {R\left( {u, v} \right){\text{|}}\forall \left( {u, v} \right) \in P} \right) $ |
转步骤6;
7) 步骤6. 执行推流, 更新残流网络:
| $\scriptstyle {{R}}\left( {{{u}}, {{v}}} \right) = {{R}}\left( {{{u}}, {{v}}} \right) - {c_f}\left( P \right), \forall \left( {{{u}}, {{v}}} \right) \in {{P}} $ |
| $ \scriptstyle {{R}}\left( {{{v}}, {{u}}} \right) = {{R}}\left( {{{v}}, {{u}}} \right) + {c_f}\left( P \right), \forall \left( {{{u}}, {{v}}} \right) \in {{P}} $ |
转步骤7;
8) 步骤7. 更新最大流

|
图 4 基于记忆化搜索策略的最大流算法流程图 |
本文所提出的基于记忆化搜索策略的最大流算法, 须在层次网络上执行搜索. 采用何种搜索策略不直接影响算法何时停止搜索增广路径, 算法的终止条件是当前层次网络中不包含汇点t. 因此, 若所采取的搜索策略能在当前层次网络中找到至少一条s-t增广路径, 则一定能在后续若干张层次网络中找到最大流.
当采用记忆化搜索策略时, 设所找到的s-t增广路径为P, 则每轮搜索会将至少lP–1 (lP为P的路径长度)个结点的访问状态标记成已访问态, 并且每轮搜索结束后仅把汇点

|
图 5 记忆化搜索策略的最坏情况 |
3.3 实例分析
初始层次网络如图1(a)所示, 当前层次为3. 图6、图7展示了记忆化搜索策略的搜索步骤, 右侧所示

|
图 6 搜索增广路径
|
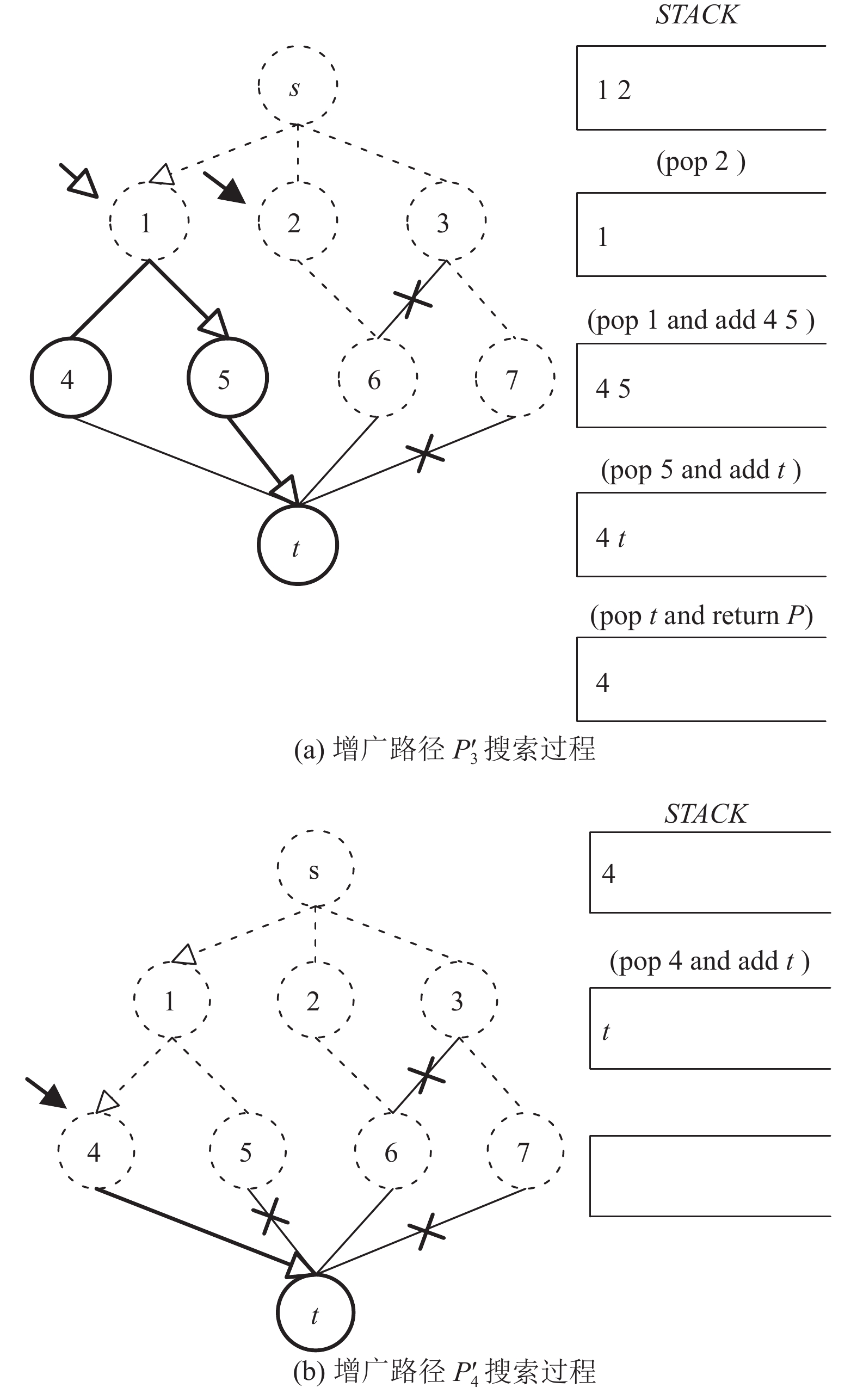
|
图 7 搜索增广路径
|
| 表 2 记忆化策略搜索过程 |
记忆化策略首次搜索与深度优先策略保持一致, 算法依次遍历结点(s, 1, 2, 3, 6, 7, t)后找到增广路径
第2次搜索从结点6开始, 假设层次网络中边(7,t)被阻塞, 算法通过(6, t)找到汇点t, 搜索所得增广路径为
第3次搜索从结点2开始, 假设层次网络中边(7, t)、(3, 6)被阻塞, 由于结点6已经在上轮搜索中已被标记成已访问态, 故算法无法通(2, 6, t)找到汇点t. 因此, 算法将从结点1继续恢复搜索, 依次遍历结点(4, 5, t)找到汇点t, 所得增广路径为
根据上一轮搜索所保存的搜索状态, 最后一轮搜索从结点4开始, 假设层次网络中边(7, t)、(3, 6)、(5, t)被阻塞, 算法通过(4, t)找到汇点t, 所得增广路径为
若当流网络中存在类似图8(a)所示的带状分支结构, 两条增广路径长度同为k+2, 则路径有效搜索步数

|
图 8 记忆化搜索策略的最优情况 |
在包含n个结点、m条边的流网络G中, 最坏情况下, 每张层次网络中仅能找到一条增广路径, 算法效率等同于基于宽度优先搜索策略的Edmonds-Karp算法, 因此最坏复杂度是
本文实验部分所有测试代码均是基于Python实现, 由Python 3.9编译, 实验测试平台配置为Intel i7 2.59 GHz CPU和16 GB内存, 64-bit Windows操作系统的计算机, 本文实验所采用的测试数据均为随机生成的流网络, 在对应ENr下分别生成10张随机流网络进行测试, 测试结果取平均值. 实验变量定义如下.
1) FVm表示最大流的流量值.
2) ENr表示随机流网络中边数与结点数的比值.
3) Vn表示有效搜索总步数, 即增广路径长度总和; Sn表示搜索总步数, 即搜索总代价; Vr是有效搜索率, 其定义为:
本文首先在数值上验证了算法的正确性, 在算法执行结束后, 将结合最大流值FVm、残流网络R、流网络G来计算流经每一条边的流量值, 计算其与本文算法所得最大流量值、源点s发出的流量值以及流入汇点t的流量值是否相等, 来验证最大流量FVm数值大小的正确性. 此外, 还将验证每个结点(除s、t以外)的存余流量(excess flow)均为0, 来确定本文算法所得最终残流网络中不存在s-t路径. 通过上述步骤, 可以证明本文算法在数值上的正确性与可行性.
本文在初始包含500个结点、5 000条边, 每次扩张5 000条边的随机流网络中, 对比了3种传统最大流算法: Ford-Fulkerson算法、Edmonds-Karp算法、Dinic算法以及本文所提的记忆化搜索算法的耗时和搜索效率. 算法耗时的测试结果如图9所示, 当流网络较为稀疏时, Ford-Fulkerson算法耗时上升明显, 是由于深度优先搜索在稀疏流网络中搜索路径的任意性导致算法所得增广路径过长, 进而导致Ford-Fulkerson算法耗时开销明显增大. 而在基于层次网络的最短增广算法中, Edmonds-Karp算法、Dinic算法以及本文算法在稀疏网络上耗时差距不大. 但随着流网络稠密程度上升, Edmonds-Karp算法、Dinic算法的耗时上升明显. 其原因是Edmonds-Karp算法所采用的宽度优先搜索策略每轮搜索大量重复, 导致其搜索代价随着网络稠密程度的增加而递增. Dinic算法通过循环利用层次网络, 减少了宽度优先搜索的调用次数, 因此其算法耗时相较于Edmonds-Karp算法有所下降. 本文算法通过记忆化策略更高效的利用层次网络中的连通路径, 进一步避免了在无效路径上的无效搜索, 因此在稠密网络中的算法耗时大幅下降.

|
图 9 算法耗时对比 |
搜索效率的对比主要针对基于层次网络的4种最大流算法, 分别是Edmonds-Karp算法、Dinic算法以及逆向Dinic算法和本文算法, 测试结果如图10和表3所示. 逆向Dinic算法是由文献[14]所提出的基于有效反向网络的最大流算法, 该算法通过不断地剪枝, 剔除

|
图 10 有效搜索率对比 |
| 表 3 搜索代价和有效搜索率测试结果 |
逆向Dinic算法的搜索代价及有效搜索率波动较大, 测试结果表明, 其有效搜索率在本文所定义的随机网络结构中难以体现较为平稳的增长趋势. 在测试过程中发现逆向Dinic算法往往在上连通性较好的网络中对有效搜索率Vr的优化明显, 但在上连通性不佳的网络中Vr接近于原始Dinic算法, 其原因是逆向Dinic算法在搜索过程中路径递归迭代次数不断增加, 若当前路径不连通时逐层路径回退会增加额外搜索代价, 且剪枝操作至多会增加
本文提出了一个基于记忆化搜索策略的最大流算法, 该算法在基于层次网络的最大流算法上优化了搜索效率, 通过记忆化存储路径搜索状态来避免算法反复搜索网络中的“无效部分”, 进而避免了大量无效增广. 实验结果表明, 算法在稠密网络中的搜索总代价与算法执行效率明显优于传统Edmonds-Karp算法和Dinic算法, 且比同类算法更具稳定性. 与此同时, 本文算法仍旧保留着与传统增广路径算法一致的简易性与可行性. 现如今, 最大流算法被广泛地运用于实际工程技术当中, 本文算法具有较高的实用价值, 为最大流算法相关工程技术的应用与开发提供了一个便捷、可行且高效的选择.
| [1] |
Alzaben N, Engels DW. End-to-end routing in SDN controllers using max-flow min-cut route selection algorithm. Procedings of the 24th International Conference on Advanced Communication Technology (ICACT). PyeongChang: IEEE, 2021. 461–467.
|
| [2] |
毛善丽, 李晓卉, 蔡彬, 等. 基于EHWSN的能量均衡动态最大流路由算法. 传感技术学报, 2017, 30(2): 291-295. DOI:10.3969/j.issn.1004-1699.2017.02.021 |
| [3] |
徐毅, 王建民, 黄向东, 等. 一种基于最大流的分布式存储系统中查询任务最优分配算法. 计算机学报, 2019, 42(8): 1858-1872. DOI:10.11897/SP.J.1016.2019.01858 |
| [4] |
Duan YP, Huang WM, Chang HB. Shape prior regularized continuous max-flow approach to image segmentation. Proceedings of the 21st International Conference on Pattern Recognition (ICPR2012). Tsukuba: IEEE, 2012. 2516–2519.
|
| [5] |
Baxter JSH, Rajchl M, Mcleod AJ, et al. Directed acyclic graph continuous max-flow image segmentation for unconstrained label orderings. International Journal of Computer Vision, 2017, 123(3): 415-434. DOI:10.1007/s11263-017-0994-x |
| [6] |
Pang SN, Zhu L, Bany T, et al. Online max-flow learning via augmenting and de-augmenting path. Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN). Rio de Janeiro: IEEE, 2018. 1–8.
|
| [7] |
Zhu L, Pang SN, Sarrafzadeh A, et al. Incremental and decremental max-flow for online semi-supervised learning. IEEE Transactions on Knowledge and Data Engineering, 2016, 28(8): 2115-2127. DOI:10.1109/TKDE.2016.2550042 |
| [8] |
Ford LR Jr, Fulkerson DR. Maximal flow through a network. Canadian Journal of Mathematics, 1956, 8: 399-404. DOI:10.4153/CJM-1956-045-5 |
| [9] |
Karzanov AV. Determining the maximal flow in a network by the method of preflows. Soviet Mathematics Doklady, 1974, 15(3): 434-437. |
| [10] |
Edmonds J, Karp RM. Theoretical improvements in algorithmic efficiency for network flow problems. Journal of the ACM, 1972, 19(2): 248-264. DOI:10.1145/321694.321699 |
| [11] |
Dinitz EA. Algorithm for solution of a problem of maximum flow in networks with power estimation. Soviet Mathematics Doklady, 1970, 11(5): 1277-1280. |
| [12] |
张柏礼, 王媛瑗, 洪亮, 等. 动态网络中最大流快速增量求解. 东南大学学报(自然科学版), 2017, 47(3): 450-455. DOI:10.3969/j.issn.1001-0505.2017.03.006 |
| [13] |
罗甜甜, 赵礼峰. 包含交叉顶点的最大流改进算法. 计算机工程, 2020, 46(11): 48-52. DOI:10.19678/j.issn.1000-3428.0056170 |
| [14] |
韩颖铮, 邓国强, 陆以勤. 基于有效反向网络的最大流算法. 通信学报, 2018, 39(S1): 179-183. |
| [15] |
赵礼峰, 邵丽萍. 求解最大流问题的算法. 计算机工程与设计, 2019, 40(8): 2224-2227, 2241. DOI:10.16208/j.issn1000-7024.2019.08.020 |
| [16] |
邵丽萍, 赵礼峰. 基于宽度优先的网络最大流求解算法. 计算机技术与发展, 2019, 29(6): 62-65. DOI:10.3969/j.issn.1673-629X.2019.06.013 |
| [17] |
Wei W, Liu Y, Zhang RQ. SPLMax: Exploiting the simple path introduced locality for maximum flow acceleration. IEEE Communications Letters, 2018, 22(7): 1330-1333. DOI:10.1109/LCOMM.2018.2830786 |
 2023, Vol. 32
2023, Vol. 32


