深度学习的出现, 使得识别和使用数据的技术, 得到了发展^[1]. 特别是卷积神经网络(CNN), 在图像处理领域^{[2, 3]}取得了巨大的成功. 然而, 现实世界还存在许多不包含位置信息和序列信息的数据, 如生物网络^[4]、化合物分子网络^[5]、社会网络^[6]等数据, 此类数据可以由图的节点及边构成. 借鉴CNN的卷积层池化层的功能, 在图数据上推广卷积和池化操作是相当有吸引力的^[7]. 将CNN中的卷积操作拓展到任意图结构数据上的方法, 称为图神经网络(GNN). 目前各种GNN算法在以节点为主的图学习任务中获得出色的表现, 如节点分类^{[8, 9]}, 链路预测^[10], 推荐系统^[11]等. 图分类任务作为一种重要的数据挖掘任务, 在很多领域均有应用前景^[12]. 例如, 在生物信息学中, 对蛋白质网络分类, 判断该蛋白是否为酶, 对某种疾病是否具有治疗能力^{[13, 14]}; 在化学信息学中, 对化合物分子图进行分类, 判断分子的诱变性、抗癌活性、毒性^{[15, 16]}; 给定分子的结构图, 判断其性质^[17]. 图中的池化操作在图的分层表示中起着关键作用, 可以挖掘图中存在的子图结构, 获取全局特征的层次信息^[18]. 针对图中池化操作进行设计, 对解决图分类问题具有较高的研究价值.

图分类任务的目标是根据给定图的节点特征以及拓扑结构来预测整个图的标签. 早期的图分类学习模型主要是通过设计全局特征提取函数来获取所有节点的特征. 虽然这种方式是可行的, 但是通过这种方式得到的图级别表示本质上是“扁平的”, 只考虑了图的特征信息, 图的层次结构信息在一定程度上被忽略了^[19]. 为了捕捉层次结构信息用于图分类, 最近一些工作根据图的不同子结构和节点的不同作用, 专注于GNN的分层池化设计^{[18, 20-22]}. 主要有两类方法, 一种是将节点分组形成节点簇, 另一种是选取代表节点形成子图. 在节点簇的池化方法中, 使用学习的方式得到节点分配矩阵, 根据分配矩阵将每个节点进行分簇, 然后将簇内节点汇集成新节点, 形成粗化图^{[18, 21]}. 由于此类方法需要额外学习分配矩阵, 导致模型的计算复杂度较高. 在选取代表节点的方法中, 核心思想是计算出图中节点的排名, 对原始图进行节点抽取, 形成粗化图^{[20, 22]}. 例如可学习的投影向量^[20], 邻域重建中心节点得分^[23]等. 由于节点排名时没有显式的使用图的邻接矩阵信息, 并且对节点的排名方式单一, 观点往往具有偏见^[24]. 不同维度的信息对节点评分侧重点可能不同, 因此在多个维度信息下协作学习稳健的节点排名是非常具有必要性的^[25].

为了解决上述问题的局限性, 我们提出了一个新的基于编码解码结构的多维度图池化方法EDMDPool. 它具有编码解码框架, 可以学习图的分层表示. 具体来说我们首先引入了一套度量方法, 来评估特征维度和拓扑结构维度下节点的两种重要性分数. 然后, 通过注意力机制^[26], 动态地将两种维度下的重要性分数进行汇总, 来生成更为稳健的节点排名. 之后, 编码结构中的池化操作根据得到的节点排名自适应的选择排名前百分之K的节点集合, 生成原始图的诱导子图, 并记录所选节点的编号, 用于解码部分恢复原始结构. 我们堆叠GNN层和MDPool层来实现一个端到端的架构, 以执行图分类任务.

1 相关工作

与CNN中池化效果相似, GNN池化可以使参数减少, 得到更好的泛化性能^[22]. 目前图池化的方法可以分为两类: 全局图池化和分层图池化.

全局图池化: 全局池化的方法使用平均操作、加和操作或神经网络将所有节点嵌入整合为特征向量作为图的表示^[22]. Set2Set使用LSTMs模型寻找图中重要节点, 聚合节点信息生成图表示^[27]. DGCNN根据顶点在图结构中的作用, 对节点嵌入进行排序后传递给传统CNN结构对图进行表示^[28]. 全局池化虽然可以应用于不同大小的图, 具有不同结构的图可以被统一处理, 但是这种方法只根据节点特征进行操作, 可能会丢失一部分结构信息.

分层图池化: 分层表示对于获取图的层次结构信息至关重要, 可以学习每层基于特征或拓扑的节点分配. 在节点分组形成节点簇的方法中, Ying等人^[18]提出DiffPool, 一种可微分池化模型, 使用GNN将节点分配到可重复的节点集合中. Diehl等人^[29]提出了EdgePool, 通过学习节点之间边的得分决定节点是否融合, 这种方式导致了每次池化节点数减半. 在选取代表节点形成子图的方法中, 顾昕等人^[30]提出节点信息保留的多头注意力图池化模型MHAPool, 与本文提出的特征维度下多头自注意力分数相似, 但本文包括了拓扑维度下节点排名信息的融合. 张红梅等人^[31]提出层内-层间联合特征提取的模型. 朱小草等人^[32]提出一种基于稀疏注意力自适应图池化方法AGP-SA, 保留图的局部特征. Lee等人^[22]提出了SAGPool, 它是一种用GNN获取自注意力得分的图池化方法. Gao等人提出了具有池化和反池化操作的Graph U-Net, 池化层根据节点在可训练投影向量p上的得分排名, 选择节点形成新子图^[20]. 在Ranjan等人^[33]的工作中, 利用新的自注意网络和改进的GNN来捕捉给定图中每个节点的重要性, 设计了ASAPool. Zhang等人^[34]提出了图自适应池方法GSAPool, 根据节点的局部结构和特征信息以多种方式评估节点的重要性. 然而现有的大多数方法, 只有限的使用了图的特征信息或拓扑结构, 忽略了不同维度数据协作贡献.

2 多维度池化图分类模型 2.1 问题定义

图分类问题的任务是根据给定信息找到图对应标签的映射关系. 具体来说, 给定一数据集 $D = \{ \left( {{G_1}, {Y_1}} \right), \left( {{G_2}, {Y_2}} \right), \left( {{G_3}, {Y_3}} \right),\cdots \}$ , 获取映射函数 $ F:G \to Y $ , 其中 $G = \left\{ {{G_1}, {G_2},\cdots, {G_n}} \right\}$ 是输入图的集合, $Y = \left\{ {{Y_1}, {Y_2}, \cdots,{Y_n}} \right\}$ 是与之相对应的标签集合. 对于数据集中任意一个图 $ G = \left( {V, E, X} \right) $ , 标签为Y, V表示节点集合, 节点数量为n, E表示图中边的集合, 边的数量为e. 我们令X作为图的特征矩阵, $ X \in {\mathbb{R}^{n \times d}} $ , 其中d为节点的特征维度. 此外, 令 $A \in {\mathbb{R}^{n \times n}}$ 作为图的邻接矩阵, 表明图中节点的连接关系, $D \in {\mathbb{R}^{n \times n}}$ 是邻接矩阵A的度矩阵.

2.2 模型框架

全局多维度池化图分类框架流程: 根据文献[28]提出的全局池化架构, 本文设计了相似的结构, 如图1(a)所示, 全局多维度池化框架由3层图卷积层堆叠, 并将每层的特征进行串联拼接后传入多维度图池化层, 经读出层获取到图的特征表示, 最后经过线性层进行分类.

编码-解码多维度池化图分类框架流程: 受文献[20, 35]中编码器和解码器结构的启发, 本文设计了基于编码-解码多维度池化的图分类框架. 如图1(b)所示, 堆叠编码块来构建编码器部分, 每个编码块包含一个GCN层和一个MDPool层, GCN层负责聚合一阶邻居节点信息, MDPool层负责缩减图的规模. 在解码器部分, 设计与编码器相同数目的解码块, 每个解码块包含一个UnPool层和一个GCN层, UnPool层负责恢复对应编码部分的图结构, GCN层负责聚合信息. 将编码块、解码块中的不同层次特征进行读出, 图的特征使用读出层输出进行拼接, 最后将图的特征送入线性层进行分类. 图2给出了由两个编码块两个解码块组成的多维度池化图分类框架的解释. 对于输入图数据, 每层之间使用GCN提取节点特征. 在编码部分, 使用MDPool缩减原始图节点数目, 生成诱导子图, 并记录节点下标及图结构用于解码部分恢复. 在解码部分, UnPool层使用记录的结构及下标恢复原始图结构. 对编码解码过程中每层子图特征进行读出, 将拼接后的特征传入MLP获取标签, 用于图分类.

在本文提出的模型框架中, 我们设计了基于节点特征维度和图拓扑结构维度协作的多维度图池化层, 为了对比单个维度下的池化层的效果, 我们设计仅包含特征维度的池化层模型和仅包含拓扑结构维度的池化层模型做验证. 我们将在第3.4节实验部分讨论该问题.

2.3 多维度图池化层

在本节中, 我们将介绍提出的多维度图池化操作MDPool, 以实现对图的下采样. 根据文献[20, 22]中图池化方式的启发, 图池化操作用来确定诱导子图的节点集, 节点集的采样根据原始节点重要性排名前百分之K的节点形成. 在这里, 我们设计了一个新的多维度图池化操作, 可以使不同维度下的节点得分进行协作, 从而产生更健壮的节点排名.

基于节点排名的图池化操作的关键是获得图中所有节点重要性排名的排序. 一般来说, 图通常包含结构信息和节点特征信息, 这两类信息对应着图的邻接矩阵A和特征矩阵X. 因此, 根据这两类信息, 评估每个节点基于特征和结构维度的排名. 图3给出了我们所提出的图池化层的说明解释. 假设在模型框架的第l层中, 邻接矩阵 ${A^l} \in {\mathbb{R}^{{N^l} \times {N^l}}}$ , 其中N^l为第l层中节点数目. 特征矩阵 $ {X^l} \in {\mathbb{R}^{{N^l} \times d}} $ , 第l层中每个节点包含d个特征. MDPool的具体操作如下.

节点特征维度: 图通常包含丰富的特征信息, 节点特征在很大程度上可以描述自身属性. 我们使用节点特征的多头自注意力^[36]分数, 作为图中节点在特征维度的得分. 将节点特征X^l做3次线性映射得到Q_i, K_i, V_i, 如下所示:

$\left\{ { \begin{gathered} {Q_i} = {X^l}W_i^Q \\ {K_i} = {X^l}W_i^K \\ {V_i} = {X^l}W_i^V \\ \end{gathered} } \right.$

(1)

其中, $W_i^Q, W_i^K, W_i^V \in {\mathbb{R}^{d \times f}}$ 为可学习的参数矩阵, $ {Q_i}, {K_i}, {V_i} \in {\mathbb{R}^{{N^l} \times f}} $ 代表多头自注意力中的第i个头的query、key、value, $i \in \left\{ {1, 2, \cdots, h} \right\}$ , h为多头自注意力中头的数目.

Q_i,K_i,V_i中的每一行表示为每个节点不同空间下的特征向量, 则经过式(2)得到注意力矩阵, 并将注意力矩阵应用于特征矩阵V_i, 过程如下所示:

$ {O_i} = {\textit{Softmax}}\left(\frac{{{Q_i}K_i^{\rm T}}}{{\sqrt f }}\right) $

(2)

$ {Z_i} = {O_i}{V_i} $

(3)

其中, ${O_i} \in {\mathbb{R}^{{N^l} \times {N^l}}}$ 表示为节点之间的注意力或者相关性, Softmax(·)函数使O_i每一行元素相加为一. 将节点特征V_i与注意力矩阵进行加权线性组合, 得到图在第i个头下的特征矩阵 ${Z_i} \in {\mathbb{R}^{{N^l} \times f}}$ , 使每个节点特征向量都含有当前图中所有节点特征向量的信息.

将每个注意力头中获取到的节点特征向量进行拼接, 得到在多头自注意力机制下的特征向量 $Z \in {\mathbb{R}^{{N^l} \times \left( {h \times f} \right)}}$ . 为了得到所有节点的排名, 我们将多头特征向量进行线性变换, 得到一维表示 ${S_1} \in {\mathbb{R}^{{N^l} \times 1}}$ :

$ Z = concat\left( {{Z_1}, \cdots, {Z_h}} \right) $

(4)

$ {S_1} = \sigma \left( {ZW} \right) $

(5)

其中, $W \in {\mathbb{R}^{\left( {h \times f} \right) \times 1}}$ 为可训练的矩阵, $\sigma \left( \cdot \right)$ 为Sigmoid非线性激活函数, 将节点得分范围限制在 $\left[ {0, 1} \right]$ .

图拓扑结构维度: 除了特征信息, 节点的重要性通常还与图拓扑结构相关. 图拓扑结构本身可以提供许多有用信息, 比如节点的度以及节点之间的最短路径等. 因此, 在这里我们使用节点的度中心性、介数中心性^[37]、接近中心性^[38]作为节点在图拓扑结构维度下得分. 我们认为使用单一中心性研究节点的重要程度具有偏差, 使用3种中心性结合不同角度信息计算节点重要性更为准确.

一个节点与其他节点关系越多, 该节点的影响力就越强, 因此, 度中心性越大的节点其重要性越大. 度中心性描述如下所示:

$ {C_D} = \frac{{degree({A^l})}}{{{{N}} - 1}} $

(6)

其中, ${C_D} \in {\mathbb{R}^{{N^l} \times 1}}$ , degree(·)函数通过计算邻接矩阵中每个节点的连接数从而得到节点的度. 由于只关注了与某一个节点直接相连的点数, 忽略间接相连的点数, 因此被视为局部中心度.

图中两个不相邻节点的相互作用取决于其他节点, 特别是处于两节点最短路径上的节点. 因此, 一节点处于多条其他节点的最短路径中, 那么该节点就是图中重要节点, 有较大的中介中心性, 其描述如下:

$ {C_B}(v) = \sum\limits_{s, t \in V} {\frac{{f(s, t\left| v \right.)}}{{f(s, t)}}} $

(7)

其中, ${C_B} \in {\mathbb{R}^{{N^l} \times 1}}$ 表示节点的介数中心性, V是节点集合, $f( s, t )$ 表示节点s到节点t最短路径的数目, $f\left( {s, t\left| v \right.} \right)$ 表示节点s到节点t最短路径上包含节点v的路径数目.

接近中心性是一节点与图中其他节点的最短距离之和的倒数, 代表了该节点与其他点的远近程度, 其描述如下:

$ {C_C}(v) = \frac{{n - 1}}{{\displaystyle\sum\limits_{u \in \left\{ {V - v} \right\}} d (v, u)}} $

(8)

其中, ${C_C} \in {\mathbb{R}^{{N^l} \times 1}}$ 表示节点的接近中心性, $d\left( {v, u} \right)$ 是节点v和节点u之间最短路径长度, n–1是节点v能够达到的节点个数.

将计算得到的3个节点中心性得分进行相加, 经过Sigmoid非线性激活函数, 得到节点在图拓扑结构维度下的重要性排名 ${S_2} \in {\mathbb{R}^{{N^l} \times 1}}$ :

$ {S_2} = \sigma \left( {{C_D} + {C_B} + {C_c}} \right) $

(9)

由于单个维度下的节点排名往往具有偏见, 每个维度下的节点重要性可能不同, 本文尝试将不同维度下的节点排名进行汇聚融合, 以生成鲁棒性更好的节点排名. 因此, 使用注意力机制自动学习每个维度得分 $\left\{ {{S_d}} \right\}_{d = 1}^D$ 下的权重 $\left\{ {{w_d}} \right\}_{d = 1}^D$ :

$ {w_d} = \frac{{\exp \left( {\sigma \left( {h{{\textit{z}}_d} + {b_d}} \right)} \right)}}{{\displaystyle\sum\limits_{k = 1}^D {\exp } \left( {\sigma \left( {h{{\textit{z}}_k} + {b_k}} \right)} \right)}} $

(10)

其中, ${w_d} \in {\mathbb{R}^{{N^l} \times 1}}$ 为维度d下的权重矩阵, h是不同维度下节点得分的拼接, z_d和b_d是维度d下的参数向量, D是维度的集合. 因此权重w_d越大, 维度d越重要. 以权重为系数, 得到最终的节点重要性得分 $S \in {\mathbb{R}^{{N^l} \times 1}}$ :

$ S = \sigma \left( {\sum\limits_{d = 1}^D {{w_d} \cdot {S_d}} } \right) $

(11)

在得到最终的节点重要性得分后, 使用得分作为评价标准选择在池化过程中应该被保留下的节点. 具体来说, 首先根据节点重要性得分对节点进行排序, 选择排名靠前的节点生成诱导子图. 记录所选节点编号, 用于生成下一层的邻接矩阵和特征矩阵, 方法如下:

$\left\{ { \begin{array}{l}{idx}={rank}\left(S, \lceil r\times{N}^{l}\rceil \right) \\ \tilde{S}=S\left({idx, :}\right) \\ {\tilde{X}}^{l}={X}^{l}\left({idx, :}\right) \\ {A}^{l+1}={A}^{l}\left({idx, idx}\right) \\ {X}^{l+1}={\tilde{X}}^{l}\odot \left(\tilde{S}{1}_{d}\right)\end{array} } \right.$

(12)

其中, r是图中节点的池化率, ${N^{^{l + 1}}} = \left\lceil {r \times {N^l}} \right\rceil$ 代表新图中节点数目. rank(·)表示返回排序后的前N^l+1个节点索引的函数. $S\left({{{idx, :}}} \right)$ 表示根据索引保留诱导子图节点的得分, ${A^l}\left( {{{idx, idx}}} \right)$ 和 ${X^l}\left( {{{idx, :}}} \right)$ 依据索引进行矩阵行或列的提取, 形成诱导子图的特征矩阵和邻接矩阵. ${1_d} \in {\mathbb{R}^d}$ 是一个长度为d, 元素全部为1的向量, $ \odot $ 为哈达玛积, 使矩阵逐元素相乘. 因此, 经过以上池化层操作, 我们得到 ${A^{l + 1}} \in {\mathbb{R}^{{N^{l + 1}} \times {N^{l + 1}}}}$ , ${X^{l + 1}} \in {\mathbb{R}^{{N^{l + 1}} \times d}}$ 作为下一层输入的邻接矩阵和特征矩阵.

2.4 其他层

图神经网络层: 图卷积网络在许多与提取图特征相关的机器学习任务中得到了最先进的性能^[8]. 因此我们使用GCN作为模型中提取特征信息的模块, 其定义为:

$ {X^{l + 1}} = \sigma \left( {{{\hat D}^{ - \frac{1}{2}}}{{\hat A}^l}{{\hat D}^{\frac{1}{2}}}{X^l}{W^l}} \right) $

(13)

其中, W^l是第l层可学习的参数矩阵, X^l是特征矩阵, 初始节点在第1次进行卷积操作时使用 ${X^0} = {X_{{\text{input}}}}$ . ${\hat A^l} = {A^l} + I$ 是对每个节点添加自环后的邻接矩阵, $\hat D$ 是添加了自环后的度矩阵. 实际上我们提出的MDPool池化算子也可以与其他图神经网络模型结合, 我们将在第3.4节实验部分讨论这些问题.

反池化层: 模型中的编码部分使用池化层缩减图的规模, 而在解码部分, 图结构数据需要被上采样以恢复其原本的节点规模. 为了实现图结构数据的上采样, 我们使用反池化层, 执行MDPool的反向操作. 如图2虚线所示, 在MDPool过程中保存图的邻接矩阵信息以及所选节点的索引. 如图4所示, 在反池化层中, 邻接矩阵直接使用对应编码层的邻接矩阵, 特征矩阵根据索引信息, 将现有特征放回图中原始位置, 其表述如下:

$ {X^{l + 1}} = {{unpool}}\left( {{0_{N \times d}}, {X^l}, {{idx}}} \right) $

(14)

其中, ${X^l} \in {\mathbb{R}^{K \times d}}$ 为待放回的节点特征, ${{idx}} \in {\mathbb{R}^K}$ 为相应池化层中的节点索引, ${0_{N \times d}}$ 是新图的初始化全为0的特征矩阵. unpool(·)函数按照idx中的索引将X^l的每一个行向量填充到 ${0_{N \times d}}$ 矩阵中去. 经过反池化操作我们将得到新图的特征矩阵 ${X^{l + 1}} \in {\mathbb{R}^{N \times d}}$ , 图中节点数目从K变成N.

读出层: 如图2所示图分类框架由多次重复的卷积层池化层模块以及反池化层卷积层模块构成. 每个模块可以得到不同规模的子图特征: ${X^1}, {X^2}, \cdots, {X^L}$ , 由于不同模块输出特征的节点数目不同, 参考读出层的设计^[39], 将所有层节点特征汇聚在一起, 形成一个固定大小的表示:

$\left\{ { \begin{split} & X{\text{\_}}max = \left[ {\mathop {\max }\limits_{i = 1}^d {X^l}\left( {:, i} \right)} \right]_{l = 1}^{l = L} \\ & X{\text{\_}}mean = \left[ {\frac{1}{{{N^l}}}\sum\limits_{j = 1}^{{N^l}} {{X^l}\left( {j, :} \right)} } \right]_{l = 1}^{l = L} \end{split} } \right.$

(15)

其中, X_max为框架中每层特征矩阵, 按特征列选取最大值形成的列表, X_mean为每层特征矩阵中所有节点特征的均值形成的列表, 列表长度均为L. 我们将不同规模的读出层输出进行拼接, 最终形成图形级别的表示:

$ Z = \sigma \left( {X{\text{\_}}max\left\| {X{\text{\_}}mean} \right.} \right) $

(16)

其中, $Z \in {\mathbb{R}^{2Ld}}$ 为图的特征, $||$ 为向量拼接操作.

损失函数: 我们将图的特征表示放入带有Softmax(·)分类器的多层感知机中, 损失函数使用交叉熵损失:

$\left\{ { \begin{split} & \hat Y = {\textit{Softmax}}\left( {MLP\left( Z \right)} \right) \\ & loss = - \sum\nolimits_{i \in {G_{{\rm{train}}}}} {\sum\nolimits_{j = 1}^C {{Y_{ij}}} \log {{\hat Y}_{ij}}} \end{split} } \right.$

(17)

其中, ${\hat Y_{il}}$ 表示训练集中图i预测为第j类的概率, Y_ij为其真实标签, C表示为类别数.

3 实验与分析 3.1 数据集及基线

本文采取了4个广泛使用的数据集来评估我们提出的图分类模型性能. 包含了生物信息学和社交网络领域的数据^[40-43], 包括二分类任务和多分类任务, 4个数据集的统计信息总结于表1. DD数据集^{[40, 41]}由蛋白质的结构图组成, 节点代表氨基酸, 边表示两个氨基酸之间距离小于6埃米, 标签为两类用于判断蛋白质是否为酶. PROTEINS数据集^{[41, 42]}是蛋白质的图表示, 节点代表蛋白质的二级结构, 边表示蛋白质二级结构在氨基酸序列中为邻居或三维空间中是邻居. 标签为两类用于判断蛋白质是否为酶. COLLAB是一个科学合作数据集^[43], 节点代表科研人员, 每一个图为科研人员的自我中心网络, 标签代表所属的研究领域. IMDB-MULTI是一个电影合作数据集^[43], 节点代表演员, 每个图为演员的自我中心网络, 标签为电影类型.

我们使用3类方法作为实验基线: (1)基于图核的方法. 此类方法使用不同核方法来进行图分类, 包括W-L子树核(1-WL)^[40], W-L最优分配核(WL-OA)^[44], Graphlet核(GR)^[45], 最短路径核(SP)^[46]. (2)基于图神经网络的方法, 包括GCN^[8], ChebNet^[47], GraphSAGE^[9], GAT^[48]. (3)基于池化的方法, 包括两个全局池化方法Set2Set^[27]和DGCNN^[28], 以及6个层次图池化模型DiffPool^[18], EdgePool^[21], SAGPool^[22], gPool^[20], ASAPool^[33], GSAPool^[34].

3.2 实验和参数设置

我们使用PyTorch以及PyG框架实现EDMDPool模型, 并使用10折交叉验证作为模型性能评估. EDMDPool中我们设置编码块解码块的个数均为3, 根据数据集中节点规模, 将节点表示维度设置为128或64. 根据数据集的规模, 将批次大小设置为64或32. 设置多头自注意力头数为2, 维度为128. 使用具有两个全连接层的MLP后跟Softmax分类器做预测, 我们使用Adam优化器来优化模型参数, 学习率设置为0.001, 对于不同数据集每层的池化率使用与gPool相同的设置, 选择200轮训练中最优的结果.

3.3 实验结果

我们在图分类任务的4个典型数据集上比较了提出的EDMDPool与基线方法的性能, 准确率以及标准差在表2给出, 粗体突出显示了最佳结果. 首先, 可以观察到, EDMDPool的性能在4个数据集中始终优于其他经典基线的表现. 具体来说, 我们的模型在DD、PROTEINS、IMDB-MULTI数据集上分别比表现最好的模型提升了1.52%、0.62%、1.8%的准确率. 在COLLAB数据集上虽然EDMDPool与SAGPool模型准确率差别不明显, 但是EDMDPool取得了较低的标准差. 与其他模型相比, EDMDPool在COLLAB数据集上的表现较为相对平庸. 并且可以看到, 我们提出的MDPool_Global全局池化的模型在COLLAB数据集上可以取得较好的表现. 那是因为COLLAB数据集中许多科研协作图只有单层的社团结构. EDMDPool具有3组编码解码模块的复杂层次结构, 可能会导致过拟合现象, 这与之前工作发现的结果一致^[19].

值得注意的是, 传统的基于图核方法由于其非端到端的学习方式, 导致该类方法不能推广到任意结构的图上, 在部分数据集上效果较差. 此外, 与具有池化模块的框架相比, GNN组均不能达到较好的效果, 主要原因是在汇聚全局节点特征时, 忽略了图的结构信息, 这进一步验证了在框架中增加池化层的必要性. 我们还可以看到, 大部分基于分层的池化方法效果超过了全局池化方法Set2Set和DGCNN. 这是因为基于全局的池化方法, 本质上图的特征表示仍是“扁平的”, 图的层次结构信息未被考虑. 在大部分基线中, 层次池化模型可以获得更好的性能, 这说明了我们使用的层次池化方式的有效性. 对于全局池化方法, 我们同样设计了MDPool_Global作对比. 可以看到, 与基线模型相比较, 我们提出的全局池化方式仍能取得较好效果, 这进一步证明了我们提出池化层的有效性.

3.4 消融实验及参数分析

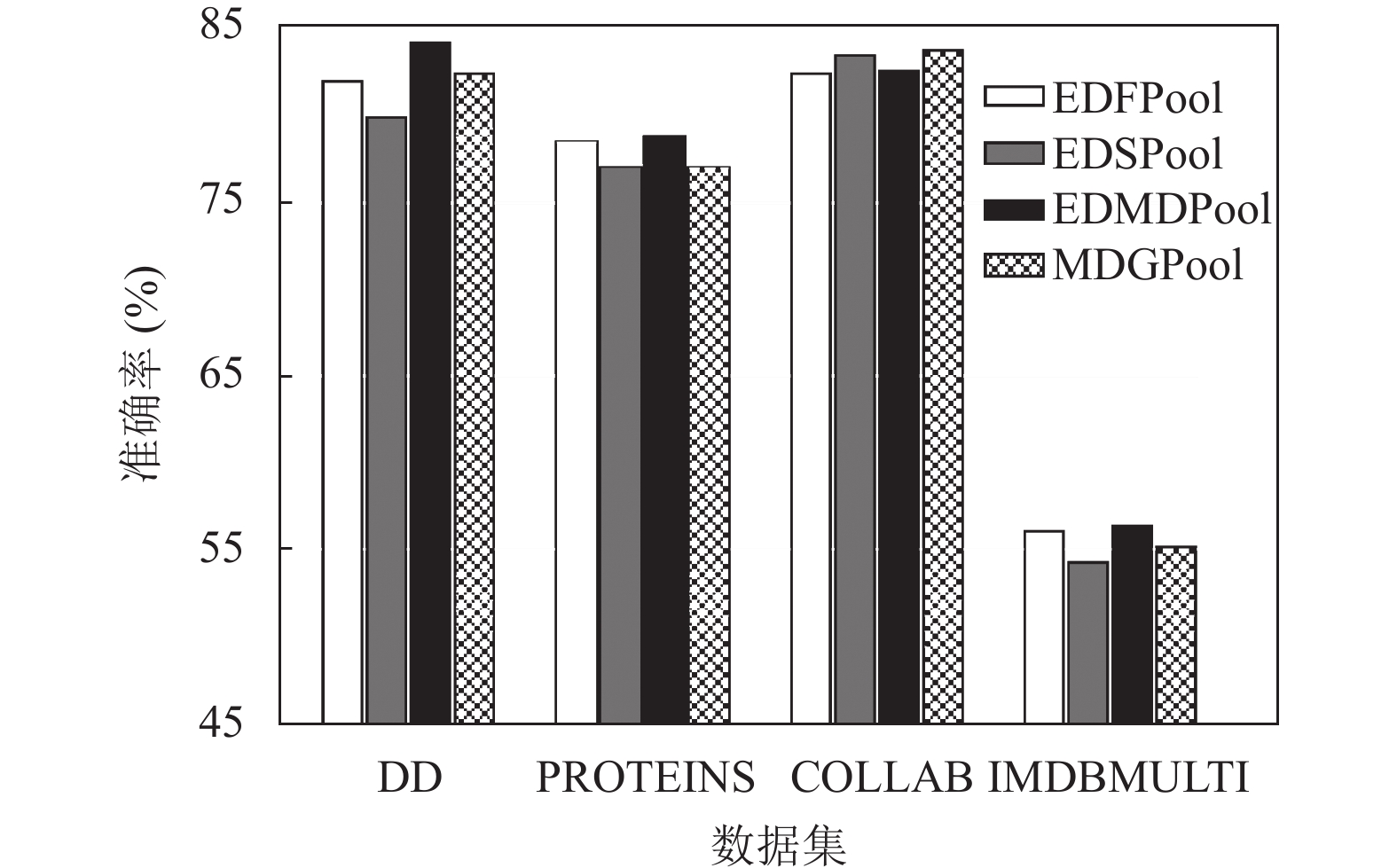
为了验证各维度下的信息都有助于图分类, 我们将EDMDPool模型与其变体比较, 其中, 仅使用节点特征的模型为EDFPool, 仅使用图拓扑结构的模型为EDSPool, 全局池化模型为MDGPool. 图5显示了各个变体的分类效果, 在DD、PROTEINS、IMDB-MULTI这3个数据集上, 单一维度下的变体的性能均不如EDMDPool, 这证明了多维度得分整合的有效性. 对于COLLAB数据集, 由于出现过拟合现象, EDMDPool的准确率低于EDSPool. 但是MDGPool, 仍比仅使用单一维度的EDSPool性能更好, 这进一步证明了多维度信息融合进行节点选取的有效性.

为了证明本文提出的MDPool池化层可以集成到任意图神经网络框架中, 我们选择了4种最广泛使用的图神经网络方法构建模型. 在两个不同领域的数据集上对他们进行了评估, 涵盖了二分类及多分类任务. 结果如表3所示, 根据所选择的数据集及GNN类型, 图数据的分类性能有所不同, 但不同GNN类型的模型都能得到相似的分类效果, 这表明了我们提出的模型对各种图神经网络方法的兼容性较好.

我们进一步研究了一些重要的超参数对EDMDPool的影响, 包括编码解码模块的深度d, 学习率r. 如图6所示, 当分别设置d=3和r=0.001时, 模型可以实现最佳性能. 随着学习率的减小分类精度呈增长趋势, 当学习率过小时, 出现局部极值点收敛现象, 精度开始降低. 对于模块的深度, 大的d可以提高分类结果, 但过大则会导致过拟合, 损害分类性能.

4 结论与展望

为了提高图分类任务的准确性, 增强图分层表示的能力, 提出了一种基于多维度信息节点选择的图池化算子MDPool. 使用节点特征维度和图拓扑结构维度下的信息分别评估节点重要性. 由不同维度下的节点排名, 协作生成鲁棒性更高的节点得分, 依据排序后的得分选择节点构成诱导子图, 实现对原始图的下采样操作. 将MDPool池化层、UnPool反池化层与现有图神经网络模型堆叠形成编码解码框架, 构建了一个端到端的图分层表示学习模型EDMDPool. 在4种数据集上进行了10倍交叉验证. 实验结果表明, EDMDPool具有较好的性能.