2. 天津大学 智能与计算学部, 天津 300350;
3. 福建医科大学附属协和医院, 福州 350001
2. College of Intelligence and Computing, Tianjin University, Tianjin 300350, China;
3. Fujian Medical University Union Hospital, Fuzhou 350001, China
近年来, 基于卷积神经网络(convolutional neural network, CNN)的目标检测(object detection)方法[1]不断创新, 主要有以YOLO[2, 3]为代表的单阶段目标检测算法和以Faster R-CNN[4]为代表的两阶段目标检测算法等. 随着深度神经网络的迅速发展, 目标检测算法已广泛应用于医学图像检测领域, 可以辅助医生完成相关手术[5]. 比如基于腔镜影像的甲状旁腺手术[6], 存在较高的甲状旁腺误伤、误切的风险, 这会给人体带来低钙血症、手脚抽搐等严重后遗症. 因此, 在手术中如何保护甲状旁腺一直是医学上关注的热点, 研究基于深度学习的甲状旁腺目标检测模型, 可以辅助医生有效地保护甲状旁腺.
通常来说, 基于CNN的目标检测器在经过主干网络进行特征提取之后, 会利用检测头中的不同分支回归目标的位置和类别. 那么对于这样的检测器而言, 都需要在训练的时候, 对图像映射到网络输出的特征图上的每一个候选位置进行正负样本的划分, 赋予合适的学习目标, 即设置一个合适的label. 在训练的时候就可以利用损失函数(loss function)去学习, 这个过程就是标签分配(label assignment)[7]. 标签分配是目标检测算法中所必须的步骤, 其结果直接决定模型所需要学习的目标, 也决定了算法的性能. 因此, 要提高检测性能, 一种方法是使用更复杂的CNN网络, 即一个更复杂的近似函数. 另一种方法是结合具体的检测场景, 结合目标的先验信息等设计一种较为合适标签分配策略来构造一个更好的样本空间从而提升模型的性能.
基于锚点(anchor)进行标签分配的检测算法, 通常在图片中只有少数几个目标target却有预先设置的大量的先验框anchor, 如YOLOv3、Faster R-CNN、SSD[8]和RetinaNet[9]等. 因此, 模型在训练的时候需要根据不同的策略进行标签分配, 使得网络在学习的时候让某些anchor负责预测对应的target. 但是这种策略很大程度依赖目标GT (ground truth)的标注. 对于一些特殊的场景而言, 比如甲状旁腺检测, 其真正的目标只是GT中的一小部分, GT无法完全代替目标, GT内部很多区域其实是属于背景却也被划分为正样本. 此外, 基于anchor的策略依赖于数据集的超参数, 当数据集被更改时, 需要花费大量的精力进行调优.
针对上述问题, FCOS[10]、CenterNet[11]等无锚方法(anchor-free)[12]将目标检测问题转换为关键点检测, 以CenterNet为例, 其不需要在特征图上进行密集的anchor覆盖, 摆脱对anchor的依赖, 因而不需要手动进行前景和背景的阈值设置, 减少不必要的超参数; 并且CenterNet中每个对象只有其中心点为关键点正样本, 所以也无需使用非极大值抑制 (non maximum suppre-ssion, NMS)[13]减少计算量, 最终只需要提取关键点的热力图中局部峰值即可, 简洁明了. 对于负样本点, Center-Net在制作标签时在对应的特征图大小中使用高斯核函数负样本热力点设置相应的权重, 等同于设置了一种软阈值而不是简单粗暴的0与1的划分, 在训练时可以加快拟合. 不过该策略只依赖于模型唯一输出的高分辨率特征图, 无法最大程度适应甲状旁腺中存在的多种不同尺度大小的目标. 此外, 直接在全局特征图上构建高斯分布设置权重的时候, 忽略了目标的形状和方向, 无法最大程度地利用这些样本点去拟合目标的形状.
因此, 鉴于CenterNet算法简洁高效、架构清晰等特点, 结合甲状旁腺检测场景, 本文以CenterNet为baseline, 从甲状旁腺的形状信息出发, 构建符合目标形状特征的热力点高斯分布, 创建更加细粒度的样本空间, 构建更加符合甲状旁腺方向特征的训练样本空间, 以最大程度地定位目标位置. 同时, 一个期望的训练样本空间还需要一个合适的目标函数来引导模型学习更高质量的特征. 当前主流的anchor-free检测算法中包含的损失函数, 一般有如下几个: 用于定位目标中心的中心点预测损失、减少读取标签数据时存在的数据截断误差的目标中心偏置损失、用于回归目标大小的宽高预测损失. 不过当前目标函数范式较少有融入目标形状信息的损失函数, 本文从甲状旁腺的形状出发, 基于关键点的高斯分布, 融入形状信息, 提出形状约束的目标损失函数, 从而更好地约束目标的位置.
综上所述, 设计一个融入目标形状信息的标签分配策略和适用于甲状旁腺的椭圆形状约束的损失函数极为重要. 为此, 本文基于CenterNet提出了一种检测性能更高、更适合甲状旁腺检测场景的新型甲状旁腺检测模型EllipseNet.
本文的贡献概括如下.
1)提出了一种基于甲状旁腺目标形状的标签分配策略, 使用高斯核函数在GT中构建椭圆形状的高斯分布, 将所有样本点更细粒度地划分为正样本、“软样本”和负样本. 以此构建出来的高斯热图使热力点的分布更灵活, 以适应目标的形状和方向.
2)基于热力点的分布, 提出融入目标形状约束的损失函数, 更好地对目标位置进行约束.
3)在模型中构建多个不同分辨率的特征图输出, 根据交并比(IoU)的计算将不同大小的目标分配给不同尺度的分支进行预测, 更好地适应目标尺度差异大的场景, 解决尺度不平衡问题.
1 相关工作基于anchor的目标检测算法, 将检测问题转换为回归先验框的位置和类别. 其存在着以下一些问题[14]: 1) anchor的设计参数过于复杂. 2)特别形状的目标检测效果差. 3)复杂的anchor在覆盖一些特殊形状样本的同时, 正负样本也变得更加不均衡.
因此, 基于anchor-free的算法相继被提出, 2018年, CornerNet算法[15]的出现开启了anchor-free的热潮. CornerNet通过寻找目标边界框的左上角和右下角的角点, 以此来实现目标的定位和分类. 2019年, Zhou等人提出ExtremeNet[16], 利用关键点预测网络来预测最顶部、最左侧、最底部、最右侧4个极值点和1个中心点共5个关键点, 如果这5个关键点是几何对齐的, 那么将这些极值点分组到一个边界框中去, 即定位到目标. 2019年, Zhou等人提出CenterNet[11], 其使用一个中心关键点来表示该对象, 其他属性直接从中心的图像特征进行回归. 使用中心关键点来代表目标, 在特征图上构建热力点高斯分布, 算法的训练难度小. CenterNet算法的网络结构由特征提取网络和检测头两大部分构成, 特征提取网络主要包含编码器和解码器(encoder-decoder)[17-19]. 特征提取完之后再利用检测头预测中心关键点的热力图, 同时回归出目标的宽高和中心点对应的偏移量, 从而定位目标的位置.
Anchor-free算法将目标检测问题转换为关键点检测, 依靠中心点来进行目标的回归, 同样在训练的时候需要进行标签分配. 比如CenterNet的标签分配策略如下: 将原图采样到的
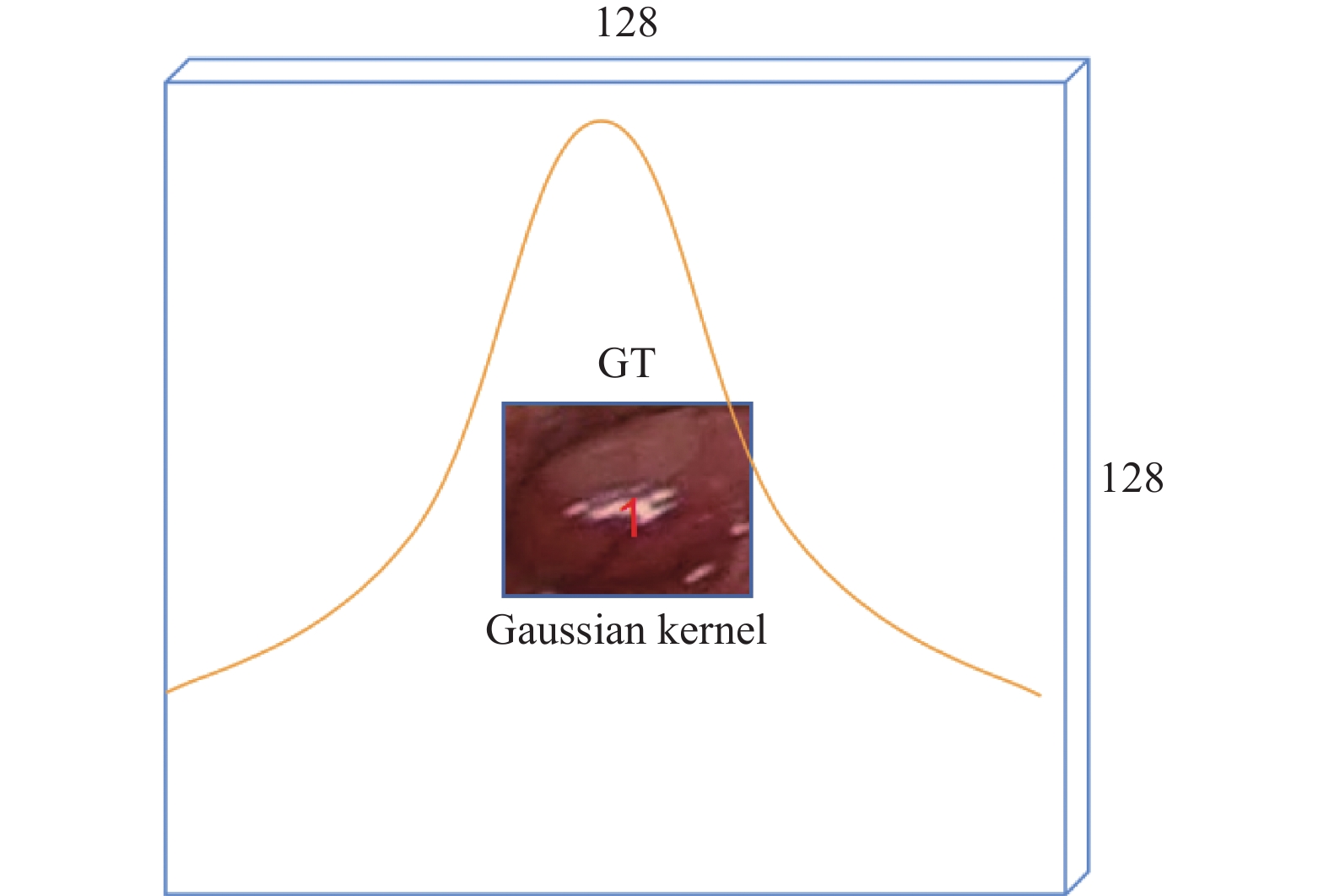
|
图 1 高斯分布 |
CenterNet的标签分配策略对实际目标充满整个GT效果显著, 但在甲状旁腺检测场景中依旧无法达到最佳检测效果. 甲状旁腺具有特殊的类椭圆形状特征, 实际的目标只是GT的一部分, 且在绝大多数情况下是属于单目标检测. 如果按照原先标签分配的思想在
本节主要介绍EllipseNet甲状旁腺检测模型, 其通过在GT内部椭圆目标形状区域构建高斯分布, 以此来最大程度地贴近标签框内部真正的目标(Real-GT), 对热力点进行更细粒度的划分, 分成正样本、“软负样本”和负样本, 使得正负样本的标签分配更加平衡; 并且提出融入目标形状的损失函数来对目标的位置进行约束. 其次, 在模型结构的设计上, 通过在检测头上构建多尺度预测输出, 使得模型能够更好地检测不同大小的目标, 适应目标尺度差异较大的甲状旁腺检测场景.
2.1 EllipseNet网络结构EllipseNet模型包括: 编码器与解码器所构成的特征提取网络、空间金字塔池化层(spatial pyramid pooling, SPP)[20]和多尺度输出的目标检测头, 如图2所示. 模型的处理流程如下: 对预处理之后的图片
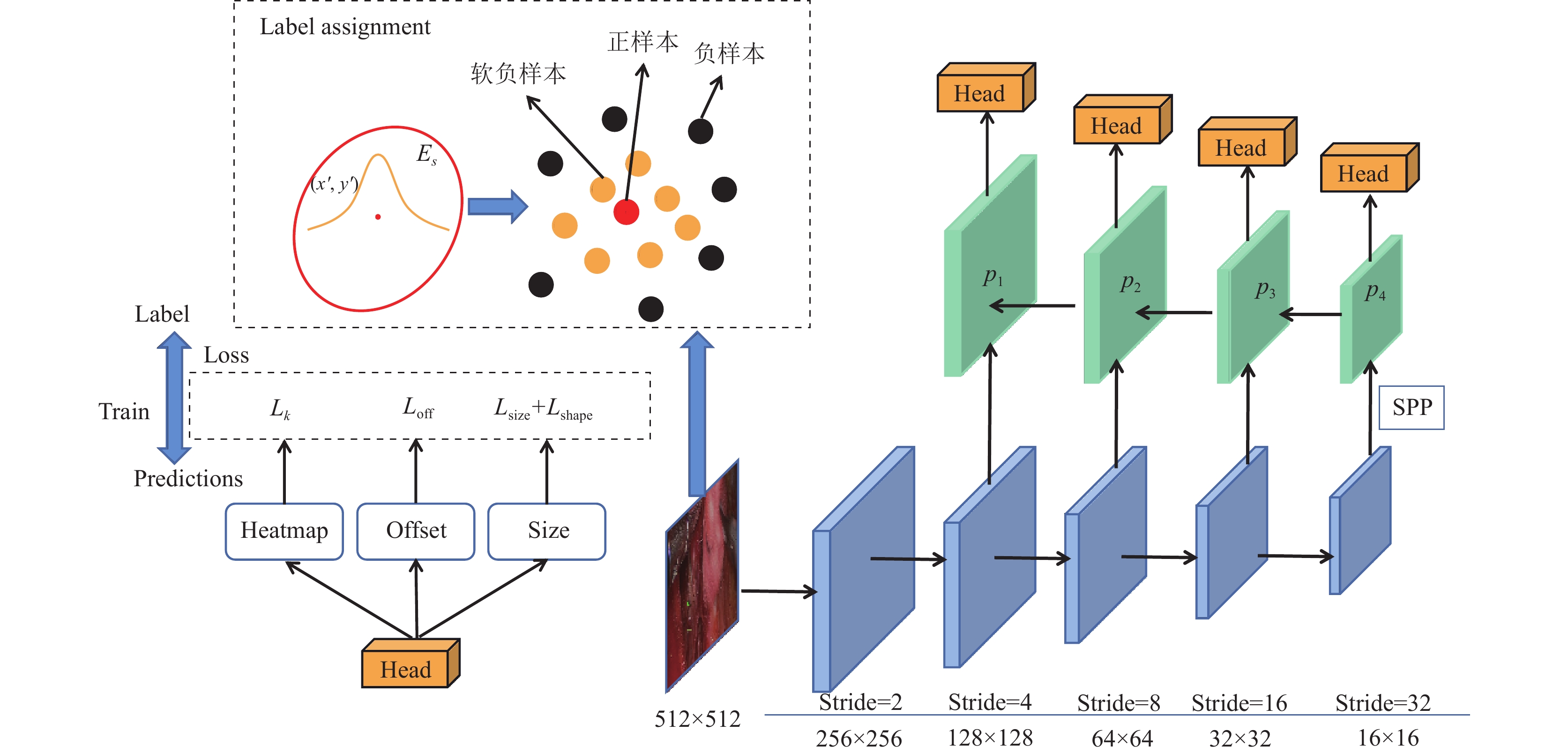
|
图 2 EllipseNet网络结构 |
2.2 椭圆形状的高斯热图
本文先采取在CenterNet中缩小热力点分布范围到整个GT区域上得到CNG (CenterNet-GT), 再在GT区域构建符合目标形状的热力点分布. CNG的具体方法如下: 将热力点的高斯分布从
结合腔镜手术中甲状旁腺的特点, 并对数据样本进行分析, 可知甲状旁腺的目标形状非常近似椭圆形. 对于这种形状特点的甲状旁腺, 目标检测常用的矩形框标注方法得到的标签(GT)是没有办法最大程度拟合到目标. 真正的目标(Real-GT)往往只是标注框内的一部分, 特别是极端情况下由于手术中目标被拉扯而会出现的更为瘦长的目标. 对于全局考虑热力点分布的话, 左上角和右下角部分远离目标中心, 是不应该作为“软负样本”, 而应该直接被划分为绝对的负样本.
因此, 根据甲状旁腺的形状特点, 如图3所示, 本文利用到目标大小与形状的先验信息在标签分配时构建符合其目标形状的椭圆形热力点高斯分布, 以此构建高斯热图, 使得正负样本的分配能最大程度拟合目标, 减少正负样本的不平衡; 同时, 减小矩形标注框中可能存在的标注误差.
本文通过两种方式来进行椭圆形状的高斯热图, 分别为垂直方向椭圆构建和倾斜方向椭圆构建.
在GT区域使用垂直方向椭圆构建高斯热图的基本思想如图4所示. 设构建出来的椭圆为
| $ E = \left\{ (x, y)\Bigg |(\frac{{{{(x - w/2)}^2}}}{{{{(h/2)}^2}}} + \frac{{{{(y - h/2)}^2}}}{{{{(w/2)}^2}}} \leqslant 1\right\} $ | (1) |

|
图 3 EllipseNet基于目标形状的高斯分布 |
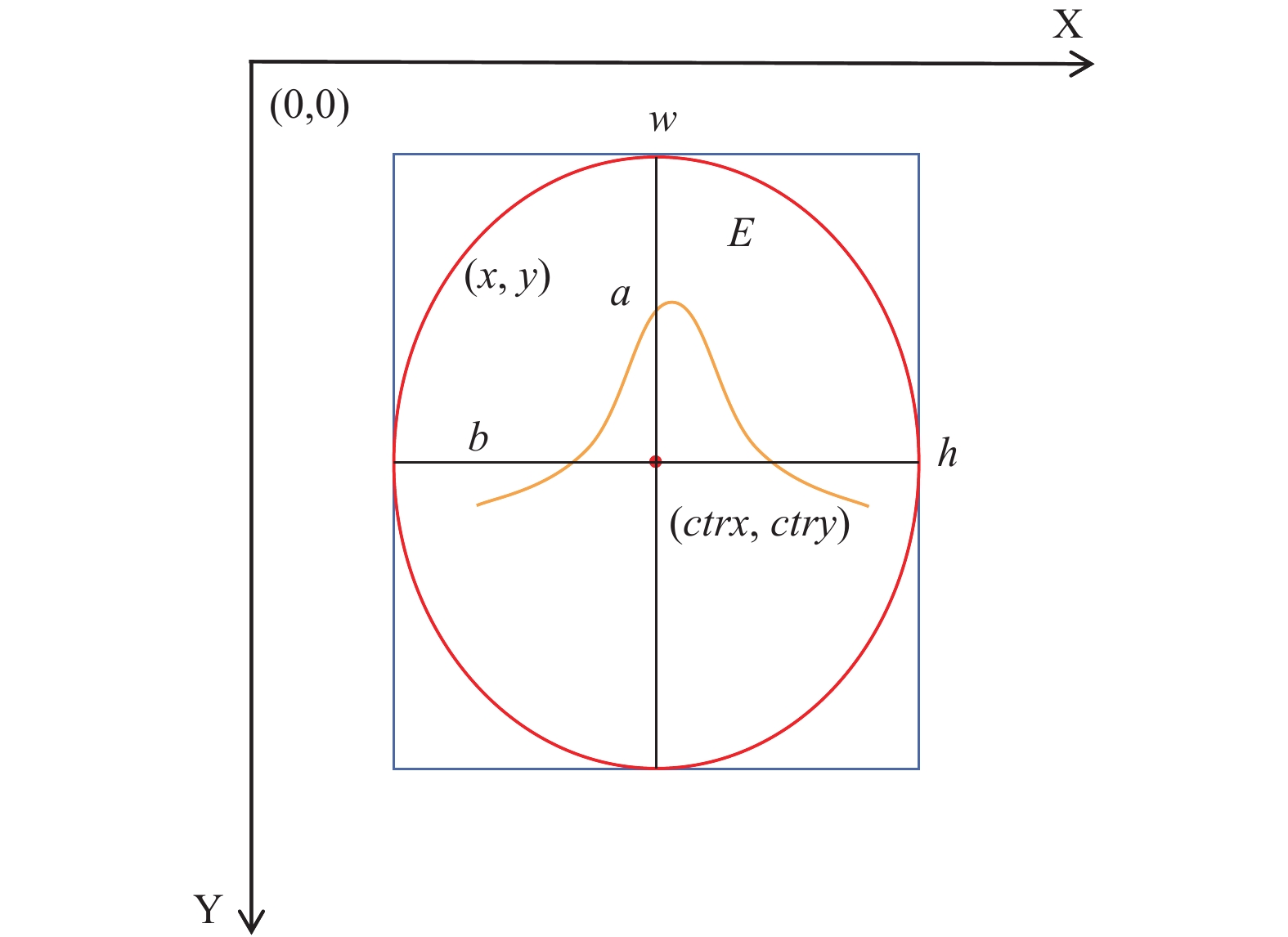
|
图 4 垂直椭圆高斯分布 |
所以在椭圆
| $ {Y}_{xyc}=\left\{\begin{array}{ll}\mathrm{exp}\left(-\dfrac{{(x-ctrx)}^{2}+{(y-ctry)}^{2}}{2{\sigma }_{p}^{2}}\right),& (x\text{, }y)\in E\\ 0,& {\rm{otherwise}}\end{array} \right.$ | (2) |
其中,
上述为构建垂直椭圆的方式, 而为了在GT区域使用倾斜方向椭圆构建Real-GT高斯分布, 本文所使用的方法为从一个垂直椭圆通过旋转一定角度得到.
首先, 讨论当椭圆中心在直角坐标系原点时, 任意一个斜椭圆
| $ \frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} + nxy = 1 $ | (3) |
假设, 该倾斜椭圆的垂直椭圆表达式为:
| $ \frac{{{x^2}}}{{{A^2}}} + \frac{{{y^2}}}{{{B^2}}} = 1 $ | (4) |
其中,
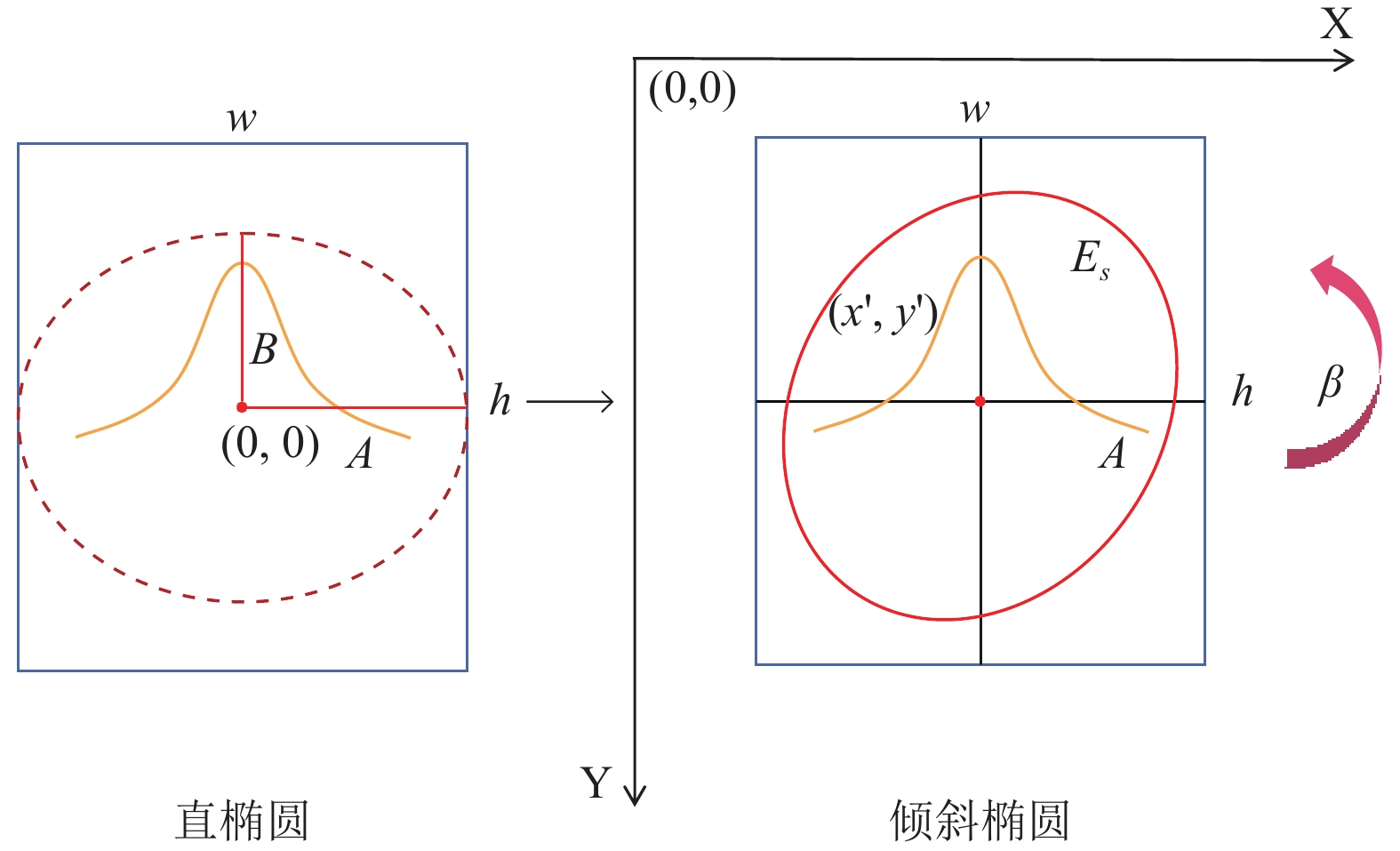
|
图 5 倾斜椭圆 |
两个椭圆上坐标点的关系表达式如下, 其中,
| $ \left[ {\frac{{x'}}{{y'}}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos\beta }&{ - \sin\beta } \\ {\sin\beta }&{\cos\beta } \end{array}} \right]\left[ {\frac{x}{y}} \right] $ | (5) |
将其转换为如下形式:
| $ \left[ {\frac{x}{y}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos\beta }&{\sin\beta } \\ { - \sin\beta }&{\cos\beta } \end{array}} \right]\left[ {\frac{{x'}}{{y'}}} \right] $ | (6) |
代入直椭圆方程表达式, 得:
| $ \begin{split} & {x'^{2}}\left(\frac{{\cos^2\beta }}{{{A^2}}} + \frac{{\sin^2\beta }}{{{B^2}}}\right) + {y'^{2}}\left(\frac{{\sin^2\beta }}{{{A^2}}} + \frac{{\cos^2\beta }}{{{B^2}}}\right) \\ & +2\left(\frac{{\cos \beta \sin \beta }}{{{A^2}}} - \frac{{\sin \beta \cos \beta }}{{{B^2}}}\right)x'y' = 1 \end{split} $ | (7) |
联合斜椭圆
| $ \left\{ \begin{gathered} \frac{{\cos^2\beta }}{{{A^2}}} + \frac{{\sin^2\beta }}{{{B^2}}} = \frac{1}{{{a^2}}} \\ \frac{{\sin^2\beta }}{{{A^2}}} + \frac{{\cos^2\beta }}{{{B^2}}} = \frac{1}{{{b^2}}} \\ 2\left(\frac{{\cos\beta \sin\beta }}{{{A^2}}} - \frac{{\sin\beta \cos\beta }}{{{B^2}}}\right) = n \\ \end{gathered} \right. $ | (8) |
将所求的
| $ \frac{{{{(x - ctrx)}^2}}}{{{a^2}}} + \frac{{{{(y - ctry)}^2}}}{{{b^2}}} + n(x - ctrx)(y - ctry) = 1 $ | (9) |
至此便可以根据上述倾斜椭圆方程在GT内构建符合Real-GT椭圆形状的高斯热图.
2.3 目标形状约束损失函数在anchor-free的关键点检测算法中, 损失函数[21]一般都包含中心点预测损失、目标大小损失以及目标中心点的偏置损失(可选). 这些损失函数中只有目标大小损失能够体现模型对目标大小约束, 但实际该损失函数只是考虑了目标GT层面上的大小回归, 本质上还是无法最大程度地在Real-GT层面进行目标形状的约束.
因此, 针对甲状旁腺的形状特点, 本文引入一种基于热力点分布的带有目标形状约束的损失函数. 输入图片下采样到对应输出尺度的热力图大小上, 其中GT是目标的标注框, Real-GT是内部的真正的目标区域, Predict是预测框. Predict预测框的定位是通过中心点与回归分支的结果计算得到, 其位置情况如图6所示.

|
图 6 预测框的位置 |
由于“软负样本”热力点的分布, 理想的Predict应该是其中心点, 也为Real-GT中心点, 同样靠近中心点分数会越接近1, 而远离中心点的分数会越小直至趋近于0. 同时, Predict所包含的区域应该是不超出GT且靠近Real-GT, 这样就能使得在检测到目标的同时, 减少标签中可能存在的矩形框标注误差的干扰.
在Real-GT上进行椭圆形状高斯分布构建的时候, 采用的是根据某一点在网格坐标系中是否满足椭圆公式来赋予权重的. GT中心点值为1, Real-GT内其他值
| $ {C}_{{\rm{Real}}{\textit{-}}{\rm{GT}}}=\displaystyle \sum _{i=ys\_min}^{ys\_max}\displaystyle \sum _{j=xs\_min}^{xs\_max}{\varphi }_{(i,j)},\;其中{\varphi }_{(i,j)} = \left\{ \begin{array}{ll}1,& {C}_{i,j} > 0\\ 0,& {\rm{otherwise}}\end{array}\right. $ | (10) |
Predict即为当前模型预测所认为的目标位置, 即其包含的热力点数目为Cpre=exp(tw)×exp(th). 此时就可以通过约束Cpre=CReal-GT, 在训练的时候调整回归分支上的tw, th的值. 再通过解码得到相应的宽高来使得预测框能够最大程度地包含目标的Real-GT, 所以目标形状约束函数公式如下:
| $ {L_{{\rm{shape}}}}{\text{ = |}}{\rm{exp}}{\text{(}}tw{\text{)}} \cdot {\rm{exp}}(th){{ - }}{C_{{\rm{Real{\textit{-}}GT}}}}{\text{|}} $ | (11) |
基于目标形状热力点分布, 设计目标形状约束损失函数与目标大小回归的损失函数, 可以使得预测框最大程度贴近GT的同时更加靠近Real-GT, 从而更好地进行目标的定位. 同时, 对于使用矩形框在标注时由于标注不当而使得GT过大或过小的情况下, 借助目标形状约束函数可以在训练的过程中通过模型所学习的正确的样本数据, 更加精准地定位目标的位置.
最终完整的损失函数在原先CenterNet的损失函数上加上本文所提出的目标约束损失函数, 公式如下, 在模型训练的时候进行目标位置的定位和目标分类.
| $ {L_{{\rm{det}}}}{\text{ = }}{L_k} + {\lambda _{{\rm{size}}}}{L_{{\rm{size}}}} + {\lambda _{{\rm{off}}}}{L_{{\rm{off}}}} + {\lambda _{{\rm{shape}}}}{L_{{\rm{shape}}}} $ | (12) |
其中,
在复杂的手术的场景中, 甲状旁腺的大小具有多样性, 尺度分布不均衡. 而解决尺度分布不平衡的问题通常是使用多尺度特征融合从而进行多尺度预测的方式, 网络的浅层擅长检测小尺寸物体, 而深层更擅长检测大尺寸物体. 因此本文在EllipseNet模型中集成了多尺度预测, 更好地适应不同大小的目标检测.
基于anchor-free的关键点检测, 没有办法根据GT与anchor的交并比来将目标分配到不同的尺度上进行预测. 因此, 本文利用在数据样本上对目标大小使用K-means (聚类)的方式来获取不同大小的宽高. EllipseNet网络架构输出的4个尺度其热力图从大到小为p1–p4即128×128–16×16, 不同尺度之间的热力图大小为2倍关系. 最终对目标样本进行4聚类得到结果如下式:
| $ {\textit{Si{{z}}e}}=\{({w}_{i}\text{, }{h}_{i})\},\;i\in \{1, 2, 3, 4\} $ | (13) |
具体将图像
算法1. 目标预测尺度分配算法
输入: 图像
输出: 图像
① XMatchScaleCalculation(GT, Size);
② max=0, k=0;
③ for i in range(4):
④ temp=IoU(GT,Size(i))
⑤ if temp>max:
⑥ max=temp, k=i
⑦ end if
⑧ end for
通过上述流程, 可以求得输入网络的图像
本节在真实手术场景下的甲状旁腺数据集上进行了实验, 以验证所提出的EllipseNet模型的有效性.
首先, 对实验条件和评价指标进行说明; 其次, 以CenterNet为baseline进行消融实验和对比实验, 通过分析各组实验的效果, 验证本文所提出的EllipseNet模型在甲状旁腺检测中具有良好的检测效果.
3.1 实验条件1)实验环境如下: CentOS 6.0操作系统, Intel(R) Xeon(R) CPU E5-2620 v4 @ 2.10 GHz处理器, 2块Tesla P4 GPU, Python 3.7.10, PyTorch 1.6.0.
2)数据集: 为了充分评估所提出的EllipseNet的性能, 本文采用真实手术场景下的甲状旁腺数据集(parathyroid dataset)进行验证, 如图7所示. 该数据集的标定由福建医科大学附属协和医院甲状腺外科治疗组完成. 该治疗组从完成的腔镜甲状腺手术中选取166例高清视频, 并对视频中可能出现甲状旁腺的片段进行截取、抽帧转换为图片进行标注. 最终构建的数据集图片13740张, 并按照8:1:1随机抽取形成训练集、验证集和测试集.

|
图 7 甲状旁腺数据集 |
3)训练参数: 输入网络的图片大小为512×512, batch size为4, 网络训练时所使用的优化器为SGD(stochastic gradient descent), 学习率(learning rate)为0.001, 动量参数(momentum)为0.9, 权重衰减系数(weight decay)为0.000 1.
3.2 评价指标本文采用AP (average precision)来评估模型的性能. 其中预测框与真实框交并比大于一定阈值时则认为预测正确, 否则认为预测错误, 如AP50则即表示阈值为0.5. 采用AP作为评价指标在要求获取较高准确率(Precision)的同时, 也要获取较高的召回率(Recall), 其中精确率和召回率的计算公式如下:
| $ Precision = \frac{{TP}}{{TP + FP}} $ | (14) |
| $ Recall = \frac{{TP}}{{TP + FN}} $ | (15) |
其中, TP为被模型预测为正类的正样本, 即检测结果为甲状旁腺, 实际也是甲状旁腺; FP表示被模型预测为正类的负样本, 即检测结果为甲状旁腺, 但实际为背景; FN表示被模型预测为负类的正样本, 即存在有甲状旁腺却没有被检测到的漏检情况. AP的计算公式如下:
| $ AP = \int_0^1 {Precision} (Recall)d(Recall) $ | (16) |
消融实验以CenterNet为baseline, 根据不同的热力点分布构建形式、是否引入目标形状约束损失函数和是否设置多尺度预测来进行实验. 具体每组实验说明如下: 1)在GT内构建垂直椭圆热力点分布构成CNV (CenterNet-Vertical). 2)在GT内构建倾斜椭圆热力点分布构成CNE (CenterNet-Ellipse). 3)构建倾斜椭圆热力点分布的同时引入目标形状约束损失函数构成CNS (CenterNet-ShapeLoss). 4)基于甲状旁腺目标形状的标签分配策略, 在GT中构建倾斜椭圆的热力点高斯分布, 同时融入目标形状约束的损失函数和多尺度预测构成本文的EllipseNet模型. 具体的消融实验结果见表1.
| 表 1 本文模型在甲状旁腺数据集的消融实验结果(%) |
实验结果显示, CNG、CNV与CNE在AP50上分别比baseline提升了3%、5.2%和6.7%, 这表明了缩小热力点分布范围从而减少大量负样本的有效性. 按照垂直椭圆、倾斜椭圆在GT内最大程度地将热力点分布在Real-GT上, 结合目标形状特征减少没有训练意义的负样本, 能更好地解决正负样本的不平衡问题. 并且由于倾斜椭圆分布是最拟合Real-GT, 最符合目标的形状和方向, 因此检测精度提升更高. 除此之外CNV、CNE在中等目标、大目标上有了不同程度的提高, 表明了在anchor-free方法中将热力点分布最大程度地放置在目标形状区域上可以得到更具有训练价值的“软负样本”, 可以显著地提升模型的检测精度.
其次, CNS在CNE的基础上引入了目标形状约束的损失函数, 在AP50上相比原baseline提升了7.5%, 比CNE提升了0.8%, 在大目标、中等目标指标上也有不同程度的提高, 表明了该损失函数的有效性.
CNS和baseline的检测效果对比如图8所示. 从两者的检测效果对比可以看出, 使用了目标形状约束的损失函数可以更精确地定位到目标的位置, 更好地捕捉到目标的边缘位置, 使得检测的框更加贴近真正的目标位置Real-GT.

|
图 8 CenterNet与CenterNet-ShapeLoss的检测效果对比 |
最后, 在CNS的基础上加入多尺度预测模块, 改变原先anchor-free算法单尺度的输出, 更好地适应甲状旁腺检测中存在的目标尺度不平衡问题, 以此提高不同大小的目标的检测精度, 构成EllipseNet模型. 由实验结果可以得知, 本文所提出的EllipseNet模型在AP50指标上从原先CenterNet的87.0%提升到95.0%, 提升了8.0%; 在中等目标指标APM和大目标APL分别提升了5.7%和5.2%. 由此可知, EllipseNet模型在不同大小的目标检测上检测精度更高, 模型的检测效果更好.
3.4 对比实验为了充分说明EllipseNet模型的检测效果, 本文还与部分主流的目标检测算法进行对比分析, 主流的算法包括两阶段目标检测算法Faster R-CNN、单阶段目标检测算法YOLOv3、EfficientDet算法[22]以及其他anchor-free算法等, 实验对比结果见表2.
| 表 2 不同模型在甲状旁腺数据集的对比实验结果(%) |
从表2可以看出, 本文所提出的算法EllipseNet相比于经典的两阶段检测算法Faster-RCNN、单阶段检测算法YOLOv3、RetinaNet、EfficientDet、YOLOX等在检测精度上都有大幅度的提升. EllipseNet模型中, 结合甲状旁腺为椭圆形目标的特点, 在构建样本空间的时候, 使用椭圆形高斯热图进行构建, 更好地划分正样本、“软负样本”、负样本, 减少没有训练意义的负样本, 更好地解决正负样本的不平衡问题; 同时, 基于高斯热力点的分布, 模型中所融入的目标形状约束损失函数更好地目标的宽高进行回归, 使得预测框更加贴近真正的目标位置Real-GT; 最后, EllipseNet模型中还借助数据样本的聚类所得的不同尺度的数据, 融入多尺度预测分支, 进一步提高检测精度, 使得最终构建的EllipseNet模型在甲状旁腺检测场景中能取得比当前主流模型得更高的检测精度.
由于真实手术场景较为复杂, 为了验证方法的鲁棒性, 本文选出了几种典型的场景和不同尺度的甲状旁腺图片进行检测和分析, 结果如图9所示. 其中, 图9(a)为不同大小的甲状旁腺; 图9(b)为手术过程中存在纱布遮挡, 同时周围背景较为复杂的甲状旁腺, 目标特征不明显, 容易出现漏检; 图9(c)为手术刀干扰下的甲状旁腺, 检测难度更高. 从检测的效果图中可以看出, 本文提出的EllipseNet模型对于不同尺度大小的甲状旁腺在手术刀遮挡、手术过程充血以及甲状腺术中场景较暗等一些复杂场景下都能取得不错的检测效果.

|
图 9 EllipseNet的检测效果 |
4 结论
本文在基于类似椭圆形状的甲状旁腺检测场景中, 提出一种椭圆形高斯热图标签分配策略, 并运用于所设计的EllipseNet模型. 首先, 基于GT构建椭圆形状的高斯函数热力点分布, 最大程度地拟合GT框中的Real-GT, 使得正负样本的分配更加细粒度; 其次, 融入目标形状信息的损失函数, 对目标的位置进行约束, 进一步提高检测的精度; 同时, 在检测模型中构建多尺度预测, 使得模型能够更好地检测到不同大小的目标, 解决甲状旁腺检测中目标尺度不平衡的问题. 实验结果表明, 本文提出的EllipseNet在AP50中达到了95%, 相比原先anchor-free检测算法CenterNet算法提升了8.0%; 与当前通用单阶段检测算法中性能较好的YOLOX算法相比, 本文模型在AP50提升了2.9%. 总之, 改进后的EllipseNet模型相比于其他多种主流的检测算法, 检测精度均有不同程度的提升.
| [1] |
Zaidi SSA, Ansari MS, Aslam A, et al. A survey of modern deep learning based object detection models. Digital Signal Processing, 2022, 126: 103514. DOI:10.1016/j.dsp.2022.103514 |
| [2] |
Wang CY, Bochkovskiy A, Liao HYM. YOLOv7: Trainable bag-of-freebies sets new state-of-the-art for real-time object detectors. arXiv:2207.02696, 2022.
|
| [3] |
Redmon J, Farhadi A. YOLOv3: An incremental improvement. arXiv:1804.02767, 2018.
|
| [4] |
Ren SQ, He KM, Girshick R, et al. Faster R-CNN: Towards real-time object detection with region proposal networks. Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal: MIT Press, 2015. 91–99.
|
| [5] |
谢富, 朱定局. 深度学习目标检测方法综述. 计算机系统应用, 2022, 31(2): 1-12. DOI:10.15888/j.cnki.csa.008303 |
| [6] |
王军轶, 高明. 甲状旁腺术中快速识别技术的进展. 中国肿瘤临床, 2019, 46(9): 479-483. DOI:10.3969/j.issn.1000-8179.2019.09.203 |
| [7] |
Huang ZC, Li W, Xia XG, et al. A general Gaussian heatmap label assignment for arbitrary-oriented object detection. IEEE Transactions on Image Processing, 2022, 31: 1895-1910. DOI:10.1109/TIP.2022.3148874 |
| [8] |
Liu W, Anguelov D, Erhan D, et al. SSD: Single shot multibox detector. Proceedings of the 14th European Conference on Computer Vision. Amsterdam: Springer, 2016. 21–37.
|
| [9] |
Lin TY, Goyal P, Girshick R, et al. Focal loss for dense object detection. Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV). Venice: IEEE, 2017. 2999–3007.
|
| [10] |
Tian Z, Shen CH, Chen H, et al. FCOS: Fully convolutional one-stage object detection. Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 9626–9635.
|
| [11] |
Zhou XY, Wang DQ, Krähenbühl P. Objects as points. arXiv:1904.07850, 2019.
|
| [12] |
Zand M, Etemad A, Greenspan M. ObjectBox: From centers to boxes for anchor-free object detection. Proceedings of the 17th European Conference on Computer Vision. Tel Aviv: Springer, 2022. 390–406.
|
| [13] |
Neubeck A, van Gool L. Efficient non-maximum suppression. Proceedings of the 18th International Conference on Pattern Recognition. Hong Kong: IEEE, 2006. 850–855.
|
| [14] |
Zhang SF, Chi C, Yao YQ, et al. Bridging the gap between anchor-based and anchor-free detection via adaptive training sample selection. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 9756–9765.
|
| [15] |
Law H, Deng J. Cornernet: Detecting objects as paired keypoints. Proceedings of the 15th European Conference on Computer Vision. Munich: Springer, 2018. 765–781.
|
| [16] |
Zhou XY, Zhuo JC, Krähenbuhl P. Bottom-up object detection by grouping extreme and center points. Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 850–859.
|
| [17] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 770–778.
|
| [18] |
Newell A, Yang KY, Deng J. Stacked hourglass networks for human pose estimation. Proceedings of the 14th European Conference on Computer Vision. Amsterdam: Springer, 2016. 483–499.
|
| [19] |
Yu F, Wang DQ, Shelhamer E, et al. Deep layer aggregation. Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 2403–2412.
|
| [20] |
He KM, Zhang XY, Ren SQ, et al. Spatial pyramid pooling in deep convolutional networks for visual recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1904-1916. DOI:10.1109/TPAMI.2015.2389824 |
| [21] |
Zou ZX, Chen KY, Shi ZW, et al. Object detection in 20 years: A survey. arXiv:1905.05055, 2019.
|
| [22] |
Tan MX, Pang RM, Le QV. EfficientDet: Scalable and efficient object detection. Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 10778–10787.
|
| [23] |
Kong T, Sun FC, Liu HP, et al. Foveabox: Beyound anchor-based object detection. IEEE Transactions on Image Processing, 2020, 29: 7389-7398. DOI:10.1109/TIP.2020.3002345 |
| [24] |
Ge Z, Liu ST, Wang F, et al. YOLOX: Exceeding YOLO series in 2021. arXiv:2107.08430, 2021.
|
 2023, Vol. 32
2023, Vol. 32


