近年来, 随着信息技术的飞速发展, 现实生活中出现了非常多具有大量特征的数据集, 从而引发了高维数据的处理问题. 高维数据的处理方法可以分为特征提取和特征选择^[1], 其中, 特征选择的主要目的是从原始特征集中选择出使得评估指标最佳的特征子集. 特征选择保留了数据的原始特征, 具有良好的可解释性, 因此得到了广泛应用.

特征选择本质上是一个组合优化问题, 因此, 很多学者利用各类智能优化算法来解决特征选择问题. Hancer等^[2]提出了一种基于改进蜂群算法的特征选择方法, 该方法将遗传算子和非支配排序过程引入到蜂群算法并应用到特征选择中. Mashhour等^[3]提出了一种基于萤火虫算法和卡方的特征选择方法, 该方法通过用每次移动后改变的细胞卡方值模拟萤火虫位置, 并通过计算一组不同的适应度函数作为特征权重来模拟萤火虫强度进而应用到特征选择中. 孙林等^[4]提出了一种基于改进帝王蝶优化算法的特征选择方法, 该方法使用差分进化算法中的变异操作替换帝王蝶算法的迁移算子, 其次融入了自适应调整策略, 对每次种群进行柯西变异, 然后引入KNN分类器构造适应度函数, 最终获得最优特征子集.

作为一种处理不确定性的有效工具, 粗糙集理论^{[5, 6]}在特征选择方面也可以发挥重要的作用. 很多学者利用粗糙集理论来进行特征选择. 王锋等^[7]提出了一种组增量式的粗糙特征选择算法. 江峰等^[8]利用粗糙集的近似精度来定义近似决策熵, 并提出了一种基于近似决策熵的特征选择算法. 董红斌等^[9]提出了一种基于关联信息熵的特征选择算法. 王鹏等^[10]提出了一种基于改进模糊决策粗糙集的最小化决策代价特征选择算法. 然而, 基于粗糙集的特征选择方法还存在计算效率低、性能难以满足要求等问题. 针对这些问题, 有不少学者将粗糙集理论与智能优化算法结合在一起来进行特征选择的相关研究, 从而可以有效发挥这两类方法各自的优势. Tawhid等^[11]提出了基于粗糙集与二进制鲸鱼优化的特征选择算法. Azar等^[12]提出了一种基于粗糙集和灰狼算法的特征选择方法. Chen等^[13]将鱼群算法与粗糙集结合在一起来进行特征选择. 高薇等^[14]提出了一种基于粗糙集与人工蜂群算法的动态特征选择方法.

人工蜂群(artificial bee colony, ABC)算法作为一种经典的群智能优化算法已被广泛应用于特征选择问题. 人工蜂群算法是由土耳其教授Karaboga等^{[15, 16]}受蜜蜂蜂群采蜜机制的启发而提出的. 该算法运算简单、具有较好的探索能力且参数较少, 因此引起了大量的关注. 但是, 收敛速度较慢、容易陷入局部最优等仍然是该算法在实际应用中面临的问题.

针对人工蜂群算法的不足, 本文将粗糙集理论^[6]引入到人工蜂群算法中, 并由此提出一种基于粒度粗糙熵与改进蜂群算法的特征选择算法FS_GREIABC. FS_GREIABC算法的主要思路如下: 首先, 针对人工蜂群算法中的适应度函数构建问题, 将粗糙集中的知识粒度与粗糙熵有机地结合在一起, 从而得到一种新的信息熵模型——粒度粗糙熵. 粒度粗糙熵中采用到的粗糙熵能够有效度量知识的完备性, 但却不能有效度量知识的粒度大小, 而知识粒度可以度量知识的粒度大小, 两者有机地结合起来能够更加全面地对信息表中的属性进行度量, 为后续的特征选择提供了一种更加全面的度量机制; 其次, 人工蜂群算法的关键步骤之一就是如何为算法选择一个合适的适应度函数, 我们提出了一种基于粒度粗糙熵的适应度函数, 针对特征选择中两个相互冲突的目标是必须完成所选特征的最小数目和最大的分类精度, 我们利用粒度粗糙熵来构造适应度函数能够更好地对特征子集进行评估; 第三, 为了提高人工蜂群算法的局部搜索能力, 考虑到云模型具有稳定性和随机性等优势^{[17, 18]}, 因此, 将云模型引入到跟随蜂阶段, 并采用一维正态云模型来调整局部搜索范围, 以增强算法的局部开采能力, 提高蜂群算法的鲁棒性和收敛速度.

本文的主要贡献如下: (1)提出了一种新的信息熵模型——粒度粗糙熵. 粒度粗糙熵将粗糙集中的知识粒度与粗糙熵这两个基本概念结合在一起, 既考虑了知识的不完备性, 又刻画了知识的粒度大小, 是一种更加全面的不确定性度量机制. (2)提出了一种基于粒度粗糙熵的适应度函数, 通过粒度粗糙熵来计算每只蜜蜂的适应度值, 从而为人工蜂群算法提供一种新的适应度计算策略. (3)为了提高ABC算法的局部搜索能力, 将云模型引入到人工蜂群算法的跟随蜂阶段, 采用一维正态云模型来改进跟随蜂阶段的搜索策略.

1 相关技术介绍 1.1 粗糙集的相关概念

在粗糙集中, 信息表^[6]是一个四元组 $ S = (U, A, V, f) $ , 其中U表示非空有限的对象集; A表示非空有限的属性集; V表示所有属性值域的并集, 即 $ V = \bigcup\nolimits_{a \in A} {{V_a}} $ ( $ {V_a} $ 是属性 $ a $ 的值域); $ f:U \times A \to V $ 表示一个函数, 使得对任意 $ a \in A $ 以及 $ x \in U $ , 都有 $ f(x, a) \in {V_a} $ .

给定一个信息表 $ S = (U, A, V, f) $ , 对于任意属性子集 $ B \subseteq A $ , 由属性子集B所确定的一个不可分辨关系如下:

$ IND(B) = \{ (x, y) \in U \times U:f(x, a) = f(y, a), \forall a \in B\} $

其中, $ IND(B) $ 是论域 $ U $ 上的一个等价关系, 它把 $ U $ 划分成不同的等价类, 所有等价类的集合就构成了 $ U $ 上的一个划分, 记为 $ U/IND(B) $ .

定义1. 知识粒度^[19]. 给定一个信息表 $ S = (U, A, V, f) $ , 对于任意属性子集 $ B \subseteq A $ , 令 $U/IND(B) = \{ {X_1}, {X_2}, \cdots, {X_t}\}$ 表示关系 $ IND(B) $ 对论域 $ U $ 的划分. $ B $ 的知识粒度 $ GK(B) $ 被定义为:

$ GK(B) = \frac{{\displaystyle\sum\limits_{i = 1}^t {|{X_i}{|^2}} }}{{|U{|^2}}} $

其中, 对任意 $ 1 \leqslant i \leqslant t $ , $ |{X_i}| $ 表示集合 $ {X_i} $ 的势, $ |U| $ 表示集合 $ U $ 的势.

可以证明, 对任意 $ B \subseteq A $ , $ \dfrac{1}{{|U|}} \leqslant GK(B) \leqslant 1 $ .

定义2. 粗糙熵^[20]. 给定一个信息表 $ S = (U, A, V, f) $ , 对于任意属性子集 $ B \subseteq A $ , 令 $U/IND(B) = \{ {X_1}, {X_2}, \cdots, {X_t}\}$ 表示关系 $ IND(B) $ 对论域 $ U $ 的划分. $ B $ 的粗糙熵 $ {E_r}(B) $ 被定义为:

$ {E_r}(B) = - \sum\limits_{i = 1}^t {\frac{{|{X_i}|}}{{|U|}}{{\log }_2}\frac{1}{{|{X_i}|}}} $

(1)

可以证明, 对任意 $ B \subseteq A $ , $ 0 \leqslant {E_r}(B) \leqslant {\log _2}|U| $ .

1.2 人工蜂群算法介绍

传统的人工蜂群算法的具体步骤如下.

① 初始化种群. 假设随机产生N个初始解, 并且 ${X_i}\;(1 \leqslant i \leqslant N)$ 为种群的第i个解. ${X_i}$ 可以用一个D维向量来表示, 其中, D是待优化目标问题的参数个数. 随机获得初始解的过程如下:

$ {X_{i, j}} = {X_{\min , j}} + Rand(0, 1) \times ({X_{\max , j}} - {X_{\min , j}}) $

(2)

其中, $ 1 \leqslant i \leqslant N $ , $ 1 \leqslant j \leqslant D $ ; $ {X_{\min , j}} $ 为搜索解空间的下限; ${X_{{\rm{max}}, j}}$ 为搜索解空间的上限.

② 计算适应度. 蜂群将位置替换为适应度最优的位置. 雇佣蜂使用目标函数来评估每个解 ${X_i}$ 的适应度, 适应度由式(3)计算:

$ fi{t_i} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{1}{{1 + {f_i}}}, {f_i} \geqslant 0} \\ {1 + {\rm{abs}}({f_i}), {f_i} \lt 0} \end{array}} \right. $

(3)

其中, $ {f_i} $ 是 ${X_i}$ 所对应的目标函数值, 而 $ fi{t_i} $ 则是 ${X_i}$ 的适应度.

③ 雇佣蜂(引领蜂)搜索. 雇佣蜂对食物源进行领域搜索, 产生候选解, 并计算候选解的适应度值. 具体而言, 雇佣蜂基于贪婪策略来选择食物源, 保留适应度最高的食物源. 根据当前的解 ${X_i}$ , 可以利用式(4)来计算新的候选解 ${V_i}$ :

$ {V_{i, j}} = {X_{i, j}} + {r_{i, j}}({X_{i, j}} - {X_{k, j}}) $

(4)

其中, $ 1 \leqslant i \leqslant N $ , $ 1 \leqslant j \leqslant D $ ; k与j为随机选取的两个下标, 并且 $ 1 \leqslant k \leqslant N $ , $ k \ne i $ ; $ {r_{i, j}} $ 是[−1, 1]区间内的一个随机数.

④ 跟随蜂阶段. 在传统的人工蜂群算法中, 跟随蜂采用轮盘赌的方式(即按照一定的概率 $ {p_i} $ )来选择已寻找到较优食物源的雇佣蜂进行跟随, 然后根据雇佣蜂搜索公式在其邻域内搜索新的食物源, 并择优保留食物源. 选择概率 $ {p_i} $ 由式(5)来计算:

$ {p_i} = \frac{{fi{t_i}}}{{\displaystyle\sum\limits_{i = 1}^{N/2} {fi{t_i}} }} $

(5)

其中, $ 1 \leqslant i \leqslant N $ , $ {p_i} $ 为第i个食物源(解) ${X_i}$ 所对应的概率, $fi{t_i}$ 则是 ${X_i}$ 的适应度.

由式(6)可知, 选择概率 $ {p_i} $ 与适应度成正比关系. 因此, 在进行特征选择时, 人工蜂群算法容易出现过早收敛、收敛到局部最优等问题. 事实上, 经过多次迭代之后, 当前较差的解也可能包含一些非常有用的信息. 为了避免过早收敛并保证物种多样性, 本文将采用一种改进的基于轮盘赌的选择策略, 使得较差的解也具有较大的选择概率. 在这种改进的选择策略中, 选择概率 $ {p_i} $ 由式(6)来计算:

$ {p_i} = \frac{{1/fi{t_i}}}{{\displaystyle\sum\limits_{i = 1}^N {(1/fi{t_i})} }} $

(6)

⑤ 侦查蜂阶段. 侦查蜂基于概率 $ pro{b_i} $ ( $ 1 \leqslant i \leqslant N $ )来选择一个食物源, 并且更新其位置信息. 每个食物源 ${X_i}$ 的选择概率 $ pro{b_i} $ 由式(7)计算得到:

$ pro{b_i} = \frac{{0.9 \times fi{t_i}}}{{max \_fit}} + 0.1 $

(7)

其中, $ 1 \leqslant i \leqslant N $ , $fi{t_i}$ 是 ${X_i}$ 的适应度, $max \_fit$ 为最大适应度.

2 基于云模型的跟随蜂搜索策略

云模型是李德毅院士等所提出的一种表示某个定性概念 $\widetilde A$ 与其定量数值之间不确定性的转换模型^{[17, 18]}. 云模型的数字特征有数值期望 $ Ex $ 、熵 $ En $ 和超熵 $ He $ . 期望 $ Ex $ 是云的重心位置, 是最能表现定性概念的点, 表示在论域空间上分布的期望; 熵 $ En $ 是云的期望曲线宽度, 它的大小反映了在论域中可被模糊概念接受的元素数, 是对定性概念模糊度的度量; 超熵 $ He $ 是云滴的厚度, 反映了云的熵的离散程度, 即熵的熵, 是对熵的不确定度的度量. 云模型综合考虑了随机性和模糊性, 由定量到定性, 用数字特征表示语言值. 再从定性到定量, 通过云发生器来模拟随机性、模糊性以及二者之间的关联性^[19]. 假设U是用数值集合表示的定量论域, C是U上的定性概念, 若定量值 $ x \in U $ 是定性概念C的一次随机体现, $x$ 对C的确定度 $ \mu (x) \in [0, 1] $ 是具有稳定倾向性的随机数, 即 $ U \to [0, 1] $ , $ \forall x \in U $ , $ x \to \mu (x) $ , 则称 $x$ 在论域U上的分布为云, 每一个 $x$ 称为云滴.

一维正态云算子 $ C(Ex, En, He) $ 的计算步骤如下^[21].

① 生成以 $ En $ 为期望、 $ He $ 为标准差的正态随机数 $Ei\;(1 \leqslant i \leqslant N)$ .

② 生成以 $ Ex $ 为期望、 $ Ei $ 为标准差的正态随机数 ${x_i}\;(1 \leqslant i \leqslant N)$ , $ {x_i} $ 对应的是论域空间中的云滴, $N$ 是云滴的总个数.

③ 计算 ${y_i} = \exp ( - {({x_i} - Ex)^2}/2$ $E{i^2})$ , 令 $ {y_i} $ 为 $ {x_i} $ 属于定性概念 $\widetilde A$ 的确定度.

人工蜂群算法的跟随蜂在搜索新的食物源时, 不够稳定且随机性较大, 当搜索次数迭代到一定的数目后, 便由于很难提高蜜源寻优的能力而陷入局部最优, 降低了算法的求解精度. 由于云模型具有稳定倾向性和随机性等优势, 本文运用正态云模型对跟随峰的搜索方式进行改进, 以提高算法的局部开采能力, 从而改善ABC算法求解精度低、收敛速度慢的缺点, 提高ABC算法的鲁棒性和收敛速度. 我们利用一维正态云模型 $ C(Ex, En, He) $ 在初始食物源附近产生新的食物源, 即在跟随蜂阶段, 假设食物源位置为 ${x_{ij}}$ , 令:

$\left\{ { \begin{split} & Ex = {x_{ij}} \\ & En = - ({X_{\max , j}} - {X_{\min , j}})(iter/iter\_max {)^2} + {X_{\max , j}} \\ & He = En/10 \end{split} } \right.$

(8)

其中, $ {X_{\min , j}} $ 为搜索解空间的下限, ${X_{{\rm{max}}, j}}$ 为搜索解空间的上限, $ iter $ 为当前迭代次数, $iter\_max$ 为最大迭代次数.

3 基于粒度粗糙熵的人工蜂群算法适应度计算

人工蜂群算法的一个关键环节就是适应度的计算, 我们有必要为该算法选择一个合适的适应度函数. 本节将在文献[18]中所提出的粗糙熵模型基础上, 进一步提出一种新的信息熵模型——粒度粗糙熵, 并利用粒度粗糙熵来构建人工蜂群算法的适应度函数. 粒度粗糙熵不仅能够刻画出知识的粒度大小, 而且还可以对知识的不完备性进行度量, 因此, 它非常适合于为人工蜂群算法构建适应度函数.

下面, 我们首先给出粒度粗糙熵的具体定义, 并对粒度粗糙熵的基本性质进行分析, 最后将粒度粗糙熵应用于人工蜂群算法的适应度计算中.

定义3. 粒度粗糙熵. 给定一个信息表 $ S = (U, A, V, f) $ , 对于任意属性子集 $ B \subseteq A $ , 令 $U/IND(B) = \{ {X_1}, {X_2}, \cdots, {X_t}\}$ 表示关系 $ IND(B) $ 对论域U的划分. 属性子集B的粒度粗糙熵 $ GK{E_r}(B) $ 被定义为:

$ GK{E_r}(B) = GK(B) \times {E_r}(B) $

(9)

其中, $ GK(B) $ 为 $ B $ 的知识粒度, $ {E_r}(B) $ 为 $ B $ 的粗糙熵.

从定义3可以看出, 粒度粗糙熵将知识粒度和粗糙熵有机地结合在一起, 既考虑了知识的不完备性, 又刻画了知识的粒度大小, 从而得到了一种更加全面的不确定性度量机制.

下面, 给出粒度粗糙熵的一些基本性质.

定理1. 给定一个信息表 $ S = (U, A, V, $ $ f) $ , 其中 $U = \{ {x_1}, {x_2}, \cdots , {x_n}\}$ . 对于任意属性子集 $ B \subseteq A $ , $ B $ 的粒度粗糙熵 $ GK{E_r}(B) $ 满足以下性质.

1) $ 0 \leqslant GK{E_r}(B) \leqslant {\log _2}|U| $ .

2)当 $ U/IND(B) = \{ \{ {x_1}\} , \{ {x_2}\} , \cdots , $ $ \{ {x_n}\} \} $ 时, $ GK{E_r}(B) $ 达到最小值.

3)当 $ U/IND(B) = \{ U\} $ 时, $ GK{E_r}(B) $ 达到最大值.

证明:

1)当 $ IND(B) $ 为 $ U $ 上的相等关系时, 即 $ U/IND(B) = \{ \{ {x_1}\} , \{ {x_2}\} , \cdots , \{ {x_n}\} \} $ 时, 我们可以得到:

$\left\{ { \begin{split} &GK(B) = \frac{{\displaystyle\sum\limits_{i = 1}^t {|{X_i}{|^2}} }}{{|U{|^2}}} = \frac{{\displaystyle\sum\limits_{i = 1}^{|U|} {{1^2}} }}{{|U{|^2}}} = \frac{{|U|}}{{|U{|^2}}} = \frac{1}{{|U|}}\\ &{E_r}(B) = - \sum\limits_{i = 1}^t {\frac{{|{X_i}|}}{{|U|}}{{\log }_2}\frac{1}{{|{X_i}|}}} = - \displaystyle\sum\limits_{i = 1}^{|U|} {\frac{1}{{|U|}}{{\log }_2}\frac{1}{1}} = 0 \end{split}} \right.$

这时, 我们有: $ GK{E_r}(B) = GK(B) \times {E_r}(B) = 0 $ .

在上述情形下, 粒度粗糙熵 $ GK{E_r}(B) $ 取得最小值0.

2)当 $ IND(B) $ 为 $ U $ 上的论域关系时, 即 $ U/IND(B) = \{ U\} $ 时, 我们可以得到:

$\left\{ { \begin{split} &GK(B) = \frac{{\displaystyle\sum\limits_{i = 1}^t {|{X_i}{|^2}} }}{{|U{|^2}}} = \frac{{|U{|^2}}}{{|U{|^2}}} = 1 \\ &{E_r}(B) = - \sum\limits_{i = 1}^t {\frac{{|{X_i}|}}{{|U|}}{{\log }_2}\frac{1}{{|{X_i}|}}} = - \frac{{|U|}}{{|U|}}{\log _2}\frac{1}{{|U|}} = {\log _2}|U| \end{split}} \right.$

这时, 我们有: $ GK{E_r}(B) = GK(B) \times {E_r}(B) = {\log _2}|U| $ .

在上述情形下, 粒度粗糙熵 $ GK{E_r}(B) $ 取得最大值 $ {\log _2}|U| $ .

根据上述证明, 可知 $ 0 \leqslant GK{E_r}(B) \leqslant {\log _2}|U| $ .

由于2)和3)的证明可以由1)的证明直接得到, 因此这里忽略具体过程.

定理2. 给定一个信息表 $ S = (U, A, V, $ $ f) $ , 对于任意两个属性子集 $ {B_1} \subseteq A $ , $ {B_2} \subseteq A $ , 如果 $U/IND({B_1})$ $\underline \prec $ $U/IND $ $({B_2})$ , 则 $ GK{E_r}({B_1}) \leqslant $ $ GK{E_r}({B_2}) $ .

证明: 假设 $ U/IND({B_1}) = \{ {X_1}, {X_2}, $ $ \cdots , {X_m}\} $ , 并且 $ U/ IND({B_2}) = \{ {Y_1}, {Y_2}, $ $ \cdots , {Y_n}\} $ . 由于 $ U/IND({B_1}) $ $\underline \prec $ $U/IND({B_2}) $ , 我们可以得到: $ m \geqslant n $ 并且存在一个集合 $ \{ 1, 2, \cdots , m\} $ 的划分 $ C = \{ {C_1}, {C_2}, \cdots , {C_n}\} $ 使得下列公式成立:

$ {Y_j} = \bigcup\limits_{i \in {C_j}} {{X_i}{, ^{}}1 \leqslant j \leqslant n} $

由定义2, 我们可以得出:

$ \begin{split} {E}_{r}({B}_{2})&=-{\displaystyle \sum _{j=1}^{n}\frac{\left|{Y}_{j}\right|}{\left|U\right|}}{\mathrm{log}}_{2}\frac{1}{\left|{Y}_{j}\right|}\\ &=-\frac{1}{\left|U\right|}{\displaystyle \sum _{j=1}^{n}\left|{\displaystyle \underset{i\in {C}_{j}}{\bigcup }{X}_{i}}\right|}{\mathrm{log}}_{2}\frac{1}{\left|{\displaystyle \underset{i\in {C}_{j}}{\bigcup }{X}_{i}}\right|}\\ &=-\frac{1}{\left|U\right|}\displaystyle \sum _{j=1}^{n}\left({\displaystyle \sum _{i\in {C}_{j}}\left|{X}_{i}\right|}\mathrm{log}{}_{2}\left(\frac{1}{{\displaystyle \sum _{i\in {C}_{j}}\left|{X}_{i}\right|}}\right)\right)\\ &=\frac{1}{\left|U\right|}\displaystyle \sum _{j=1}^{n}\left({\displaystyle \sum _{i\in {C}_{j}}\left|{X}_{i}\right|}\mathrm{log}{}_{2}\left({\displaystyle \sum _{i\in {C}_{j}}\left|{X}_{i}\right|}\right)\right) \end{split} $

由于 $ m \geqslant n $ , 并且对任意 $ 1 \leqslant i \leqslant m $ , $ |{X_i}| \geqslant 1 $ , 因此, 我们可以得出如下结论: 对于每一个 $ 1 \leqslant j \leqslant n $ , 都有 $ \displaystyle\sum\limits_{i \in {C_j}} {|{X_i}|} {\log _2} $ $ \left(\displaystyle\sum\limits_{i \in {C_j}} {|{X_i}|} \right) \geqslant \displaystyle\sum\limits_{i \in {C_j}} {|{X_i}|} {\log _2}|{X_i}| $ .

根据上述结果, 我们可以进一步得出:

$ \begin{split} {E}_{r}({B}_{2})=&\frac{1}{\left|U\right|}{\displaystyle \sum _{j=1}^{n}\left({\displaystyle \sum _{i\in {C}_{j}}\left|{X}_{i}\right|}{\text{log}}_{2}\left({\displaystyle \sum _{i\in {C}_{j}}\left|{X}_{i}\right|}\right)\right)}\\ \geqslant& \frac{1}{\left|U\right|}\displaystyle \sum _{j=1}^{n}\left({\displaystyle \sum _{i\in {C}_{j}}\left|{X}_{i}\right|}{\text{log}}_{2}|{X}_{i}|\right)\\ =&\frac{1}{\left|U\right|}{\displaystyle \sum _{i=1}^{m}\left|{X}_{i}\right|{\text{log}}_{2}\left|{X}_{i}\right|}\\ =&-{\displaystyle \sum _{i=1}^{m}\frac{\left|{X}_{i}\right|}{\left|U\right|}{\mathrm{log}}_{2}\frac{1}{\left|{X}_{i}\right|}} \\ =&{E}_{r}({{B}_{1}}) \end{split} $

另一方面, 根据文献[17], 我们可以得出: 如果 $U/IND{({B_1})}$ ${\underline \prec } $ $U/IND({B_2}) $ , 则 $ GK({B_1}) $ $ \leqslant GK({B_2}) $ . 这样, 根据定义3, 可以得出: $ GK{E_r}({B_1}) = GK({B_1}) \times {E_r}({B_1}) \leqslant GK({B_2}) \times {E_r}({B_2}) = GK{E_r}({B_2}) $ .

传统的人工蜂群算法采用式(4)计算适应度, 本文则为人工蜂群算法提供一种基于粒度粗糙熵的适应度函数, 具体定义如下:

定义4. 基于粒度粗糙熵的适应度函数. 假设当前有N个解(食物源), 对任意 $ 1 \leqslant i \leqslant N $ , 令 $ {X_i} $ 表示第 $ i $ 个解, 并且令 $ {B_i} $ 为 $ {X_i} $ 所对应的属性子集. 解 $ {X_i} $ 的适应度由式(10)计算:

$ fi{t_i} = \frac{1}{{1 + GK{E_r}({B_i})}} $

(10)

其中, $ 1 \leqslant i \leqslant N $ , $ GK{E_r}({B_i}) $ 是属性子集 $ {B_i} $ 的粒度粗糙熵, $ fi{t_i} $ 则是 $ {X_i} $ 的适应度.

由定理1可知, 对任意 $ 1 \leqslant i \leqslant N $ , $ fi{t_i} $ 的取值范围为 $ [{(1 + {\log _2}|U|)^{ - 1}}, 1] $ .

4 特征选择算法

本节首先给出一种计算粒度粗糙熵的算法(即算法1), 然后给出特征选择算法FS_GREIABC (即算法2).

算法1. 粒度粗糙熵的计算

输入: 给定的信息表 $\scriptstyle S = (U, A, V, f) $ , 任意属性子集 $\scriptstyle B \subseteq A $ .

输出: 属性子集 $\scriptstyle B $ 的粒度粗糙熵 $\scriptstyle GK{E_r}(B) $ .

1) 初始化: 令 $\scriptstyle {E_{(r)}}(B) = 0 $ , 并且令 $\scriptstyle GK(B) = 0 $ .

2) 通过计数排序的方法^[8]计算划分 $\scriptstyle U/IND(B) $ (假设 $\scriptstyle U/IND(B) = \{ {X_1} $ , $\scriptstyle {X_2}, $ $\scriptstyle \cdots , {X_t}\} $ ).

3) 根据划分 $\scriptstyle U/IND(B) $ 计算每个等价类 $\scriptstyle {X_i} $ 的势 $\scriptstyle |{X_i}| $ , 其中, $\scriptstyle 1 \leqslant i \leqslant t $ .

4) 对任意 $\scriptstyle 1 \leqslant i \leqslant t $ , 循环执行:

　　　令 $\scriptstyle {E_r}(B) = {E_r}(B) - \frac{{|{X_i}|}}{{|U|}}{\log _2}\frac{1}{{|{X_i}|}} $ .

5) 对任意 $\scriptstyle 1 \leqslant i \leqslant t $ , 循环执行:

　　　令 $\scriptstyle GK(B) = GK(B) + \frac{{|{X_i}{|^2}}}{{|U{|^2}}} $ .

6) 计算粒度粗糙熵 $\scriptstyle GK{E_r}(B) $ , 即令 $\scriptstyle GK{E_r}(B) = GK(B) \times {E_r}(B) $ .

7) 返回属性子集 $\scriptstyle B $ 的粒度粗糙熵 $\scriptstyle GK{E_r}(B) $ .

算法2. FS_GREIABC

输入: 给定的信息表 $\scriptstyle S = (U, A, V, f) $ .

输出: 最终选择的特征子集.

1) 初始化: 随机产生初始种群, 得到N个初始解 $\scriptstyle {X_1}, {X_2}, \cdots , {X_N} $ , 设置蜜源个数(雇佣蜂个数) FoodCount、观察蜂个数OnlookerCount、最大迭代次数MaxIterCount以及云滴数nc.

2) 对信息表S进行离散化处理.

3) 对任意 $\scriptstyle 1 \leqslant j \leqslant FoodCount $ , 循环执行:

4) 　根据算法1计算种群中各只蜜蜂的粒度粗糙熵 $\scriptstyle GK{E_r}({B_j}) $ ;

5) 　根据式(11)计算种群中各只蜜蜂的适应度值 $\scriptstyle fi{t_j} $ .

6) 对任意 $\scriptstyle 1 \leqslant t \leqslant MaxIterCount $ , 循环执行:

7) 　雇佣蜂阶段: 对任意 $\scriptstyle 1 \leqslant j \leqslant $ $\scriptstyle FoodCount $ , 各蜜源根据式(5)依次更新.

8) 　跟随蜂阶段:

9) 　　对任意 $\scriptstyle 1 \leqslant m \leqslant nc $ , 循环执行:

10)　　　 根据式(9)计算各食物源一维正态云模型的参数Ex、En、He并构造一维正态云模型;

11) 　　　根据式(7)计算选择蜜源 $\scriptstyle {X_i} $ 的概率 $\scriptstyle {p_i} $ ;

12)　　 对任意1≤k≤OnlookerCount, 循环执行: 选择较好的蜜源 $\scriptstyle {X_i} $ 进行跟随.

13) 　侦查蜂阶段: 对任意 $\scriptstyle 1 \leqslant j \leqslant $ $\scriptstyle FoodCount $ , 循环执行: 选择放弃蜜源并根据式(8)产生新蜜源来替代旧蜜源.

14) 获得全局最佳蜜源bestfood.

15) 对最佳蜜源进行0-1编码.

16) 得到当前最优的特征子集并返回该特征子集.

5 实验 5.1 实验数据与实验设置

为了验证FS_GREIABC算法的性能, 我们首先选取了10个UCI数据集^[22]进行特征选择实验, 具体包括: 1) Heart; 2) German; 3) Diabetes; 4) Ionosphere; 5) Smart_grid; 6) Sonar; 7) Musk2; 8) Spmbase_disc; 9) WDBC; 10) Dress. 这10个数据集的详细信息如表1所示.

除上述10个UCI数据集之外, 为了将FS_GREIABC算法与实际应用更好地结合在一起, 我们还考虑将该算法应用于软件缺陷预测领域. 当前软件的规模和复杂度日益增长, 因此, 软件的可靠性备受关注. 在软件工程中, 如果可以找出软件系统中有可能存在缺陷的模块及其分布, 对软件开发者合理配置资源以及提高软件质量将起到至关重要的作用. 软件缺陷预测便是这样一种技术, 它对软件模块中是否存在缺陷进行预测, 能够根据历史数据以及已经发现的缺陷等软件度量数据, 提前预测哪些模块有出错的倾向. 合理地预测软件缺陷可以有效帮助测试者快速定位并弥补软件缺陷, 从而达到显著减少软件开发成本和提高软件可信度的效果.

当前的研究通常将缺陷预测的实现形式化为一个机器学习问题, 很多机器学习技术被用于软件缺陷预测. 然而, 现有的缺陷预测方法在实际应用中还存在许多问题. 例如, 这些方法在高维数据情况下(如存在大量冗余、不相关的度量元), 预测精度不高, 而在实际应用中高维的缺陷预测数据是非常普遍的^[23].

针对软件缺陷预测中所存在的高维数据问题, 本文尝试采用FS_GREIABC算法来进行特征选择, 通过对度量元进行有效降维, 从而提高软件缺陷预测模型的性能. 我们选取了5个来自于Jureczko和Madeyski^[24]所整理的Promise数据集进行特征选择实验, 具体包括: 1) Ant-1.3; 2) Camel-1.0; 3) Jedit-4.3; 4) Synapse-1.0; 5) Log4j-1.0. 这5个数据集的详情信息如表2所示.

由于粗糙集理论更适合于处理离散型属性, 因此, 对于上述数据集中的连续型属性, 我们统一采用Weka平台中所提供的等宽离散化算法进行了离散化处理, 其中, bins=5.

我们基于Python语言实现了FS_GREIABC算法, 实验所采用的硬件环境具体如下: 1.8 GHz Intel处理器、8.0 GB内存. 我们将FS_GREIABC算法与以下5种具有代表性的基于智能优化技术的特征选择算法进行了对比: 1)哈里斯鹰算法(HHO)^[25]; 2)樽海鞘算法(SSA)^[26]; 3)鲸鱼算法(WOA)^[27]; 4) Jaya算法^[28]; 5)正余弦算法(SCA)^[29].

为了有效评价FS_GREIABC算法及其他对比算法的性能, 本文分别采用了如下3种性能评价指标: Accuracy、F1-score和AUC. 其中, Accuracy代表分类正确率, 正确率越高, 分类效果越好;F1-score代表由Accuracy和Recall的调和平均值, 取值范围为[0, 1], 当F1-score取得1时, 代表模型的输出结果最好, 当F1-score取得0时, 代表模型的输出结果最差; AUC代表ROC曲线下方的面积, 用来判断二分类预测模型的优劣, 其考虑了因数据不均衡而导致的预测偏差问题, 当AUC越接近1时, 代表模型的分类效果越好, 当AUC低于0.5时, 代表模型的分类效果较差.

对于每一个实验数据集, 我们通过随机抽样的方式将其划分成训练集和测试集, 其中, 70%的样本作为训练集, 其余30%的样本作为测试集. 我们采用机器学习中常用的一种分类算法——CART在特征选择之后的训练集上训练分类器, 并利用测试集来测试分类器的分类性能(即计算该分类器的Accuracy值、F1-score值以及AUC值). 此外, 我们还比较了不同特征选择算法所选择的特征子集的大小.

在实验过程中, 我们发现, 对于FS_GREIABC算法, 不同的参数会达到不同的效果. 通过多次实验, 我们逐步调节FoodCount、OnlookerCount、MaxIterCount、nc的值, 并选择能够获得最优实验结果的参数值. 最终, 将FoodCount设置40、OnlookerCount设置为40、MaxIterCount设置为100、nc设置为 500. 对于5个对比算法, 它们的参数均采用相关文献中所提供的参数值进行设置.

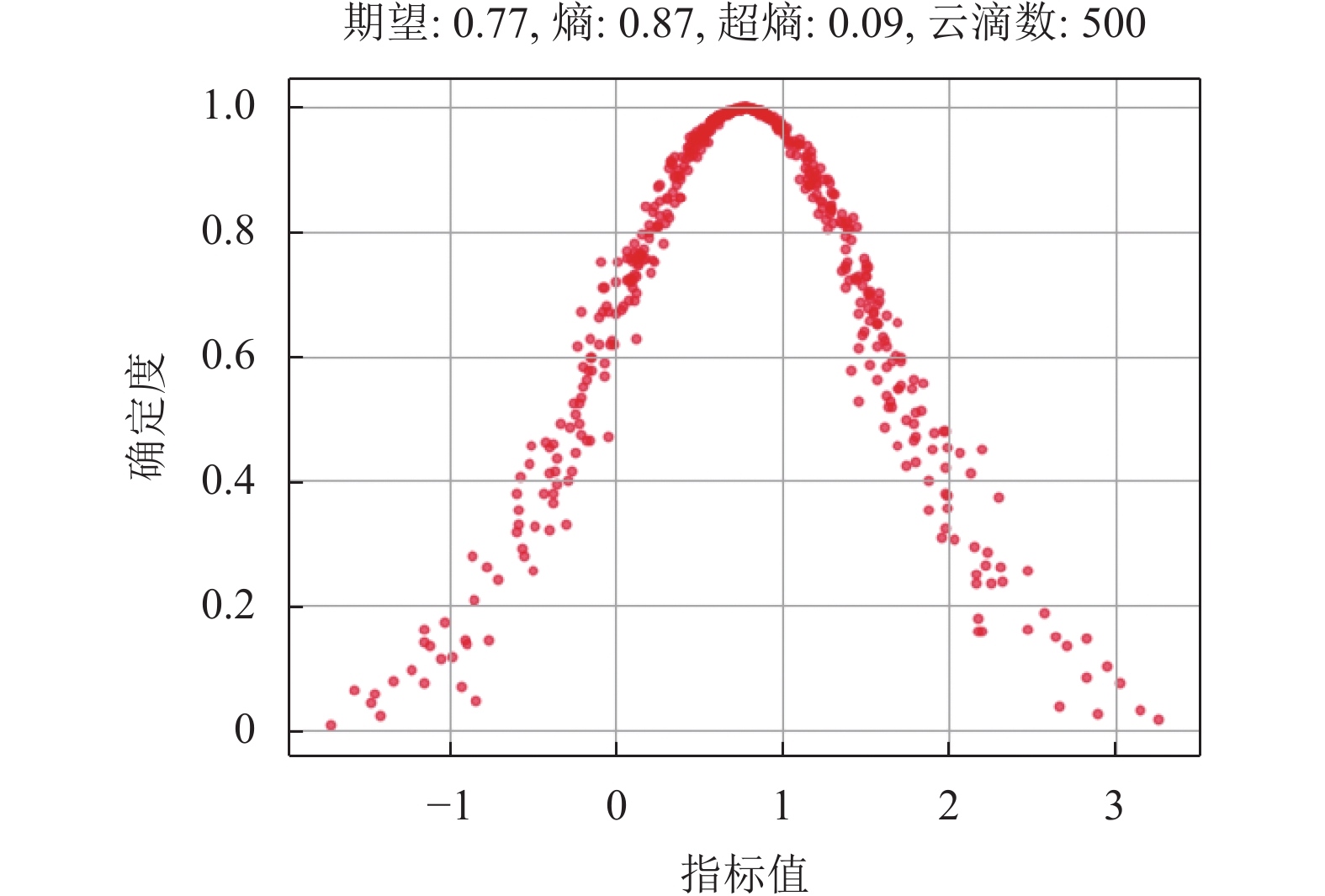
5.2 实验结果

图1–图3分别表示实验过程中在Heart、Diabetes以及Ionosphere这3个数据集上采用500个云滴所构造出的云模型示图.

从图1–图3可以看出, 熵 $En$ 的取值越大, 则云滴的取值范围越广, 相应地跟随蜂的搜索范围就越广; 反之, 跟随蜂的搜索范围就越窄. 此外, 超熵的取值越大, 则云滴越厚, 相应地食物源的分布就越离散.

表3给出了在不同数据集上6种特征选择算法所选择的特征子集的大小.

从表3可以看出FS_GREIABC算法所选择的特征数量在大部分数据集上都要少于或等于5种对比算法. 除了在Smart_grid和Sonar这两个数据集上要差于HHO之外, FS_GREIABC在其他数据集上都表现最好(即其所选择的特征数量最少). 事实上, 在Smart_grid和Sonar这两个数据集上, FS_GREIABC的表现也非常接近于表现最好的HHO算法. 因此, 从整体上看, 相对于HHO、SSA、WOA、Jaya、SCA这5种对比算法, FS_GREIABC算法能够获得更小的特征子集.

表4–表6分别给出了6种特征选择算法在Accuracy值、F1-score值以及AUC值上的对比结果.

从表4看出, FS_GREIABC算法的Accuracy值在大部分数据集上都要高于或等于5种对比算法. 除了在Smart_grid和Dress这两个数据集上分别低于Jaya和SCA算法之外, 在其余13个数据集上, FS_GREIABC算法都具有最高的Accuracy值. 事实上, 在Smart_grid和Dress数据集上, FS_GREIABC算法的Accuracy值也只是略低于Jaya和SCA算法, 比其余4个算法都要高. 因此, 从Accuracy这个评价指标来看, FS_GREIABC算法的性能要优于5种对比算法, 即FS_GREIABC在提升分类器的分类性能方面表现更好.

从表5可看出, FS_GREIABC算法的F1-score值在大部分数据集上都要高于5种对比算法. 除了在Smart_grid数据集上, 在其余14个数据集上, FS_GREIABC算法都具有最高的F1-score值. 事实上, 在Smart_grid数据集上, FS_GREIABC算法的性能也是非常接近于最优的算法. 因此, 从F1-score这个评价指标来看, FS_GREIABC算法的性能要优于5种对比算法.

从表6可以看出, FS_GREIABC算法的AUC值在所有15个数据集上都要高于或等于5种对比算法. 除了在German数据集上, 在其余14个数据集上, FS_GREIABC算法的AUC值都要高于其他算法. 因此, 从AUC这个评价指标来看, FS_GREIABC算法的性能要优于5种对比算法.

综合表3–表6中的实验结果, 我们可以得出: 本文所提出的基于粒度粗糙熵与改进蜂群算法的特征选择算法FS_GREIABC具有更好的特征选择性能.

6 结论

本文利用粗糙集理论和云模型来改进传统的人工蜂群算法, 并由此提出一种新的特征选择算法FS_GREIABC. FS_GREIABC通过粒度粗糙熵来计算每个解的适应度. 作为一种新的信息熵模型, 粒度粗糙熵不仅可以对知识的不完备性进行度量, 而且还能够刻画出知识的粒度大小. 此外, 为了提高人工蜂群算法的局部搜索能力, FS_GREIABC采用一维正态云模型来改进跟随蜂阶段的搜索策略. 实验结果表明, FS_GREIABC所选择的特征子集不仅更小, 而且基于这些特征子集所训练的分类器也具有更好的分类性能.

FS_GREIABC通过粒度粗糙熵来为人工蜂群算法构建适应度函数. 由于粒度粗糙熵是基于经典的粗糙集模型定义的, 该模型更适合于处理离散型属性, 因此, 对于连续型属性, 必须提前进行离散化处理. 然而, 离散化过程必然会带来信息的损失问题. 针对上述问题, 下一步将考虑如何把本文所提出的特征选择方法推广到邻域粗糙集或模糊粗糙集等扩展的粗糙集模型中, 这些模型不需要经过离散化阶段就可以直接处理连续型属性.