2. 太原理工大学 软件学院, 晋中 030600
2. School of Software, Taiyuan University of Technology, Jinzhong 030600, China
阿尔茨海默病(Alzheimer’s disease, AD)是一种不可逆的神经退行性疾病, 该疾病在发展过程中, 除了会表现出不同的病理特征, 还会表现出不同的临床症状. 此疾病按照患病程度的不同分为3个阶段, 患病状态, 正常状态和轻度认知障碍(mild cognitive impairment, MCI)[1], MCI是阿尔兹海默症早期的一种状态, 患者早期表现为记忆能力的缺失, 脑结构中海马和内嗅皮层发生损伤, 随着更多神经元死亡, 大脑结构和功能开始发生明显的变化, 最终导致患者死亡. 此阶段的患者有很大的可能性发展为AD[2], 研究人员表示若能在早期就对患者进行干预和治疗, 或许能延缓病情, 甚至停止病情恶化. 但是如前文所述, 轻度认知障碍患者的临床症状并不明显, 医生用肉眼也很难从神经影像中准确判断出脑区发生的萎缩现象, 由于医生的经验和主观性, 对AD患者早期脑区变化的诊断存在很大的不确定性, 患者很难得到及时且准确的诊断, 因此通过计算机辅助诊断方法准确地对正常老年人、MCI患者和AD患者进行分类识别对阿尔兹海默症的干预有着极其重要的意义.
在图卷积网络(graph convolutional network, GCN)发展之前, 阿尔兹海默症的分类任务是将磁共振影像信息与机器学习(machine learning, ML)算法相结合, 建立阿尔兹海默症的分类器和预测器[3], 但是机器学习未能考虑被试之间的关系[4], 且特征选择独立于后续的分类器, 可能无法与后续的分类器很好的协调, 潜在地导致诊断性能下降[5]. 近年来, 基于图结构数据的深度学习方法引起了研究者的关注[6], 与传统方法相比, 图卷积网络表现出了更好的性能, 它将被试视为独立的个体, 建模被试间的关联信息. 2017年, Ktena等人[7]使用GCN来度量图之间的结构相似性, 通过向图中的边提供结构和功能信息, 对自闭症谱系障碍进行了分类, 结果表明, GCN在学习大脑网络表征方面是有效的. Parisot等人[8]使用GCN对自闭症障碍和阿尔茨海默病进行分类时, 测试了图的结构对GCN的影响. 但基于图的研究都是将节点表示为在特定时间点针对某个被试采集的一系列数据, 节点间边的权重是通过成对节点间的皮尔森相关系数(Pearson correlation coefficient, PCC)[9]或欧几里得距离[10]来描述. 这种表示方法只适用于简单图, 即节点之间的关系是成对的, 在实际生活中, 被试之间的相似关系要更复杂, 是超越成对连接的.
超图[11]可以捕捉真实世界的高阶交互, 建模多个被试间的复杂关系. HGNN[12]是第1个应用于引文网络中的基于超图的神经网络模型, 该模型能够处理复杂的超图结构数据; 在脑疾病领域, 基于超图的神经网络也受到高度关注, 在超图中, 节点表示被试, 超边表示多个被试的高阶相似信息, 从而提高分类性能. Xiao等人[13]提出了一种基于超图学习的方法, 该方法构建了一个超图相似性矩阵来表示全卷积神经网络, 稀疏回归方法生成超边, 超边权重通过超图学习得到. 与传统的图方法和现有的未加权超图方法相比, 所提出的方法能够更好地捕捉多个超节点之间的关系. Ji等人[14]提出了一种用于功能脑网络分类的超图注意力网络, 以进一步提取超图中的信息, 其中包括节点和超边之间的特征. 但基于超图的神经网络方法大多数都是通过连通分量扩展将超图的超边分解, 利用一条超边上节点之间的成对加权边代替整条超边, 再对其执行图卷积操作, 本质上仍是在超边分解得到的简单图上进行节点信息聚合, 对于阿尔兹海默症分类任务来说, 一条超边上表达的是多个被试间具有相似的特征信息, 不同超边上的被试特征具有差异性, 如果简单地将超边分解为被试间的成对关系, 超边所表达的信息就会引入噪声. 类似地, 在超图中, 被称为张量的高阶矩阵被用于多重计算, 如文献[15]中提出的一种非负张量分解方法, 用于以超图的形式对具有复杂关系的数据集进行聚类. 基于张量的方法大多数情况下, 假设超图的超边大小相等, 即超边权值相等, 但对于阿尔兹海默症分类任务来说, 具有突出特征的被试所在的超边应更重要, 在分类学习过程中这种超边的权重应该更高[16].
因此, 现有的研究虽然已经将超图引入到神经网络中实现在超图结构中编码高阶数据相关性, 但目前基于超图的阿尔兹海默症分类研究假设被试间的高阶复杂关系可以拆分为被试间简单的成对关系[13], 直接或间接地使用连通分量扩展将超边分解为多条边[17, 18], 或使用星型扩展将超图转换为异构图[19], 实际上最终都是对转换后的简单图进行下游挖掘任务. 正如文献[20]中所描述的, 在一条完整超边内存在的关系可能并不存在于该超边的不完全子集内. 超边的高阶信息没有得到完全地表达, 在神经网络中用超图表达阿尔兹海默症患者间的高阶关系的优势并没有发挥出来.
针对以上的挑战, 本文基于线-超图神经网络(line-hypergraph neural network, L-HGNN)模型对阿尔兹海默症进行自动分类. 在神经网络中, 通过线图[21]实现被试间复杂关系的整体表达, 同时受图注意力网络(graph attention network, GAT)[16]的启发, 在线图中加入自注意力机制根据节点特征为每条超边赋予不同的权重, 有侧重地进行信息聚合.
本文的主要工作如下.
1)用超图描述被试间的复杂关联, 通过稀疏线性回归模型构建超图用于神经网络模型.
2)基于超图提出一种线-超图神经网络, 并引入自注意力机制来提高AD分类准确性.
3)在ADNI数据集上对线-超图神经网络进行了实验, 实验结果表明该方法可以有效地提高准确率.
1 相关介绍 1.1 模型设计图1所示为L-HGNN的网络结构, 基于线-超图神经网络的阿尔兹海默症分类模型主要分为3个部分: 1)超图构建, 对数据集进行预处理得到特征向量, 通过稀疏线性回归模型将被试间的关系构建为超图, 超图的每个节点代表一个被试都携带一个特征向量, 随着超图在神经网络中进行传播学习. 2) 基于超图与线图转换进行特征嵌入学习, 在保持超图整体结构不变的基础上, 进行高阶邻域节点特征和超边特征学习; 并引入注意力策略, 对邻域节点信息进行有侧重地聚合. 3) 在超图和线图的转换中实现图上特征的提取和筛选, 最后经过Softmax层输出最终分类结果.

|
图 1 L-HGNN整体流程 |
1.2 超图构建
超图的定义为:
| $ H = \left\{ {\begin{array}{*{20}{c}} {1,\quad {\rm{if}}\;{v_H} \in {e_H}} \\ {0,\quad {\rm{if}}\;{v_H} \notin {e_H}} \end{array}} \right. $ | (1) |
其中, 关联矩阵的行元素为节点, 列元素为超边, 如果节点
超图中, 超节点度表示与该节点连接的超边个数, 超边度表示超边所包含的节点的数量, 每个超节点的度和超边的度分别被定义为:
| $ {D_E} = \sum\nolimits_{{e_H} \in {E_H}} {H({v_H}, {e_H})} $ | (2) |
| $ {D_E} = \sum\nolimits_{{v_H} \in {V_H}} {H({v_H}, {e_H})} $ | (3) |
用超图对阿尔兹海默症患者统一建模可以捕获被试间的更细粒度的相关性, 将超图中的节点表示为被试, 超边表示被试间的关系, 首先需要提取被试的特征然后通过科学计算来得到被试间的关联关系, 进而构建超图. 特征提取过程及关联矩阵计算方法如下.
1) 特征提取
本文使用了来自ADNI数据集中的结构磁共振影像和表型信息(姓名, 年龄), 有关数据集的详细介绍在第2.1节. 对结构磁共振影像进行特征提取, 利用Desikan-Killiany cortical atlas图集[22]将每个被试的脑结构影像划分为138个感兴趣区域(regions of interest, ROI), 每个半球69个. 再通过FreeSurfer软件对基于ROI的形态学特征(平均皮质厚度、灰质体积)进行提取. 最后利用提取出的138个脑区结构特征和表型信息进行计算, 得到超图关联矩阵.
特征提取具体步骤如下: 使用5.1.0版本的FreeSurfer ( http://surfer.NMR.mgh.Harvard.edu/)对所有sMRI数据进行大脑皮质重建和体积分割. 处理流程包括: 偏差场校正、颅骨分离、灰白质分离等. 首先将磁共振成像数据标准化为标准解剖模板[23], 并进行偏差场校正. 然后使用分水岭算法对得到的图像进行颅骨剥离[24], 随后分割成皮质下白质和深层灰质结构[25, 26]. 并生成高精度的灰、白质分割面和灰质、脑脊液分割面[27], 根据这两个表面可以计算任何位置的皮质厚度及其他面数据特征如皮质外表面积、曲率、灰质体积等, 这些参数可以映射到通过白质膨胀算法得到的大脑皮质表面上直观显示. 计算软脑膜表面每个节点的各种形态特征, 包括体积(皮质厚度、表面积和灰质体积)和几何(沟深度、度量失真和平均曲率)测量[28]. 这种方法已经在很多基于MRI的分类方法中取得了成功[23], 皮质厚度和灰质体积的测量程序已经通过组织学分析[29]和手工测量[30].
2) 关联矩阵计算
在超图的构建中, 本文使用了稀疏线性回归模型, 通过该方法对多个被试之间的复杂相关性建模已被证明在反映全局数据结构方面是有效的, 并且对数据噪声也是鲁棒的[30,31]. 利用提取到的特征信息和表型信息来描述被试, 用稀疏表示的方法将一个被视表示为其他被视的线性组合, 获得该被试与其他被试的关联性, 过滤掉无关紧要的连接, 产生描述被视间关联的超图关联矩阵, 具体如图2所示.
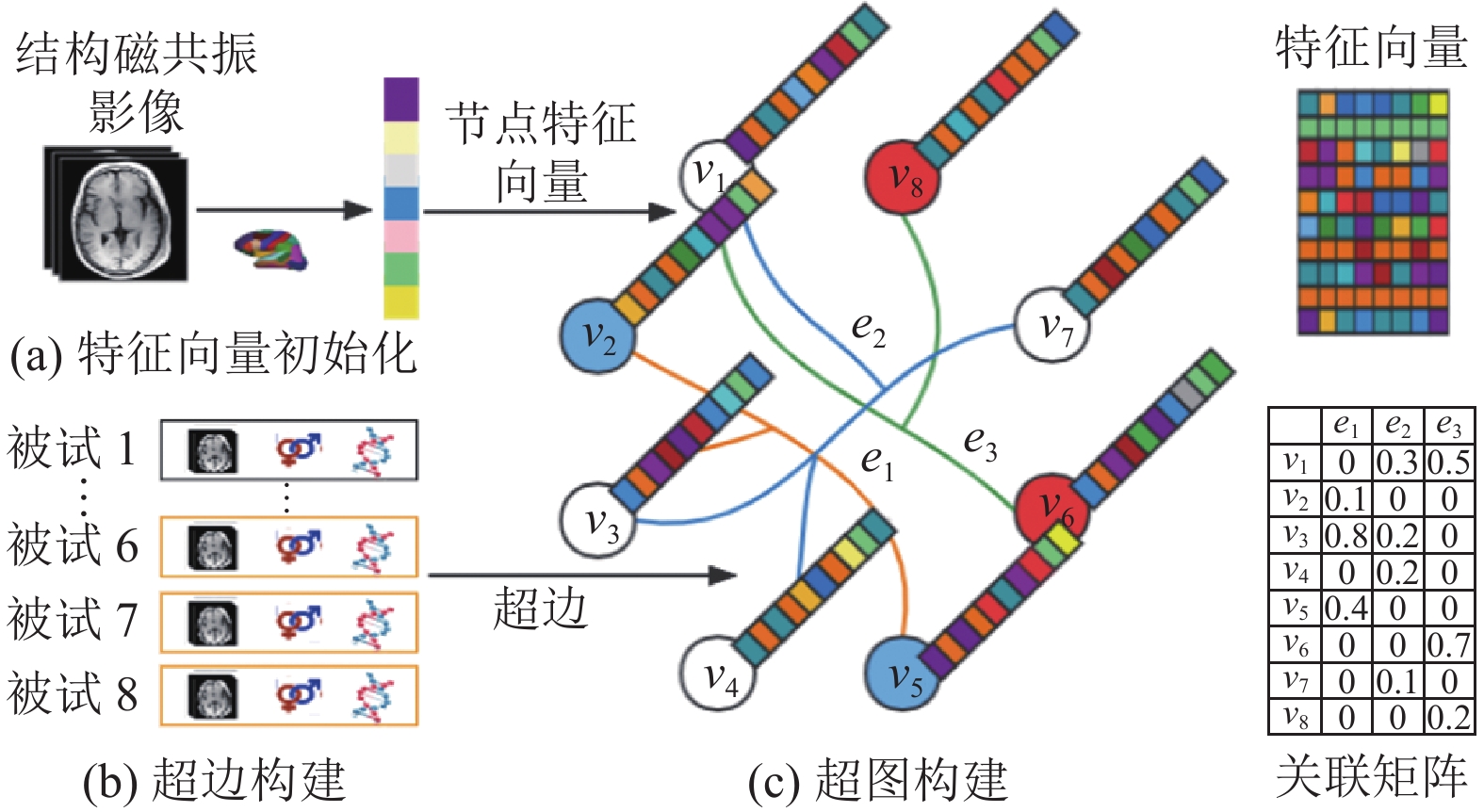
|
图 2 超图构建 |
稀疏线性回归模型表示过程如式(1)所示:
| $ {\min_{S_m} }\mathop {\left\| {\mathop x\nolimits_m - \mathop T\nolimits_m \mathop S\nolimits_m } \right\|}\nolimits_2 + \lambda {\left\| {\mathop S\nolimits_m } \right\|_1} $ | (4) |
其中,
利用式(4)中学习到的每个被试的权重向量, 稀疏表示权重矩阵S就被定义为
| $ {H_{{v_i}, {e_j}}} = \left\{ {\begin{array}{*{20}{l}} {{S_{i, j}},\quad {\rm{if}}\;\left| {{S_{i, j}}} \right| \geqslant \theta } \\ {0,\qquad {\rm{if}}\;\left| {{S_{i, j}}} \right| < \theta } \end{array}} \right. $ | (5) |
值得注意的是, 在式(4)中, 正则化参数
本文提出的L-HGNN模型可以借助线图实现超图整体特征学习, 将构建好的超图作为L-HGNN的输入, 利用线图让超节点和超边在每一层中交替, 超节点特征和超边特征在每一层中交替进行信息传播, 堆叠多个这样的层, 以端到端的方式在交叉熵损失上训练, 最终用于阿尔兹海默症分类.
超图到线图的转换类似于简单图到线图的转换. 图3是简单图和超图转换为线图的例子, 将超图中的每个超边转化为线图中的一个节点, 如果对应的超边在超图中共享至少一个超节点, 则转化后的两个节点在线图中连接.

|
图 3 图和超图到线图的转换 |
为避免连接两条高阶超边的权重在线图中的权重过高, 本文使用关联矩阵的行规范化和列规范化来形成线图的邻接矩阵, 即:
| $ {A_L} = D_E^{ - 1}{H^{\rm{T}}}D_V^{ - 1}H \in {R^{\left| E \right| \times \left| E \right|}} $ | (6) |
其中,
在超图中, 节点可以同时被多条超边共同覆盖, 因此, 在式(6)中将超图的超边转换为线图的节点进行嵌入学习时, 线图节点间边的权重由两条超边共同覆盖的节点数决定, 但超边间相关性的权重应取决于超边间节点的特征. 注意力机制[16]可以学习邻居节点对目标结点的重要性权重, 节点权重的学习就独立于图结构, 自注意力机制是注意力机制的一种特殊形式, 自注意力机制可以注意到整个输入中不同部分的相关性, 它更擅长捕捉特征的内部相关性, 减少对外部信息的依赖. 因此, 本文使用自注意力机制为超边学习不同的权重, 线图的权重学习邻接矩阵就表示为:
| $ {A_{{\rm{att}}}} = {A_L}{P}({\sigma _{{\rm{att}}}}(X_L^l\theta _{{\rm{att}}}^l)) $ | (7) |
其中,
从超图的超节点特征中导出的线图的节点特征矩阵可以表示为
| $ {X^{l + 1}} = \sigma \left( {H\left( {{A_{{\rm{att}}}}X_L^l + {\varepsilon ^l}X_L^l} \right){W^l}} \right) $ | (8) |
其中, 第l层中线图的节点特征更新规则就定义为:
本模型堆叠3层对特征矩阵和关联矩阵进行处理进而提取超图特征, 提取得到的特征最后经过一个Softmax操作, 可以得到被试的分类类别概率, 选择最大的概率对应的标签即为被试的分类结果.
2 实验和结果 2.1 ADNI数据库本文使用的数据集来自阿尔兹海默症神经影像学计划的公共数据集[32], ADNI数据库是2003年由迈克尔·韦纳领导的一个公私合作项目. ADNI研究包括ADNI-1、ADNI-2、ADNI-GO、ADNI-3这4个阶段, 研究所使用的数据集可在 http://adni.loni.usc.edu进行下载.
本次研究从ADNI中选取了1 480名被试的MRI数据和表型信息以及所有研究对象的类标签. 该数据集中包含403名正常对照(normal control, NC), 713例MCI, 364例AD. 下载了ADNI-1数据集中提供的l.5TT1加权结构磁共振影像数据186例AD、396例MCI、227例NC. 下载了ADNI-2和ADNI-3阶段的3TT1加权sMRI数据, 包括178例AD, 317例MCI, 176例NC. 表1列出了所研究被试的人口统计学信息.
| 表 1 使用的数据集的被试人口统计信息 |
2.2 实验设置
为保证实验的可信性, 本实验选择了计算性能高效且能自动调整学习率的Adam优化器. 通过辅助实验, 保持其他超参数不变, 观察一个超参数的影响, 找到最优的超参数组合. 本文将初始学习率设置为0.03, 训练周期为200, 且在每100个训练周期将学习率减少2倍. 隐藏层维度d固定为128. 通过堆叠3层L-HGNN来对输入的矩阵信息进行处理, 损失函数使用交叉熵:
| $ Loss = - \sum\limits_{v \in {V^s}} {\sum\limits_{k \in L} {{y_{v, k}}} \ln {{\hat y}_{v, k}}} $ | (9) |
其中,
实验采用10倍交叉验证策略评估分类性能, 具体来说, 将所有被试分成10个大小基本一致的子集, 其中9个子集是训练集, 一个是测试集. 为避免交叉验证过程中随机划分的偏差, 本文将上述测试过程重复了30次, 每次都重新打乱被试顺序.
2.3 评价指标为评估该模型的分类性能, 本文采用准确性(accuracy, ACC)、敏感性(sensitivity,SEN)、特异性(specificity, SPE)和曲线下面积(area under ROC, AUC)作为评估指标. 这些评估指标定义为:
| $ ACC = \frac{{TP + TN}}{{TP + FP + TN + FN}} $ | (10) |
| $ {\textit{SEN}} = \frac{{TP}}{{TP + FN}} $ | (11) |
| $ {\textit{SPE}} = \frac{{TN}}{{TN + FP}} $ | (12) |
| $ AUC = \frac{{\displaystyle\sum\nolimits_{i \in P} {ran{k_i} - \dfrac{{M \times (M + 1)}}{2}} }}{{M \times N}} $ | (13) |
其中, TP、TN、FN和FP分别表示真阳性、真阴性、假阴性和假阳性, F代表真阳性和假阳性,
为了验证L-HGCN中在阿尔兹海默症分类性能上的有效性, 将L-HGNN与传统图卷积网络、超图卷积网络和HyperGCN[33]进行了对比. 并在ADNI数据集上分别进行了3种分类(AD和MCI、AD和NC、NC和MCI)来验证模型在阿尔兹海默症发展史上的分类有效性. 实验所使用的对比模型如下.
1) GCN: 由文献[7]提出的图卷积神经网络模型, 将图像处理中的卷积成功推广到图结构上, 是比较经典的图神经网络模型.
2) HGNN: 目前比较流行的超图神经网络方法, 该方法利用超图拉普拉斯算子进行表示学习, 被认为是在超图的连通分量扩展上使用图卷积.
3) HyperGCN: 也是目前比较流行的超图神经网络方法, 基于超图的谱论结合半监督学习并利用GCN进行超节点的特征提取及分类, 将超图拉普拉斯近似为一个简单的图, 然后在其中使用图卷积对超图进行节点分类.
表2中报告了L-HGNN与其他3种神经网络模型(GCN[7]、HGNN[12]、HyperGCN[33])在3种情况下的分类效果. 从表2可知, 使用同样的测试样本的情况下, L-HGNN的分类性能要优于其他模型, 且3种分类实验可以证明该模型在阿尔兹海默症疾病的分类诊断是有效的, 对AD的早期诊断具有重要的应用价值.
与GCN的关系建模方法相比, 基于超图的HGNN、HyperGCN、L-HGNN在分类性能上都有所改进. 其中, L-HGNN相对于GCN, 在ACC指标上最高可提高8.5个百分点, 最低可提高6.1个百分点. 结果表明, 与简单图结构方法相比, 在阿尔兹海默症分类问题中超图结构能更好地表示被试间的关系从而改进基于简单图的方法, 较好的分类性能可以归因于所采用的超图结构. 与HGNN、HyperGCN相比, L-HGNN平均分类准确度最高分别增加了6.5和5.3个百分点, 本文将此归因于HGNN和HyperGCN进行超图信息聚合时, 忽略了超边信息, 且HGNN本质上还是通过连通分量扩展进行高阶信息传递的. 这说明, 在超图特征嵌入过程中使用线图来学习超边特征有利于超图的完整信息在神经网络模型中表示. 此外, 阿尔兹海默症的早期诊断和干预很重要, 本文方法对阿尔兹海默症发展过程中的3个阶段(MCI、AD、NC)分别进行二分类, 可以看出AD与NC的二分类效果最好, MCI与NC的分类效果最差, 这是因为阿尔兹海默症早期的大脑结构变化并不明显, 发展至AD脑结构已经发生了明显的变化. 但在MCI与NC的分类实验中虽然准确率较低, 但与其他方法相比, L-HGNN的分类准确性有较大的提升, 这说明该模型对阿尔兹海默症的早期分类诊断具有实际应用意义.
| 表 2 不同图神经网络和超图神经网络的性能比较 |
2.5 超图稀疏度影响
超图描述了阿尔兹海默症患者之间的潜在关系, 超图的不同构建会对模型的最终分类性能产生影响, 在本文中使用稀疏线性回归方法进行超图构建, 该方法中, 参数

|
图 4 不同稀疏度超图的分类结果对比 |
在之前的对比工作中,
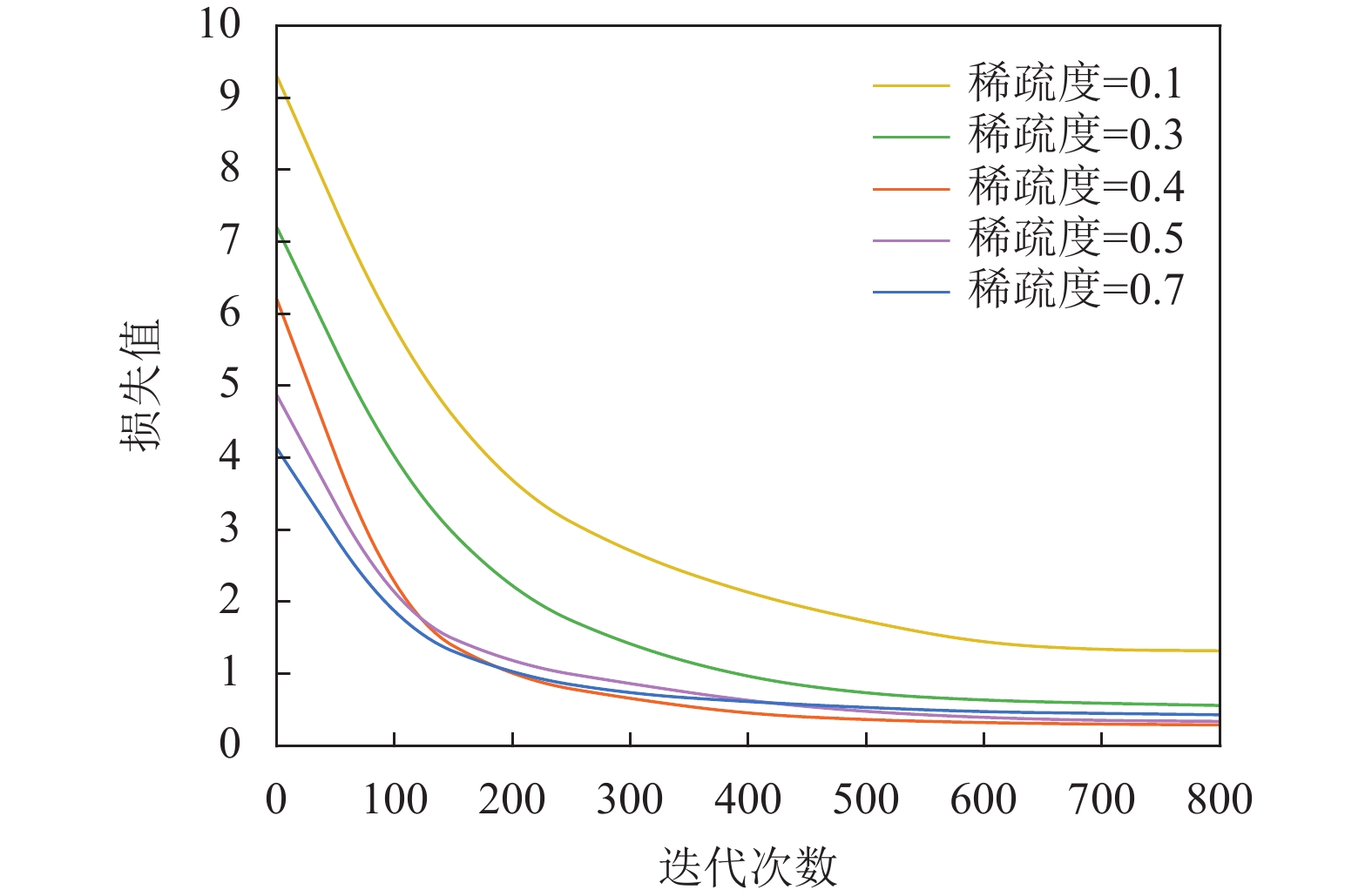
|
图 5 损失值随迭代次数的变化 |
在训练模型的过程中, 损失函数的收敛对于理解结果的稳定性很重要. 在图5中可以观察到L-HGNN在不同稀疏度下损失函数的收敛性能. 图中的稀疏度是根据第2.4节的经验选取了
神经网络隐藏层维度d是影响模型分类准确度的一个重要参数. 为了能够选择出最适合的值, 本文设计了相关实验.
在经过Softmax层之前, L-HGNN会将超节点映射到d维空间, 本实验将隐藏层维度 分别设置为8、16、32、64、128与256. 在不同稀疏度构建的超图数据集上进行分类, 结果如图6所示, 横坐标表示隐藏层维度, 纵坐标表示分类准确率, 分类准确率随着隐藏层维度的增加明显升高, 维度提高至128时, 分类精度达到饱和.
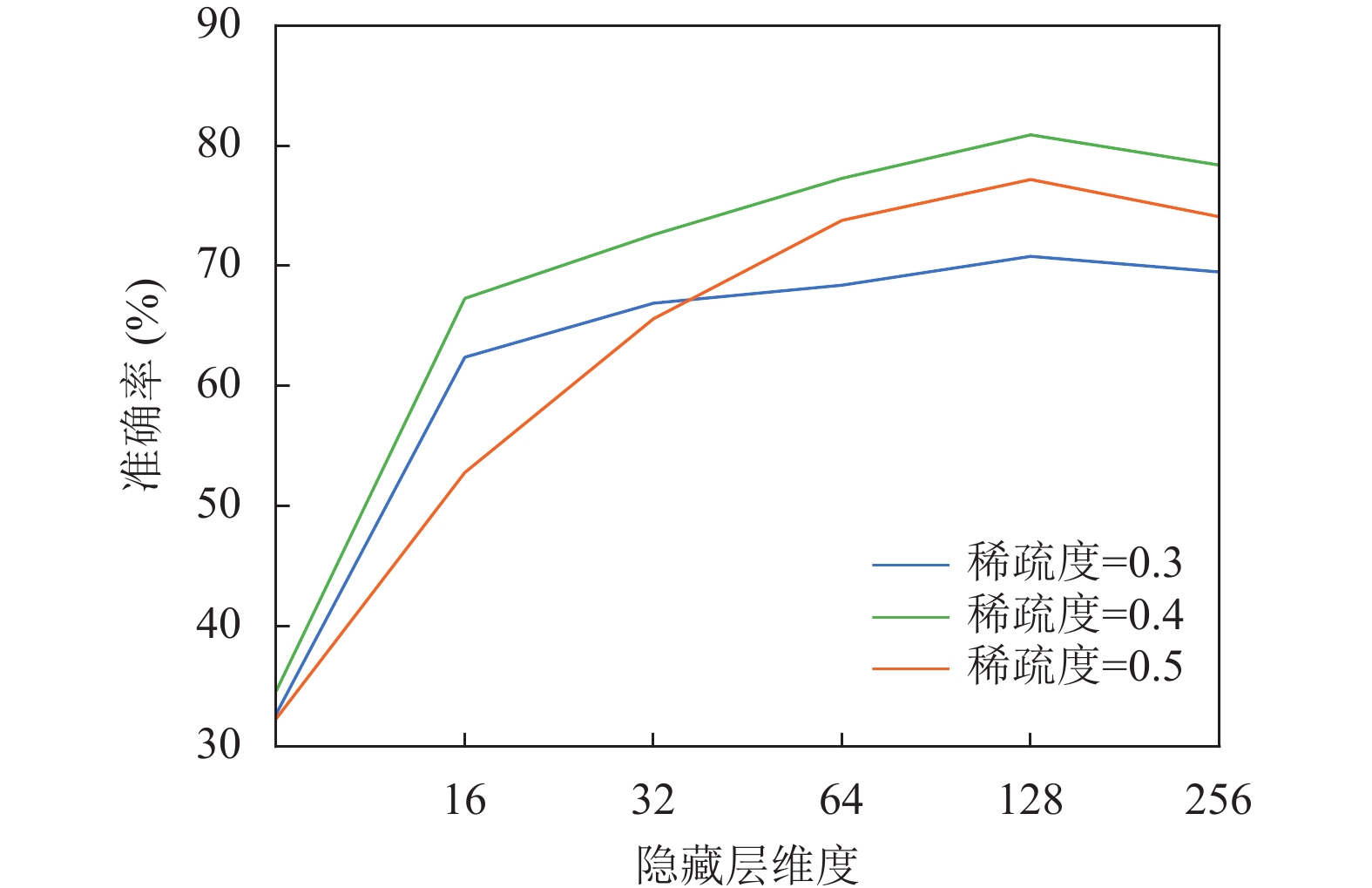
|
图 6 不同隐藏层维度下的分类准确率 |
结果显示, 如果隐藏层维度不够大, L-HGNN就无法捕获足够的信息表示超节点, 本节的实验结果还显示了L-HGNN在不同稀疏度超图数据集上表现出一致的行为.
图7显示了在不同训练集规模下模型分类性能的表现, 保持不同规模训练集中不同类别的标签数量平衡, 将训练集规模从1%增加至50%, 结果显示, 一开始随着训练集的增加, L-HGNN的分类性能明显提高, 在10%后几乎饱和, 结果表明, L-HGNN可以在标记的超节点数量很少的情况下达到较好的分类性能.

|
图 7 不同训练集规模下的分类准确率 |
3 结束语
本文提出了一种新的框架, 利用结构磁共振成像数据和表型数据来寻找阿尔茨海默病患者的相关性, 使用超图神经网络学习超图的结构与节点特征等信息, 实现阿尔兹海默症分类, 并证明了它优于现有的图神经网络方法和超图神经网络方法. 本文提出的方法将每个被试作为超图结构中的一个节点, 用稀疏线性回归模型根据被试的成像信息和表型信息建模被试间的相似性, 从而构建超图, 该超图输入到L-HGNN模型中进行训练, 用于节点分类. 在L-HGNN每一层中, 输入的超图被隐式转换为线图, 在保证超图整体结构不变的基础上, 将超边特征有侧重地嵌入节点特征中. 具有多层的L-HGNN网络的所有参数都可以通过端到端的方式获得. 通过实验, L-HGNN能够在本文使用的数据集上提高最先进的超节点分类性能, 有力支持了其在神经科学研究和临床实践中的潜在用途和影响.
| [1] |
Weller J, Budson A. Current understanding of Alzheimer’s disease diagnosis and treatment. F1000Research, 2018: 7.
|
| [2] |
陈玖. 基于神经影像特征的遗忘型轻度认知损害患者痴呆转化模型构建与临床应用研究. 南京: 东南大学, 2017.
|
| [3] |
Mateos-Pérez JM, Dadar M, Lacalle-Aurioles M, et al. Structural neuroimaging as clinical predictor: A review of machine learning applications. NeuroImage: Clinical, 2018, 20: 506-522. DOI:10.1016/j.nicl.2018.08.019 |
| [4] |
Marizzoni M, Ferrari C, Jovicich J, et al. Predicting and tracking short term disease progression in amnestic mild cognitive impairment patients with prodromal Alzheimer’s disease: Structural brain biomarkers. Journal of Alzheimer’s Disease, 2019, 69(1): 3-14. DOI:10.3233/JAD-180152 |
| [5] |
Lian CF, Liu MX, Zhang J, et al. Hierarchical fully convolutional network for joint atrophy localization and Alzheimer’s disease diagnosis using structural MRI. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020, 42(4): 880-893. DOI:10.1109/TPAMI.2018.2889096 |
| [6] |
Zhou J, Cui GP, Hu SD, et al. Graph neural networks: A review of methods and applications. AI Open, 2020, 1: 57-81. DOI:10.1016/j.aiopen.2021.01.001 |
| [7] |
Ktena SI, Parisot S, Ferrante E, et al. Metric learning with spectral graph convolutions on brain connectivity networks. NeuroImage, 2018, 169: 431-442. DOI:10.1016/j.neuroimage.2017.12.052 |
| [8] |
Parisot S, Ktena SI, Ferrante E, et al. Spectral graph convolutions for population-based disease prediction. Proceedings of the 2017 International Conference on Medical Image Computing and Computer-assisted Intervention. Quebec City: Springer, 2017. 177–185.
|
| [9] |
Liu MX, Zhang J, Yap PT, et al. View-aligned hypergraph learning for Alzheimer’s disease diagnosis with incomplete multi-modality data. Medical Image Analysis, 2017, 36: 123-134. DOI:10.1016/j.media.2016.11.002 |
| [10] |
Eynard D, Kovnatsky A, Bronstein MM, et al. Multimodal manifold analysis by simultaneous diagonalization of Laplacians. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(12): 2505-2517. DOI:10.1109/TPAMI.2015.2408348 |
| [11] |
Bretto A. Hypergraph Theory: An Introduction. Cham: Springer, 2013. 132.
|
| [12] |
Feng YF, You HX, Zhang ZZ, et al. Hypergraph neural networks. Proceedings of the 33rd Conference on AAAI Conference on Artificial Intelligence. Honolulu: AAAI, 2019. 3558–3565.
|
| [13] |
Xiao L, Wang JQ, Kassani PH, et al. Multi-hypergraph learning-based brain functional connectivity analysis in fMRI data. IEEE Transactions on Medical Imaging, 2020, 39(5): 1746-1758. DOI:10.1109/TMI.2019.2957097 |
| [14] |
Ji JZ, Ren YT, Lei ML. FC-HAT: Hypergraph attention network for functional brain network classification. Information Sciences, 2022, 608: 1301-1316. DOI:10.1016/j.ins.2022.07.041 |
| [15] |
Shashua A, Zass R, Hazan T. Multi-way clustering using super-symmetric non-negative tensor factorization. Proceedings of the 9th European Conference on Computer Vision. Graz: Springer, 2006. 595–608.
|
| [16] |
Velickovic P, Cucurull G, Casanova A, et al. Graph attention networks. Proceedings of the 6th International Conference on Learning Representations. Vancouver: ICLR, 2018. 1–12.
|
| [17] |
王国力, 孙宇, 魏本征. 医学图像图深度学习分割算法综述. 计算机工程与应用, 2022, 58(12): 37-50. DOI:10.3778/j.issn.1002-8331.2112-0225 |
| [18] |
Zhang MH, Cui ZC, Jiang SL, et al. Beyond link prediction: Predicting hyperlinks in adjacency space. Proceedings of the 32nd AAAI Conference on Artificial Intelligence and 30th Innovative Applications of Artificial Intelligence Conference and 8th AAAI Symposium on Educational Advances in Artificial Intelligence. New Orleans: AAAI, 2018. 543.
|
| [19] |
Agarwal S, Branson K, Belongie S. Higher order learning with graphs. Proceedings of the 23rd International Conference on Machine Learning. Pittsburgh: Association for Computing Machinery, 2006. 17–24.
|
| [20] |
Pu L, Faltings B. Hypergraph learning with hyperedge expansion. Proceedings of the 2012 Joint European Conference on Machine Learning and Knowledge Discovery in Databases. Bristol: Springer, 2012. 410–425.
|
| [21] |
Evans TS, Lambiotte R. Line graphs of weighted networks for overlapping communities. The European Physical Journal B, 2010, 77(2): 265-272. DOI:10.1140/epjb/e2010-00261-8 |
| [22] |
Desikan RS, Cabral HJ, Hess CP, et al. Automated MRI measures identify individuals with mild cognitive impairment and Alzheimer’s disease. Brain, 2009, 132(8): 2048-2057. DOI:10.1093/brain/awp123 |
| [23] |
Talairach J, Tournoux P. Co-planar stereotaxic atlas of the human brain: 3-dimensional proportional system: An approach to cerebral imaging. Thieme, 1988: 1–122.
|
| [24] |
Ségonne F, Dale AM, Busa E, et al. A hybrid approach to the skull stripping problem in MRI. NeuroImage, 2004, 22(3): 1060-1075. DOI:10.1016/j.neuroimage.2004.03.032 |
| [25] |
Fischl B, Salat DH, Busa E, et al. Whole brain segmentation: Automated labeling of neuroanatomical structures in the human brain. Neuron, 2002, 33(3): 341-355. DOI:10.1016/S0896-6273(02)00569-X |
| [26] |
Fischl B, van der Kouwe A, Destrieux C, et al. Automatically parcellating the human cerebral cortex. Cerebral Cortex, 2004, 14(1): 11-22. DOI:10.1093/cercor/bhg087 |
| [27] |
Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis: I. Segmentation and surface reconstruction. Neuroimage, 1999, 9(2): 179-194. |
| [28] |
Fischl B, Dale AM. Measuring the thickness of the human cerebral cortex from magnetic resonance images. Proceedings of the National Academy of Sciences of the United States of America, 2000, 97(20): 11050-11055. DOI:10.1073/pnas.200033797 |
| [29] |
Rosas HD, Liu AK, Hersch S, et al. Regional and progressive thinning of the cortical ribbon in Huntington’s disease. Neurology, 2002, 58(5): 695-701. DOI:10.1212/WNL.58.5.695 |
| [30] |
Wright J, Yang AY, Ganesh A, et al. Robust face recognition via sparse representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227. DOI:10.1109/TPAMI.2008.79 |
| [31] |
Qiao LS, Chen SC, Tan XY. Sparsity preserving projections with applications to face recognition. Pattern Recognition, 2010, 43(1): 331-341. DOI:10.1016/j.patcog.2009.05.005 |
| [32] |
Jack Jr CR, Bernstein MA, Fox NC, et al. The Alzheimer’s disease neuroimaging initiative (ADNI): MRI methods. Journal of Magnetic Resonance Imaging, 2008, 27(4): 685-691. DOI:10.1002/jmri.21049 |
| [33] |
Yadati N, Nimishakavi M, Yadav P, et al. HyperGCN: A new method of training graph convolutional networks on hypergraphs. Proceedings of the 33rd International Conference on Neural Information Processing Systems. Vancouver: Curran Associates Inc., 2019. 1511–1522.
|
 2023, Vol. 32
2023, Vol. 32


