在5G、物联网与产业互联网发展的推动下, 物联网设备的类别越来越细化[1, 2]. 目前, 物联网技术已经发展出许多计算密集型的应用类别, 例如虚拟现实、在线交互游戏、无人驾驶等[3]. 然而, 大部分应用设备受限于自身的计算资源和能量等问题, 在设备上执行这类任务会产生大量的能耗. 为解决这个问题, 用户会购买云计算(cloud computing, CC)服务或移动边缘计算(mobile edge computing, MEC)服务, 并将任务卸载到云服务器或边缘服务器上计算[4-7].
作为传统的用户任务卸载方式, CC拥有许多集中式服务器并可以提供大量的计算资源[8, 9]. 然而, 通过广域网将任务卸载到云端所需要的时延将会抵消掉在云端计算节省的时间. 与传统CC范式不同, MEC范式可以将CC服务从集中式的远程服务器扩展到距离用户更近的分布式服务器[10, 11]. 用户通过将任务整体[12]或部分[13, 14]卸载至MEC服务器并请求提供计算资源, 可以降低传输时延. 同时, 相比于CC, MEC服务提供商收取的计算资源费用对用户更友好, 用户可以请求更多的计算资源来满足自己的QoS.
在实际生活场景中, 用户希望减小自己购买计算资源时付出的成本, 同时服务提供商希望最大化自己的利益, 因此博弈论成为解决MEC系统中效益问题的重要方法[15-17]. 通过将用户与服务器提供商之间的交互进行建模, 可以分析并计算出双方的最优策略. 随着边缘服务提供商的增加以及边缘基站的部署, 在市场竞争中, 用户更需要根据不同的定价以及算力来制定自己的卸载策略, 以最优化自身效益.
现有的大部分研究都只是简单考虑了“云-边-端”三层架构, 认为MEC服务器是一个计算资源有限但距离用户更近的CC服务器; 并且部分研究为了最大化单方效益, 会舍弃掉另一方的部分利益, 陷入局部最优. 在本文中, 考虑了边缘服务器随机分布情况. 用户为了减少卸载和计算成本, 可以选择不同的边缘服务器. 其次, 与部分研究相似, 为了验证最优效益存在, 证明了移动设备与边缘服务器之间存在纳什均衡. 最后设计了一种基于贪心思想的改进双重拍卖算法来获得最优解. 与已有算法相比, 该算法会记录系统中的所有拍卖可能, 并选择最优组合进行拍卖, 实现边缘服务器分布式场景中用户效益的最优卸载; 同时, 算法中加入了资源整合机制, 可以最大化边缘服务器资源利用率, 实现资源受限情况下的最优效益. 本文的主要贡献如下.
1) 构建了一个用户与MEC服务器随机分布的场景, 用户可以将任务卸载至任意一个边缘服务器上进行计算, 并将MEC服务器与移动设备之间的交互建模为Stackelberg博弈.
2) 证明了MEC服务器与用户、用户之间存在唯一的纳什均衡点, 并提出了一种基于贪心思想的改进双重拍卖算法来求得系统最优整体效益.
3) 仿真实验的结果验证了所提算法的有效性. 在MEC服务器随机分布的场景下, 本文所提算法可以显著提高系统中用户效益和边缘服务器效益.
1 相关工作现有关于MEC的研究主要关注移动设备任务卸载和边缘服务器计算资源分配. 文献[18]将非正交多址(NOMA)技术引入MEC系统中, 并为了进一步提高频谱的利用效率, 提出了一种用于子信道分配的低复杂度次优匹配算法, 该算法可以最大程度地提高卸载效率. 文献[19]考虑时延敏感型任务的卸载问题, 将该问题建模为传输功率、子载波和计算资源分配联合优化, 并将原始问题拆解为3个子问题, 通过一个迭代算法顺序处理. 通过等价参数凸规划获得最优解. 文献[20]研究MEC中协同计算任务卸载和资源分配联合问题, 通过对计算卸载决策、协同选择、功率分配进行分别建模从而最小化系统时延. 作者提出了一种基于拉格朗日对偶分解、生津公式法和单调优化法的联合迭代算法来解决提出的问题. 文献[21]考虑超密集网络下的任务卸载问题, 使用博弈论寻找到各用户的最优卸载服务器后, 再通过启发式萤火虫算法来优化用户任务卸载比例带来的时延和能耗问题, 在多次迭代中不断逼近最优值. 文献[22]注重优先级任务的卸载问题, 根据用户任务的平均处理价值分配优先级, 并根据优先级分配其相应的计算资源, 从而减少系统总时延和能耗.
上述工作主要优化时延和能耗的加权问题, 没有考虑经济效益情况. 在考虑MEC社会效益的研究中, 大部分工作主要使用拍卖算法或其他激励机制来实现效益最优. 文献[23]提出了一种新的分层结构, 通过将请求计算卸载的移动设备与边缘服务器之间建立一种投标与要价的双边交互, 并将计算资源和通信资源以利润最大化的方式进行拍卖, 从而满足用户QoS标准. 文献[24]从博弈论出发, 构建了CC服务器与MEC服务器之间一种全新的协作关系, 从顶层向下层进行任务卸载, 并对卸载的任务进行出价奖励. 通过验证两者之间的纳什均衡关系来证明最优任务卸载量和出价存在, 并进行多次迭代找到该最优解. 这套关系同样可以适用于边缘服务器与移动设备之间. 文献[25]研究了工业物联网中如何提升社会效益, 对MEC服务器与移动设备之间的双向交互进行建模, 构建了一个通用的双重拍卖框架来解决交互问题并最大化社会效益. 在满足各项经济属性的前提下, 通过真实的双重拍卖算法将MEC服务器的计算资源出售, 从而最优化效益. 文献[26]将MEC服务器与用户之间的竞争性交易以3层拍卖模型表示, 并把整个拍卖过程拆分为3个独立且有顺序的子问题. 作者提出了一种真实的组合拍卖算法来联合优化服务成本和无线信道资源. 文献[27]在不考虑信道资源的情况下, 基于市场定价利润最优化问题设置了一个激励机制, 同时针对用户随机性, 设计了一种在线多轮拍卖算法. 文献[28]提出了一种基于双重拍卖的多对多计算资源分配算法, 以最大限度提高效益. 作者从网络经济学的角度研究MEC中的跨服务器资源分配方案, 并将MEC服务器与用户之间的双边交互建模为双重动作, 从而解决多种用户任务跨服务器交互问题.
现有使用拍卖理论来优化MEC社会效益的研究没有考虑边缘服务器随机分布场景下, 用户对服务器的选择产生的效益影响. 例如文献[18-23]侧重于能耗最优化, 并没有考虑服务收费问题; 文献[24-28]虽然考虑了计算服务成本, 但并没有考虑不同边缘服务器之间的位置差异对用户的卸载影响, 且没有考虑边缘服务器计算资源受限情况. 用户选择不同位置的边缘服务器会产生不同的传输时延和能耗, 进而影响用户请求计算资源量, 最终影响用户效益. 在这篇文章中, 考虑MEC服务器随机分布且计算资源受限情况下对于用户卸载选择的影响, 使用Stackelberg博弈对MEC服务器与移动设备之间进行建模, 并且在该场景下提出了基于贪心思想的改进双重拍卖算法来最优化MEC服务器资源受限情况下的移动设备效益. 与传统双重拍卖的价高者得和其他文章为简化时间而忽略部分交易的双重拍卖不同, 本文提出的双重拍卖算法可以在首轮拍卖中满足价高者得的用户局部效益最优, 进而在第2轮拍卖中实现系统整体效益最优.
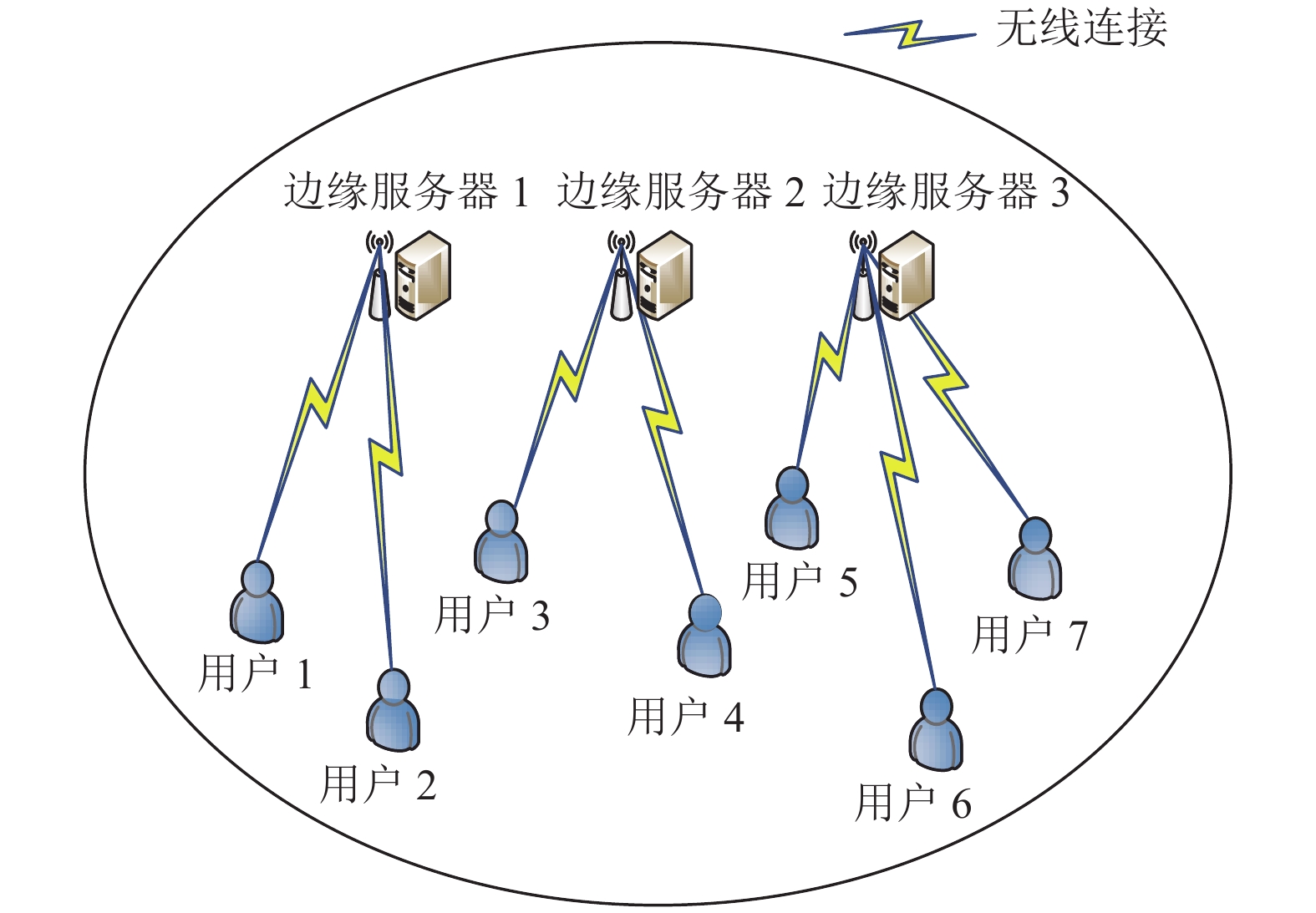
2 系统架构和问题建模 2.1 系统架构如图1所示, MEC系统网络架构由M个用户、N个边缘服务器组成, 用户与边缘服务器之间通过无线信道连接. 假设每个用户拥有一个不可分割的待卸载任务, 即共有M个任务, 用U={U1, U2, …, UM}表示. 用户的属性可以表示为Ui ={Ci,
|
图 1 MEC系统网络架构 |
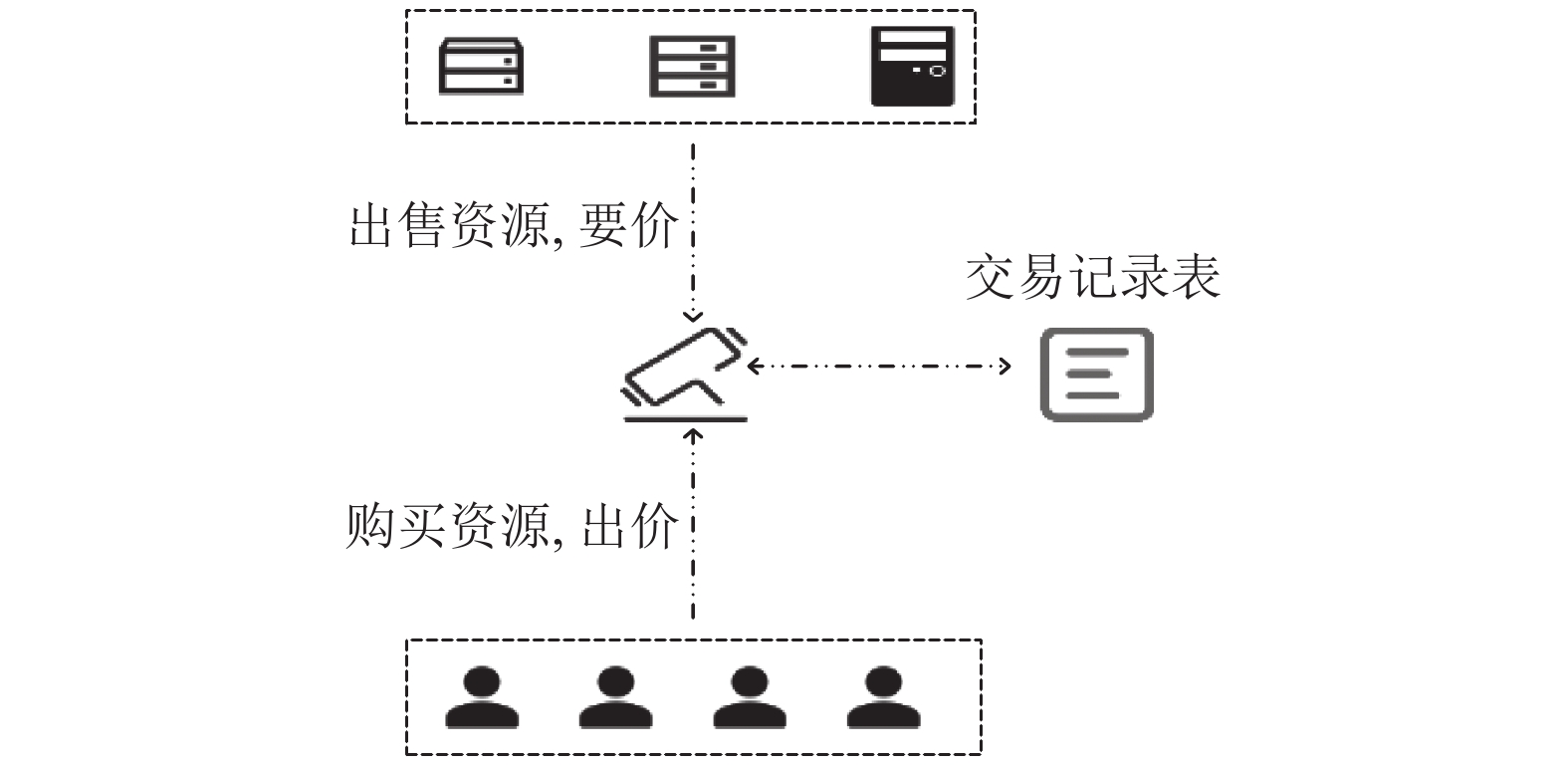
双重拍卖模型如图2所示, 由买方(用户)、卖方(边缘服务器)以及第三方拍卖者组成. 其中交易双方分别向拍卖方提供需求资源量、出价以及出售资源量、要价. 在拍卖进行时, 拍卖方会将每次交易倾向条目储存在交易记录表中, 并在拍卖结束后统一达成交易.
2.2 传输模型多服务器多用户随机分布的边缘计算模型常应用于大型商场或商业区场景中, 因此采用自由空间路径损耗模型来描述用户任务卸载至边缘服务器过程. 对于不同用户传输, 采用正交频分多址方式, 并假设每个用户拥有的信道带宽为Bi . 由香农公式知, 忽略用户之间的信道干扰, 用户i将任务卸载到边缘服务器j的上行链路传输速率为:
| vi,j=Bilog2(1+PTiHi,jσ2) | (1) |
其中, Hi,j表示用户i与边缘服务器j之间的信道增益, 与文献[29]相似, Hi,j=
|
图 2 双重拍卖示意图 |
在得知用户与边缘服务器的传输速率后, 可以求得用户将任务卸载至边缘服务器的时延. 不考虑传输过程中的速度损耗, 用户i卸载任务至边缘服务器j的传输时延可以表示为:
| TCi,j=Civi,j | (2) |
与文献[30]的计算方法相似, 系统中用户i将任务卸载至边缘服务器j的传输能耗可以表示为:
| ECi,j=PTi×Civi,j | (3) |
在本节中, 对用户的计算资源请求量与边缘服务器的资源定价之间进行博弈建模. 由于Stackelberg博弈是两阶段完全信息动态博弈, MEC服务提供商作为领导者首先在第1阶段制定自己的定价策略, 用户作为追随者在得知定价策略后确定自己的资源请求策略. 为了建立博弈模型, 首先对用户卸载策略进行描述, 之后定义MEC服务提供商与用户的效用函数, 它们的目标都是最大化自己的效用函数值.
在多用户多服务器的边缘计算场景中, 各服务器的定价会对用户的卸载倾向以及系统整体性能产生较大的影响. 由于每个用户都在所有边缘服务器的覆盖范围内, 因此用户可以选择不同的边缘服务器来卸载它们的任务, 以达到自身成本最小化的目的. 同时, 希望更多的用户将任务卸载到边缘服务器上, 这样传输时延以及成本会更低. 用户对各边缘服务器的喜好程度可以表示为:
| oi,j=β1SjRi,j+β21di,j+β3Costi,j | (4) |
其中,
基于式(4), 每个用户可以选择一个合适的边缘服务器卸载任务并购买计算资源. 进一步需要研究用户与边缘服务器之间的博弈交互. 用户与边缘服务器之间不断改变自己的策略以适应对方的策略, 并最终达到两者最优效用. 用户与边缘服务器的效用函数建模如下.
2.3.1 用户效益用户成本由两部分组成: 1)用户购买计算资源的出价; 2)用户任务的卸载能耗. 为了最优化系统中用户效益, 在拍卖时需要优先考虑每个用户对应成本最小的边缘服务器. 对于卸载至边缘服务器上计算的用户, 他们需要支付任务通过无线信道传输所产生的能耗以及购买计算资源的出价. 用户i在将任务卸载至边缘服务器j上计算的成本可以表示为:
| Costi,j=αiRi,jpj+(1−αi)PTi×Civi,j | (5) |
其中, Ri,j表示用户i向边缘服务器j请求的计算资源量.
如果用户购买了大量的计算资源, 那么这些任务的执行时间会减少, 因此用户可以从完成这些任务中获得的报酬就会增加. 然而, 当用户拥有足够的计算资源以后, 计算能力的提升以及从任务中获得的报酬的增加都会减缓. 因此, 用户卸载至边缘服务器上完成任务获得的收益可以用自然对数函数建模[27], 表示随着
| UPi=λiln(1+μ−1jRi,j)−Costi,j | (6) |
其中,
边缘服务提供商通过出售边缘服务器中的计算资源来获得效益, 并且该效益与单位计算资源的收费有关. 边缘服务器的效益可以用边缘服务器出售计算资源获得的收益减去计算用户任务的能耗求得. 由于边缘服务器需要提供计算服务, 因此边缘服务提供商需要付出额外的成本来维护边缘服务器的使用. 边缘服务器的计算能耗与用户卸载的任务大小以及用户请求的计算资源量有关. 边缘服务器j的计算能耗可以表示为:
| ECj=M∑i=1ηi,jPjRi,jfj | (7) |
相应的, 边缘服务器j的效益可以表示为:
| UPj=M∑i=1ηi,jRi,jpj−ECj | (8) |
本文的首要目标是通过优化用户任务卸载决策以及请求资源量来最大化系统中用户的总收益. 优化问题P1建模如下:
| {P1:max Uuser={M∑i=1UPi}约束条件:C1:N∑j=1ηi,j=1,∀i∈MC2:TCi,j+TEi,j⩽TDi,∀i∈[1,M] | (9) |
其中, 约束条件C1限制每个用户只能卸载至一个边缘服务器上; 约束条件C2说明用户在边缘服务器上的计算时延与传输时延之和要小于用户任务的截止时间. 由于用户到不同边缘服务器的传输时延是不同的, 因此其计算时延也是不同的, 可得知用户在每个边缘服务器上的请求资源有最小值.
本文的次要目标是通过优化单位计算资源收费来最大化边缘服务提供商的效益. 优化问题P2建模为:
| {P2:maxUES={N∑j=1UPj}约束条件:C3:0⩽Ri,j⩽Dj,∀i∈[1,M],j∈[1,N]C4:N∑j=1M∑i=1ηi,jRi,j⩽DjC5:pj>0,j∈[1,N] | (10) |
其中, 约束条件C3限制每个用户对任意一个边缘服务器请求的计算资源, 表示请求的计算资源量要小于等于边缘服务器所拥有的计算资源量; 约束条件C4表示每个边缘服务器上各卸载任务请求的资源量之和要小于等于该边缘服务器所拥有的计算资源量; 约束条件C5表示必须要收费大于0, 如果边缘服务提供商收益小于它维护服务付出的成本, 那么它将不会继续提供服务.
不难看出, 用户效益最大化与边缘服务器效益最大化之间纯在冲突, 因为若希望用户效益提高, 则需要减少用户向边缘服务器支付的计算资源成本, 然而这样会减少边缘服务器的效益. 因此, 需要找到一个用户最优卸载策略和最优计算资源请求策略, 在对边缘服务器效益产生较小影响的情况下, 最大化系统中用户整体效益.
3 问题分析与拍卖算法描述 3.1 Stackelberg博弈问题分析该博弈问题中, 边缘服务器作为领导者, 且每个边缘服务器拥有一个最优定价策略, 可以表示为P*=(
| {UPi(R∗i,j,R∗−i,j,p∗j)⩾UPi(Ri,j,R∗−i,j,p∗j)UPj(R∗i,j,p∗j)⩾UPj(R∗i,j,pj) | (11) |
其中,
定理1. 在用户选择边缘服务器博弈中存在纳什均衡.
证明: 如式(6)所示, 用户的效益函数它是一个关于请求资源Ri,j的连续函数. 它对于请求资源Ri,j的一阶偏导数为:
| ∂Upi∂Ri,j=λiμj+Ri,j−αipj | (12) |
相应的, 该函数对于请求资源Ri,j的二阶偏导数为:
| ∂2UPi∂(Ri,j)2=−λi(1+μj)(μj+Ri,j)2 | (13) |
因为
定理2. 对于给定边缘服务器收费pj, 用户i对于边缘服务器j的最优计算资源请求量可以表示为:
| R∗i,j=max(λiαipj−μj,CiTDi−TCi) | (14) |
证明: 由定理1知, 用户效益是关于请求资源的凸函数. 根据凸函数的性质, 函数的极值点就是函数的最大值点. 令式(12)=0, 可以求得用户效益取得最大值时的计算资源为:
| R′i,j=λiαipj−μj | (15) |
其中,
定理3. 每一个用户有且仅有一个最优的计算资源请求策略.
证明: 如果边缘服务器的收费为0, 那么用户在请求计算资源时便不会考虑不同边缘服务器的收费差异, 只考虑距离带来的传输能耗问题; 如果边缘服务器的收费非常高, 那么用户无论选择哪个边缘服务器所带来的效益都不高. 因此本文只考虑每个边缘服务器都是合理收费情况, 此时分别让最优请求计算资源量对收费求一阶偏导数和二阶偏导数有:
| ∂R∗i,j∂pj=−λiαip2j | (16) |
| ∂2R∗i,j∂(pj)2=2λiαip3j | (17) |
由于pj >0,
综上, 易知用户的计算资源请求量是关于收费pj的一个递减的下凹函数. 因此, 对于一个给定范围的收费, 该函数是一个严格的凹函数. 所以用户计算资源请求策略是最优且唯一的, 该定理证得.
定理4. 用户与边缘服务器之间存在纳什均衡.
证明: 根据定理1和定理2可知, 当边缘服务器的收费pj确定时, 用户总是可以达到纳什均衡. 下一步, 通过分析边缘服务器的效益来证明用户与边缘服务器之间的纳什均衡. 分别让边缘服务器的效益函数对收费求一阶偏导数和二阶偏导数有:
| ∂UPj∂pj=M∑i=1ηi,j(Pjλiαifjp2j−μj) | (18) |
| ∂2UPj∂(pj)2=M∑i=1−ηi,jPjλiαifjp3j | (19) |
不难看出, 式(18)>0、式(19)<0. 这说明对于给定范围的收费pj, 随着它的增大, 边缘服务器的效益会逐渐增加, 这是因为用户购买计算资源的单价上升, 所以边缘服务器的效益逐渐增加; 同时, 这种增加的趋势在逐渐变慢, 这是因为用户购买计算资源的单价上升, 所以用户购买计算资源量会减少, 边缘服务器效益增加速度会有缓和. 因此, 用户与边缘服务器之间存在纳什均衡, 定理证得.
3.2 双重拍卖算法描述在第3.1节中, 证明了用户与边缘服务器之间存在纳什均衡, 且各服务器对于计算资源的收费会直接影响各用户对于该服务器请求的计算资源, 而用户请求计算资源量与自身以及边缘服务器的效益相关. 在博弈中, 各个用户通过计算出最优的计算资源请求量来最大化自己的效益, 同时需要尽可能将边缘服务器的计算资源与用户进行匹配, 从而最大化系统内用户整体效益.
传统双重拍卖算法中, 交易双方向第三方拍卖者提供自己出售(需求)的物品量和对应要价(出价)后, 遵循价高者得原则, 即将出价最高的用户优先拍卖. 在计算资源不受限的情况下, 这种拍卖策略可以实现效益最优化. 但在资源受限场景中, 传统双重拍卖算法容易陷入局部最优, 因为可能会出现部分交易占用大量资源, 从而导致较多用户无法完成拍卖的情况.
为了解决上述问题, 在本节中, 提出了一种基于贪心思想的改进双重拍卖算法(improved double auction algorithm based on greed, IDAG)来解决用户与边缘服务器之间的效益最大化问题. 在IDAG算法中, 首先从用户的角度出发, 将各用户与其对应成本最小的边缘服务器进行拍卖匹配, 使得各用户自身的效益最大化, 这样会占用边缘服务器的大部分计算资源, 拍卖失败的用户会加入失败队列; 其次从系统的角度出发, 通过改变交易策略, 从而省下额外的计算资源, 并将这些计算资源拍卖给失败用户, 从而实现整个系统的效益最大化. 该算法的具体步骤如算法1.
算法1. 基于贪心思想的改进双重拍卖算法
输入: 用户集合U, 边缘服务器集合E
输出: 成功拍卖用户WU , 用户效益Uuser, 边缘服务器效益UES
1) 通过式(4)和式(14)计算用户喜好矩阵和用户请求资源矩阵, 初始化各边缘服务器匹配用户队列
For each user in U//遍历用户集合中的所有用户
2) 从用户喜好矩阵中选择用户i最喜爱的边缘服务器j. 若Ri,j ≤Sj, 则将用户i拍卖给该边缘服务器, 并将该用户加入
End for
3) 对各边缘服务器按计算资源收费升序排列, 此时边缘服务器匹配用户队列可表示为
For each user in
4) 从
End for
For each user in WL//循环失败匹配队列, 重新拍卖
5) 判断用户ui是否有可以重新拍卖的边缘服务器, 如果
End for
for each
6) 分别用式(6)和式(8)计算用户效益Uuser和边缘服务器效益UES ;
End for
If ║UES(t)–UES(t–1)║>ε
7) 改变各边缘服务器资源定价pj
End if
在算法1中, 步骤2)为第一轮拍卖, 目的是各用户贪婪资源分配. 在首轮计算资源拍卖结束后, 对于各拍卖成功的用户, 他们的效益是最优的, 因为他们在成本最低的边缘服务器上获得了计算资源. 但此时仍可能存在资源浪费现象, 因为部分用户会在一些成本较低的边缘服务器上占用过多计算资源, 从而导致部分用户拍卖失败, 用户整体效益不是最优的. 因此需要进行第2轮计算资源拍卖, 将失败用户与边缘服务器进行重新匹配.
在第2轮拍卖开始前, 需要先在边缘服务器之间进行用户交换, 即步骤4), 目的是节省出部分计算资源给失败用户. 在边缘服务器之间的任务交换过程中会出现如下3种情况.
① 如果用户任务i在Ej上的请求计算资源小于等于Ej的剩余资源, 则将该用户从
② 如果用户任务i在Ej上的请求计算资源大于该边缘服务器的剩余计算资源, 且任务i在EN上的计算资源小于
③ 如果不满足②中的两个条件, 说明Ej可以进行交换. 如果
之后, 失败用户开始重新进行拍卖. 通过判断每一个失败任务对不同边缘服务器的请求资源是否满足
与传统双重拍卖算法相比, 本文提出算法的不同在于: 1)我们将
算法的步骤2)需要遍历整个用户集合, 共有M个用户, 因此需要的时间为O(M); 步骤4)要进行资源整合, 会对收费最高服务器队列的用户进行遍历, 该队列最大数量为用户总数M, 因此需要的时间为O(M). 遍历每一个用户时, 需要访问剩余N–1个边缘服务器, 以判断是否有剩余计算资源供整合, 每个用户所需时间为O(N–1), 因此步骤4)的总时间为O(MN); 步骤5)对失败用户重拍卖, 最大数量为用户总数, 因此需要的时间为O(M). 遍历每一个用户时, 需要访问N个边缘服务器, 以判断是否有剩余计算资源供失败用户重新拍卖, 每个用户所需时间为O(N), 因此步骤5)的总时间为O(MN). 综上, 算法1的时间复杂度为O(MN).
需要注意的是, 贪心策略在大多数问题上容易陷入局部最优. 比如0-1背包问题中, 使用贪心策略不能保证背包可以装满, 部分闲置空间会使背包价值下降. 但本文假设用户任务无法拆分情况, 并且为了保证用户QoS标准, 每个用户都有硬时延要求, 因此各用户请求资源有最小值, 无法将边缘服务器计算资源完全拍卖. 且在实际生活场景, 很难做到资源的完美消耗. 所以本文提出的算法可以实现完全卸载情况下的整体最优.
4 仿真结果与分析 4.1 实验设置本文的仿真实验设置的应用场景为多用户需要计算卸载的大型小区, 假设系统中共有5个边缘服务器, 用户数量从80个到130个递增. 不同服务器之间具有定价、算力以及物理位置的差异, 同时服务器的初始定价与其算力成正比. 用户和边缘服务器随机分布在半径为1000 m的区域, 如图3所示. 式(4)中的参数设置为β1=0.1, β2=0.1, β3=0.8. 其他参数及具体数据范围如表1所示. 取20次实验结果的平均值, 并且同以下4种基准算法进行对比:
随机匹配算法 (random matching algorithm, RMA): 用户随机与边缘服务器进行拍卖.
顺序匹配算法 (sequential matching algorithm, SMA): 类似于传统双重拍卖算法, 用户按照边缘服务器价格由低到高拍卖.
文献[25]提出的(breakeven based double auction, BDA): 将边缘服务器出价的中间值作为breakeven点, 并以此过滤掉部分不符合拍卖的用户.
文献[31]提出的(double action of multi-type multi-resource based on dynamic pricing, DAMMDP): 成功交易的价格是由边缘服务器决定的, 并且该价格是用收费更高的边缘服务器来代替. 收费最高的边缘服务器参与拍卖时价格不变.

|
图 3 用户与边缘服务器随机分布图 |
| 表 1 仿真参数设定 |
4.2 仿真结果分析
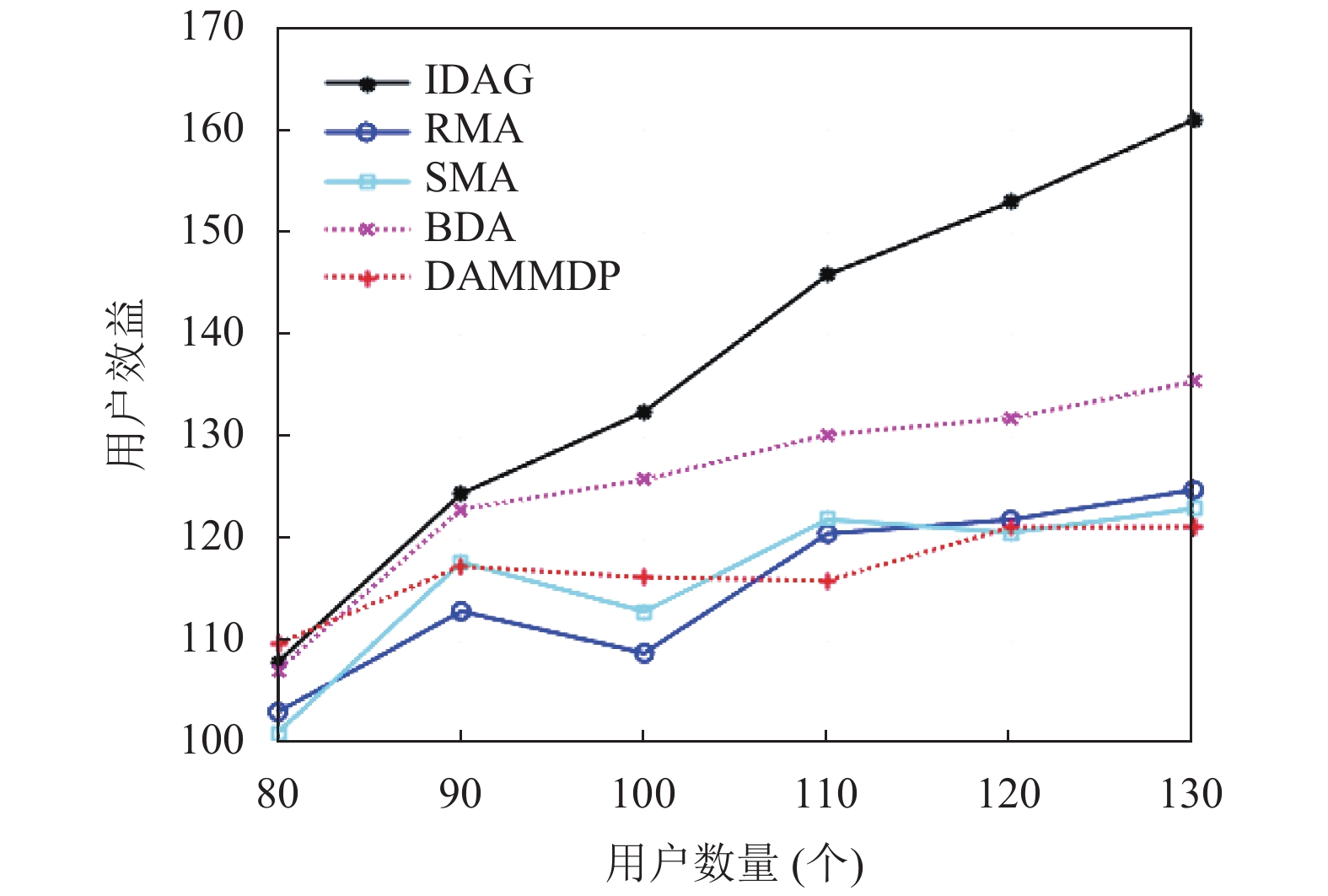
图4–图6展示了不同的用户数量对于成功匹配用户总体效益、边缘服务器效益、成功匹配用户数量的影响. 可以发现, 当用户数量较少时, 各算法在效益和成功匹配数量上的表现是接近的, 因为此时边缘服务器中所拥有的计算资源还没有被完全占用, 每个用户都可以匹配给相应的边缘服务器. 当用户数量继续上升时, 边缘服务器的计算资源几乎被分配完, 此时各算法之间的差异增大.
|
图 4 用户数量与用户效益的关系 |

|
图 5 用户数量与边缘服务器效益的关系 |

|
图 6 用户数量与成功匹配用户数的关系 |
图4可以看出, 随着用户数量的增加, IDAG算法的成功匹配用户效益在不断增加, 与其他算法的差距增大. 这是因为当边缘服务器计算资源消耗殆尽时, 通过二次拍卖将部分计算资源结余出来留给匹配失败的用户, 因此成功匹配的用户更多, 且效益增加. 其他算法随着用户增加后, 失败匹配用户逐渐增加, 并且没有边缘服务器之间的任务交换, 因此成功匹配用户效益增长程度逐渐趋平. 随着用户数量的增加, 随机匹配、顺序匹配和DAMMDP算法都出现了波动. 这是因为在随机匹配和顺序匹配中, 用户任务数据量的改变会产生较大的影响. 但当用户数量到达110以后, 这两种方法的用户效益趋于稳定. 因为用户已经将系统内边缘服务器的计算资源全部占用. 对于DAMMDP算法, 由于其为了增加成功匹配用户数量, 在定价阶段将所有用户的出价提高, 从而导致随着用户的增多, 成功匹配用户的整体效益出现下降. 而BDA算法为了提高系统用户总效益, 会删除掉成本较高的边缘服务器和用户任务, 因此随着用户数量的增加, 其用户效益仍在增加. 但由于没有资源重分配过程, 因此当系统内计算资源完全占用后, 用户效益难以增加.
图5中, 用户数量从80到90时, 边缘服务器的效益出现的急剧提高. 这是因为边缘服务器的计算资源被大量占用, 且边缘服务器的效益与分配的计算资源正相关, 因此效益提升. 当用户数量继续增加, 边缘服务器的计算资源已经被用户任务占用完全, 效益难以提升, 趋于稳定. 可以看出, BDA策略和DAMMDP策略的效果较差, 这是因为BDA会删去成本较高边缘服务器的, 因此边缘服务器的效益会降低; 而DAMMDP会提高用户成本, 从而使得这类用户的拍卖优先级降低, 使得边缘服务器效益降低.
从图6中可以看出, BDA算法和DAMMDP算法的成功匹配用户数相比于随机匹配和顺序匹配效果更优, 但代价就是效益的降低. 在一些需要增加成功匹配用户数量且对算法运行时间较为敏感的场景中, BDA算法和DAMMDP算法更具有优势. 由于IDAG算法有资源重分配过程, 因此即使当用户数量到达100以后系统内计算资源占用完毕, 本文提出的算法仍然可以使更多用户与边缘服务器匹配.
IDAG算法相对于基准算法在成功匹配用户效益、边缘服务器效益的提升分别为: 33.4%、8.2%.
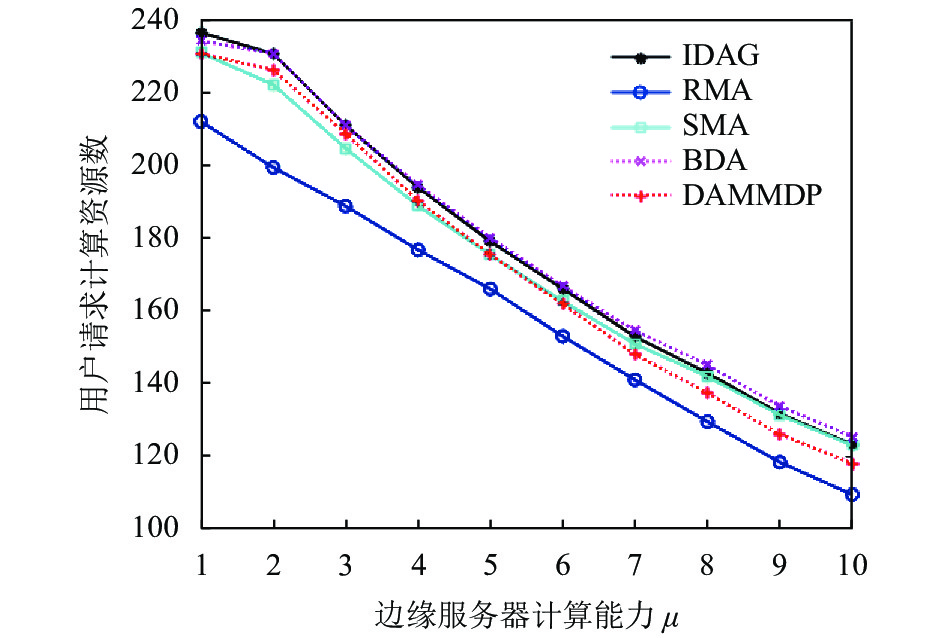
图7和图8展示了当用户数量为100、用户效益系数为5时(
从图7中可以看出, 随着计算能力的提高, 系统中成功匹配用户的效益在不断提高, 这是因为单位计算资源的数据处理能力在同步提高. 用户的任务数据量不变, 从而用户请求的计算资源量就会减少, 因此成功匹配用户的成本会减少, 效益会提高. 同时, 从图8中可以发现, 正如前面提到的, 用户对于计算资源的请求量在不断减少.
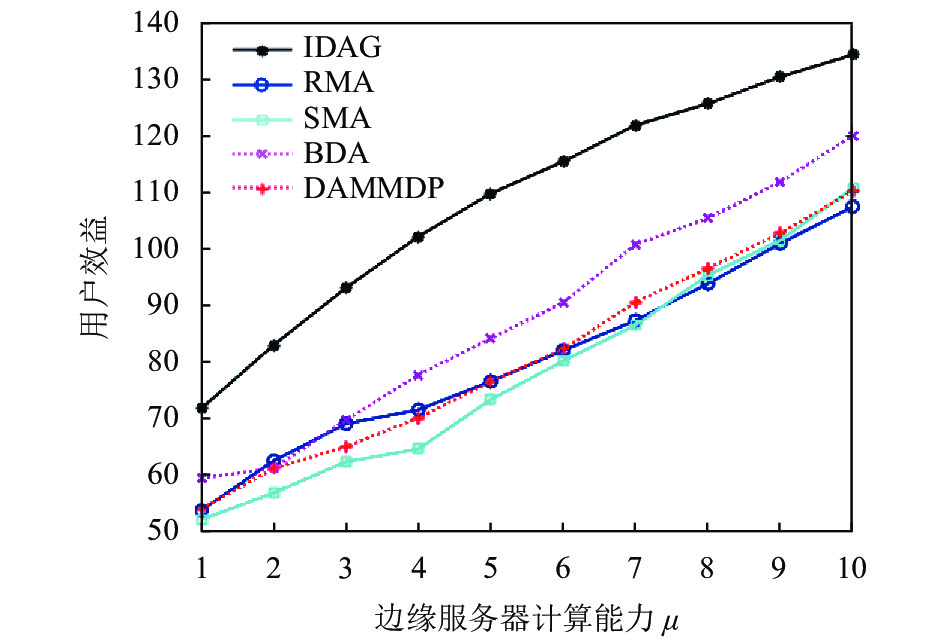
|
图 7 边缘服务器计算能力对用户效益的影响 |
|
图 8 边缘服务器计算能力对请求计算资源量的影响 |
图9和图10展示了当用户数量为100、边缘服务器计算能力
总的来说, IDAG算法无论在用户效益、边缘服务器效益还是系统总体效益都相较于4种基准算法有较为明显的提升. 同时, 在成功匹配用户数量上也表现不俗, 并且也达到了理想的平衡. 因此, 在边缘服务器与用户随机分布的场景中, 本文提出的IDAG算法有着优异的性能.

|
图 9 用户效益参数对用户效益的影响 |

|
图 10 用户效益参数对计算资源请求量的影响 |
5 结论
本文研究了边缘服务器随机分布的MEC场景中用户和边缘服务器效益问题. 首先通过将用户与边缘服务器之间的交互过程建模为Stackelberg博弈, 并验证了该博弈存在唯一的纳什均衡点. 为找到最优任务卸载和计算资源请求策略, 提出了一种基于贪心思想的改进双重拍卖算法. 实验结果表明, 与其他基准算法相比, 提出的IDAG算法可以有效提高系统内成功拍卖的用户效益和边缘服务器效益, 并且能使更多用户将任务卸载至边缘服务器计算. 在未来, 这项工作将加强云服务器对于整体策略的影响, 并将用户QoS标准作为计算用户效益的一个重要指标.
| [1] |
Abbas N, Zhang Y, Taherkordi A, et al. Mobile edge computing: A survey. IEEE Internet of Things Journal, 2018, 5(1): 450-465. DOI:10.1109/JIOT.2017.2750180 |
| [2] |
Hassan N, Yau KLA, Wu C. Edge computing in 5G: A review. IEEE Access, 2019, 7: 127276-127289. DOI:10.1109/ACCESS.2019.2938534 |
| [3] |
Hassan N, Gillani S, Ahmed E, et al. The role of edge computing in Internet of Things. IEEE Communications Magazine, 2018, 56(11): 110-115. DOI:10.1109/MCOM.2018.1700906 |
| [4] |
Huda SMA, Moh S. Survey on computation offloading in UAV-enabled mobile edge computing. Journal of Network and Computer Applications, 2022, 201: 103341. DOI:10.1016/j.jnca.2022.103341 |
| [5] |
Mach P, Becvar Z. Mobile edge computing: A survey on architecture and computation offloading. IEEE Communications Surveys & Tutorials, 2017, 19(3): 1628-1656. |
| [6] |
Kong LH, Tan JL, Huang JQ, et al. Edge-computing-driven Internet of Things: A survey. ACM Computing Surveys, 2023, 55(8): 174. |
| [7] |
Qiu HM, Zhu K, Luong NC, et al. Applications of auction and mechanism design in edge computing: A survey. IEEE Transactions on Cognitive Communications and Networking, 2022, 8(2): 1034-1058. DOI:10.1109/TCCN.2022.3147196 |
| [8] |
Sadeeq MM, Abdulkareem NM, Zeebaree SRM, et al. IoT and cloud computing issues, challenges and opportunities: A review. Qubahan Academic Journal, 2021, 1(2): 1-7. DOI:10.48161/qaj.v1n2a36 |
| [9] |
Zhou ZY, Liu PJ, Feng JH, et al. Computation resource allocation and task assignment optimization in vehicular fog computing: A contract-matching approach. IEEE Transactions on Vehicular Technology, 2019, 68(4): 3113-3125. DOI:10.1109/TVT.2019.2894851 |
| [10] |
Pham QV, Fang F, Ha VN, et al. A survey of multi-access edge computing in 5G and beyond: Fundamentals, technology integration, and state-of-the-art. IEEE Access, 2020, 8: 116974-117017. DOI:10.1109/ACCESS.2020.3001277 |
| [11] |
Liu YQ, Peng MG, Shou GC, et al. Toward edge intelligence: Multiaccess edge computing for 5G and Internet of Things. IEEE Internet of Things Journal, 2020, 7(8): 6722-6747. DOI:10.1109/JIOT.2020.3004500 |
| [12] |
Zhang K, Mao YM, Leng SP, et al. Energy-efficient offloading for mobile edge computing in 5G heterogeneous networks. IEEE Access, 2016, 4: 5896-5907. DOI:10.1109/ACCESS.2016.2597169 |
| [13] |
Wang YT, Sheng M, Wang XJ, et al. Mobile-edge computing: Partial computation offloading using dynamic voltage scaling. IEEE Transactions on Communications, 2016, 64(10): 4268-4282. |
| [14] |
Ning ZL, Dong PR, Kong XJ, et al. A cooperative partial computation offloading scheme for mobile edge computing enabled Internet of Things. IEEE Internet of Things Journal, 2019, 6(3): 4804-4814. DOI:10.1109/JIOT.2018.2868616 |
| [15] |
Tran TX, Pompili D. Joint task offloading and resource allocation for multi-server mobile-edge computing networks. IEEE Transactions on Vehicular Technology, 2019, 68(1): 856-868. DOI:10.1109/TVT.2018.2881191 |
| [16] |
Zhan YF, Guo S, Li P, et al. A deep reinforcement learning based offloading game in edge computing. IEEE Transactions on Computers, 2020, 69(6): 883-893. DOI:10.1109/TC.2020.2969148 |
| [17] |
Asheralieva A, Niyato D. Bayesian reinforcement learning and Bayesian deep learning for blockchains with mobile edge computing. IEEE Transactions on Cognitive Communications and Networking, 2021, 7(1): 319-335. DOI:10.1109/TCCN.2020.2994366 |
| [18] |
Xue JB, An YN. Joint task offloading and resource allocation for multi-task multi-server NOMA-MEC networks. IEEE Access, 2021, 9: 16152-16163. DOI:10.1109/ACCESS.2021.3049883 |
| [19] |
Zhao MX, Yu JJ, Li WT, et al. Energy-aware task offloading and resource allocation for time-sensitive services in mobile edge computing systems. IEEE Transactions on Vehicular Technology, 2021, 70(10): 10925-10940. DOI:10.1109/TVT.2021.3108508 |
| [20] |
Kuang ZF, Ma ZH, Li Z, et al. Cooperative computation offloading and resource allocation for delay minimization in mobile edge computing. Journal of Systems Architecture, 2021, 118: 102167. DOI:10.1016/j.sysarc.2021.102167 |
| [21] |
刘振鹏, 郭超, 王仕磊, 等. 基于博弈论和启发式算法的超密集网络边缘计算卸载. 计算机工程, 2022, 48(12): 54-61, 71. DOI:10.19678/j.issn.1000-3428.0063734 |
| [22] |
董思岐, 吴嘉慧, 李海龙, 等. 面向优先级任务的移动边缘计算资源分配方法. 计算机工程, 2020, 46(3): 18-23. DOI:10.19678/j.issn.1000-3428.0054490 |
| [23] |
Kiani A, Ansari N. Toward hierarchical mobile edge computing: An auction-based profit maximization approach. IEEE Internet of Things Journal, 2017, 4(6): 2082-2091. DOI:10.1109/JIOT.2017.2750030 |
| [24] |
Zhou H, Wang ZN, Cheng N, et al. Stackelberg-game-based computation offloading method in cloud-edge computing networks. IEEE Internet of Things Journal, 2022, 9(17): 16510-16520. DOI:10.1109/JIOT.2022.3153089 |
| [25] |
Sun W, Liu JJ, Yue YL, et al. Double auction-based resource allocation for mobile edge computing in industrial Internet of Things. IEEE Transactions on Industrial Informatics, 2018, 14(10): 4692-4701. DOI:10.1109/TII.2018.2855746 |
| [26] |
Su Y, Fan WH, Liu YA, et al. A truthful combinatorial auction mechanism towards mobile edge computing in industrial Internet of Things. IEEE Transactions on Cloud Computing, 2022.
|
| [27] |
Wang QY, Guo ST, Liu JD, et al. Profit maximization incentive mechanism for resource providers in mobile edge computing. IEEE Transactions on Services Computing, 2022, 15(1): 138-149. DOI:10.1109/TSC.2019.2924002 |
| [28] |
Yue YL, Sun W, Liu JJ. Multi-task cross-server double auction for resource allocation in mobile edge computing. Proceedings of the 2019 ICC IEEE International Conference on Communications (ICC). Shanghai: IEEE, 2019. 1–6.
|
| [29] |
Wang YP, Lang P, Tian DX, et al. A game-based computation offloading method in vehicular multiaccess edge computing networks. IEEE Internet of Things Journal, 2020, 7(6): 4987-4996. DOI:10.1109/JIOT.2020.2972061 |
| [30] |
Gao LX, Chen X, Yin B, et al. Computation offloading based on game theory in multi-access edge computing for 6G network. Proceedings of the 14th International Conference on Communication Software and Networks (ICCSN). Chongqing: IEEE, 2022. 63–68.
|
| [31] |
Yan Y, Zhang JX, Wei YK, et al. Double action mechanism for vehicle edge computing resource allocation and pricing. Proceedings of the 4th International Conference on Information Communication and Signal Processing (ICICSP). Shanghai: IEEE, 2021. 547–552.
|
 2023, Vol. 32
2023, Vol. 32



