2. 复旦大学 智能复杂体系基础理论与关键技术实验室, 上海 200433
2. Research Institute of Intelligent Complex Systems, Fudan University, Shanghai 200433, China
近年来, 计算机技术快速发展, 人们对人工智能的研究越来越深入. 在人工智能的发展历史中, 研究学者对从人类大脑中获得信息传输原理和本质的研究从未中断, 他们希望从大脑传输信息的理论出发, 让机器能够以类脑的方式进行工作, 从而让机器拥有感知、学习、记忆、决策、判断等能力, 并将其运用到现实生活中的各个领域[1]. 1943年生理学家McCulloch和数学家Pitts提出了第一个神经元模型(M-P模型), 从此开启了人们对人工神经网络的研究[1,2]. 在过去的几十年中, 随着问题复杂度的增加以及海量数据的累积, 控制神经网络的计算成本已经成为目前研究的一个重要课题. 目前, 实现神经网络高效性的方法有: 知识蒸馏[3-5]、量化和剪枝[6-8], 其中对网络进行剪枝的方法在近年来得到广泛研究与应用.
对剪枝算法进行分类的方法有很多: 1)根据剪掉的网络元素分为神经元剪枝和连接剪枝; 2)根据剪枝前后网络结构是否改变分为结构化剪枝和非结构化剪枝; 3)根据训练阶段是否剪枝分为静态剪枝和动态剪枝. Ponnapalli等人提出了一种基于局部相对灵敏度指标概念的前馈人工神经网络形式化选择和剪枝技术[9]. 其基于对前馈神经网络子群中相对冗余的权值进行并行剪枝, 从而在减少模型残差、提高网络泛化能力、降低网络复杂度等方面具有更好的剪枝效果. Han等人提出了一种根据连接的重要性对网络进行修剪的方法[6]. 该算法主要原理是: 网络经过训练之后, 对网络中“不重要”的连接进行剪枝, 然后再对剪枝后的稀疏连接的网络进行训练从而获得最终权重. 该方法使得网络参数显著减少, 并且精度不受影响, 从而使得网络更加高效节能. Collins等人提出了一种在CNN训练过程中使用鼓励卷积和全连接层中的较少连接采用非零值的正则化器, 从而使得深度网络中隐藏层之间的连接稀疏, 该方法也减少了内存消耗, 并且在准确性方面损失很小[10]. Srinivas等人通过对神经元进行修剪, 去除相似的神经元, 从而减少冗余达到修剪的效果, 同样实现了减少耗能[11]. Jin等人通过迭代硬阈值方法来训练瘦深度神经网络(skinny deep neural networks, SDNNs), 实现了减少网络在训练过程中的能量消耗[12]. 2018年, 彩票假说(lottery ticket hypothesis, LTH)揭示了在密集型网络中存在子网络, 当对该子网络进行单独训练时, 其性能能够与密集型网络相匹配[13]. 除此之外, 也有研究从稀疏网络出发, 提出了在训练过程中 对网络结构进行调整以提高稀疏网络的性能[14].
近年来, 随着人工智能和类脑计算的发展, 人们对于人工神经网络的研究不再只是从数学计算出发, 而是试图将对大脑网络的研究和人工神经网络结合起来[15]. 随着影像技术和信息采集技术的发展, 人们对于大脑的网络结构和功能等方面有了进一步研究[16]. 研究表明, 大脑体积约占人体体积的2%, 其耗能占身体总耗能的20%左右, 其功率大约20 W[17]. 由此可见, 相比于计算机, 大脑在信息处理等方面具有更高的效率. 大脑的高效性与其网络连接特性密不可分, 所以, 结合大脑网络的连接特性, 训练更加高效节能的网络是实现网络高效性的一个重要方法.
1 大脑网络的连接特性近20年来, 随着复杂网络分析技术被广泛应用到社交网络、生物网络以及脑网络的研究中, 复杂网络的概念也逐渐被人们所熟知. 在对网络的研究中, 人们把个体表示为节点, 个体之间的关系或相互作用表示为边, 这些点和边共同构成了复杂网络. 然而在对脑网络的研究中, 人们通常将其分为结构网络和功能网络. 在大脑的结构网络中, 通常将神经元作为节点, 神经元之间的突触连接作为边对其进行研究. 而在大脑的功能网络中, 节点通常是大脑的某一个区域, 边一般指区域之间的关系或相互作用[18]. 20世纪末, 随着影像技术和信息采集技术的发展, 人们对大脑网络有了进一步的研究. 大量的研究表明, 大脑网络的连接表现出以下特性: 稀疏性、小世界特性、无标度特性以及在进化、成长发育过程中的动态连接特性.
1.1 大脑网络的稀疏性人类大脑消耗的能量与GPU相比要少很多, 但处理信息能力要高出约109倍, 大脑如此高效的一个重要原因是大脑网络的稀疏性[19]. 并且有研究发现, 当大脑中的神经元越多时, 其与其他神经元连接的比例会越小. 在成人大脑中大约有860亿个神经元以及约1015个突触, 其连接比例大约在10%左右, 所以大脑网络的连接是稀疏的.
1.2 大脑网络的小世界特性在许多生物网络、社交网络、交通网络中发现, 自然界中的很多网络并不是规则网络或完全随机的网络, 而是一种介于两种网络连接模式之间的具有特殊连接模式的网络. 1998年Watts等人提出了介于规则网络和随机网络之间的网络连接状态, 即小世界网络[20]. 科学家认为, 小世界网络所具备的局部的紧密连接和少量的长程连接特性有利于大脑以较低的连接和能量成本实现信息的高效整合与分离, 并且认为这是人脑在长期进化过程中在网络成本和效率平衡之后自然选择的结果.
1.3 大脑网络的无标度特性19世纪末20世纪初, 著名的经济学家Pareto在研究人群的收入统计特征时发现, 大约20%的人拥有80%的财富, 而剩下80%的人只占据着大约20%的财富, 因此提出了著名的“八二法则”. 而在真实的社交网络、交通网络、脑网络中单个节点的连接程度形成了一个分布, 对于大多数网络该分布呈现幂律衰减. 也就是说, 少数节点(Hub)拥有大量连接, 而大部分节点具有少量连接, 并将这种网络称为无标度网络[21].
在先前的研究中指出, 在结构层面, 由于突触连接数量的饱和效应, 皮层网络要么看起来不是无标度的, 要么表现出最大度数较低的无标度架构, 其对高度连接的Hub节点的出现起到阻碍作用[22]. 相反, 功能性大脑网络表现出幂律度分布以及小世界属性[23, 24]. 2005年, Humphries等人通过对脊椎动物大脑脑干的内侧网状结构 (RF)进行研究, 结果表明, 内侧RF可以看作是小世界网络, 但不是无标度类型的网络[25]. 而在关于功能连接的研究中, Eguiluze等人通过功能磁共振成像提取相关大脑部位的功能连接网络, 研究发现, 功能连接的分布以及连接的概率与距离的关系都是无标度的, 并且具有较小的特征路径长度和比随机网络高几个数量级的集聚系数[23]. 所以, 大脑的功能网络表现出无标度特性.
1.4 大脑网络的成长与发展大脑常常由于进化、个体发育、依赖经验的细化以及脑损伤或疾病而发生大脑网络结构的变化. 小世界网络[20]和无标度网络[21]的增长机制已经被提出, 但是由于生物系统中空间的有效性, 这种增长机制在生物神经网络中受到限制. 目前, 也有研究针对生物系统空间的有效性生成不同类型的小世界和无标度网络[26, 27]. 而在一些研究中, 提到了重连接的思想[28].
在生物神经网络中会有突触的修剪和重塑. 突触重塑是生物个体发育过程中神经环路的形成以及生物对生理或环境变化的适应过程中普遍存在的生物学现象[29]. 研究表明, 果蝇幼虫神经肌肉接头处的突触在成长过程中经历了剧烈而广泛的重塑, 以产生成年特异性突触. 而突触的修剪是在人成长过程中由于发育等因素必定会出现的一种现象, 它主要包括退化和消失. 一般来说, 皮层中的灰质体积在青春期之前会增加, 这反映了突触的生长, 但在青春期之后又会减少, 这反映了突触的修剪. 这种修剪很大程度上取决于环境影响并代表学习[30]. 人类从婴儿时期到成人时期, 大脑的尺寸会增长到原来的5倍, 其主要原因是神经元之间突触连接的增加, 以及神经纤维的髓鞘形成. 而随着年龄的增加, 突触连接老化, 一些连接被删除, 从而导致突触连接的体积再次减少. 除此之外, 突触连接还可能出现异常情况, 通常与疾病相关.
科学家认为, 生物神经网络之所以能够形成高效且节能的神经网络结构, 是经过生物进化而来的. 而在生物进化过程中, 必定伴随着由于适应周围环境而产生的网络结构的变化. 同时在先前的研究中也发现, 在成长发育过程中, 神经元之间的突触连接也在发生变化. 所以, 大脑网络结构是动态变化的, 其受到生长发育、进化、周围环境、衰老、病变以及学习等因素的影响.
2 训练高效网络算法为了实现高效节能的神经网络, 结合大脑网络的连接特性, 提出了训练高效神经网络的算法.
(1)大脑网络的稀疏性是大脑能够进行高效运转的重要原因之一, 所以提出了直接对稀疏的网络进行训练. 实验采用稀疏连接的LeNet-300-100网络[31], 网络结构如图1所示, 每一层神经元的数量分别为: nin=784、n1=300、n2=100、nout=10, 每一层神经元之间连接的比例分别为: P1、P2、Pout, 网络以随机的方式进行连接, 其所对应的参数量分别为: theta1= nin×n1×P1、theta2 = n1×n2×P2、thetaout = n2×nout×Pout.
(2)大脑网络中突触的连接并不是随机的, 每个神经元连接的神经元个数也存在差异, 即大脑网络的小世界特性和无标度特性. 小世界特性是指网络具有较高的集聚系数以及较低的平均路径长度[20], 无标度特性指网络中单个节点的连接程度形成无标度分布[21]. 也就是说, 在生物脑网络中, 单个节点的连接存在差异, 大多数节点有相对较少的连接, 而极少数的节点存在较多的连接. 在我们的实验中, 直接对稀疏网络进行训练时, 采用了随机连接的方法, 这种方法在理论上会使得每个节点的连接数所形成的分布是高斯分布, 并不是生物脑网络所呈现出来的无标度分布. 为进一步提高网络性能, 提出了对稀疏连接的神经网络进行结构约束, 即使得网络中神经元的度分布更接近生物脑网络中神经元之间连接的度分布, 从而训练高效的神经网络.

|
图 1 4层稀疏连接的网络 |
(3)大脑网络受到生长发育、进化、环境、衰老、疾病等因素的影响, 其网络结构处在变化之中. 结合大脑网络在成长发育过程中突触修剪与重塑的特点, 使得网络在训练过程中能够得到调整与约束, 即在训练过程中改变网络连接, 使其具备与大脑网络相似的连接特性, 从而训练高效的神经网络. 而在先前的研究中, Bellec等人提出在训练过程中改变网络连接以提高网络性能. 其原理是: 当对一个稀疏的网络进行训练时, 根据网络连接权重调整的幅度对网络的结构进行调整, 即在训练过程中某一个连接权重调整相对较大时, 则认为该连接需要进行重连, 随即删除该连接, 并且加入新的连接[14]. 该方法虽然应用到大脑网络成长与发展的特点, 但其在重连时也是随机选取, 同样会造成网络中神经元的度分布更加接近于高斯分布而不是与生物脑网络类似的无标度分布. 为了进一步提高网络性能, 提出了在重连接的过程中不再是随机选取连接, 而是有偏好地进行重连, 进而使网络结构具备生物脑网络的连接特性, 从而训练高效的神经网络.
3 实验分析分别对所提出的训练高效网络的算法进行实验分析, 网络结构示意图如图1所示. 该网络通过反向传播算法实现简单的分类任务, 并在MNIST数据集上对网络进行训练和测试. 在训练过程中使用随机梯度下降对网络进行优化, 并且设置batch_size=10, epoch=20, 初始学习率lr=0.1, 衰减率lr_decay= 0.8[6,14,32].
3.1 训练稀疏网络由于大脑网络的稀疏性是大脑能够进行高效运转的重要原因之一, 所以提出对一个稀疏连接的网络进行训练, 测试了不同稀疏度下网络的正确率. 并且, 定义网络的效率为Eta =Accuracy/Cost, 其中Accuracy为网络的正确率, Cost为稀疏网络与全连接网络的参数量之比, 即连接成本. 如图2所示, 当训练全连接网络时, 网络的正确率为98.44%, 随着网络连接成本的减少, 网络的正确率减少, 网络效率增加, 当网络的连接成本减少到一定程度时, 网络效率会达到最大值.

|
图 2 不同连接成本下稀疏网络的正确率和效率 |
3.2 训练连接异质性网络
在先前的研究中, 为了减少计算成本, 提出了对经过训练的网络进行剪枝, 然后对剪枝后的稀疏网络进行再训练[6]. 通过实验复现得到: 对训练后的网络进行剪枝再训练, 当剪掉约90%的边时, 网络的正确率依然能够保持与全连接网络的正确率相平, 即P1=0.1、P2=0.1、Pout=0.25时, 网络的正确率约98.31%. 该方法在减少计算成本的同时, 又确保了网络的正确率, 使网络更加高效. 但当直接对稀疏网络进行训练时, 发现在相同稀疏度下其正确率总是低于对网络进行剪枝再训练时的正确率. 所以, 对相同稀疏度的经过剪枝再训练的网络以及直接训练的稀疏网络进行了分析, 即当P1=0.1、P2=0.1、Pout=0.25时, 计算网络每一层中的每个神经元与下一层中的神经元连接的个数, 即出度, 并且计算了其度分布.
如图3所示, 实验结果表明, 经过剪枝再训练的网络, 每一层神经元的度存在差异, 其中第1层的神经元的度分布更是表现出类似于无标度网络的幂律分布, 而当对稀疏网络进行训练时, 其度分布更像是高斯分布. 并且在对复杂网络的研究中也明确指出, 现实生活中的很多网络都表现出了无标度特性. 所以, 我们将经过剪枝的网络的连接权重重新赋值, 并对其进行训练, 网络的正确率约97.76%. 该方法使得稀疏网络的连接更具有异质性, 其正确率要高于直接对稀疏网络进行训练, 但低于对网络进行再训练时的正确率.

|
图 3 直接对稀疏网络进行训练与对网络进行剪枝之后神经元的度分布 |
对网络进行剪枝再训练的方法, 虽然使得网络最终的计算成本降低了, 但要先对全连接网络进行训练, 然后再剪枝, 实际上增加了计算量, 而训练高效网络的最终目的是减少网络的计算成本. 直接训练低连接成本的网络是从根本减少网络计算成本的重要方法之一. 对训练集所含信息量, 即所有训练样本像素的均值与网络经过剪枝后第一层神经元的出度之间的关系进行了分析, 如图4所示, 第1层中的784个神经元的出度与输入像素的大小之间存在一定的相关性. 所以, 设置第1层神经元与下一层神经元的连接与输入像素的大小相关, 即当输入像素较高时该神经元被连接的概率较大. 实验结果表明, 当根据输入信号对网络的结构进行约束时, 网络的正确率比直接对稀疏网络进行训练时的正确率高约0.53%.
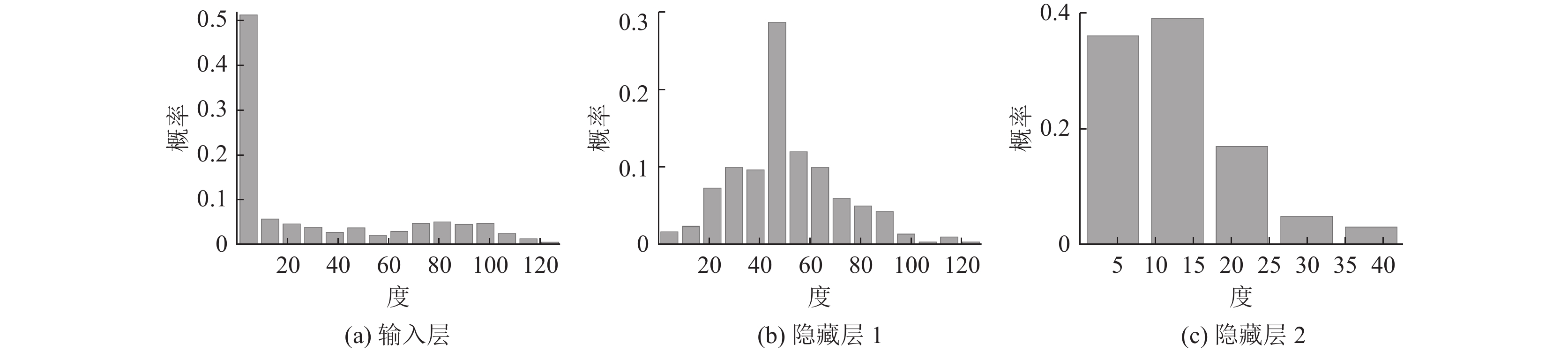
除此之外, 计算网络中每一层神经元与下一层神经元连接的个数, 并计算其度分布. 如图5所示, 当根据输入信号对网络的结构进行约束时, 输入层神经元出度的分布情况更接近于无标度分布, 而隐藏层神经元由于仍保持随机连接, 所以其度分布更接近于高斯分布.

|
图 4 经过剪枝的网络输入层神经元的度与输入像素 |
3.3 重连接算法
2017年, Bellec等人提出了Deep R算法, 该算法提出: 当对一个稀疏的网络进行训练时, 根据网络连接权重调整的幅度对网络的结构进行调整[14]. 通过实验复现得到, Deep R算法对稀疏网络的正确率提高了约0.02%. 然而, 根据无标度网络的增长机制——BA模型, 提出了不同于Deep R 的算法, 即在网络的训练过程中, 当某一个连接权重调整相对较大时, 则认为该连接应该被删除, 但加入新的连接时不再是随机选择, 而是本身连接比较多的神经元被连接的可能性会较大, 这会促使网络连接的异质性. 实验结果表明, 该方法使得网络的正确率与直接训练稀疏网络时的正确率相平. 对出现该结果的原因进行分析, 认为是在对网络进行初始化时, 神经元的度存在一定的异质性, 而我们并不能保证输入信号多的神经元能够连接更多的下一层神经元, 所以在训练过程中即使网络连接的异质性更加明显, 但也可能造成了输入信号的浪费, 从而使得网络的正确率相对较低. 出于这样的考虑, 在对网络进行初始化时, 仍然对网络的连接进行了约束, 使得输入信号越多的神经元与下一层神经元连接的可能性越大, 并且在训练的过程中根据权重的变化以及输入层神经元度的大小对网络连接进行剪枝和重连. 实验结果表明, 该方法使得网络的正确率比直接对稀疏网络进行训练时的正确率提高了约0.47%. 与此同时, 计算了3种方法下输入层和隐藏层神经元的度分布, 如图6所示, 结果表明, 当在初始化时对网络结构进行约束, 并且在训练过程中进行有偏好的重连时, 第1层神经元的度分布更接近于无标度网络的幂律分布.
|
图 5 根据输入信号对网络结构进行约束时神经元的度分布 |

|
图 6 3种方法下输入层和隐藏层神经元的度分布 |
表1是对本文所提出的提高网络效率的方法以及先前的一些方法的比较. 其中FC指训练全连接网络, SC指训练稀疏网络, Prune_Retrain指剪枝再训练, Prune_Init_Retrain指剪枝之后对权重重新赋值然后再训练, SC_Input指根据输入对稀疏网络的结构进行约束并训练, Deep R指重连接算法, BA_Deep R指结合生成无标度网络的规则—BA模型, 进行网络重连接, SC_Input+BA_Deep R则是两种方法的结合.
| 表 1 方法性能比较 (%) |
如表1所示, 根据输入信号对网络的结构进行约束时, 网络的效率提高更加明显, 其次是在此基础上结合BA算法对网络进行重连接的方法. 虽然先前所提出的对网络进行剪枝再训练的方法在正确率上要稍高于本文所提出的方法, 但其需要先对全连接网络进行训练, 而本文所提出的方法则只需要对稀疏网络进行训练. 结合大脑网络的连接特性以及剪枝后网络的结构特征, 通过改变稀疏网络的结构来提高稀疏网络的正确率, 从而提高了网络的效率. 先前所提出的Deep R算法也是直接对稀疏网络进行训练, 但本文所提出的方法在相同参数下正确率要略高于Deep R算法. 其次, 记录了不同方法在训练过程中正确率的变化情况. 如图7所示, 根据输入信号对网络的结构进行约束的方法(SC_input)以及在此基础上结合BA算法对网络进行重连接的方法(SC_input+BA_Deep R)使得网络在训练过程中能够以更短时间达到正确率的稳定, 并且使得网络在训练过程中正确率的变化情况也更加接近训练全连接网络时正确率的变化. 所以, 根据大脑网络的连接特性对人工神经网络的结构进行约束时, 网络的效率得到很大程度的提高.
4 结论与展望基于大脑网络的连接特性, 本文提出了训练更加高效的网络的方法, 在保证网络性能的同时减少了网络的计算成本. 本文通过对网络结构进行改变, 从而实现了网络的稀疏性、动态连接特性、以及无标度特性, 进而提高了网络的正确率. 本文所提出的训练高效网络的方法只是在简单的多层网络中进行了测试, 而将其应用到像AlexNet、GoogLeNet等更为复杂的神经网络将会是我们需要进一步研究的内容. 其次, 对于训练更加高效的神经网络这一课题, 起源于脑科学, 被称为第三代人工神经网络的脉冲神经网络(spiking neural network, SNN)由于其事件驱动的特点, 具有低能耗的优点[33]. 并且在近年来也有研究提出对SNN进行剪枝, 训练更加高效的神经网络, 这也将会是在未来的研究中值得深入的方向[34].

|
图 7 训练过程中网络正确率的变化 |
| [1] |
毛健, 赵红东, 姚婧婧. 人工神经网络的发展及应用. 电子设计工程, 2011, 19(24): 62-65. DOI:10.3969/j.issn.1674-6236.2011.24.022 |
| [2] |
McCulloch WS, Pitts W. A logical calculus of the ideas immanent in nervous activity. The Bulletin of Mathematical Biophysics, 1943, 5(4): 115-133. DOI:10.1007/BF02478259 |
| [3] |
Hinton G, Vinyals O, Dean J. Distilling the knowledge in a neural network. arXiv:1503.02531, 2015.
|
| [4] |
Li H. Exploring knowledge distillation of deep neural nets for efficient hardware solutions. Technical Report, Stanford: University of Stanford, 2018.
|
| [5] |
Park W, Kim D, Lu Y, et al. Relational knowledge distillation. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach: IEEE, 2019. 3962–3971.
|
| [6] |
Han S, Pool J, Tran J, et al. Learning both weights and connections for efficient neural network. Proceedings of the 28th International Conference on Neural Information Processing Systems. Montreal: MIT Press, 2015. 1135–1143.
|
| [7] |
Liang TL, Glossner J, Wang L, et al. Pruning and quantization for deep neural network acceleration: A survey. Neurocomputing, 2021, 461: 370-403. DOI:10.1016/j.neucom.2021.07.045 |
| [8] |
Liu Z, Sun MJ, Zhou TH, et al. Rethinking the value of network pruning. Proceedings of the 7th International Conference on Learning Representations. New Orleans: ICLR, 2019. 1–21.
|
| [9] |
Ponnapalli PVS, Ho KC, Thomson M. A formal selection and pruning algorithm for feedforward artificial neural network optimization. IEEE Transactions on Neural Networks, 1999, 10(4): 964-968. DOI:10.1109/72.774273 |
| [10] |
Collins MD, Kohli P. Memory bounded deep convolutional networks. arXiv:1412.1442, 2014.
|
| [11] |
Srinivas S, Babu RV. Data-free parameter pruning for deep neural networks. Proceedings of the British Machine Vision Conference 2015. Swansea: BMVC, 2015. 31.1–31.12.
|
| [12] |
Jin XJ, Yuan XT, Feng JS, et al. Training skinny deep neural networks with iterative hard thresholding methods. arXiv:1607.05423, 2016.
|
| [13] |
Frankle J, Carbin M. The lottery ticket hypothesis: Finding sparse, trainable neural networks. Proceedings of the 7th International Conference on Learning Representations. New Orleans: ICLR, 2018. 1–42.
|
| [14] |
Bellec G, Kappel D, Maass W, et al. Deep rewiring: Training very sparse deep networks. Proceedings of the 6th International Conference on Learning Representations. Vancouver: ICLR, 2017. 1–24.
|
| [15] |
沈静. 基于小世界拓扑的神经网络研究与应用[硕士学位论文]. 北京: 北京邮电大学, 2021.
|
| [16] |
蒲慕明, 徐波, 谭铁牛. 脑科学与类脑研究概述. 中国科学院院刊, 2016, 31(7): 725-736. DOI:10.16418/j.issn.1000-3045.2016.07.001 |
| [17] |
刘永. 人体的奇异能力. 百科知识, 2006(21): 29-30. |
| [18] |
汪小帆, 李翔, 陈关荣. 复杂网络理论及其应用. 北京: 清华大学出版社, 2006.
|
| [19] |
张秋玥, Luciana, 钱天培. 稀疏学习: 从人脑得到灵感, 让深度学习突破算力限制. https://baijiahao.baidu.com/s?id=1641099255924772685&wfr=spider&for=pc.2019. (2019-08-06).
|
| [20] |
Watts DJ, Strogatz SH. Collective dynamics of ‘small-world’ networks. Nature, 1998, 393(6684): 440-442. DOI:10.1038/30918 |
| [21] |
Barabási AL, Albert R. Emergence of scaling in random networks. Science, 1999, 286(5439): 509-512. DOI:10.1126/science.286.5439.509 |
| [22] |
Sporns O, Zwi JD. The small world of the cerebral cortex. Neuroinformatics, 2004, 2(2): 145-162. DOI:10.1385/NI:2:2:145 |
| [23] |
Eguiluz VM, Chialvo DR, Cecchi GA, et al. Scale-free brain functional networks. Physical Review Letters, 2005, 94(1): 018102. DOI:10.1103/PhysRevLett.94.018102 |
| [24] |
Sporns O, Chialvo DR, Kaiser M, et al. Organization, development and function of complex brain networks. Trends in Cognitive Sciences, 2004, 8(9): 418-425. DOI:10.1016/j.tics.2004.07.008 |
| [25] |
Humphries MD, Gurney K, Prescott TJ. The brainstem reticular formation is a small-world, not scale-free, network. Proceedings of the Royal Society B: Biological Sciences, 2006, 273(1585): 503-511. DOI:10.1098/rspb.2005.3354 |
| [26] |
Kaiser M, Hilgetag CC. Spatial growth of real-world networks. Physical Review E, 2004, 69(3): 036103. DOI:10.1103/PhysRevE.69.036103 |
| [27] |
Kaiser M, Hilgetag CC. Modelling the development of cortical systems networks. Neurocomputing, 2004, 58–60: 297–302.
|
| [28] |
Sur M, Leamey CA. Development and plasticity of cortical areas and networks. Nature Reviews Neuroscience, 2001, 2(4): 251-262. DOI:10.1038/35067562 |
| [29] |
Liu ZW, Chen Y, Wang D, et al. Distinct presynaptic and postsynaptic dismantling processes of Drosophila neuromuscular junctions during metamorphosis. Journal of Neuroscience, 2010, 30(35): 11624-11634. DOI:10.1523/JNEUROSCI.0410-10.2010 |
| [30] |
Craik FIM, Bialystok E. Cognition through the lifespan: Mechanisms of change. Trends in Cognitive Sciences, 2006, 10(3): 131-138. DOI:10.1016/j.tics.2006.01.007 |
| [31] |
LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 |
| [32] |
Feng YX, Li YM. An overview of deep learning optimization methods and learning rate attenuation methods. Hans Journal of Data Mining, 2018, 8(4): 186-200. DOI:10.12677/HJDM.2018.84020 |
| [33] |
Maass W. Networks of spiking neurons: The third generation of neural network models. Neural Networks, 1997, 10(9): 1659-1671. DOI:10.1016/S0893-6080(97)00011-7 |
| [34] |
Kim Y, Li YH, Park H, et al. Lottery ticket hypothesis for spiking neural networks. arXiv:2207.01382, 2022.
|
 2023, Vol. 32
2023, Vol. 32



