早期目标跟踪通常假设每个目标在给定的时间步长最多可以产生一个量测值^[1]. 利用现代更精确的传感器, 目标可能占据传感器的多个分辨单元, 从而在给定时间步长产生多个量测, 这些目标被称为扩展目标^[2]. 扩展目标跟踪的应用包括使用汽车雷达的车辆跟踪、使用地面或者海上雷达站跟踪足够近的飞机或者船舶等.

Mahler首先将随机有限集 (random finite set, RFS) 引入到扩展目标跟踪^[3], 将扩展目标状态集和量测数据集均建模为随机有限集, 避免了数据关联问题. Koch提出利用对称正定的随机矩阵 (random matrix, RM) 方法将目标外形建模成椭圆^[4], 并首次将贝叶斯方法应用于椭圆外形的扩展目标跟踪, 在忽略传感器误差的假设条件下给出贝叶斯估计的封闭形式解. 文献[5]首先将该方法用于概率假设密度(probability hypothesis density, PHD)滤波器, 提出了基于随机矩阵的扩展目标高斯逆威沙特概率假设密度 (Gaussian inverse Wishart-probability hypothesis density, GIW-PHD) 滤波器, 实现对扩展目标的运动学特征和外形状态估计. 文献[6]将扩展目标量测比建模为伽玛分布, 提出能够实时估计目标量测比率与扩展目标状态的伽玛高斯逆威沙特 (gamma Gaussian inverse Wishart, GGIW) 模型, 文献[7]将GGIW模型应用于扩展目标多伯努利 (multi-Bernoulli, MB) 滤波器. 针对上述滤波器未能直接形成目标轨迹的问题, 文献[8]将广义标签多伯努利算法应用于扩展目标跟踪, 并将目标状态建模为GGIW分布, 通过标签追溯目标的运动轨迹. Granström等人提出了泊松多伯努利混合 (Poisson multi-Bernoulli mixture, PMBM) 算法, 并在扩展目标跟踪中取得比 $ \delta $ -GLMB算法更好的滤波性能^{[9, 10]}, 文献[11]对PMBM算法做出改进, 提出一种泊松多伯努利(Poisson multi-Bernoulli, PMB)算法, 该算法假设目标状态服从GGIW分布, 将描述后验分布的多个伯努利混合近似为单个伯努利以减少计算量, 维持稳定的滤波性能.

衍生是扩展目标的重要运动方式, 在军事的体现有战斗机发射导弹、飞机在航母上起飞等. 文献[12]首先提出了扩展目标衍生的研究工作, 基于随机矩阵提出了一种衍生目标状态期望值与原始目标状态期望值相同的衍生模型, 衍生目标的扩展也保持了原始目标扩展的预期值. 当原始目标的外形尺寸与衍生出的目标尺寸不一致时, 这样的简单衍生模型并不适用. 针对该问题, 文献[13]提出多假设模型, 考虑了衍生目标的合理备选方案, 并验证所提的模型提高了GGIW-PHD滤波器对衍生扩展目标的跟踪性能. 之后将学者们多假设模型结合CPHD、 $ \delta $ -GLMB和PMBM等滤波器开展了一系列的研究工作^[14-16], 提高了滤波器对衍生目标的跟踪性能.

本文在文献[11]的基础上, 提出一种改进的GGIW-PMB滤波算法. 在滤波算法的预测阶段利用多假设模型^[12]对衍生事件建模, 根据给定的假设值, 产生多个衍生假设分量, 将衍生分量建模为GGIW形式, 最后在PMB滤波框架下利用量测数据对每个假设分量更新, 实现原始目标和衍生目标的有效跟踪, 增强算法的适用性.

1 扩展目标模型

假设在 $ k $ 时刻扩展目标状态为:

$ {X_k} = \left\{ {\xi _k^i = \left( {\gamma _k^i, x_k^i, X_k^i} \right)} \right\}_{i = 1}^{{N_{x, k}}} $

(1)

其中, $ {N_{x, k}} $ 表示 $ k $ 时刻目标的数量, $ \gamma _k^i $ 表示第 $ i $ 个目标 $ k $ 时刻的泊松均值, $ x_k^i $ 表示第 $ i $ 个目标的运动学状态, 例如目标的位置、速度等其他参数, $ X_k^i $ 表示第 $ i $ 个目标的外形及尺寸.

目标运动模型为:

$ x_{k + 1}^i = ({F_{k + 1|k}} \otimes {I_d})x_k^i + \varpi _{k + 1}^i $

(2)

其中, $ {F_{k + 1|k}} $ 为状态转移矩阵, $ \varpi _{k + 1}^i $ 为协方差为 $ {Q_{k + 1|k}} \otimes X_{k + 1}^i $ 的零均值高斯白噪声.

假设 $ {{\textit{z}}_x} = \left\{ {{\textit{z}}_k^j} \right\}_{j = 1}^{{N_{{\textit{z}}, k}}} $ 为 $ k $ 时刻扩展目标的量测集, 则量测模型可表示为:

$ {\textit{z}}_k^j = \left( {{H_k} \otimes {I_d}} \right)x_k^i + e_k^j $

(3)

其中, $ e_k^j $ 是协方差为 $ X_k^j $ 的高斯白噪声, $ {H_k} $ 为量测矩阵. $ k $ 时刻的量测集合包括目标产生的量测和杂波产生的量测, 且表示为两者的并集:

$ {Z_k} = {{\textit{z}}_x}({\textit{z}}) \cup {{\textit{z}}_c}({\textit{z}}) $

(4)

其中, $ {{\textit{z}}_c}({\textit{z}}) $ 表示杂波量测.

假设 $ k $ 时刻, $ {\gamma _k} \sim GAM\left( {{\gamma _k}, {\alpha _k}, {\beta _k}} \right) $ 表示泊松分布的均值; $ {x_k} \sim N\left( {{x_k};{m_k}, {P_k} \otimes {X_k}} \right) $ 表示目标质心的运动状态; $ {X_k} \sim IW({X_k};{v_k}, {V_k}) $ 表示目标的扩展状态. 令 $ {Z^k} = \{ {Z_1}, \cdots , {Z_k} \} $ 代表直到 $ k $ 时刻所有量测的集合, 假设扩展目标状态估计服从GGIW分布:

$ \begin{split} p\left( {{\xi _k}} \right) =& GAM\left( {{\gamma _k};{\alpha _k}, {\beta _k}} \right)N\left( {{x_k};{m_k}, {P_k} \otimes {X_k}} \right) \cdot IW\left( {{X_k};{v_k}, {V_k}} \right)\\ =& GGIW\left( {{\xi _k}, {\zeta _k}} \right) \end{split} $

(5)

其中, $ {\xi _k} \triangleq \left( {{\gamma _k}, x, {X_k}} \right) $ 为 $ k $ 时刻扩展目标的待估计状态; $ {\zeta _k} = \left( {{\alpha _k}, {\beta _k}, {m_k}, {P_k}, {v_k}, {V_k}} \right) $ 为GGIW分量的参数.

2 PMB滤波器

PMB分为泊松点过程(Poisson point process, PPP)部分和多伯努利(MB)部分, 其中PPP部分表示目标存在但未被传感器检测到的目标, 由符号 $ {X^u} $ 表示; MB部分表示多目标演化过程中存在并被传感器检测到的目标的分布情况, 由符号 $ {X^d} $ , 且 $ X = {X^u} \cup {X^d} $ , $ {X^u} \cap {X^d} = \phi $ .

假设 $ k - 1 $ 时刻的后验PMB密度参数为:

$ {D^u}, {\left( {{r^i}, {f^i}\left( \cdot \right)} \right)_{i \in {\mathbb I}}} $

(6)

则 $ k $ 时刻的预测PMB密度参数为:

$ D_{k|k - 1}^u, {\left( {r_{k|k - 1}^i, f_{k|k - 1}^i\left( \cdot \right)} \right)_{i \in {\mathbb I}}} $

(7)

其中,

$ D_{k|k - 1}^u\left( X \right) = {D^b}\left( X \right) + \left\langle {{D^u}, {p_s}{f_{k|k - 1}}} \right\rangle $

(8)

$ r_{k|k - 1}^i = \left\langle {{f^i}, {p_s}} \right\rangle {r^i} $

(9)

$ f_{k|k - 1}^i = \frac{{\left\langle {{f^i}, {p_s}{f_{k|k - 1}}} \right\rangle }}{{\left\langle {{f^i}, {p_s}} \right\rangle }} $

(10)

其中, $ r $ 为伯努利分量的权重, $ {f^i}\left( \cdot \right) $ 表示第 $ i $ 个伯努利的密度函数, $ f\left( \cdot \right) $ 为状态转移模型, $ {D^b} $ 代表泊松点过程新生强度.

假设给出预测步的PMB密度参数如式(7)和量测集合 $ {Z^k} $ , 将预测步得到的PMB密度进行更新, 得到的后验为PMBM形式, 其参数为:

$ \hat D_{k|k}^u, {\left\{ {\left( {W_{k|k}^j, {{\left\{ {\left( {\hat r_{k|k}^{j, i}, \hat f_{k|k}^{j, i}} \right)} \right\}}_{i \in {\mathbb I}}}} \right)} \right\}_{j \in \mathbb J}} $

(11)

其中, PPP部分的更新为:

$ {D^u}\left( {X} \right) = \left( {1 - {p_D}} \right)D_{k|k - 1}^u\left( {X} \right) $

(12)

$ {p_D} $ 表示独立于目标状态的检测概率.

对于之前存在的目标, 每个单目标假设可能包含误检的目标, 或者使用量测更新的目标. 对于误检的目标, 伯努利密度参数为:

$ {r^{i, j}} = \frac{{r_{k|k - 1}^i\left\langle {f_{k|k - 1}^i, \left( {1 - {p_D}} \right)} \right\rangle }}{{1 - r_{k|k - 1}^i + r_{k|k - 1}^i\left\langle {f_{k|k - 1}^i, {p_D}} \right\rangle }} $

(13)

$ {f^{j, i}}\left( {X} \right) = \frac{{\left( {1 - {p_D}} \right)\left( {X} \right)f_{k|k - 1}^i\left( {X} \right)}}{{\left\langle {f_{k|k - 1}^i, \left( {1 - {p_D}} \right)} \right\rangle }} $

(14)

其中, 单目标假设的更新轨迹对应的伯努利参数为:

$ {r^{j, i}} = 1 $

(15)

$ {f^{j, i}}\left( {X} \right) = \frac{{l\left( {X} \right)f_{k|k - 1}^i\left( {X} \right)}}{{\left\langle {f_{k|k - 1}^i, l\left( {X} \right)} \right\rangle }} $

(16)

其中, $ l\left( {X} \right) $ 为单个伯努利分量的似然函数, $ {r^{j, i}}\left( \cdot \right) $ 表示第 $ j $ 个多伯努利中第 $ i $ 个伯努利的存在概率, $ {f^{j, i}}\left( \cdot \right) $ 表示第 $ j $ 个多伯努利中第 $ i $ 个伯努利的密度函数.

为了减少多伯努利的数量, 需要从PMBM滤波器中获得保留尽可能多信息的PMB滤波器, 实现该滤波器需要最小化PMBM与PMB之间的KL散度^[11], 将多伯努利混合部分近似为单个伯努利分量来处理, 即:

$ \arg \mathop {\min }\limits_f {D_{KL}}\left( {{f_{k|k}}\left( {{X_k}} \right)\parallel {{\hat f}_{k|k}}\left( {{X_k}} \right)} \right) $

(17)

其中, $ {\hat f_{k|k}}\left( {{X_k}} \right) $ 被限制为PMB, 则更新后的PMB密度参数为:

$ D_{k|k}^u, {\left( {\hat r_{k|k}^i, \hat f_{k|k}^i} \right)_{i \in {\mathbb I}}} $

(18)

其中, $ D_{k|k}^u $ 表示PPP部分的强度, $ \hat r_{k|k}^i $ 表示第 $ i $ 个伯努利存在概率, $ \hat f_{k|k}^i $ 表示第 $ i $ 个伯努利密度.

3 改进的GGIW-PMB滤波算法

假设在 $ k - 1 $ 时刻, 后验密度函数是GGIW混合的形式:

$ D_{k - 1}^u(X) = \sum\limits_{n = 1}^{{N^u}} {\omega _{k - 1}^{u, n}} GGIW\left( {X;\zeta _{k - 1}^{u, n}} \right) $

(19)

其中, $ \zeta _{k - 1}^{u, n} = \left\{ {{\alpha _{k - 1}}, {\beta _{k - 1}}, {m_{k - 1}}, {P_{k - 1}}, {v_{k - 1}}, {V_{k - 1}}} \right\} $ , $ \omega _{k - 1}^{u, n} $ 表示GGIW分量的权重, 第 $ i $ 个伯努利分量也是GGIW的形式:

$ f_{k - 1}^i = GGIW\left( {X;\zeta _{k - 1}^i} \right) $

(20)

● 预测. 若有衍生事件发生, 则需要考虑原目标和衍生目标的预测, 所以预测阶段包括未发生衍生事件分量的预测和衍生分量的预测两部分. $ k $ 时刻未发生衍生事件的GGIW分量的预测过程为:

$ \begin{split} D_{k|k - 1}^u\left( X \right) =& \sum\limits_{n = 1}^{{N^b}} {\omega _k^{b, n}} GGIW\left( {X;\zeta _k^{b, n}} \right) \\ & + \sum\limits_{n = 1}^{{N^u}} {\omega _{k|k - 1}^{u, n}} GGIW\left( {X;\zeta _{k|k - 1}^{u, n}} \right) \end{split} $

(21)

$ \omega _{k|k - 1}^{u, n} = \omega _{k - 1}^{u, n}{p_S} $

(22)

$ r_{NT, k|k - 1}^i = {p_S}r_{k - 1}^i $

(23)

$ f_{NT, k|k - 1}^i\left( X \right) = GGIW\left( {X;\zeta _{k|k - 1}^i} \right) $

(24)

其中, $ \omega _k^{b, n} $ 为新生目标的权重, $ \zeta _k^{b, n} $ 新生目标的GGIW分量, $ {p_S} $ 表示目标的存活概率, 其中GGIW分量参数的计算如下:

$ \left\{ \begin{gathered} {\alpha _{k|k - 1}} = \frac{{{\alpha _{k - 1}}}}{\eta } \\ {\beta _{k|k - 1}} = \frac{{{\beta _{k - 1}}}}{\eta } \\ {m_{k|k - 1}} = F{m_{k - 1}} \\ {P_{k|k - 1}} = F{P_{k - 1}}{F^{\rm{T}}} + Q \\ {v_{k|k - 1}} = 2d + 2 + {{\rm{e}}^{ - {T_s}/\tau }}\left( {v - 2d - 2} \right) \\ {V_{k|k - 1}} = {{\rm{e}}^{ - {T_s}/\tau }}M{V_{k - 1}}{M^{\rm{T}}} \\ \end{gathered} \right. $

(25)

其中, $ M $ 为转化矩阵, $ {T_s} $ 采样时间, $ \tau $ 为运动相关常数, $ \eta $ 为量测率参数.

假设衍生事件发生在量测产生之间, 即在扩展目标跟踪滤波的预测步骤中, 且每个目标在每个时刻只产生一个衍生目标. 由于衍生目标相对于原目标的运动状态发生了变化, 若直接忽略对衍生目标的预测, 将会导致在衍生时刻无法检测跟踪到衍生目标, 对于该问题本文利用多假设模型对衍生目标建模, 在预测阶段根据给定的衍生假设值, 产生多个假设的衍生先验信息, 其中每个假设代表一个可能的衍生事件, 即假设衍生事件发生在 $ k $ 时刻, 未发生衍生事件的GGIW分量参数如式(25), 则衍生目标状态为:

$ \xi _{t, k|k - 1}^{\left( {l, \kappa } \right)} = \left\{ {\gamma _{k|k - 1}^{(t)}, x_{k|k - 1}^{(t)}, X_{k|k - 1}^{(t)}} \right\}_{t = 1}^2, \; l = 1, 2, \cdots , d $

(26)

其中, $ \kappa $ 为衍生假设值, $ d $ 为扩展目标的外形维度. 然后将衍生目标状态建模成GGIW形式, 假设 $ \zeta _{1, k|k - 1}^{\left( {l, \kappa } \right)} $ 和 $ \zeta _{2, k|k - 1}^{\left( {l, \kappa } \right)} $ 分别为给定每一个衍生假设值 $ \kappa $ 和每个扩展状态维度 $ l $ 对应的衍生估计对的GGIW分量, 参数计算如下:

$ \zeta _{k|k - 1}^{\left( {1, l, \kappa } \right)} = \left( {{\alpha _{k|k - 1}}, \frac{{{\beta _{k|k - 1}}}}{\kappa }, m_{k|k - 1}^{\left( {1, l, \kappa } \right)}, P_{k|k - 1}^{\left( {1, l, \kappa } \right)}, v_{k|k - 1}^{\left( {l, \kappa } \right)}, \kappa V_{k|k - 1}^{\left( {l, \kappa } \right)}} \right) $

(27)

$ \begin{split} & \zeta _{k|k - 1}^{\left( {2, l, \kappa } \right)} = \\ & \left( {{\alpha _{k|k - 1}}, \frac{{{\beta _{k|k - 1}}}}{\kappa }, m_{k|k - 1}^{\left( {2, l, \kappa } \right)}, P_{k|k - 1}^{\left( {2, l, \kappa } \right)}, v_{k|k - 1}^{\left( {l, \kappa } \right)}, (1 - \kappa )V_{k|k - 1}^{\left( {l, \kappa } \right)}} \right) \end{split} $

(28)

其中,

$ m_{k|k - 1}^{\left( {1, l, k} \right)} = {m_{k|k - 1}} + \left( {1 - \kappa } \right)\sqrt {{e_l}} {H^{\rm{T}}}{v_l} $

(29)

$ m_{k|k - 1}^{\left( {2, l, \kappa } \right)} = {m_{k|k - 1}} - \kappa \sqrt {{e_l}} {H^{\rm{T}}}{v_l} $

(30)

$ P_{k|k - 1}^{\left( {i, l, \kappa } \right)} = {P_{k|k - 1}} , i = 1, 2 $

(31)

假设有 $ K $ 个不同的衍生假设值 $ \kappa $ , 则在预测阶段将产生 $ 2dK $ 个不同的GGIW假设分量. 由同一目标衍生出的两个目标是相关的, 而由不同目标衍生出的两个目标是相互独立的. 基于KL-DIV准则对衍生分量的联合密度分布作近似^[15]:

$ r_{T, k|k - 1}^i = {p_S}{\omega _{sp}}r_{k - 1}^i $

(32)

$ \bar f_T^i({X_{1:2, k, k - 1}}) \triangleq \bar f_T^i({X_{1, k|k - 1}}, {X_{2, k|k - 1}}) $

(33)

$ \begin{split} \bar f_T^i\left( {{X_{1:2, k|k - 1}}} \right) \approx &\sum\limits_{l = 1}^d {\delta \left( l \right)} GGIW\left( {X_{1, k|k - 1}^{\left( {l, \kappa } \right)};\zeta _{1, k|k - 1}^{\left( {l, \kappa } \right)}} \right) \\ &\times GGIW\left( {X_{2, k|k - 1}^{\left( {l, \kappa } \right)};\zeta _{2, k|k - 1}^{\left( {l, \kappa } \right)}} \right) \\ = &\sum\limits_{l = 1}^d {\delta \left( l \right)} \prod\limits_{t = 1}^2 {f_T^i} \left( {X_{t, k|k - 1}^{\left( {i, \kappa } \right)}} \right) \end{split} $

(34)

其中, $ \bar f_T^i\left( {{X_{1:2, k|k - 1}}} \right) $ 是联合概率密度, $ {\omega _{sp}} $ 为衍生权重, 结合未发生衍生事件分量的PMB密度 $ f_{NT}^i $ , 因此可得到近似的预测PMB密度形式:

$ D_{k|k - 1}^u, {\left( {\hat r_{k|k - 1}^i, \hat f_{k|k - 1}^i} \right)_{i \in {\mathbb I}}} $

(35)

$ \left( {\hat r_{k|k - 1}^i, \hat f_{k|k - 1}^i} \right) = \left\{ {\left( {r_{NT, k|k - 1}^i, f_{NT, k|k - 1}^i} \right), \left( {r_{T, k|k - 1}^i, f_{T, k|k - 1}^i} \right)} \right\} $

(36)

● 更新. 假设给出如式(5)的预测PMB密度分布, 更新阶段的概率密度由以下4个部分组成.

(1) PPP漏检

$ \begin{split} & {D^u}\left( {X} \right) = \\ & \sum\nolimits_{n = 1}^{{N^u}} {\left( {\omega _1^{u, n}{GGIW}\left( {{X;}\zeta _1^{u, n}} \right) + \omega _2^{u, n}{GGIW}\left( {{X;}\zeta _2^{u, n}} \right)} \right)} \end{split} $

(37)

其中,

$ \omega _1^{u, n} = (1 - {p_D})\omega _{k|k - 1}^{u, n} $

(38)

$ \omega _2^{u, n} = {p_D}{\left( {\frac{{\beta _{k|k - 1}^{u, n}}}{{\beta _{k|k - 1}^{u, n} + 1}}} \right)^{\alpha _{k|k - 1}^{u, n}}}\omega _{k|k - 1}^{u, n} $

(39)

$ \zeta _1^{u, n} = \zeta _{k|k - 1}^{u, n} $

(40)

$ \zeta _2^{u, n} = \left\{ {\alpha _{k|k - 1}^{u, n}, \beta _{k|k - 1}^{u, n} + 1, m_{k|k - 1}^{u, n}, P_{k|k - 1}^{u, n}, v_{k|k - 1}^{u, n}, V_{k|k - 1}^{u, n}} \right\} $

(41)

(2) PPP更新

根据文献[17]的距离划分方法对量测集 $ {Z^k} $ 划分, 得到划分后的量测单元 $ C $ , PPP部分的更新如下:

$ r_C^u = \left\{ \begin{gathered} 1, \qquad\quad\;\;\;\; {\rm{if}} \; |C| > 1 \\ \frac{{{L_C}}}{{{\kappa ^C} + {L_C}}},\quad {\rm{if}} \; |C| = 1 \\ \end{gathered} \right. $

(42)

$ f_C^u\left( {X} \right) = \frac{{\displaystyle\sum\nolimits_{n = 1}^{{N^u}} {\omega _{k|k - 1}^{u, n}{p_D}L_C^{u, n}{GGIW}\left( {{X;}\zeta _C^{u, n}} \right)} }}{{\displaystyle\sum\limits_{n = 1}^{N{}^u} {\omega _{k|k - 1}^{u, n}{p_D}L_C^{u, n}} }} $

(43)

$ L_C^u = \sum\limits_{n = 1}^{{N^u}} {\omega _{k|k - 1}^{u, n}{p_D}l_C^{u, n}} $

(44)

其中, $ {\kappa ^C} = \lambda c({\textit{z}}) $ 表示杂波强度, 其中 $ \lambda $ 为杂波率, $ c({\textit{z}}) $ 为杂波空间分布; $ \zeta _C^{u, n} $ 和 $ l_C^{u, n} $ 的具体计算见文献[9].

(3) MBM漏检

$ r_\phi ^{j, i} = \frac{{r_{k|k - 1}^iq_D^i}}{{1 - r_{k|k - 1}^i + r_{k|k - 1}^iq_D^i}} $

(45)

$ f_\phi ^{j, i}\left( {X} \right) = \omega _1^i{GGIW}\left( {{X;}\zeta _1^i} \right) + \omega _2^i{GGIW}\left( {{X;}\zeta _2^i} \right) $

(46)

$ L_\phi ^{j, i} = 1 - r_{k|k - 1}^i + r_{k|k - 1}^iq_D^i $

(47)

其中,

$ q_D^i = 1 - p_D^i + p_D^i{\left( {\frac{{\beta _{k|k - 1}^i}}{{\beta _{k|k - 1}^i + 1}}} \right)^{\alpha _{k|k - 1}^i}} $

(48)

$ \omega _1^i = {\left( {q_D^i} \right)^{ - 1}}\left( {1 - {p_D}} \right) $

(49)

$ \omega _2^i = {\left( {q_D^i} \right)^{ - 1}}p_D^i{\left( {\frac{{\beta _{k|k - 1}^i}}{{\beta _{k|k - 1}^i + 1}}} \right)^{\alpha _{k|k - 1}^i}} $

(50)

$ \zeta _1^i = \zeta _{k|k - 1}^i $

(51)

$ \zeta _2^i = \left\{ {\alpha _{k|k{\text{ - }}1}^i, \beta _{k|k - 1}^i + 1, m_{k|k - 1}^i, P_{k|k - 1}^i, v_{k|k - 1}^i, V_{k|k - 1}^i} \right\} $

(52)

(4) MBM更新

$ r_C^{j, i} = 1 $

(53)

$ f_C^{j, i}\left( {X} \right) = {GGIW}\left( {{X;}\zeta _C^{j, i}} \right) $

(54)

$ L_C^{j, i} = r_{k|k - 1}^i{p_D}l_C^{j, i} $

(55)

PMB滤波器的更新步骤与PMBM滤波器类似, 详细的GGIW更新过程的参数计算参考文献[9].

4 实验仿真

在区域 $[ - 200 \; {\rm{m}}, 200 \; {\rm{m}}] \times [ - 200 \; {\rm{m}}, 200 \; {\rm{m}}]$ 内, 对4个目标进行跟踪, 时间采样间隔设置为 $ T = 1 \; {\rm{s}} $ , 时间步长为100 s. 杂波数目服从杂波率 $ \lambda $ 为60的泊松分布且杂波在监测范围内服从均匀分布. 扩展目标的外形状态为 ${X_k} = {R_k}{\rm{diag}}([{A^2}, {a^2}])$ , 其中 $ {R_k} $ 表示转移矩阵, $ A $ 和 $ a $ 分别表示椭圆外形的长轴和短轴.

初始的两个目标及其各自的衍生目标参数设置如下:

$\left\{ {\begin{array}{l} {A_1} = 0.8, {a_1} = 1, {\gamma _1} = 10, {t_{b, 1}} = 1, {t_{d, 1}} = 100\\ {A_2} = 0.8, {a_2} = 0.5, {\gamma _2} = 5, {t_{b, 2}} = 51, {t_{d, 2}} = 90\\ {A_3} = 0.8, {a_3} = 1, {\gamma _3} = 10, {t_{b, 3}} = 4, {t_{d, 3}} = 100 \\ {A_4} = 0.8, {a_4} = 0.5, {\gamma _4} = 5, {t_{b, 4}} = 51, {t_{d, 4}} = 80 \end{array}} \right. $

每个扩展目标每个时刻产生的量测数量服从泊松分布, $ {\gamma _i} $ , $ {t_{b, i}} $ 和 $ {t_{d, i}} $ ( $ i = 1, 2, 3, 4 $ )分别表示对应泊松分布的均值和每个扩展目标的新生时间和消失时间. 其他的参数设置为: $P = {\rm{diag}}\left\{ {1, 1} \right\}$ , $ v = 2 $ , $V = {\rm{diag}}\left\{ {12, 12} \right\}$ , $ \alpha = 32 $ , $ \;\beta = 4 $ , 运动相关 $ \tau = 10 $ , 量测率参数 $ \eta = 2 $ , 外形维度 $ d = 2 $ , 转化矩阵 $ M = \left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right] $ , $ H = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&0&1&0 \end{array}} \right] $ , 传感器的检测概率设为 $ {p_D} = 0.95 $ , 目标存活概率为 $ {p_S} = 0.99 $ . 衍生权重为 $ {\omega _{sp}} = 0.05 $ , 衍生假设为 $ \kappa = \{ 0.25, 0.5, 0.75 \} $ . 新生目标的权重 $ \omega _k^b = 0.01 $ .

假设场景中目标均做匀速直线运动, 目标的状态转移矩阵和噪声协方差分别为:

$ F = \left[ {\begin{array}{*{20}{c}} 1&1&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right] , Q = \left[ {\begin{array}{*{20}{c}} {\dfrac{{{T^4}}}{4}}&{\dfrac{{{T^3}}}{2}} \\ {\dfrac{{{T^3}}}{2}}&{{T^2}} \end{array}} \right] \cdot {0.1^2} \otimes \left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right] $

为验证所提算法的有效性, 我们进行了50次蒙特卡洛实验, 同时选取广义最优子模式分配(GOSPA)距离^[18]评估算法的性能, 其定义为:

$ \begin{gathered} d_p^{\left( {c, 2} \right)}\left( {X, \hat X} \right) = \\ {\left[ {\mathop {\min }\limits_{\theta \in {\Theta ^{\left( {|X|, |\hat X|} \right)}}} \sum\limits_{\left( {i, j} \right) \in \theta } {d_{GW}^{\left( c \right)}{{\left( {{x^i}, {{\hat x}^j}} \right)}^p} + \frac{{{c^p}}}{2}\left( {|X| - |\theta | + |\hat X| - |\theta |} \right)} } \right]^{\frac{1}{p}}} \\ \end{gathered} $

(56)

其中,

$ d_{GW}^{\left( c \right)}\left( {x, \hat x} \right) = \min \left( {c;{d_{GW}}\left( {{x^i}, {{\hat x}^j}} \right)} \right) $

(57)

其中, $ {d_{GW}}\left( {x, \hat x} \right) $ 为高斯Wassterstein距离(Gaussian Wassterstein distance, GWD)^[19], $ c $ 是基线距离的截止值, $ p $ 是异常值的惩罚程度, 在本文仿真实验中取 $ c = 10 $ , $ p = 1 $ .

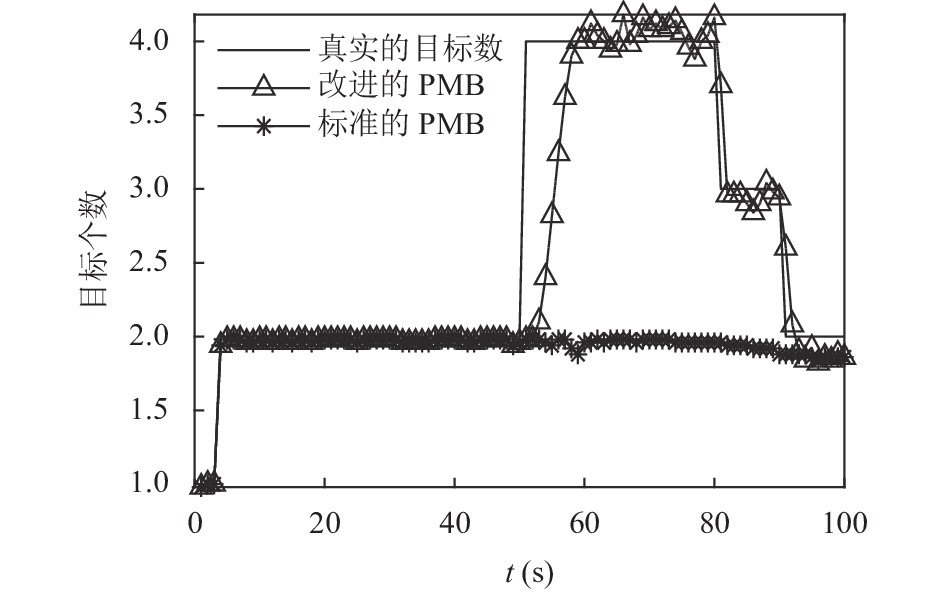
图1(a)和图1(b)分别为标准的PMB算法和改进的PMB算法的跟踪轨迹. 通过对比图1两张图的跟踪轨迹可知, 衍生事件发生后, 改进的PMB算法利用多假设模型对衍生事件预测, 相比于标准的PMB算法能更有效地跟踪目标轨迹, 同时根据图2可知, 改进的PMB算法对目标数目的估计也更接近真实的目标数目.

GOSPA误差评估算法的整体性能, 图3显示了标准PMB算法和改进的PMB算法的GOSPA误差. 在扩展目标 $ k = 51 $ 时刻之前, 两种算法的GOSPA误差相近, 说明在未发生衍生事件之前两种算法都能有效地跟踪目标. 在 $ k = 51 $ 时刻, 衍生事件发生后, 由于衍生目标与原目标的轨迹相近导致两种算法均出现较大的误差, 之后改进的PMB算法的GOSPA误差有下降的趋势且小于标准的PMB算法的GOSPA误差, 说明改进的PMB算法能够有效地检测到衍生目标并进行跟踪.

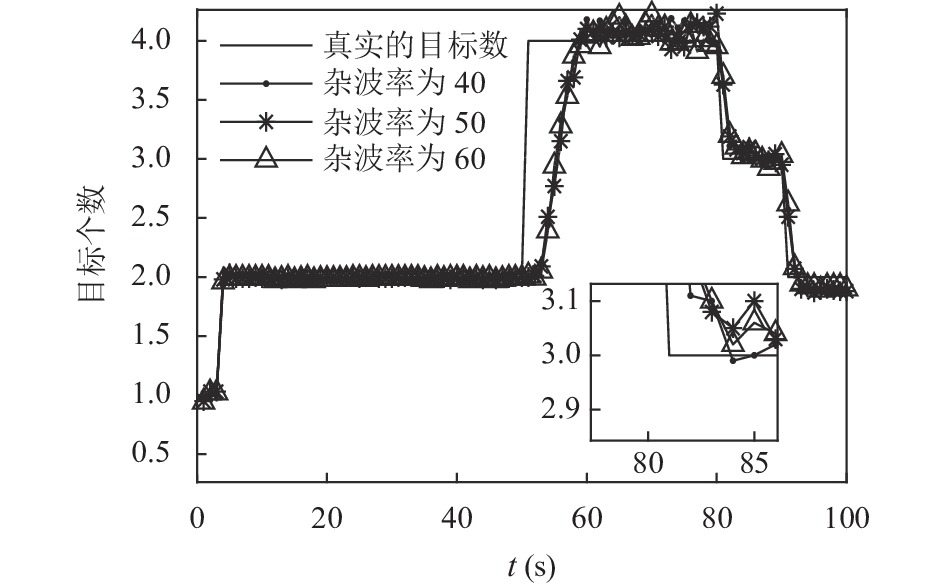
为了验证改进的PMB算法在不同条件下的估计性能, 在其他仿真环境相同的条件下, 分别设置跟踪区域内的杂波率为 $ \lambda = 40 $ , $ \lambda = 50 $ , $ \lambda = 60 $ , 以此来观察分析实验结果. 由图4可以看出, 在给定的3种不同的杂波率下, 所提算法都能有效地准确估计目标的数目. 根据图5显示的GOSPA距离误差可知, 3种不同的杂波率下算法对运动状态和外形的估计效果相差较小, 由此说明不同的杂波率对所提算法影响不大, 符合标准的PMB滤波算法适用于高杂波的性质.

5 结论

针对标准PMB滤波器未对衍生扩展目标建模的问题, 本文利用多假设模型在PMB滤波的预测阶段对衍生事件进行预测, 利用随机矩阵法建模不同尺寸的椭圆外形, 使之更符合扩展目标衍生的假设. 仿真结果表明, 改进的算法能更有效地检测到衍生目标并进行跟踪, 但该算法对衍生的估计精度依赖于衍生假设值的选取, 因此如何合理地选取假设值提高衍生目标的估计精度还需要进一步研究.