沉积相建模对于地质学研究的许多课题至关重要, 例如储层建模[1]、古地质学研究[2]. 沉积相建模主要根据少数已知的井相观测数据(测井数据)推测整个工区的地质性质, 例如河流或者岩石类型. 传统地质建模方法主要包括两点统计模拟[3]和多点统计模拟(MPS)[4, 5]. 两点统计模拟, 主要通过变差函数模拟空间关系以再现逼真的地质模式. 但受限于只能建模两点间空间关系, 无法产生复杂的非线性地质模式. MPS应用一张训练图像代替变差函数并建立搜索树学习图像中多个点的空间关系, 可以产生非线性的地质模式, 从而弥补了两点统计模拟的局限. 但MPS仍然存在一些难以克服的问题, 如难以获取适合的高平稳性的训练图像[6]、对建模参数高度敏感[7]等. 此外, 单张训练图像难以提供丰富的先验知识, 导致MPS的建模结果无法反映地质模型的不确定性[8], 再现的地质模式单一. 单纯应用地质学方法难以应对这些问题, 因此地质建模迫切需要新的思想.
近几年, 深度学习在各研究领域大放光彩, 其不依赖于单张图像的表现, 而是总结历史学习数据以泛化数据的一般规律, 在新数据上产生更稳定的结果. 生成对抗网络(generative adversarial networks, GAN)[9]作为一种先进的深度学习模型, 已在许多场景中展现出强大的建模能力[10]. 地质学者尝试将GAN应用于地质学科问题, 例如利用GAN生成逼真的3D地质模型[11]、超分辨率的岩石薄片图像[12]等. 尽管GAN在地质学科已经取得了一些成就, 但GAN无法满足条件化建模场景, 例如沉积建模中空间观测值的约束. 条件生成对抗网络(conditional generative adversarial nets, CGAN)[13]作为GAN的一种变体, 在GAN的基础上加入条件概率, 实现了条件映射. 2018年, Dupont等人[8]尝试将CGAN应用于沉积图像建模. 将空间观测值(井相数据)映射为视觉形式的井相图, 将其作为生成网络的输入, 并将OBM[14]模拟的河流图像作为目标图像, 学习从井相图像域到河流图像域的映射, 产生了逼真且符合井相约束的河流图. 2019年, Chan等人[15]通过堆叠推理网络探索地质图像生成过程的参数化. 2020年, Gao等人[16]选取400个三角洲图像作为训练数据, 将CGAN应用于三角洲图像的条件建模. 2021年, Canchumuni等人[17]测试了不同的GAN模型进行相图像的生成以及参数化. 但这些工作仅关注将测井数据作为条件, 忽略了对地质属性的调节, 例如河流模式的方位角和河流宽度等. 如何实现在井相数据之外进一步调节生成图像的地质模式, 生成模式可控的地质图像是目前值得探索的课题.
本文提出引入属性标签调节生成图像的条件建模方法, 其中属性标签是表示地质属性类别的数字代码. 将属性标签与井相图联合作为生成条件, 并在以往工作[8]实现了井相图到地质图像的图像转换框架的基础上, 扩展一个属性分类器用于预测图像的属性类别, 以辅助属性标签进行模式调节. 此外, 本文利用半监督聚类实现自动标签化, 将少量标注数据作为监督信息, 利用K-means聚类将标签传播到未标注数据, 减少标注标签的人工成本, 实现更高的聚类精度. 针对聚类产生标签噪声的问题, 模型使用对称交叉熵损失替代常用的交叉熵损失, 缓解标签噪声对模型的负面影响. 本文在一个包含复杂形态的真实河流数据集上进行了实验, 结果证明所提出方法的有效性.
本文的主要贡献可以总结为以下3点.
(1) 本文设计一种新的沉积相图条件生成模型, 通过引入属性标签扩展以往工作中的沉积相图建模网络, 实现对于沉积相图的地质模式调节.
(2) 本文利用半监督聚类自动为地质图像分配属性标签, 实现更高的聚类精度. 以对称交叉熵损失替代原始交叉熵损失, 提高网络对噪声标签的鲁棒性.
(3) 本文采集并构建一个真实河流数据集, 在其上进行大量的实验, 结果证明了本方法在沉积相图像的条件生成与调节上的有效性.
1 基础知识 1.1 半监督聚类目前, 已有的数据训练方法主要分为有监督学习、无监督学习和半监督学习[18]. 有监督学习利用一组完全标签化数据学习数据与标签之间的相关性. 有监督模型通常会产生高精度的预测结果, 但数据标签的标注会产生大量的人工成本, 难以处理大数据场景. 无监督学习与有监督学习相反, 不需要任何标签信息, 只通过挖掘数据本身的内在特征学习数据间分布关系. 无监督学习的优势在于完全免去人工标注的成本, 但同时导致不太理想的预测效果. 现实场景中大量的标签数据难以获得, 但少量的标签化数据投入的成本较少. 因此, 半监督学习将少量的有标签数据看作监督信息, 以此来训练和学习大量的无标签数据, 综合了有监督和无监督学习的优点.
聚类是将对象集合划分到不同的类, 每个类称作一个簇, 每个簇的对象彼此相似并与其他簇的对象相异[19]. 传统的聚类方法为无监督聚类方法, 例如K-means聚类[20], 按照样本间的距离度量将距离近的样本划分到同一簇中, 距离远的样本划分到不同簇. 然而, 即使聚类时预先指定类别数, 聚类依据的具体特征信息却无法指定, 因此划分的类别会出现不符合实际期望的情况. 半监督聚类则是利用已标注样本计算各类别中样本的均值向量, 并将其作为聚类的初始质心. 通过这种方式将有标签数据的类别信息传播到无标签数据, 实现更高精度的聚类.
1.2 生成对抗网络生成对抗网络(GAN)[9]是2014年由Goodfellow等人提出的对抗式生成模型, 由生成器网络
| $ \begin{split} & \mathop {\min }\limits_G \mathop {\max }\limits_D {E_{x\sim p(x)}}[\log D(x)] + {E_{{\textit{z}}\sim p({\textit{z}})}}[\log (1 - D(G({\textit{z}})))] \end{split} $ | (1) |
其中,
| $ \begin{split} & \mathop {\min }\limits_G \mathop {\max }\limits_D {E_{x\sim p(x)}}[\log D(x|y)] + {E_{{\textit{z}}\sim p({\textit{z}})}}[\log (1 - D(G({\textit{z}}, y)|y))] \end{split} $ | (2) |
之后许多GAN及其变体的相关工作[21]相继被提出, 其中与本文相关的是Pix2Pix[22]和ACGAN[23]. Pix2Pix[22]是2019年Isola等人提出的图像转换框架, 该模型通过CGAN实现从图像到图像的转换, 实现了模型框架和目标函数的通用化. ACGAN将类别标签作为CGAN的输入条件, 并引入一个分类器进行分类任务, 可以生成特定类别的图像. 本文以Pix2Pix作为基线模型, 并在其上扩展了一个属性分类器, 将图像转换与类别引导结合到一起, 实现多条件的图像生成.
2 结合半监督聚类的多条件生成网络 2.1 整体框架给定一组配对的训练数据
本文首先对地质图像进行半监督聚类, 将有标签数据的标签信息传播到无标签数据, 为其更准确地分配属性类别标签. 这一部分将在第2.2节详细介绍. 之后, 将属性标签与井点图像联合馈入生成器网络作为生成条件, 通过条件判别器将生成图像拉近真实数据分布. 为了配合属性标签, 扩展一个属性分类器预测图像的属性类别, 辅助生成器生成具有特定类别特征的图像. 通过各个组件的配合, 生成符合井相分布且地质结构可控的地质图像. 此外, 采用具有噪声标签鲁棒性的对称交叉熵损失替代传统的交叉熵损失, 以缓解聚类产生的噪声标签对建模结果的负作用. 这一部分将在第2.3节详细介绍.
2.2 半监督K-means聚类获取属性标签为了自动获取地质图像的属性标签, 本文采用半监督K-means聚类来实现. 具体来说, 首先对
| $ {\mu _i} = \frac{1}{{|{C_i}|}}\sum\limits_{x \in {C_i}} x $ | (3) |
其中,
| $ d(x, \mu ) = \sqrt {\sum\limits_{i = 1}^m {{{({x^i} - {\mu ^i})}^2}} } $ | (4) |
其中,
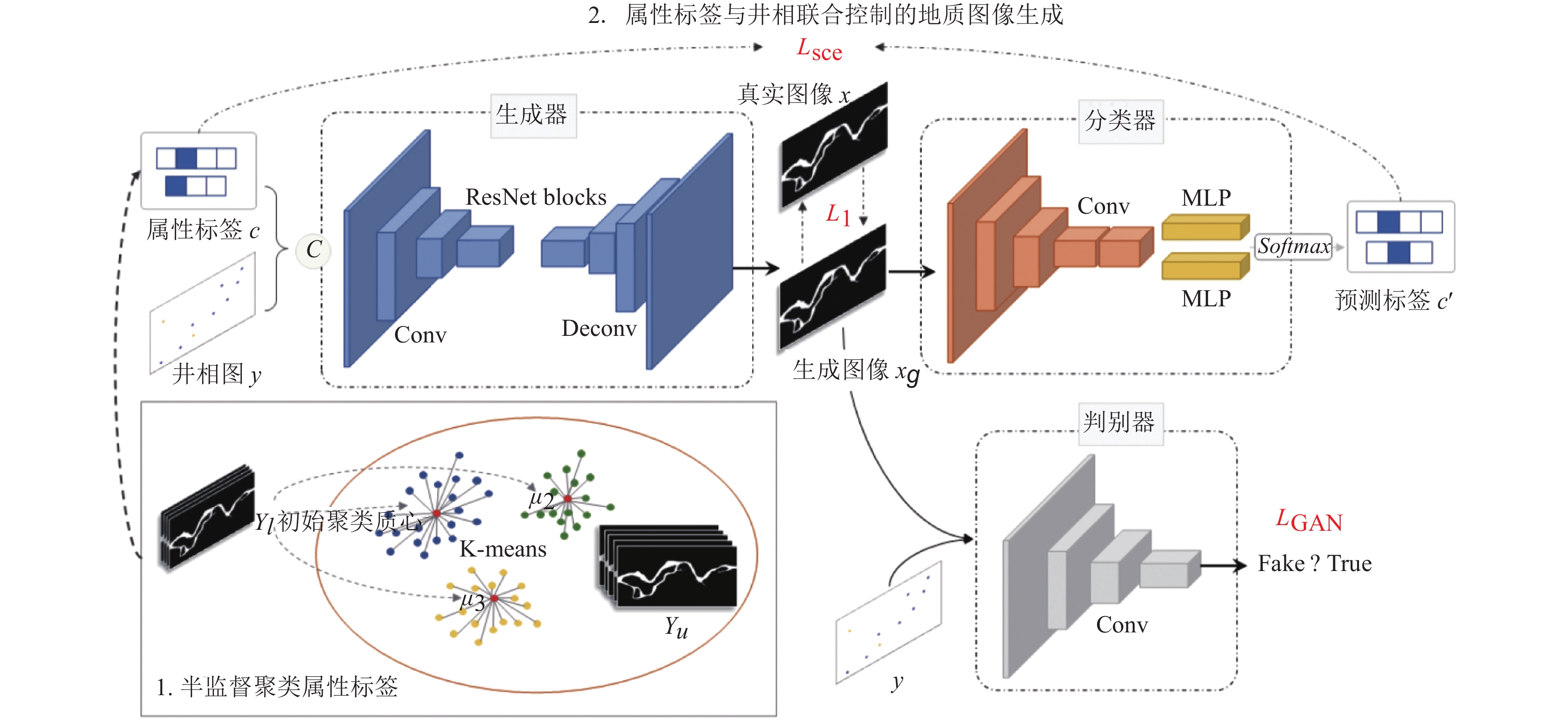
|
图 1 模型架构 |
2.3 属性标签与井相联合控制的图像生成网络
属性标签与井相联合控制的图像生成网络主要包括生成器、条件判别器和属性分类器3个组件.
对于生成器, 其输入是井点图像
| $ {x_g} = {\mathcal{G}_\theta }(y, c, {\textit{z}}) $ | (5) |
其中,
对于判别器, 将生成图像和真实图像分别与井相图
| $ {L_{{\rm{GAN}}}} = \log D(x|y) + \log (1 - D({x_g}|y)) $ | (6) |
为进一步稳定参数收敛, 在生成图像与该井相图对应的地质图像之间加入
| $ {L_1} = ||x - {x_g}|{|_1} $ | (7) |
属性标签与井相联合控制的图像生成网络的关键是扩展的属性分类器
具体来说, 分类器
| $ p = C(x) $ | (8) |
其中,
分类任务中常用交叉熵损失
| $ {L_{{\rm{ce}}}} = - \sum\nolimits_{k = 1}^K {q(k|x)\log p(k|x)} $ | (9) |
其中,
| $ q(k|x) = \left\{ \begin{gathered} 1, \; {\text{ }} k = c \\ 0, \; {\text{ otherwise}} \\ \end{gathered} \right. $ | (10) |
由于聚类时可能会产生噪声标签, 因此交叉熵损失严格惩罚预测值向标签靠近, 会导致噪声标签对模型性能产生负作用. 本文利用噪声鲁棒的分类损失
| $ {L_{{\rm{rce}}}} = - \sum\nolimits_{k = 1}^K {p(k|x)\log q(k|x)} $ | (11) |
总的分类损失
| $ {L_{{\rm{sce}}}} = \alpha {L_{{\rm{ce}}}} + \beta {L_{{\rm{rce}}}} $ | (12) |
其中,
综合以上, 网络的总损失函数如式(13)所示:
| $ L = {\lambda _1}{L_1} + {\lambda _2}{L_{{\rm{GAN}}}} + {\lambda _3}{L_{{\rm{sce}}}} $ | (13) |
其中,
本文遵循已有工作[8]的设置, 通过两种地质结构(河流类型和岩石类型)来探索条件地质建模的一般性. 由于地质图像有限且难以采集, 以往工作通常使用工具模拟地质图像作为训练集[8,16]. 本文采集黄河地区的河流卫星图像, 对其进行像素过滤及二值化等处理后作为地质图像集. 并且, 编写计算机程序为河流图像自动构建模拟的井相点图, 并提供井点数、点大小、坐标点范围、点间最大最小距离(控制井相点的稀疏性)等数据接口, 以获得不同需求的井相图. 图2井相图中不同颜色的圆点代表不同的地质性质, 蓝点代表河流相, 黄点代表背景岩石. 地质图像集由3000张二值化图像组成, 每张图像构建2张不同的井相图以模拟井相分布的随机性. 最终配对后的数据集包括6000个训练图像对.

|
图 2 训练数据对示例 |
150张有标签地质图像用于半监督聚类, 为3000张地质图像聚类属性标签. 标签表示河流方位和河流宽度两种属性, 其中河流方位分为东西向、南北向、东北-西南向和东南-西北向4个类别, 聚类后分别包括939、806、669和586张地图像; 河流宽度分为3个类别, 聚类后分别包括1781、895和324张图像. 图3展示了两种属性标签的示例.

|
图 3 图像的属性标签示例 |
3.2 实验细节
本文中的网络均基于卷积网络实现. 使用Adam优化器且参数设置为
为了验证半监督聚类的有效性, 采用精确率(Precision)来定量地评估每个类别的聚类性能, 采用准确率(Accuracy)来评价总样本的聚类性能:
| $ Precision = \frac{{{T_p}}}{{{T_p} + {F_p}}} $ | (14) |
| $ Accuracy = \frac{{{T_p} + {T_n}}}{N} $ | (15) |
其中,
结合表1和图4可以看出, 和无监督聚类相比, 本文的半监督聚类在各类别上的聚类精确率更高, 虽然存在错误聚类但总体聚类性能良好, 且半监督聚类较清晰地区分了类边界. 而无监督聚类的类边界模糊(图4中圆框圈出), 聚类精度相较半监督聚类差异较大. 此外, 无监督聚类对于初始质心的随机值选择很敏感, 需要多次实验尝试以得到理想的簇划分. 相比之下, 半监督聚类可以利用少量标签数据更有效地聚类样本且聚类结果稳定, 具有更优越的性能.
| 表 1 聚类结果对比 (%) |

|
图 4 聚类结果可视化对比 |
我们量化了在100张测试井相图上的1200张生成图像对于井相条件的匹配度, 即实现的地质图像中对应井相图中井相点处的地质结构符合井相条件的程度, 结果为100%. 结果显示, 实现的地质图像很好地遵从了井相条件, 符合条件地质建模的必要目的.
图5展示了在同一个井相分布下结合不同属性标签的生成图像示例. 图中每行表示同一个河流方位标签的生成样本, 每列表示同一个河流宽度标签的生成样本. 从图5可以直观地看出, 在给定相同的井相图下, 模型生成的图像严格遵从井相分布, 并随着属性标签的变化表现出该标签具有的地质结构特性. 由此证明, 所提出的结合半监督聚类的沉积相图多条件生成方法可以有效灵活地调节生成图像, 实现模式更可控的沉积相图.
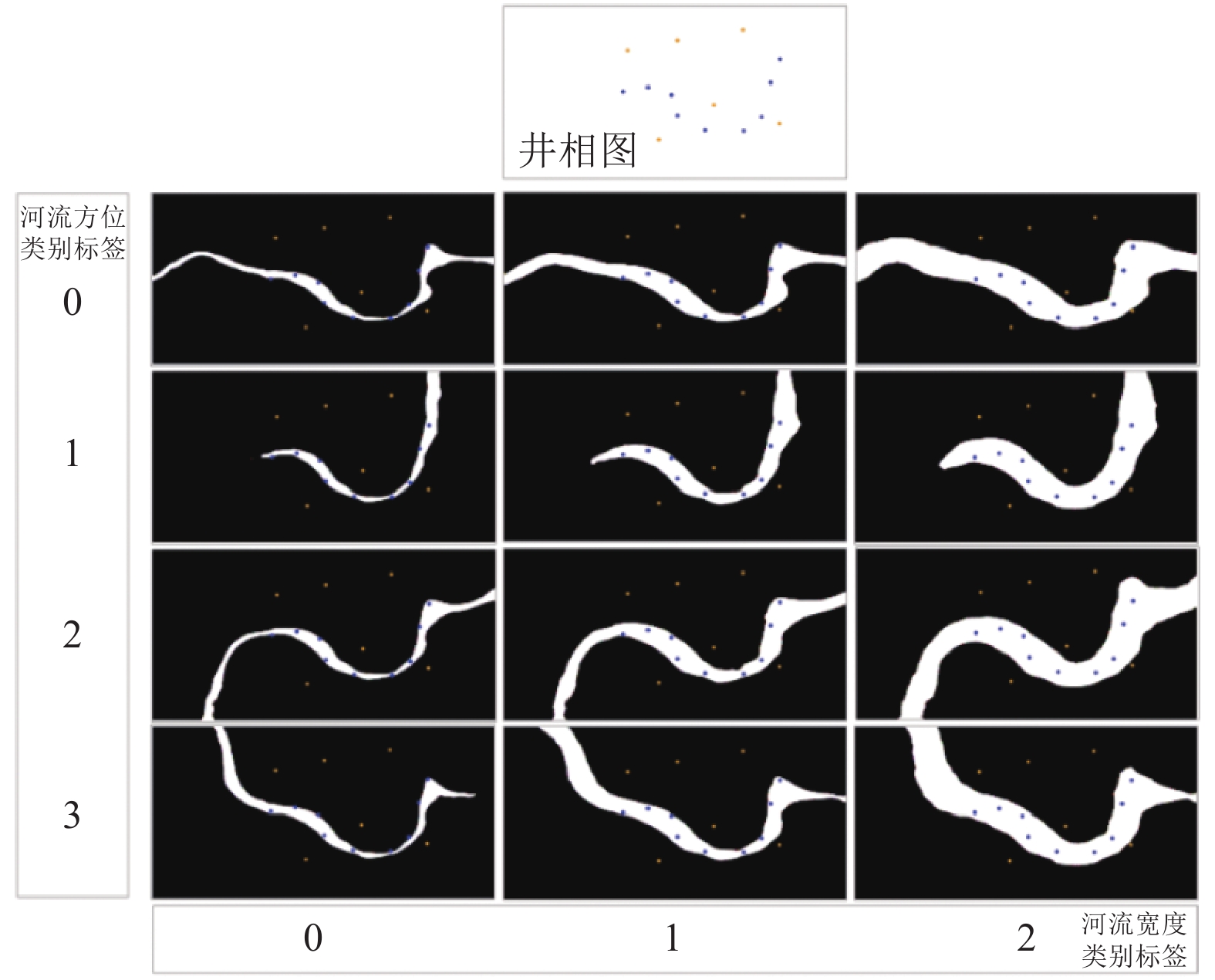
|
图 5 生成结果示例 |
以验证

|
图 6 分类损失对比实验结果示例 |
图7是模型训练过程中
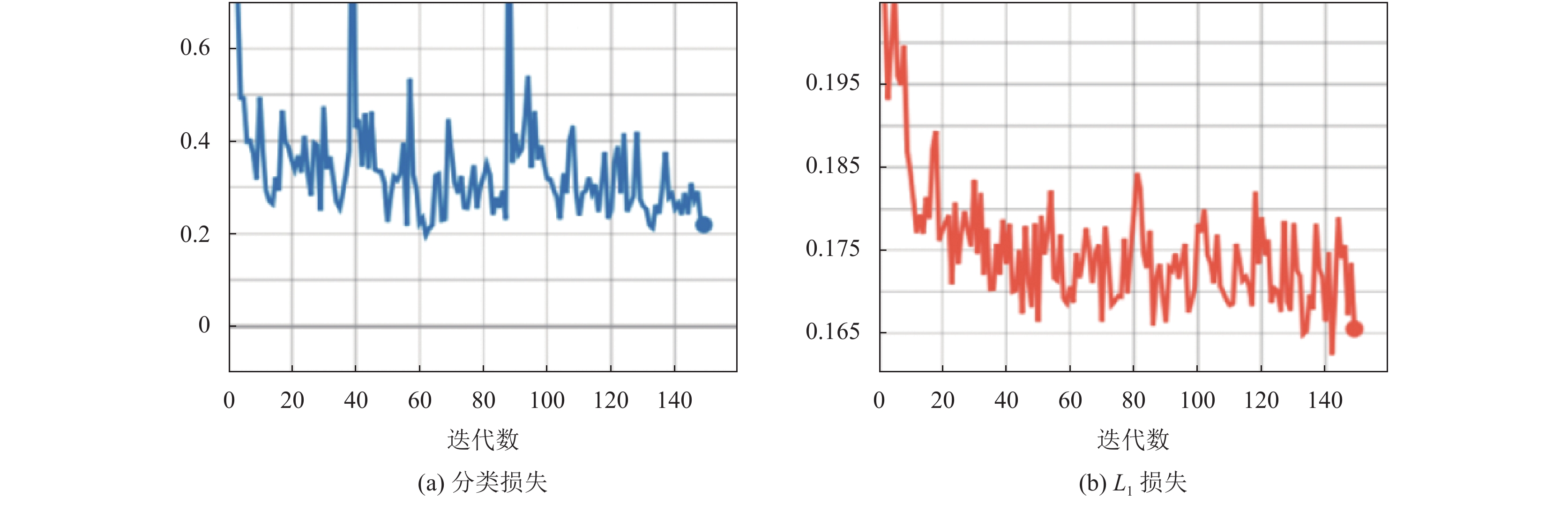
|
图 7 训练过程可视化 |
4 结论与展望
本文提出一种结合半监督聚类的地质图像条件建模方法, 该方法在以往建模工作的基础上, 扩展了一个条件生成与分类网络. 通过引入额外的属性标签和属性分类器调节图像的地质属性表现, 生成模式可控的地质图像. 此外, 为减小属性标签的标注成本, 通过半监督聚类, 为数据自动分配属性标签. 对于聚类可能产生的错误标签, 利用对称交叉熵损失加入对模型预测结果的鼓励, 提高了模型的噪声标签鲁棒性. 在未来的工作中, 我们将进一步探索更灵活的地质模式控制方法, 为地质建模研究提供可行的方案.
| [1] |
于兴河, 陈建阳, 张志杰, 等. 油气储层相控随机建模技术的约束方法. 地学前缘, 2005, 12(3): 237-244. DOI:10.3321/j.issn:1005-2321.2005.03.025 |
| [2] |
林良彪, 陈洪德, 姜平, 等. 川西前陆盆地须家河组沉积相及岩相古地理演化. 成都理工大学学报(自然科学版), 2006, 33(4): 376-383. DOI:10.3969/j.issn.1671-9727.2006.04.009 |
| [3] |
陈培元, 姜楠, 杨辉廷, 等. 由两点到多点的地质统计学储层建模. 断块油气田, 2012, 19(5): 596-599. DOI:10.6056/dkyqt201205012 |
| [4] |
Strebelle SB. Sequential simulation drawing structures from training images [Ph.D. Thesis]. Stanford: Stanford University, 2000.
|
| [5] |
Zhang TF, Switzer P, Journel A. Filter-based classification of training image patterns for spatial simulation. Mathematical Geology, 2006, 38(1): 63-80. DOI:10.1007/s11004-005-9004-x |
| [6] |
吴胜和, 李文克. 多点地质统计学——理论、应用与展望. 古地理学报, 2005, 7(1): 137-144. DOI:10.3969/j.issn.1671-1505.2005.01.013 |
| [7] |
文子桃, 林承焰, 陈仕臻, 等. 多点地质统计学建模参数敏感性分析. 西安石油大学学报(自然科学版), 2017, 32(1): 44-51. DOI:10.3969/j.issn.1673-064X.2017.01.007 |
| [8] |
Dupont E, Zhang TF, Tilke P, et al. Generating realistic geology conditioned on physical measurements with generative adversarial networks. arXiv:1802.03065, 2018.
|
| [9] |
Goodfellow IJ, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets. Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal: MIT Press, 2014. 2672–2680.
|
| [10] |
Dash A, Ye JY, Wang GL. A review of generative adversarial networks (GANs) and its applications in a wide variety of disciplines—From medical to remote sensing. arXiv:2110.01442, 2021.
|
| [11] |
Zhang TF, Tilke P, Dupont E, et al. Generating geologically realistic 3D reservoir facies models using deep learning of sedimentary architecture with generative adversarial networks. Petroleum Science, 2019, 16(3): 541-549. DOI:10.1007/s12182-019-0328-4 |
| [12] |
Liu Y, Guo C, Cao J, et al. A new resolution enhancement method for sandstone thin-section images using perceptual GAN. Journal of Petroleum Science and Engineering, 2020, 195: 107921. DOI:10.1016/j.petrol.2020.107921 |
| [13] |
Mirza M, Osindero S. Conditional generative adversarial nets. arXiv:1411.1784, 2014.
|
| [14] |
Deutsch CV, Wang LB. Hierarchical object-based stochastic modeling of fluvial reservoirs. Mathematical Geology, 1996, 28(7): 857-880. DOI:10.1007/BF02066005 |
| [15] |
Chan S, Elsheikh AH. Parametric generation of conditional geological realizations using generative neural networks. Computational Geosciences, 2019, 23(5): 925-952. DOI:10.1007/s10596-019-09850-7 |
| [16] |
Gao XY, He WX, Hu Y. Modeling of meandering river deltas based on the conditional generative adversarial network. Journal of Petroleum Science and Engineering, 2020, 193: 107352. DOI:10.1016/j.petrol.2020.107352 |
| [17] |
Canchumuni SWA, Castro JDB, Potratz J, et al. Recent developments combining ensemble smoother and deep generative networks for facies history matching. Computational Geosciences, 2021, 25(1): 433-466. DOI:10.1007/s10596-020-10015-0 |
| [18] |
Schmarje L, Santarossa M, Schröder SM, et al. A survey on semi-, self- and unsupervised learning for image classification. IEEE Access, 2021, 9: 82146-82168. DOI:10.1109/ACCESS.2021.3084358 |
| [19] |
Zhou S, Xu HJ, Zheng ZN, et al. A comprehensive survey on deep clustering: Taxonomy, challenges, and future directions. arXiv:2206.07579, 2022.
|
| [20] |
杨俊闯, 赵超. K-means聚类算法研究综述. 计算机工程与应用, 2019, 55(23): 7-14, 63. DOI:10.3778/j.issn.1002-8331.1908-0347 |
| [21] |
Wang ZW, She Q, Ward TE. Generative adversarial networks in computer vision: A survey and taxonomy. ACM Computing Surveys, 2022, 54(2): 37. |
| [22] |
Isola P, Zhu JY, Zhou TH, et al. Image-to-image translation with conditional adversarial networks. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017. 5967–5976.
|
| [23] |
Odena A, Olah C, Shlens J. Conditional image synthesis with auxiliary classifier GANs. Proceedings of the 34th International Conference on Machine Learning. Sydney: JMLR.org, 2017. 2642–2651.
|
| [24] |
Wang YS, Ma XJ, Chen ZY, et al. Symmetric cross entropy for robust learning with noisy labels. Proceedings of the IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 322–330.
|
 2023, Vol. 32
2023, Vol. 32


