1 引言

随着物联网技术、人工智能和区块链等技术的不断发展, 智慧医疗也在逐步发展. 可穿戴设备、智能传感器等产生大量的医疗数据. 为方便数据共享, 越来越多的医疗机构开始将医疗数据存储到云服务器中. 但是医疗数据涉及了大量的患者隐私信息, 一旦云服务器被攻击或者在共享过程中被未经授权的用户获取, 可能造成医疗数据被篡改或者患者隐私信息遭到泄露. 因此保证存储在云服务器中的医疗数据不被未经授权的用户获取是非常重要的^[1–3].

Goyal等^[4]为了解决电子病历共享过程中隐私泄露问题, 提出了一种基于密文策略属性加密算法的细粒度访问控制方案, 并将加密后的电子病历存储在云服务器上, 通过云服务器实现医疗机构之间的电子病历共享. 基于密文策略的属性加密方案不仅实现了细粒度的数据访问控制也可以对电子病历进行了加密. Yang等^[5]将区块链和属性加密相结合, 实现了医疗数据的安全共享. 首先, 对医疗数据进行加密, 并将密文存储到云服务器中. 而后将加密数据的存储地址和医疗相关信息上传到区块链中, 这样不仅可以确保数据高效率的存储, 而且缓解了区块链的存储开销. 其次, 为了解决医疗数据隐私和签名者身份泄露问题, 同时也要保证医疗数据源真实可信的问题, 该方案将基于属性的加密(attribute-based encryption, ABE)和基于属性的签名(attribute-base signature, ABS)相结合. Wu等^[6]为了解决电子病历安全共享问题, 提出了一种基于联盟区块链和代理重加密的电子病历共享方案. 此方案中的电子设备连接到区块链网络, 通过自动执行区块链链代码确保数据访问的安全性; 基于属性的访问控制方法保证了对数据的细粒度访问; 代理重加密技术可以保证相对敏感数据的安全共享和传输.

Sun等^[7]利用区块链和智能合约技术, 提出了一种分布式电子病历搜索方案. 首先基于属性的加密方法加密数据, 而后将其存储到星际文件系统(interplanetary file system, IPFS)中. 然后, 将电子病历的加密关键字索引信息存储到区块链上, 通过部署在区块链上的智能合约实现关键字搜索. 应作斌等^[8]将变色龙哈希和零知识证明结合解决区块链上恶意用户追踪溯源问题. 然后提出基于多个解密机构的属性基加密方案, 解决了密钥管理中的单点故障问题. Lee等^[9]引入区块链和智能合约技术, 建立一个医疗区块链. 实现患者共享病历时对其隐私进行保护. Lai等^[10]为了解决医疗数据安全共享问题, 将可追踪环签名和区块链相结合. 首先提出一种分布式密钥生成的无证书可追踪环签名算法, 以保证数据完整性和隐私保护. 其次, 智能合约结合访问控制和自控制对象(self controlled objects, SCO)可以实现解密外包和数据共享. 此外, 该方案利用IPFS存储海量的医疗隐私数据, 并对哈希索引进行加密存储, 提高了数据共享的效率. 最后, 结合区块链选择代理节点, 并使用共识机制将SCO包上传到区块链节点进行数据共享. Jiang等^[11]将Tangle集成到物联网区块链中, 并在数据管理背景下构建了跨链交互式分散模型^[12], 解决了数据存储和物联网区块链的隐私问题.

从上述方案讨论可以看出, 目前在医疗数据领域, 利用区块链来进行医疗数据的访问控制, 解决医疗数据的隐私泄露问题. 但随着医疗数据的不断增加, 应用的不断增多, 区块链的存储瓶颈成为发展瓶颈, 同时也出现了医疗机构之间数据共享不畅, 出现数据孤岛问题^[13]. 同时数据隐私也是数据共享面临的关键问题. 针对医疗数据孤岛问题和医疗数据共享过程中的数据隐私问题. 本文主要研究工作如下.

1)提出一种基于跨链的医疗数据安全共享方案, 解决医疗数据共享过程中加密数据的搜索和细粒度访问控制.

2) 访问策略隐藏, 未经授权的数据用户不能从访问策略中获得任何属性信息. 同时, 将访问控制和关键字搜索, 数据加密相结合, 只有两者都匹配, 用户才能解密数据.

3)利用IPFS存储医疗数据密文, 区块链只存储密文在IPFS中的存储地址和密钥的密文. 这不仅缓解了区块链的存储压力, 也实现了细粒度的数据访问控制.

2 预备知识 2.1 属性基加密

属性基加密(ABE)^[14]的思想来源于模糊身份基加密(fuzzy identity-based encryption, FIBE), 属性基加密的思想是让密文和密钥与属性集合和访问结构产生关联, 当且仅当属性集合满足访问结构的时候, 方能解密成功.

2.2 可搜索加密

当数据存储在一个不可信的服务器时, 为了让服务器不能够了解到数据内容, 需要对数据加密后再存储. 为了实现在加密后的数据上进行关键词检索, 提出了可搜索加密(searchable encryption, SE)的思想^[15]. SE分为对称可搜索加密(symmetric searchable encryp-tion, SSE)和非对称可搜索加密(asymmetric searchable encryption, ASE). 两者的区别在于SSE使用对称加密算法, 加密和解密的密钥一样; ASE使用非对称加密算法.

2.3 双线性映射

$G$ 和 ${G_T}$ 是两个阶为素数 $p$ 的乘法循环群, $g \in G$ . 定义一个满足双线性、可计算性和退化性^[16]的双线性映射 $e:G \times G \to {G_T}$ .

(1)双线性: 对于 $\forall x, y \in G$ , $\exists \alpha , \beta \in {{\rm Z}_p}$ , 使得等式 $e({x^\alpha }, {y^\beta }) = e{(x, y)^{\alpha \beta }}$ 成立.

(2)可计算性: 对于 $\forall x, y \in G$ , 存在一个有效的算法计算 $e(x, y)$ .

(3)非退化性: $\exists g \in G$ , 使得 $e(g, g) \ne 1$ .

2.4 困难性假设

Decisional bilinear Diffie-Hellman (DBDH)困难问题假设^[17], $g \in G$ . 随机选取 $a, b, c, {\textit{z}} \in {{\rm Z}_p}$ , 挑战者给予敌手两个元组 $(g, {g^a}, {g^b}, {g^c}, e{(g, g)^{abc}})$ 和 $(g, {g^a}, {g^b}, {g^c}, e{(g, g)^{\textit{z}}})$ , 敌手对 $e{(g, g)^{abc}}$ 和 $e{(g, g)^{\textit{z}}}$ 进行判定是否相等, 如果相等, 敌手输出1; 否则, 输出0. 如果没有一个多项式时间算法以不可忽略的优势解决DBDH困难问题假设, 则DBDH假设成立.

Decisional Diffie-Hellman (DDH)困难问题假设^[18], $g \in G$ , 随机选取 $a, b, c, {\textit{z}} \in {{\rm Z}_p}$ , 挑战者给予敌手两个元组 $({g^a}, {g^b}, {g^c})$ 和 $({g^a}, {g^b}, {g^{ab}})$ . 如果没有一个多项式时间算法以不可忽略的优势 $\varepsilon $ 区分 ${g^{ab}}$ 和 ${g^c}$ , 则DDH假设成立.

2.5 符号描述

本文涉及的符号描述如表1所示.

3 本文方案 3.1 系统模型

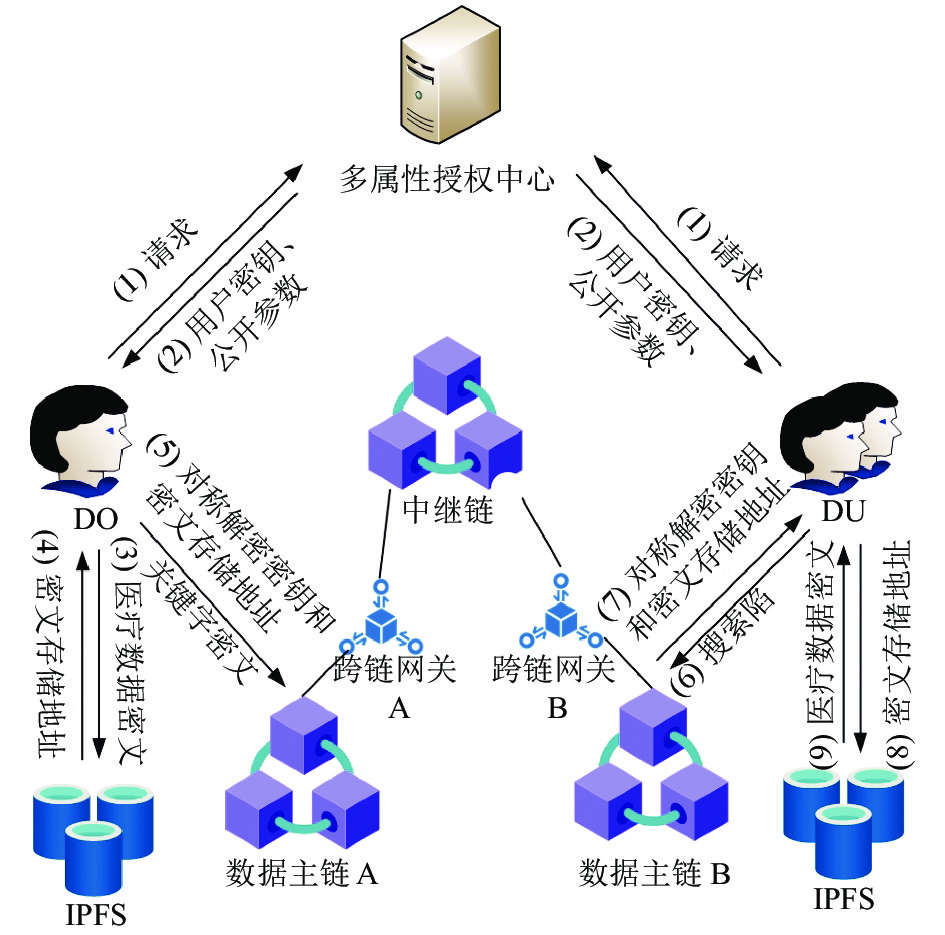
如图1所示, 本文提出的系统模型由6个实体组成: 属性授权中心、患者、数据使用者、IPFS和区块链.

1)属性授权中心(attribute authorities, AA). 属性授权中心负责管理用户属性并生成用户属性密钥.

2)患者(data owner, DO). 医疗数据所有者, 使用对称加密算法对医疗数据进行加密并将其存储到IPFS中. 同时为对称加密密钥和搜索关键字设置访问控制策略, 并将其上传到区块链.

3)数据使用者(data user, DU). 主要是医护人员或研究员, 用户生成关键字搜索陷门, 区块链节点进行搜索匹配, 当关键字匹配, 且数据使用者的属性满足患者所设置的访问控制策略时, 数据使用者便可以获得用于解密医疗数据密文的密钥, 从而对医疗数据密文进行解密.

4) IPFS. 存储医疗数据所有者将加密后的数据. 在降低区块链存储开销的同时, 实现密文数据的分布式存储.

5)数据主链. 存储医疗数据的关键字密文和IPFS中的地址以及对称加密密钥的密文. 保证医疗数据的不可篡改.

6)中继链. 主要用于数据主链的跨链管理, 以及跨链信息验证与存储.

7)跨链网关. 是中继链和数据主链的中转站, 负责监听数据主链的跨链请求消息, 用于转发跨链请求.

3.2 属性基可搜索加密医疗数据共享方案定义

1)系统初始化阶段

输入一个安全参数 $\kappa $ , 生成系统公共参数 $PP$ . 获得属性授权中心公钥 $APK$ 和私钥 ${\textit{ASK}}$ .

2)密钥生成阶段.

输入公共参数 $PP$ 、属性授权中心 $AA$ 私钥 ${\textit{ASK}}$ 和用户属性集 $\zeta $ , 输出用户私钥 ${\textit{SK}}_u$ .

3)数据加密阶段

使用对称加密算法加密原始的医疗数据, 将密文上传到IPFS中存储, IPFS返回其存储地址 ${u}$ , 而后使用CP-ABE加密对称加密密钥. 同时, 对关键字 $kw$ 进行加密. 最后, 将数据密文的摘要, IPFS存储地址 $u$ 、对称加密密钥加密结果以及关键字密文存储到区块链上.

4)数据搜索阶段

输入公共参数 $PP$ , 用户密钥 ${\textit{SK}}_u$ , 关键字 $w$ 获得陷门 ${T_w}$ . 将其上传到区块链节点, 如果用户上传的关键字匹配成功, 则返回加密医疗数据的密钥密文 $CT$ 和医疗数据在IPFS中的存储地址 $\mu $ .

5)数据使用者解密阶段

首先, 数据使用者从区块链获得密钥密文 $CT$ , 如果数据使用者的属性满足数据用户设定的访问控制策略, 数据使用者便可以解密密文获得医疗数据密文的解密密钥 $\sigma $ . 最后, 数据使用者DU根据下载链接 $u$ 下载密文 ${C_M}$ , 获得 ${C_M}$ 后, 使用解密出的密钥 $\sigma $ 解密密文 ${C_M}$ , 得到医疗数据明文 $M$ .

3.3 跨链交互

当数据主链A的用户想要获得数据主链B上的患者的数据时, 数据主链A的用户可以通过该跨链架构查询获取数据. 跨链查询流程如图2所示.

首先, 数据主链A发起跨链查询请求. 跨链网关A监听到跨链请求事件. 跨链网关A将跨链请求转发到中继链. 中继链收到跨链请求后, 首先对请求进行验证, 验证通过后, 将请求信息存储到中继链节点上并转发给跨链网关B, 网关B将收到的请求转给数据主链B, 数据主链根据请求, 调用相应的智能合约. 因为查询反馈也是跨链的, 所以数据主链B将查询到的数据返回给数据主链A的过程, 与数据主链A发送跨链查询给数据主链B的过程一致. 既跨链网关B转发数据给中继链, 中继链转发给跨链网关A, 跨链网关A将数据转给数据主链A.

3.4 安全模型

本文方案安全模型通过敌手Att和挑战者C之间的挑战游戏进行刻画, 具体过程如下.

游戏1. 关键字不可区分性.

1)初始化阶段. 首先挑战者C运行初始化算法, 获得公共参数 $PP$ 并生成属性授权中心的密钥, 并将其发送给敌手Att.

2)密钥询问阶段. 敌手Att向挑战者C进行属性私钥询问, 但所询问的属性不能满足要挑战的访问结构 $({M^*}, {\rho ^*})$ . 挑战者C生成属性私钥, 并将生成的属性私钥返回给敌手Att.

3)挑战阶段. 敌手Att向挑战者C发送两个等长关键字 ${w_0}$ 和 ${w_1}$ . 挑战者C随机选择 $b \in \{ 0, 1\} $ , 在访问结构 $({M^*}, {\rho ^*})$ 下, 对消息 ${w_b}$ 进行加密, 加密完成后将密文发送给敌手Att.

4)猜测阶段. 敌手Att输出猜测 ${b^{'}} \in \{ 0, 1\} $ , 当 ${b^{'}} = b$ 时, 敌手Att赢得挑战游戏.

定义1. 如果存在敌手Att能够在多项式时间内以优势 $Ad{v_{Att}} = \left| {\Pr [b = {b^{'}}] - \dfrac{1}{2}} \right|$ 赢得上述挑战游戏, 则我们的方案是安全的.

游戏2. 陷门不可区分性.

1)初始化阶段. 首先挑战者C运行初始化算法, 获得公共参数 $PP$ 并生成属性授权中心的密钥, 并将其发送给敌手Att.

2)密钥询问阶段. 敌手 ${Att}$ 向挑战者 ${ C }$ 进行私钥 ${\textit{SK}}_u$ 询问. 挑战者 ${ C }$ 生成私钥 ${\textit{SK}}_u$ , 并发送给敌手 ${ Att }$ . 陷门询问阶段. 敌手 ${ Att }$ 对关键字 $w$ 进行询问, ${ C }$ 生成搜索陷门 ${T_w}$ , 并将其发送给 ${ Att }$ .

3)挑战阶段. 敌手 ${ Att }$ 向挑战者 ${ C }$ 发送两个等长关键字 ${w_0}$ 和 ${w_1}$ . 挑战者 ${ C }$ 随机选择 $b \in \{ 0, 1\} $ , 生成加密关键字 ${T_{{w_b}}}$ 并发送给 ${ Att }$ .

4)猜测阶段. 敌手 ${ Att }$ 输出猜测 ${b^{'}} \in \{ 0, 1\} $ , 当 ${b^{'}} = b$ 时, 敌手 ${ Att }$ 赢得挑战游戏.

定义2. 如果存在敌手 ${ Att }$ 能够在多项式时间内以优势 $Ad{v_{Att}} = \left| {\Pr [b = {b^{'}}] - \dfrac{1}{2}} \right|$ 赢得上述挑战游戏, 则我们的方案是安全的.

3.5 属性基可搜索加密医疗数据共享方案构造

(1) 系统初始化阶段

输入安全参数 $\kappa $ . 选择阶为素数 $p$ 的乘法循环群 $G$ 和 ${G_T}$ , 其中 $g$ 为 $G$ 的生成元. 定义双线性映射 $e:G \times G \to {G_T}$ . 选择哈希函数 ${H_1}:{\{ 0, 1\} ^*} \to {\mathbb{Z}_p}$ , ${H_2}:{\{ 0, 1\} ^*} \to G$ . 生成系统公共参数 $PP = \{ e, p, g, {H_1}, {H_2}G, {G_T}\} $ . 属性授权中心随机选择 $\alpha , \beta , \mu \in {\mathbb{Z}_p}$ , 计算属性授权中心公钥 $APK = \{ e{(g, g)^\alpha }, {g^\beta }, {g^\mu }\} $ 和密钥 ${\textit{ASK}} = \{ \alpha , \beta , \mu \}$ .

(2) 密钥生成阶段

属性授权中心AA根据用户属性集 $\zeta $ 为用户计算属性私钥.

1) 随机选取 $t \in {\mathbb{Z}_p}$ , 计算 ${\textit{SK}}_{u1} = {g^{\alpha + \mu t}}$ .

2) 对 $\forall att \in \zeta $ (att表示用户属性), 随机选取 $r \in {\mathbb{Z}_p}$ , 计算 ${\textit{SK}}_{ua} = {g^{\mu r}}$ , ${\textit{SK}}_{ua}^{'} = {g^t}{H_2}{(att)^{ - r}}$ .

最后, 输出用户密钥 ${\textit{SK}}_u = \{ {\textit{SK}}_{u1} = {g^{\alpha + \mu t}}, \forall att \in \zeta : {\textit{SK}}_{ua} = {g^{\mu r}}, {\textit{SK}}_{ua}^{'} = {g^t}{H_2}{(att)^{ - r}}\}$ , 并通过安全信道发送给用户.

(3) 数据加密阶段

1) 医疗数据第1次加密与存储. 患者首先使用AES对称加密算法, 通过AES加密算法的密钥 $\sigma $ 对原始医疗数据 $M$ 进行加密, 得到数据的密文.

$ {C_M} = En{c_{AES}}(\sigma , M) $

为了降低区块链的存储开销, 将密文 ${C_M}$ 存储到IPFS中, 随后IPFS返回一个密文下载链接 $\mu $ .

2)数据第2次加密与存储. 用户设置访问控制策略 $(X, \rho )$ , $X$ 是一个 $l \times n$ 的矩阵, $\rho $ 是一个映射函数, 将 $X$ 中的每一行x映射到用户属性. ${X_i}$ 表示 $X$ 的第 $i$ 行. 随机选择 $s \in {\mathbb{Z}_p}$ , 随机选取 ${\chi _1}, {\chi _2}, \cdots,{\chi _n} \in {\mathbb{Z}_p}$ , 设置向量 $\overrightarrow v = (s, {\chi _1}, {\chi _2}, \cdots, {\chi _n})$ , 计算 ${\lambda _i} = {X_i}\overrightarrow v$ , 对密钥 $\sigma $ 进行加密, 获得密文 $ {C}_{0}=\sigma \cdot e{(g, g)}^{\alpha s} $ , $C = {g^s}$ , $ {C_{1, i}} = {g^{\mu {\lambda _i}}} $ , ${C_{2, i}} = {H_1}{(\rho (i))^{{\lambda _i}}}, \forall i \in \zeta $ .

(3)关键字加密阶段

数据拥有者DO对关键字 $kw$ 加密, ${C_w} = ({H_1}(kw) \cdot {H_2}(\rho (i)))^{{\lambda _i}}$ , $C_w^{'} = e({g^{\mu s}}, {g^\beta })$ .

数据拥有者将密文的存储地址 $\mu $ , 密文摘要, 对称密钥 $\sigma $ 的密文 $CT = \{ {C_0}, C, {C_{1, i}}, {C_{2, i}}{C_w}, C_w^{'}\} $ 上传到区块链中.

(4) 数据搜索阶段

数据使用者DU先进行陷门生成, 输入关键字 $w$ , 对于 $\forall att \in \zeta $ , 数据使用者DU随机选择 ${\vartheta _i} \in {\mathbb{Z}_p}$ , 计算 ${T_1} = {({H_1}(w), {H_2}(att))^{{\vartheta _i}}}$ , ${T_2} = {g^{\mu {\vartheta _i}}}$ . 所以, 陷门 ${T_w} = \{ {T_1}, {T_2}\} $ .

数据搜索, 用户提交搜索陷门 ${T_w}$ , 如果用户属性满足数据拥有者设定的访问控制策略 $(X, \rho )$ , 存在一个常数集 ${\{ {\omega _i} \in {\mathbb{Z}_p}\} _{i \in I}}$ , 其中 $I = \{ i:\rho (i) \in \zeta \} $ , 使得 $\displaystyle\sum\limits_{i \in I} {{\omega _i}{\lambda _i}} = s$ . 计算:

$ \begin{split} \theta & = \frac{{\displaystyle\prod\limits_{i \in I} {e{{({g^\beta } \cdot {T_1}, {C_{1, i}})}^{{\omega _i}}}} }}{{\displaystyle\prod\limits_{i \in I} {e{{({T_2}, {C_w})}^{{\omega _i}}}} }} \\ & = \frac{{\displaystyle\prod\limits_{i \in I} {e{{({g^\beta } \cdot {{({H_1}(w) \cdot {H_2}(att))}^{{\vartheta _i}}}, {g^{\mu {\lambda _i}}})}^{{\omega _i}}}} }}{{\displaystyle\prod\limits_{i \in I} {e{{({g^{\mu {\vartheta _i}}}, {{({H_1}(kw) \cdot {H_2}(\rho (i)))}^{{\lambda _i}}})}^{{\omega _i}}}} }} \\ & = \prod\limits_{i \in I} {e({g^\beta }, {g^{\mu {\lambda _i}{\omega _i}}}) = e({g^\beta }, {g^{\mu s}})} \end{split} $

验证 $\theta $ 是否等于 $C_w^{'} = e({g^{\mu s}}, {g^\beta })$ , 如果相等, 则搜索成功, 区块链节点将密文和数据存储地址发送给用户. 如果不相等, 则表示搜索失败. 终止算法运行.

(5) 数据使用者解密阶段

如果用户属性满足访问控制策略, 则计算 $D = e({C_{1, i}}, {\textit{SK}}_{ua}^{'}) \cdot e({C_{2, i}}, {\textit{SK}}_{ua}) = e{(g, g)^{t\mu s}}$ , 用户再根据自己的私钥计算出对称密钥:

$ {\sigma {'}} = \frac{{{C_0} \cdot D}}{{e(C, {\textit{SK}}_{u1})}} = \frac{{\sigma \cdot e{{\left( {g, g} \right)}^{\alpha s}}e{{(g, g)}^{t\mu s}}}}{{e({g^s}, {g^\alpha }{g^{\mu t}})}} = \sigma $

数据使用者根据IPFS下载链接 $u$ 下载密文, 根据对称密钥 $\sigma $ 对密文进行解密, 得到明文信息 $M = De{c_{AES}} (\sigma , {C_M})$ .

4 安全性分析 4.1 关键字安全

定理1. 如果在多项式时间内, 敌手 ${ Att }$ 可以以不可忽略的优势 $\varepsilon $ 赢得挑战游戏, 则挑战者 $C$ 能够以 $\dfrac{\varepsilon }{2}$ 的优势解决DBDH困难问题.

通过刻画敌手 ${ Att }$ 和挑战者 $C$ 之间的挑战游戏证明方案的安全性.

1)初始化阶段. 首先挑战者 $C$ 运行初始化算法, 获得公共参数 $PP = \{ e, p, g, {H_1}, {H_2}G, {G_T}\} $ . 随机选取 $\alpha , \beta , \mu \in {\mathbb{Z}_p}$ , 生成属性授权中心的主密钥, 并将 $APK = \{ e{(g, g)^\alpha }, {g^\beta }, {g^\mu }\} $ 返回给敌手 ${ Att }$ .

2)密钥询问阶段. 敌手 ${ Att }$ 向挑战者 $C$ 进行私钥询问, 挑战者 $C$ 运行密钥生成算法生成 ${\textit{SK}}$ , 然后将 ${\textit{SK}}$ 返回给 ${ Att }$ . 但所询问的属性不能满足要挑战的访问结构 $({M^*}, {\rho ^*})$ .

3)挑战阶段. 敌手 ${ Att }$ 向挑战者 $C$ 发送两个长度相等的关键字 ${w_0}$ 和 ${w_1}$ . 挑战者 $C$ 随机选择 $b \in \{ 0, 1\} $ , 在访问结构 $({M^*}, {\rho ^*})$ 下, 对消息 ${w_b}$ 进行加密, 获得密文 $CT$ . 随机选择 $s, {\chi _1}, {\chi _2}, \cdots,{\chi _n} \in {\mathbb{Z}_p}$ , 设置向量 $\overrightarrow v = (s, {\chi _1}, {\chi _2}, \cdots, {\chi _n})$ , 计算 ${\lambda _i} = {M_i}\overrightarrow v $ , $ {C}_{0}=\sigma \cdot e{(g, g)}^{\alpha s} $ , $C = {g^s}$ , $ {C_{1, i}} = {g^{\mu {\lambda _i}}} $ , ${C_{2, i}} = {H_1}{(\rho (i))^{{\lambda _i}}}, \forall i \in \zeta $ . ${C_w} = {({H_1}(kw) \cdot {H_2}(\rho (i)))^{{\lambda _i}}}$ , $C_w^{'} = e({g^{\mu s}}, {g^\beta })$ . 然后将密文 $CT = \{ {C_0}, C, {C_{1, i}}, {C_{2, i}}{C_w}, C_w^{'}\} $ 发送给敌手 ${ Att }$ .

4)猜测阶段. 敌手 ${ Att }$ 输出猜测 ${b^{'}} \in \{ 0, 1\} $ , 如果 ${b^{'}} = b$ , 挑战者 $C$ 输出1, 敌手 ${ Att }$ 破解DBDH困难问题的优势为 $Ad{v_{Att}} = \left| {\Pr [b = {b^{'}}] - \dfrac{1}{2}} \right| \leqslant \varepsilon$ , 否则, 输出0.

因此, 如果敌手 ${ Att }$ 以不可忽略的优势赢得挑战游戏, 那么挑战者 $C$ 就能解决DBDH困难问题.

4.2 陷门安全

定理2. 如果在多项式时间内, 敌手 ${ Att }$ 以不可忽略的优势赢得挑战游戏, 则挑战者 $C$ 能构建一个算法去解决DDH困难问题.

通过刻画敌手 ${ Att }$ 和挑战者 $C$ 之间的挑战游戏证明方案的安全性.

1) 初始化阶段. 首先挑战者 $C$ 运行初始化算法, 获得公共参数 $PP = \{ e, p, g, {H_1}, {H_2}G, {G_T}\} $ . 随机选取 $\alpha , \beta , \;\mu \in {\mathbb{Z}_p}$ , 生成属性授权中心的主密钥, 并将 $APK = \{ e{(g, g)^\alpha }, {g^\beta }, {g^\mu }\} $ 发送给敌手 ${ Att }$ .

2) 密钥询问阶段. 敌手 ${ Att }$ 向挑战者 $C$ 进行私钥询问, 计算私钥 ${\textit{SK}}_u = \{ {\textit{SK}}_{u1} = {g^{\alpha + \mu t}}, \forall att \in \zeta :{\textit{SK}}_{ua} = {g^{\mu r}}, {\textit{SK}}_{ua}^{'} = {g^t}{H_2}{(att)^{ - r}}\}$ ,

然后将私钥 ${\textit{SK}}_u$ 发送给敌手 ${ Att }$ . 陷门询问, 计算陷门, 输入关键字 $w$ , 对于 $\forall att \in \zeta $ , 随机选择 ${\vartheta _i} \in {\mathbb{Z}_p}$ , 计算 ${T_1} = {({H_1}(w), {H_2}(att))^{{\vartheta _i}}}$ , ${T_2} = {g^{\mu {\vartheta _i}}}$ . 所以, 陷门为 ${T_w} = \{ {T_1}, {T_2}\}$ .

3) 挑战阶段. 敌手 ${ Att }$ 向挑战者 $C$ 发送两个等长关键字 ${w_0}$ 和 ${w_1}$ . 挑战者 $C$ 随机选择 $b \in \{ 0, 1\} $ , 计算关键字 ${w_b}$ 陷门, 获得陷门 ${T_w}$ . 并返回给 ${ Att }$ .

4) 猜测阶段. 敌手 ${ Att }$ 输出猜测 ${b^{'}} \in \{ 0, 1\} $ , 如果 ${b^{'}} = b$ , 挑战者C输出1, 敌手 ${ Att }$ 破解DDH困难问题的优势为 $Ad{v_{Att}} = \left| {\Pr [b = {b^{'}}] - \dfrac{1}{2}} \right| \leqslant \varepsilon $ , 否则, 输出0.

因此, 如果敌手 ${ Att }$ 以不可忽略的优势赢得挑战游戏, 那么挑战者 $C$ 就能解决DDH困难问题.

5 性能分析和仿真实验分析 5.1 功能性分析

如表2所示, 本文方案与文献[19-22]在访问控制策略、可搜索、策略隐藏和区块链技术方面的功能对比, 可以看出, 本文方案在功能上有一定的优势.

5.2 仿真实验分析

本节仿真实验是基于Ubuntu 20.04系统, i5-7500 3.40 GHz, 8 GB运行内存, 构建Hyperledger Fabric v1.4.2联盟链.

5.2.1 区块链网络性能

测试区块链查询数据与写入数据的性能. 不同并发量下区块链的读写性能如图3所示, 实验结果表明, 随着并发量的增加, 区块链的读写时延也在逐渐地增加, 在并发量为300 TPS时, 查询平均时延为2 134.41 ms, 写入的平均时延为4 239.72 ms.

5.2.2 数值实验分析

本节实验是在虚拟机上运行Linux系统, 利用JPBC库, 采用Java语言进行编程.

图4是用户密钥生成时间与用户属性个数之间的关系, 将本文方案与文献[19,23]方案进行对比, 由图4可知, 用户的属性数量影响着用户密钥生成时间耗费. 随着用户属性数量的增加, 用户密钥生成时间也在增加.

图5是本文方案的加解密时间与属性个数的关系. 加密时间由AES算法加密数据的时间和CP-ABE算法加密AES密钥的时间组成. 解密时间由CP-ABE算法解密AES密钥的时间和AES算法解密数据的时间组成. 从图5可知, 用户加解密所消耗的时间与用户的属性数量呈线性关系. 数据解密时间的整体消耗要低于加密时间消耗.

6 结束语

为了解决医疗机构之间医疗数据共享困难的问题, 本文提出基于跨链的医疗数据安全共享方案. 为了保护的患者隐私信息, 使用CP-ABE算法进行细粒度的访问控制. 此外, 利用可搜索加密技术使数据用户可以快速查找到数据同时, 不泄露任何搜索信息. 同时使用IPFS存储医疗数据密文, 将存储地址和密钥存储到区块链中, 以缓解区块链存储压力. 实验结果表明了本文方案在医疗数据传输和共享方面是可行的.