2. 福建省网络安全与密码技术重点实验室(福建师范大学), 福州 350007
2. Fujian Provincial Key Laboratory of Network Security and Cryptology (Fujian Normal University), Fuzhou 350007, China
随着自动驾驶汽车、智能建筑、水处理和分配厂等信息物理系统中互连设备和传感器的快速增长, 物联网的出现进一步推动网络物理系统应用于各种任务, 越来越需要监控这些设备免受攻击, 对于电网、通信网络等关键基础设施尤为重要. 但随着传感器数据复杂性和维度的增加, 人们无法手动监视这些数据, 需要自动异常检测方法以快速检测高维数据中的异常.
由于传感器收集的数据中缺乏异常的标签, 同时异常往往是不可预测和多样化的, 通常把异常检测视为无监督学习问题. 近年来, 研究人员已经开发了许多经典的无监督方法, 包括基于统计过程控制的方法[1]、基于线性模型的方法[2]和基于支持向量机的方法[3]. 如今的信息物理系统产生的多元时间序列是高度复杂的, 而且内在相关性是非线性, 然而这些方法只是简单的对传感器之间的关系进行建模, 仅能捕获线性关系.
因此, 研究人员开始利用基于深度学习的技术对高维数据进行异常检测, 从而开发出更智能和效益高的方法来识别异常[4]. 比如基于自编码器的异常检测方法[1]和基于长短期记忆网络的异常检测方法[5]. 但是大多数的方法没有学习传感器彼此的关系, 在对有大量潜在相互关系的高维传感器数据进行建模时有困难. 近年来, 研究人员基于生成对抗网络的方法[6]提出新的异常检测对抗训练框架, 但是生成对抗网络存在模式崩溃和不收敛的问题, 使得模型训练困难[7]. 图能很好地展现关系复杂的高维数据, Defferrard等人提出图神经网络[8]成功对图结构数据进行建模. 图神经网络以图结构数据作为输入, 若应用于多元时间序列的异常检测, 需要将时间序列中的复杂关系转换为图并与模型一起学习.
考虑到上述问题, 本文提出一个基于图自编码器的时间序列异常检测方法GAE-AD, 该方法先学习传感器之间的关系图, 然后使用两个图自编码器进行GAN式对抗训练, 最后通过计算重构误差值进行异常检测. 本文主要贡献如下: (1)本文提出了基于图自编码器的对抗训练框架的异常检测方法, 可以学习传感器之间依赖关系的图结构数据并结合自编码器和对抗训练的优势. (2)对两个数据集进行了实验, 结果表明本方案与基线方法相比, 提升了对异常的检测准确率, 在F1值和召回率两个异常检测指标上优于基线方法.
本文第2节介绍了相关工作. 第3节介绍本文提出的基于图自编码器的时间序列异常检测方法. 第4节在测试数据集上评估本文的方法. 第5节总结本文的工作.
2 相关工作在许多领域中都会应用时间序列, 时间序列中的异常包含重要信息且会对整体产生重大影响. 异常检测方法主要有基于相似度、基于预测和基于重构等方法.
基于相似度的方法: 基于相似度的方法将远离大部分正常点的对象定义为异常值. 经典的方法包括基于聚 类的方法、基于距离的方法、基于密度的方法.
基于聚类的方法: 群集中样本点与其他样本点的距离、隶属性用来评估样本点的离群值, 比如CBLOF[9], 将数据聚类以区分大小簇, 然后计算样本点与大簇的聚类中心点的距离, 作为异常得分.
基于距离的方法: 用群集中样本点到其他变量的距离作为异常值, 具有大的异常值的点被定义为异常. 比如K-nearest neighbor是一种常用的有监督学习算法[10], 计算测试样本与其最近K个样本的距离作为异常得分, 得分大于阈值的样本分类为异常点.
基于密度的方法: 用测试样本点在指定的区域内其他样本点的数量来定义密度, 在低密度区域的样本点分类为异常点. 比如LOF[11], 将测试样本点周围样本点密度的平均值与其位置的密度之比定义为异常得分, 异常得分越大于1, 表明测试样本点位置的密度相对于周围样本点越小, 它是异常点的可能性越大.
这些方法都是基于相似度的概念, 它们之间差异在于如何定义测试样本点与其他样本点的相似程度. 虽然基于相似度的方法简单, 易于推广. 但是在时间序列中, 不同的时刻具有前后相关性, 基于相似度的方法无法捕获这些相关性.
基于预测的方法: 该方法的思路是通过判断测试样本点的预测输入与其真实值之间的差异是否超过预设的阈值, 若超过则将该样本点识别为异常. 比如时序预测模型ARIMA方法[12], 该方法需要将时间序列转换为平稳、突变较少的序列, 使用前一时间段内的样本点来预测下一时刻的样本输入值. ARIMA一共有7个参数, 选择合适的参数比较困难, 同时需要进行大量的参数估计, 导致ARIMA训练开销大. 基于迭代决策树GBDT[13]的异常检测, 通过梯度提升来对决策树迭代, 寻找最优的模型参数和学习率, 最终形成一个强学习器来预测输入值. 该方法缺点在于提取有效特征需要人工经验, 同时检测结果不稳定. 因为要使用前一个时间段来预测下一时刻的输入值, 所以基于预测的异常检测方法有滞后. 同时基于预测的方法容易受到异常点和周期性因素的影响, 适合平稳的时间序列.
基于重构的方法: 该方法通过构建一个编码-解码网络执行重构任务, 该网络能正常重构正常样本, 而对异常样本的重构效果较差. 将测试样本的原始值和重构结果之间的差值定义为重构误差. 如果测试样本的重构误差值越大, 则该样本是异常的可能性越高. 基于自编码器的方法是最朴素的重构思想, 比如LSTM-AE[14], 自编码器由编码器和解码器两部分组成, 编码器提取输入矢量的隐藏表示, 解码器根据隐藏表示通过与编码器相同的变换进行重构, 使重构结果与原始输入误差最小. 但是基于自编码器的神经网络结构的泛化性较强, 使得训练模型也能很好重构异常样本, 致使检测的误报率上升. 基于生成对抗网络的方法, 比如MAD-GAN[15], 用两个长短期循环神经网络来替换生成器和判别器, 生成器的输入是测试样本的时间序列, 根据其生成假的时间序列并传递给判别器, 由判别器来区分生成序列和实际的训练序列. 基于GAN框架的时间序列异常检测模型需要的超参数较多, 同时异常也是在不断变化的, 需要一定的人工经验来纠正.
通过图的方法可以用边来表示特征之间和不同时刻的依赖关系, 根据构造的边来进行建模. 将传感器的时间序列转换为图结构进行异常检测, 可以更好地学习前后时刻和关联传感器之间的依赖关系. 本文的基于图自编码器的时间序列异常检测方法吸收了图表示依赖关系的特点, 同时利用自编码器对测试样本进行重构来检测异常.
图自编码器: 图自编码器(GAE)是将自编码器的编码器和解码器用两个图神经网络构造, 是一个可以半监督和无监督学习图结构数据的神经网络. Kipf等人提出一种变分图自编码器[16], 该方法使用图卷积网络来构造编码器和解码器, 以图的邻接矩阵和节点信息作为输入, 学习图结构数据的隐藏向量表示. 变分图自编码器训练中使用图卷积网络, 训练开销会比较大. 图自编码器的优点是继承了无监督和半监督的特征, 编码和解码过程是对包含了深层次的拓扑结构信息和节点信息的图结构数据进行的, 有利于对图结构数据的信息传递、特征提取和表示.
在这项工作中, 将时间序列数据之间的关系转化为图结构, 引入两个图自编码器构成对抗训练结构进行重构, 并且用重构误差作为异常得分, 提高了异常检测的性能.
3 基于GAE的异常检测将多变量数据序列的训练数据表示为Dtrain={Dtrain,1, … , Dtrain,n}, 由于采用无监督的方法来学习异常检测模型, 所以训练数据由正常数据组成, 没有发生异常; 测试数据表示为Dtest={Dtest,1, …, Dtest,m}. 在时刻t, Dtrain,t∈RN是一个N维向量, 当N=1时, 是单变量时间序列.
异常检测是一个二分类问题, 所以训练模型对于测试数据Dtest的输出是二进制标签y(i)∈{0, 1}, 若y(i)=1, 表示时刻i出现了异常.
3.1 构建关系图收集数据的传感器之间有着完全不同的特征, 但它们也可能以某种方式相互关联. 例如, 测量水位和水速的传感器, 二者之间的特征相差甚远, 但是水速的变化, 也会影响着水位的数据. 因此, 用以表示每个传感器的方式要能多维度捕捉传感器不同行为背后的联系.
因此, 为每个传感器引入一个能表示其特征的嵌入向量:
| gi∈Rd,i∈{1,2,⋯,N} | (1) |
其中, gi表示第i个传感器在连续的d个时刻内数值所组成的向量.
嵌入向量gi之间变化的相似性代表着传感器之间行为的相似性, 嵌入向量相似的传感器之间大概率有着高度相互关联. 这些嵌入向量将用于后续学习图的结构. 传感器关系如图1所示.
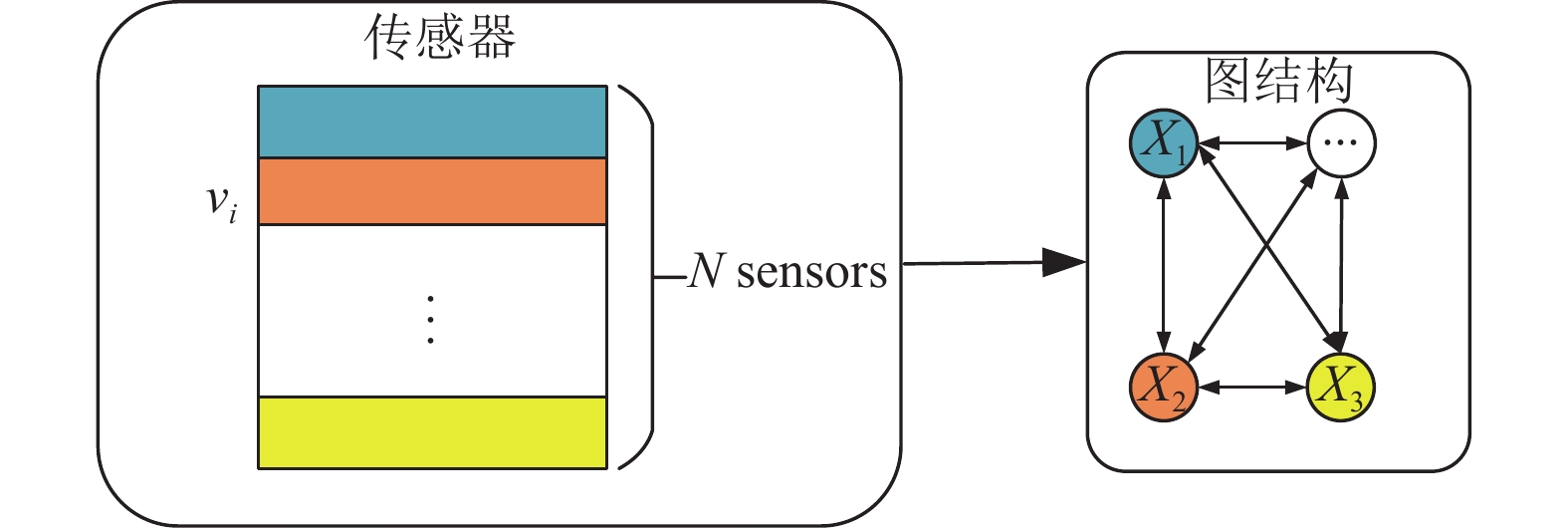
|
图 1 传感器关系图 |
3.2 学习图的结构
通过图结构来学习传感器之间的关联. 因为无向图是对称的, 无法表示传感器之间的不对称的依赖关系和因果关系. 所以本文将采用有向图连接特征, 展示不同传感器之间的依赖, 图的节点表示传感器, 节点之间的边代表它们的依赖关系. 使用邻接矩阵A来表示上述的有向图, 其中Aij表示从节点i到节点j存在有向边.
根据图结构里存在的先验信息可以为每个传感器i创建一组关系Bi, 即传感器i可能需要依赖的传感器:
| Bi⊆{1,2,⋅⋅⋅,N}−{i} | (2) |
若没有先验信息, 传感器i的依赖关系包含除了自身外的所以传感器.
为了量化Bi中的依赖关系, 计算传感器i的嵌入向量与传感器j∈Bi的嵌入向量之间的相似性:
| eji=gTigj‖gi‖⋅‖gj‖,j∈Bi | (3) |
本文先计算eji, 即传感器i的嵌入向量与传感器j之间的归一化点积.
综上所述, 给出构建图数据的算法(算法1). 步骤1: 输入测试数据集所用的特征F和特征数量n构造候选关系, 第i个特征Fi的候选关系是除自身之外的n–1个特征的集合, 即{F1, …, Fi–1, Fi+1, …, Fn}. 步骤2: 如果特征Fi是数据集的特征之一, 构造Fi与其候选关系的边. 步骤3: 根据步骤2所构造边的特征数据计算图数据, 并对其归一化.
算法1. 图数据构建
Input: 输入样本的特征和特征数n
Output: 训练用的图数据
1. 根据特征和特征数n建立候选关系矩阵
2. 利用候选关系构造边
3. 根据步骤2中的构造好的边计算图数据并进行归一化
然后选择k个这样的归一化点积, k是时间窗口大小, 用来模拟当前时间点和之前时间点, 以此将时间序列划分成子序列. 给定长度为k的时间窗口, 组成邻接矩阵:
| Aji={j∈{eki:k∈Bi}} | (4) |
后续模型的训练将用到该邻接矩阵.
3.3 训练模型图自编码器(GAE)[17]是用于无监督学习、高效编码的神经网络, 结合了编码器和解码器, 其目的在于重构编码器的输入, 利用反向传播, 使得解码器的输出目标和输入相同.
编码器获取输入X并将其映射到一组潜在变量Z, 解码器将潜在变量Z映射会输入空间作为重构结果R. 原始输入X与重构结果R之间的误差称为重构误差. 本文的目的是最小化该重构误差. 重构误差定义如下:
| {f:X→Zg:Z→Rf,g=argmin‖X−g[f(X)]‖2 | (5) |
基于图自编码器的异常检测GAE-AD使用重构误差作为异常分数, 分数超过阈值的点被分类为异常. 如果异常非常小, 与正常数据比较接近, 则重构误差会很小, 导致该异常无法检测. 这是因为自编码器旨在重构输入数据以接近正态性. 所以, 图自编码器在训练之前应当识别输入的数据是否是正常数据. 而由于在训练时, 使用的数据不包含异常, 所以, 在测试时, 图自编码器能很好地重构正常数据, 而由于训练过程中不包含异常数据, 对异常数据的重构效果不好, 所得到的重构误差较大.
生成对抗网络(GAN)是判断输入是否为异常的一种方法, GAN是基于两个网络之间极大极小博弈. 一个网络是生成网络, 旨在生成样本使判别网络无法区分其真实性; 另一个是判别网络, 目标是尽量区分数据源自于真实数据还是生成网络生成的. 基于生成对抗网络的异常检测使用正常数据训练, 用判别网络作异常检测器, 但是生成对抗网络会出现模式崩溃和不收敛的问题, 这是由于生成网络和判别网络之间的不平衡[8].
本文方法GAE-AD分为两阶段对抗训练的图自编码器结构. 这是因为自编码器在对抗训练中能获得稳定性, 解决了生成对抗网络的模式崩溃和不收敛的问题, 同时也能对输入数据进行良好的重构.
本文框架GAE-AD由两个编码器网络encoder1 (E1)、encoder2 (E2)和两个解码器网络decoder1 (D1)、decoder2 (D2)组成, 构成了两个图自编码器GAE1和GAE2, 如图2.

|
图 2 GAE-AD模型 |
首先对两个图自编码器进行训练(算法2), 学习重构正常的输入W; 然后, 两个图自编码器以对抗的方式进行训练, 如同生成对抗网络极大极小博弈, GAE1试图欺骗GAE2, 而GAE2要尽量区分数据是输入的W还是来自于GAE1重构的.
算法2. 训练算法
Input: 输入样本W=W1, …, Wn, 训练次数N
Output: 训练好的GAE1和GAE2
1. 初始化E1、E2、D1、D2, n←1
2. while n!=N do
3. fori=1 to T do
4. Zi←E1(Wi)
5. Wi1←D1(Z1)
6. Z2←E2(Wi1)
7. Wi2←D2(Z2)
8.
9. 使用lossGAE1、lossGAE2更新E1、E2、D1、D2权重
10. end for
11. n←n+1
12. end while
第1个阶段: 图自编码器训练. 在这个阶段, 输入数据W有编码器E1压缩到潜在空间Z, 然后由解码器D1进行重构. 第1阶段的图自编码器训练如下:
| GAE1(W)=D1(E1(W)) | (6) |
第2个阶段: 对抗训练. 这个阶段的目标是训练GAE2区分数据是真实数据还是来源于GAE1, 同时GAE1继续学习以欺骗GAE2. GAE1的输出通过编码器E2压缩到潜在空间Z, 再由GAE2 的解码器D2重构. 使用生成对抗网络的训练方法, 生成器的目标是最小化输入W和GAE2重构结果的不同, 鉴别器则旨在最大化二者之间的差异以实现异常检测. 第2阶段训练的如下:
| GAE2(W)=D2(E2(W)) | (7) |
综上, 两个阶段类似生成对抗网络的极大极小博弈, 公式描述如下:
| minGAE1maxGAE2V(GAE1,GAE2)=minGAE1maxGAE2‖W−GAE2(GAE1(W))‖2 | (8) |
第1个阶段的训练目标是最小化重构误差║Wi–Wi1║2, 来学习数据潜在特征, 第2个阶段的训练目标是将重构误差║Wi–Wi2║2降至最低. 对两个阶段设置了重构误差的权重比例, 随着训练迭代而变化. 最终将两个阶段的训练损失结合起来所得到的损失函数式(9)所示:
| lossGAE1←1n‖Wi−W1i‖2+(1−1n)‖Wi−W2i‖2 | (9) |
在检测阶段(算法3), 异常得分定义为:
| score(W′)=12‖W′−GAE1(W′)‖2+12‖W′−GAE2(GAE1(W′))‖2 | (10) |
如果时刻i的异常分数高于阈值threshold, 则该时刻被分类为异常.
算法3. 异常检测算法
Input: 输入测试数据W'=
Output: 分类结果: y1, …, ym
1. 初始化异常分数score←[]
2. fori=1 to m do
3.
4.
5. score.append(0.5║
6. if score≥λ then
7. yi←1
8. else
9. yi←0
10. end if
11. end for
4 实验本文使用的数据集是基于水处理物理试验台系统的两个传感器数据集: SWaT和WADI, 均是由新加坡科技设计大学的iTrust机构采集并开源. 安全水处理数据集(SWaT)来自新加坡公共事业委员会[16]. 它代表了小规模的信息物理系统, 集成了数据和物理实体来控制和监控系统行为. 配水数据集(WADI)是SWat的延伸, 由一个大量配水管道组成的配水系统[18], 是个更完整、更现实的水处理、储存和分配网络.
如表1所示, SWaT数据集有51个特征, 总的样本数目为946719, 其中正常工作下的训练样本有568031个, 带有异常的测试样本数为378688, 有11.97%的异常. WADI有127个特征, 总共有577658个样本, 其中正常工作下的训练样本有346594个, 带有异常的测试样本数为231064, 异常占比5.99%.
| 表 1 数据集统计信息 |
这两个数据集包含两周的正常运行数据, 这些数据作为训练. 在接下来的几天里, 在不同的时间间隔进行了受控的物理攻击以模拟异常情况, 这段时间内的数据用作测试数据.
本文使用Python 3.8作为编程基础, PyTorch 1.10.0、cuda 11.1实现和测试. 使用Windows 10、Intel(R)Core(TM) i7-10750H CPU、RTX3060、16 GB内存的计算机运行程序. 实验选取的滑动窗口k=12, 模型的训练迭代次数N=50, 批大小batch=8, 模块的编码网络和解码网络均是图神经网络.
4.1 基准模型本文选择了5个异常检测模型作为基准模型, 与本文提出的基于图自编码器的异常检测模型GAE-AD进行比较.
LSTM-VAE[19]: 用长短期记忆网络替换变分自编码器的前馈神经网络以结合二者, 对多维信号的底层分布进行建模, 并使用预期的分布信息重建原始的时间序列, 通过重构误差检测异常.
DAGMM[20]: 深度自编码高斯模型将自编码器和高斯混合模型联合起来的无监督异常检测模型, 网络结构分为压缩网络和估计网络, 压缩网络将样本映射到异常检测信息的低维空间, 估计网络评估低维空间中样本的高斯混合建模, 最后使用重构误差判定异常.
Isolation Forest[21]: IF是基于决策树的算法, 在给定的数据集中构建iTrees的集合, 经过重复划分递归后, 在iTrees上具有较短平均路径长度的样本被归为异常, 较长平均路径长度则表示为正常.
AE[22]: 使用自编码器的编码器和解码器来重构数据样本, 将重构误差作为异常分数, 如果测试样本的异常分数高于预设的阈值, 则判断为异常.
USAD[23]: 基于重构的无监督方法, 由1个编码器和2个解码器构成, 在训练过程中学习如何放大异常样本输入的重构误差, 利用重构误差识别异常.
4.2 评估指标准确率(P)、召回率(R)和F1值用于评估异常检测性能. TP表示异常样本经过模型分类为异常的个数. FN表示异常样本经过模型分类为正常的个数.FP表示正常样本经过模型分类为异常的个数.
| {P=TPTP+FPR=TPTP+FNF1=2P×RP+R | (11) |
其中, P为检测的准确率, 表示检测到的异常样本的百分比; R为召回率, 表示正确识别出来的异常样本的百分比, R越高表示漏报的异常越少; F1值兼顾准确率和召回率, 是评估模型异常检测性能的主要指标.
4.3 结果分析为了展示本文模型GAE-AD的整体性能, 对比了5个基准模型在多变量时间序列SWaT和WADI数据集上的检测性能, 比较结果如表2、图3、图4所示. 由表2可知, 本文方案在两个测试数据集上的召回率和F1值均为最高, 异常检测整体性能最好.
| 表 2 模型性能(%) |

|
图 3 SWaT上模型性能 |
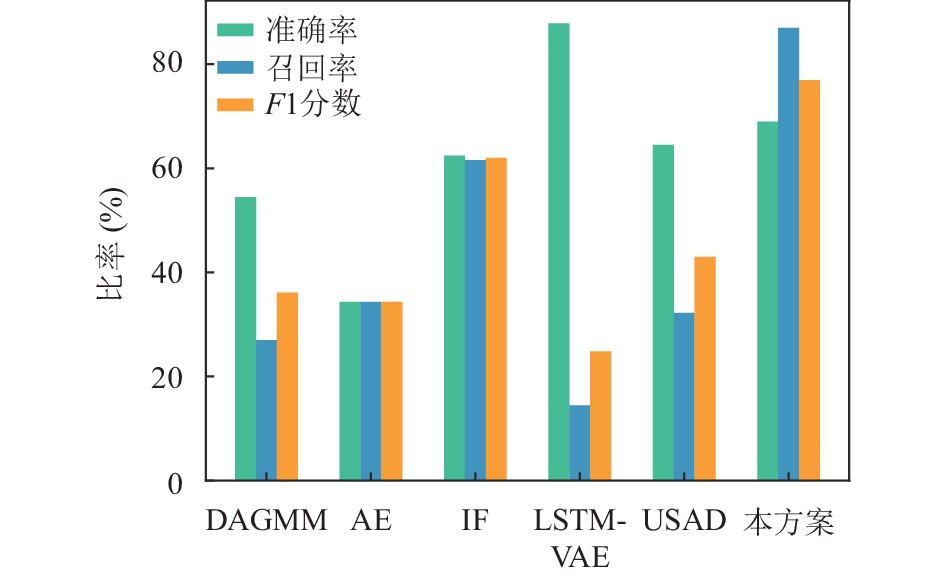
|
图 4 WADI上模型性能 |
DAGMM性能最差的原因是它没有利用时间序列中的时间信息, 对于时间序列, 这些信息十分重要, 不同时刻的观测数据是相关的, 历史数据有助于重构当前时刻的样本. 在本文模型GAE-AD中, 输入是一系列观测数据, 包含了时间序列的时间信息和关系, 使用图结构数据可以学习这些信息和关系.
IF方法适用于低维的数据. 在每次切分数据空间时, IF是随机选取一个维度, 如果数据维度高, 在构建好树后, 会有大量的维度信息没有使用. 本方案基于图自编码器这一深度学习方法, 可以提取高维时间序列数据的特征.
AE、USAD和LSTM-VAE都能保留时间序列的时间信息, 能很好地重构输入样本, 使得这3种方法无法检测接近正常样本的异常. GAE-AD通过基于图自编码器的对抗训练弥补了这一缺点, 能更好地识别出异常样本, 使召回率相对于5个基准模型有了大幅提升.
从表1可以看出, WADI的特征维度远高于SWaT, 因此WADI也比SWaT也更加不平衡, 所以在反映异常检测整体性能的F1值上, 6个模型在WADI数据集上的性能相对于SWaT数据集出现了下降.
图5展示了AE、LSTM-VAE、USAD、GAE-AD这4个模型的损失函数曲线, 横坐标为迭代次数, 纵坐标为损失函数值. 从图5可以看出, 训练初期梯度更新信息变化较大, 但是随着迭代次数增加, 损失值趋于稳定并且保持在一定范围内振荡. 相比其他3个模型, 本文提出的GAE-AD收敛速度最快, 最先达到稳定状态, 并且它的损失值是最小的. 说明GAE-AD与其他3个模型相比, 具有损失小、收敛快的优势.

|
图 5 不同模型损失函数曲线 |
5 结语
本文对多变量时间序列进行异常检测, 提出基于图自编码的异常检测模型GAE-AD. 通过实验表明其提高了异常检测的性能. 本文考虑到时间序列相关性引入了图自编码器; 同时针对生成对抗网络的模式崩溃和不收敛的问题, 引入了两个自编码器组成对抗训练架构; 将传感器收集的时间序列数据转换为图结构数据并且划分成多个子序列, 能更好地学习前后时刻之间的关系, 有助于发现时间序列中的上下文异常和提升异常检测的召回率, 通过实验表明其提升了异常检测的性能. 在多变量时间序列SWaT和WADI数据集上评估本文模型, 并且与其他基准模型对比, 发现GAE-AD模型获得了最好的总体性能(最高F1分数).
通过对比DAGMM、AE、IF、LSTM-VAE、USAD这5种异常检测模型在SWaT和WADI两个多变量时间序列数据集上异常检测性能可知, 基于图自编码器的多维时间序列异常检测方法GAE-AD能更好学习时间序列的前后时刻关系, 放大学习异常样本的重构误差, 更好地区分正常和异常样本以提升召回率. 但是本方案的准确率较低, 如何提升本文方法异常检测准确率是后续研究方向.
| [1] |
Aggarwal CC. Outlier Analysis. 2nd ed., New York: Springer, 2017.
|
| [2] |
Shyu ML, Chen SC, Sarinnapakorn K, et al. A novel anomaly detection scheme based on principal component classifier. Proceedings of the Foundations and New Directions of Data Mining Workshop. IEEE, 2003. 172–179.
|
| [3] |
Schölkopf B, Platt JC, Shawe-Taylor J, et al. Estimating the support of a high-dimensional distribution. Neural Computation, 2001, 13(7): 1443-1471. DOI:10.1162/089976601750264965 |
| [4] |
Kwon D, Kim H, Kim J, et al. A survey of deep learning-based network anomaly detection. Cluster Computing, 2019, 22(1): 949-961. |
| [5] |
Qin Y, Song DJ, Cheng HF, et al. A dual-stage attention-based recurrent neural network for time series prediction. Proceedings of the 26th International Joint Conference on Artificial Intelligence. Melbourne: AAAI Press, 2017. 2627–2633.
|
| [6] |
Goodfellow IJ, Pouget-Abadie J, Mirza M, et al. Generative adversarial nets. Proceedings of the 27th International Conference on Neural Information Processing Systems. Montreal: MIT Press, 2014. 2672–2680.
|
| [7] |
Arjovsky M, Bottou L. Towards principled methods for training generative adversarial networks. Proceedings of the 5th International Conference on Learning Representations. Toulon: OpenReview.net, 2017. 1050.
|
| [8] |
Defferrard M, Bresson X, Vandergheynst P. Convolutional neural networks on graphs with fast localized spectral filtering. Proceedings of the 30th International Conference on Neural Information Processing Systems. Barcelona: Curran Associates Inc., 2016. 3844–3852.
|
| [9] |
He ZY, Xu XF, Deng SC. Discovering cluster-based local outliers. Pattern Recognition Letters, 2003, 24(9–10): 1641–1650.
|
| [10] |
冯贵兰, 周文刚. 基于Spark平台的并行KNN异常检测算法. 计算机科学, 2018, 45(S2): 349-352, 366. DOI:10.11896/j.issn.1002-137X.2018.11A.071 |
| [11] |
杭菲璐, 郭威, 陈何雄, 等. 基于iForest和LOF的流量异常检测. 计算机应用研究, 2022, 39(10): 3119-3123. DOI:10.19734/j.issn.1001-3695.2022.03.0121 |
| [12] |
Moayedi HZ, Masnadi-Shirazi MA. Arima model for network traffic prediction and anomaly detection. Proceedings of 2008 International Symposium on Information Technology. Kuala Lumpur: IEEE, 2008. 1–6.
|
| [13] |
Wen ZY, He BS, Kotagiri R, et al. Efficient gradient boosted decision tree training on GPUs. Proceedings of 2018 IEEE International Parallel and Distributed Processing Symposium (IPDPS). Vancouver: IEEE, 2018. 234–243.
|
| [14] |
陈磊, 秦凯, 郝矿荣. 基于集成LSTM-AE的时间序列异常检测方法. 华中科技大学学报(自然科学版), 2021, 49(11): 35-40. DOI:10.13245/j.hust.211107 |
| [15] |
Li D, Chen DC, Jin BH, et al. MAD-GAN: Multivariate anomaly detection for time series data with generative adversarial networks. Proceedings of the 28th International Conference on Artificial Neural Networks. Munich: Springer, 2019. 703–716.
|
| [16] |
Kipf TN, Welling M. Variational graph auto-encoders. arXiv:1611.07308, 2016.
|
| [17] |
吴博, 梁循, 张树森, 等. 图神经网络前沿进展与应用. 计算机学报, 2022, 45(1): 35-68. DOI:10.11897/SP.J.1016.2022.00035 |
| [18] |
Ahmed CM, Palleti VR, Mathur AP. WADI: A water distribution testbed for research in the design of secure cyber physical systems. Proceedings of the 3rd International Workshop on Cyber-Physical Systems for Smart Water Networks. Pittsburgh: ACM, 2017. 25–28.
|
| [19] |
Park D, Hoshi Y, Kemp CC. A multimodal anomaly detector for robot-assisted feeding using an LSTM-based variational autoencoder. IEEE Robotics and Automation Letters, 2018, 3(3): 1544-1551. DOI:10.1109/LRA.2018.2801475 |
| [20] |
Zong B, Song Q, Min MR, et al. Deep autoencoding Gaussian mixture model for unsupervised anomaly detection. Proceedings of the 6th International Conference on Learning Representations. Vancouver: OpenReview.net, 2018.
|
| [21] |
Liu FT, Ting KM, Zhou ZH. Isolation forest. Proceedings of the 8th IEEE International Conference on Data Mining. Pisa: IEEE, 2008. 413–422.
|
| [22] |
Chow JK, Su Z, Wu J, et al. Anomaly detection of defects on concrete structures with the convolutional autoencoder. Advanced Engineering Informatics, 2020, 45: 101105. DOI:10.1016/j.aei.2020.101105 |
| [23] |
Audibert J, Michiardi P, Guyard F, et al. USAD: Unsupervised anomaly detection on multivariate time series. Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. ACM, 2020. 3395–3404.
|
 2023, Vol. 32
2023, Vol. 32



