2. 福建师范大学 福建省网络安全与密码技术重点实验室, 福州 350007
2. Fujian Provincial Key Lab of Network Security and Cryptology, Fujian Normal University, Fuzhou 350007, China
近些年来, 由于区块链技术的去中心化、数据不可篡改和去信任化等特性, 区块链技术被广泛运用于金融领域. 其中, 由Linux基金会主导发起并由IBM公司开发的一个模块化、可拓展的开源系统Hyperledger Fabric (HLF)从众多区块链系统中脱颖而出.
虽然HLF较比特币、以太坊在交易效率方面已有了很大的突破, 它被认为是最适合作为企业级应用程序开发的区块链系统[1], 但与传统金融每秒交易的处理量相比, 其效率仍不尽人意, 几乎无法直接运用于现代金融领域[2]. 又因为区块链系统本身的不可篡改和去中心化的特性, 一旦区块链系统产生交易错误, 其损失难以控制, 金融系统交易受阻, 会造成不可弥补的损失.
HLF区块链系统引入了一种新的“执行—排序—验证” (execute-order-validate, EOV)的体系架构, 这种架构允许交易执行和验证的并行化[3], 在一定程度上解决了现有区块链系统的不确定性、资源消耗大和易被性能攻击等问题. 但是在实际交易过程中, HLF系统中的排序节点在处理事务交易时并不会检查事务语义, 而是直接按照事务到达的先后顺序来进行排序处理的. 同时, 由于HLF系统中一个区块内可能包含上千笔交易, 所以HLF系统在事务交易进行至排序阶段时, 极易产生序列化冲突问题. 这种序列化冲突也称“块内冲突”, 严重影响了交易效率, 占用了大量的计算资源和存储资源来计算和存储一些未交易成功的无效事务.
首先, Baliga等人[4]通过调整链码参数、增加通道和增加对等节点的数量优化 HLF 系统性能. Gorenflo等人[5]通过减少交易期间的计算与I/O消耗提升HLF系统吞吐量. 上述方案均在系统层面对HLF进行优化, 其结果并不尽人意. Xu等人[6]设计了一种基于Redis数据库的“共享锁”机制来对抗并发冲突问题. 许沁琪[7]利用缓存交易写集的方式在执行阶段检测交易是否冲突, 以减小冲突交易在HLF系统的资源消耗. 上述方案对HLF系统执行阶段的冲突问题提出了优化改进, 并未关注到排序服务存在的问题.
Sharma等人[8]发现了HLF系统的排序服务存在着很大的逻辑缺陷, 在优化了HLF系统的排序服务, 使其具有语义检查能力后, 对交易事务进行重新排序, 以此减少序列化冲突问题的产生. Sousa等人[9]使用拜占庭容错(BFT)优化改进了HLF系统的排序服务. Sun等人[10]认为文献[8]的重排序算法存在可信问题, 故提出了一种基于贪心算法的可信重排序算法.
上述优化方案均在其排序阶段对交易事务进行了预处理, 删除了某些容易引发序列化冲突的交易事务后再对这批交易进行排序处理. 考虑到现实金融交易过程中, 若某客户机发起的交易被重复“判定”为易冲突交易, 那么客户机可能需要发起多次交易提案才能交易成功, 这显然不符合实际交易场景.
因此, 需要一种对大量交易进行全局排序的排序优化方案. 将这些交易按重要程度进行连线即为本文方案的核心思想. 复杂网络理论中最重要的模型Barabási-Albert模型[11], 就是建立在重要节点优先连边的基础上的, 但困难的是找出哪些节点才是重要节点[12]. 李劲等人[13]提出了一种描述节点间不相似性的距离度量方法. Li等人[14]提出了一种节点的多元度量方法. Pal[15]提出了一种基于完全图的排序方法. Behera[16]在文献[15]的基础上提出了一种名为“对应比较图”的用于排序的完全图模型.
本文基于对应比较图的排序方案, 针对HLF系统中交易事务进行至排序阶段时极易产生的序列化冲突问题.
(1)定义了交易事务重要度的概念, 将一个区块内的全部交易事务进行重要性度量.
(2)根据这些交易事务及其重要度构建对应比较图.
(3)在生成的对应比较图上运行深度优先搜索算法(DFS), 进行拓扑排序.
本文方案是对客户机发起的一批次交易事务进行全局排序, 缓解了客户机需要重复发起同一交易提案的问题. 并且通过实验分析表明, 本文优化方案有效减少了系统中的无效事务, 提升了系统的交易效率.
1 相关知识 1.1 Hyperledger FabricHLF是一个许可的区块链系统, 它只追踪分类账数据结构的执行历史, 并未内置加密货币, 其所有节点都需要在加入系统之前进行身份验证, 这些节点的身份由证书颁发机构(CA)和成员服务提供商(MSP)提供和维护. HLF区块链系统中的节点可大致为两类: (1)执行链码、发起提案和验证提案的对等节点. (2)对交易提案进行排序并生成区块的排序节点.
HLF 舍弃了大多数区块链系统采用的“排序—执行”的体系设计, 引入了一种“执行—排序—验证”的区块链体系结构, 如图1所示.
(1)执行阶段. 系统进行交易的模拟、背书、创建读写集和收集背书结果. 在此阶段, 首先, 由客户机将已签名的交易提案发送给背书节点背书, 背书节点根据交易提案中的参数调用链码生成读写集. 其次, 背书节点对生成的读写集进行签名并连同背书声明一齐返回给客户机. 最后, 客户机接收到返回的背书结果, 并且会从多个背书节点收集足够多的背书结果用于验证, 若验证成功, 则向排序服务广播交易提案.
(2)排序阶段. 排序服务在接收到的交易事务之间进行全局排序, 创建交易块并传递给网络中的所有对等节点进行验证. HLF不会检查交易内容, 它只会在满足某些要求时将一批交易按顺序打包到一个块中, 例如接收一定数量的交易事务或交易事务达到时限.
(3)验证阶段. 所有对等节点根据背书策略和签名验证接收到的块内的事务, 即VSCC (validation system chaincode)验证, 若验证通过, 该事务则为一个有效事务, 对于一个有效交易事务, 对等节点将会使用其写入集, 更新当前状态数据库, 然后处理下一个交易事务. 若未验证通过满足, 该事务将被标记为无效事务.

|
图 1 Hyperledger Fabric体系结构 |
1.2 序列化冲突
Hyperledger Fabric通过EOV模型来实现链码的高并发执行, 但同时也会产生大量的不可序列化的交易事务, 这些事务会在验证阶段被对等节点验证失败并被判定为无效事务, 但这些无效事务依旧会被打包成区块上传至链上, 严重影响了系统的交易效率及成功交易事务的吞吐量. 并且这些无效事务通常占比很大, 计算并存储这些无效的交易占用了大量的计算资源与存储资源.
如表1所示, 这些交易事务被判定为无效的主要原因是其记录读取集变量的账本状态在读取集生成到账本更新的期间发生了变化.
| 表 1 读写集变化导致验证失败的示例 |
在HLF系统中, 排序服务以黑盒的方式处理交易事务且不以任何方式检查事务语义, 所以排序服务会按照事务到达的先后顺序对事务进行排序. 表1中的一系列交易就是由于交易顺序的不恰当, 在第2笔交易事务还未进行验证前, 第1笔交易事务Tx1的版本号已经由v1更新为了v2, 但随后的3笔事务在验证读集时仍在读取v1, 交易事务的读写集不一致导致后续的一系列事务无法成功验证, 从而产生了一系列的无效交易事务. 这就是HLF的序列化冲突, 由于这种交易冲突是发生在同一个区块内部, 所以也称“区块内冲突”.
2 方案设计本文方案使用的主要符号及其含义如表2.
2.1 交易事务重要度定义在对HLF系统交易重要程度定义中, 本文方案将结合相关性与多样性的概念, 在相关性与多样性之间取得平衡, 共同定义本文方案中交易事务的重要性概念.
| 表 2 主要符号及其含义 |
首先给出相关性度量的定义, 个性化PageRank是图数据上实现相关性查询的有效方法[17]. 令G为一个包含n个节点的图, 节点的个性化PageRank排序向量可由如下迭代公式表示:
| r=aATr+(1−α)q | (1) |
其中,
| p=qB1×n | (2) |
矩阵B为一个
| C=αAT+(1−α)p | (3) |
给定一个排序列表S(
| F(S)=2∑i∈Sr(i)−∑i,j∈SC(i,j)r(j) | (4) |
若将矩阵A的转置代入式(4)中得:
| F(S)=2∑i∈Sr(i)−α∑i,j∈SA(j,i)r(j)−(1−α)∑j∈Sr(j)∑i∈Sq(i) | (5) |
式(5)与式(4)为等价关系.
因此, 计算HLF系统交易重要度的问题就可定义为:
| S′←argmax | (6) |
其中,
使用拓扑排序算法对HLF排序机制优化的基础就是完全图的构建. 对应比较图是一个完全图, 它就是将每个包含了交易事务索引和重要度值的元素表示为一个顶点, 将每次重要度值的大小比较结果表示为一条弧, 从重要度小的节点指向重要度大的节点, 由此构造出一个存储了所有比较结果的图.
如图2所示, 图中顶点的元素信息为(交易事务索引, 重要度值), 所以这个弧不仅比较了重要度值, 还表示了交易顺序.

|
图 2 对应比较图 |
设G为欲构造的图,
算法1. 弧添加算法
Function addARC(G, S', u, v)
w = adj[u].front
while adj[u].index > 0 do
if S'[v] < S'[w] then
INSERT(adj[u], w.index, v)
G.size++
return
if adj[u].index = adj[u].length then
APPEND(adj[u], v)
G.size++
elsew = w.next
算法1中弧添加的基本思想就是不断地从一个重要度值最小的顶点遍历到下一个重要度值最小的顶点, 即从对应比较图中遍历到重要度值最小的顶点(2, 3), 再遍历到(6, 4). 并对邻接列表正向或反向的排序实现弧的添加. 新顶点插入的基本思想是从第1个元素到最后一个元素遍历, 然后在邻接列表中的正确位置插入新顶点以实现排序的总体不变性.
接着, 由第2.1节可以得知
算法2. 图构造算法
Function constructGRAPH(S', k, r)
G = null graph of order k
for i =1 to k do
for t = 1 to rdo
j = (i + t) mod k
if S'[i] < S'[j] then
addARC(G,S',i,j)
else
addARC(G,S',j,i)
return G
算法2中, G是一个k阶空图, r为节点与其他节点在图中的比较范围, 例如当r等于1时, 节点仅与其左右相邻节点进行比较并添加弧. 这时就得到了一个包含HLF交易重要度信息的对应比较图.
2.3 基于对应比较图的拓扑排序算法对应比较图包含如下独特的性质.
(1)如果G是一个对应比较图, 则G是无环图, 因此, G是一个有向无环图.
(2)如果G是一个对应比较图, 则G有一个拓扑排序.
(3)如果G是一个对应比较图, 在G上运行深度优先搜索算法(DFS)生成一个堆栈, 并按完成时间递减排序, 那么这个堆栈就是G的拓扑排序.
基于上述对应比较图的特性, 将第2.2节中包含HLF交易重要度信息的对应比较图输入拓扑排序算法(算法3).
算法3. 拓扑排序算法
Function GraphSort(G)
x = max.index(S')
S* = {x}
DFS(G, S*)
return array(S', S*)
拓扑排序算法的主要思想就是从数组S'的最大值元素开始在图G上运行深度优先算法. 其中, 变量x存储了线性时间内运行的S'的最大元素的索引, 引入深度优先搜索算法, DFS(G, S*)是运行深度优先搜索算法的函数, 其中, S*是深度优先搜索算法生成的堆栈, 即S*是深度优先搜索算法完成后图G的拓扑排序. 最后返回值array(S', S*)是根据索引列表S*从排序列表S'中构造的一个数组.
这个数组将一个区块内的交易事务的索引按重要度从大到小排列, 排序节点将按照索引对这一批交易事务进行交易排序. 以图2为例, 按拓扑排序算法(算法3)在图上运行深度优先搜索, 即可获得一条如图3所示的哈密顿路径.

|
图 3 哈密顿路径 |
因为存在一条哈密顿路径, 在运行深度优先搜索时只需要进行5条边和6个顶点的遍历, 那么DFS的堆栈即为拓扑排序数组{3, 4, 5, 6, 8, 9}, 所以排序后的交易事务索引数组为{2, 6, 3, 5, 1, 4}, 如此, 就完成了依据重要度值的对应比较图拓扑排序, 排序服务就会按照交易事务索引对块内的一批交易事务进行排序.
3 方案分析上述优化方案为HLF系统的交易事务引入了一种重要度定义, 通过将多样性与相关性这两项指标相平衡从而更准确的定义交易事务的重要度属性. 然后将重要度值与交易事务的索引构造成对应比较图G, 再对G进行拓扑排序.
因此, 本节将从重要度定义的可靠性证明以及对优化前后的HLF系统的吞吐量、交易时间和有效事务占比等性能指标进行实验测试, 分析本文优化方案的可行性.
3.1 方案可靠性分析本节将对本文第2.1节的目标函数, 即式(4)作方案可靠性分析及证明. 目标函数由两项相减得到本文方案定义的重要度排序序列. 前一项为2倍的排序分数和, 用于度量相关性. 后一项为是任意两个节点
本文方案的可靠性证明, 即下述3个条件的证明.
(1)
(2) F(S)是单调非递减的, 即
(3) F(S)是S的一个子模. 即:
| F(I \cup R) - F(I) \geqslant F(J \cup R) - F(J) |
其中,
令
| \begin{split} & F(J) - F(I) \\ &=2\sum\limits_{i \in T} {{r}(i) - \sum\limits_{i \in I} {\sum\limits_{j \in J} {{C}(i, j){r}(j) - } } } \sum\limits_{i \in T} {\sum\limits_{j \in J} {{C}(i, j){r}(j)} } \\ &= \left(\sum\limits_{j \in T} {{r}(j) - } \sum\limits_{j \in T} {\sum\limits_{i \in I} {{C}(i, j){r}(j)} } \right) \\ &\quad + \left(\sum\limits_{i \in T} {{r}(i) - }\right. \left. \sum\limits_{i \in T} {\sum\limits_{j \in J} {{C}(i, j){r}(j)} } \right) \end{split} | (7) |
又因为矩阵C是一个列随机矩阵, 即其每列的和都为1, 且r中的每个元素都是非负的, 故式(7)的前半部分有:
| \begin{split} \left(\sum\limits_{j \in T} {{r}(j) - } \sum\limits_{j \in T} {\sum\limits_{i \in I} {{C}(i, j){r}(j)} } \right) & = \sum\limits_{j \in T} {{r}(j)(1 - \sum\limits_{i \in I} {{C}(i, j)} } \\ & = \sum\limits_{j \in T} {{r}(j)\sum\limits_{i \notin I} {{C}(i, j)} } \geqslant 0 \end{split} | (8) |
同理, 式(7)的后半部分有:
| \begin{split} \left(\sum\limits_{i \in T} {{r}(i) - } \sum\limits_{i \in T} {\sum\limits_{j \in J} {{C}(i, j){r}(j)} } \right) & = \sum\limits_{i \in T} {({r}(i) - \sum\limits_{j \in J} {{C}(i, j){r}(j)} )} \\ & = \sum\limits_{i \in T} {\sum\limits_{j \notin J} {{C}(i, j){r}(j)} } \geqslant 0 \end{split} | (9) |
将式(8)和式(9)代入式(7)中得:
| F(J) - F(I) \geqslant 0 | (10) |
即
令
| \begin{split} & (F(I \cup R) - F(I)) - (F(J \cup R) - F(J)) \\ & = \left(\sum\limits_{i \in J} {\sum\limits_{i \in R} {{C}(i, j){r}(j) - \sum\limits_{i \in I} {\sum\limits_{j \in R} {{C}(i, j){r}(j)} } } } \right) \\ & \quad + \left(\sum\limits_{i \in R} {\sum\limits_{j \in J \cup R} {{C}(i, j){r}(j) - \sum\limits_{i \in R} {\sum\limits_{j \in I \cup R} {{C}(i, j){r}(j)} } } } \right) \\ & = \sum\limits_{j \in R} {\sum\limits_{i \in T} {{C}(i, j){r}(j)} } + \sum\limits_{i \in R} {\sum\limits_{j \in T} {{C}(i, j){r}(j) \geqslant 0} } \end{split} | (11) |
即
本节将通过实验测试分析对比原始方案与本文优化方案. 本文的方案优化是为了适应现阶段金融交易的效率需要且同时缓解客户机在现实交易中需频繁发起交易提案的问题, 所以本文方案的性能分析重点主要为吞吐量及块内交易有效事务比.
为了分析本文方案的交易处理性能, 本文优化了HLF系统的排序机制, 并对交易流程进行了模拟实验, 具体实验环境及实验配置见表3.
| 表 3 实验环境及配置 |
本文使用Hyperledger Caliper基准测试工具进行以下实验测试. 本文采用了IBM公司官方提供的专门用于HLF区块链模拟性能测试的实验案例, 此HLF网络中有一个名为mychannel的通道, 由org1、org2、org3这3个组织共同负责管理维护, 此案例网络由2个对等节点和1个排序节点组成, 在此基础上, 本文实验方案设置了100个客户机节点进行模拟交易以测试本方案性能, 并通过Golang语言实现本方案的链码以控制交易事务排序机制.
首先, 本文对优化方案与原始方案的有效事务与总交易事务数量比进行测试对比, 设置每秒发起的交易事务数量(transaction per second, TPS)为1 100, 交易持续时间(txDuration)参数为30, 测试连续30 s内每秒完成的交易总量、有效事务数量和无效事务数量, 并重复10次取均值, 得到的实验结果如图4、图5所示, 每秒均为一组实验数据, 共30组.
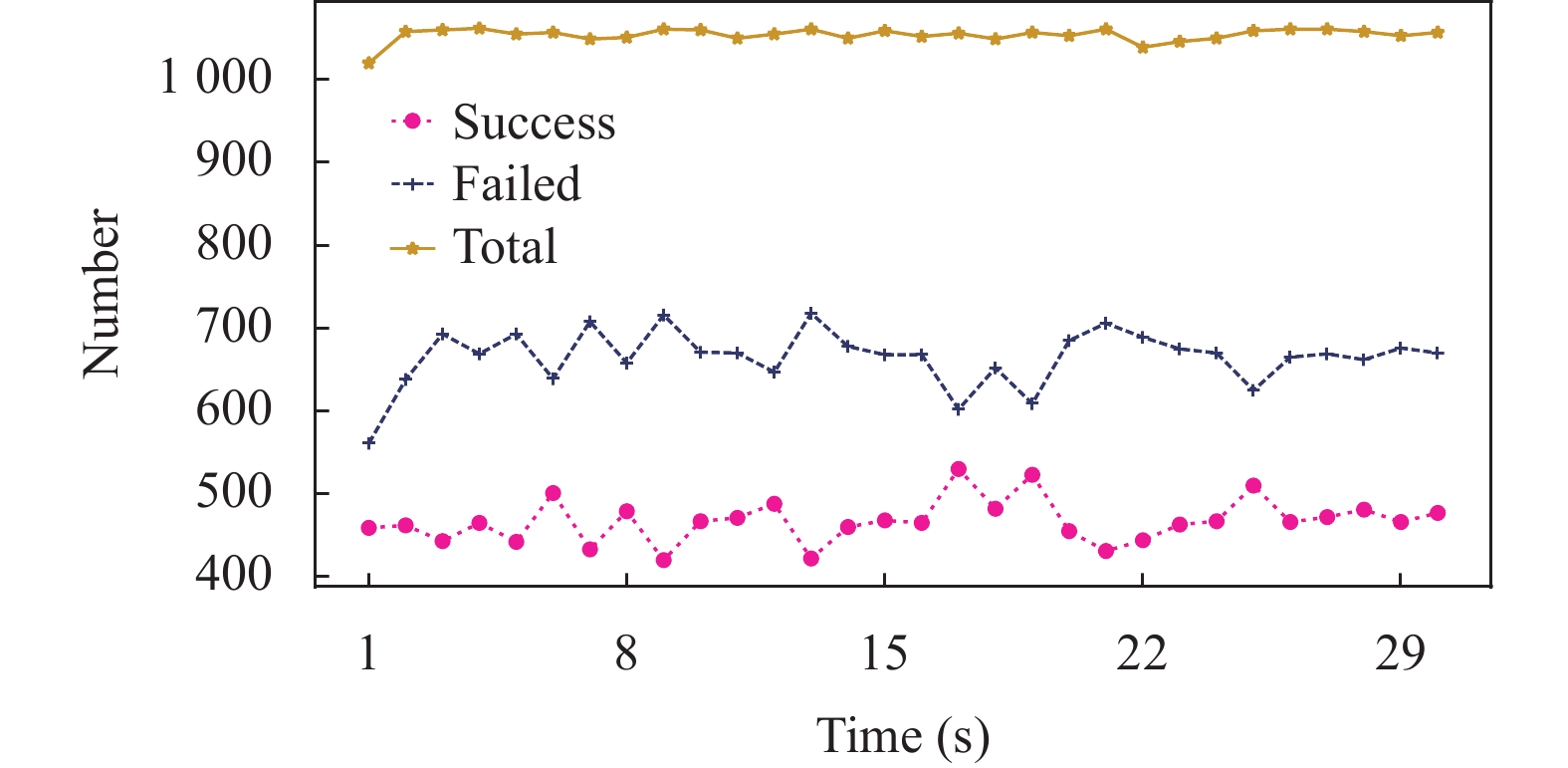
|
图 4 优化方案有效事务比 |
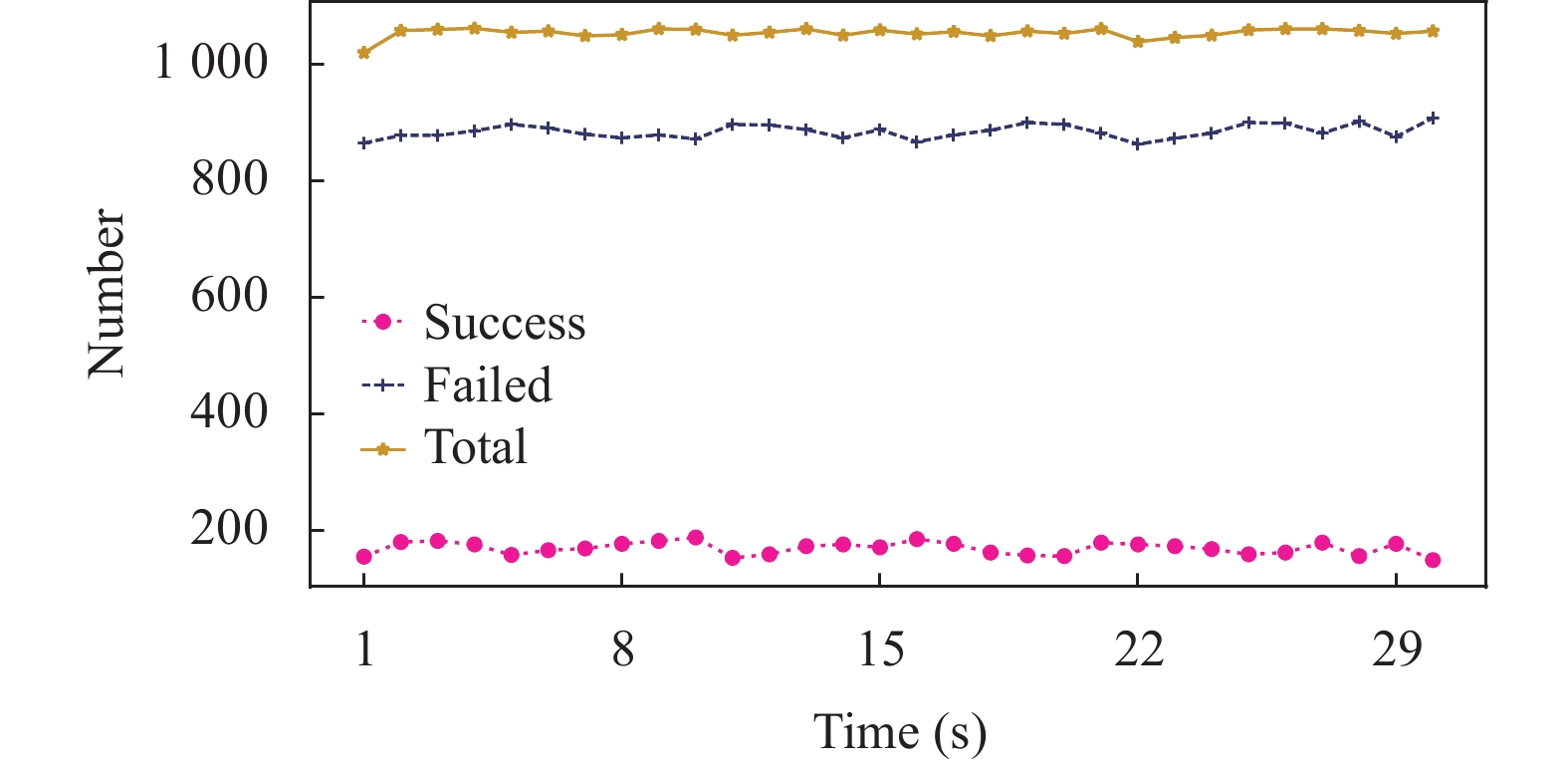
|
图 5 原始方案有效事务比 |
可以看出本文优化后的方案中有效事务的数量大都处于450至500之间, 30 s持续期间内提交的有效事务数量的平均值为467, 由于交易期间会产生通道阻塞和交易并发等问题, 实际完成的交易总量平均值为1 050, 约占交易总量的44.48%. 原始方案中有效事务的数量均处于150左右, 30 s持续期间内提交的有效事务数量的平均值为169, 实际完成的交易总量平均值为1 054, 约占交易总量的16.03%. 本文优化方案较原始方案有效事务占比提升约28.45%, 说明本文方案的交易效率较原始方案确有提升, 有效地解决了HLF系统中排序阶段易产生的序列化冲突问题.
其次, 本文对系统本身的吞吐量性能进行对比测试, 对比优化方案与原始方案在控制交易事务发起数量的情况下系统的吞吐量性能. 对比结果如图6所示.
图6中, 横坐标表示每秒发起的交易数量, 设置每秒发起的交易事务数量为10、20、40、60、80、100. 可以看出, 优化方案较原始方案在事务发起数量逐渐增加后, 系统的吞吐量性能由略微提升, 说明本优化方案在未影响原始方案的基本性能的同时, 吞吐量性能还有所提升.
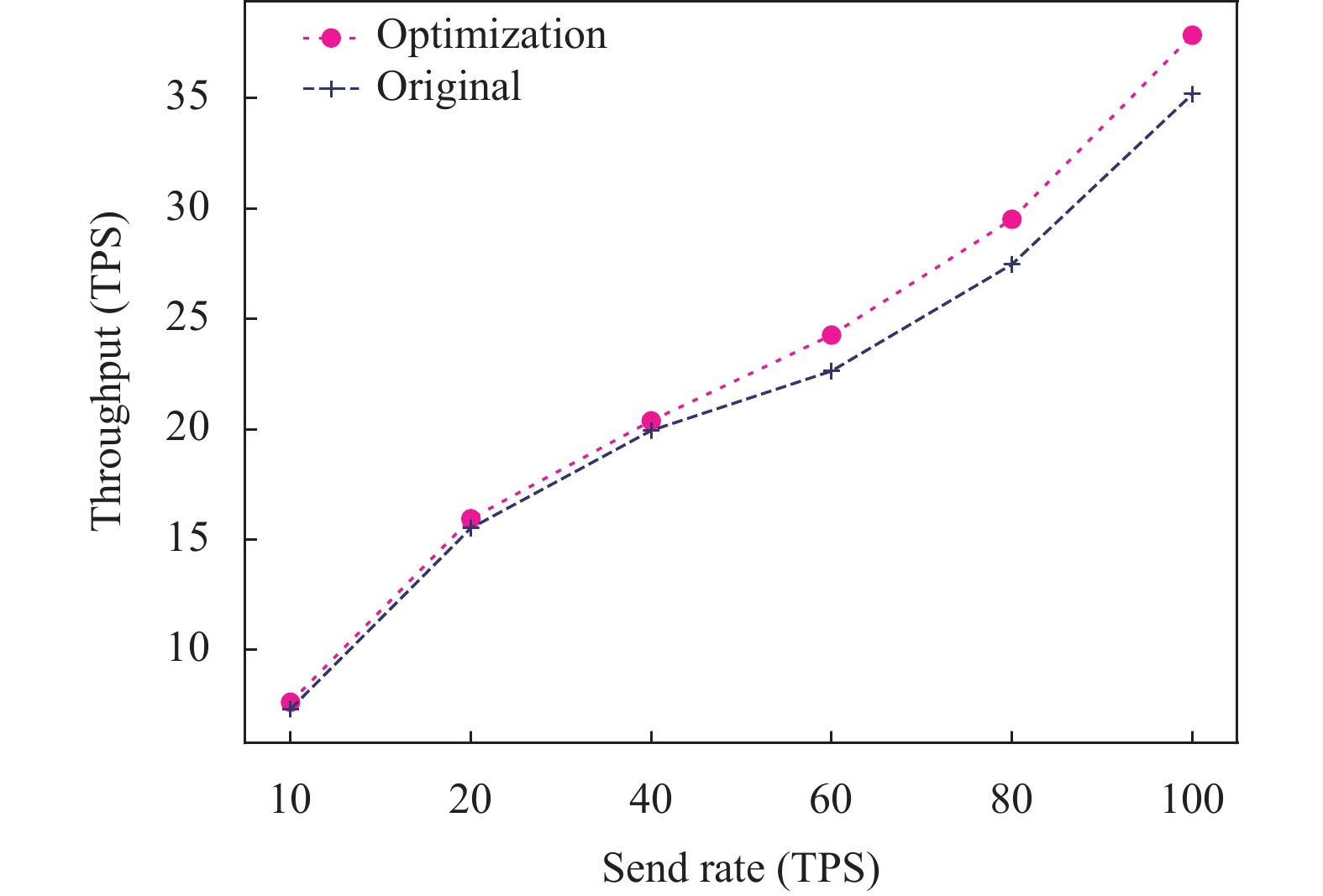
|
图 6 吞吐量性能测试 |
此外, 本文在实验过程中发现, 其中最明显的一个对等节点的CPU平均占用率从原始方案的34.32%减少到优化方案的16.31%. 综上所述, 本文方案的交易效率较原始方案确有提升, 有效地解决了HLF系统中排序阶段易产生的序列化冲突问题, 同时节省了大量的计算与存储资源.
4 总结针对HLF系统中交易进行至排序阶段时容易出现的序列化冲突问题, 提出了基于对应比较图的HLF排序机制优化方案, 为交易事务定义重要度并对重要度参数进行对应比较图的拓扑排序, 并根据索引为交易事务全局排序. 最后通过实验对比分析原始方案与本文优化方案的吞吐量性能及有效事务占比, 实验结果表明本文优化方案确实有效解决了HLF系统中的序列化冲突问题, 提升了系统交易效率, 节省了大量的计算与存储资源.
| [1] |
Dinh TTA, Wang J, Chen G, et al. Blockbench: A framework for analyzing private blockchains. Proceedings of the 2017 ACM International Conference on Management of Data. Chicago: ACM, 2017. 1085–1100.
|
| [2] |
Gupta S, Hellings J, Rahnama S, et al. Building high throughput permissioned blockchain Fabrics: Challenges and opportunities. Proceedings of the VLDB Endowment, 2020, 13(12): 3441-3444. DOI:10.14778/3415478.3415565 |
| [3] |
Androulaki E, Barger A, Bortnikov V, et al. Hyperledger Fabric: A distributed operating system for permissioned blockchains. Proceedings of the 13th EuroSys Conference. Porto: ACM, 2018. 30.
|
| [4] |
Baliga A, Solanki N, Verekar S, et al. Performance characterization of Hyperledger Fabric. Proceedings of the 2018 Crypto Valley Conference on Blockchain Technology (CVCBT). Zug: IEEE, 2018. 65–74.
|
| [5] |
Gorenflo C, Lee S, Golab L, et al. FastFabric: Scaling Hyperledger Fabric to 20 000 transactions per second. Pro-ceedings of the 2019 IEEE International Conference on Blockchain and Cryptocurrency (ICBC). Seoul: IEEE, 2019. 455–463.
|
| [6] |
Xu L, Chen W, Li ZX, et al. Locking mechanism for concurrency conflicts on Hyperledger Fabric. Proceedings of the 20th International Conference on Web Information Systems Engineering. Hong Kong: Springer, 2020. 32–47.
|
| [7] |
许沁琪. Fabric区块链系统事务执行性能优化技术[硕士学位论文]. 深圳: 中国科学院大学(中国科学院深圳先进技术研究院), 2021.
|
| [8] |
Sharma A, Schuhknecht FM, Agrawal D, et al. Blurring the lines between blockchains and database systems: The case of Hyperledger Fabric. Proceedings of the 2019 International Conference on Management of Data. Amsterdam: ACM, 2019. 105–122.
|
| [9] |
Sousa J, Bessani A, Vukolic M. A byzantine fault-tolerant ordering service for the Hyperledger Fabric blockchain platform. Proceedings of the 48th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN). Luxembourg: IEEE, 2018. 51–58.
|
| [10] |
Sun QC, Yuan YY, Guo T, et al. A trusted solution to Hyperledger Fabric reordering problem. Proceedings of the 8th International Conference on Dependable Systems and Their Applications (DSA). Yinchuan: IEEE, 2021. 202–207.
|
| [11] |
Barabási AL, Albert R. Emergence of scaling in random networks. Science, 1999, 286(5439): 509-512. DOI:10.1126/science.286.5439.509 |
| [12] |
任晓龙, 吕琳媛. 网络重要节点排序方法综述. 科学通报, 2014, 59(13): 1175-1197. DOI:10.1360/972013-1280 |
| [13] |
李劲, 岳昆, 蔡娇, 等. 基于距离度量的多样性图排序方法. 软件学报, 2018, 29(3): 599-613. DOI:10.13328/j.cnki.jos.005455 |
| [14] |
Li RH, Yu JX. Scalable diversified ranking on large graphs. IEEE Transactions on Knowledge and Data Engineering, 2013, 25(9): 2133-2146. DOI:10.1109/TKDE.2012.170 |
| [15] |
Pal RK. CompleteGraphSort: A complete graph structure based sorting algorithm. Proceedings of the 2011 IEEE International Conference on Computer Science and Auto-mation Engineering. Shanghai: IEEE, 2011. 193–197.
|
| [16] |
Behera BD. Sorting an array using the topological sort of a corresponding comparison graph. Theoretical Computer Science, 2020, 845: 76-97. DOI:10.1016/j.tcs.2020.09.004 |
| [17] |
Haveliwala TH. Topic-sensitive PageRank: A context-sensitive ranking algorithm for Web search. IEEE Transactions on Knowledge and Data Engineering, 2003, 15(4): 784-796. DOI:10.1109/TKDE.2003.1208999 |
 2023, Vol. 32
2023, Vol. 32



