近年来, 微小型机器人广泛应用于环境监测、农业植保、灾害救援等领域, 其对导航、避障、巡检等自主化需求增加, 深度感知是实现这些功能必不可少的关键技术. 单目相机具有能耗低、体积小、易标定等特点, 出现了很多利用单目相机深度估计的研究. 基于单目相机相关的深度估计可分为传统的MVS深度估计、基于网络的单目深度估计、基于网络的MVS深度估计. 基于网络的单目深度估计会对数据集产生严重的依赖性, 泛化性较差. 基于网络的MVS深度感知再纹理缺失、光照变化等环境下比传统方法展现出更为精准的深度预测效果, 因此将重点对基于网络的轻量化MVS深度估计进行研究.

MVS旨在从多张图片估计出一个或多个深度图从而进行3D重建^[1], 基于深度学习的MVS方法主要包括基于深度图、体素、点云的方法. 基于体素与点云需要大量内存不利于网络模型的整体运行, 难以进行部署. 基于深度图的方法相较于体素与点云的方法不会产生大量内存消耗同时可以轻松进行滤波处理. 早期基于深度图方法的MVS-Net^[2]在数据集^{[3, 4]}较传统MVS方法展现出卓越的性能, 但该模型在计算时消耗大量内存与时间. 为了限制内存和时间消耗, Badki等人^[5]将深度估计转化为二进制分类问题, 虽然其精度并不是最先进的, 但其速度达到了较先进的水平. Yu等人^[6]通过构造一个稀疏代价体来学习稀疏深度图, 然后使用高精度RGB图像和2D卷积对稠密化, 从而产生较为精准的深度图. 一些研究人员采样级联的方法^[7-9]从粗到细的优化深度图, 有效地在速度和精度间进行了权衡. Yang等人^[10]通过采用轻量级的极线注意力机制有效地将单目和多视图进行结合, 在公开基于网络MVS的方法中达到了最为先进的精度与速度.

当前, 基于网络的MVS深度估计网络结构复杂, 冗余, 需要耗费大量的硬件资源, 而大多数嵌入式设备计算能力低, 无法满足使用要求, 想要在嵌入式平台上实现高效的深度感知, 主要难点就是如何平衡算法的精度与计算的耗时性. 为了平衡算法的精度与计算的耗时性出现了一系列的轻量级神经网络模型^{[11, 12]}, 这类算法通过引入深度可分离卷积与SE-Net^[13]注意力机制等方式在精度损失较小的情况下, 有效地减少了网络计算的吞吐量. 受上述启发, 提出基于MVS2D极线注意力机制与MobileNetV3-Small的MVS深度感知网络(Mobile-MVS2D), 在精度损失有限情况下大幅降低网络参数以及计算量.

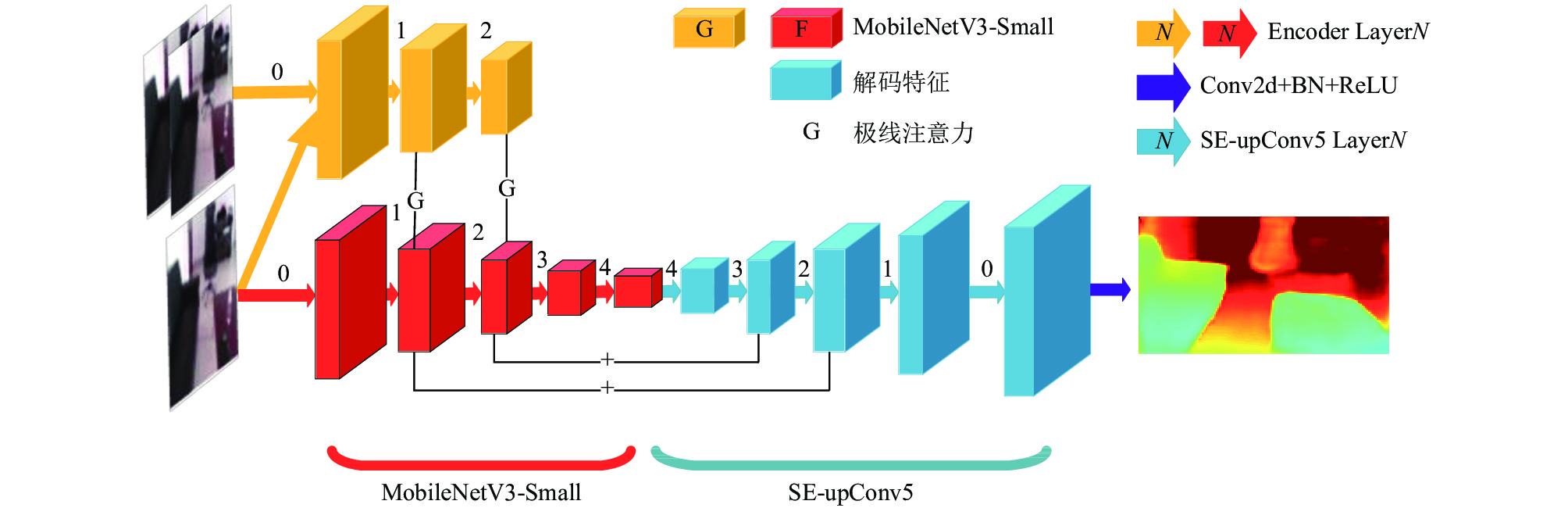
1 Mobile-MVS2D模型构建与实现

所提出的Mobile-MVS2D模型结构如图1所示. 网络主要由3部分组成: 编码器(特征提取)、基于MVS2D的极线注意力机制(G)、解码器(SE-upConv5). 其中编码器采用MobileNetV3-Small, 图片和参考图片经过编码器进行特征提取, 在编码器的Layer2、Layer3通过基于2D卷积的轻量化的极线注意力机制将参考帧图片信息与源图片信息进行耦合. 在编码阶段, 高层的编码信息具有较高的分辨率, 但编码信息较少, 底层的编码信息分辨率较低, 但编码信息更多. 在解码阶段, 解码器采样双线性插值进行上采样、为了获取更多的特征信息在解码的Layer3、Layer2采用轻量级的跳跃连接.

1.1 模型问题与编码层设置

模型的目的是在给定n张与源图像相同尺寸的参考图片 $ \{ {I_i}\} _{i = 1}^n $ , 在已知相机参数 $ K \in {R^{3 \times 3}} $ 、源图像与参考图像之间的相对运动 ${T_i} = \left( {{R_i}|{t_i}} \right)$ , ${R_i} \in {\textit{SO}}\left( 3 \right)$ , ${t_i} \in {R^3}$ 下恢复源图像 ${I_0} \in {R^{h{{ \times }}w{{ \times }}3}}$ 为每个像素 ${p_0}$ 对应深度. 若源图像 ${I_0}$ 的每个像素 ${p_0}$ 对应的齐次坐标为 $ {\overline p _0} = {\left( {{{\overline p }_{0, x}}, {{\overline p }_{0, y}}, 1} \right)^{\rm{T}}} $ , ${p_0}$ 对应的深度 ${d_0}$ , 则根据成像原理在相机坐标系下的3D点为 $ {p_0}\left( {{d_0}} \right) = {d_0}\left( {{K^{ - 1}}{p_0}} \right) $ . 同样的, 根据相机运动方程可以将参考图片i坐标系中 $ {p_0}\left( {{d_0}} \right) $ 的3D坐标和齐次坐标可分别定义为 $ {p_i}\left( {{d_0}} \right) $ 和 $ {\overline p _i}\left( {{d_0}} \right) $ , 如式(1)所示:

$\left\{ { \begin{split} &{p_i}\left( {{d_0}} \right) = {R_i}{p_0}\left( {{d_0}} \right) + {t_i} \\ &{\overline p _i}\left( {{d_0}} \right) = K{p_i}\left( {{d_0}} \right) \end{split} } \right.$

(1)

网络模型的编码层主要是一个具有L层的编码前馈学习网络F, 将 ${F_j} \in {R^{{h_j} \times {{{w}}_{{j}}} \times {{{m}}_{{j}}}}}$ 表示第j层编码器的输出. ${{m}}_{j}、{{h}}_{{j}}、{{w}}_{{j}}$ 分别表示为j层输出特征维度、宽度、高度. 连续两层之间通过MobileNetV3-Small进行编码. 用通用的卷积 ${C_{{j}}}:{R^{{h_j} \times {{{w}}_{{j}}} \times {{{m}}_{{j}}}}} \to {R^{{h_{j + 1}} \times {{{w}}_{{{j + 1}}}} \times {{{m}}_{{{j + 1}}}}}}$ 每一个Layer总编码映射, 每一层的通用公式可表示为式(2), 每一单层结构与MobileNetV3-Small一致, 每一C_j所包含的MobileNetV3-Small结构如表1所示, 表中 $H{{ \times }}W{{ \times }}{C_n}$ 、 $H{{ \times }}W{{ \times }}{C_{{\rm{out}}}}$ 分别为编码器特征输入输出的高、宽维度, $Add$ 为使用极线注意力. $ {A_j} \in {R^{{h_j} \times {w_j} \times {m_j}}} $ 基于MVS2D^[10]极线注意力机制, 在Layer1、Layer2层使用. 参考图的特征提取与源图的特征提取都采用训练好的MobileNetV3-Small进行迁移学习.

$ {F_{j + 1}} = {C_j}\left( {{A_j} + {F_j}} \right) $

(2)

1.2 模型问题与编码层设置

极线注意力机制的目的是求参考帧 ${I_n}$ 在Layer1、Layer2层的特征通过对极几何(极线注意)投影到源图像 ${I_0}$ 对应的特征层编码信息进行融合, 根据MVS2D极线注意力机制, 可以将参考帧与源图像的耦合定义为 ${A_i}\left( {{p_0}} \right)$ (式(3)), 由3部分组成. $ A_j^{ep}\left( {{p_0}, \left\{ {{I_i}} \right\}_{i = 1}^n} \right) $ 表示使用可训练代码(卷积)对 $ {{p}}_{0} $ 与对应参考图像之间的匹配结果进行编码. $A_j^0:{R^{{{m_j}}}} \to {R^{{{m_j}}}}$ 由1×1的卷积构成, 是对 ${p_0}$ 在j层的特征进行可训练线性映射, 以增强源图像的特征信息灵活性.

$ {A_j}\left( {{p_0}} \right) = A_j^{ep}\left( {{p_0}, \left\{ {{I_i}} \right\}_{i = 1}^n} \right) + A_j^0\left( {{F_j}\left( {{p_0}} \right)} \right) + {F_j}\left( {{p_0}} \right) $

(3)

$ A_j^{ep}\left( {{p_0}, \left\{ {{I_i}} \right\}_{i = 1}^n} \right) $ 由参考图像特征在 ${p_0}$ 极线上的样本组成. 样本是对深度值 ${d_0}$ 进行采样然后根据式(1)获得. 将用 $p_i^k$ 表示第i个参考图像上的第k个样本. 为了保持源图像与参考图像特征一致性, 采用一个同样的MobileNetV3-Small ( $G$ )编码器进行特征提取, 对源图像与参考图像在第j层的特征分别用 $ {G_j}\left( {{I_0}, {p_0}} \right) \in {R^j} $ 和 $ {G_j}\left( {{I_i}, p_i^k} \right) \in $ $ {R^j} $ 进行表示, 为了遵循缩放点积注意力(scaled-dot product attention)^[14], 对提取的特征引入 $f_0^j:{R^{{{m_j}}}} \to {R^{{{m_j}}}}$ 和 $f_i^j:{R^{{{m_j}}}} \to {R^{{{m_j}}}}$ 进行可训练线性映射. 对于 $ {p_0} $ 与 $ p_i^k $ 之间的匹配分数定义为 $ w_{ik}^j $ :

$ w_{ik}^j = {\left( {f_0^j\left( {{G_j}\left( {{I_0}, {p_0}} \right)} \right)} \right)^{\rm{T}}}\left( {f_{ref}^j\left( {{G_j}\left( {{I_i}, p_{_i}^k} \right)} \right)} \right) $

(4)

为了解决参考图像中部分特征映射到源图像边界外和对匹配分数 $ w_{ik}^j $ 进行桥接, 引入 ${c_{jk}} \in {R^{{{m}}_j}}$ 表示第k个训练样本的掩码. 用 $v_{{\rm{in}}}^j \in {R^{{{m_j}}}}$ 和 $v_{{\rm{out}}}^j \in {R^{{{m_j}}}}$ 分别表示边界内与边界外的信息, 可定义为:

$ v_{ik}^j = \left\{ \begin{gathered} v_{{\rm{in}}}^j, \;\;\;\;\;0 \leqslant {\overline p _{i, x}} \leqslant w, \; 0 \leqslant {\overline p _{i, y}} \leqslant h, \; 0 \leqslant {\overline p _{i, {\textit{z}}}} \\ v_{{\rm{out}}}^j, \;\;\;\;{\rm{otherwise}} \\ \end{gathered} \right. $

(5)

其中, $\overline p _i^k = {\left( {\overline p _{_{i, x}}^k, \overline p _{_{i, y}}^k, 1} \right)^{\rm{T}}}$ , $p_i^k = {\left( {p_{_{i, x}}^k, p_{i, y}^k, 1} \right)^{\rm{T}}}$ . 为了提高 ${G_j}$ 的表现力引入 $A_j^1:{R^{{{m_j}}}} \to {R^{{{m_j}}}}$ 对 $ {p_0} $ 进行线性映射. 结合式(4)与式(5)可得:

$ \begin{split} A_j^{ep}\left( {{p_0}, \left\{ {{I_i}} \right\}_{i = 1}^n} \right) =& A_j^1\left( {{G_j}\left( {{p_0}} \right)} \right) \\ & + \sum\nolimits_{i = 1}^n {\sum\nolimits_{k = 1}^K {N\left( {\frac{{w_{ik}^j}}{{\sqrt {{m_j}} }}} \right)} } \left( {v_{ik}^j \cdot {c_{jk}}} \right) \end{split} $

(6)

其中, N为 $ \dfrac{{w_{ik}^j}}{{\sqrt {{m_j}} }} $ 的 Softmax 归一化函数, $ 1 \leqslant k \leqslant K $ . 由式(3)与式(6)可得 $ {A_j}\left( {{p_0}} \right) $ :

$ \begin{split} {A_j}\left( {{p_0}} \right) =& A_j^1\left( {{G_j}\left( {{p_0}} \right)} \right) + \sum\nolimits_{i = 1}^n {\sum\nolimits_{k = 1}^K {N\left( {\frac{{w_{ik}^j}}{{\sqrt {{m_j}} }}} \right)} } \left( {v_{ik}^j \cdot {c_{jk}}} \right) \\ & + A_j^0\left( {{G_j}\left( {{p_0}} \right)} \right) + A_j^0\left( {{F_j}\left( {{p_0}} \right)} \right) \end{split} $

(7)

1.3 SE-upConv5解码器模型

Wofk等人^[15]基于深度可分离网络提出快速解码结构upConv5, 虽然相对普通的U-Net^[16]解码结构在内存消耗上与运行速度上有了极大的提升, 但基于深度可分离网络的upConv5, 在处理低层编码信息会产生大部分卷积无效的情况. 对此将引入SE-Net^[13], 通过上采样层通道之间的非线性关系提高解码器的全局信息表现能力. 所提出的SE-upConv5如图2所示. 每一层的解码流程为上一次解码特征N×C_n×W×H, 经过1×1的卷积核进行维度升维N×C_up×W×H然后进行DW卷积操作到N×C_dw×W×H, 之后是SE-Module模块进行解码信息的全局提升, 再通过1×1的卷积进行降维到N×C_down×W×H, 然后进行双线性插值到N×C_n+1×W×H, 为了进一步提高不同层级编码器信息与特征的提取程度我们将双线性插值后的解码层[Layer4, Layer3, Layer2]与之相同的编码特征层进行加和计算从而得到最终的解码层为N×C_n+1×2W×2H. 其中每一层的各级维度如表2所示. 表2中H、W、C_n、C_up、C_dw、C_down、Add分别表示输入特征层的高、输入层宽、输入层维度、Conv1×1升维后卷积维度、深度可分离卷积维度、Conv1×1降维维度、是否与编码层信息融合.

1.4 损失函数

基于神经网络的MVS深度估计任务中标准的损失函数为深度图的有效真实值与对应预测深度值之间的差. 不同类型的损失函数对MVS网络估计的精度和训练速度有很大的影响, 为了有效恢复图片的精度, 将采用的损失函数为文献[17]所提出的损失函数, 其由3部分组成, 其整体定义为 $L({{d}}, {d^ * })$ , ${L_{{\rm{depth}}}}({{d}}, {d^ * })$ 表示预测深度值和真实深度值之间均差, ${L_{{\rm{grad}}}}({{d}}, {d^ * })$ 为像素梯度损失对深度图的深度边缘进行梯度约束, ${L_{{\textit{SSIM}}}}({{d}}, {d^ * })$ 利用结构相似性对图像进行约束. 其中 ${{{d}}_p}$ 表示预测深度, ${{d}}_{{p}}^*$ 表示真实深度值, N表示所有带真实标签的像素.

$ L({{d}}, {d^ * }) = \lambda {L_{{\rm{depth}}}}({{d}}, {d^ * }) + {L_{{\rm{grad}}}}({{d}}, {d^ * }) + {L_{\textit{SSIM}}}({{d}}, {d^ * }) $

(8)

$ {L_{{\rm{depth}}}}({{d}}, {d^ * }) = \frac{1}{N}\sum\nolimits_p^n {\left| {{d_p} - d_p^ * } \right|} $

(9)

$ {L_{{\rm{grad}}}}({{d}}, {d^ * }) = \frac{1}{N}\sum\nolimits_p^n {\left| {{g_x}\left( {{d_p} - d_p^ * } \right) + {g_y}\left( {{d_p} - d_p^ * } \right)} \right|} $

(10)

$ {L_{{\textit{SSIM}}}}({{d}}, {d^ * }) = \frac{{1 - {\textit {SSIM}}\left( {{d_p} - d_p^ * } \right)}}{2} $

(11)

2 实验过程与结果分析

本节将展现所提出的Mobile-MVS2D网络模型在公开数据集ScanNet^[18]与现实场景两部分进行实验测试. 在ScanNet数据集上, 与现有部分开源方法^[2,6,9,10]进行对比. 在现实场景中, 将基于四旋翼所采集的室内数据在与世界SLAM的VINS扩展框架上进行深度估计与三维重建, 嵌入式设备Jeston Xavier NX上进行了位姿估计与深度感知测试.

2.1 实验环境

实验训练环境: 硬件为CPU为 Intel Xeon(R) Silver 4214, 48核, 单核2.20 GHz, 显卡为RTX 5000, 内存为16 GB, 运行内存为8 GB. 软件环境为PyTorch 1.7.0, Python 3.7, Ubuntu 18.04, CUDA 10.2, cuDNN 8.2.1.

嵌入式设备: Jeston Xavier NX, 实际运行内存6 GB, GPU为384-core NVIDIA Volta GPU和48 Tensor Cores, 算力为6T (Float16), CPU为6核, 单核1.4 GHz. 软件环境为 PyTorch 1.9.0, Python 3.6, Ubuntu 18.04, CUDA 10.2.

实验设置: 输入图像的分辨率为640×480; 输入图像个数为3; 采用Adam优化器, 其中 $ \epsilon = {10^{ - 8}}$ , $\; \beta = \left(0.9, 0.999\right) $ , 对于ScanNet数据集, 采用的初始学习率为 $2{{\rm{E}}{ - 3}}$ , 在第5轮和第10轮的时候学习率分别降低0.05; 训练batch为12; Batch_Size为80, 训练时长4–5天.

2.2 ScanNet数据集实验对比 2.2.1 数据集介绍

实验选用的ScanNet数据集包含807个独立场景, 其中包含不同相机轨迹捕获的图像序列, 为了保证训练速度, 将参考MVS2D中采样方式进行采样, 对807个独立场景进行采样1:20的采样, 选其中 700个数据集进行为训练数据集, 对剩余数据集再进行1:40的采样. 最终选用72574组图片(一幅源图像和两幅参考图像)进行训练和666组图片(包含107个独立场景)用于测试.

2.2.2 算法评估标准及结果对比

将根据深度估计中公认的评价指标对相关网络进行评估, 其中 ${d_i}$ 表示预测深度, $d_i^ * $ 表示真实深度值, N表示所有带真实标签的像素. 评价公式为绝对值相对偏差 (AbsRel)、线性均方根误差(RMSE)、线性均方根误差(RMSE)、相对平方差(SqRel), 不同阈值下的准确度 ${\delta _i}$ : 相对误差在阈值内预测像素的百分比.

$ Abs{Re} l = \frac{1}{N}\sum {\left| {\frac{{d_i^ * - {d_i}}}{{{d_i}}}} \right|} $

(12)

$ {\textit{RMSE}} = \sqrt {\frac{1}{N}\sum\nolimits_i^n {{{\left| {{d_i} - d_i^ * } \right|}^2}} } $

(13)

$ {\textit{SqRel}} = \frac{1}{N}{\sum {\left( {\frac{{d_i^ * - {d_i}}}{{d_i^ * }}} \right)} ^2} $

(14)

$ \max \left(\frac{{{d^ * }}}{{{d}}}, \frac{{{d}}}{{{d^ * }}}\right) \leqslant {\delta _i}, \; {\delta _i} = 1.25, {1.25^2}, {1.25^3} $

(15)

Time (ms): 为了更加适配嵌入式设备Jeston NX, 本实验中将模型设置为半径度(Float16), 图片的尺寸为640×480, 在Jeston NX上进行实时的模型速率的验证. 为了保证数据的准确性, 将进行300次的推理然后选其平均值.

表3给出了在公开数据集ScanNet上公开算法^{[2, 6,9,10]}的对比结果(部分数据来源于MVS2D), 其中MVS2D基于多层极线注意力机制, 其在精度与速度在公开算法中为最优结果. 同时, 可视化了所提出的MVS算法在ScanNet数据集上的预测结果, 如图3所示, 为了更好说明算法的效果, 同样可视化了MVS2D预测结果进行对比, 可视化工具为Python中matplotlib工具包中热力图显示模块, 可以看出所提出的算法在ScanNet数据上展现出了较高的精度, 对于低纹理与被遮挡的地方有较好的补充, 同时在Jeston Xavier NX 上的推理速度仅为0.17 s.

2.3 真实环境实验展示 2.3.1 VINS扩展方法

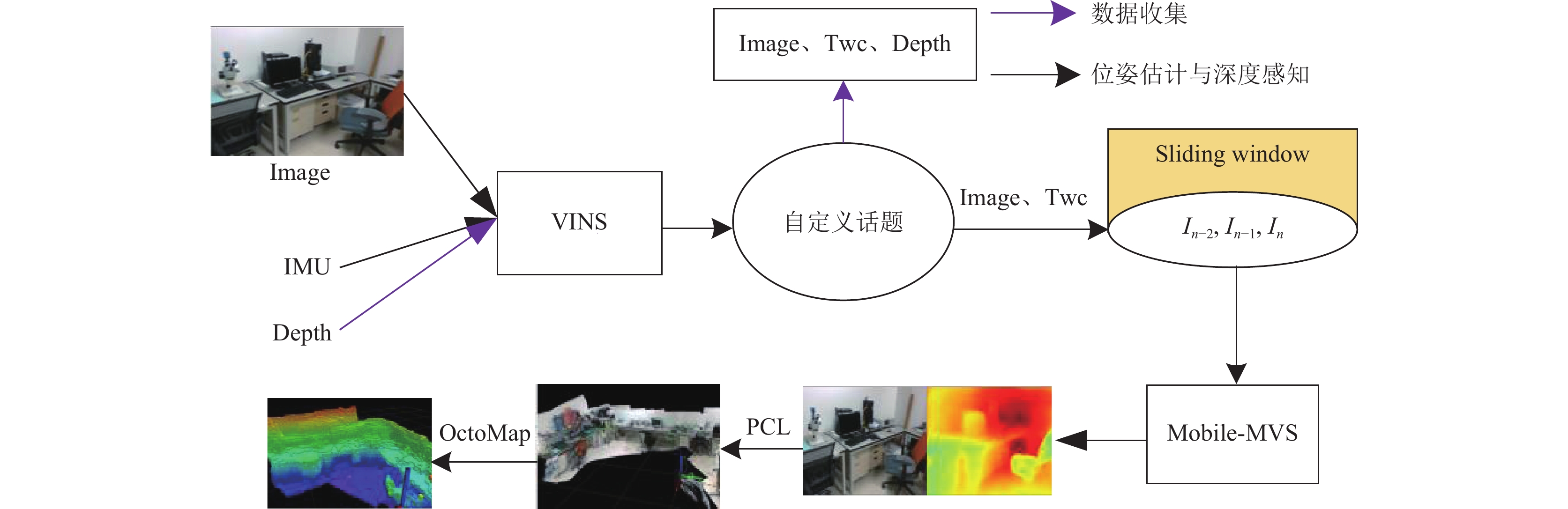
为了验证所提出方法的扩展性与简化现实环境下MVS数据收集流程, 同时满足机器人多元化需求与多设备之间的高效通信, 将基于ROS通信机制, 采用一种级联的方法对当下流行的嵌入式视觉SLAM框架VINS^[19]进行扩展. 其流程如图4所示.

所提出的VINS扩展框架主要包含两个部分: 数据收集、位姿估计与深度感知. 位姿估计感知. 位姿估计与深度感知处理流程为: 图片与IMU数据经过VINS获取图片与对应的位姿, 通过ROS特有的自定义话题传入到Mobile-MVS中进行处理, 在处理过程中为了防止数据冗余与造成内存拥挤, 采用一种基于滑动窗口的形式, 对之前图片的信息进行有效利用, 经Mobile-MVS进行深度预测获得图片对应的深度图, 利用针孔成像原理对深度图与RGB图片进行拼接, 为了进一步保证点云输出的实时性, 将对点云进行八叉树(OctoMap)算法压缩, 生成轻量化可用于机器人导航、避障的点云地图.

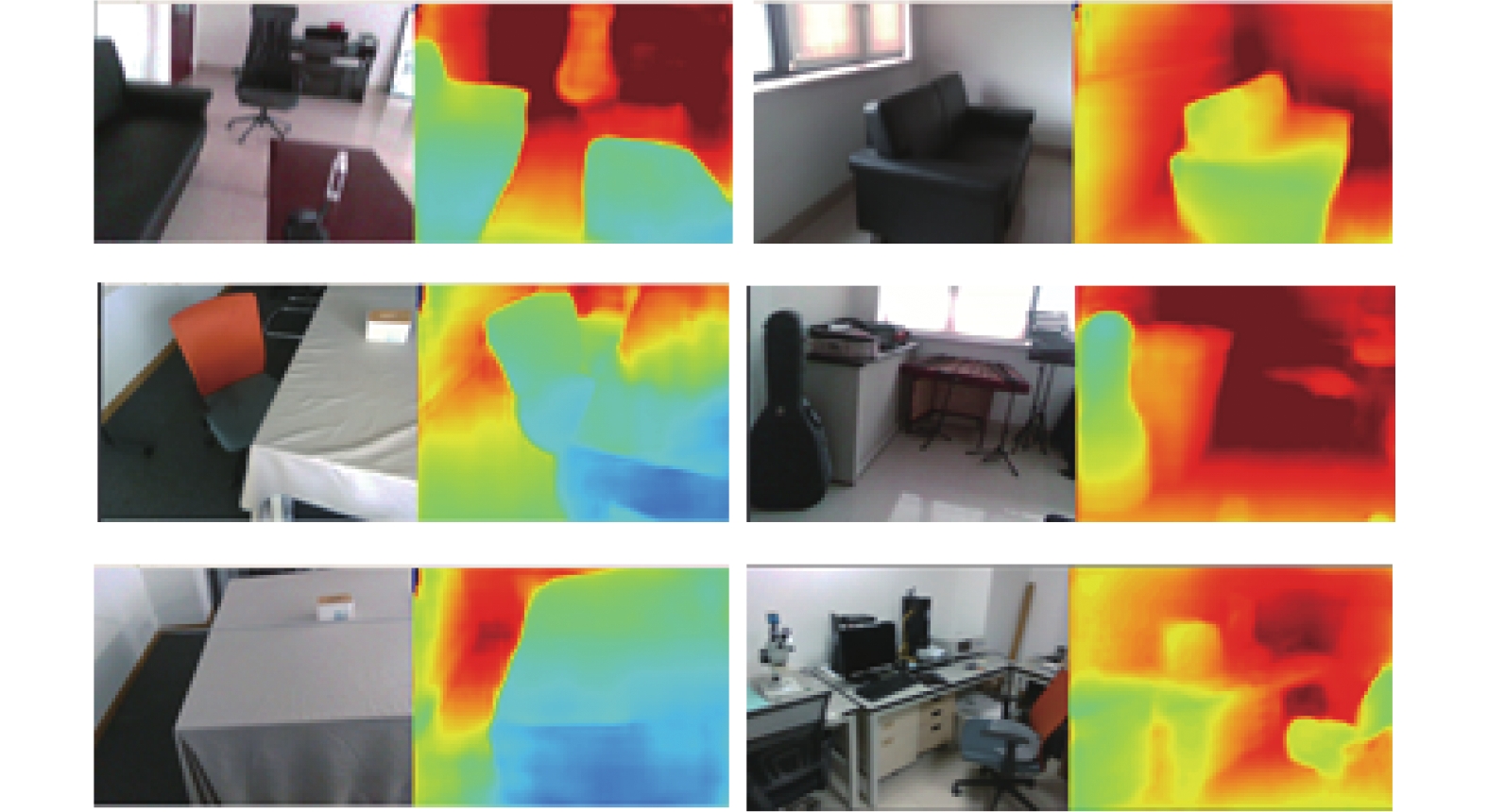
2.3.2 VINS扩展框架的实验结果对比

为了进一步展示提出方法的鲁棒性, 将以四旋翼机器人搭载D435I相机对室内真实环境的RGB图片、IMU数据、深度图进行收集. RGB和深度图片收集的像素为640×480、帧率为30 f/s. IMU数据收集的帧率为200 Hz. 所有的数据均在无人机绕室内正常飞行, 最终以ROS的数据格式bag进行存储. 利用所采集的数据在基于VINS扩展框架在CPU为锐龙R7-5800H、16 GB运行内存、显卡为RTX3050Ti的电脑端实现了实时的位姿估计和深度感知与三维重建, 经所提出鲁棒的训练集收集方法训练后, 其深度感知效果与三维重建效果分别如图5和图6所示. 为了进一步展现所提出方法的精度, 同样方法对D435i所采集的深度图、RGB图、IMU数据在VINS下进行三维重建, 由可视化地图可看出所提出方法具有较好的可扩展性与精度. 为了体现所提出算法在嵌入式设备上Jeston Xavier NX实现了10 Hz的位姿估计与5 Hz的像素为480×384的深度图感知, 可以满足当下嵌入式机器人对于避障等算法实时性要求.

3 结束语

为了解决低算力嵌入式平台算力吞吐量低的问题, 本文基于MVS2D深度感知网络的极线注意力机制, 引入高效的编码MobileNetV3-Small与SE-Net网络, 设计了一款轻量级的MVS深度感知网络Mobile-MVS2D. 本文研究的内容主要从以下方面进行展开: (1)为了加速模型的推理速度与训练速度, 采样MobileNetV3-Small进行信息编码(特征提取)与迁移学习, 为了增强解码信息在解码层引入SE注意力机制, 提出一种新的SE-upConv5结构. (2)为了增强模型在现实环境的表达能力, 基于VINS提出一种简易的数据集收集、深度估计与三维重建框架. 结果如下: 1) 在ScanNet数据集可以达到较高的精度, 相对于当下公开算法精度最高与速度最快的MVS网络架构MVS2D在图像尺寸为640×480、精度为Float16、数量为3的图片下, 在精度损失有限情况下, 速度提升了20%左右, 预测一张图片在嵌入式设备Jeston NX上仅需168 ms, GPU仅消耗1 GB. 2) 在所提出的VINS三维重建框架下实现了较高质量的点云地图, 同时在嵌入式设备上Jeston Xavier NX实现了10 Hz的位姿估计与5 Hz的像素为480×384的深度图感知.