基于SATLike3.0局部搜索求解器的算法改进

引用本文

于瀚一, 陈寅. 基于SATLike3.0局部搜索求解器的算法改进. 计算机系统应用, 2023, 32(5): 300-307.http://www.c-s-a.org.cn/1003-3254/9074.html

Yu HY, Chen Y. Algorithm Improvement Based on Local Search Solver SATLike3.0. Computer Systems and Applications, 2023, 32(5): 300-307(in Chinese).http://www.c-s-a.org.cn/1003-3254/9074.html

基于SATLike3.0局部搜索求解器的算法改进

于瀚一¹, 陈寅^1,2

1. 华南师范大学计算机学院, 广州 510631;
2. 华南师范大学人工智能学院, 佛山 528225

收稿日期：2022-10-20; 修改日期：2022-11-18; 采用时间：2022-11-30; csa 在线出版时间：2023-02-24

通讯作者：陈寅, E-mail: ychen@scnu.edu.cn.

摘要：部分最大可满足性问题是可满足性问题的重要变体, 它可以同时处理硬约束和软约束, 因此可以对广泛的现实问题进行建模. 局部搜索求解器是为该问题寻找高质量解的主流方法, 它依赖于问题实例的初始数据状态. 本文针对局部搜索求解器SATLike3.0的初始解生成过程, 提出了优先满足硬约束的改进策略, 最终得到的算法名为HFCRP-F. 该算法作用于构造初始解和初始权重配置阶段, 主要包括优先传播尚未满足的硬约束中的未赋值变量, 以及根据已找到的解为约束增加初始权重, 由此指导后续的局部搜索过程. 本文采用MaxSAT Evaluation 2018–2021中的数据集对HFCRP-F和SATLike3.0进行测试, 结果表明HFCRP-F处理加权实例的性能明显优于SATLike3.0, 同时处理非加权实例的性能与SATLike3.0基本持平.

关键词: SATLike3.0 动态局部搜索算法反馈机制初始解生成初始权重配置

Algorithm Improvement Based on Local Search Solver SATLike3.0

YU Han-Yi¹, CHEN Yin^1,2

1. School of Computer Science, South China Normal University, Guangzhou 510631, China;
2. School of Artificial Intelligence, South China Normal University, Foshan 528225, China

Abstract: The partial maximum satisfiability problem is an important variant of the satisfiability problem. It can handle both hard and soft constraints simultaneously and thus can model a wide range of realistic problems. Local search solvers are the mainstream method to find high-quality solutions to the partial maximum satisfiability problem, and they rely on initial data states of problem instances. Aiming at the initial solution generation process of a local search solver, namely, SATLike3.0, this study proposes an improvement strategy that gives priority to satisfy the hard constraints, and the obtained algorithm is dubbed HFCRP-F. The algorithm works on the stages of initial solution construction and initial weight configuration, including propagating unassigned variables in unsatisfied hard constraints and adding initial weights to constraints based on found solutions, so as to guide the subsequent local search process. HFCRP-F and SATLike3.0 are tested by using data sets from MaxSAT Evaluation 2018–2021. The results reveal that HFCRP-F performs much better than SATLike3.0 in processing weighted instances and shows nearly the same performance as SATLike3.0 in processing non-weighted instances.

Key words: SATLike3.0 dynamic local search algorithm feedback mechanism initial solution generation initial weight configuration

1 引言

可满足性(SAT)问题广泛存在于科学和工业场景中, 其计算方法可以应用到包括人工智能、机器视觉、密码学、运筹学、数学等多个领域, 能够用来解释图着色问题、调度问题和选路问题等经典问题^{[1, 2]}.

部分最大可满足性问题(partial maximum satisfiability, PMS)和其加权版本(weighted partial maximum satisfiability, WPMS)是可满足性问题的重要变体^[3], 通过引入硬约束、软约束等概念实现了更强的表达力^[4], 因此获得了研究者的关注.

系统搜索与局部搜索^[5]是解决此类问题的两大方向, 目前局部搜索方法已被证明可以高效求解组合优化问题. 相比于系统搜索方法一定会得到最优解或不可满足证明的完备性, 局部搜索方法通常可以快速地找到一组高质量解, 更及时地响应现实需求. 近年来格局检测、权重调整等策略的提出证明了局部搜索算法仍有较大研究潜力, 并且研究人员已经积累了将其应用于科学和工程领域各类问题的成功经验: 著名的商用优化求解器Gurobi中集成了局部搜索方法^[6], 已被应用至沃尔玛的供应链场景中^[7]. 由此可见发展局部搜索算法对解决理论和现实问题都是必要的.

目前基于动态权重调整的局部搜索求解器是解决(W)PMS问题最先进的方法之一. 在局部搜索的过程中, 该类求解器不断调整各个子句的权重以跳出局部最优. SATLike是首个在工业实例上具备竞争力的动态局部搜索求解器, 它集成了新颖的权重调整机制和基于单元传播的初始解构造方法^{[8, 9]}; FPS改进了SATLike的变量选择机制, 在无法通过翻转一个变量得到更优解时考虑翻转一组变量^[10]; NuWLS-c针对SATLike的权重配置策略提出了更细粒度的解决方案且在MaxSAT Evaluation (MSE) 2022中表现优异^[11].

本文通过对SATLike3.0重要组件的分析, 得出了改良初始解生成过程的方案, 并辅以轻量级的反馈机制, 实现了SATLike3.0求解质量的提升. 具体是提出了基于优先传播硬变量和利用局部最优解指导变量极性选择的局部搜索求解器初始解生成算法, 利用局部搜索求解器依赖于程序初始数据状态的特点, 帮助SATLike3.0找到更优解. 我们选择SATLike3.0作为基准求解器的原因在于它是MSE 2018的获胜者之一, 并且被集成于最先进的不完备求解器当中, 提高SATLike3.0的性能对推动不完备求解器的发展有积极意义.

本文第2节对(W)PMS问题、求解的关键技术和专有名词进行介绍. 第3节对基准算法SATLike3.0进行介绍. 第4节提出算法改进的思路和具体实现. 第5节通过在标准数据集上测试对新旧算法进行比较评估. 第6节提出我们对于改进策略的思考. 第7节对本文的工作内容进行总结和展望.

2 预备知识和定义

(W)PMS问题: 通常采用CNF范式表示. 一个CNF公式是子句集合的合取, 子句是文字集合的析取, 而文字是一个布尔变量或者它的非; 一个子句若有至少一个文字为真, 则这个子句被满足, 否则是未满足的子句; 当所有子句被满足时, 整个CNF公式才被满足. (W)PMS在此基础上引入了硬子句和软子句, 其中硬子句为必须要被满足的子句, 软子句需要尽可能多地满足. 用CNF表述的(W)PMS问题实例即为给定命题公式, 找到一组变量的赋值, 使得其满足所有的硬子句, 并满足最多(权重)数量的软子句. 若一组解使得所有硬子句被满足, 则可称这组解是公式的一组可行解.

单元传播: 仅包含一个文字的子句被称为单元子句. 为了满足这种子句, 必须使其仅有的文字为真. 那么公式中所有包含这个文字的子句都可以被删除(由于这个文字为真而被满足); 公式中所有包含这个文字的非的子句都可以删除这个文字的非(这个文字的非一定为假, 所以对子句是否被满足没有影响).

硬变量: 所有出现在硬子句中的变量称为硬变量; 其余变量为软变量. 需要为变量赋值从而使其代表的文字为真或假.

软得分sscore(v): 考虑将变量赋值为真或假, 软得分为将当前变量赋值后, 被满足软子句数量(权重)的增量的最大值.

翻转变量的得分score(v): 假设变量v已被赋值, 翻转这个变量的得分为翻转之后被满足子句数量(权重)的增量.

代价cost: 对于PMS, 如果所有硬子句被满足, 那么cost为未满足软子句的数量, 否则为正无穷; 对于WPMS, 如果所有硬子句被满足, 那么cost为未满足软子句的权重, 否则为正无穷.

3 SATLike3.0

SATLike3.0^[12]是一种局部搜索求解器. 局部搜索一般的流程为: 随机生成一组初始赋值; 选择一个未被满足的子句中的变量并翻转; 每当找到一组更优解则记录当前解的信息; 当翻转变量的次数达到了上限, 会重新生成一组初始解并继续搜索; 满足了全部子句或达到预设的超时时间则退出算法, 返回找到的最优解信息. SATLike3.0也遵循这个流程, 但初始解生成方法使用了UPDeci算法, 局部搜索过程也采取了一定的贪心策略.

3.1 初始解生成算法UPDeci

UPDeci^[13]利用单元传播技术, 在为变量赋值的同时化简公式. 传播变量的优先级从高到低依次为硬单元子句中的变量、软单元子句中的变量、未赋值的变量. 由于单元传播机制会缩减未满足子句的长度, 因此该算法执行过程中会不断产生新的单元子句. 算法在得到一组完整的赋值后结束.

3.2 局部搜索过程

SATLike3.0基于变量的score选取并翻转变量. 如果存在score为正数的多个变量, 则随机采样常数个后翻转其中的一个变量; 否则更新子句的权重, 随后翻转未满足的硬子句或软子句中score最大的变量.

子句权重更新的策略为有(1–sp)的概率为未满足的子句增加权重, 有sp的概率为已满足的子句减少权重. sp取决于问题类型及规模, 其值不大于0.01^[14].

4 HFCRP-F 4.1 改进思路

在当前不存在单元子句时, UPDeci会随机为一个未赋值的变量赋值. 对于某些实例来说, 这个过程会频繁执行, 因此可以添加额外的策略进行改进; 参考局部最优解进行赋值的方法已被证实是有效的, 因此可以从局部最优解中提取信息引导算法^[15-17].

优先传播硬变量: UPDeci会对一些变量随机赋值, 这会为初始解提供多样性. 然而局部搜索过程拥有一定的纠错能力, 因此我们希望可以更快地搜索到可行解并对其进行优化. 在不存在单元子句时, 我们会使算法优先传播未满足的硬子句中的变量. 这样既保证了硬子句中的变量比软子句中的变量有较高的优先级, 又使得初始解的多样性得到了保证——当硬子句全部被满足或矛盾时算法退化为原策略.

反馈机制: 在传播硬单元子句时如果遇到矛盾, UPDeci会检查sscore(v)是否为非正数, 是则会随机为变量赋值. 这里我们可以参考当前的局部最优解, 将此最优解中的值赋给变量.

反馈机制的增强: SATLike3.0依赖于子句权重的差别——算法中的初始解生成过程(UPDeci)和局部搜索过程均使用子句的权重计算变量的得分. 考虑到算法每次都基于不同的初始情况进行搜索, 子句的初始权重要重新初始化. 然而我们仍然可以从已找到的局部最优解中提取信息: 总是被满足的子句有更大概率出现在最优解中, 因此可以增加它们的初始权重, 以引导算法倾向于优先满足这些“确定”的子句.

4.2 具体实现

根据上文针对UPDeci的改进思路, 一方面随机传播尚未满足的硬子句中的变量, 另一方面实现了反馈机制, 得到的初始解生成算法名为UPDeci-HFCRP-F. 整个动态局部搜索算法名为HFCRP-F (hard falsified clauses random propagation with feedback).

4.2.1 初始解生成算法UPDeci-HFCRP-F

如算法1所示, 在传播硬子句遇到矛盾的情况下会首先检查sscore(v), 如果小于等于0则会参局部最优解进行赋值; 并且在随机选择变量赋值之前插入了优先传播硬变量的过程: 先选择一个未满足的硬子句, 再选择该子句中第一个未赋值的文字, 赋予其真值.

4.2.2 初始权重配置

开辟一个子句额外初始权重数组. 每当搜索过程中找到一个更优解, 为每个当前解中被满足的软子句初始额外权重加1. 这个操作会影响初始解生成时变量的选值和局部搜索过程初期的决策, 进而对局部搜索过程产生深远的影响.

算法1. UPDeci-HFCRP-F

输入: (W)PMS问题实例 $\scriptstyle F $

输出: $\scriptstyle F $ 中变量的一组完整赋值

1.　 while 存在未赋值的变量 do

2.　　 if 存在未满足的硬单元子句 then

3.　　　 $\scriptstyle c:= $ 选择一个硬单元子句;

4.　　　 if $\scriptstyle c $ 遇到矛盾 then

5. 　　　　 $\scriptstyle x:= $ 其中的变量;

6.　　　　 if $\scriptstyle sscore\left(x\right) > 0 $ then

7. 　　　　　根据 $\scriptstyle sscore\left(x\right) $ 为 $\scriptstyle x $ 赋值, 化简 $\scriptstyle F $ ;

8.　　　　 else

9. 　　　　　参考局部最优解为 $\scriptstyle x $ 赋值, 化简 $\scriptstyle F $ ;

10.　　　 else

11. 　　　　使用 $\scriptstyle c $ 执行单元传播

12.　　 else if 存在未满足的软单元子句 then

13.　　　 $\scriptstyle c:= $ 选择一个软单元子句;

14.　　　 if $\scriptstyle c $ 遇到矛盾 then

15. 　　　　 $\scriptstyle x:= $ 其中的变量;

16. 　　　　随机为 $\scriptstyle x $ 赋值, 化简 $\scriptstyle F $ ;

17. 　　　 else

18. 　　　　使用 $\scriptstyle c $ 执行单元传播;

19. 　　 else if 存在未满足的硬子句

20.　　　 $\scriptstyle c:= $ 选择一个未满足的硬子句;

21.　　　 $\scriptstyle x:= $ 其中一个未赋值变量;

22.　　　将 $\scriptstyle x $ 在 $\scriptstyle c $ 中的文字赋予真值, 化简 $\scriptstyle F $ ;

23.　　 else

24. 　　　 $\scriptstyle x:= $ 一个未赋值变量;

25. 　　　随机为 $\scriptstyle x $ 赋值, 化简 $\scriptstyle F $ ;

26. 　 return 一组完整赋值;

5 实验结果与分析 5.1 实验设置

数据集: 我们在MSE 2018–2021不完备赛道中的PMS和WPMS实例上测试HFCRP-F以及原始算法SATLike3.0, 将对应的数据集记为pms 2018、wpms 2018等. 需要注意的是, 我们将至少包含一个硬子句的问题实例视作(W)PMS.

算法实现: HFCRP-F用C++编写, 使用g++工具“-O3”参数编译, 与SATLike3.0一致.

实验环境: 所有实验在Windows 10的WSL子系统运行(Ubuntu 20.04), 计算机配置为AMD Ryzen 7 4800U @ 1.80 GHz.

对比指标: 两个求解器在每个实例上都运行300 s, 记录其找到的最优解信息(最优cost、对应时间). 对于每个数据集, 我们会统计两个求解器分别的获胜次数(找到比对方更低的代价)和求出最终解的平均时间, 记为“#win”和“time”; 每个数据集包含的实例个数记作“#inst”; 我们还使用MSE 2019的不完备分数比较两个求解器的求解质量, 记作“score”. 如果求解器在一个实例上没有找到可行解, 则将time记为600 s、score记为0.

$ score={\displaystyle \sum _{}^{}\frac{所有求解器找到的最优解\text{+1}}{当前求解器找到的最优解\text{+1}}} $

(1)

实验结果: 如表1所示, HFCRP-F在所有数据集的score都优于SATLike3.0; HFCRP-F在pms 2021的获胜次数略低于SATLike3.0, 而在其余的数据集上占据优势, 尤其在wpms 2019和wpms 2020上优势明显. 综上, HFCRP-F在解的质量方面取得了显著进步.

表 1 实验结果

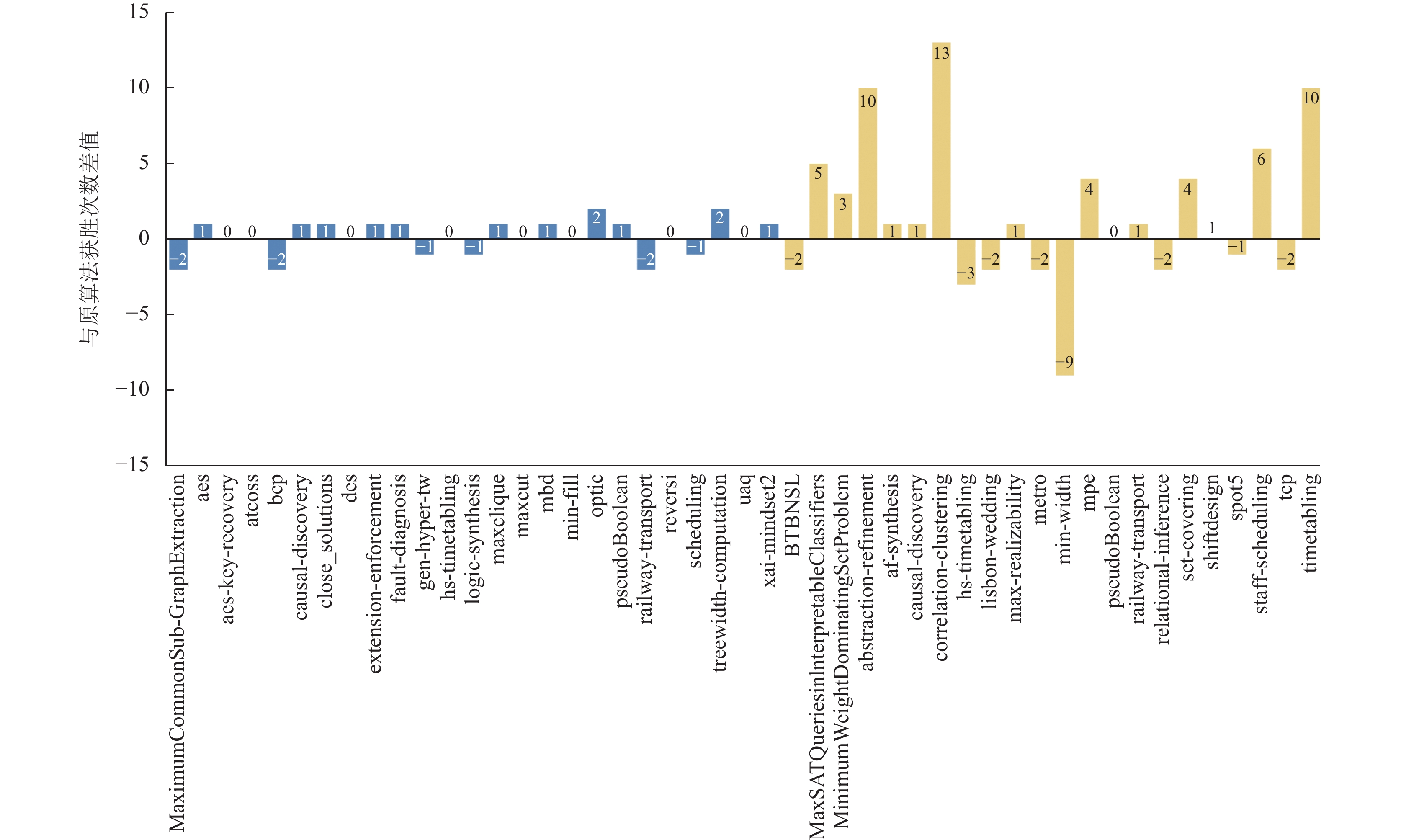
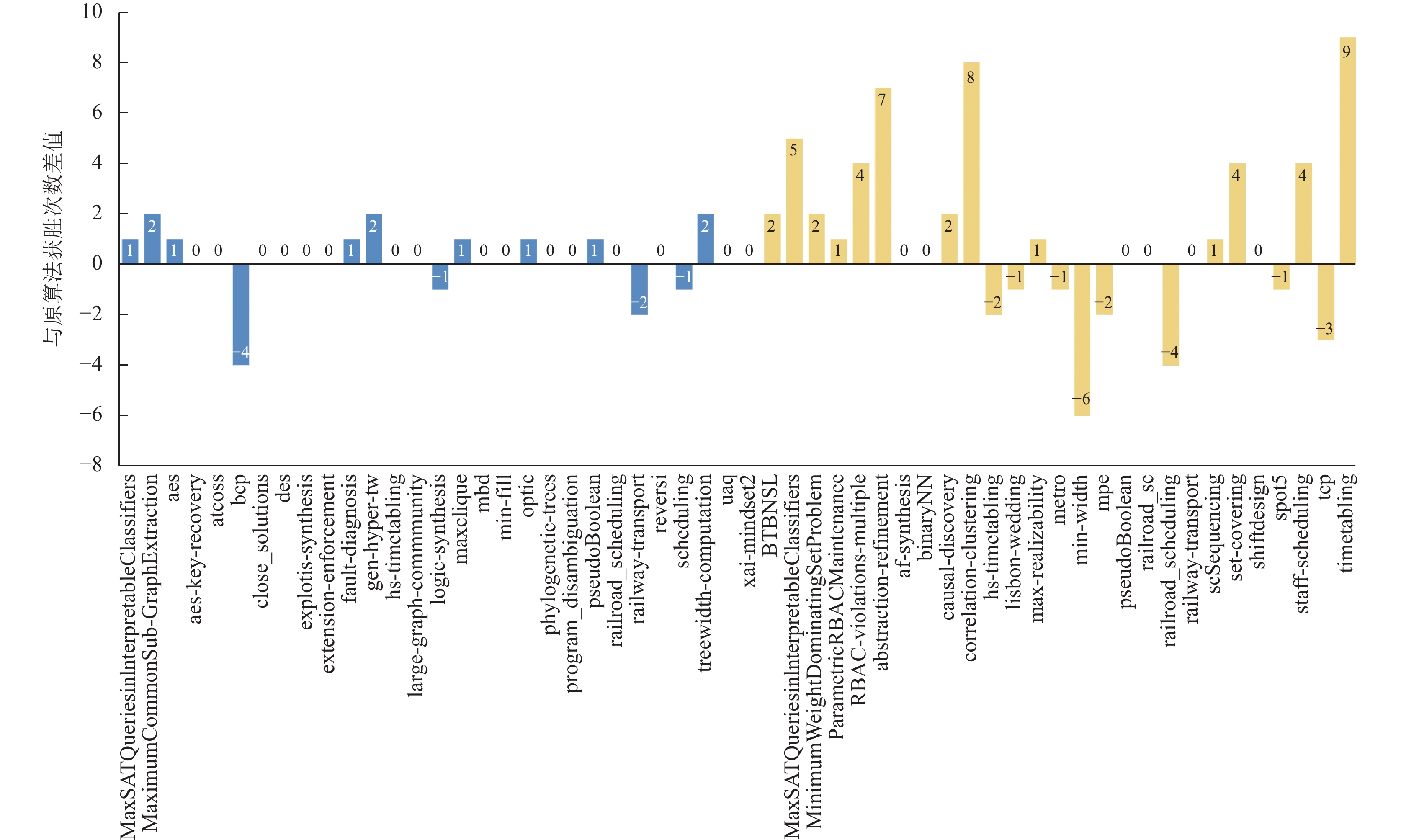
更多实验细节如图1–图3所示. y轴表示HFCRP-F找到更低cost的频数, x轴表示不同的问题实例类. PMS和WPMS实例的统计结果分别用蓝色和黄色表示. 结果显示两个求解器各有自己擅长求解的问题, 而HFCRP-F尤其更擅长求解WPMS问题.

5.2 主要改进机制工作流程示例

本节将演示仅为UPDeci添加优先传播硬变量机制的初始解构造过程, 记作“UPDeci-HRP”.

如图4所示: 命题公式用“F”表示, 硬子句用“H”表示, 软子句用“S”表示, 括号内的数字代表文字; 我们将逐步展示两种方法构造初始解的过程, 其中, 序号的下标表示执行的动作, 上标表示操作的对象. 例如, ${①}_{{\rm{hup}}}^{-5}$ 表示根据“hup”规则传播变量“5”, 值为假(以下简称传播“–5”). “hup” (hard unit propagation)表示单元传播硬子句; “sup” (soft unit propagation)表示单元传播软子句; “ran” (random)表示随机选择一个未赋值的变量, 赋值后传播. 需要注意的是, “ran”动作的结果并不固定, 我们只是列出了一种可能的计算结果. 以硬子句 $\{ ( - 2 \vee 4 \vee 5) \wedge ( - 5) \wedge ( - 4 \vee 5 \vee - 2)\}$ , 软子句 $\{ (1 \vee 2) \wedge ( - 2 \vee 3)\} $ 的命题公式为例, 说明UPDeci与UPDeci-HRP工作流程上的差异.

图 1 (w)pms 2019实验结果

图 2 (w)pms 2020实验结果

图 3 (w)pms 2021实验结果

图 4 UPDeci与UPDeci-HRP工作流程对比

UPDeci优先传播硬单元子句, 其次是软单元子句, 再次是未赋值的变量. 因此对于图4中的公式, UPDeci首先传播“−5” (①); 此时没有单元子句, 因此随机传播一个未赋值变量, 假设传播“2” (②); 随后在传播“4”时遇到了矛盾, 由于sscore(4)不为正数, 因此随机赋值, 假设赋值为假(③, ④); 最后传播软单元子句“3”并随机为变量“1”赋值(⑤, ⑥). 最终, UPDeci生成的初始解为{1, 2, 3, −4, −5}, 该解的代价为硬子句(−2, 4, 5)的权重.

同样对于该实例, 当不存在单元子句时, UPDeci-HRP优先传播一个未赋值的硬变量(②), 使得接下来仅需确定性地执行两轮单元传播即构造了一组代价为0的可行解.

5.3 对改进思路的进一步理解

SATLike3.0的搜索过程: 每个未满足的子句都“有意愿”使自己满足, 表现为将自身权重作为score或sscore贡献给其中的变量, 结果是未满足的子句争夺变量的“赋值权”, 其目的是促使算法为其中的变量赋予真值; 已满足的子句也会捍卫变量的极性, 表现为用自身权重降低变量的score或sscore. 值得注意的是, 已满足的子句只会在其中只有一个为真的文字时才会“阻止”改变这个文字的值, 因为一旦将这个文字变为假, 那么子句本身将从满足变为不满足状态.

在初始解生成过程中, 只在遇到矛盾的硬单元子句时参考局部最优解. 初始解的多样性是至关重要的. 尽管搜索过程具有一定的“纠错”能力, 但如果总是围绕相似的初始解搜索, 则必然会导致性能降级. 此外这个过程可以与HFCRP配合: HFCRP优先传播未赋值的硬变量, 如果它带来了好的决策, 那么就很有希望将结果留在搜索到的局部最优解中, 因此在处理矛盾时参考局部最优解可能是一个好的选择.

只调节软子句权重: 求解器为软子句设置了权重上限, 因此为了使整个公式被满足, 硬子句的权重会在一次次调整中增长到足够大的数值, 以至于不惜牺牲一定的代价换取硬子句的满足. 因此我们没有关注硬子句的权重配置. 这也是没有从历史搜索的结果中提取软子句权重的一部分原因——许多软子句的权重达到了上限, 无法反映出子句权重的差异.

对于搜索第1个可行解的影响: 反馈机制依赖于第1个可行解, 因此此时只有HFCRP生效. HFCRP在初始解生成阶段尝试满足硬子句, 然而它缩小了初始解的空间, 并且影响了翻转变量的得分, 因此可能对找第1个可行解有害. 不过从实验结果来看, HFCRP-F总体受益于该机制.

6 结论与展望

我们主要的贡献是结合了优先传播硬变量和从局部最优解提取信息两个方面, 更加确定性地处理了SATLike3.0中严格执行随机策略的部分.

向较大规模的随机领域添加合适的策略可以更快地引导算法达到局部最优, 但也增加了计算复杂度, 进而可能增加求解时间. 相比原算法, 我们的算法在WPMS上取得了成功, 在PMS上擅长处理的问题族却与原算法有较大差别, 然而本文并没有探讨出这些差异的来源, 原因在于通过强制改变算法流程的手段粒度较大, 尝试只通过调整权重达成类似的效果或许是更好的解决方案.

目前已有研究在结合CDCL求解器和局部搜索求解器的应用上取得突破, 如Cai等^[18]提出了将局部搜索过程中得到的统计信息加以利用, 指导CDCL求解引擎的运作过程. 未来会继续研究局部搜索算法利用历史搜索信息的方式, 以及该类型求解器与CDCL求解器的混合使用.

参考文献

[1]	Demirović E, Musliu N, Winter F. Modeling and solving staff scheduling with partial weighted MaxSAT. Annals of Operations Research, 2019, 275(1): 79-99. DOI:10.1007/s10479-017-2693-y
[2]	Xu H, Rutenbar RA, Sakallah K. Sub-SAT: A formulation for relaxed Boolean satisfiability with applications in routing. IEEE Transactions on Computer-aided Design of Integrated Circuits and Systems, 2003, 22(6): 814-820. DOI:10.1109/TCAD.2003.811450
[3]	王国俊. 数理逻辑引论与归结原理. 北京: 科学出版社, 2003.
[4]	Miyazaki S, Iwama K, Kambayashi Y. Database queries as combinatorial optimization problems. Proceedings of the International Symposium on Cooperative Database Systems for Advanced Applications. Kyoto: CODAS, 1996. 477–483.
[5]	艾森阳, 宋振明, 沈雪. 基于变量混合特征的分支启发式策略. 计算机系统应用, 2020, 29(3): 200-205. DOI:10.15888/j.cnki.csa.007288
[6]	Achterberg T. What’s new in Gurobi 9.0. https://www.gurobi.com/wp-content/uploads/2019/12/Gurobi-90-Overview-Webinar-Slides-1. pdf. (2022-05-11)[2022-11-18].
[7]	Industry solution sheet: Supply chain. https://www.gurobi.com/wp-content/uploads/2022/08/IndustrySolutionSheet-SupplyChain.pdf?x58432. (2022-02-11)[2022-11-18].
[8]	Lei ZD, Cai SW. Solving (weighted) partial MaxSAT by dynamic local search for SAT. Proceedings of the 27th International Joint Conference on Artificial Intelligence. Stockholm: AAAI Press, 2018. 1346–1352.
[9]	Lei Z, Cai S, Geng F, et al. SATLike-c: Solver description. MaxSAT Evaluation 2021, 2019, 19.
[10]	Zheng JZ, Zhou JR, He K. Farsighted probabilistic sampling based local search for (weighted) partial MaxSAT. arXiv:2108.09988, 2021.
[11]	Chu Y, Cai SW, Lei ZD, et al. NuWLS-c: Solver description. In: Bacchus F, Berg J, Järvisalo M, et al., eds. MaxSAT Evaluation 2022: Solver and Benchmark Descriptions. Helsinki: University of Helsinki, 2022.
[12]	Cai SW, Lei ZD. Old techniques in new ways: Clause weighting, unit propagation and hybridization for maximum satisfiability. Artificial Intelligence, 2020, 287: 103354. DOI:10.1016/j.artint.2020.103354
[13]	Cai SW, Luo C, Zhang HC. From decimation to local search and back: A new approach to MaxSAT. Proceedings of the 26th International Joint Conference on Artificial Intelligence. Melbourne: AAAI Press, 2017. 571–577.
[14]	Hutter F, Tompkins DAD, Hoos HH. Scaling and probabilistic smoothing: Efficient dynamic local search for SAT. Proceedings of the 8th International Conference on Principles and Practice of Constraint Programming. Ithaca: Springer, 2002. 233–248.
[15]	Demirović E, Chu G, Stuckey PJ. Solution-based phase saving for CP: A value-selection heuristic to simulate local search behavior in complete solvers. Proceedings of the 24th International Conference on Principles and Practice of Constraint Programming. Lille: Springer, 2018. 99–108.
[16]	Nadel A. Anytime weighted MaxSAT with improved polarity selection and bit-vector optimization. Proceedings of 2019 Formal Methods in Computer Aided Design (FMCAD). San Jose: IEEE, 2019. 193–202.
[17]	Nadel A. Polarity and variable selection heuristics for SAT-based anytime MaxSAT. Journal on Satisfiability, Boolean Modeling and Computation, 2020, 12(1): 17-22. DOI:10.3233/SAT-200126
[18]	Cai SW, Zhang XD. Deep cooperation of CDCL and local search for SAT. Proceedings of the 24th International Conference on Theory and Applications of Satisfiability Testing. Barcelona: Springer, 2021. 64–81.