计算机系统应用  2023, Vol. 32 Issue (5): 188-195   PDF    
引用本文
代刚, 吴湘宁, 邓玉娇, 涂雨, 张锋, 方恒. 基于孪生深度特征融合残差网络的PCB缺陷分类模型. 计算机系统应用, 2023, 32(5): 188-195.http://www.c-s-a.org.cn/1003-3254/9073.html   
Dai G, Wu XN, Deng YJ, Tu Y, Zhang F, Fang H. PCB Defect Classification Model Based on Siamese Deep Feature Fusion Residual Network. Computer Systems and Applications, 2023, 32(5): 188-195(in Chinese).http://www.c-s-a.org.cn/1003-3254/9073.html   
基于孪生深度特征融合残差网络的PCB缺陷分类模型
代刚, 吴湘宁, 邓玉娇, 涂雨, 张锋, 方恒     
智能地学信息处理湖北省重点实验室(中国地质大学(武汉)), 武汉 430078
收稿日期：2022-10-19; 修改日期：2022-11-18; 采用时间：2022-11-30; csa 在线出版时间：2023-02-28
基金项目：国家自然科学基金(U21A2013); 智能地学信息处理湖北省重点实验室开放基金(KLIGIP-2018B14)
通讯作者：吴湘宁, E-mail: wxning@cug.edu.cn.
摘要：在电子工业领域中, 印刷电路板(printed circuit board, PCB)缺陷检测已经变得越来越重要. PCB的部分微小损伤或者不规则损伤与其密集复杂的排线等视觉纹理信息高度相关. 传统卷积神经网络提取特征向量, 容易丢失纹理特征等中级视觉特征信息, 导致对于细微损伤和不规则损伤的检测效果不明显. 针对这一问题, 提出了基于孪生深度特征融合残差网络(Siamese deep feature fusion residual network)的PCB损伤分类模型. 模型的骨干网络采用ResNet50. 特征提取阶段将纹理信息等中级视觉特征和神经网络最终输出的高级语义特征融合为一个32维的特征向量. 两个特征的向量的相似性用L2距离表示, 用于判断PCB是否有缺陷. 在训练阶段应用了三元损失和交叉熵损失, 多个损失函数的组合提高了网络的准确性. 通过实验验证了模型的有效性, 在测试数据集上的准确率达到了(95.42±0.31)%的准确率, 实现了模型在PCB缺陷分类检测的可行性.
关键词: 孪生网络    残差网络    特征融合    缺陷分类    印刷电路板 (PCB)    
PCB Defect Classification Model Based on Siamese Deep Feature Fusion Residual Network
DAI Gang, WU Xiang-Ning, DENG Yu-Jiao, TU Yu, ZHANG Feng, FANG Heng     
Hubei Key Laboratory of Intelligent Geo-information Processing (China University of Geosciences), Wuhan 430078, China
Abstract: In the electronic industry, defect detection of printed circuit board (PCB) has become more and more important. Some minor or irregular damage of PCBs is closely related to visual texture information, such as dense and complex PCB cables. Feature vectors extracted from the traditional convolutional neural network are prone to lose the intermediate visual feature information such as texture features, which results in an insignificant detection effect for minor and irregular damage. To solve this problem, this study proposes a PCB damage classification model based on a Siamese deep feature fusion residual network, and the model’s backbone network is ResNet50. In the feature extraction stage, the intermediate visual features such as texture information and the high-level semantic features finally output by the neural network are fused into a 32-dimensional feature vector. The similarity between the vectors of the two features is represented by the L2 distance, which is used to judge whether the PCB is defective. Triplet loss and cross-entropy loss are applied in the training phase, and the combination of multiple loss functions improves the accuracy of the network. The validity of the model is verified by experiments, and the accuracy on the test data set reaches (95.42±0.31)%. This indicates the feasibility of the model in PCB defect classification and detection.
Key words: Siamese network     residual network     feature fusion     defect classification     printed circuit board (PCB)    

1 引言

印刷电路板(printed circuit board, PCB)是电子工业中的重要部件, 在智能家电、医疗保健、生物传感器等领域都有着广泛的应用[1]. PCB作为各类电子元器件的支撑体和电气连接的载体, 保证其稳定的质量显得尤为重要, PCB的质量检测成为其生产制造过程中质量控制的关键步骤[2]. 近年来, 随着我国PCB生产的迅速发展, 其缺陷检测也成为一个重要的研究课题.

早期PCB的缺陷检测主要依靠流水线工人在高亮度光源条件下的人工检测. 然而人工检测具有主观性, 存在误检和漏检的情况, 进而导致检测准确率低下的问题. 此外, 高亮度的检测环境不支持工人长时间工作, 不仅会使检测效率降低, 还会给工人的眼睛带来伤害.

为了解决人工检测存在的问题, 自动光学检测(automatic optical inspection, AOI)技术在PCB的缺陷检测中得到研究人员的重视, 并在相关领域取得了成果[3, 4]. AOI技术不仅克服了人工检测效率低、成本高的问题, AOI技术作为一种非接触式的检测技术, 避免了检测时与PCB表面的接触造成的损伤. 但是AOI技术通常使用的方法有图像识别方法[5]和基于模板匹配的方法[6], 这些方法对于光照条件和检测样本的几何性质敏感, 因此该方法对于不同类型的PCB样本泛化能力不高[7].

近年来, 深度学习方法已经被证明在图像分类和缺陷检测等问题领域有着出色的性能[4, 7]. 基于深度学习的方法分为两个主要框架: 检测网络[8]和分割网络[9]. 检测网络的任务是检测和分类缺陷所在的边界框, 可以进一步分为单阶段和两阶段检测算法.

单阶段检测算法主要有YOLO系列算法[8]、单次检测器(SSD)[10]等, 检测速度快但是准确率低. 两阶段检测算法主要有区域卷积神经网络(R-CNN)系列算法[11]. 两阶段检测算法通常具有较高的检测精度, 但检测速度需要进一步提高. Ding等人提出了一种结合Fast R-CNN和特征金字塔的微小缺陷检测网络(TDD-net)来检测PCB的细微缺陷[12]. 相比之下, 分割网络将通过逐像素分割获得缺陷区域而不是边界框[9], 这可以进一步提高检测精度并获得缺陷的面积和形状等. 例如, Li等人提出了一种端到端的多任务学习网络来检测手机的缺陷[9].

孪生网络是一种人工神经网络, 作为卷积神经网络的前沿模型, 孪生网络因其能够从成对的图像中学习并提取有用信息的能力而受到广泛关注. 它使用相同的权重和相同的架构, 同时在两个不同的输入向量上协同工作以生成可比较的输出向量[13]. Ling等人提出了一种深度孪生语义分割网络应用于PCB焊接的细微缺陷检测, 由于该网络是逐像素对缺陷进行分割, 具有较高精度, 但是模型的训练速度和检测速度都有待提高[14]. Miao等人提出一种成本敏感的孪生网络模型(CSS-Net), 该模型对于PCB的真实缺陷具有较高的检测精度, 但对于灰尘等不影响PCB质量的微缺陷检测精度较低, 该类缺陷仍需人工进行进一步检测[15].

为了克服前文描述方法的局限性, 提升PCB损伤检测的精度和速度, 本文提出基于孪生纹理特征融合残差网络的PCB缺陷分类模型. 在工业应用中, 只需判断PCB是否有缺陷, 并对有缺陷的PCB做报废处理, 无需判定缺陷的具体位置及种类, 因此, 相比于语义分割网络和目标检测网络等算法, 模型有更高的检测速度. PCB的排线复杂且密集, 缺陷通常包含微小缺陷和不规则缺陷. 通常PCB的微小缺陷和不规则缺陷往往和PCB的焊接点、排线分布等纹理信息有很高的相关性. 通过特征融合残差网络提取PCB的纹理特征和高级语义特征并对其进行融合, 输出32维特征向量, 提高了对包含小目标损伤和不规则损伤PCB的检测精度. 通过比较特征向量与提供特征向量记录的L2距离判断PCB产品是否拥有缺陷. 训练阶段使用三元[16]损失和交叉熵损失, 提高了网络的准确性. 并采用多组对比实验和独立重复实验证明了所提出模型的可行性.

2 算法介绍 2.1 模型整体设计

基于孪生深度特征融合残差网络PCB缺陷分类模型在训练阶段和推理阶段的整体设计如图1所示.

训练阶段如图1(a)所示, 将PCB图像三元组数据集(详见第2.3节)输入到3个共享参数的孪生深度特征融合残差网络进行训练, 计算3张PCB图的三元损失, 通过反向传播迭代更新网络参数, 使有缺陷和无缺陷的PCB图之间的特征向量L2距离最大化, 从而达到区分两者的目的. 接下来将测试集中的PCB图像依次送入网络提取特征向量, 并分别与该PCB同类型标准板图像的特征向量(也通过训练后的网络获得)计算L2距离, 得到一个L2距离的集合. 由于无缺陷的PCB与标准板之间L2距离小, 有缺陷的PCB与标准板之间L2距离大, 因此无缺陷样本和有缺陷样本与标准板样本的L2距离在一维数轴上呈相对集中分布, 在数轴上设置一条分割线, 将其左边样本判定为无缺陷, 右侧样本判定为有缺陷, 不断移动分割线的位置并重新计算分类精度, 最后取分类精度最高的分割线位置作为判定阈值.

推理阶段如图1(b)所示. 先将待检测PCB图像输入到已完成训练的网络提取特征向量e, 再将e与该PCB同类型标准板图像的特征向量r计算L2距离. 若此L2距离低于判定阈值, 表明该PCB图像中没有缺陷, 反之则存在缺陷.

图 1 基于孪生深度特征融合残差网络PCB缺陷分类模型在训练阶段和推理阶段的整体设计

2.2 特征融合残差网络

特征融合残差网络如图2所示, 网络的主干是针对纹理等中级视觉特征信息提取进行改进之后的ResNet50. 网络由49个卷积层和2个全连接层组成. 跳连接是指图中卷积层左侧跳过3个卷积层的弧形箭头的连接. 其中虚线的跳连接会增加输出数据的维度, 而实线的跳连接则不会[17]. 网络中虚线的直线箭头是实现特征融合的方式. 4个不同卷积层的输出在最大池化后连接起来, 形成纹理等中级视觉特征信息和神经网络最终输出的高级语义特征信息的连接. 为保证视觉等特征信息得到充分的利用, 连接后的结果进一步作为全连接层“fc 4096”的输入.

在推理阶段, 由“fc 32”层计算一个32维特征向量(在实验部分会证明32维特征向量是最优选择), 并通过“Norm”操作进行归一化. 该特征向量是网络提取的PCB图像的纹理信息、语义特征信息的表示. 在训练阶段, 网络通过多个损失函数进行反向传播. 其中三元损失(triplet loss)函数在孪生连体架构中使用. 交叉熵(cross-entropy loss)损失是通过“fc 83”层构建的分类器实现的, 因为厂商提供的PCB数据集共有83种不同类型的PCB局部图像.

PCB的纹理特征信息属于中级视觉特征. 深层神经网络在提取高级语义特征信息常会忽略低级信息. 但是在PCB缺陷检测中, PCB的低层次信息和高层次信息同等重要, 因此4个不同尺度的卷积层输出共同参与特征向量的表示, 克服了普通卷积神经网络对纹理特征信息难以提取的缺点.

图 2 特征融合残差网络

2.3 孪生网络和多重损失

提取特征向量采用三联体孪生残差网络, 图3为孪生网络架构, 架构骨干网络使用特征融合残差网络. 训练阶段输入的是3个不同的PCB图像. 分别命名为anchor、positive、negative. 其中positive为有缺陷的PCB图像, negative为没有缺陷的PCB图像, anchor既可以是有缺陷PCB图像, 也可以是无缺陷PCB图像. 网络以共享权重提取3个特征向量, 用以计算三元损失. 三元损失收集相同纹理特征的向量距离并分离不同纹理特征. anchor图像的特征向量通过具有83类输出的全连接分类器(“fc 83”层)计算交叉熵损失, 交叉熵用来分离不同种类PCB的特征.

三元损失的计算公式如式(1)所示:

$ {{triplet\_loss = }}\sum\limits_{{i}}^N {{{{[}||f_i^a - f_i^p||_2^2 - ||f_i^a - f_i^{{n}}||_2^2 + \alpha {]}}_ + }} $ (1)

其中, f a、f p和f n分别是从anchor、positive、negative的PCB图像中提取的特征向量. ||·||2表示L2范数. [·]+表示当数值小于零的时候取零. $ \alpha $ 表示不同对之间的强制执行边距. N是梯度下降学习中epoch的大小. triplet loss会将anchor与其同类PCB图像提取的特征向量之间的距离最小化, 与其不同类PCB图像提取的特征向量之间的距离最大化. 例如anchor是一张有缺陷的PCB图像, 那么它和positive之间的距离会最小化, 与negative之间的距离会最大化. 最小化triplet loss会在拥有缺陷PCB图像和正常PCB图像提取的特征向量之间产生可靠且可验证的边距 $ \alpha $ .

图 3 孪生网络架构

交叉熵损失的计算公式如式(2)所示:

$ \begin{split} &{cross{\_}entropy\_loss=-}{\displaystyle \sum _{k=1}^{K}{y}_{k}}\mathrm{log}{p}_{k} \\ &{p}_{k}={\textit{Softmax}}\text{(}{x}_{k}\text{)}=\frac{{{\rm{e}}}^{{x}_{k}}}{{\displaystyle {\sum }_{i}{{\rm{e}}}^{{x}_{i}}}} \end{split} $ (2)

其中, xi是对应于第i个类的分类器输出. pk是第k个类别的预测概率, yk是真实分类(ground truth)标签. 最小化交叉熵损失函数的过程使xk比其他xi尽可能大. 选择83作为“fc 83”层的维度, 因为训练集中的所有图像都来自83个不同类别PCB产品局部图像.

3 实验结果与分析 3.1 数据集

本文所用到的PCB损伤缺陷图像数据集来自于某PCB厂商, 应厂商要求, 该数据集无法开源. 原始数据集由一个包含25 000张有缺陷PCB图像的true数据集和一个包含25 000张无缺陷PCB图像的false数据集组成, 所有图像均为jpg格式, 尺寸为224×224. 由图像文件名的前缀可以区分图像所属的PCB类别(83类). 分别从两个数据集中随机选出2 500张图像, 组成一个包含2 500张有缺陷图像、2500张无缺陷图像的测试集. 再从true和false数据集各自剩下的22 500张图像中随机抽取、组合获得15 000个图像三元组(anchor, positive, negative), 生成方式为: 每次先随机从true数据集中抽取一张图像P1作为图像三元组的positive, 再从false数据集中与P1同类别的PCB图像中随机抽取一张图像P2作为图像三元组的negative. 第i次随机抽取的时候, 若i为奇数, 则从true数据集中随机抽取一张与P1同类别的图像P3作为图像三元组的anchor; 若i为偶数, 则从false数据集中抽取与P1同类型的图像P3作为三元组的anchor.

3.2 实验结果

训练阶段完成之后得到训练完成的模型, 测试集图像通过模型获得对应的特征向量. 再将所得特征向量与该测试样本同类型标准板图像的特征向量计算L2距离, 将这个L2距离与训练阶段得到的判定阈值比较后得到判定结果.

为了对模型的性能进行合理有效的评估, 分别对不同的残差网络、不同的输出特征向量维度、不同的特征融合结构和不同的损失函数进行了多组消融实验, 验证了模型所采用的各个结构或模块的有效性. 如图4所示, 图4(a)展示了模型使用不同损失函数下的学习曲线, 图4(b)展示了模型使用不同特征融合结构下的学习曲线, 图4(c)展示了模型使用不同输出特征向量维度下的学习曲线, 图4(d)展示了模型使用不同残差网络下的学习曲线. 为了减少随机性的影响, 对所有的实验均进行了6次重复独立的训练并得到相应的数据.

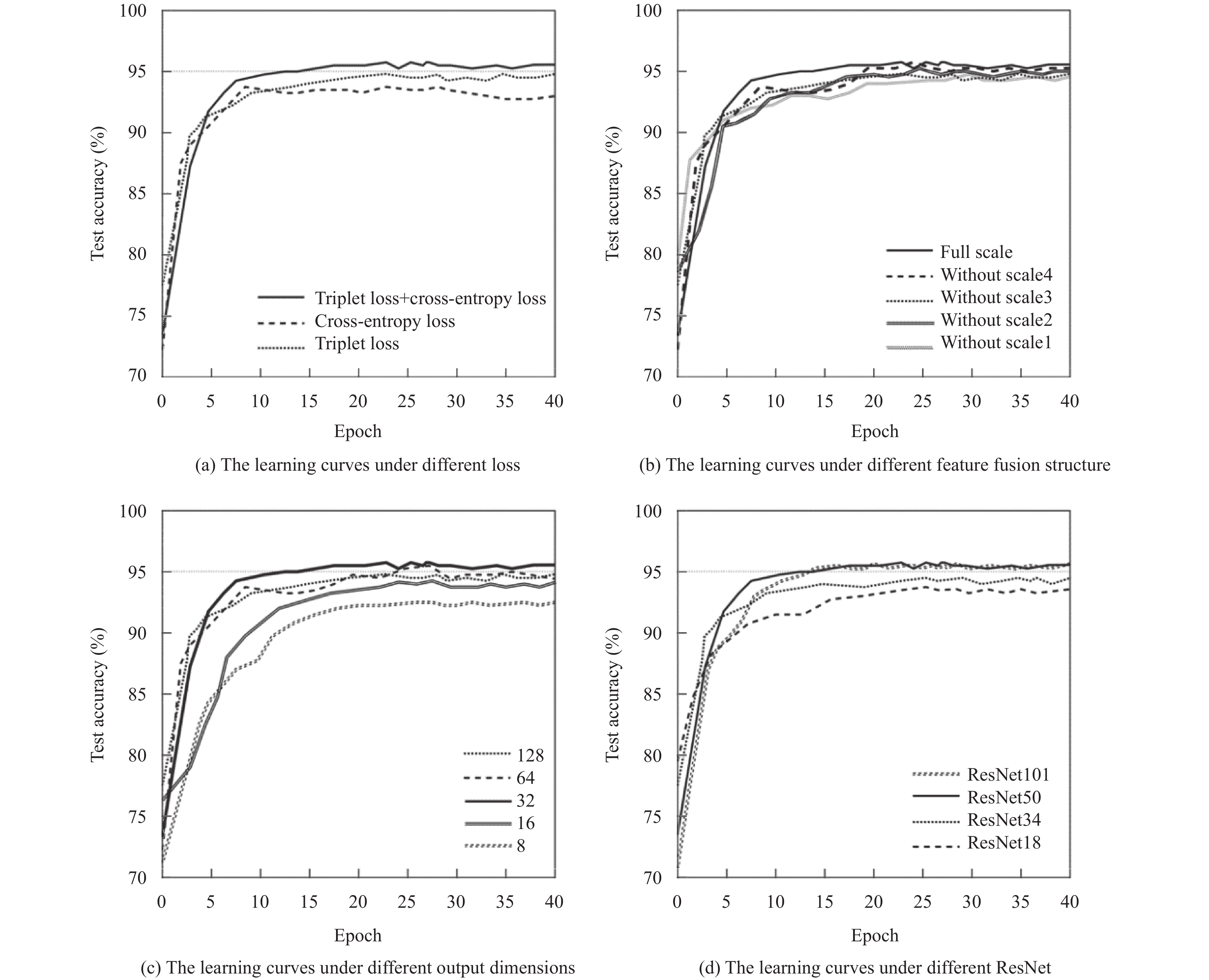
图 4 不同损失函数、特征融合结构、输出维度、残差网络下的学习曲线

为了探索模型采用的骨干网络对于PCB图像缺陷分类检测的效果, 本文分别采用ResNet18、ResNet34、ResNet50和ResNet101这几种在深度上有差别的骨干网络进行对比. 表1给出了采用不同类型骨干网络对于模型精度的影响.

表 1 采用不同骨干网络的分类精度(%)

根据表1的数据可得, 随着不同骨干网络深度的加深, 分类的精度不断提升. ResNet101相比ResNet50在深度上增加了很多, 但是分类的精度并没有特别明显的提升, 而且重复独立实验中分类结果的稳定性更差. 随着网络层数的增加, 训练时间也更长. 综上, 最终模型采用了分类精度、分类稳定性和训练时间均比较适中的ResNet50.

为了说明模型输出特征向量的维度对于模型测试精度的影响, 实验探索了不同维度输出特征向量下模型对于测试数据集的精度. 表2是不同输出特征向量维度下模型的测试精度.

由表2数据可知, 当输出特征向量的维数太小的时候, 对于视觉纹理特征信息表示不充分, 导致对于精度降低. 而输出特征向量的维数太大的时候, 又会导致过拟合, 从而使得分类精度降低, 如果要达到相同的训练效果, 就需要更多的训练数据. 因此, 权衡后最终将模型输出表示为32维特征向量.

表 2 不同输出维度下的测试精度

为了说明特征融合的作用, 在具有不同的特征融合结构的网络上进行了相关的实验. 表3为网络分别在没有scale1、scale2、scale3、scale4特征融合尺度下的分类精度, full scale为scale1、scale2、scale3、scale4都有的特征融合尺度下的分类精度. 测试时, 只需分别断开图2中concat层中相应scale的连接即可.

表 3 不同特征融合结构下的测试精度(%)

根据表3中的数据可知, 与全尺度特征融合的模型相比, 缺少任何一种尺度的特征融合都会导致一定程度的分类精度降低.

不同的损失函数具有不同的特点, 三元组损失函数用于分离特征向量, 而交叉熵损失函数增加了不同局部类型PCB图像聚类中心之间的距离, 从而增强它们的区分度. 使用不同损失函数的结果如表4所示. 当仅使用三元组损失和交叉熵损失时, 准确率分别下降了 0.97% 和 1.84%. 结果表明, 三元组损失和交叉熵损失的效果是协同的, 不可替代的.

表 4 不同损失函数下的测试精度(%)

4 结束语

本文提出一种基于孪生深度特征融合残差网络的PCB损伤分类模型. 模型通过孪生残差网络将提取的PCB图像中级视觉特征和高级语义特征融合表示为 32 维特征向量. 两个特征向量之间的L2距离表示其纹理特征的相似性, 用于PCB损伤检测. 通过比较L2距离和通过网络训练阶段计算的验证阈值, 可以验证PCB产品是否拥有缺陷损伤. 所提出的网络利用特征融合架构来提取多尺度特征, 从而获得可靠的多级融合特征表示. 孪生网络架构通过融合多重损失函数和交叉熵损失函数提高了预测的准确率. 实验结果证明了孪生深度特征融合残差网络在提取和表达PCB图像纹理等中级视觉特征和高级语义特征方面的有效性. 模型在测试数据集上达到(95.42±0.31)%的准确率, 显示出对于PCB缺陷有效的检测能力.

参考文献
[1]
Zhuge MC, Fan DP, Liu N, et al. Salient object detection via integrity learning. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2023, 45(3): 3738-3752.
[2]
朱寒, 林丽, 王健华, 等. 基于改进模板匹配及图像差分法的PCB板缺陷多级检测方法. 应用光学, 2020, 41(4): 837-843.
[3]
Bhatt PM, Malhan RK, Rajendran P, et al. Image-based surface defect detection using deep learning: A review. Journal of Computing and Information Science in Engineering, 2021, 21(4): 040801. DOI:10.1115/1.4049535
[4]
Czimmermann T, Ciuti G, Milazzo M, et al. Visual-based defect detection and classification approaches for industrial applications—A survey. Sensors, 2020, 20(5): 1459. DOI:10.3390/s20051459
[5]
Wu FP, Zhang XM, Kuan YC, et al. An AOI algorithm for PCB based on feature extraction. Proceedings of the 2008 7th World Congress on Intelligent Control and Automation. Chongqing: IEEE, 2008. 240–247.
[6]
Tsai DM, Huang CK. Defect detection in electronic surfaces using template-based Fourier image reconstruction. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2019, 9(1): 163-172. DOI:10.1109/TCPMT.2018.2873744
[7]
Zhou XE, Wang YN, Zhu Q, et al. A surface defect detection framework for glass bottle bottom using visual attention model and wavelet transform. IEEE Transactions on Industrial Informatics, 2020, 16(4): 2189-2201. DOI:10.1109/TII.2019.2935153
[8]
Xin HJ, Chen ZB, Wang BY. PCB electronic component defect detection method based on improved YOLOv4 algorithm. Journal of Physics: Conference Series, 2021, 1827: 012167. DOI:10.1088/1742-6596/1827/1/012167
[9]
Li Y, Li JF. An end-to-end defect detection method for mobile phone light guide plate via multitask learning. IEEE Transactions on Instrumentation and Measurement, 2021, 70: 2505513.
[10]
Shi W, Lu ZS, Wu W, et al. Single-shot detector with enriched semantics for PCB tiny defect detection. The Journal of Engineering, 2020, 2020(13): 366-372. DOI:10.1049/joe.2019.1180
[11]
Božič J, Tabernik D, Skočaj D. End-to-end training of a two-stage neural network for defect detection. Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR). Milan: IEEE, 2021. 5619–5626.
[12]
Ding RW, Dai LH, Li GP, et al. TDD-net: A tiny defect detection network for printed circuit boards. CAAI Transactions on Intelligence Technology, 2019, 4(2): 110-116. DOI:10.1049/trit.2019.0019
[13]
Chopra S, Hadsell R, LeCun Y. Learning a similarity metric discriminatively, with application to face verification. Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Diego: IEEE, 2005. 539–546.
[14]
Ling ZG, Zhang AR, Ma DX, et al. Deep Siamese semantic segmentation network for PCB welding defect detection. IEEE Transactions on Instrumentation and Measurement, 2022, 71: 5006511.
[15]
Miao YL, Liu ZW, Wu XN, et al. Cost-sensitive Siamese network for PCB defect classification. Computational Intelligence and Neuroscience, 2021, 2021: 7550670.
[16]
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 770–778.
[17]
Schroff F, Kalenichenko D, Philbin J. FaceNet: A unified embedding for face recognition and clustering. Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015. 815–823.