随着数据时代的到来, 海量信息不断产生并在网络中传输, 信息的主要承载方式也逐渐从文本转为图像以及视频. 由于图像中包含的信息广泛, 甚至涉及个人隐私、公司机密等重要内容, 并且在传输过程中容易受到噪声及黑客的攻击, 导致信息泄露和篡改, 对个人及公司都会造成严重威胁, 所以迫切需要良好的图像加密技术. 单幅图像传输的信息有限, 故针对多图像进行加密的技术受到研究者们的广泛关注.

混沌系统因其具有初值敏感性、非周期性和轨道不可预测性等特性, 能满足多图像加密技术中对密钥敏感、实现“一图一密”等要求, 故而研究者们将多图像加密与混沌系统^[1]结合起来. 例如: 文献[2]将混沌系统与位平面相结合实现多图像加密. 文献[3]利用PWLCM映射进行双层交叉耦合操作实现多图像加密. 除此之外, 研究者们还将混沌系统与脱氧核糖核酸(DNA)编码^[4]、细胞自动机^[5]、变换域^[6-8]等方法结合实现多图像加密. 随着加密技术的不断提高, 研究者们发现使用低维混沌系统存在密钥空间小, 安全性能较低等问题^[9], 超混沌系统具有运行轨迹复杂, 不容易被预测的优势, 因此, 人们逐渐开始使用高维混沌系统^[10]甚至超混沌系统^[11]实现多图像加密. 然而在已提出的多图像加密算法中, 大部分加密算法是将多幅图像同时加密为一幅密文, 而密文经过解密算法可以同时得出多幅明文图像, 且每幅明文的解密密钥相同. 这样对于具有多权限解密和用户部分解密需求的客户来说, 这些加密方案将受到限制. 为解决这个问题, 张笑^[12]提出基于级联分数傅里叶变换的多图像加密算法, 通过傅里叶变换的实部实现层层加密, 使得具有高权限的用户可以拥有更多的安全密钥并访问更多的图像信息. 除此之外, 研究者们还通过联合变换相关器^[13]、球面衍射^[14]、卷积运算及圆柱形衍射^[15]等方法实现多权限加密.

在本文中, 利用混沌系统实现多权限的多图像加密算法. 整个加密系统实行分层加密, 针对用户权限的高低加密不同的明文信息, 每个用户只能通过各自的私钥解密得到部分图像. 通过PWLCM混沌系统的交叉耦合操作加密高级用户对应的明文图像, 得到类噪声结果图, 再通过最低有效位算法将类噪声图像嵌入到低级用户对应的明文图像中, 最后通过2D-CTMM混沌系统进行扩散和双层阶梯置乱得到密文图像, 以期实现多权限和用户部分解密的多图像加密.

1 相关知识 1.1 PWLCM混沌系统

在图像加密中, 选择任何混沌映射时, 都必须考虑混沌映射的两个重要特征, 即“简单性”和“遍历性”. 相比其他一维混沌系统, 分段线性混沌映射在相位分布上相对均匀且方程简单, 满足以上这两个特征^[16], 因此本文将采用PWLCM系统产生随机序列, 其动力学方程定义如下:

$ {x_{i + 1}} = {F_p}({x_i}) = \left\{ \begin{gathered} {{{x_i}} \mathord{\left/ {\vphantom {{{x_i}} {p, \quad {\kern 1pt} 0 \leqslant {x_i} \leqslant p}}} \right. } {p, \quad {\kern 1pt} 0 \leqslant {x_i} \lt p}} \\ {{{x_i} - p} \mathord{\left/ {\vphantom {{{x_i} - p} {0.5 - p, \quad p \leqslant {x_i} \leqslant 0.5}}} \right. } {0.5 - p, \quad p \leqslant {x_i} \lt 0.5}} \\ {F_p}(1 - {x_i}), \quad 0.5 \leqslant {x_i} \lt 1 \\ \end{gathered} \right. $

(1)

其中, p为控制参数, 其取值范围为(0, 0.5), $ {x_i} \in [0, 1) $ 为状态变量. 在本文加密算法中, 为了得到更加不可预测的混沌序列, 利用PWLCM映射进行双层交叉耦合操作, 其产生的行为轨迹更加复杂且不容易被预测, 可以达到更好的图像置乱效果.

1.2 2D-CTMM混沌系统

低维混沌系统运行速度较快, 但它存在密钥空间小, 行为轨迹容易被预测, 安全性能较低等问题. 而高维混沌系统行为轨迹难以预测, 结构复杂, 这导致加密速率降低. 在权衡加密速率和加密安全性后, 本文结合一维帐篷混沌映射^{[17, 18]}和一维cubic混沌映射^[19]提出了二维cubic-帐篷混沌映射(2D-CTMM), 这是一种新的混沌系统, 将两个一维混沌系统进行组合, 相比其他高维混沌系统, 2D-CTMM结构简单; 对比低维混沌系统, 它的行为轨迹不容易被预测. 在满足加密安全性的前提下, 2D-CTMM具有相对较高的运行速率, 其系统方程如式(2)所示:

$ \left\{ \begin{gathered} {x_{i + 1}} = \left\{ \begin{gathered} (4a{x_i}(1 - {x_i}^2) + 4b{y_i}/0.5)\bmod 1\;({y_i} \lt 0.5) \\ (4a{x_i}(1 - {x_i}^2) + 4b(1 - {y_i}) \cdot 0.5)\bmod 1\;({y_i} \geqslant 0.5) \\ \end{gathered} \right. \\ {y_{i + 1}} = \left\{ \begin{gathered} (4a{y_i}(1 - {y_i}^2) + 4b{x_i}/0.5)\bmod 1\;({x_i} \lt 0.5) \\ (4a{y_i}(1 - {y_i}^2) + 4b(1 - {x_i}) \cdot 0.5)\bmod 1\;({x_i} \geqslant 0.5) \\ \end{gathered} \right. \\ \end{gathered} \right. $

(2)

其中, a和b为2D-CTMM系统的控制参数, $ \bmod $ 为取余函数. 由于2D-CTMM混沌系统的模块化操作是全局有界的, 它总是可以将该值折叠成一个固定的范围, 所以控制参数的取值可以设置为任何较大的值, 在本文中, 设置参数取值范围为 $ a, b \in [1, 100] $ .

1.3 2D-CTMM混沌系统性能分析

李雅普诺夫指数(Lyapunov exponent, LE) 是衡量系统动态特性的一个关键的定量指标, 描述了系统轨迹的收敛速度或发散速度. 当一个系统中存在多个大于零的李雅普诺夫指数时, 表明这个混沌系统存在超混沌行为^[20].

对比其他二维混沌映射, 二维逻辑帐篷映射(two-dimensional logistic tent modular map, 2D-LTMM)^{[21, 22]}表现出更好的混沌特性, 故在本文中对比了2D-CTMM和2D-LTMM的李雅普诺夫指数曲线如图1所示. 其中设置初始值为 $ x0 = 0.528, y0 = 0.135 $ , 控制参数 $ b = 50, a \in [1, 100] $ . 由图1可得, 2D-CTMM在整个区间范围内都处于超混沌行为, 并且对比2D-LTMM, 2D-CTMM具有更大的LE值, 说明其具有更复杂的混沌特性.

2 多图像加密算法

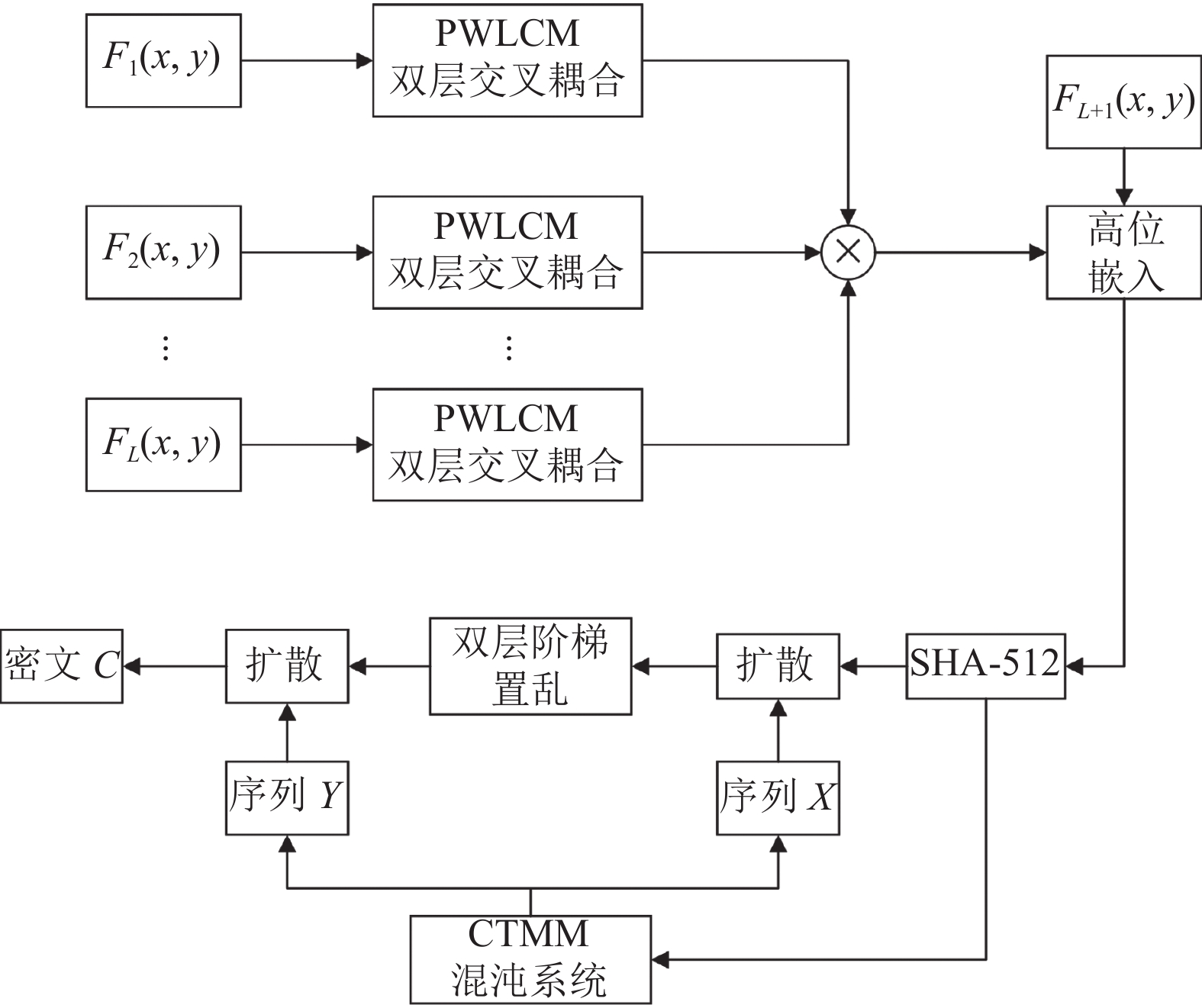
本文提出了基于超混沌系统的多权限多图像加密算法. 为了实现多权限加密, 整个加密方案实行分层加密, 通过图像嵌入手段将高权限用户图像加密与低权限用户图像加密进行联系. 方案中利用哈希算法得到混沌系统初始值, 将明文信息与加密方案相关联, 并根据混沌序列完成图像的置乱和扩散, 对每幅明文图像都实现了“一图一密”, 使算法具备抵挡选择明文攻击的能力; 其次采用最低有效位实现图像的嵌入, 对比通过替换离散小波变换等频域变换的高频部分实现图像嵌入的方式, 最低有效位可以实现无损加密, 可以更好地还原高权限用户图像; 最后通过双层阶梯置乱, 得到效果更好的置乱图像, 进而完成整体加密过程. 具体加密流程图如图2所示.

2.1 PWLCM双层交叉耦合

针对高权限用户图像加密, 本文采用PWLCM双层交叉耦合操作来完成. 混沌系统的初始值由随机数和哈希算法计算得出, 将加密方案与明文信息相关联, 可以实现“一图一密”. PWLCM双层交叉耦合流程图如图3所示, 具体加密方案如下.

步骤1. 由用户随机输入8个在(0, 1)范围内的随机数作为PWLCM双层交叉耦合初始值和参数.

步骤2. 分别对L幅大小为 $ N \times N $ 原始明文图像通过哈希算法(SHA-512)得到每幅图像对应的唯一哈希值h, 利用式(3)更新得到4个PWLCM混沌系统的初始值和参数.

$ \left\{ \begin{gathered} x1 = km1 - 0.01 \cdot \bmod (h1 \oplus h2 \oplus \cdots \oplus h8/255, 1) \\ p1 = kn1 - 0.05 \cdot \bmod (h9 \oplus h10 \oplus \cdots \oplus h16/255, 1) \\ x2 = km2 - 0.01 \cdot \bmod (h17 \oplus h18 \oplus \cdots \oplus h24/255, 1) \\ p2 = kn2 - 0.05 \cdot \bmod (h25 \oplus h26 \oplus \cdots \oplus h32/255, 1) \\ x3 = km3 - 0.01 \cdot \bmod (h33 \oplus h34 \oplus \cdots \oplus h40/255, 1) \\ p3 = kn3 - 0.05 \cdot \bmod (h41 \oplus h42 \oplus \cdots \oplus h48/255, 1) \\ x4 = km4 - 0.01 \cdot \bmod (h49 \oplus h50 \oplus \cdots \oplus h56/255, 1) \\ p4 = kn4 - 0.05 \cdot \bmod (h57 \oplus h58 \oplus \cdots \oplus h64/255, 1) \\ \end{gathered} \right. $

(3)

其中, h表示哈希算法结果, km1,km2,km3, km4,kn1, kn2,kn3, kn4为随机数, $ \oplus $ 为异或符号.

步骤3. 根据PWLCM系统初始值x1和x2及参数p1和p2, PWLCM-1和PWLCM-2交叉迭代^[23] $ N \times N $ 次, 得到两个序列X1, Y1.

步骤4. 根据PWLCM系统初始值x3和x4及参数p3和p4, PWLCM-3和PWLCM-4交叉迭代次 $ N \times N $ , 得到序列X2, Y2, 并将X1, Y1,X2,Y2这4个序列调整为大小 $ N \times N $ 的二维矩阵.

步骤5. 利用二维矩阵X1对明文图像进行异或, 改变明文图像像素值, 达到扩散效果.

步骤6. 将二维矩阵Y1按行进行排序得到每行的行排序索引, 根据索引对异或结果实现行置乱.

步骤7. 使用X2,Y2分别重复步骤5和6方法完成列置乱, 得到 ${I_i{'}}(x, y)$ , 其中 $ i \in [1, L] $ .

2.2 嵌入阶段

本文中嵌入阶段采用最低有效位方法, 通过将类噪声图像的高4位替换载体图像的低4位达到嵌入效果, 并将低4位矩阵保存为密钥, 可以实现无损嵌入. 具体步骤如下.

步骤1. 将L幅原始图像经过PWLCM双层交叉耦合后的结果 ${I_i{'}}(x, y)$ 进行异或合并为一幅类噪声图像. 通过式(4)得到对应图像解密的私钥 $ {f_j}(x, y) $ .

$ {f_j}(x, y) = {I_1{'}}(x, y) \oplus \cdots \oplus {I_i{'}}(x, y) \oplus \cdots \oplus {I_L{'}}(x, y), i \ne j $

(4)

步骤2. 通过最低有效位算法, 将类噪声图像的高4位嵌入到第L+1幅明文图像的低4位中, 得到半加密图像, 并将低4位矩阵保存为解密密钥, 以实现无损嵌入.

2.3 二次加密

本文加密算法中, 采用二次加密以便更好地改变明文图像像素位置和像素值. 本节采用新的超混沌系统CTMM实现图像的置乱和扩散, 并同样利用哈希算法得到混沌系统初始值, 使算法具有抵抗明文攻击的能力. 具体步骤如下.

步骤1. 半加密图像通过SHA-512哈希算法以及式(3), 式(5)–式(8)得到CTMM混沌系统的初始值(x0,y0)及参数a和b.

$ x0 = (km1 + km2)/2 $

(5)

$ y0 = (km3 + km4)/2 $

(6)

$ a = fix(\bmod (kn1 + kn2 + kn1 \times kn2 \cdot {10^{15}}, 100)) $

(7)

$ b = fix(\bmod (kn3 + kn4 + kn3 \times kn4 \cdot {10^{15}}, 100)) $

(8)

其中, 在式(7)和式(8)中, $ fix $ 为向下取整.

步骤2. 利用混沌系统初始值(x0,y0)及参数a和b, 迭代CTMM混沌系统 $ N \times N $ 次, 得到两个混沌序列X和Y.

步骤3. 将两个序列X和Y调整为大小 $ N \times N $ 的二维矩阵序列, 得到新的序列X和Y.

步骤4. 利用二维矩阵X对半加密图像进行异或操作, 改变半加密图像像素值, 达到扩散效果.

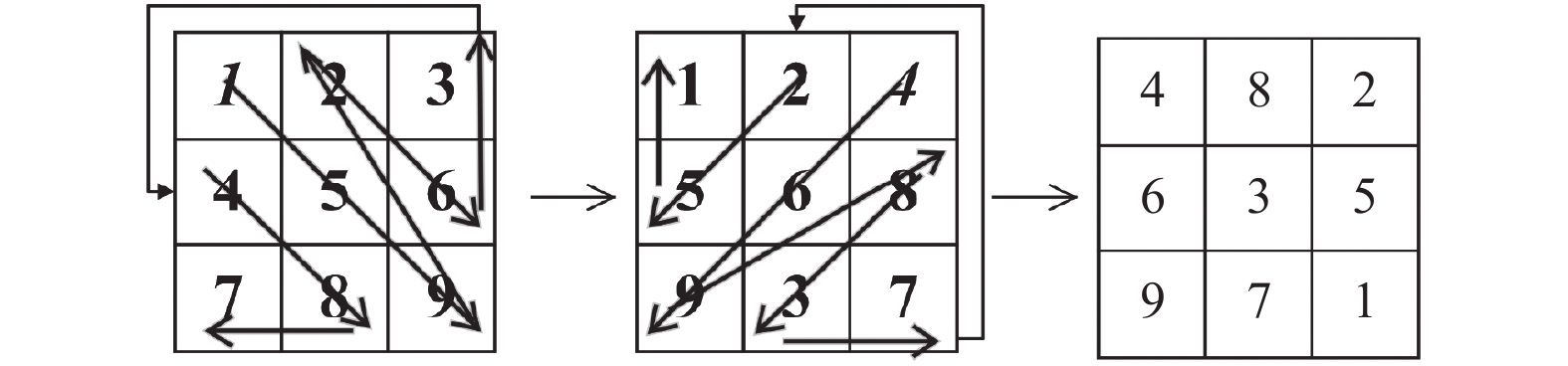
步骤5. 将异或结果进行双层阶梯置乱, 第1次阶梯置乱从左上角开始以斜右下的方向执行阶梯状扫描; 第2次阶梯置乱从右上角以斜左下的方向执行阶梯状的扫描方式, 依次将二维图像数据的像素位置完成置乱以至结束. 具体置乱方式如图4所示, 其中斜体数字为起始点.

步骤6. 利用二维矩阵Y对置乱后图像进行二次扩散, 得到密文C.

3 相应的解密算法

本文提出的多权限多图像加密算法属于对称加密, 加密与解密使用的密钥相同, 故解密过程为加密算法的逆过程. 本文在保证图像加密安全性的前提下, 通过分层加密实现不同权限用户解密得到不同的明文图像. 合法的解密用户根据权限大小得到相应的解密密钥, 对于低权限用户, 只能解密得到一幅有意义的半加密图像, 可以有效减少对高权限图像的暴力攻击; 对于高权限用户而言, 通过各自的私钥进行解密得到互不相同的图像信息. 解密密钥包括: km1,km2, km3,km4, kn1, kn2,kn3, kn4, 其中在PWLCM交叉耦合阶段以及2D-CTMM混沌系统阶段各一次. 除此之外, 加密过程中产生的哈希值以及在嵌入阶段的解密图像 $ {f_j}(x, y) $ 也是必不可少的. 具体解密过程如下.

步骤1. 通过加密方传过来的2D-CTMM混沌系统产生的随机数及明文图像对应的哈希结果, 可以得出混沌系统初始值和参数对应的密钥.

步骤2. 利用混沌系统初始值和参数迭代CTMM混沌系统产生序列X,Y, 并调整大小为 $ N \times N $ 的二维矩阵.

步骤3. 利用二维矩阵Y对密文进行异或操作, 得到置乱图像.

步骤4. 对置乱图像经过双层阶梯置乱的逆过程进行逆置乱, 首先从图像的左下至右上的方向, 以对角线为界, 按阶梯状逐个扫描像素; 再从右下至左上的方向, 以对角线为界, 按阶梯状逐个扫描像素完成阶梯逆置乱.

步骤5. 利用二维矩阵X对逆置乱后结果进行扩散, 得到半加密图像, 至此低权限用户解密完毕.

步骤6. 高权限用户通过不同的私钥 $ {f_j}(x, y) $ , 与半加密图像进行异或, 进入各自解密通道.

步骤7. 通过PWLCM系统对应的密钥, 对其进行双层交叉耦合操作, 产生的序列按照加密过程的逆顺序依次对图像进行逆列置乱、异或、逆行置乱、异或操作, 最终得到各自的解密图像.

4 仿真实验及安全性分析

本文采用4幅大小为512×512的灰度图像进行实验, 实验的主机环境为Intel Core I7-6700, 8 GB的机带RAM, 具有3.41 GHz 的处理器, 以及 64 位Windows 10操作系统. 实验使用Matlab (R2019b)软件实现仿真测试. 密钥设置如下: PWLCM混沌系统阶段为 $[km1, km2, km3, km4, kn1, kn2, kn3, kn4]$ = [0.7832, 0.2718, 0.3526, 0.4671, 0.9843, 0.4953, 0.2389, 0.6829], CTMM混沌系统阶段为: $ [km1, km2, km3, km4, kn1, kn2, kn3, kn4] $ = [0.4637, 0.9327, 0.5673, 0.9082, 0.8943, 0.3285, 0.5892, 0.6417].

4.1 加解密结果图

为了直观地观测加解密效果, 本节对其进行仿真实验, 并统计图像直方图. 结果如图5所示. 从结果图中可以看出, 密文像素分布均匀, 并且在视觉上解密图像和明文图像难以进行区分. 观察直方图结果可知, 半加密图像与明文图像Baboon的直方图相似, 对于高权限图像来说, 不管在视觉上还是直方图分析, 都不容易被攻击者发现, 大大减少了发生入侵的可能性.

4.2 相邻像素相关性

相邻像素相关性常用来反映图像相邻位置像素值的关联程度, 包括了水平、垂直以及对角线3个方向. 一个良好的加密算法, 其密文的邻近像素相关性将极限趋近于零. 相邻像素相关性的实验结果见表1.

通过观察表1中数据可知, 所提算法明文图像的像素相关性非常趋近于1, 表明具有强相关性, 经过加密算法密文图像像素分布均匀, 相关性弱, 表明本文通过PWLCM双层交叉耦合及CTMM混沌系统产生的混沌序列实现图像置乱的方法可以有效减弱图像像素之间的相关性. 相较于文献[23-25], 所提算法表现出更好的相邻像素相关性, 表明该研究方案可以有效地扰乱图像像素.

4.3 信息熵

信息熵也是反映加密效果的一个指标, 体现了加密体系的混乱程度. 在本节中将所提算法与相近算法进行对比, 结果见表2. 根据表中数据, 可以得出所提算法的密文信息熵非常接近理想值8, 可以有效抵抗统计攻击. 但由于整个加密系统中采用的超混沌系统CTMM是由两个简单的一维混沌系统组合得到, 相对其他超混沌系统结构较为简单, 且没有使用更为复杂的置乱方式, 故加密系统的混乱程度低于其他相近文献.

4.4 密钥空间

良好的加密系统应该具有抵抗穷举攻击的能力, 这就与加密体系中密钥空间密切相关. 本文提出的加密算法密钥包括km1,km2, km3, km4,kn1,kn2,kn3,kn4, 并且分为PWLCM交叉耦合阶段以及CTMM混沌系统阶段. 除此之外, 还包括了哈希值以及图像私钥. 由于整个系统处于双精度, 在64位Windows 10操作系统下, 每个密钥的精度为 $ {10^{15}} $ , 则整个算法的密钥空间可以达到 $ {(10{}^{15})^{16}} = {10^{240}} $ . 表明所提算法的密钥空间已经足够大, 可以抵御穷举攻击.

4.5 差分攻击分析

在本节中采用像素数目变化率(number of pixels change rate, NPCR)和统一平均变化强度(unified average change intensity, UACI)^[26]进行测量. 通过改变明文图像中一个像素值, 来计算密文之间的NPCR和UACI, 结果如表3所示. 可以看出本文算法的NPCR和UACI都在理论范围内, 表明本方案中通过利用随机数和哈希算法结果产生混沌系统初始值和参数的方式, 有效地将加密方案与明文信息相关联, 当明文图像发生微小变化时, 整个加密系统的初值会随之变化, 通过混沌系统会产生完全不同的混沌序列, 致使可以有效做到“一图一密”, 这表明本文算法可以有效抵御差分攻击.

4.6 密钥敏感性分析

密钥敏感性反映了加密算法对密钥的敏感程度. 密钥敏感性越强, 表明只有在解密密钥完全正确时才可以正确解密出原始信息. 为检验本文算法的密钥敏感性, 通过将密钥做微小改变, 并计算密文之间的NPCR和UACI值进行分析, 结果见表4.

表4展示了所提算法的密钥敏感性, 其中 km1–kn4 表示PWLCM交叉耦合阶段密钥, kp1–kq4 表示CTMM阶段密钥, 分别将每个密钥做出微小改变后计算两幅密文之间的NPCR和UACI值. 结果显示NPCR值均超过99%, UACI值超过33%, 表明所提算法对所有的密钥都具有较高敏感性. 实验验证, 本文将两个一维混沌系统结合产生的CTMM超混沌系统对初值足够敏感, 只要密钥发生变换, 产生的混沌序列随之变换, 以至于对图像具体像素进行的置乱和扩散操作会完全不同, 最终得到完全不同的密文图像, 可以有效抵抗已知明文攻击.

4.7 鲁棒性

由于图像在传输过程中可能会遭到噪声和数据丢失的影响, 使得解密图像变得困难. 因此本节对密文添加不同噪声和切割部分密文来模拟在传输过程中受到的影响. 图6显示了经过不同噪声影响和切割部分密文后的密文和对应的Lena解密图. 即使密文在传输过程中受到影响, 通过正确的密钥信息, 解密图像内容依然可以进行分辨, 表明所提出的算法具有一定的抗噪声性能.

5 结语

本文提出基于混沌系统的多权限多图像加密算法, 实现了多权限用户和用户部分解密工作. 通过PWLCM混沌系统的交叉耦合操作实现高权限图像加密, 设计2D-CTMM混沌系统和双层阶梯置乱实现低权限图像加密, 利用最低有效位算法将高低权限联系在一起, 最终实现多权限多图像加密.

通过以上仿真实验分析, 相比于其他相近文献, 所提出的多权限图像加密算法的密文具有更加良好的像素相关性, 差分攻击实验结果也表明密文对明文具有较强的敏感性, 可以抵抗差分攻击. 所提算法的密钥空间足够大, 并且当每个密钥有微小变化时, 整个密文也会完全不同, 表明可以抵抗穷举攻击. 通过鲁棒性分析实验, 表明本文提出算法可以有效抵抗传输过程中的噪声以及数据丢失的影响. 对比文献[23-25], 所提算法的密文信息熵较低, 说明整个加密体系的混乱程度不足, 在以后的研究过程中不断加以改进.