2. 中北大学 电子测试技术国家重点实验室, 太原 030051
2. State Key Laboratory of Electronic Test Technology, North University of China, Taiyuan 030051, China
随着电路板制造工艺逐渐向精密化和高度集成化的方向发展, 传统的人工检测手段已经无法满足电路板检测的需求. 为了能够检测电路板在电子装配环节的质量, 飞针测试机已经成为电路板检测中一种必不可少的检测设备[1-3]. 飞针测试机是针对PCB (printed circuit board)板进行测试的一种仪器, 其工作时使用多个独立控制的探针移动到测试中的元件焊点上提取信息, 再通过内置的测试仪器分析采集到的电信号达到电路板测试的目的.
目前针对飞针测试机的研究大多集中在图像处理和运动控制等方向, 对被测元件的检测路径规划的研究较少. 焊点的测试路径优化与旅行商问题(traveling salesman problem, TSP)相似: 探针从初始位置出发, 经过被测元件焊点位置扎下测试, 如此按照规划的测试路线行进, 直到测试完电路板所有元件回到初始位置测试结束. 在此过程中, 测试路径规划的优劣可以直接影响到飞针测试机的测试效率, 一种合适的路径规划算法会大大提升对电路板的测试效率.
林梅[4]将果蝇算法用于激光切割路径规划, 可以有效地减少空行程, 提高切割效率, 但其也有参数复杂、泛用性小等缺陷. 黄兴旺[5]将一种改进的粒子群算法应用于小型无人船路径规划, 使用了一种多子域分组的方式改进了粒子群算法收敛精度低的缺陷, 使其收敛精度提高12%, 但其算法计算时间长不适用于小型电路板测试路径规划. 黄韬等[6]将融合聚类算法和模拟退火算法用于焊点检测路径规划, 缩短了测试总路径, 但其算法的最优适应度不佳, 并且模拟退火算法的收敛速度缓慢, 效率低下. 吴亚帅等[7]将驴和走私者算法应用于印刷电路板焊点路径优化, 有效地缩短了测试时间, 平均规划时间可低至2 s, 但是其算法在最优适应度方面并无优势. Xiao等[8]将一种改进的蚁群算法应用于电路板表面缺陷检测, 改进了蚁群算法易陷于局部最优的缺点, 在不改变总测试时间的情况下可将测试路径平均长度缩短13.7%, 但是蚁群算法本身运行时间较长, 实机测试操作效果不佳.
从当前的研究结果来看, 智能优化算法已成为电路板元件测试路径规划的重要方法, 可以有效地提高检测效率、减少检测时间. 粒子群算法是一种经典的智能优化算法[9, 10], 其优点在于迭代速度快, 收敛时间短, 但也存在着易于陷入局部最优的缺陷. 本文提出了一种改进的粒子群算法(H-PSO), 在粒子群算法的基础上加入混沌初始化用于约束和更新搜索的最大速度, 同时引入了遗传算法的交叉、变异的思想改进粒子群算法易于趋于局部最优的缺陷, 进一步提升了算法的全局搜索能力, 另外加入分区的方法解决两针相撞的问题同时提高测试效率. 通过对算法的有效性分析和飞针测试机实机操作证实本方法可以有效地提高飞针测试的效率.
1 焊点测试路径数学模型飞针测试机的测试过程为: 测试机探针组件从电路板的第一个焊点出发, 依次按照规划的路径对所有元件进行测试, 直到遍历检测完电路板上的所有元件完成测试. 根据测试需求的不同, 飞针测试机有双针联合测试与单针分区测试两个模式, 两者规划的路径有所不同.
1.1 双针联合测试双针联合测试是指飞针测试机的两个探针组件协同运动, 每次测试都扎在同一个元件的两端从而构成回路. 使用这种测试方式可以测得元件的VI曲线, 获得被测元件更多的信息. 可以描述为在有n个待测元件的集合D={(x1, y1), (x2, y2) , …, (xn, yn)}中找到一条路径T使得测试路径最短.
1.2 单针分区测试单针分区测试每次测试两针都扎在不同的元件上, 通过飞针组件一端接地测得元件信息. 使用这种测试方式可以提高飞针测试机的工作效率, 但测得的信息更少. 由于飞针x, y两轴的电机导轨的硬件限制, 飞针1无法运动到飞针2的下方, 即飞针运动的坐标中飞针2的y坐标数值只能大于飞针1的坐标数值. 为避免两针相撞, 需要根据y轴坐标值分区测试: 在待测元件集合D中, 按照y轴数值大小将坐标排序后, 将集合D平均分为D1和D2两部分, 再将集合D1、D2分别路径规划, 使得总测试路径最短.
1.3 适应度函数适应度函数也被称为目标函数, 路径规划的目的是使测试路径总长度S尽可能短, 所以S的值越小越接近最优解. 式(1)表示路径中所有相邻节点的距离总和, S为路径总长度.
| S=∑ni=1√(xi+1−xi)2+(yi+1−yi)2 | (1) |
粒子群算法是一种启发式搜索算法[11-13], 它模拟了鸟类在觅食中个体与集体共享信息的行为方式, 在解决非线性、不可微和多模态问题时快速有效, 但是其过快的收敛能力在提高了计算速率的同时也容易收敛局部最优解. 粒子通过以下公式来更新自己的速度和位置:
| Li(t+1)=Li(t)+vi(t+1) | (2) |
| vi(t+1)=vi(t)+c1r1[pbesti(t)−Li(t)]+c2r2[gbesti(t)−Li(t)] | (3) |
其中, Li(t+1)为t+1时刻粒子位置, Li(t)为t时刻粒子位置, vi(t+1)为t+1时刻粒子速度, vi(t)为t时刻粒子速度, c1、c2为学习因子, pbesti(t)为个体最优, gbesti(t)为全局最优, r1、r2为随机数.
初始化中的速度最大值和最小值非常重要, 最大值越小全局搜索能力越强, 但是会导致搜索速度下降. 最小值过小会难以快速迭代. 使用如下公式来规定初始速度数值大小.
| vmax,i=δ(Lmax,i−Lmin,i) | (4) |
| vmin,i=δ(Lmin,i−Lmax,i) | (5) |
混沌系统用于描述数学系统中的一种不规则行为, 其主要特征是不可预测性和对初始条件的极端敏感性, 其公式为:
| Xt+1=K×Xt(1−Xt) | (6) |
其中, K为常数, 通常取0–4之间, X需要取值在0到1之间, 否则后续迭代会趋向于–∞.
粒子群算法主要使用速度更新来促进全局搜索, 为此可以使用logistic方程更新过快的粒子速度, 减缓其收敛速度, 提升其全局搜索能力, 具体如以下公式所示:
| Cvold=mod(abs(vi(t+1),vmax))vmax | (7) |
| Cvnew=4×Cvold×(1−Cvold) | (8) |
| v′i(t+1)=sign(vi(t+1))×Cvnew×vmax | (9) |
遗传算法是一种生物进化启发式算法[14, 15], 其运行包括种群生成、适应度评估、选择、交叉和变异操作等过程. 比起粒子群算法, 遗传算法中的变异操作更具随机性、全局搜索能力更强, 对于非连续变化的变量使用变异操作会有更好的效果. 为了提高全局搜索效率可以把遗传算法交叉、变异与淘汰的思想运用在粒子群算法迭代更新的过程中. 令适应度优的粒子交叉, 加快局部收敛速度; 令适应度差粒子自我变异, 提高全局搜索能力.
计算每个粒子适应度值, 第i个粒子适应度值设为si, 种群中粒子适应度的最大值定义为smax, 最小值定义为smin, 由以下公式计算交叉概率pc和遗传概率pm:
| pc=smax−sismax−smin | (10) |
| pm=si−sminsmax−smin | (11) |
设定阈值pl, 令pc>pl的粒子执行交叉操作, 令pm>pl的粒子执行变异操作. 先使用式(12)轮盘赌法选中粒子父代, 再由式(13)和式(14)进行粒子的交叉操作获得新的子代放回种群中. 变异操作如式(15)所示, 使用均匀变异的方法生成新的粒子.
| pm=si∑nj=1sj | (12) |
| ˆLi=rLi+(1−r)Li+1 | (13) |
| ˆLi+1=rLi+1+(1−r)Li | (14) |
| ˙Li=Lmin+r(Lmax−Lmin) | (15) |
其中, pi为粒子个体被选中的概率, Li、Li+1为父代粒子,
步骤1. 读取焊点坐标位置并且计算坐标间的距离矩阵.
步骤2. 初始化种群, 记录个体粒子的当前最优解和群体粒子的当前全局最优解, 同时根据式(4)、式(5)规定粒子最大最小速度.
步骤3. 根据式(1)计算适应度评估当前群体, 根据式(10)对满足pc>pl的粒子执行交叉操作, 根据式(11)对满足pm>pl的粒子执行变异操作, 同时应用式(9)更新最大速度.
步骤4. 再次计算每个粒子的适应度值, 根据式(2)、式(3)更新个体最优位置pbest、全局最优位gbest位置.
步骤5. 算法迭代, 重复步骤3、步骤4直到达到最大迭代次数.
2.4 混合粒子群算法思想测试根据路径规划需要, 使用多个TSP测试集对本文的算法性能进行分析对比, 测试集分别为st70、krA200、rand400; 使用粒子群算法和遗传算法进行对照, 规划结果和收敛曲线如图1–图3所示, 结果汇总如表1所示.

|
图 1 st70规划结果 |
|
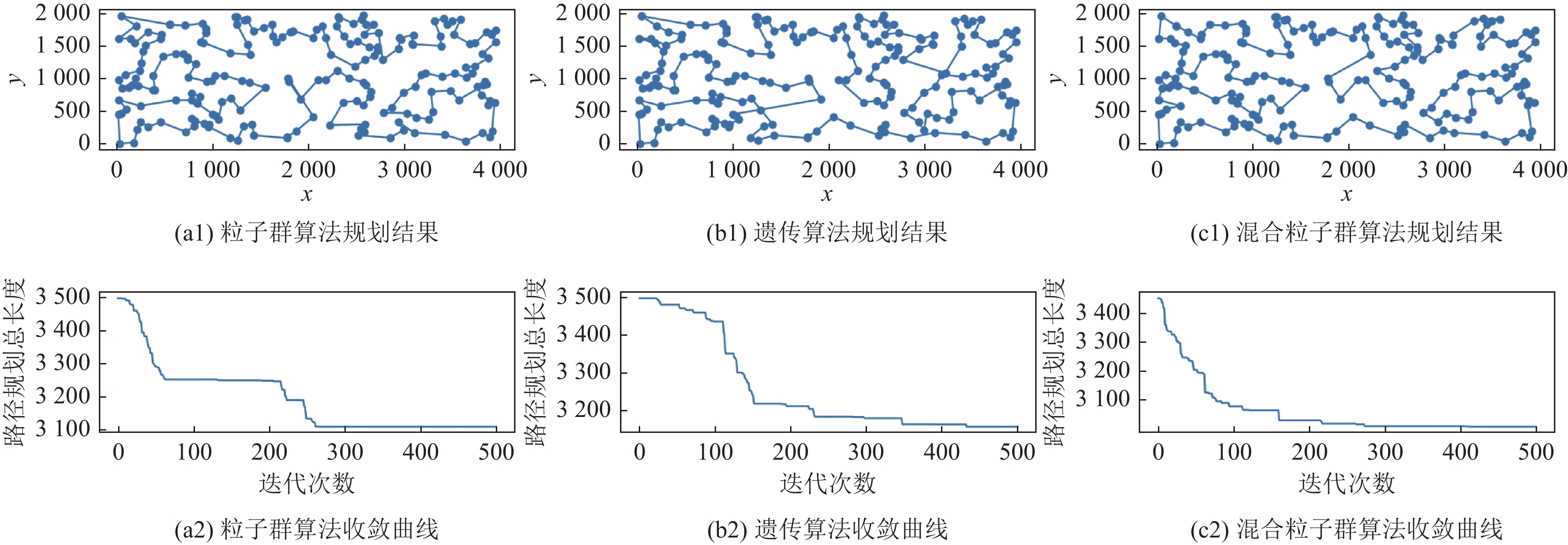
图 2 krA200规划结果 |

|
图 3 rand400规划结果 |
对比st70、krA200、rand400测试集3种算法路径规划结果, 可知: 粒子群算法运行速度最快, 但是其算法运行结果不够稳定, 易陷入局部最优, 其最优适应度值最差. 遗传算法最优适应度好于粒子群算法但是运行速度最慢, 达到最优值所需迭代数也较多. 混合粒子群算法运行速度稍慢于粒子群算法, 但是由于其全局搜索能力更强, 达到最优适应度所需的迭代次数更少, 所以达到最优收敛值所用的时间最短, 其最优适应度在3种算法中也最优, 比粒子群算法和遗传算法有大约10%的提升.
| 表 1 3种算法对3种测试集路径规划结果 |
3 电路板测试路径规划 3.1 焊点坐标提取
选择两个形状、功能、元件分布不同的两个电路板分别测试, 展示路径规划的性能. 首先根据电路板的设计图, 使用AD16以表格的形式导出被测电路板坐标, 将坐标输出给飞针测试机用于电路板检测. 测试电路板如图4所示, 被测元件焊点坐标如图5所示.

|
图 4 测试电路板 |

|
图 5 被测元件焊点坐标 |
3.2 路径优化算法对比分析与实测
为了验证混合粒子群算法对于电路板焊点路径规划的性能, 使用其他两种路径规划算法进行对比. 所选算法分别为遗传算法和粒子群算法, 对比试验的程为使用AD软件提取坐标后, 分别使用3种算法进行路径优化, 将优化后的路径输入到飞针测试机上实机测试并且对比. 优化算法运行环境为Windows 10操作系统, 运行环境为一种双飞针测试机.
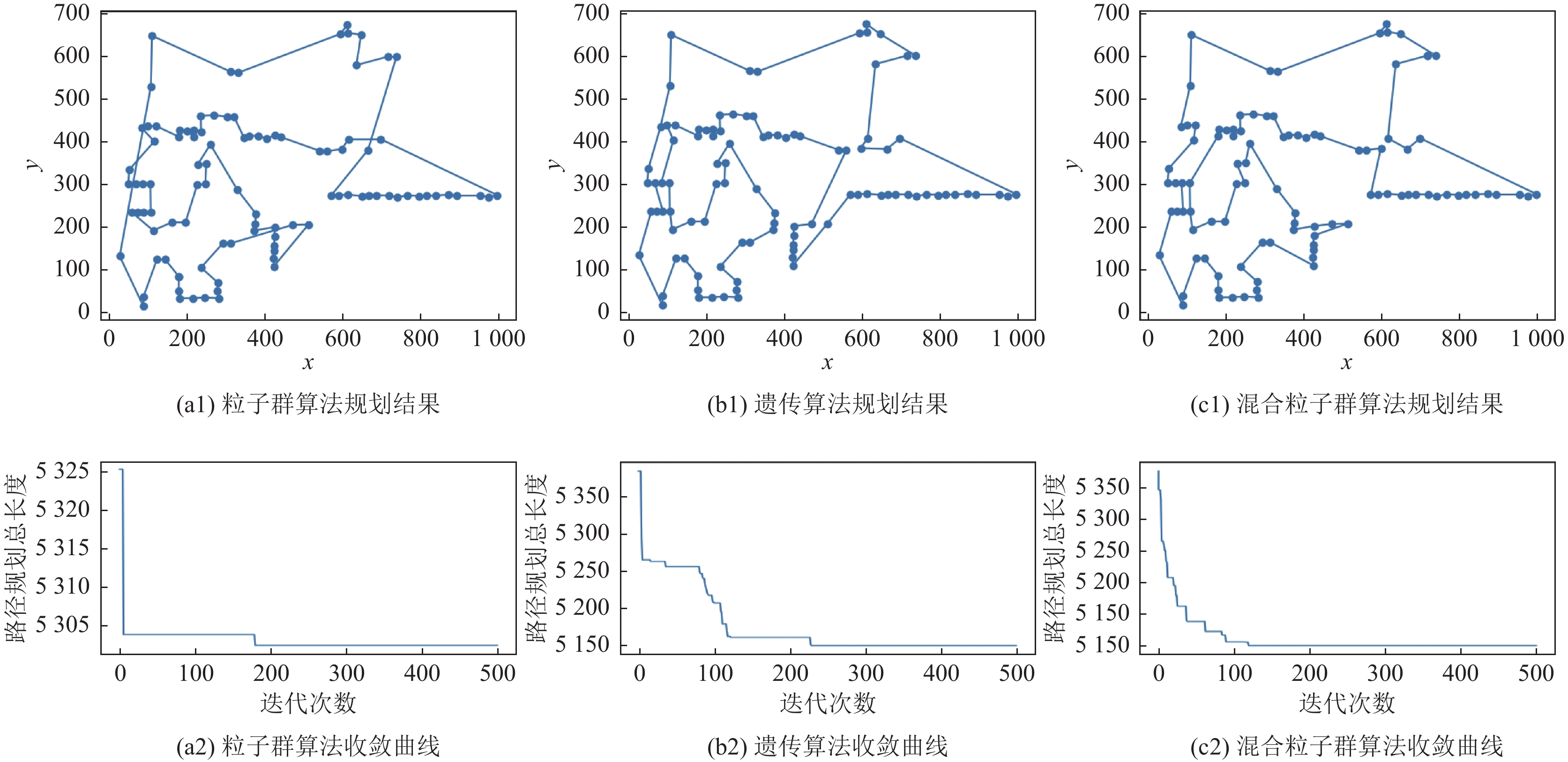
实验中, 根据各个算法的特性, 各测试算法的相关参数如下所示: 粒子群算法中粒子数目为100, 最大迭代数500, c1、c2为2, 惯性权重ωmin取0.4、ωmax取0.9; 遗传算法中种群个数为100, 最大迭代数500, 选择概率0.2, 交叉概率0.9, 变异概率0.1; 混合粒子群算法粒子数100, 最大迭代数500, 常数c1、c2为2, 惯性权重ωmin取0.4、ωmax取0.9, 交叉变异阈值为0.8. 算法参数设定后进行运行对比, 混合粒子群算法、遗传算法、粒子群算法路径规划结果如图6、图7所示.
|
图 6 测试1号板双针测试路径规划结果图 |
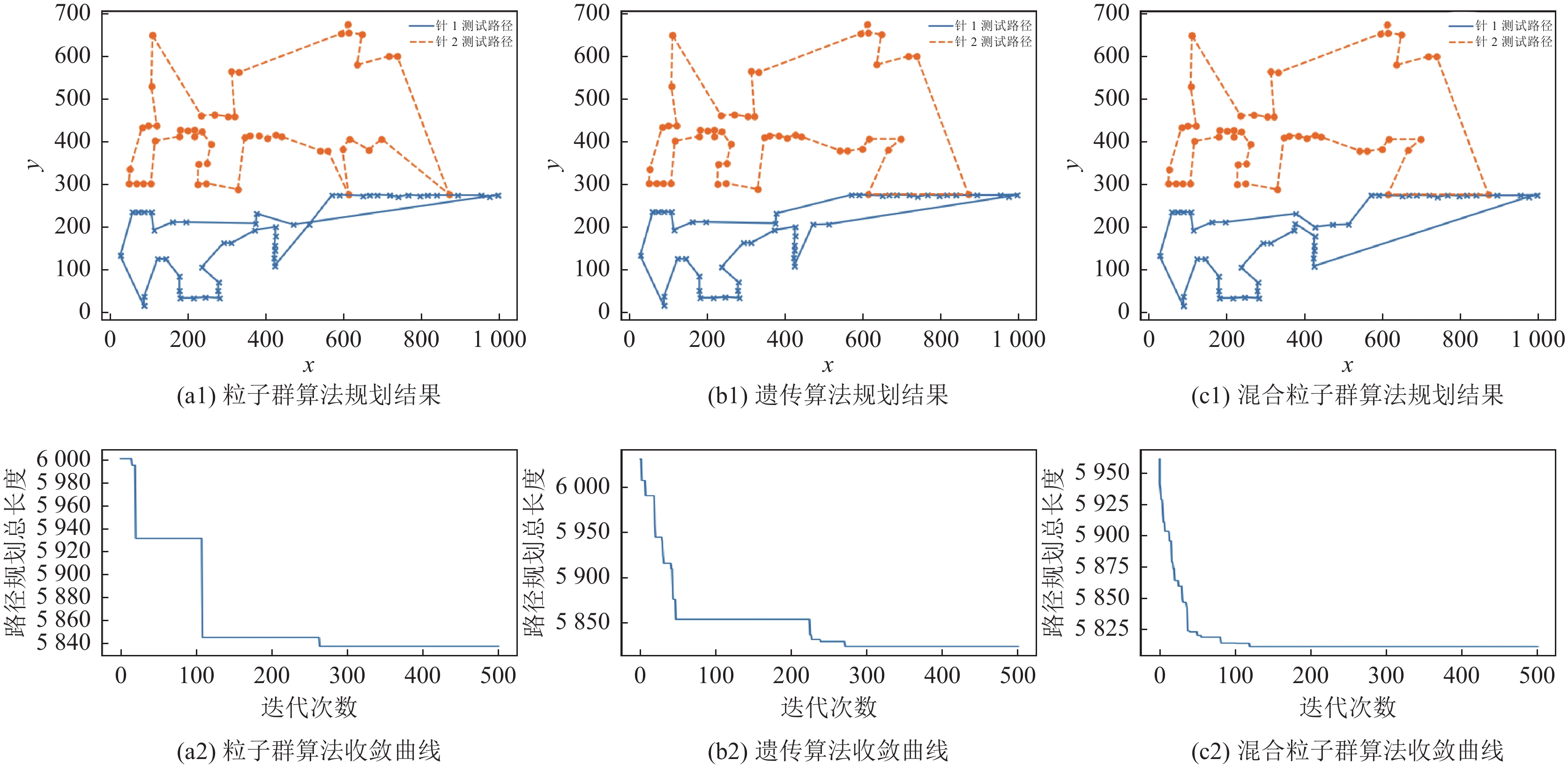
|
图 7 测试1号板单针分区测试路径规划结果 |
对比图6、图8可知: 在双针联合测试路径规划中, 两种电路板使用粒子群算法规划路径的效果最差, 分别为5300.183和3200.054. 与此相对的, 混合粒子群算法规划最短路径长度均为最优, 分别为5016.330和3178.762. 与此同时混合粒子群算法在规划所用时间也有优势比起粒子群算法和遗传算法分别有30%和50%的提升, 可知混合粒子群算法在规划效率上优于对比的两种算法. 对比图7、图9, 可发现在计算能力要求更高的单针分区测试路径规划中, 混合粒子群算法全局搜索能力强的优势体现得更加明显, 并且随着电路板的复杂程度提升逐渐扩大优势. 由此分析可见混合粒子群算法全局搜所能力更强, 可以生成更短的路径, 并且所需要的迭代数更少, 使得路径规划的时间更短, 同时随着计算量的增加, 这个优势变得越来越显著.
在规划路径之后, 将规划后的结果以表格的形式导入双飞针测试机进行电路板实机测试. 飞针测试机运行参数如表2所示.
实机测试结果的汇总见表3、表4, 可知比起飞针电路板测试机本身的测试路径, 3种路径优化算法都能有效地减少测试总路径长度从而减少测试时间, 提高测试效率, 其中混合粒子群算法全局搜索能力更强, 可以避免陷于局部最优, 获得全局更短的路径, 与此同时算法需要迭代次数更少, 算法规划路径所用时间更短.

|
图 8 测试2号板双针分区测试路径规划结果 |

|
图 9 测试2号板单针分区测试路径规划结果 |
| 表 2 飞针测试机参数 |
| 表 3 测试1号板3种算法实机测试结果 |
| 表 4 测试2号板3种算法实机测试结果 |
4 结论
本文针对飞针测试机在检测电路板的过程中测试时间长、测试效率低、单针检测容易撞针等问题, 提出了一种基于改进粒子群算法的电路板测试路径规划算法. 通过仿真验证和实机测试证明本算法可以有效地减少测试总路径, 提高测试机的检测效率, 为解决电路板自动测试中的路径规划问题提供了有效的理论依据和解决办法.
| [1] |
黄东亮, 戴苏榕, 刘昊亮. 飞针测试机的测量方法研究与实践. 电子技术, 2021, 50(2): 28-29. |
| [2] |
Solorzano C, Tsai DM. Environment-adaptable printed-circuit board positioning using deep reinforcement learning. IEEE Transactions on Components, Packaging and Manufacturing Technology, 2022, 12(2): 382-390. DOI:10.1109/TCPMT.2022.3142033 |
| [3] |
Johnson MR. The increasing importance of utilizing non-intrusive board test technologies for printed circuit board defect coverage. Proceedings of 2018 IEEE AUTOTESTCON. National Harbor: IEEE, 2018. 1–5.
|
| [4] |
林梅. 激光切割路径的自适应飞行半径果蝇算法优化. 机械设计与研究, 2021, 37(4): 146-149. DOI:10.13952/j.cnki.jofmdr.2021.0154 |
| [5] |
黄兴旺. 基于多子域分组粒子群优化算法的小型无人船路径规划. 船舶工程, 2021, 43(12): 158-165. DOI:10.13788/j.cnki.cbgc.2021.12.25 |
| [6] |
黄韬, 董远川, 王野平. 印制电路板飞针测试机基准网络电测路径规划. 印制电路信息, 2022, 30(4): 43-46. DOI:10.3969/j.issn.1009-0096.2022.04.009 |
| [7] |
吴亚帅, 刘新妹, 殷俊龄, 等. 基于DSO算法的印刷电路板焊点测试路径优化. 科学技术与工程, 2021, 21(14): 5840-5846. DOI:10.3969/j.issn.1671-1815.2021.14.028 |
| [8] |
Xiao Z, Wang ZA, Liu D, et al. A path planning algorithm for PCB surface quality automatic inspection. Journal of Intelligent Manufacturing, 2022, 33(6): 1829-1841. DOI:10.1007/s10845-021-01766-3 |
| [9] |
Abhishek B, Ranjit S, Shankar T, et al. Hybrid PSO-HSA and PSO-GA algorithm for 3D path planning in autonomous UAVs. SN Applied Sciences, 2020, 2(11): 1805. DOI:10.1007/s42452-020-03498-0 |
| [10] |
Teng ZJ, Lv JL, Guo LW. An improved hybrid grey wolf optimization algorithm. Soft Computing, 2019, 23(15): 6617-6631. DOI:10.1007/s00500-018-3310-y |
| [11] |
梁景泉, 周子程, 刘秀燕. 粒子群算法改进灰狼算法的机器人路径规划. 软件导刊, 2022, 21(5): 96-100. |
| [12] |
张真诚. 机器人路径规划的改进粒子群-蚁群算法. 电子测量技术, 2021, 44(8): 65-69. DOI:10.19651/j.cnki.emt.2105919 |
| [13] |
许诺. 基于改进PSO算法的UAV三维路径规划研究. 电子测量技术, 2022, 45(2): 78-83. DOI:10.19651/j.cnki.emt.2108102 |
| [14] |
El-Shafiey MG, Hagag A, El-Dahshan ESA, et al. A hybrid GA and PSO optimized approach for heart-disease prediction based on random forest. Multimedia Tools and Applications, 2022, 81(13): 18155-18179. DOI:10.1007/s11042-022-12425-x |
| [15] |
Liu YY, Dai JJ, Zhao SS, et al. Optimization of five-parameter BRDF model based on hybrid GA-PSO algorithm. Optik, 2020, 219: 164978. DOI:10.1016/j.ijleo.2020.164978 |
 2023, Vol. 32
2023, Vol. 32



