高速公路中的通行时间分布预测, 即给定路段和车辆的出发时间, 预测车辆在该路段通行时间的分布. 由于车速的差异或堵车的发生, 同一出发时间经过同一路段的多辆车可能具有不同的通行时间, 相比于预测通行时间的期望, 预测车辆的通行时间分布可以更全面地反映路段在未来的通行状况, 进而可以更精准的辅助高速公路中的路径规划, 事故事件预警等任务. 因此准确的通行时间分布预测对于高速公路的精细化管理有着重要的意义. 在高速公路中, 车辆运行轨迹数据通过固定式交通信息检测器获得, 这类检测器不仅可以获取到大量的数据, 而且精确性高, 成本低. 如何挖掘高速公路中车辆运行轨迹数据中的有用信息, 并且结合高速公路的拓扑结构信息, 实现准确的通行时间分布预测, 是具有挑战性的.

针对高速公路的通行时间预测问题, 现有的方法主要分为3类: 线性系统理论、非线性系统理论、组合模型.

线性理论方法主要包括历史趋势方法^[1]、时间序列模型^[2]、卡尔曼滤波模型^[3]等. 这类根据历史趋势进行预测的方法比较直观, 但是这类方法无法实现短时间内道路交通流变化较大情况下的通行时间预测^[4] .

相比于线性理论方法, 非线性理论方法可以更好地建模较短时间间隔内交通流的变化特征, 从而更准确地实现通行时间预测, 该类方法主要包括神经网络、支持向量机等. 韩勇等人采用BP神经网络模型来预测相邻信号交叉口之间的车辆运行时间, 将影响车辆出行时间的因素作为网络模型的输入, 预测车辆的通行时间^[5]. 刘松等人通过采集车辆在高速公路进出口收费站的刷卡数据获取通行时间, 利用门控循环神经网络对通行时间进行预测, 该工作取得了比BP神经网络更高的预测精度^[6]. 由于支持向量机在一些工作中被证明可以基于较少数据样本量实现准确的预测, 并且泛化能力较好, 因此也被广泛应用于通行时间预测^[7]. Theja等人提出一种基于支持向量机的模型应用于不同交通条件下的通行时间预测模型, 并与神经网络模型进行了性能上的比较, 说明了基于支持向量机的方法在通行时间预测中的优势与不足^[8].

非线性理论方法更多的是运用海量数据进行计算, 没有将交通流理论进行结合. 一些研究将多个模型或方法组合起来应用于通行时间预测, 以解决单一模型存在的局限性. 丁宏飞等人提出了将支持向量机和BP神经网络相结合的组合预测方法, 结果表明组合预测方法相比单一的BP神经网络或者支持向量机具有更好的预测效果^[9]. Gao等人提出了一种基于支持向量回归和遗传算法相结合的通行时间预测算法, 结合实际交通数据, 证明了这种组合是可行的, 在通行时间预测方面优于历史平均法、多元线性回归法和BP神经网络^[10].

但是, 上述方法难以基于路网拓扑结构捕获路网信息的复杂时空相关性. 为此, 一些工作基于图卷积网络建模道路通行时间与车速的时空相关性实现通行时间的预测^[11-13]. 但是, 这些基于图卷积网络的方法都需要根据距离或者相似性预先定义路网的连接关系图. 这就需要大量的先验知识, 并且预测效果相对于预定义图的质量非常敏感^[14]. 根据先验知识预定义的图通常不能包含路网中完整的空间信息, 并且不能直接和通行时间预测任务建立相关性, 因此这些基于预定义图实现图卷积运算的方法不能较好地适应通行时间预测任务.

本文提出一种基于面向高速公路通行时间分布预测的时空混合密度网络(spatial-temporal mixture density networks, STMDN). 本文使用自适应图卷积网络捕获路网信息的空间相关性, 以解决传统图卷积^[15]运算依赖于预定义邻接矩阵从而产生较大预测偏差的问题. 在时间维度, 本文基于注意力机制^[16]自适应建模路网信息的非线性时间相关性, 并通过卷积层进一步聚合相邻时间片间的信息. 然后, 本文将基于自适应时空建模得到的路段嵌入表示作为混合密度网络^[17]的输入, 实现路段的通行时间分布预测. 最后, 本文基于真实高速公路数据的实验验证了提出方法的有效性. $ {}^{} $

1 相关理论 1.1 通行时间分布预测

(1)高速公路路网. 将高速公路路网定义为一个有向图 $ G=(L, E) $ , 其中 $ L=\{{l}_{0}, {l}_{1}, \cdots , {l}_{M}\} $ 是 $ \left|L\right|=M $ 个路段的集合. $ E $ 是 $ \left|E\right|=\mathrm{Q} $ 条边的集合, 如果路段 $ {l}_{i} $ 和路段 $ {l}_{j} $ 共享同一节点, 则路段 $ {l}_{i} $ 和路段 $ {l}_{j} $ 存在连接关系, $ {e}_{ij}\in E $ 表示连接路段 $ {l}_{i} $ 和路段 $ {l}_{j} $ 的边.

(2)图信号矩阵. 在第 $ t $ 个时间间隔内, 观测到高速公路路网 $ G $ 上的图信号用矩阵 ${\mathbf{X}}_{t}=({\mathbf{x}}_{t, 1}, {\mathbf{x}}_{t, 2}, \cdots , {\mathbf{x}}_{t, M}{)}^{{\rm{T}}}\in {\mathbb{R}}^{M\times C}$ 表示, 其中, $ {\mathbf{x}}_{t, l}\in {\mathbb{R}}^{C} $ 表示第 $ t $ 个时间间隔内路段 $ l $ 的 $ C $ 个观测量的取值.

(3)一次通行时间的查询请求表示为一个元组 $ (l, s) $ , 其中 $ l $ 表示查询路段, $ s $ 表示查询时间, 查询时间前 $ T $ 个时间间隔的图信号矩阵表示为 $ \mathit{\chi }=({\mathbf{X}}_{s-T+1}, {\mathbf{X}}_{s-T+2}, \cdots , {\mathbf{X}}_{s})\in {\mathbb{R}}^{T\times M\times C} $ . 本研究的目标是在给定图信号矩阵 $ \mathit{\chi } $ 的条件下预测路段 $ l $ 在时间 $ s $ 下通行时间的分布 $ p\left(y\right|\mathit{\chi }, l, s) $ .

(4)训练样本. 由 $ N $ 个样本构成的输入为 $ \mathbf{S}=({\mathbf{s}}_{1}, {\mathbf{s}}_{2}, \cdots , {\mathbf{s}}_{N}) $ , 其中每个样本都为一个三元组 $ {\mathbf{s}}_{j}=(\mathit{\chi }, l, s) $ , 三元组元素分别表示该样本查询时间前 $ T $ 个时间间隔的图信号矩阵, 该样本对应的查询路段, 查询时间. $ N $ 个样本的目标值表示为 $\mathbf{y}=({{y}}_{1}, {{y}}_{2}, \cdots , {{y}}_{N})$ .

1.2 自适应图卷积

图卷积网络因其具有捕获图结构上空间相关性的能力已被广泛用于交通流预测领域. 目前普遍使用的图卷积计算公式如下:

$ \mathbf{H}=\left({\mathbf{I}}_{{N}}+{\mathbf{D}}^{-\frac{1}{2}}\mathbf{A}{\mathbf{D}}^{-\frac{1}{2}}\right)\mathbf{X}\mathbf{W}+\mathbf{b} $

(1)

其中, $ \mathbf{A}\in {\mathbb{R}}^{N\times N} $ 为图邻接矩阵, $ \mathbf{D} $ 是度矩阵, $ \mathbf{X}\in {\mathbb{R}}^{N\times C} $ 为图信号输入, $ \mathbf{H}\in {\mathbb{R}}^{N\times F} $ 为经卷积计算后的输出, $ \mathbf{W}\in {\mathbb{R}}^{C\times F} $ 和 $ \mathbf{b}\in {\mathbb{R}}^{F} $ 为可学习参数. 图卷积操作通过一组共享的参数 $ \mathbf{W}\mathrm{和}\mathbf{b} $ 聚合节点自身及其邻居信息, 实现空间特征提取.

传统图卷积模型普遍使用预定义的邻接矩阵 $ \mathbf{A} $ , 邻接矩阵 $ \mathbf{A} $ 基于距离或历史时间序列相似性计算. 此种方法的弊端在于节点特征在图结构上的传播将完全依赖于预定义的图结构, 由于预定义图结构难以保证其能完全包含高速公路路网中复杂的空间相关性, 通行时间预测的准确度难以保证.

为解决上述问题, 自适应图卷积通过数据驱动的方式, 通过学习图节点的表示, 计算出自适应邻接矩阵用于图卷积运算. 具体来说, 首先为每个图节点随机初始化一个节点嵌入矩阵 ${\mathbf{E}}_{{v}}\in {\mathbb{R}}^{N\times {d}_{e}}$ , 该矩阵中的每一行表示一个节点的嵌入表示, $ {d}_{e} $ 即为节点嵌入维度. 通过节点表示 ${\mathbf{E}}_{{v}}$ 与其自身转置 ${{\mathbf{E}}^{{\rm{T}}}_{{v}}}$ 的乘积计算节点相似度:

$ {\mathbf{D}}^{-\frac{1}{2}}\mathbf{A}{\mathbf{D}}^{-\frac{1}{2}}={{\textit{Softmax}}}\left({R}{e}{L}{U}\left({\mathbf{E}}_{{v}}\cdot {\mathbf{E}}_{{v}}^{{\rm{T}}}\right)\right) $

(2)

自适应邻接矩阵不需要任何先验知识, 在训练过程中通过梯度下降学习邻接矩阵参数, 通过数据驱动的方式发现路网信息中的空间相关性.

我们使用式(2)中使用自适应方法计算得到的 $ {\mathbf{D}}^{-\frac{1}{2}}\mathbf{A}{\mathbf{D}}^{-\frac{1}{2}} $ 应用到式(1), 实现对各个时间片的空间图进行自适应图卷积运算, 以得到各个时间步空间图的嵌入表示表示 $ {\mathbf{H}}_{t} $ :

$ {\mathbf{H}}_{t}=\left(\mathbf{I}+{{\textit{Softmax}}}\left({R}{e}{L}{U}\right({\mathbf{E}}_{{v}}\cdot {\mathbf{E}}_{{v}}^{{\rm{T}}}\left)\right)\right){\mathbf{X}}_{t}\mathbf{W}+\mathbf{b} $

(3)

其中, $ {\mathbf{X}}_{t} $ 为第 $ t $ 个时间片下的图信号矩阵.

1.3 混合密度网络

混合密度网络采用神经网络映射输入数据与混合分布参数之间的关系, 从而实现对条件概率分布的拟合. 混合密度网络融合了人工智能与非参数估计方法的优势, 混合分布通过多个子分布参数的灵活组合具有更强的拟合能力, 并且神经网络可以映射高维非线性关系.

以采用全连接网络将输入映射到混合高斯分布的参数为例, 假设由 $ N $ 个样本构成的输入为 $ \mathbf{X}=({\mathbf{x}}_{1}, {\mathbf{x}}_{2}, \cdots , {\mathbf{x}}_{N}) $ , 其中 $ {\mathbf{x}}_{i}\in {\mathbb{R}}^{d} $ , $ d $ 为样本特征维度. 样本对应的目标值为 $\mathbf{y}=({{y}}_{1}, {{y}}_{2}, \cdots , {{y}}_{N})$ . 对于第 $ j $ 个样本对应的混合分布中的第 $ i $ 个高斯分布, 全连接网络的映射表示为函数 $ {h}_{i}\left({\mathbf{x}}_{j}\right) $ , 通过输出层输出 $ C $ 个高斯分布的权重参数 $ {\omega }_{i}\left({\mathbf{x}}_{j}\right) $ , 均值 $\; {\mu }_{i} $ ( $ {\mathbf{x}}_{j} $ ), 标准差 $ {\sigma }_{i}\left({\mathbf{x}}_{j}\right) $ , $ i=1, \cdots , C $ . 第 $ j $ 个样本的混合高斯分布的概率密度函数为:

$ p\left({{y}}_{j}|{\mathbf{x}}_{j}\right)=\sum _{i=1}^{C}{\omega }_{i}\left({\mathbf{x}}_{j}\right)\frac{1}{(2\pi {)}^{\frac{1}{2}}{\sigma }_{i}({\mathbf{x}}_{j})}\mathrm{exp}\left\{-\frac{({y}_{j}-{\mu }_{i}{({\mathit{x}}_{j}))}^{2}}{2{\sigma }_{i}^{2}\left({\mathit{x}}_{j}\right)}\right\} $

(4)

其中, $ {\omega }_{i}\left({\mathbf{x}}_{j}\right) $ 为第 $ i $ 个高斯分布的权重参数, 满足 $ {\omega }_{i}\left({\mathbf{x}}_{j}\right)\geqslant 0 $ 且 $ \displaystyle\sum _{i=1}^{C}{\omega }_{i}\left({\mathbf{x}}_{j}\right)=1 $ . 混合密度函数的输出层可通过 ${{\textit{Softmax}}}$ 函数保证权重参数 $ {\omega }_{i}\left({\mathbf{x}}_{j}\right) $ 为正实数且和为 $ 1 $ , $ {\omega }_{i}\left({\mathbf{x}}_{j}\right) $ 的计算可形式化定义为:

$ {\omega }_{i}\left({\mathbf{x}}_{j}\right)={{\textit{Softmax}}}\left({h}_{i}\left({\mathbf{x}}_{j}\right)\right)=\frac{{{\rm{exp}}}\left({h}_{i}\right({\mathbf{x}}_{j}\left)\right)}{{\displaystyle\sum }_{i=1}^{C}{{\rm{exp}}}\left({h}_{i}\right({\mathbf{x}}_{j}\left)\right)} $

(5)

另外, 均值 $ \;{\mu }_{i} $ ( $ {\mathbf{x}}_{j} $ ), 标准差 $ {\sigma }_{i}\left({\mathbf{x}}_{j}\right) $ , $ i=1, \cdots , C $ 的计算可形式化定义为:

$ {\mu }_{i}\left({\mathbf{x}}_{j}\right)={h}_{i}\left({\mathbf{x}}_{j}\right) $

(6)

$ {\sigma }_{i}\left({\mathbf{x}}_{j}\right)=\mathrm{exp}\left({h}_{i}\left({\mathit{x}}_{j}\right)\right) $

(7)

在得到混合高斯分布的参数以及权重参数后, 根据极大似然估计的假设, 希望输出分布在目标值 $ \mathbf{y} $ 处概率值最大. 设 $ \mathbf{y} $ 中的目标值均为独立分布, 混合密度网络的损失函数 $ l\left(\theta \right|\mathbf{X}, \mathbf{y}) $ 可通过对数似然函数 $ \mathrm{l}\mathrm{n}P\left(\mathbf{y}\right|\theta , \mathbf{X}) $ 表示:

$ l\left(\theta |\mathbf{X}, \mathbf{y}\right)=\mathrm{l}\mathrm{n}P\left(\mathbf{y}|\theta , \mathbf{X}\right)=\sum _{j=1}^{N}\mathrm{l}\mathrm{n}P\left({y}_{j}|\theta , {\mathbf{x}}_{j}\right) $

(8)

混合密度网络根据极大似然估计的假设, 通过梯度上升算法训练网络, 获得最优网络参数 $ {\theta }^{*} $ :

$ {\theta }^{*}={{\rm{argmax}}}_{\theta }l\left(\theta |\mathbf{X}, \mathbf{y}\right) $

(9)

2 模型介绍

本文提出的基于时空混合密度网络的通行时间分布预测模型(STMDN)的整体结构如图1所示, 首先, 以查询时间 $ s $ 前 $ T $ 个时间间隔的图信号矩阵 $ \mathit{\chi }=({\mathbf{X}}_{s-T+1}, {\mathbf{X}}_{s-T+2}, \cdots , {\mathbf{X}}_{s}) $ 为输入, 通过自适应图卷积建模路网信息的空间相关性, 得到各个路段的嵌入表示 $ \mathcal{H}=({\mathbf{H}}_{s-T+1}, {\mathbf{H}}_{s-T+2}, \cdots , {\mathbf{H}}_{s}) $ . 在时间维, 基于注意力机制捕获路网信息的时间相关性, 得到聚合时空信息的路段嵌入表示 ${\mathcal{H}}'=({\mathbf{H}}'_{s-T+1}, {\mathbf{H}}'_{s-T+2}, \cdots , {\mathbf{H}}'_{s})$ . 然后, 通过卷积层进一步聚合相邻时间片的信息, 得到所有路段编码后的嵌入表示 $\mathbf{Z}=({\mathbf{z}}_{1}, \cdots , {\mathbf{z}}_{{M}})$ 作为混合密度网络的输入, 输出混合高斯分布中各个分布的均值 $ \;{\mu }_{i} $ , 方差 $ {\sigma }_{i} $ 以及权重参数 $ {\omega }_{i} $ , 其中 $ i=1, \cdots , C $ , 以此得到查询路段的通行时间分布 $ p\left(y\right|\mathit{\chi }, l, s) $ .

2.1 自适应空间相关性建模

由于预定义图结构难以保证其能完全包含高速公路路网中复杂的空间相关性, 并且无法直接与通行时间预测任务建立直接的关联性, 因此可能带来很大的预测偏差. 本文采用式(3)定义的自适应图卷积建模路网中路段的空间相关性. 通过自适应空间相关性建模得到的查询时间 $ t $ 前 $ T $ 个时间步的路段嵌入表示为 $ \mathcal{H}=({\mathbf{H}}_{s-T+1}, {\mathbf{H}}_{s-T+2}, \cdots , {\mathbf{H}}_{s})\in {\mathbb{R}}^{M\times T\times F} $ .

2.2 自适应时间相关性建模

在时间维度上, 不同时间片的路网信息之间存在显著的相关性, 并且在不同情况下, 相关性也不同. 在这里, 我们贯彻自适应的理念, 引入注意机制对时间序列的不同部分赋予不同相关性. 我们使用式(10)和式(11)计算出时间注意力矩阵:

$ \mathbf{C}=\mathbf{V}\cdot \sigma \left( \left( {(\mathcal{H})}^{{\rm{T}}}{\mathbf{U}}_{1}\right) {\mathbf{U}}_{2} \left({\mathbf{U}}_{3}\mathcal{H}\right)+\mathbf{e} \right) $

(10)

$ {\mathbf{C}}'_{i, j}=\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left({\mathbf{C}}_{i, j}\right)}{{\displaystyle\sum }_{j=1}^{T}\mathrm{e}\mathrm{x}\mathrm{p}\left({\mathbf{C}}_{i, j}\right)} $

(11)

其中, $ \mathbf{V}, \mathbf{e}\in {\mathbb{R}}^{T\times T} $ , $ {\mathbf{U}}_{1}\in {\mathbb{R}}^{N} $ , $ {\mathbf{U}}_{2}\in {\mathbb{R}}^{F\times M} $ , $ {\mathbf{U}}_{3}\in {\mathbb{R}}^{F} $ 是可学习参数. 时间相关性矩阵 $ \mathbf{C} $ 的值由数据决定, 其中某元素 $ {\mathbf{C}}_{i, j} $ 表示时间片 $ i $ 和 $ j $ 的相关性. 最后, 使用 ${{\textit{Softmax}}}$ 函数对矩阵进行标准化. 我们用计算得到时间注意力矩阵与卷积后的时空图表示相乘, 得到新的时空图表示:

$ {\mathcal{H}}'=\mathcal{H}{\mathbf{C}}'=\left({\mathbf{H}}_{s-T+1}, {\mathbf{H}}_{s-T+2}, \cdots , {\mathbf{H}}_{s}\right){\mathbf{C}}' $

(12)

此时, 对 ${\mathbf{H}}'_{t}, \forall t\in [0, T]$ 中任意元素 ${\mathbf{H}}'_{t, i, j}$ , 其中已包含与其自适应相关的空间、时间维度聚合后的信息. 在上述基础上, 我们在时间维度上应用 $ R $ 个标准卷积层进一步聚合相邻时间片间的信息. 对其中第 $ r $ 步卷积, 可表示为:

$ {\mathcal{H}}'^{\left(r\right)}={{\textit{ReLU}}}\left(\mathrm{\Phi }*{\mathcal{H}}'^{\left(r-1\right)}\right)\in {\mathbb{R}}^{{F}_{r}\times M\times {T}_{r}} $

(13)

其中, $ * $ 表示标准卷积操作, $ \mathrm{\Phi } $ 为时间维卷积核参数, $ {F}_{r} $ 表示第 $ r $ 步卷积后图节点的特征维度, $ {T}_{r} $ 表示经第 $ r $ 步卷积后时间维度大小. 最终输出为:

$ \mathbf{Z}={{\textit{ReLU}}}\left(\mathrm{\Phi }*{\mathcal{H}}'^{\left(R\right)}\right)\in {\mathbb{R}}^{{F}_{{\rm{out}}}\times M} $

(14)

$ {F}_{{\rm{out}}} $ 表示最终图节点的输出维度, $\mathbf{Z}=({\mathbf{z}}_{1}, \cdots , {\mathbf{z}}_{{M}})$ 表示通过自适应时空相关性建模获得的 $ M $ 个路段嵌入表示.

2.3 通行时间分布预测

同一路段在单一时间步可能有多辆车通过, 由于车速的差异或堵车的发生, 这些车辆的通行时间可能是不同的. 为更全面的建模各个路段在不同时间步的通行时间, 我们将预测给定查询时间 $ s $ , 查询路段 $ l $ , 图信号矩阵 $ \mathit{\chi } $ 的条件下的通行时间分布. 通过混合密度网络, 可以在自适应建模路网中复杂时空相关性的基础上实现通行时间分布的预测. 第 $ j $ 个样本的通行时间 $ {y}_{j} $ 的分布表示为:

$ P\left({y}_{j}|{\mathbf{s}}_{j}\right)=\sum _{i=1}^{C}{\omega }_{i}\left({\mathbf{s}}_{j}\right)\mathcal{N}\left({\mu }_{i}\left({\mathbf{s}}_{j}\right), {\sigma }_{i}\left({\mathbf{s}}_{j}\right)\right) $

(15)

其中, $ \mathcal{N}(\cdot ) $ 表示高斯分布. 根据自适应时空相关性建模获得的路段嵌入表示 $ {\mathbf{z}}_{j} $ , 可以由式(16)计算混合分布的权重参数:

$ {\omega }_{i}\left({\mathbf{s}}_{j}\right)={{\textit{Softmax}}}\left({\mathbf{z}}_{j}\right)=\frac{{{\rm{exp}}}\left({f}_{i}\right({\mathbf{z}}_{j}\left)\right)}{{\displaystyle\sum }_{i=1}^{C}{{\rm{exp}}}\left({f}_{i}\right({\mathbf{z}}_{j}\left)\right)} $

(16)

混合分布的均值和方差计算定义为:

$ {\mu }_{i}\left({\mathbf{s}}_{j}\right)={f}_{i}\left({\mathbf{z}}_{j}\right) $

(17)

$ {\sigma }_{i}\left({\mathbf{s}}_{j}\right)=\mathrm{exp}\left({f}_{i}\right({\mathbf{z}}_{j})) $

(18)

其中, $ {f}_{i} $ 为全连接层.

2.4 模型训练

在得到混合高斯分布的参数后, 根据极大似然估计的假设, 希望输出值分布在目标值 $ \mathbf{y} $ 处概率值最大. 设 $ \mathbf{y} $ 中的目标值均为独立分布, 混合密度网络的损失函数 $ l\left(\theta \right|\mathbf{S}, \mathbf{y}) $ 可通过对数似然函数 ${\rm{ln}}P\left(\mathbf{y}\right|\theta , \mathbf{S})$ 表示:

$ l\left(\theta |\mathbf{S}, \mathbf{y}\right)=\mathrm{l}\mathrm{n}P\left(\mathbf{y}|\theta , \mathbf{S}\right)=\sum _{j=1}^{N}\mathrm{l}\mathrm{n}P\left({y}_{j}|\theta , {\mathbf{s}}_{j}\right) $

(19)

混合密度网络根据极大似然估计的假设训练网络, 为了使 $ P\left(\mathbf{y}\right|\theta , \mathbf{S}) $ 具有极大值, 通过梯度上升算法优化网络参数, 最终获得最优网络参数 $ {\theta }^{*} $ :

$ {\theta }^{*}={{\rm{argmax}}}_{\theta }l\left(\theta |\mathbf{S}, \mathbf{y}\right) $

(20)

3 实验 3.1 数据集与数据处理

本文使用的数据集来自桂林市区域的高速公路, 车辆通行时间由高速公路收费设备(收费站、门架)采集. 我们提取了2021年1月的13万车次在36条主要路段上的通行时间数据, 同时按照7:2:1的比例沿时间线划分了训练集、验证集、测试集.

3.2 基准方法与评价指标

我们将STMDN与其他4种现有可用于时间分布预测的经典模型进行了对比.

MLP^[18]: 多层感知机, 通过设置隐藏层捕获高阶函数关系.

LSTM^[19]: 一种经典的循环神经网络模型, 广泛用于处理序列数据.

ASTGCN^[20]: 一种用于交通流预测的基于注意力的时空图卷积模型, 其在时间和空间为都应用了集合注意力机制的卷积操作.

AGCRN^[14]: 一种应用了自适应图卷积和循环神经网络的交通流预测模型.

上述所有模型的输入数据与本文模型的输入相同, 但根据不同模型所需的数据格式进行了相应的调整.

本文采用均方误差(root mean square error, RMSE)、平均绝对误差(mean absolute error, MAE)、平均绝对百分比误差(mean absolute percentage error, MAPE)作为评价指标, 具体公式如下:

$\left\{ { \begin{split} &{{\textit{RMSE}}}=\sqrt{\frac{1}{n}\sum _{i=1}^{n}{({y}_{i}-{\widehat{y}}_{i})}^{2}} \\ &{{\textit{MAE}}}=\frac{1}{n}\sum _{i=1}^{n}\left|{y}_{i}-{\widehat{y}}_{i}\right| \\ &{{\textit{MAPE}}}=\frac{100{\text{%}}}{{n}}\sum _{{i}=1}^{{n}}\left|\frac{{{y}}_{{i}}-{\widehat{{y}}}_{{i}}}{{{y}}_{{i}}}\right| \end{split} } \right.$

3.3 实验环境与设置

本文模型基于PyTorch框架实现, 自适应图神经网络的节点嵌入维度为64, 图卷积, 时间注意力卷积, 隐藏层大小均设置为128, 混合密度网络中全连接层的嵌入维度为64. 时间注意力卷积模块在时间维度堆叠了3层卷积得到最终预测结果. 模型训练采用了Adam优化算法, 初始学习率0.0001, 训练批次大小128.

本文实验使用Python 3.6编写, PyTorch框架版本1.10.2, 硬件配置如表1所示.

3.4 实验结果

图2展示了模型Loss以及3项评价指标的收敛过程. 可以看到, 模型在训练初期收敛速度较快, 随着训练轮数增加, 模型最终收敛并在评价指标上取得较好的结果.

我们以秒为单位进行预测, 并将STMDN与前述的4种基准方法进行了比较, 表2展示了其在桂林高速公路数据集上的预测结果.

从表2可以看出, 我们提出的模型STMDN在3种评价指标中均达到了最佳性能. 其中, MLP是经典深度学习结构, 可以用于几乎所有预测任务, 但由于其结构单一, 在预测通行时间时缺少相应的模块建模路网信息的时空相关性, 导致效果并不理想. LSTM有能力捕获时间序列上长短期依赖, 但是其难以捕获空间维度上路网信息的相关性, 因此效果仍然有限. ASTGCN和AGCRN作为时空预测领域的模型, 都集成了空间和时间两个维度的处理模块. 然而, ASTGCN在图卷积模块中基于注意力机制计算得到的邻接矩阵对相关性的捕获能力仍弱于自适应矩阵, 因为基于预定义的图难以建模路网信息中完整的空间相关性. 此外, 以上所有模型都仅能够针对于通行时间均值进行预测, 本文模型通过引入混合密度网络实现了对通行时间的分布预测. 本文模型通过独特设计, 巧妙地将自适应图学习、注意力机制与混合密度网络结合, 学习路网信息的时空特征的同时建模了目标值的条件概率分布, 从而实现了最佳效果.

为了进一步研究本文模型中不同模块的效果, 我们设计了原模型的3个变体进行消融实验, 我们将这3个变体与本文模型进行比较, 各变体模型描述如下.

STMDN_wo_T: 在STMDN的基础上, 不使用时间注意力机制建模路网信息的时间相关性.

STMDN_wo_S: 在STMDN的基础上, 不使用自适应图卷积建模路网信息的空间相关性.

STMDN_wo_M: 在STMDN的基础上, 不使用混合密度网络建模通行时间的分布, 直接预测通行时间均值, 并且使用均方误差作为损失函数训练模型.

消融实验结果如表3所示, 首先, 在不建模路网信息的时间相关性的情况下(STMDN_wo_T), 模型效果在各项指标的表现都显著降低. 由于路段的通行时间, 以及车速等信息在时间维度上具有相关性, 因此本文基于注意力机制自适应地学习路网信息的时间相关性对于准确的通行时间预测是有效的. 在不建模路网信息的空间相关性的情况下(STMDN_wo_S), 模型效果也有所降低, 由于不同路段的车速和通行时间变化是存在相关性的, 比如上游路段发生的拥堵通常会影响下游路段的通行时间和车速, 因此本文通过自适应图卷积捕获路网信息的空间相关性是有效的. 最后, 在不使用混合密度网络的情况下(STMDN_wo_ M), 模型效果显著降低, 因为建模通行时间的分布可以更全面地反映各个路段在不同时间的通行时间, 并且可以建模通行时间的波动性, 因此建模通行时间的分布有助于模型更准确地预测通行时间.

3.5 案例分析

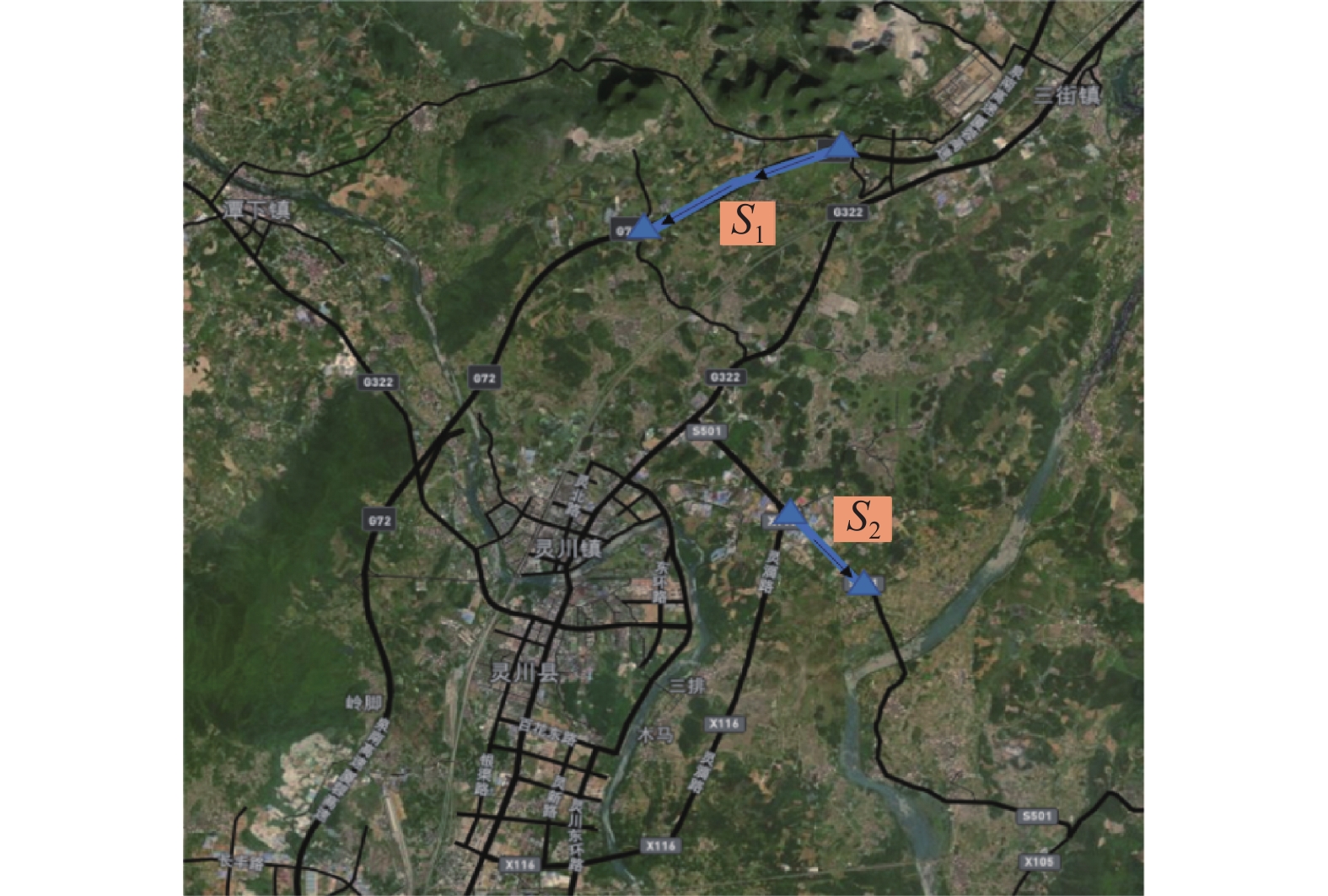
本文在桂林高速公路的两个路段进行案例分析, 其位置如图3中的 $ {S}_{1}, {S}_{2} $ 所示.

案例分析结果如图4所示. 其中横坐标表示通行时间(time), 纵坐标表示概率密度函数(probability density function, pdf). 图4(a)和图4(b)分别表示的是2021年1月30日和31日14:30驶入桂林高速公路 $ {S}_{2} $ 路段的车辆在该路段的真实通行时间分布(label)和使用STMDN预测得到的通行时间分布, 从图中可以看出STMDN较准确地预测了真实的通行时间分布. 图4(c)和图4(d)分别表示的是2021年1月30日和31日13:10驶入桂林高速公路 $ {S}_{1} $ 路段的车辆在该路段的真实通行时间分布(label)和使用STMDN预测得到的通行时间分布. 从该图可以看出, 真实车辆通行时间集中在400–500 s, 由STMDN预测得到的通行时间分布可以很好地反映这一现象, 并且STMDN可以较准确的建模通行时间分布的长尾部分. 相比于预测通行时间的均值, 预测通行时间的分布能更全面地反映道路的通行状况, 因此可以更精准的辅助高速公路中的路径规划, 事故事件预警等管理目标.

4 结论与展望

为更全面地反映高速公路中各个道路的通行状况, 本文提出一种面向高速公路通行时间分布预测的时空混合密度网络. 本文使用自适应图卷积网络捕获路网信息的空间相关性, 解决基于预定义图的图卷积运算难以包含路网信息完整空间相关性的问题, 此外, 本文基于注意力机制自适应建模路网信息的时间相关性, 然后通过卷积层进一步聚合相邻时间片间的信息. 然后, 本文将基于自适应时空相关性建模得到的路段嵌入表示输入混合密度网络, 以建模通行时间的分布, 并根据极大似然估计, 采用梯度上升的方式训练模型, 得到最优模型参数, 以预测通行时间分布. 最后, 本文通过实验证明了提出方法的有效性. 基于本文提出的方法, 今后我们将进一步研究由多个路段组成的路线的通行时间分布预测.