2. 季华实验室 新型显示技术与装备研究中心, 佛山 528200
2. New Display Technology and Equipment Center, Ji Hua Laboratory, Foshan 528200, China
近些年来, 随着互联网与多媒体技术的高速发展, 每分每秒都有庞大的图像数据在互联网上传输, 如何从大规模的图像数据中快捷、准确地查询检索到用户所需图像数据, 成为图像检索技术领域研究的一个热点问题[1]. 图像检索主要可分为两大类: 以人工标注图像文本信息为主的基于文本的图像检索(text-based image retrieval, TBIR), 以及以图像语义内容为主的基于内容的图像检索(content-based image retrieval, CBIR). 其中, 基于内容的图像检索技术是一种相对比较有优势方案, 它是从图像中提取图像的特征信息, 将特征信息存储, 并以特征信息为依据进行图像检索, 不需要繁杂的人工交互和干预. 但一张图像所蕴含的信息, 往往需要高维度特征矢量才能有效表达, 而处理高维度特征矢量需要消耗大量的存储空间和计算资源. 为了保证图像检索质量和计算效率, 哈希方法逐渐受到欢迎, 它能将图像的高维特征信息映射到低维汉明空间的二进制编码(即哈希编码), 解决上述特征存储空间大、计算复杂度高的难题.
关于哈希图像检索研究, Gionis等人提出局部敏感哈希(locality sensitivity hashing, LSH)算法[2], 首次将哈希应用到图像检索领域, 设计了一种位置敏感的哈希函数随机映射哈希码; Shen等人提出监督离散哈希(supervised discrete hashing, SDH)算法[3], 采用一种离散循环坐标下降法生成哈希编码; Liu等人提出核监督哈(kernel-based supervised hashing, KSH)算法[4], 利用核函数为原始数据提供非线性映射以生成有判别性的哈希码; 迭代量(iterative quantization)算法[5]与乘积量化(product quantization, PQ)算法[6]通过最小化重构误差建立哈希方程; 谱哈希(spectral hashing, SH)算法[7]与锚点图哈希(anchor graph hashing, AGH)算法[8]利用图学习构建数据的哈希编码[9]. 但由于图像数据维度高, 特征提取困难的问题, 上述传统方法都无法达到令人满意的效果.
随着深度学习在计算机视觉领域的成功应用, 越来越多研究表明深度神经网络在图像特征表示方面有出色的性能. 因此, 深度学习被运用到图像哈希检索领域以解决高维度、大规模的图像检索. 深度哈希方法通过卷积神经网络出色的特征表达能力学习哈希方程, 解决传统方法在高维度图像上特征提取难的问题, 生成判别力强的哈希码. Xia等人提出卷积神经网络哈希(convolutional neural network hashing, CNNH)算法[10], 采用两阶段策略, 其中第1阶段用非深度学习的方法学习各个数据的近似哈希码, 第2阶段通过深度网络学习一个哈希函数来拟合第1阶段的哈希码. 深度神经网络哈希(deep neural network hashing, DNNH)算法[11]通过改进CNNH算法, 使特征提取和哈希编码可以在同一学习过程中优化. 深度哈希网络(deep hashing network, DHN)[12]在DNNH算法上进一步改进, 在保留成对相似度的同时, 引入正则化控制量化损失. Liu等人提出深度监督哈希(deep supervised hashing, DSH)算法[13], 引入正则化约束, 使神经网络的实数输出更趋近于离散值. Li等人提出深度二元组监督哈希(deep pairwise-supervised hashing, DPSH)算法[14], 该算法利用标签对, 同时学习图像特征及其哈希编码. 受到DPSH算法启发, Wang等人提出深度三元标签监督哈希(deep supervised hashing with triplet labels, DTSH)算法[15], 使用三元组损失函数进行端到端学习. Cao等人提出哈希网络(hashnet: deep learning to hash by continuation)[16], 通过平衡训练数据对和引入量化函数的近似来改进DHN算法. Li等人提出深度离散哈希(deep supervised discrete hashing, DSDH)算法[17], 将神经网络最后一层的输出直接限制为二进制编码, 并在训练过程中使用交替优化的方式. 深度柯西哈希(deep cauchy hashing, DCH)算法[18]与汉明距离间隔最大化哈西(maximum-margin hamming hashing, MMHH)算法[19]将数据相似对和不相似对建模为一个分布, 利用分布的特性降低由数据不平衡造成的局部优化, 提高对噪声数据的鲁棒性. Jiang等人提出非对称深度监督哈希(asymmetric deep supervised hashing, ADSH)算法[20], 以非对称方式处理查询和数据库, 实现高效训练. Zhang等人提出改进的深度哈希网络(improved deep hashing network, IDHN)[21], 在归一化语义标签上将数据对的相似性量化, 通过量化的相似度信息增强多标签数据集的图像检索性能. 中心相似度量化(Central similarity quantization, CSQ)算法[22]与正交哈希(deep hashing with a single cosine similarity based learning objective, OrthoHash)算法[23]使用Hadamard矩阵预先设定哈希中心, 通过拉近相似数据与其对应的哈希中心之间的汉明距离进行相似度学习.
以上深度哈希方法都着眼于如何优化相似度度量方法以及降低量化误差, 所设计网络模型的目标本质上还是分类. 主要有两个原因导致模型性能受限: (1) 16位哈希编码可以区分百万种类别, 因此必定存在编码冗余(即哈希编码的冗余性), 而现有方法的网络任务没有利用冗余的编码; (2)网络哈希编码层仅使用全连接层学习哈希函数, 并行地输出整段哈希编码, 这种方法预先假定了哈希编码每一位的生成相互独立, 忽略了哈希编码自身的内在联系(即哈希编码的关联性).
因此, 本文首次将深度哈希视为信息论中的编码过程, 利用编码的冗余性和关联性对哈希码进行校验. 在编码传输过程中, 编码信息由于信道的各种干扰而产生错误, 利用冗余编码位可对传输后的内容进行校验. 如图1通用编码校验框架所示, 编码校验即由某种判错纠错的目的计算生成校验码, 例如奇偶校验码、汉明编码等. 而由于哈希图像检索生成的编码存在冗余, 因此可将冗余的编码位用作编码校验, 也就是在相同位数编码的情况下, 利用冗余编码位进行编码校验实现更加准确的信息编码. 同时, 由于校验码的生成依据是前部分的信息码, 信息码和校验码拼接组成哈希编码的编码方式增强了哈希编码自身的关联性.

|
图 1 通用编码校验框架 |
更具体地, 本文提出的方法将哈希编码分段进行, 在图1通用编码校验框架中体现如下: 网络生成的编码(信息码)会产生由实数向量转化为二进制编码的量化损失(即编码在信道传输产生错误的过程), 进而造成信息码错误, 或者生成判别力不足的哈希编码. 此时, 利用冗余的编码位(校验码)对存在量化损失的实数向量进行校验, 由于哈希图像检索的目的是对不同类别图像生成具有判别力的哈希编码, 冗余编码位会在含有歧义、判别能力不足的样本上通过校验码计算模块生成额外的、具有判别力的校验码, 因此可以将该校验码和原编码拼接作为哈希编码. 如图2编码校验示例所示, 原始的一对在实数空间上具有较大差异的向量在二值化编码之后得到了相同的一对哈希编码, 在汉明空间上不具有判别能力. 此时, 若对原始实数向量添加冗余编码位, 生成额外的校验码, 拼接的实数向量对二值化后, 由于附加的校验码部分而具有判别性, 形成更加可靠的哈希编码.

|
图 2 编码校验示例 |
而上述过程中, 将原本无关联性的哈希编码分段输出, 在足够信息码位的前提下, 其他冗余的编码位为校验码, 由上一段信息码的特征得到, 最后将各码段拼接作为哈希编码. 本文将这种串行哈希编码的网络命名为SHNet (serial hash network), 采用mAP作为检索性能评价标准, 使用SHNet在4个公开的数据集CIFAR-10[24]、ImageNet[25]、MS COCO[26]、NUS-WIDE[27]上与目前具有代表性的深度哈希方法进行对比实验, 实验结果表明, SHNet取得了更高的检索性能.
2 基于串行哈希编码的网络SHNet检索的详细流程如图3所示, 可分为3个部分, 第1部分介绍本文提出的串行编码方式(第2.1节), 使用图3所示串行哈希编码层在每个子编码器输出等长的子编码段, 最后将若干段子编码段拼接作为串行哈希编码层的输出, 即哈希编码; 第2部分介绍如何根据数据集的标签生成哈希中心(第2.2节)预先生成哈希中心; 第3部分介绍损失函数(第2.3节), 通过二元交叉熵损失训练缩小图像哈希编码与其对应的哈希中心之间在汉明空间上的距离. 在检索过程, 使用训练好的网络结构作为哈希方程, 将检索图像以及数据库图像编码成二值哈希码, 使用检索图像哈希码与数据库图像的哈希码计算汉明距离, 根据汉明距离排序的方法得到最后的检索结果.
2.1 串行哈希编码网络结构如图3所示, 整体的网络结构由主干网络和串行哈希编码层两部分组成. 主干网络采用预训练的ResNet50[28]对图像数据进行特征提取. 哈希编码层部分如图3中串行哈希编码层部分所示, 图中串行哈希编码层采用4个子编码器

|
图 3 SHNet图像检索的工作流程 |

|
图 4 子编码器的网络结构 |
设主干网络输出的图像特征向量为
对于第1个子编码器, 有:
| I1=ψ1I(x) | (1) |
| h1=ψ1C(I1) | (2) |
其中,
对于第2个子编码器:
| I2=ψ2I(x+I1) | (3) |
| h2=ψ2C(I2) | (4) |
由式(3)、式(4)递推可得:
| In=ψnI(x+In−1) | (5) |
| hn=ψnC(In) | (6) |
子编码器
| h={h1,h2,⋯,hn} | (7) |
除了第1个子编码器, 每个子编码器都会收到已输出的子码段的编码信息和主干网络的原始图像特征信息用作编码校验, 输出等长的子编码段. 本文不对每一子编码段功能(信息码或校验码)做具体定义, 而是由神经网络为达到更好检索的目的自行训练. 其中, 每个子编码器输出等长的哈希码. 本文所使用的子编码段为16 bit (过小使编码器深度过大, 有梯度消失或者过拟合的风险, 故此处选择存储单位一字节为一段子编码长度), 如图3网络使用4个子编码器串行级联, 则最终生成64 (16×4) bits的哈希码. 同理, 若最终需要生成32 (16×2) bits的哈希码, 则使用2个子编码器串行级联.
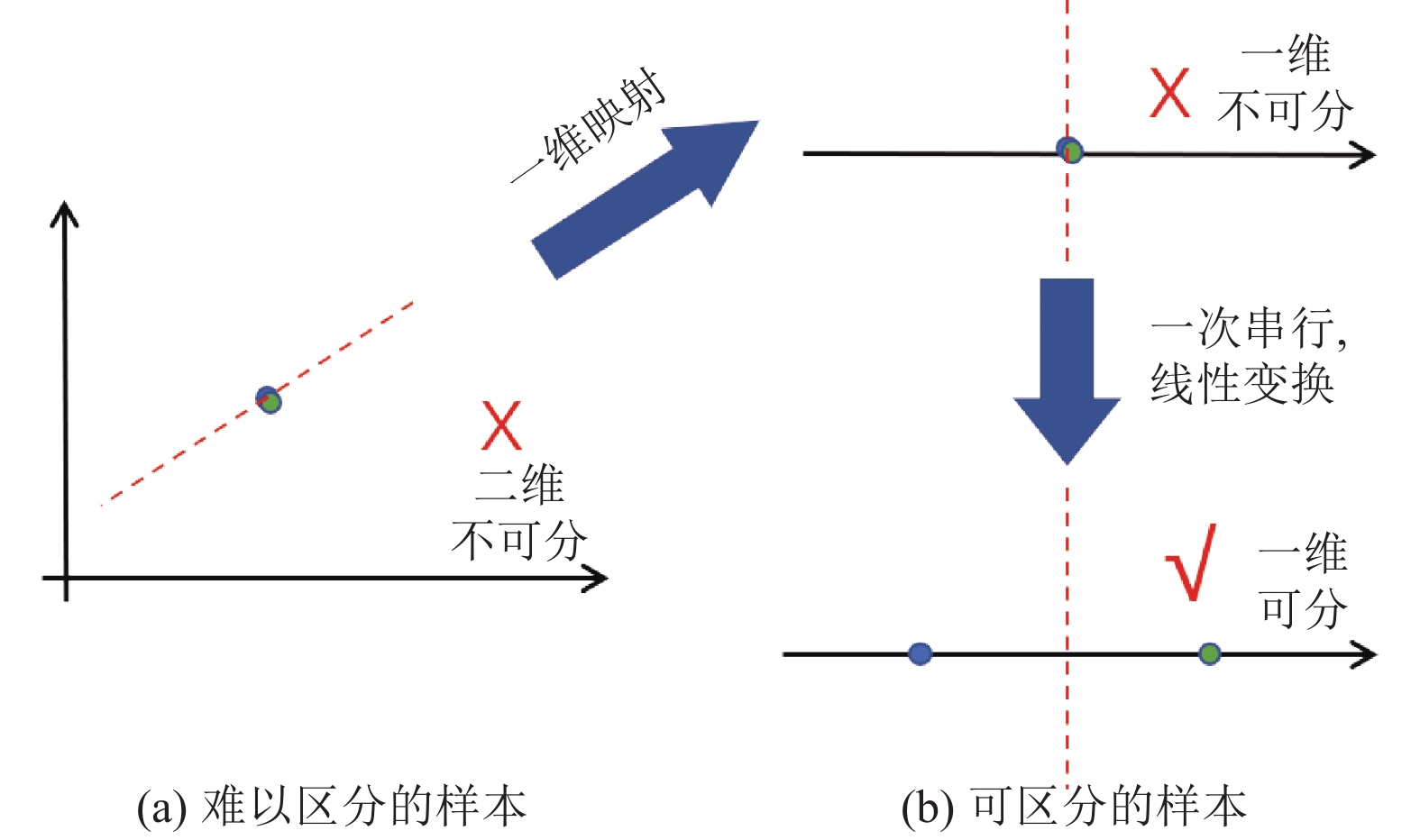
该串行哈希编码的方式实际上是将全连接的分界面转换为线性空间的嵌套. 如图5为一个简单样本分类示例, 假设有两个在二维空间中难以线性区分的样本(图5(a)所示), 那么其在一维空间的映射也同样难以区分, 无论如何优化, 都无法优化出一个能够区分的线性分界面. 然而, 倘若其在一维空间中再做一次线性变换(全连接层等效于对原始空间做线性变换), 样本在空间中的判别性就能显示出来(图5(b)所示), 这也是利用冗余编码位在分界面上的真正作用. 并行输出哈希编码对应高维度空间的线性分类, 串行输出哈希编码对应低维度空间的线性分类嵌套, 通过将高维度线性分界面分解为多个低维度线性空间的嵌套实现更复杂的分界面, 从而充分利用维度冗余性与比特位关联性来提高模型性能的上限.
|
图 5 样本分类示例 |
2.2 哈希中心的生成
设训练集包含
Hadamard矩阵是由+1和-1组成的正交矩阵, 即该矩阵的任意两个行向量或列向量都是正交的, 汉明距离为
对于单标签数据集, 设数据集label为
1) 生成大小为K×K的Hadamard矩阵
2) 根据编码长度
a) 如果哈希码位数
b) 如果
c) 如果
3) 将哈希中心矩阵
4) 得到单标签数据集的哈希中心矩阵
对于多标签数据集, 由于每个数据
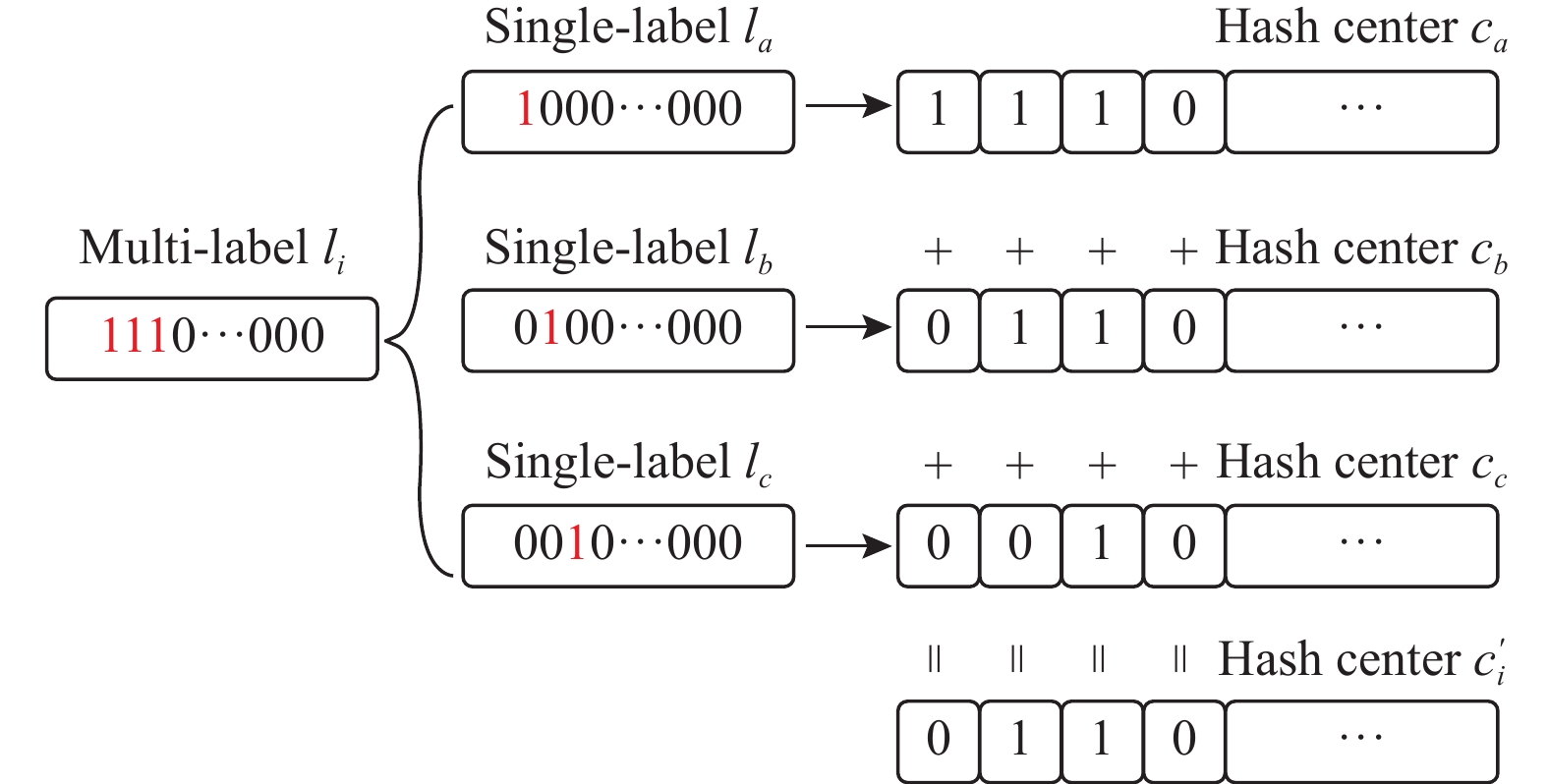
|
图 6 多标签的哈希中心的生成 |
综上, 数据
通过设计损失函数确定相似度度量策略, 得到神经网络的输入与预期结果的差距, 从而指导网络的训练向正确方向进行. 主流的相似度度量策略有以下几类: 二元组方法, 三元组方法, 中心点方法. 其中二元组方法的算法复杂度为
| LD=1KN∑i∑k∈K[c′i,kloghi,k+(1−c′i,k)log(1−hi,k)] | (8) |
其中,
在网络训练过程中, 生成的哈希码应向对应的哈希中心收敛, 然而输出编码为实数, 因此需要加入双峰拉普拉斯先验项, 对哈希编码进行二值约束, 强制哈希码向
| LQ=N∑i(‖|2hi−1|−1‖1) | (9) |
其中,
| LQ=N∑iK∑k=1(logcosh(|2hi,k−1|−1) | (10) |
综上, 将两部分损失函数整理得到最终形式:
| minΘL=LD+λLQ | (11) |
其中,
本次实验在一台机器上进行, 基于CUDA 和cuDNN进行 GPU 加速, 机器配置如表1所列.
本次实验采用Anaconda 4.11.0进行包管理, 使用PyTorch 1.7.1实现所提模型.
3.2 实验数据集将SHNet与当下主流的深度哈希方法在以下4个数据集上进行对比.
CIFAR-10: 是一个10类别的单标签图像数据集, 其中包括50000张训练集图片, 10000张测试集图片. 实验中使用1000张图片作为检索集, 5000张图片作为训练集, 剩余54000张图片作为图像数据库.
| 表 1 实验机器配置信息 |
ImageNet: 是一个1000类别的单标签数据集, 该数据集包含1.2M以上的训练集图像和50k的训练集图像. 实验中从该数据集的训练集中取100个类别的所有图像数据作为本实验的图像数据库, 使用该数据库中的所有验证集图像作为检索集, 再从中每类各选取100张图片, 共10000张图像作为训练集图像.
MS-COCO: 是一个80个类别的多标签图像数据集, 其中包括82783张训练集图像, 40504张测试集图像, 实验中随机抽取5000张图像作为检索集, 10000张图像作为训练集, 剩余的图像作为图像数据库.
NUS-WIDE: 是一个81类别的多标签分类数据集, 实验中随机选取5000张图片作为检索集, 10000张图片作为训练集, 剩下的图片作为图像数据库.
3.3 评价指标关于对比指标, 本文采用与CSQ论文中相同的4种评估指标: 平均准确率mAP, 精度召回曲线PR, 不同样本数量下检索精度曲线P@N, 汉明距离在2以内的样本在不同bits下的检索精度曲线P@H=2. 其中, 对于CIFAR-10数据集采用所有图片的检索结果计算mAP, 对于ImageNet数据集采用mAP@1000 (使用前1000个检索结果计算mAP), 对于MS COCO数据集和NUS_WIDE数据集则采用mAP@5000 (使用前5000个检索结果计算mAP).
3.4 实验对比方法为了验证SHNet在哈希图像检索任务上的优越性, 实验选取了该领域具有代表性的7种state-of-the-art深度哈希检索网络作为比较, 其中包括CNNH, DNNH, DHN, DTSH, Hashnet, DCH, CSQ.
3.5 实验设置在训练过程中, SHNet采用用自适应矩估计(Adam)优化器, Adam的初始学习率设置为10–5, 一阶矩估计的指数衰减率β1设置为0.9, 二阶矩估计的指数衰减率β2 设置为0.009, 权重衰减参数设置为0.005; 哈希编码层的学习率是特征层的10倍, 批归一化(batchnorm)的动量(momentum)设置为0.1. 输入图像的批大小(batchsize)为64.
为了实验公平的比较, 本文方法和所有对比方法在数据集上都采用相同的数据集划分策略和相同的预处理策略. 在网络架构上, 所有对比方法都采用了与本文一致的 ResNet50网络结构作为骨架网络. 在训练策略上, 输入图片的批大小(batchsize)均为64张. 在训练参数上, 均采用原始参考文献中建议的最优参数作为训练.
3.6 结果分析表2列出了7种深度哈希图像检索方法与SHNet在4个数据集上的不同哈希编码长度(16 bits, 32 bits, 64 bits)的平均准确率(mAP)结果.
| 表 2 8种深度哈希方法在各数据集上的mAP结果 |
从表2中可看出, 综合来说, 本文提出的SHNet要优于其他7种state-of-the-art深度哈希检索方法. 其中, 在CIFAR数据集上, 相较于其他7种方法, SHNet取得了最高的mAP, 用于对比的方法中表现最优的方法是DHN, SHNet对比DHN在不同长度哈希码的mAP结果上分别取得了2.2%、0.9%、0.4%的mAP提升. 相较于CSQ, SHNet取得了3.4%、2.4%、2.9%的mAP提升. 在ImageNet数据集上, 相较于其他方法SHNet取得了最高的mAP , SHNet的mAP在不同长度哈希码上均优于CSQ, 分别取得了1.4%、1.9%、2.6%的提升. 在MS COCO数据集上, CSQ在的16 bit和32 bit上取得了最高的mAP, 但在64 bit上, SHNet相较于CSQ取得了1.5%的mAP提升. 在NUS-WIDE数据集上, SHNet取得了最高的mAP, 相较于CSQ方法, 分别取得了2.7%、2.3%、2%的mAP提升. 总体而言, 在CIFAR-10, ImageNet, NUS-WIDE这3个数据集上, SHNet相较于CSQ在检索性能上平均提升了2.9%、2%、2.2%.
为了进一步验证SHNet方法的有效性, 图7给出了CNNH, DNNH, DHN, DTSH, Hashnet, DCH, CSQ这7种深度哈希检索方法和SHNet方法在ImageNet数据集上的其他评价指标对比结果, 图7(a)给出了各种方法下的精度召回曲线图(P-R), 图7(b)表示各种方法下前1000个搜索结果的精度曲线图(P@N), 图7(c)表示各种方法在汉明距离DH=2时的检索精度折线图. 由图7中3个子图所示, 本论文提出的SHNet方法要显著优于其他7种深度哈希方法.
总的来说, 通过上述定量实验, 在相同的实验条件下, 实验得到的SHNet检索性能优于其他主流方法. 因为用以对比的主流深度哈希方法使用并行方式进行哈希编码, 忽略了编码自身的内在联系, 导致其编码性能受限. 而本文提出的SHNet方法所采用的串行哈希编码策略, 充分利用编码内部的关联性, 增强编码过程中的编码信息, 同时有效运用哈希码的冗余部分进行编码校验, 使得生成的哈希码更加紧凑, 检索性能更强.
图8中我们使用t-SNE[31]可视化SHNet和CSQ在ImageNet数据集上生成的64 bits哈希编码(为了便于可视化, 我们只选取相同的ImageNet数据集的前10类数据进行可视化), 通过图8中数据分布可以看出, SHNet相较于CSQ生成的哈希码具有更好的聚拢效果, 同类数据之间的分布被很好地控制在了哈希中心周围, 形成了明显的球形分布. 这表明了SHNet相较于CSQ有着更好的图像相似度检索性能. 这是由于CSQ所采用的并行的编码方式对应着高维度空间上的线性分类, 而SHNet采用多个子编码器级联实现串行编码, 该编码方式的机理是在低维度空间上进行多次线性分类的嵌套, 通过将高维度线性分界面分解为多个低维度线性空间的嵌套可实现更复杂的分界面, 从而充分利用维度冗余性与编码比特位关联性来提高模型性能的上限.

|
图 7 SHNet与其他深度哈希方法在ImageNet上的评估对比 |

|
图 8 SHNet和CSQ生成的哈希编码的t-SNE可视化 |
4 结论与展望
本文摒弃了传统深度哈希方法使用的并行编码方式, 提出了基于串行哈希编码的深度哈希方法SHNet. SHNet基于编码校验原理设计了一种新颖的串行校验编码的网络编码结构, 以串行编码方式生成哈希编码, 通过网络结构传递编码信息增强了编码内部的关联性并利用冗余编码位的校验能力提升编码性能. 本文以4个数据集CIFAR-10、ImageNet、MS-COCO、NUS-WID为实验数据集, 使用 CNNH, DNNH, DHN, DTSH, Hashnet, DCH, CSQ这7种主流深度哈希检索方法和本文提出的SHNet方法进行mAP对比实验, 并且使用t-SNE可视化了SHNet和CSQ在ImageNet数据集上生成的哈希编码, 经以上实验结果证明, 串行哈希编码方式生成的哈希编码具有更好的检索性能, 在多个数据集上的检索效果优于其他7种主流深度哈希方法. 下一步的工作是将把串行校验编码方式应用到无监督的深度哈希图像检索领域.
| [1] |
刘海龙, 李宝安, 吕学强, 等. 基于深度卷积神经网络的图像检索算法研究. 计算机应用研究, 2017, 34(12): 3816-3819. DOI:10.3969/j.issn.1001-3695.2017.12.067 |
| [2] |
Gionis A, Indyk P, Motwani R. Similarity search in high dimensions via hashing. Proceedings of the 25th International Conference on Very Large Data Bases. San Francisco: ACM, 1999. 518–529.
|
| [3] |
Shen FM, Shen CH, Liu W, et al. Supervised discrete hashing. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015. 37–45.
|
| [4] |
Liu W, Wang J, Ji RR, et al. Supervised hashing with kernels. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Providence: IEEE, 2012. 2074–2081.
|
| [5] |
Gong YC, Lazebnik S, Gordo A, et al. Iterative quantization: A procrustean approach to learning binary codes for large-scale image retrieval. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(12): 2916-2929. DOI:10.1109/TPAMI.2012.193 |
| [6] |
Jégou H, Douze M, Schmid C. Product quantization for nearest neighbor search. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(1): 117-128. DOI:10.1109/TPAMI.2010.57 |
| [7] |
Weiss Y, Torralba A, Fergus R. Spectral hashing. Proceedings of the 21st International Conference on Neural Information Processing Systems. Vancouver: ACM, 2008. 1753–1760.
|
| [8] |
Liu W, Wang J, Kumar S, et al. Hashing with graphs. Proceedings of the 28th International Conference on Machine Learning. Bellevue: ACM, 2011. 1–8.
|
| [9] |
Wang JD, Zhang T, Song JK, et al. A survey on learning to hash. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(4): 769-790. DOI:10.1109/TPAMI.2017.2699960 |
| [10] |
Xia RK, Pan Y, Lai HJ, et al. Supervised hashing for image retrieval via image representation learning. Proceedings of the 28th AAAI Conference on Artificial Intelligence. Québec City: ACM, 2014. 2156–2162.
|
| [11] |
Lai HJ, Pan Y, Liu Y, et al. Simultaneous feature learning and hash coding with deep neural networks. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015. 3270–3278.
|
| [12] |
Zhu H, Long MS, Wang JM, et al. Deep hashing network for efficient similarity retrieval. Proceedings of the 30th AAAI Conference on Artificial Intelligence. Phoenix: AAAI, 2016. 2415–2421.
|
| [13] |
Liu HM, Wang RP, Shan SG, et al. Deep supervised hashing for fast image retrieval. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 2064–2072.
|
| [14] |
Li WJ, Wang S, Kang WC. Feature learning based deep supervised hashing with pairwise labels. Proceedings of the 25th International Joint Conference on Artificial Intelligence. New York: ACM, 2016. 1711–1717
|
| [15] |
Wang XF, Shi Y, Kitani KM. Deep supervised hashing with triplet labels. Proceedings of the 13th Asian Conference on Computer Vision. Taipei: Springer, 2017. 70–84.
|
| [16] |
Cao ZJ, Long MS, Wang JM, et al. HashNet: Deep learning to hash by continuation. Proceedings of the IEEE International Conference on Computer Vision. Venice: IEEE, 2017. 5609–5618.
|
| [17] |
Li Q, Sun ZN, He R, et al. Deep supervised discrete hashing. Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: ACM, 2017. 2479–2488.
|
| [18] |
Cao Y, Long MS, Liu B, et al. Deep cauchy hashing for hamming space retrieval. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Salt Lake City: IEEE, 2018. 1229–1237.
|
| [19] |
Kang R, Cao Y, Long MS, et al. Maximum-margin hamming hashing. Proceedings of the IEEE/CVF International Conference on Computer Vision. Seoul: IEEE, 2019. 8251–8260.
|
| [20] |
Jiang QY, Li WJ. Asymmetric deep supervised hashing. Proceedings of the AAAI Conference on Artificial Intelligence. New Orleans: AAAI, 2018. 409.
|
| [21] |
Zhang Z, Zou Q, Lin YW, et al. Improved deep hashing with soft pairwise similarity for multi-label image retrieval. IEEE Transactions on Multimedia, 2020, 22(2): 540-553. DOI:10.1109/TMM.2019.2929957 |
| [22] |
Yuan L, Wang T, Zhang XP, et al. Central similarity quantization for efficient image and video retrieval. Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle: IEEE, 2020. 3080–3089.
|
| [23] |
Hoe JT, Ng KW, Zhang TY, et al. One loss for all: Deep hashing with a single cosine similarity based learning objective. Proceedings of the 35th Conference on Neural Information Processing Systems. NeurIPS, 2021. 24286–24298.
|
| [24] |
Krizhevsky A, Hinton G. Learning multiple layers of features from tiny images. Technical Report, University of Toronto, Toronto. 2009.
|
| [25] |
Russakovsky O, Deng J, Su H, et al. Imagenet large scale visual recognition challenge. International Journal of Computer Vision, 2015, 115(3): 211-252. DOI:10.1007/s11263-015-0816-y |
| [26] |
Lin TY, Maire M, Belongie S, et al. Microsoft COCO: Common objects in context. Proceedings of the 13th European Conference on Computer Vision. Zurich: Springer, 2014. 740–755.
|
| [27] |
Chua T S, Tang J, Hong R, et al. NUS-WIDE: A real-world Web image database from National University of Singapore. Proceedings of the ACM International Conference on Image and Video Retrieval. Santorini: ACM, 2009. 48.
|
| [28] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 770–778.
|
| [29] |
Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. Proceedings of the 32nd International Conference on Machine Learning. Lille: ACM, 2015. 448–456.
|
| [30] |
Hyvärinen A, Hurri J, Hoyer PO. Natural Image Statistics: A Probabilistic Approach to Early Computational Vision. New York: Springer, 2009.
|
| [31] |
Donahue J, Jia YQ, Vinyals O, et al. DeCAF: A deep convolutional activation feature for generic visual recognition. Proceedings of the 31st International Conference on Machine Learning. Beijing: JMLR, 2014. 647–655.
|
 2023, Vol. 32
2023, Vol. 32



