云计算^{[1, 2]}、智慧城市^[3]、物联网^[4]以及大数据的快速发展给数据中心的建设和管理带来极大的冲击, 推动数据中心向分布式、一体化、低功耗以及智能化模式转变^[5]. 数据中心^[6-10]为云服务提供丰富的存储和计算资源, 海量的云IP流量对数据中心的运营管理提出了更高的要求和目标. 不同的云服务数据在时延、吞吐率和带宽的需求上也存在着差异性. 例如, 声音流和视频流对延迟要求较高; 文件和邮件服务对延迟需求不高, 但要求保证精准的数据准确率. 据统计, 从2015年到2020年, 对时延需求敏感的视频流在云IP流量中的工作负载占比从29%增长至34%^[11], 进一步给数据中心网络性能带来了严峻的考验.

数据对传输延迟要求的不同, 使得在数据交换过程中需满足其差异化时延需求. 为了实现数据中心高速传输并减少时延, 当前的研究一般采用Crossbar 光交换结构作为Core交换器, 并在Core交换器和ToR (top-of-rack)交换器之间采用高速光连接. 然而, 光交换器存在重配置开销的问题, 即在进行交叉连接重配置的过程中, 交换器或由多个交换器构成的交换网络不能进行数据交换. 在交换器具有重配置开销的场景下, 大部分现有的交换调度算法没有考虑数据包的差异化时延需求, 而是对所有数据包都进行统一调度.

目前调度算法的研究多侧重如何最小化加速比、降低时延等. 例如, DOUBLE算法^[12]提出了 $ {N_s} = 2N $ ( $ {N_s} $ 表示配置矩阵个数, N表示流量矩阵行列数据包个数)的配置矩阵策略, 获取了加速比S=2的结果, 但是忽略了重配置开销对系统的影响. EXACT算法^[13]采取了经典的Birkhoff-von Neumann矩阵分解法^[14-17], 产生了 $ {N_s} = {N^2} - 2N + 2 $ 个配置矩阵, 得到了最小加速比S=1, 但是由于EXACT算法需要大量的配置矩阵, 从而需要一个比较大的累积时间T来保证 $ T > \delta {N_s} $ ( $ \delta $ 表示重配置开销), 导致系统产生巨大的延迟. ADAPT和SRF算法^[13]改进了以往研究加速比过大的缺点, 在保证100%投递率和给定延时保证的前提下最小化加速比.

Wu等^[18]提出了3个流量矩阵调度算法(MIN, αⁱ-SCALE 和QLEF), 以最小化系统的时延为最终目标, 同时获取100%的投递率. QLEF算法在最小化时延的基础上使加速比更小, 系统性能更佳. 文献[19]提出了一种新的填补空白时隙的调度算法降低系统时延, 与大部分填补空白时隙算法不同, 采用选择性的填补策略提高运行效率, 减少运行时间, 即只对超过限制需求的空白时隙填补, 提高了50%的吞吐率, 降低了18%的时延.

这些调度算法虽然对降低平均时延以及保证100%的投递率进行了有效研究, 但是却忽略了不同数据流对于延迟的需求情况, 不能够满足端到端的延迟条件限制.

文献[20]研究了输入队列交换机的调度问题, 对MaxWeight算法进行了改进, 与MaxWeight的高复杂度不同, 作者研究了几种低复杂度算法, 其重流量性能与MaxWeight相同. 在非均匀流量的情况下, 一大类低时间复杂度算法具有与MaxWeight相同的重流量性能. 但文章并没有研究差异化时延调度, 仅针对流量不同做了研究. 还有一些研究工作^[21-23]围绕逐个时隙(slot-by-slot)、物联网延迟敏感任务、根据用户数据流选择数据中心等方面进行了算法设计研究. 但这些算法忽略了重配置开销对时延的影响, 不能满足大数据的传输需求.

国内在传输调度算法的研究多侧重减少整体数据时延, 没有考虑差异化时延的需求. 文献[24]研究了光网络中使用消息调度表对流量进行离线时间调度, 保证传输的实时性和时间确定性. 唐旭等^[25]提出了QPTS (队列优先级驱动的任务调度)算法, 确保经过数据中心的数据流的实时传输, 减少系统处理过程中产生的时延. 王耀民等^[26]提出了一种数据中心差异化流量调度策略, 改进斐波那契树优化(FTO)算法, 得到多个符合条件的差异化流量管理方案.

如何改善光交换器的交换调度效率, 同时实现无丢包、差异化时延保证的交换性能, 成为决定数据中心云服务性能的一个重要因素. 基于此, 本文设计两种光交换调度算法, 根据数据包的差异化时延需求优先传递对时延要求严格的数据, 兼顾大部分数据的时延需求, 在保证投递率的基础上实现光交换数据传输最大时延满足率.

1 数学建模 1.1 影响时延的因素

影响数据包延迟的因素有很多, 包括重配置开销、加速比以及配置矩阵的设计等, 其中重配置开销和加速比对延迟的影响较大. 在交换机进行流量调度的过程中, 通过调度算法将汇聚在输入端口的流量矩阵根据输入输出端口的不同划分成若干配置矩阵, 每一个配置矩阵负责传输一部分数据, 而每一个配置过程需要经历几个时隙的时间, 在这个时间段内有效地降低加速比或配置矩阵的数量, 能够降低整个系统的开销, 使系统能在规定时间内传递全部数据包, 保证投递率.

除此之外, 配置矩阵的执行顺序大大影响了不同数据包的时延, 需要通过精心的设计其执行顺序达到满足不同时延的目的.

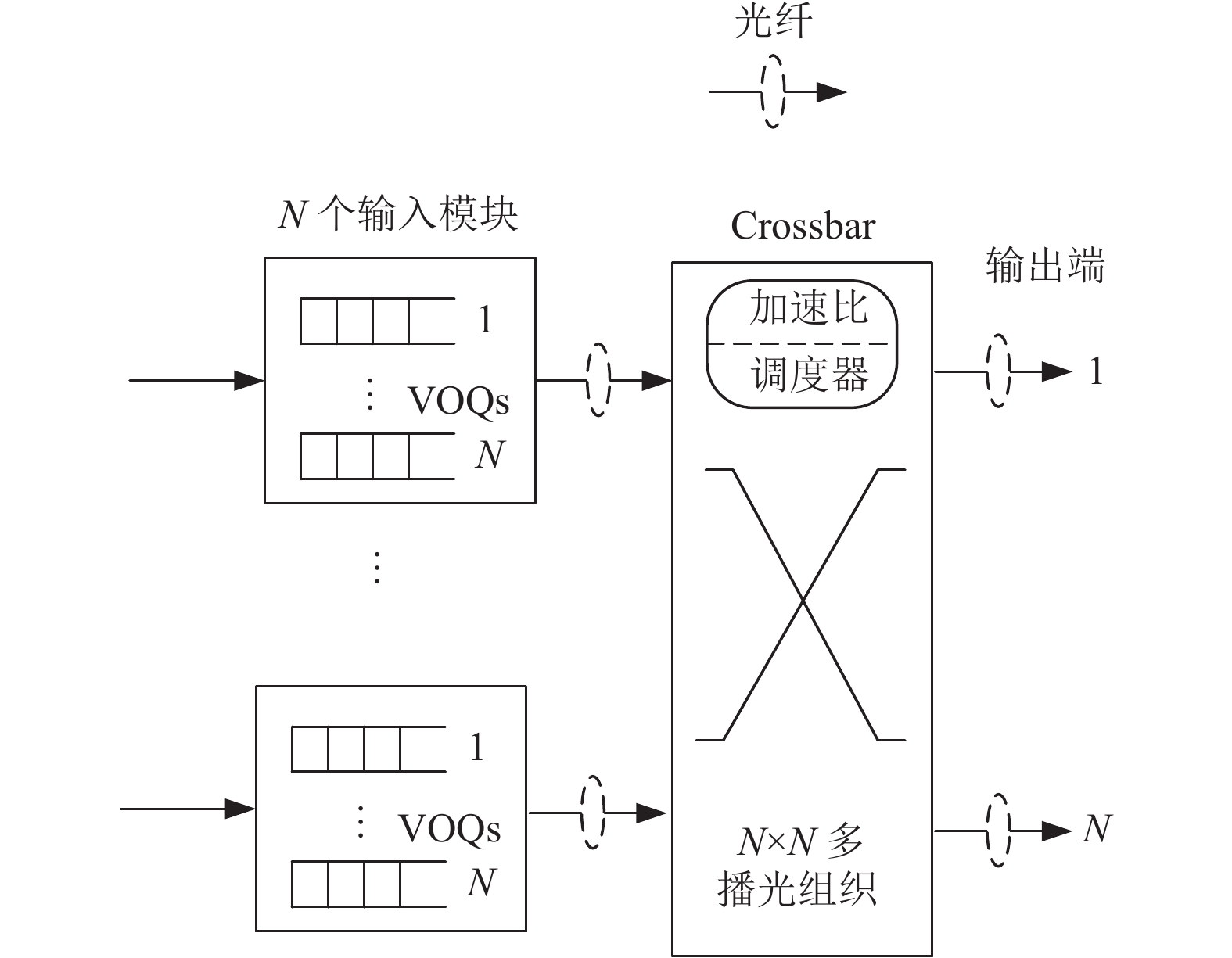
1.2 系统模型

系统基于N×N 输入队列缓冲(IQ)的Crossbar光交换机, 对具有差异化时延需求的数据包提供合理的包调度策略, 如图1所示. 输入端设置缓冲区, 在T时刻内聚集的数据包根据输入输出端口不同, 存储在特定的虚拟输出队列缓冲区(virtual output queued, VOQ)中^[18,27,28]. 每个输入端口的缓冲区存放N组数据, 对应N个输出端口. 在输入端汇集的数据包形成一个一一对应的输入输出端口流量矩阵C(T). 调度问题可以理解为通过调度算法将流量矩阵分解为不同的配置矩阵进行传输的过程.

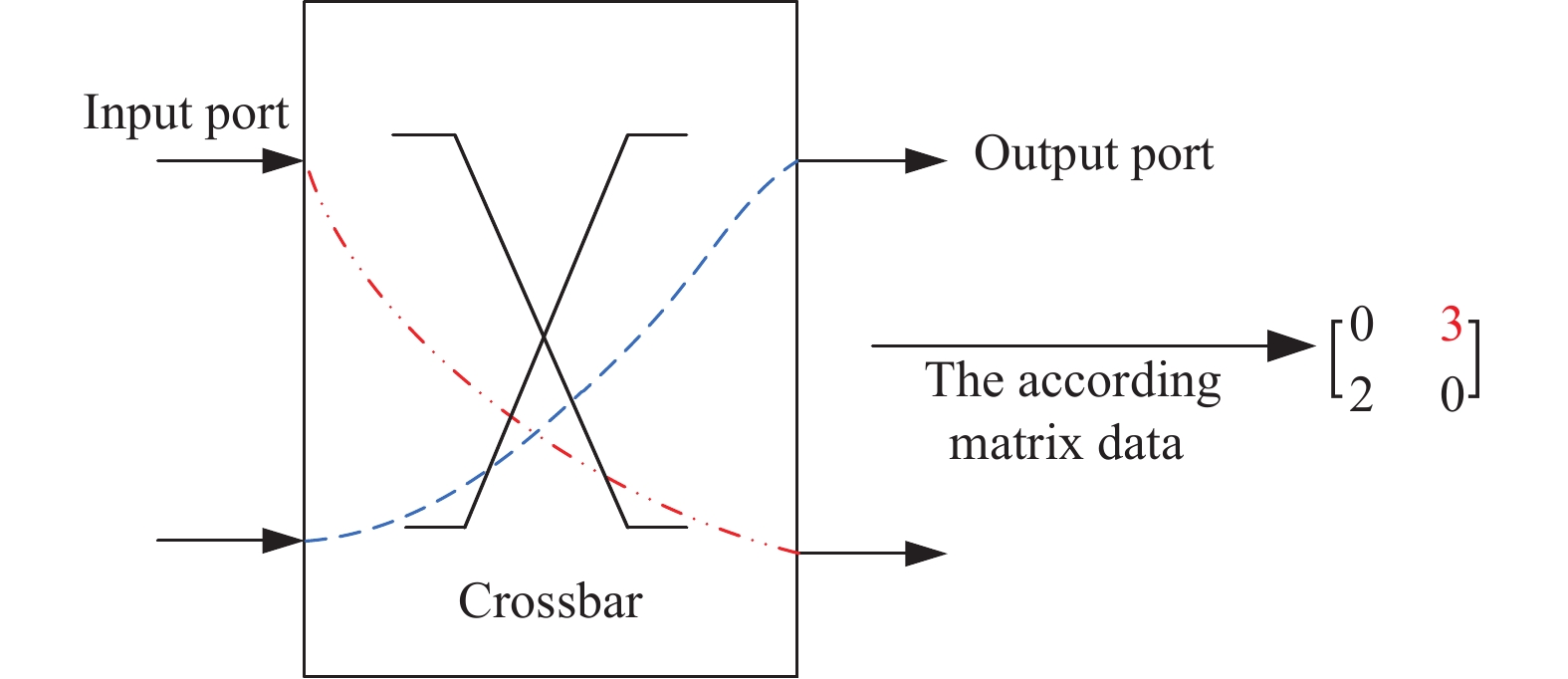
图2描述了一个简易的差异化时延处理的光交换机系统模型. 在这个2×2的Crossbar交换机模型中. 红色双点线代表对时延需求敏感的数据流, 蓝色虚线代表对时延需求不高的数据流. 右侧的矩阵代表输入端对应输出端的数据包流量矩阵, 其中红色的数据包(C₀₁=3)对时延需求较严格. 系统根据数据包的特性进行区别处理, 优先传输C₀₁.

1.3 调度过程

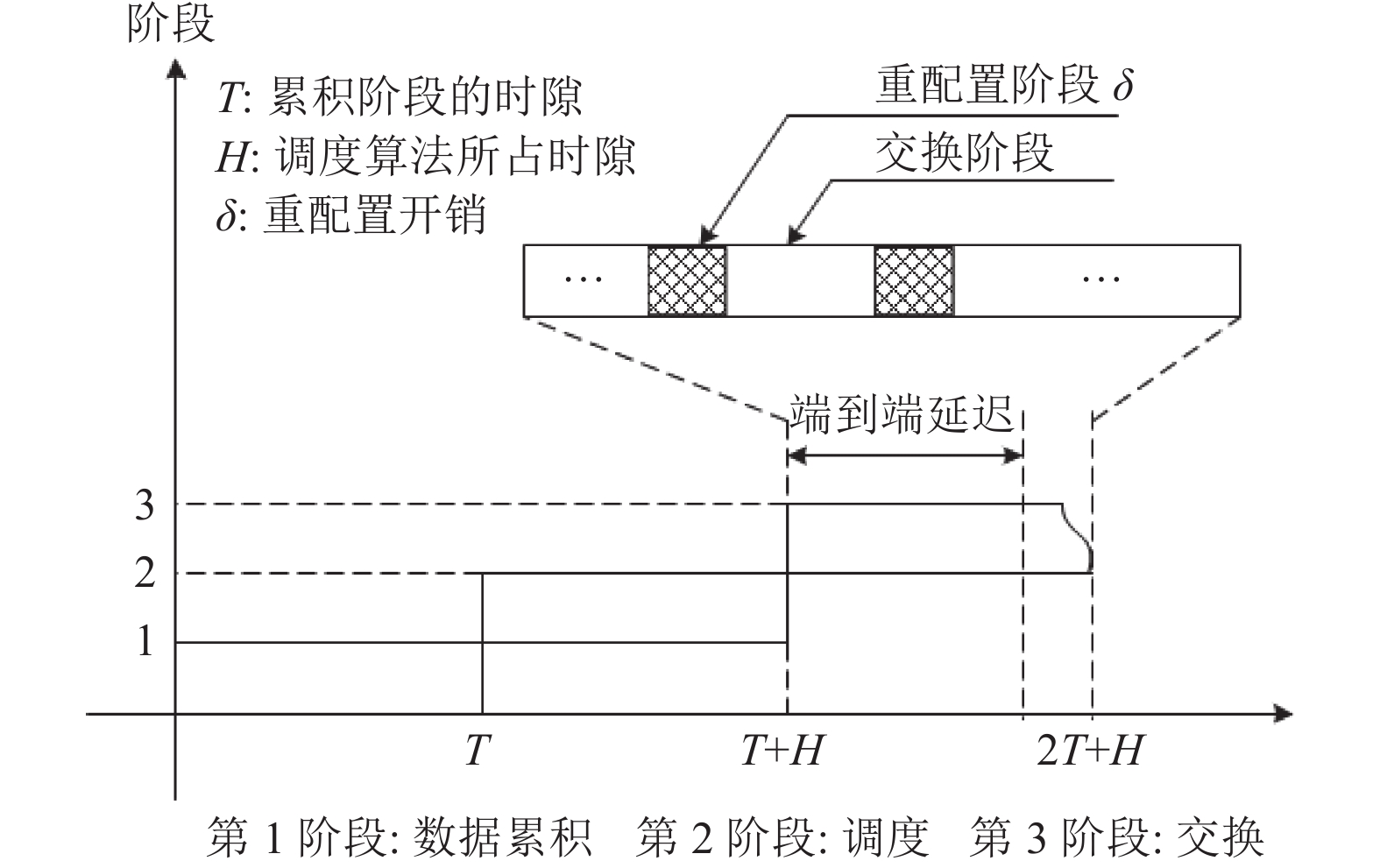
光交换调度一般分为若干阶段, 每个阶段完成系统特定的任务, 如图3所示. 交换机以流水线的方式工作, 数据包调度统共分为3个阶段: 数据累积(traffic accumulation)、调度(scheduling)以及交换(switching)过程.

① 汇聚阶段

在第1阶段, 系统经过T时隙的数据累积, 生成流量矩阵 $ C = \{ {c_{ij}}\} $ , 元素 $ {c_{ij}} $ 代表从输入端口i向对应的输出端口j传送的数据包的个数. 经过T时隙的累积, 流量矩阵行或列和最大为T, 即满足:

$ \sum\limits_{i = 0}^{N - 1} {{c_{ij}}} \leqslant T,\; \sum\limits_{j = 0}^{N - 1} {{c_{ij}}} \leqslant T $

(1)

除流量矩阵外, 定义一个时延约束矩阵 $ D = \{ {d_{ij}}\} $ , 矩阵 $ D $ 中的每个元素 $ {d_{ij}} $ 代表输入端口i与输出端口j之间所允许的最大时延. 算法设计的目标为尽量满足每个数据包 $ {c_{ij}} $ 的时延需求 $ {d_{ij}} $ .

② 调度阶段

执行调度算法的过程为第2阶段. 通过配置算法, 在H个时隙内将流量矩阵分解成 $ {N_s} $ 个配置状态矩阵 $ {P_n} = \{ P_{ij}^{(n)}\} ({N_s} \geqslant n \geqslant 1) $ . 其中, $ {P_n} $ 是交换机的配置矩阵, 且为0-1矩阵, 该矩阵中的元素 $ P_{ij}^{(n)} = 1 $ 代表输入端i与输出端j之间建立了连接, $ P_{ij}^{(n)} = 0 $ 则表示其没有数据进行通信. 为了不引起冲突, 配置矩阵每行和每列最多只能有一个元素为1, 意味着一个输入/输出端口只能对应一个输出/输入端口.

每一个配置矩阵表示交换机的一种配置状态, 在输入和输出端之间建立连接并进行通信. 当这一个状态的配置传输完毕后, 交换机必须进行重新配置, 调整输入输出连接装置以便于传递下一组数据. 所以, 交换机必须进行 $ {N_s} $ 次重配置才能将全部数据包全部传输完毕. 交换机在重配置阶段会占用一定的时隙, 由此带来的开销称之为重配置开销, 记为 $ \delta $ . 一般来说, 重配置开销包含以下几个方面^[13].

(a)更新互联模式. 根据光交换技术的不同, 这个步骤大概要需要花费10 ns到几微秒的时间^[12].

(b)光收发模块重新同步需要花费10−20 ns或更长时间^[29].

(c)将不同输入端的光信号进行排列也需要额外的时钟^[30].

即使应用当前最快的光传输技术, 系统的重配置开销仍旧要一个多时隙的时间, 在64字节处理单元, 10 Gb/s线速的系统里一个时隙的时间是50 ns.

③ 交换阶段

第3阶段为数据包的交换过程. 为了避免虚拟输出队列的冲突和阻塞, 包交换必须要在T时隙内完成.

另外, 已知流量矩阵具有 $ {N^2} $ 个数据, 基于冲突考虑, 每一个配置矩阵传递的数据包个数不能超过N个, 所以为了保证将流量矩阵的全部数据包100%传递到输出端, 配置矩阵的个数 $ {N_s} $ 不能小于N, 否则, $ {N_s} $ 个配置矩阵将不足以覆盖整个流量矩阵 $ C $ ^{[24, 31]}. 所以为了获得100%的投递率, $ {N_s} $ 个配置矩阵必须完全覆盖流量矩阵 ${C}$ , 即满足如下公式:

$ \sum\limits_{n = 1}^{{N_s}} {{\varPhi _n}P_{ij}^{(n)}} \geqslant {c_{ij}},\; i, j \in \{ 0, 1, \cdots, N - 1\} $

(2)

其中, ${\varPhi _{{n}}}$ 表示每个配置矩阵 $ {P_n} $ 的权重系数, 即配置状态 $ {P_n} $ 在第3阶段中所要维持的时隙数目. 配置状态 $ {P_n} $ 在第3个步骤中的执行顺序不同, 端到端的时延也会不同. 这是差异化时延的核心问题, 算法根据这一点对不同时延需求的数据包进行排序, 确定配置矩阵的执行顺序, 达到差异化时延的需求保证.

调度算法生成的 $ {N_s} $ 个配置矩阵完成的时间顺序不同, 故总是存在一些数据包先于其他数据包传输完, 即存在一个特定的输入输出端口对(i,j), 其流量传输经历了 $ {N_{ij}} $ 次配置矩阵即完成了数据传输工作, 满足式(3):

$ \sum\limits_{n - 1}^{{N_{ij}}} {{\varPhi _n}P_{ij}^{(n)} \geqslant {c_{ij}},\; \forall i, j \in N} $

(3)

为了使系统在数据传输过程中尽量减少传输延迟, 调度算法应尽力减少每一对输入输出端口对之间数据包传输的时延, 充分利用包传输过程中产生的空闲时隙. 如果端口对(i,j)在 $ {N_{ij}} $ 个配置矩阵之后完成了输入端口i和输出端口j的数据传输, 那么存在时隙剩余现象的位置只可能在第 $ {N_{ij}} $ 个配置矩阵当中. 假设经过 $ {N_{ij}} - 1 $ 个配置状态的调度之后, 输入输出端口对(i, j)之间的传输数据总量 $ {c_{ij}} $ 剩余了一个余量还未传输, 定义该剩余量为 $ {\Delta _{ij}} $ . 根据前面的描述, 得知每个配置矩阵 $ {N_i} $ 维持的时间为权重 $ {\varPhi _i} $ . 而这个剩余量 $ {\Delta _{ij}} $ 不需要占用下一个完整的配置矩阵调度时间 $ {\varPhi _{{N_{ij}}}} $ , 仅需一部分时钟即可传输完毕. 这样产生了空闲时隙, 即该配置矩阵剩下的量. 这一过程如式(4)所示:

$ \sum_{n-1}^{N_{i j}-1} \varPhi_n P_{i j}^{(n)}+\Delta_{i j}=c_{i j}, \forall i, j \in N $

(4)

进一步知道, $ ({\varPhi _{{N_{ij}}}} - {\Delta _{ij}}) $ 即为输入端口i和输出端口j在调度过程中所浪费的时隙数目.

另外, 由于交换机的重配置过程无法传输数据, 导致交换机内部的传输时间超过了T个时隙, 为了保证输出端口不出现阻塞冲突以及100%的投递率, 交换机的内部传输速度要大于外部的传输速度, 从而产生了加速比的概念. 定义加速比为S, 要保证交换机交换时间不能超过T, 则必须满足式(5):

$ \delta {N_s} + \frac{1}{S}\sum\limits_{n = 1}^{{N_s}} {{\varPhi _n}} \leqslant T $

(5)

其中, 左边第1项 $ \delta {N_s} $ 代表系统运行 $ {N_s} $ 个配置所耗费的重配置时间; 第2项代表 $ {N_s} $ 个配置矩阵传输数据所花费的时隙长度. $ {N_s} $ 和 $ {\varPhi _n} $ 这两个元素需要通过调度算法确定. 参考现有的研究^[11], 配置矩阵的个数 $ {N_s} $ 范围满足式(6):

$ N \leqslant {N_s} \leqslant {N^2} - 2N + 2 $

(6)

系统在输入端汇聚数据后, 已经确定了流量矩阵和每组数据的时延需求, 在输入端口和输出端口建立连接后, 交换数据时, 应该尽量满足每一对输入输出端口对所对应的时延要求. 假定 $ {\tau _{ij}} $ 表示输入端口i和输出端口j传输数据产生的实际时延, 则这个时延应满足式(7):

$ {\tau _{ij}} = \delta {N_{ij}} + \frac{1}{s}\sum\limits_{n = 1}^{{N_{ij}} - 1} {{\varPhi _n} + {\Delta _{ij}}} \preccurlyeq {d_{ij}},\; \forall i, j \notin \in N $

(7)

其中, 符号“ $ \preccurlyeq $ ”表示在设计调度算法时, 需要尽量满足式(7)所表示的不等式, 达到每个输入输出端口对的时延需求.

1.4 优化目标

不同的数据包对时延要求不同, 在流量矩阵形成后, 即形成了对应的时延需求矩阵, 系统的QoS保证需要尽量使得实际时延不能超过 $ {d_{ij}} $ , 同时, $ {d_{ij}} $ 又是一个比时钟T更为严格的时延, 即满足:

$ {d_{ij}} \leqslant T $

(8)

式(7)中的时延需求相对式(8)更加严格, 在实际运行中输入端口和输出端口产生的时延需要遵守式(7)所限定的范围.

已知系统中共有 $ {N^2} $ 个数据包, 假设交换机最终传输的数据包中有 $ |J| $ 个数据包的时延需求得到了满足, 这里 $ J $ 表示所有时延需求得到满足的输入输出端口对(i,j)的集合, 符号 $\left|\cdot \right|$ 表示一个集合中元素的个数, 因此用下面的集合描述 $ J $ :

$ J = \{ (i, j)|{\tau _{ij}} \leqslant {d_{ij}}, i, j \in N\} $

(9)

本文工作的目的是尽量满足所有数据包的时延需求, 即最大程度满足每个数据包 $ {c_{ij}} $ 对应时延矩阵D的时延需求约束 $ {d_{ij}} $ . 由于交换机的技术因素、算法执行情况以及实际情况的差异等原因, 可能有部分数据包无法被满足所需的延迟需要. 故在设计调度算法时, 排除一切非人为因素外的不可抗力外, 希望达到满足时延需求的数据包个数最大化, 所以本课题的优化目标为:

$ \max \left\{ \zeta = \frac{{|J|}}{{{N^2}}} \times 100{\text{%}} \right\} $

(10)

其中, $ \zeta $ 称为时延满足率, 表示 $ {N^2} $ 个数据包中时延需求被满足的比例. 差异化调度的最终目标是最大化时延满足率. 为了实现式(10)所描述的优化目标, 在对流量矩阵进行矩阵分解时, 需要综合考虑式(3)所确定的容量约束和式(7)描述的时延约束, 研究这两个约束如何影响差异化时延的实现.

2 SDF算法说明

SDF (stringent delay first)算法的核心思想是使用贪心策略反复执行调度分配算法, 在调度过程中总是选择那些对时延要求最严格的端口进行包调度, 从而达到满足时延要求的目的.

2.1 get_configuration函数

为了使SDF算法更加清晰简洁, 设计子函数get_configuration获取一个配置矩阵 $ {P_n} $ . 函数利用贪心策略选择时延约束中对时延需严格的数据进行传输, 函数过程如算法1所示.

算法1. get_configuration函数

BEGIN:

( $\scriptstyle{P_n}, I, \left\langle {{i_{\min }}, {j_{\min }}} \right\rangle ) = get\_configuration(C, D, \tau , \delta , S$ )

{

　　set $\scriptstyle {P_n} = {O_{N \times N}}, I = \varPhi$

　　set count=0;

　　for(count=1–N)

　　{ $\scriptstyle \left\langle {{i^*}, {j^*}} \right\rangle = {\arg _{\forall dij \in D}}\min \{ {d_{ij}}, \tau + \delta + \frac{{{c_{ij}}}}{S}$ $\scriptstyle \preccurlyeq$ $\scriptstyle {d_{ij}}\}$

　　　set $\scriptstyle {P_{{i^*}{j^*}}} = 1$

　　　set $\scriptstyle {d_{{i^*}j}} = + \infty , \forall j$

　　　set $\scriptstyle {d_{i{j^*}}} = + \infty , \forall i$

　　　if (count=1) then set $\scriptstyle \left\langle {{i_{\min }}, {j_{\min }}} \right\rangle = \left\langle {{i^*}, {j^*}} \right\rangle$

　　　else if $\scriptstyle({c_{{i^*}{j^*}}} \ne 0)$ then set $\scriptstyle I = I \cup \{ \left\langle {{i^*}, {j^*}} \right\rangle \}$

　　　　 count= count+1;

　　　}

　　　return $\scriptstyle {P_n}, I, \left\langle {{i_{\min }}, {j_{\min }}} \right\rangle$

}END.

算法1中矩阵D中的最小元素标记为 $ {d_{{i^*}{j^*}}} $ .

流量矩阵中存在一些元素, 其对时延的要求比较特殊, 无论系统如何配置调度规则, 都不可能满足这些元素的时延需求, 所以优先处理其他被满足的数据包进行传输. 给出下面的约束条件, 只有满足该式的数据包, 才具有优先参与排队调度的权利:

$ \tau + \delta + \frac{{{c_{ij}}}}{S} \preccurlyeq {d_{ij}} $

(11)

其中, $ \tau $ 表示该调度过程持续到当前时刻共耗费的时钟数, $ \delta $ 代表重配置开销, $ {c_{ij}}/S $ 表示完成该数据包的交换花费的时钟数, 左边的累加和表示调度传输元素 $ {c_{ij}} $ 所花费的总时间.

因为不能保证输入输出端口对(i,j)存在流量传输, 而且也不能保证其交换时间一定满足式(11)的约束, 因此采用符号“ $ \preccurlyeq $ ”表示满足不等式约束的端口对(i,j)会被优先选择.

2.2 SDF算法描述

SDF算法主要通过一个while循环完成对流量矩阵的分解过程. 在每一次循环内, 通过调用get_configuration函数获取一个配置矩阵 $ {P_n} $ 、最紧迫时延的位置( $ {i_{\min }}, {j_{\min }} $ )和选中元素位置集合I. 获取配置矩阵 $ {P_n} $ 的先后顺序决定了其执行顺序, 最先获取的最先执行. 集合I用来保存一趟循环后选择的端口对集合, 计算集合I中数值大于 $ {c_{{i_{\min }}{j_{\min }}}} $ 元素的个数, 记做K.

接下来, 生成配置矩阵 $ {P_n} $ 的权重 $ {\varPhi _n} $ . 为了获取权重系数 $ {\varPhi _n} $ 的值, 预先设定一个大于零的常数 $ \theta $ , 通过比较 $ \left\lceil {{\theta \mathord{\left/ {\vphantom {\theta {\left| I \right|}}} \right. } {\left| I \right|}}} \right\rceil $ 和K的值, 再根据下面的公式确定 $ {\varPhi _n} $ :

$ {\varPhi _n} = \left\{ {\begin{array}{*{20}{l}} {\left\lceil {\dfrac{1}{{\left\lceil {\theta |I|} \right\rceil }} \displaystyle\sum\limits_{k = 1, (i, j) \in I}^{\left\lceil {\theta |I|} \right\rceil } {c_{ij}^k} } \right\rceil ,\; {\rm{if}}}\;K\geqslant{\left\lceil {\theta |I|} \right\rceil } \\ {{c_{{i_{\min }}{j_{\min }}}},\; {\rm{else}}} \end{array}} \right. $

(12)

其中, $\left\lceil {} \right\rceil$ 表示一个整数的上限, $ {\varPhi _n} $ 代表每一个配置矩阵 $ {P_n} $ 执行的时间.

很显然, 通过调节参数 $ \mathrm{\theta } $ 的取值调整权重以实现最佳效果. 这里 $ \mathrm{\theta } $ 的取值有下面几种情况:

1)当 $ \theta = {1 \mathord{\left/ {\vphantom {1 |}} \right. } |}I| $ 时, 系统会选择最大的 $ {c_{{i^*}{j^*}}} $ 作为 $ {\varPhi _n} $ 的值.

2)当 $ \theta > 1 $ 时, 则选取 $ {c_{{i_{\min }}{j_{\min }}}} $ 作为权重.

3)其他情况则通过计算得到权重.

SDF算法的详细步骤如算法2所示.

算法2. SDF 算法描述

BEGIN:

set $\scriptstyle n = 1, \tau = 0, \varepsilon = \sum\limits_{i, j} {{d_{ij;}}}$

while $\scriptstyle (C \ne {O_{N \times N}})$

{

　if $\scriptstyle ({c_{ij}} = 0)$ then set $\scriptstyle {d_{ij}} = \varepsilon ;$

　( $\scriptstyle {P_n}, I, \left\langle {{i_{\min }}, {j_{\min }}} \right\rangle ) = \scriptstyle get\_configuration(C, D, \tau , \delta , S)$

　 $\scriptstyle {C^{\prime}} = \left\{ {\begin{array}{*{20}{c}}\scriptstyle {c_{ij}^k|\left\langle {i, j} \right\rangle \in I, c_{ij}^1 \geqslant c_{ij}^2 \geqslant \cdots \geqslant c_{ij}^K} \\ \scriptstyle { \geqslant {c_{{i_{\min }}{j_{\min }}}} \geqslant c_{ij}^{K + 1} \geqslant c_{ij}^{K + 2} \geqslant \cdots \geqslant c_{ij}^{|I|}} \end{array}} \right\}$

　set $\scriptstyle \lambda = \left\lceil {{\theta \mathord{\left/ {\vphantom {\theta {\left| I \right|}}} \right. } {\left| I \right|}}} \right\rceil $ ;

　if $\scriptstyle (K \geqslant \lambda )$ then set $\scriptstyle {\varPhi _n} = \left\lceil {\frac{1}{\lambda }\sum\limits_{k = 1}^\lambda {c_{ij}^k} } \right\rceil ;$

　else set $\scriptstyle {\varPhi _n} = {c_{{i_{\min }}{j_{\min }}}}; $

　if $\scriptstyle ({c_{ij}} - {\varPhi _n}{p_{ij}} < 0) $ , then set $\scriptstyle {c_{ij}} = 0 $ ;

　else set $\scriptstyle {c_{ij}} = {c_{ij}} - {\varPhi _n}{p_{ij}} $ ;

　set $\scriptstyle \tau = \tau + \delta + \frac{{{\varPhi _n}}}{S}; $

　set $\scriptstyle n = n + 1.$

}

END.

2.3 SDF算法复杂度分析

SDF调用函数 $ get\_configuration(C, D, \tau , \delta , S) $ , 该函数从 $ {N^2} $ 个数据中找到N个最小元素, 其算法复杂度为O( $ {N^2} $ ). 另外, SDF每次调用子函数找到一个配置矩阵, 直到找到 $ {N_s} $ 个配置矩阵, 覆盖流量矩阵C的全部数据流量, 所以要调用 $ {N_s} $ 次get_configuration函数. $ {N_s} $ 的数值并不是系统初始化的, 而是根据系统的参数(流量矩阵、时延矩阵、重配置开销、加速比等等)而生成的, 所以近似给出SDF的算法复杂的为O( $ {N^2}{N_s} $ ), $ {N_s} $ 满足: $ N \leqslant {N_s} \leqslant {N^2} - 2N + 2 $ .

3 m-SDF算法说明 3.1 SDF算法不足

SDF忽略了多个配置矩阵组合的累积效应以及它们之间的相互关联性. 没有充分利用由于不合理的配置所产生的空白时隙. 针对SDF的缺点和不足, 本节考虑给出另外一种解决方案m-SDF, 使m个配置矩阵之间互相协作, 利用调度过程中的空白时隙, 进一步减少系统时延.

3.2 m-SDF算法描述

为了描述方便, 首先给出一个定义.

定义1. m重配置矩阵集. m重(m-order)配置矩阵 $ {P^m} $ 指的是由m个配置矩阵行列对应元素叠加而成的矩阵, 并且该矩阵的行累加和以及列累加和不得超过m(m=1, 2, 3,…).

函数get_multiple_config给出了m重配置矩阵集 $ {P^m} $ 及其相应的配置矩阵 $ {P_n} $ 的详细设计方法, 具体如算法3.

算法3. get_multiple_config函数

BEGIN:

( $\scriptstyle {P_n}, I, \left\langle {{i_{\min }}, {j_{\min }}} \right\rangle ) = \scriptstyle get\_multiple\_config(C, D, \tau , \delta , S, m$ )

{

Step 1. 构造一个m-order 配置矩阵 $\scriptstyle {P^m}$

Step 1.1. 从时延矩阵D中选择不同行同列的N个最小元素, 元素的选取满足如下约束规则:

$\scriptstyle\left\langle {{i^*}, {j^*}} \right\rangle = {\arg _{\forall d_{ij} \in D}}$ min $\scriptstyle \{ {d_{ij}}, \tau + \delta + \frac{{{c_{ij}}}}{S} \preccurlyeq d_{ij}\}$

将最小值的索引位置记为 $ \scriptstyle\left\langle {{i_{\min }}, {j_{\min }}} \right\rangle $ .并且将刚才选择的N个索引位置保存在集合L中. 置 $\scriptstyle {P^m} = {P^1} $ , $\scriptstyle {P^1} $ 各个元素的取值由以下规则确定:

$\scriptstyle P_{ij}^1 = \left\{\scriptstyle {\begin{array}{*{20}{l}} \scriptstyle {1,\; {\rm{if}}\left\langle {i, j} \right\rangle \in L} \\ \scriptstyle {0,\; {\rm{else}}} \end{array}} \right.$ 　　　　　　　　　　　　　　　　　　 (13)

Step 1.2. 检索时延矩阵D中所有未被选中的元素 $\scriptstyle {{d}}_{{{i}}{{{'}}}{{j}}{{{'}}}}$ , 如果该元素满足下面的条件:

　　 $\scriptstyle \left\{ {\begin{array}{*{20}{c}}\scriptstyle {\tau + 2\delta + \frac{{{c_{{i^{\prime}}{j^*}}} + {c_{{i^{\prime}}{j^{\prime}}}}}}{S} \leqslant {d_{{i^{\prime}}{j^{\prime}}}}} \\ \scriptstyle {\sum\limits_j {P_{{i^{\prime}}j}^m \leqslant m \;{\rm{and}}\; \sum\limits_i {P_{i{j^{\prime}}}^m \leqslant m} } } \end{array}} \right.$ 　　　　　　　　　　　　　　　(14)

则令 $\scriptstyle P_{{i^{\prime}}{j^{\prime}}}^m = P_{{i^{\prime}}{j^{\prime}}}^m + 1 $ , 同时标注 $\scriptstyle {d_{{i^{\prime}}{j^{\prime}}}} $ 为选中状态. 这里注意索引 $\scriptstyle \left\langle {{i^{\prime}}, {j^{*}}} \right\rangle $ 表示集合L中第 $\scriptstyle {i^{\prime}} $ 行的元素位置.

Step 2. 计算 $\scriptstyle N \times N $ 邻接矩阵 $\scriptstyle {P^w} $ , 计算规则如下:

　　 $\scriptstyle P_{i, j}^w = \left\{ {\begin{array}{*{20}{l}} \scriptstyle {\rho - {{({c_{{i_{\min }}{j_{\min }}}} - {c_{ij}})}^2},\; {\rm{if}}\;P_{i, j}^m > 0} \\ \scriptstyle {0, \;{\rm{else}}} \end{array}} \right.$ 　　　　　　　　　　　 (15)

其中, $\scriptstyle \rho $ 代表系统事先定义的常数, 并且 $\scriptstyle \rho > > \max \{ {c_{ij}}^2\} $ .

Step 3. 使用匈牙利算法(Kuhn-Munkres algorithm)^[32] 获取矩阵 $\scriptstyle {P^w}$ 最佳匹配关系. 基于最优化结果, 可以得到相应的配置矩阵 $\scriptstyle {P_n}$ 以及索引集合I.

Step 4. 返回 $\scriptstyle {P_n}, I $ 及 $\scriptstyle \left\langle {{i_{\min }}, {j_{\min }}} \right\rangle $ .

END.

式(14)中, 索引( $ {i^{\prime}}, {j^*} $ )表示配置矩阵 $ {P^1} $ 的第 $ {i^{\prime}} $ 行里面已经被选中的元素位置, ( $ {i^{\prime}}, {j^{\prime}} $ )表示交换机计划下一个要传送的数据包索引位置. 第1个约束条件表示若在当前时间内继续交换新的流量 $ {c_{{i^{\prime}}{j^{\prime}}}} $ , 那么必须保证在下一配置状态内仍然有足够的时间传输之前被选中的数据包 $ {c_{{i^{\prime}}{j^{*}}}} $ . 第2个约束条件用来限制m重配置矩阵集 $ {P^m} $ 的重数. 在m-SDF算法中, $ {P^m} $ 作为配置矩阵 $ {P_n} $ 的备选集合, 为许多流量提供了额外的调度机会, $ {P^m} $ 的这种包容性使得调度更加灵活. 式(15)中, $ \rho $ 是系统预先定义好的常数, 而且 $ \;\rho > > \max \{ {c_{ij}}^2\} $ .

m-SDF算法的主体部分和SDF的主体基本相同, 只是调用了不同的生成配置矩阵的函数get_multiple_config.

3.3 算法复杂度分析

m-SDF调用函数get_multiple_config, 算法复杂度主要由前3步决定. 第1步从 $ {N^2} $ 个数据中找到N个最小元素, 复杂度为O( $ {N^2} $ ). 第2步对时延矩阵D中所有元素进行核查, 复杂度也为O( $ {N^2} $ ). 第3步与二分图最佳匹配算法的时间复杂度相同, 为O( $ {N^2} $ ). 这3步算法执行的方法为顺序执行, 所以get_multiple_config函数的时间复杂度为O( $ {N^2} $ ).

4 仿真结果

仿真实验根据Crossbar光交换特性和实际传输需求, 模拟流量矩阵和相应的时延约束矩阵. 数据采用8×8矩阵, 使用cplex优化软件+VC编写程序. 实验机器的配置为: 3.4 GHz的Intel双核处理器, 4.0 GB内存, Windows操作系统. 设定时隙T=40, 流量矩阵维数N=8, 重配置开销 $ \mathrm{\delta } $ (时隙)=3进行仿真实验验证该算法的时延满足率效果.

4.1 SDF仿真结果

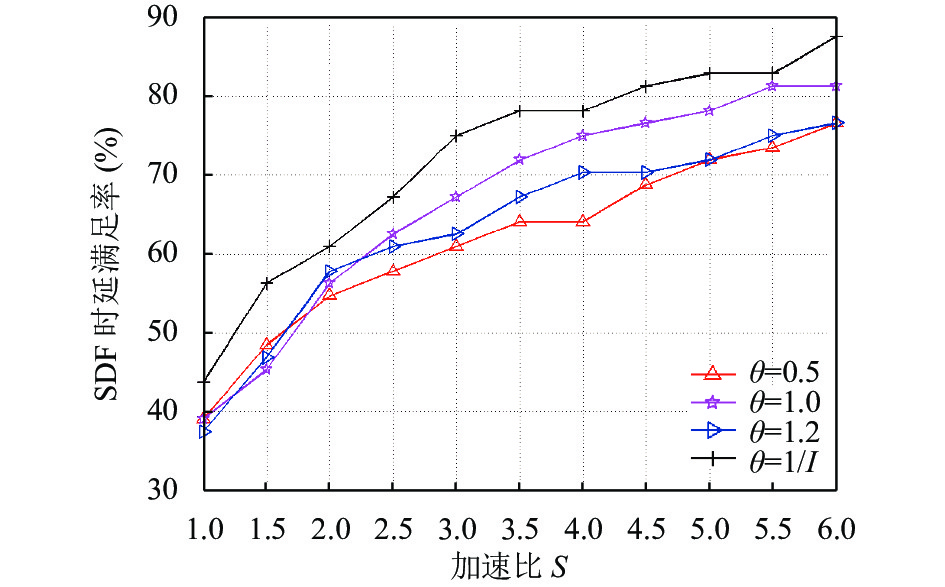
图4展示了SDF算法随着加速比S的递增, $ \theta $ 取不同的常数的数据包时延满足率 $ \zeta $ (delay constraint satisfaction ratio)效果图, 从图4中看出:

(1)随着加速比的增加, 由于数据传输速率提高, 数据包的时延满足的概率大大提升.

(2)当 $ \theta = {1 \mathord{\left/ {\vphantom {1 |}} \right. } |}I| $ 时, 由于配置状态的数量最少, 时延满足率最高, 系统性能最好. 尽管这种情况会给系统带来比较大的时隙浪费, 但是总重配置开销最小. $ \theta > 1 $ 是算法的一种特例, 在这种情况下, 根据式(12)得出, 权重 $ {\varPhi _n} $ 的取值总是 $ {c_{{i_{\min }}{j_{\min }}}} $ , 此时分解出的配置状态数量最多.

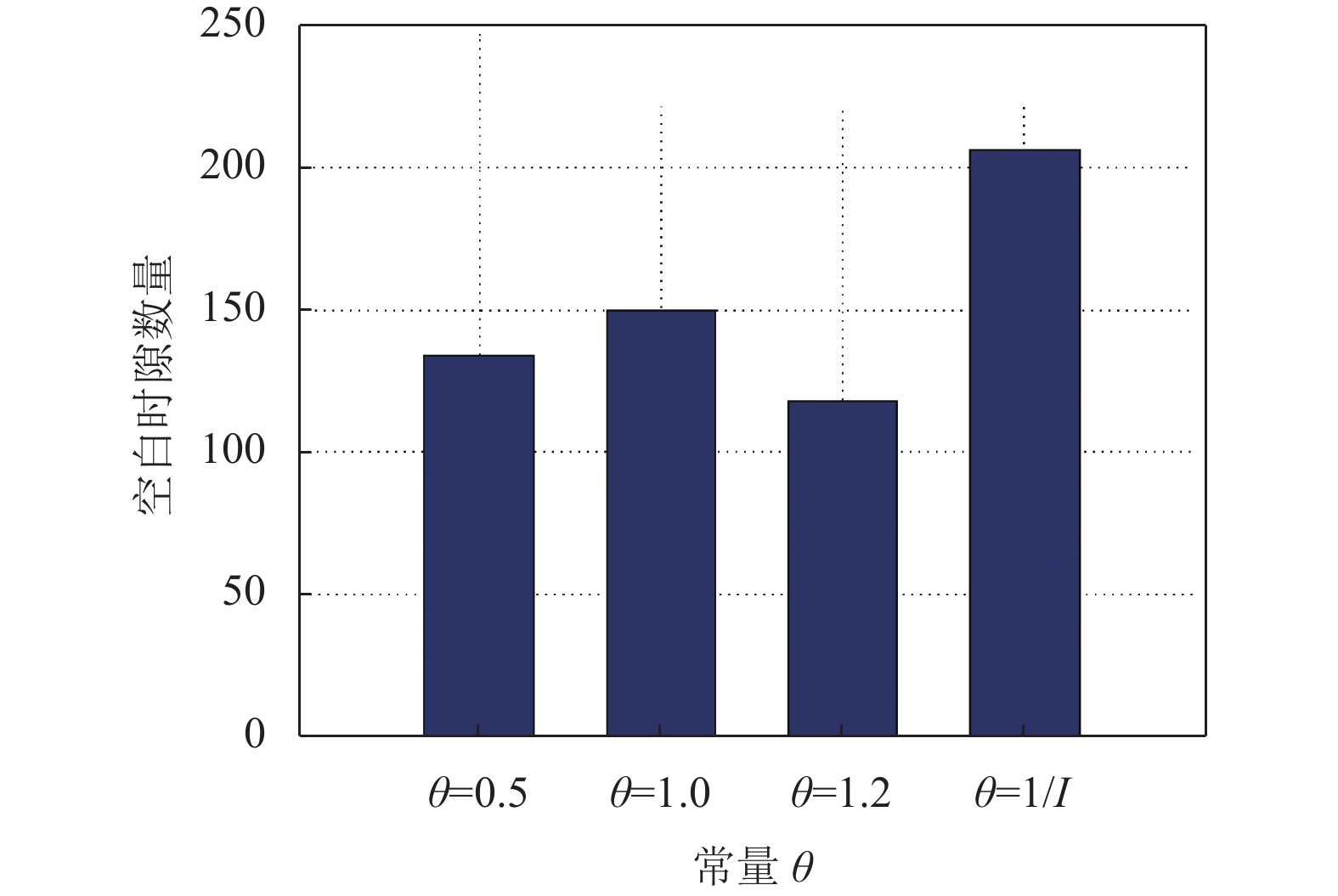
图5展示了SDF算法当加速比S=2, 在不同 $ \theta $ 取值时的空白时隙, 从中可以看出, 当 $ \theta = {1 \mathord{\left/ {\vphantom {1 |}} \right. } |}I| $ 时, 因为配置状态较少, 从而时隙浪费比较大, 而当 $ \theta > 1 $ 时, 空白时隙数量较少.

4.2 m-SDF算法实验仿真结果

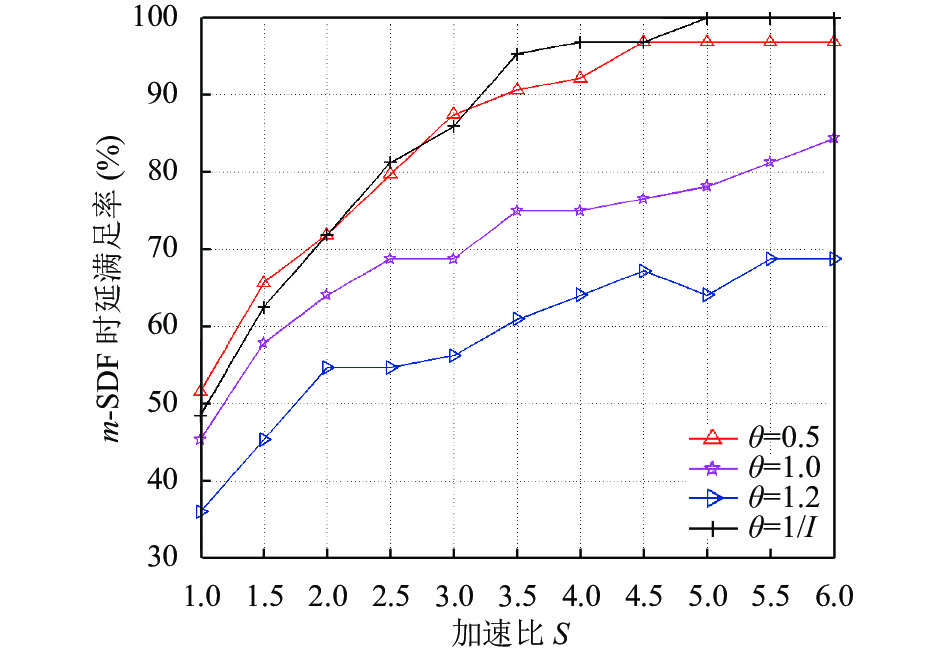
图6展示了随着加速比S的递增, $ \mathrm{\theta } $ 取不同的常数的m-SDF算法数据包时延满足率效果图.

从图6可以看出:

(1)随着加速比的增加, m-SDF的时延满足率也逐渐增大.

(2)当 $ \theta = {1 \mathord{\left/ {\vphantom {1 |}} \right. } |}I| $ 时, 由于配置状态的数量最少, 时延满足率最高.

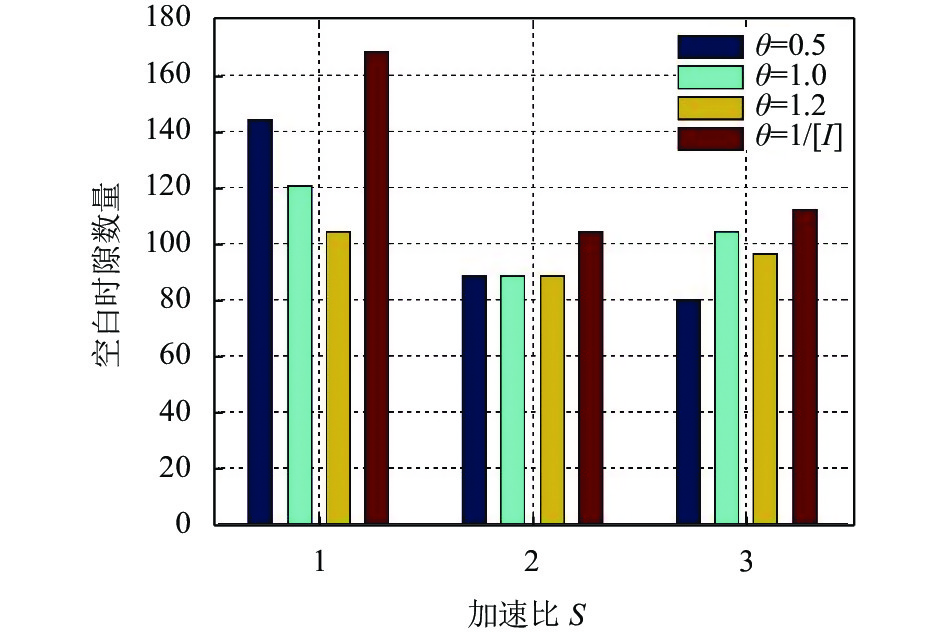
图7展示了m-SDF算法在取不同加速比, 不同 $ \theta $ 值时的空白时隙对比图. 当 $ \theta > 1 $ 时, 空白时隙数量较少. 从每一组柱状图看出, 不管加速比为何值, 当 $ \theta = {1 \mathord{\left/ {\vphantom {1 |}} \right. } |}I| $ 时, 由于配置状态较少导致时隙浪费比较大, 产生了较大的空白时隙.

另外, m的值决定了产生的多个配置状态之间的关联程度, m越大代表着其关联程度也越大, 因此交换机的数据传输性能也越好.

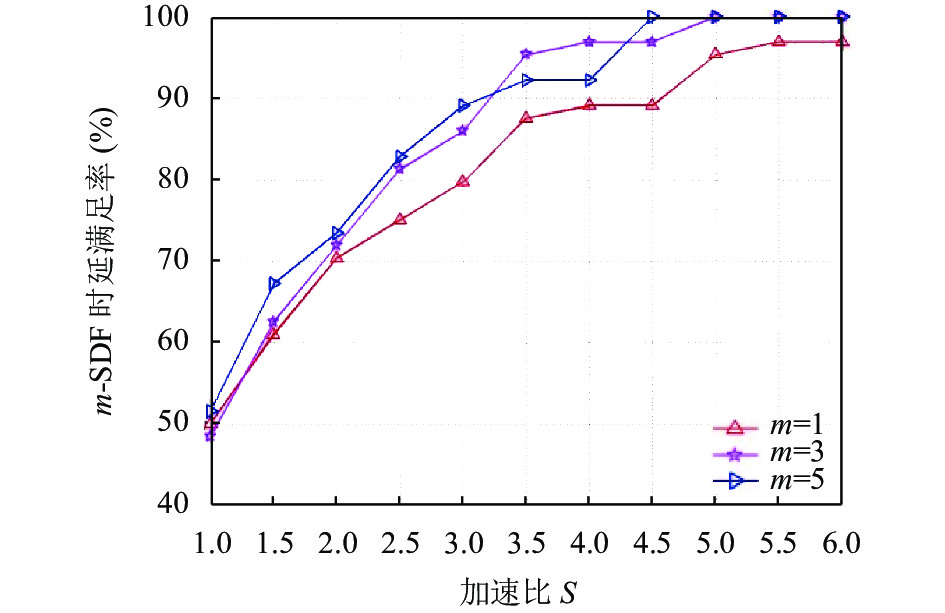
图8显示了不同m取值下的时延满足率对比图, 图中展示了当m分别取1, 3, 5时的时延满足程度. 当m=5时, 时延满足程度最高.

4.3 仿真结果对比与分析

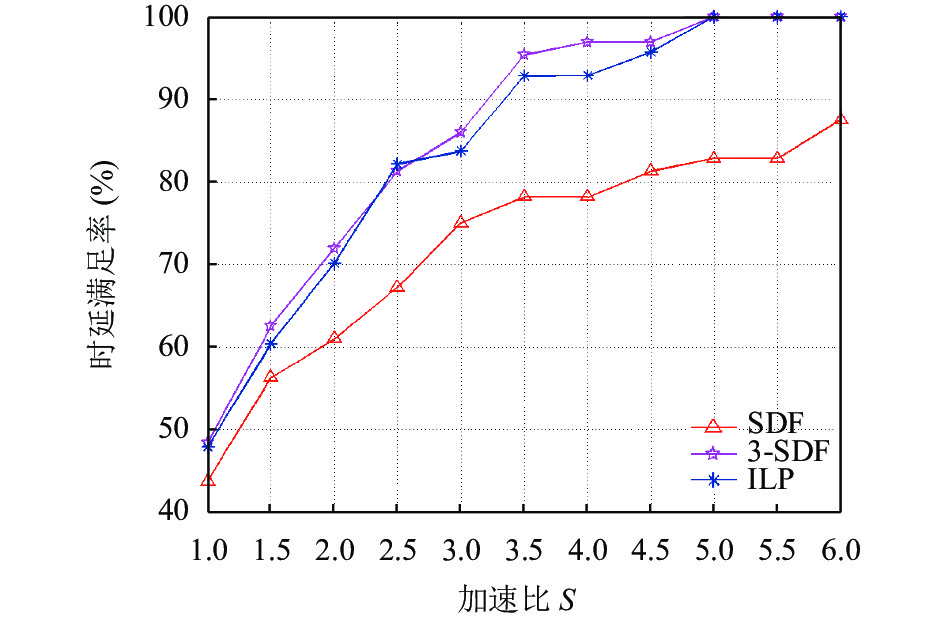
为了评估启发式算法(SDF和m-SDF)的解与最优解之间的差别, 利用ILP求解调度问题的最优解, 和启发式算法进行比较. 并以3-SDF为例进行系统仿真. 图9给出了3种算法的仿真结果对比图. 从图中看出: (1) ILP 最优解和启发式算法m-SDF之间的差别不大. (2) 3-SDF时延效果比SDF的更好. (3) 当加速比的值递增时, 时延满足率 $ \zeta $ 的值也逐渐增加.

5 总结

光分组交换技术逐渐成为光网络研究领域的前沿. 然而, 现有的分组调度机制忽略了重配置开销对时延的影响. 在实际的应用中, 这些机制无法满足端到端的差异化时延需求. 对此, 本文详细阐述并分析光交换调度模型和影响差异化时延的因素, 提出了两种启发式调度算法SDF和m-SDF, 对带有VOQ输入队列的光交换机数据包进行流量调度, 最大化数据包对时延约束的满足率. 大量的仿真实验验证了算法的有效性和灵活性.