污水处理过程是一个复杂的生物化学反应过程, 具有强非线性、时滞性、耦合性、不确定性等特点, 其关键水质参数COD的检测是污水处理厂稳定、高效运行的保障^{[1, 2]}. 现如今, COD的检测方法可以分为3类: 水质离线化验方法、水质在线检测方法以及水质软测量方法. 离线化验方法存在时滞性, 在线检测装置普遍存在仪表安装和维护成本十分昂贵等问题, 而现有的机理模型很难体现污水处理的特性, 软测量精度还需要进一步提高. 因此, 建立可靠、精确的污水处理模型对关键水质参数进行软测量是污水处理过程领域需要解决的问题, 具有重要的研究意义. 针对以上问题, 基于数据驱动的关键水质参数软测量模型得到广泛关注, 神经网络具有非线性拟合能力, 在污水水质参数软测量中应用广泛. 何丹等把线性降低权系数和变异算子引入粒子群算法中, 提出了改进粒子群算法的BP神经网络预测污水处理的COD和悬浮固体(suspended solids, SS)浓度, 并与BP神经网络和遗传算法优化的BP神经网络进行对比, 预测性能大大提高^[3]. 张明涛等用多核LS-SVM建立污水处理过程中出水能耗和水质罚款模型, 用分子动理论和人工记忆算法优化该模型, 提高了该模型收敛速度和精确度^[4]. 谢武明等用经遗传算法优化的BP神经网络的权值和阈值, 使权值和阈值在可选范围取得最佳值, 并对污水处理电耗进行预测, 与未经优化的BP神经网络相比, 预测精度得到了极大的改善^[5]. 李晋贤等用和声算法优化RBF神经网络的隐含层节点数预测污水出水COD指标, 通过与标准的RBF神经网络相比具有较高的预测精度和良好的泛化能力^[6]. 任忠铭等提出一种引力搜索算法的出水生化需氧量(biochemical oxygen demand, BOD)预测方法, 将均方根误差作为适应度函数, 根据特征变量转变为0-1组合问题来选出最优特征子集并作为RBF神经网络的输入, 在保证预测精度的情况下, 证明了算法的有效性^[7]. 任东红等把轮盘赌策略以及交叉和变异引入到粒子群算法中, 提出了混合粒子群算法的集成神经网络软测量模型, 可以有效地预测污水处理过程中的关键水质参数, 软测量精度较高^[8]. 乔俊飞等提出了粒子群优化算法对回声状态神经网络权重训练, 并对污水处理过程水质参数总磷进行预测, 结果表明该模型具有较好非线性拟合能力和准确的预测能力^[9]. 由于不同的智能优化算法具有各自的特性, 因此, 采用不同智能优化算法软测量模型得到的污水水质软测量精度不同.

自20世纪70年代遗传算法被提出以来, 不少学者根据对大自然中生物种群及物理现象的认识分析, 相继提出了许多智能优化算法, 包括: 细菌觅食优化算法^[10]、蛙跳算法^[11]、人工蜂群算法^[12]、鲸鱼优化算法^[13]、和声搜索算法^[14]、布谷鸟算法^[15]、麻雀搜索算法(sparrow search algorithm, SSA). 其中麻雀搜索算法^[16]2020年被薛建凯提出, 具有较强的全局寻优能力、参数少、易于实现、收敛快的优点. 尽管如此, 麻雀搜索算法也和其余智能优化算法一样, 在解决实际问题时, 容易陷入局部最优值, 并且在迭代过程中种群多样性会有所减少, 导致精度降低. 针对麻雀搜索算法的不足, 本文对麻雀搜索算法进行改进, 引入改进麻雀搜索算法的位置更新公式以及遗传算法中的自适应交叉和变异操作优化RBF神经网络的中心值、宽度值以及权值, 通过某大型污水处理厂的实测数据进行仿真实验, 以均方根误差和平均绝对百分比误差验证了AGAISSA的性能优势.

1 模型的建立 1.1 辅助变量的选取

COD是衡量水体有机污染的一项重要指标, 可以反映水体的受污染程度, 如果想要高效准确地预测出水COD指标, 辅助变量的选取也很重要. 本文辅助变量通过机理分析选取, 如表1所示.

1.2 污水处理水质软测量模型

本文提出了基于RBF神经网络^{[17, 18]}污水处理过程水质软测量模型, RBF神经网络有很强的非线性逼近能力, 可映射任意复杂的非线性关系, 并且学习规则简单, 便于设计实现. RBF神经网络的结构图如图1所示, 为典型的3层前向神经网络, 即输入层、隐含层、输出层. 输入层选用表1作为输入变量, 隐含层选用高斯函数作为激活函数, 高斯函数是非线性函数, 可以依据输入样本的变化不断学习, 其表达式为:

$ h(x) = \exp \left( - \frac{1}{{2\sigma _i^2}}{\left\| {x - {c_i}} \right\|^2}\right),\;\;\;i = 1, 2, 3, \cdots , m $

(1)

其中, $ x $ 是 $ n $ 维输入向量, 通过以上分析 $ n = 17 $ ; $ {c_i} $ 是第 $ i $ 个隐含层节点的中心, 即中心值; $ {\sigma _i} $ 是第 $ i $ 个隐含层节点的宽度, 即宽度值; 输出层的输出为:

$ Y = \sum\limits_{i = 1}^m {{w_i}\exp \left( - \frac{1}{{2{\sigma _i}^2}}{{\left\| {x - {c_i}} \right\|}^2}\right)} $

(2)

其中, $ {w_i} $ 为权值. 输出层选用出水COD作为输出指标, $ m $ 为隐含层节点个数, 根据经验公式, 隐含层节点数表达式为:

$ m = M(n + 1) $

(3)

其中, $ M $ 为输出层节点数, 通过输入层的分析可知 $ n = 17 $ , 故隐含层节点数为18. RBF神经网络中 $ {\sigma _i} $ 、 $ {w_i} $ 、 $ {c_i} $ 的取值直接影响RBF神经网络的预测性能, 因此, 本文采用AGAISSA优化RBF神经网络的 $ {\sigma _i} $ 、 $ {w_i} $ 、 $ {c_i} $ 参数以提高RBF神经网络的预测性能.

2 算法的实现 2.1 麻雀搜索算法

SSA算法受麻雀觅食和反捕食行为而提出的一种新型群智能优化算法, 其原理如下.

麻雀在觅食的过程中由发现者、加入者、预警者3部分构成. 在SSA中, 适应度较高的发现者在搜索食物过程中会引导种群搜索和觅食, 加入者为获取更高的适应度会跟随发现者觅食, 当麻雀种群意识到有危险时, 则会发生反捕食行为.

发现者位置更新如下:

$ X_{i, j}^{t + 1} = \left\{ \begin{gathered} X_{i, j}^t \cdot \exp \left( {\frac{{ - i}}{{\alpha \cdot N}}} \right), \quad {\rm{if}}\;{R_2} \lt ST \\ X_{i, j}^t + Q \cdot L, \quad \quad \quad \, \;{\rm{if}}\;{R_2} \geqslant ST \\ \end{gathered} \right. $

(4)

其中, $ t $ 代表迭代次数, $ j=1, 2, \cdots , d $ , $ d $ 表示待优化问题变量的维度, $ N $ 是个常数, 表示最大迭代次数, $ {X_{i, j}} $ 表示第 $ i $ 个麻雀在第 $ j $ 维中的位置信息, $ \alpha $ 为 $ (0, 1] $ 之间的随机数, $ ST $ 和 $ {R_2} $ 分别表示安全值和预警值, $ L $ 为 $ 1 \times d $ 且元素均为1的矩阵, $ Q $ 为服从正态分布的随机数. 当 $ {R_2} \lt ST $ 时, 表明麻雀种群觅食环境相对安全, 没有捕食者入侵, 发现者可以搜索更广泛的食物. 当 $ {R_2} \geqslant ST $ 时, 表明种群中的部分麻雀发现了捕食者的入侵, 同时向种群中的其他麻雀发出警告, 这时麻雀种群都会快速飞到安全的地方觅食.

加入者位置更新如下:

$ X_{i, j}^{t + 1} = \left\{ \begin{gathered} Q \cdot \exp \left( {\frac{{X_{{\rm{worst}}}^t - X_{i, j}^t}}{{{i^2}}}} \right),\quad \quad \;{\kern 1pt} \, \, {\rm{if}}\;i \gt n/2 \\ X_p^{t + 1} + \left| {X_{i, j}^t - X_P^{t + 1}} \right| \cdot {A^ + } \cdot L , \quad \, {\rm{if}}\;i \leqslant n/2 \\ \end{gathered} \right. $

(5)

其中, $ {X_p} $ 是当前发现者占据的最优位置, ${X_{{\rm{worst}}}}$ 表示当前最差位置, $ A $ 为随机包含−1和1两个元素的 $ 1 \times d $ 矩阵, ${A^ + } = {A^{\rm{T}}}{(A{A^{\rm{T}}})^{ - 1}}$ , $ n $ 为麻雀总数, 当 $i \gt {{n}}/2$ 时, 表明第 $ i $ 个加入者没有觅食, 适应度较低, 正处于饥饿状态, 需要飞到其他地方觅食, 以获得更高的能量. 当 $ i \leqslant n/2 $ 时, 表明第 $ i $ 个加入者将在当前最优位置 $ {X_p} $ 附近范围找到合适的位置觅食.

预警者位置更新如下:

$ X_{i, j}^{t + 1} = \left\{ \begin{gathered} X_{{\rm{best}}}^t + \beta \cdot \left| {X_{i, j}^t - X_{{\rm{best}}}^t} \right|,\quad \quad \quad {\rm{if}}\;{f_i} \gt {f_{{\rm{best}}}} \\ X_{i, j}^t + K \cdot \left( {\frac{{\left| {X_{i, j}^t - X_{{\rm{worst}}}^t} \right|}}{{\left( {{f_i} - {f_{{\rm{worst}}}}} \right) + \varepsilon }}} \right),\quad\, {\rm{if}}\;{f_i} = {f_{{\rm{best}}}} \\ \end{gathered} \right. $

(6)

其中, ${X_{{\rm{best}}}}$ 是当前最优位置, $\; \beta $ 为服从均值为0, 方差为1的正态分布随机数, $ {f_i} $ 为麻雀个体当前的适应度值, $ K $ 为 $ [ - 1, 1] $ 之间的随机数, ${f_{{\rm{best}}}}$ 和 ${f_{{\rm{worst}}}}$ 为全局最优和最差的适应度值. $ \varepsilon $ 为一个极小的数, 避免分母为0. 当 ${f_i} \gt {f_{{\rm{best}}}}$ 时, 此时麻雀处于种群边缘觅食, 很容易遭到捕食者攻击; ${f_i} = {f_{{\rm{best}}}}$ 时, 处于种群中间的麻雀会意识到危险, 则会飞往其他麻雀的位置觅食, 以减小被捕食的概率.

2.2 改进的麻雀搜索算法

(1 )预备知识

迭代函数 $ \phi (x) $ 在 $ \left[ {a, b} \right] $ 上连续可导, 且满足:

$({\rm{i}})$ $ x \in \left[ {a, b} \right] $ 时, $ a \leqslant \phi (x) \leqslant b $ .

$({\rm{ii}})$ 存在一正数, 满足 $ 0 \lt L \lt 1 $ , 且任意 $ x \in \left[ {a, b} \right] $ , 有 $ \left| {\phi '(x)} \right| \leqslant L $ .

对任意 $ x \in \left[ {a, b} \right] $ , 迭代法 $ {x_{k + 1}} = \phi ({x_k}) $ 均收敛于 $ {x^*} $ .

证明: 设 $ f(x) = x - \phi (x) $ , 则 $ f(x) $ 在 $ \left[ {a, b} \right] $ 上连续可导:

$ f(a) = a - \phi (a) \leqslant 0 $

(7)

$ f(b) = b - \phi (b) \geqslant 0 $

(8)

故 $ f(x) = 0 $ 在 $ [a, b] $ 上至少有一个根.

由 $ \left| {\phi '(x)} \right| \leqslant L \lt 1 $ :

$ f'(x) = 1 - \phi '(x) \gt 0 $

(9)

则 $ f(x) $ 在 $ \left[ {a, b} \right] $ 上单调递增, 有 $ x = \phi (x) $ 在 $ \left[ {a, b} \right] $ 内有唯一解 $ {x^*} $ .

$ {x_{k + 1}} = \phi ({x_k}) $

(10)

由微分中值定理:

$ {x_{k + 1}} - {x^*} = \phi ({x_k}) - \phi ({x^*}) = \phi '(\xi )({x_k} - {x^*}) $

(11)

$ {x_{k + 1}} - {x_k} = \phi ({x_k}) - \phi ({x_{k - 1}}) = \phi '(\mathop \xi \limits^ - )({x_k} - {x_{k - 1}}) $

(12)

由于 $ \left| {\phi '(x)} \right| \leqslant L $ :

$ \left| {{x_{k + 1}} - x{}_k} \right| \leqslant L\left| {{x_k} - {x_{k - 1}}} \right| $

(13)

$ \begin{split} \left| {{x_{k + 1}} - {x^*}} \right|& \leqslant L\left| {{x_k} - {x^*}} \right|\\ &= L\left| {{x_{k + 1}} - {x^*} - ({x_{k + 1}} - {x_k})} \right|\\ &\leqslant L\left| {{x_{k + 1}} - {x^*}} \right| + L\left| {({x_{k + 1}} - {x_k})} \right| \end{split} $

(14)

$ \left| {{x_{k + 1}} - {x^*}} \right| \leqslant \frac{L}{{1 - L}}\left| {{x_{k + 1}} - {x_k}} \right| $

(15)

$ \begin{split} \left| {{x_k} - {x^*}} \right|& \leqslant \frac{L}{{1 - L}}\left| {{x_k} - {x_{k - 1}}} \right| \\ &\leqslant \frac{{{L^2}}}{{1 - L}}\left| {{x_{k - 1}} - {x_{k - 2}}} \right|\\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\vdots\\ &\leqslant \frac{{{L^k}}}{{1 - L}}\left| {{x_1} - {x_0}} \right| \end{split} $

(16)

由于 $ L \lt 1 $ , $ \mathop {\lim }\limits_{k \to \infty } ({x_k} - {x^*}) = 0 $ , 因此, 对任意初值 $ {x_0} $ , 迭代法 $ {x_{k + 1}} = \phi ({x_k}) $ 均收敛于 $ {x^*} $ .

(2) 改进发现者位置

对发现者位置的改进, 引入正弦函数对其改进, 并去掉随机数 $ \alpha $ , 改进后的公式:

$ X_{i, j}^{t + 1} = \left\{ \begin{gathered} X_{i, j}^t \cdot \sin \left( {\frac{{ - i}}{N}} \right),\quad {\rm{if}}\;{R_2} \lt ST \\ X_{i, j}^t + Q \cdot L, \quad \quad {\kern 1pt} {\kern 1pt} {\rm{if}}\;{R_2} \geqslant ST \\ \end{gathered} \right. $

(17)

证明改进发现者位置公式的收敛性如下:

由预备知识 $ {x_{k + 1}} = \phi ({x_k}) $ , 只需证明 $ \left| {\phi '(x)} \right| \lt 1 $ 即可.

$ X_{i, j}^{t + 1} = X_{i, j}^t \cdot \sin \left( {\left. {\dfrac{{ - i}}{N}} \right)} \right. $ , $\phi '(x) = \sin \left( {\left. {\dfrac{{ - i}}{N}} \right)} \right.$ , 由于 $ i $ 为第 $ i $ 个麻雀的位置信息, 故 $ i $ 为1并以1为单位增加到发现者数量为7的数, 故 $ {i_{\min }} = 1 $ , $ {i_{\max }} = 7 $ , $ N = 30 $ , 故 $\dfrac{{ - i}}{N} \ne \dfrac{\pi }{2} \pm k\pi, \; k = 1, 2 , \cdots , m$ , 因此 $\left| {\phi '(x)} \right| = \left| {\sin \left( {\left. {\dfrac{{ - i}}{N}} \right)} \right.} \right| \lt 1$ , 说明改进发现者位置公式收敛.

(3) 改进加入者位置

对加入者位置的改进, 引入正弦函数以及反比例函数对其改进, 改进后的公式:

$ X_{i, j}^{t + 1} = \left\{ \begin{gathered} \frac{{\exp (X_{{\rm{worst}}}^t - X_{{\rm{best}}}^t)}}{{{i^2}}} + \frac{{\sin (i/n)}}{{X_{i, j}^t}}\, ,\; {\rm{if}}\;i \gt n/2 \\ X_p^{t + 1} + \left| {X_{i, j}^t - X_P^{t + 1}} \right| \cdot {A^ + } \cdot L ,\quad {\kern 1pt} {\kern 1pt} \, {\kern 1pt} \;{\kern 1pt} {\kern 1pt} {\rm{if}}\;i \leqslant n/2 \\ \end{gathered} \right. $

(18)

证明改进加入者位置公式的收敛性如下:

由预备知识 $ {x_{k + 1}} = \phi ({x_k}) $ , 只需证明 $ \left| {\phi '(x)} \right| \lt 1 $ 即可.

$X_{i, j}^{t + 1} = \dfrac{{\exp (X_{{\rm{worst}}}^t - X_{{\rm{best}}}^t)}}{{{i^2}}} + \dfrac{{\sin (i/n)}}{{X_{i, j}^t}}$ , 因此 $\phi '(x) = - \dfrac{{\sin (i/n)}}{{{{(X_{i, j}^t)}^2}}}$ , 由于 $ i $ 是由发现者数量+1并以单位1增加到种群规模为10的数. 即 $ {i_{\min }} = 8 $ , $ {i_{\max }} = 10 $ , $i/n \ne \dfrac{\pi }{2} \pm k\pi , \; k = 1, 2, \cdots , m$ , 由于加入者在不断跟随发现者的位置以得到更多的资源, 故加入者每次更新的位置范围较大, 即 $\left| {\phi '(x)} \right| = \left| { - \dfrac{{\sin (i/n)}}{{{{(X_{i, j}^t)}^2}}}} \right| \lt 1$ , 说明改进加入者位置公式收敛.

(4) 改进预警者位置

对预警者位置的改进, 引入正弦函数对其改进, 改进后的公式:

$ X_{i, j}^{t + 1} = \left\{ \begin{gathered} X_{{\rm{best}}}^t + \beta \cdot \sin (X_{i, j}^t - X_{{\rm{worst}}}^t),\quad \;{\kern 1pt} {\kern 1pt} \, {\kern 1pt} {\rm{if}}\;{f_i} \gt {f_{{\rm{best}}}} \\ X_{i, j}^t + K \cdot \left( {\frac{{\left| {X_{i, j}^t - X_{{\rm{worst}}}^t} \right|}}{{\left( {{f_i} - {f_{{\rm{worst}}}}} \right) + \varepsilon }}} \right), \quad {\kern 1pt} \, {\kern 1pt} \, {\rm{if}}\;{f_i} = {f_{{\rm{best}}}} \\ \end{gathered} \right. $

(19)

证明改进预警者位置公式的收敛性如下:

由预备知识 $ {x_{k + 1}} = \phi ({x_k}) $ , 只需证明 $ \left| {\phi '(x)} \right| \lt 1 $ 即可.

$X_{i, j}^{t + 1} = X_{{\rm{best}}}^t + \beta \cdot \sin (X_{i, j}^t - X_{{\rm{worst}}}^t)$ , 对其求导 $\phi '(x) = \beta \cdot \cos (X_{i, j}^t - X_{{\rm{worst}}}^t)$ , 由于 $ \;\beta $ 为服从均值为0, 方差为1的正态分布随机数, 即 $f(x) = \dfrac{1}{{\sqrt {2\pi } }}{{\rm{e}}^{\frac{{ - {x^2}}}{2}}}$ 在0处取得最大值为 $ f(0) = \dfrac{1}{{\sqrt {2\pi } }} \lt 1 $ , $ \;\beta $ 的值域为 $ \left(0, \dfrac{1}{{\sqrt {2\pi } }}\right] $ , 余弦函数值域为 $ [ - 1, 1] $ , 故导数的绝对值小于1, 说明改进预警者位置公式收敛.

2.3 自适应遗传算法改进的麻雀搜索算法

交叉操作与变异操作在遗传算法^{[19, 20]}中起着关键性的作用, 对不同问题具有较好的鲁棒性, 能够避免种群陷入局部最优值. 在麻雀种群发现食物与跟随以及侦察预警过程中, 对麻雀个体的适应度排序, 选出当前的最佳适应度麻雀个体进行交叉与变异操作, 通过子代与父代适应度比较, 淘汰适应度差的个体, 这样可以增加麻雀种群的多样性, 充分利用麻雀群体的优良特性, 使其跳出局部最优值, 从而精度得到进一步提高. 算法公式如下.

① 交叉操作

选择种群中的麻雀个体使他们随机地进行相互配对, 然后使配对好的麻雀个体通过选定的概率 $ {P_c} $ 发生交叉操作. 对于交叉的两个麻雀 $ {X_i} $ , $ {X_j} $ , 其位置交叉的公式如下:

$ \left\{ \begin{gathered} X_i^{k + 1} = \gamma \cdot X_i^k + (1 - \gamma ) \cdot X_j^k \\ X_j^{k + 1} = (1 - \gamma ) \cdot X_i^k + \gamma \cdot X_j^k \\ \end{gathered} \right. $

(20)

其中, $ \gamma $ 是区间 $ (0, 1) $ 之间的随机数.

② 变异操作

对麻雀个体的位置以选定的概率 $ {P_m} $ 发生变异. 假设个体最优值 $ {P_i} $ 的第 $ d $ 维变量为 $ P_i^d $ , 对 $ P_i^d $ 施加随机扰动的策略进行变异操作. 公式如下:

$ P_i^d = P_i^d \cdot (1 + \mu ) $

(21)

其中, $ \;\mu $ 为随机扰动变量, 服从均值为0, 方差为1的正态分布.

其中, 交叉操作 $ {P_c} $ 和变异操作 $ {P_m} $ 是影响算法性能指标的重要因素^{[21, 22]}, 在实际应用中, 很难确定最好的交叉操作 $ {P_c} $ 与变异操作 $ {P_m} $ 进而达到预期效果. 本文提出了自适应交叉和变异操作, 使 $ {P_c} $ , $ {P_m} $ 能够自动调节, 自适应交叉和变异操作定义公式如下:

$ {P_c} = \left\{ \begin{gathered} 1 - ({P_{c1}}/({f_1} + {f_3}/{f_2})), {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{if}}{\kern 1pt} fitness(1) \lt {f_1} \\ {P_{c1}}, \quad \quad \quad \quad \quad \quad \quad\;\; {\rm{if}} \; fitness(1) \geqslant {f_1}\; \\ \end{gathered} \right. $

(22)

$ {P_m} = \left\{ \begin{gathered} {P_{m1}}/({f_1} + {f_3}/{f_2}) , \quad \,\;{\rm{if}} \;fitness(1) \lt {f_1} \\ {P_{m1}} , \quad \quad \quad \quad \quad \quad \;\, {\rm{if}}\;fitness(1) \geqslant {f_1} \\ \end{gathered} \right. $

(23)

其中, $ {P_{c1}} $ , $ {P_{m1}} $ 为常数, $ {f_1} $ 为整个种群适应度的平均值, $ {f_2} $ 为整个种群适应度的最大值, $ {f_3} $ 为整个种群适应度的最小值, $ fitness(1) $ 为全局最优适应度.

自适应遗传算法改进的麻雀搜索算法流程图如图2所示.

3 仿真实验

本次仿真实验采用污水处理厂365组数据为样本, 选用345组数据作为训练样本, 20组数据为测试样本, 初始种群规模为10, 最大迭代次数为30, 安全值为0.6, 发现者的比例为0.7, 预警值为0到1之间的随机数, 用Matlab软件对RBF神经网络、GA-RBF神经网络、SSA-RBF神经网络、AGAISSA-RBF神经网络模型进行实验, 最后用均方根误差(root mean square error, RMSE)和平均绝对百分比误差(mean absolute percentage error, MAPE)来评价预测值与实测值的偏差.

$ {\textit{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{j = 1}^N {{{(actua{l_j} - predic{t_j})}^2}} } $

(24)

$ {\textit{MAPE}} = \frac{1}{N}\sum\limits_{j = 1}^N {\frac{{\left| {actua{l_j} - predic{t_j}} \right|}}{{\left| {actua{l_j}} \right|}} \times 100{\text{%}} } $

(25)

其中, $ predic{t_j} $ 为预测值, $ actua{l_j} $ 为实测值, $ N $ 为样本总数.

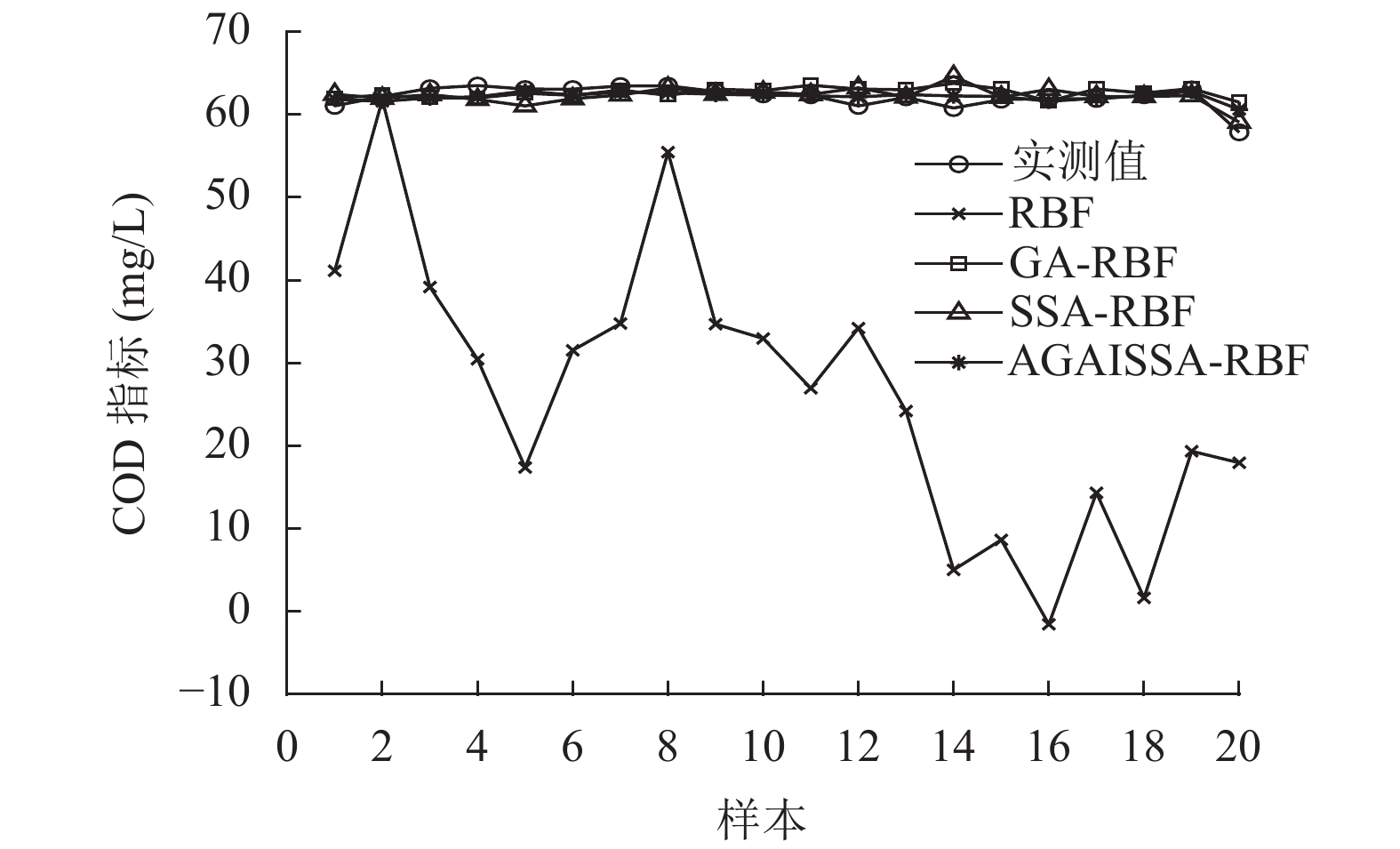
预测值和实测值对比图如图3所示, 由图3可知, RBF神经网络预测值远远低于实测值, GA-RBF神经网络和SSA-RBF神经网络的预测值会在实测值的较小范围内波动, 而在引入AGAISSA时, AGAISSA-RBF神经网络部分预测值与实测值重合, 其他未重合的数据点也非常接近实测值, 说明麻雀种群在寻优过程中, 引入自适应交叉和变异操作, 会使模型精度更高.

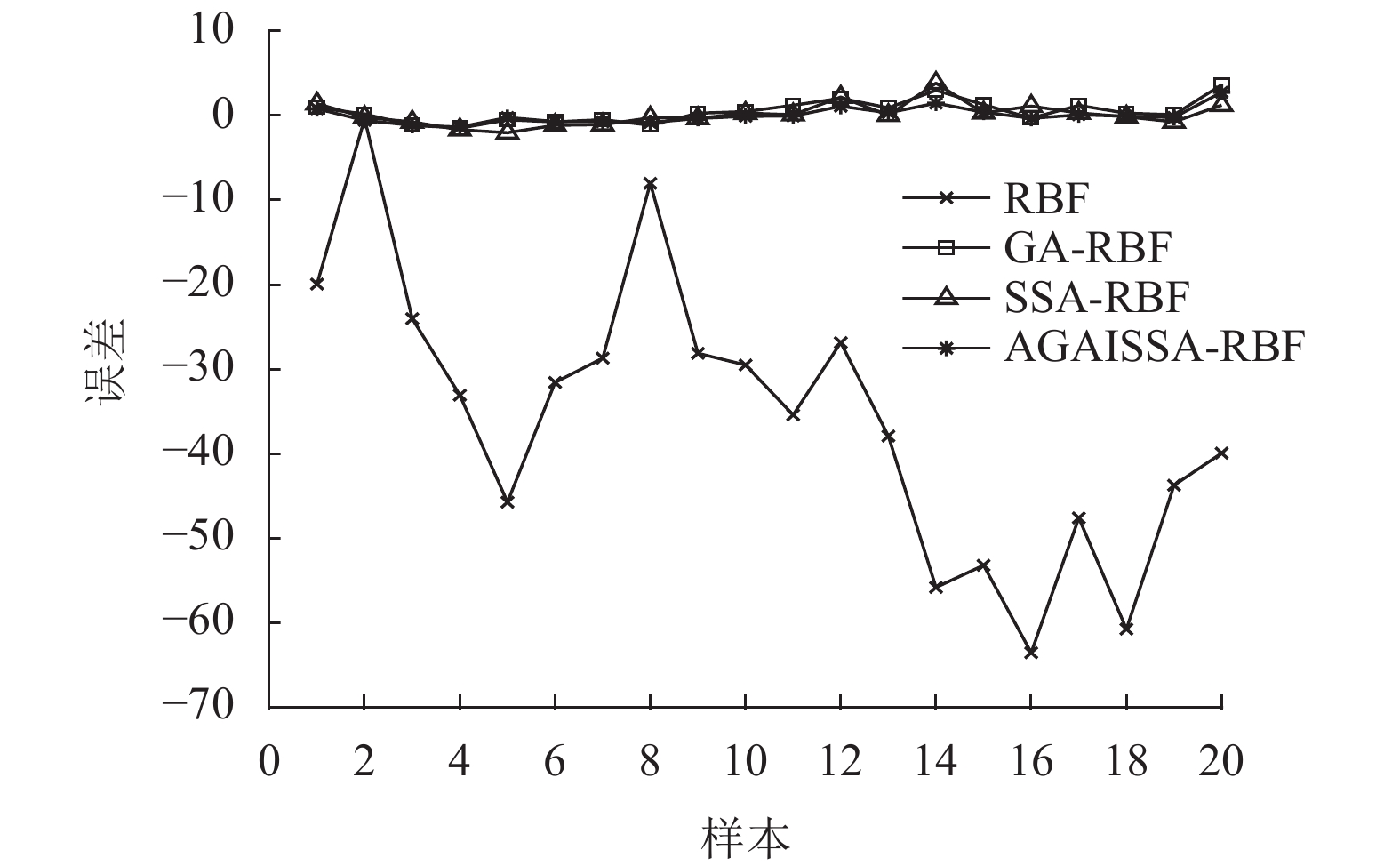
预测误差对比图如图4所示, 从图4我们可以看出, RBF神经网络的预测误差变化范围很大, 预测误差远小于0; GA-RBF神经网络和SSA-RBF神经网络的预测误差相对RBF神经网路的预测误差具有明显的改善; 而AGAISSA-RBF神经网络的预测误差非常接近于0, 说明, AGAISSA可以增加麻雀种群多样性, 使其跳出局部最优值, 从而使AGAISSA-RBF神经网络具有更高的预测精度.

迭代收敛曲线对比图如图5所示, 从图5我们可以看出, GA在第5代开始收敛, SSA在第7代开始收敛, AGAISSA在第17代开始收敛, 尽管AGAISSA收敛速度较慢, 但AGAISSA最佳适应度优于SSA和GA最佳适应度.

均方根误差对比图如图6所示, 从图6我们可以看出RBF神经网络、GA-RBF神经网络、SSA-RBF神经网络、AGAISSA-RBF神经网络的均方根误差分别为39.06、1.39、1.32、0.93, 依次呈递减趋势, 说明引入自适应遗传算法可以使软测量模型的精度得到进一步的改善.

平均绝对百分比误差对比图如图7所示, 从图中我们可以看出RBF神经网络的平均绝对百分比误差为57.49%、GA-RBF神经网络的平均绝对百分比误差为1.73%、SSA-RBF神经网络的平均绝对百分比误差为1.55%、AGAISSA-RBF神经网络的平均绝对百分比误差为1.11%, 平均绝对百分比误差值越小, 预测精度越高, 因此可以说明AGAISSA-RBF神经网络的模型精度较高.

4 结论与展望

本文提出了解决污水处理水质参数软测量问题的一种新型AGAISSA算法, 将遗传算法中的自适应交叉操作和变异操作引入改进麻雀搜索算法中, 有效地改变了麻雀个体的适应度, 避免了麻雀搜索算法陷入局部极值, 提高了算法的全局寻优能力. 通过对AGAISSA算法的性能指标分析, 验证了该算法的优势性. 运用AGAISSA-RBF神经网络模型预测污水出水COD, 相对于RBF神经网络、GA-RBF神经网络、SSA-RBF神经网络找到了更优的预测模型, 有效降低了污水出水COD预测偏差. 由于麻雀搜索算法提出较短, 以后还可以结合其他智能优化算法进行相关改进, 并运用到复杂工业建模中, 提高算法的实用性.