近年来由于城市工业生产和交通运输事业的高速发展, 以及城市人口的急剧增长, 从人类生产与生活中排出的大量废气已对城市环境产生了巨大污染. 而目前, 城市的大气污染情况亦日趋加重, 人类最基本的生存质量正在被损害, 甚至会渐渐地危及人类身体健康[1]. 因此, 国家和社会也越来越重视空气质量的状况. 空气质量预测模型的构建对于每个城市环境治理工作来说, 同样十分必要[2].
空气质量的持续改善离不开有效的科学支持和系统的管理决策, 有效管控的基础是首先要对空气质量影响因素和变化趋势进行准确预测[3]. 空气质量预测模型主要涉及两种类型, 分别是数值模型和统计模型, 其中数值模型虽然不需要有大量的历史数据就可以完成, 但是对研究对象的全面理解是必不可少的; 对于统计模型, 尽管它对于部分研究对象来说计算简便, 但对空气质量指数(AQI)这类非线性和不确定特征较为明显的对象却很难得到良好的预测效果[4]. 鉴于此, 近年来众多学者开始采用混合模型进行预测, 而由于神经网络具有较强的非线性拟合能力, 同时将神经网络与其他优化算法进行结合变得越来越普遍. 如史学良等[5]建立了一种EEMD-LSTM预测模型, 首先采用EEMD方法将获得的空气质量指数AQI值分成若干有效部分, 可以得到不同尺度的IMF分量和残余分量, 再利用经PSO改进的LSTM模型进行预测, 该模型具有较高的预测效率和精度. Yang等[6]首先使用主成分分析法对获得的空气质量指数数据进行降维, 然后利用遗传算法全局搜索优势, 克服神经网络难以得到最优解的缺点, 使得研究对象的误差波动越来越小, 同时可以看出所提模型在迭代率和预测精度方面的性能较好. Chen等[7]采用一种经过鲸鱼优化算法改进的Elman神经网络模型对空气质量指数进行预测, 即引入自适应惯性权值来提高WOA的全局搜索能力, 然后将其应用于对Elman进行优化, 提高了预测精度较低的问题. 许毅蓉等[8]提出一种基于智能型算法来预测空气综合质量指数的方法. 利用模拟退火(SA)结合支持向量机的(SVM)智能型算法自动调整参数, 最终得到最佳分类准确率. Gilik等[9]创建了混合CNN+LSTM深度神经网络, 利用时空关系预测城市多个位置的空气污染物浓度. 通过对模型的超参数进行调整, 确定了最合适的模型结构, 证明该模型具有更准确地预测性能. Nurcahyanto等[10]利用递归神经网络(RNN)对PM10浓度、湿度和温度进行年度和季节室内空气质量预测, 并结合了实时数据预测的室内空气质量管理系统IAQP方法. 通过观测设置的不同传感器的结果可以看出所提出的模型具有良好的结果和可行性. 陈峰[11]提出一种基于蚁群算法, 同时加入了支持向量机算法的预测模型, 利用蚁群算法的自动搜索能力来优化支持向量机算法里的各种参数, 用动态预测模型代替静态模型, 从而使得AQI预测结果更加准确. Septiawan等[12]采用一种可以应用于递归神经网络(RNN)网络架构的BPTT (back propagation through time)算法, 通过比较Elman RNN、Jordan RNN和混合网络架构来预测空气污染物浓度的时间序列数据, 进而确定空气质量. 研究表明文章所提的3种体系结构适用于预测空气质量.
尽管神经网络算法预测效果良好, 但是在预测精度方面仍有较大的提升空间. 为了进一步提高预测的精确度, 本文提出一种混合遗传算法和蚁群算法进而优化BP神经网络的模型. 即将遗传算法(GA)加入到蚁群算法(ACO)进而优化BP神经网络. 首先利用遗传算法优化蚁群中的信息素分布, 然后用蚁群算法搜索神经网络的最优权值和阈值, 并采用西安市的空气质量日历史数据进行模型验证.
1 基本算法 1.1 BP神经网络算法BP神经网络是一种采用误差返向传播(back propagation)算法的多层前馈网络, 由输入层、隐含层、输出层组成, 自提出以来被应用到众多领域, 是目前使用得最为成功的神经网络模型之一[13]. 其基本结构图如图1, 图中各参数的含义见表1.
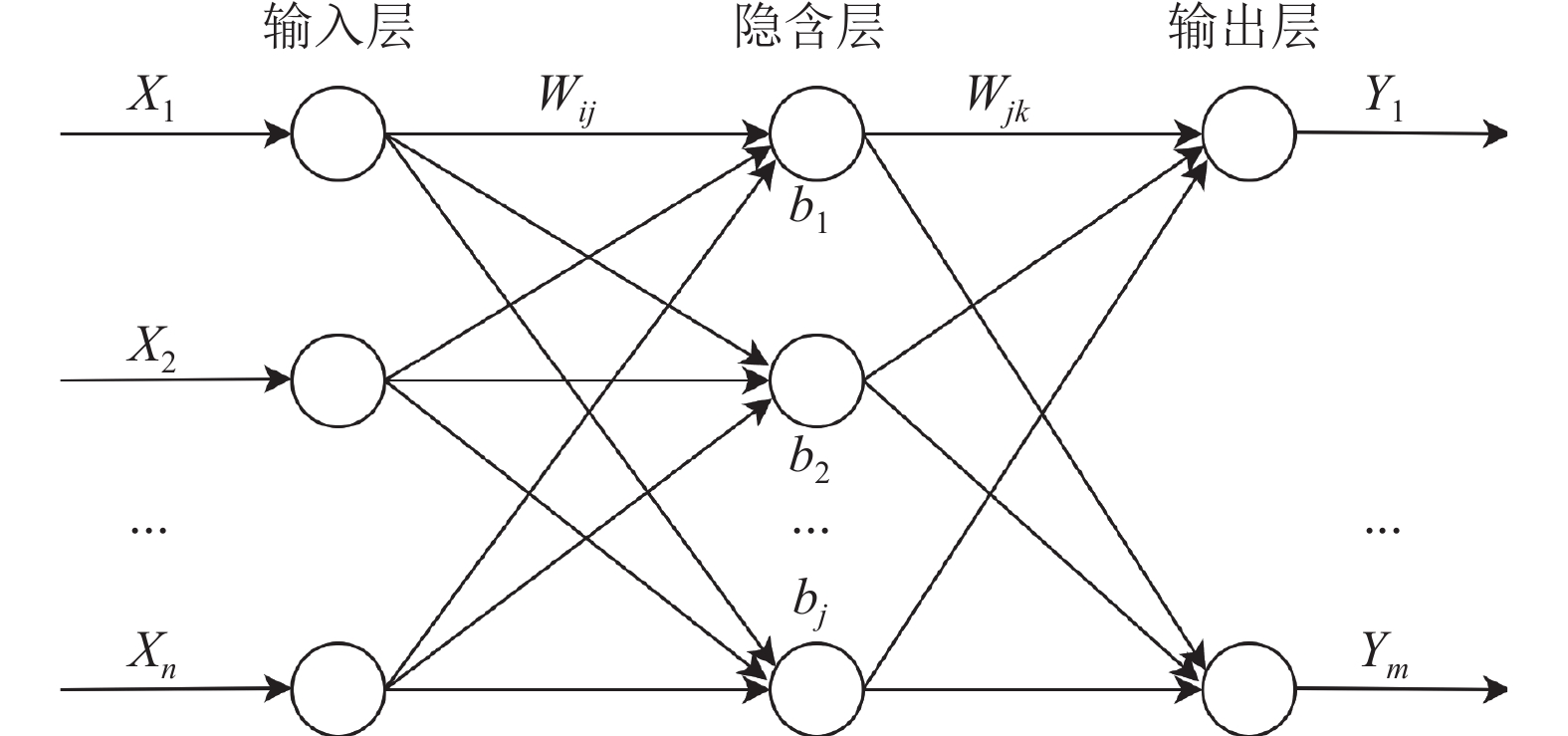
|
图 1 BP神经网络结构图 |
通过对BP神经网络进行学习的过程可发现, 其学习效果和收敛速率主要由初始权值的选择决定. 比较合理的初始权值能够使得网络模型很快收敛并且获得最优解, 反之, 将会导致一系列典型问题的发生, 例如网络收敛速度变慢, 较易陷入局部极小值等[13, 14]. 故本文采用混合遗传蚁群算法GA-ACO优化BP神经网络建立预测模型, 即通过将遗传算法加入到蚁群算法的求解过程, 进而求取出最佳信息素, 然后调整和优化BP神经网络初始权值、阈值, 提高了BP神经网络的收敛速度, 克服了易陷入局部极值的问题, 可以得到较好的预测效果.
| 表 1 BP神经网络参数含义 |
1.2 遗传算法与蚁群算法
遗传算法(GA)是一种模拟自然界遗传机制, 以生物进化论为理论基础而形成的过程搜索最优解算法[15]. 主要包括选择操作、交叉操作、变异操作. 在进行选择操作时, 个体被选中的概率与适应度值相关, 个体适应度值愈突出, 入选的可能性愈大, 最常用的方法是轮盘赌法[16]. 每个个体的适应度值和选择概率如下:
| Fi=k(n∑i=1|yi−oi|) | (1) |
| pi=fiN∑i=1fi | (2) |
| fi=k/Fi | (3) |
其中,
交叉操作: 一般采用实数交叉法, 第
| akj=akj(1−b)+aljb | (4) |
| alj=alj(1−b)+akjb | (5) |
其中,
变异操作: 通过选择第
| aij={aij+(aij−amax)⋅f(g),r>0.5aij+(amin−aij)⋅f(g),r⩽ | (6) |
| f(g) = r_2^{}{(1 - g/G_{{\rm{max}}}^{})^2} | (7) |
其中,
蚁群算法(ACO)是一种启发式随机搜索算法, 它模拟了自然界中蚂蚁寻径过程[17]. 基本原理: 蚂蚁在觅食时, 最初是随机择路而行, 同时会分泌一种化学物质, 称为信息素, 残留于所行路径中, 之后, 随着迭代次数增加, 某条路径中信息素越来越多. 最终, 这些蚂蚁会选择某一条信息素最丰富的路走, 如此一来便找到了一条最优的路径[18, 19].
步骤1. 构建解空间. 首先每只蚂蚁的起始位置都是任意的, 然后统计每只蚂蚁
| {p}_{ij}^{k}(t)=\left\{ {\begin{array}{l}\frac{{\displaystyle [{\tau }_{ij}^{}(t)]}^{\alpha }\cdot {[{\eta }_{ij}^{}(t)]}^{\beta }}{{\displaystyle \sum _{s\in {J}_{k}^{}(i)}{[{\tau }_{is}^{}(t)]}^{\alpha }\cdot {[{\eta }_{is}^{}(t)]}^{\beta }}}, \; j\in {J}_{k}^{}(i)\\ 0, \; 其他\end{array} } \right. | (8) |
其中,
步骤2. 更新信息素. 记录在当前迭代次数上的最佳解(最短路径), 并对不同城市的路线中的信息素含量做出了调整.
| \tau _{ij}^{}(t{\text{ + }}n) = (1 - \rho ) \cdot \tau _{ij}^{}(t) + \Delta \tau _{ij}^{} | (9) |
| \Delta \tau _{ij}^{} = \sum\limits_{k = 1}^m {\Delta \tau _{ij}^k} | (10) |
其中,
| \Delta {\tau }_{ij}^{k}=\left\{ {\begin{array}{l}\dfrac{Q}{{L}_{k}^{}}, \; 蚂蚁k在本次循环中的路径(i, j)\\ 0, \; 其他\end{array} } \right. | (11) |
其中,
步骤3. 判断是否结束. 如果迭代次数少于最大迭代次数, 迭代次数加1, 同时清空所有蚂蚁经过路线的记录表, 并返回步骤1; 否则结束计算, 将得到的最优解进行输出处理.
2 混合预测模型的构建方法 2.1 混合GA-ACO优化BP神经网络算法模型首先遗传算法和蚁群算法都可以对BP神经网络的参数性能进行改善, 蚁群算法与其他启发式算法相比, 具有很强的鲁棒性和搜索较好解的能力, 易与多种启发式算法结合, 以改善算法性能. 遗传算法是一种全局优化搜索算法, 能够避开局部极小点, 而且在进化过程中无需提供所要解决问题的梯度信息.
本文所提出的混合遗传蚁群算法优化BP神经网络模型主要是将利用蚁群算法处理的BP神经网络的初始权值和阈值进行适应度计算, 其中对于满足适应度条件信息素的直接进行蚁群算法的整个流程, 并重复迭代直至选择出最优的权值和阈值. 对于不满足适应度条件的就进行遗传算法的选择、交叉、变异操作, 将获得的最优个体按照蚁群算法的状态转移概率公式进行选择路径并记录具体的参数值, 并且进行信息素浓度计算, 再次计算适应度是否满足所设条件, 对上述过程进行循环迭代, 直至获得BP神经网络的最优权值和阈值结束.
所提混合预测模型流程图如图2所示, 主要目的在于进一步使所取的神经网络初始权值和阈值更加合理, 提高神经网络的收敛速度, 进而找到最优解. 其中BP神经网络在此模型中主要起到预测的作用; 在GA-ACO优化部分, 主要采用遗传算法来优化蚁群算法, 然后将得到的最优权值与阈值应用于BP神经网络. 具体实施步骤如下.
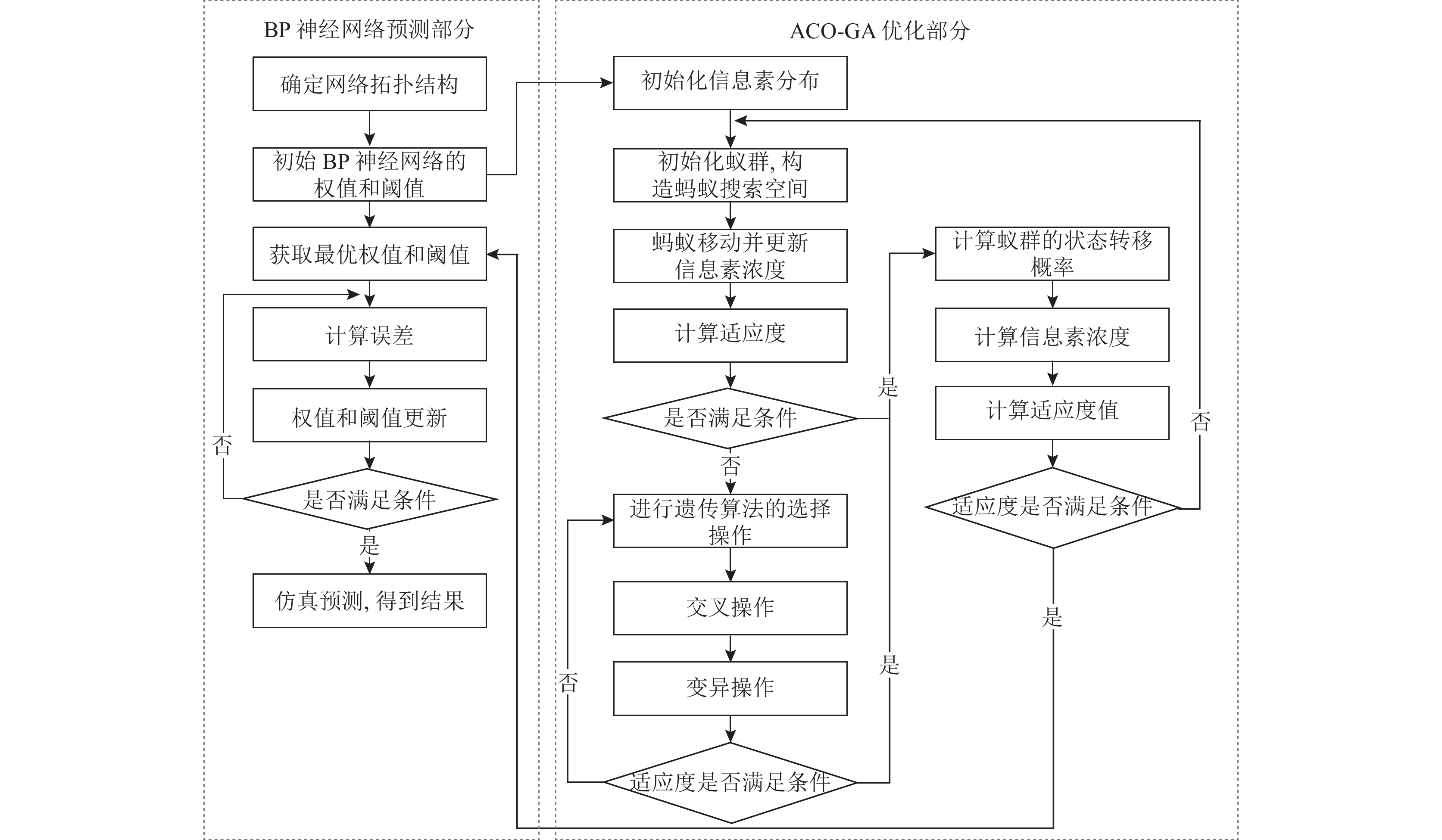
|
图 2 混合GA-ACO-BP算法流程图 |
步骤1. 参数初始化. 对BP神经网络的权值
| E_i^{}{\text{ = }}\frac{1}{2}\sum\limits_{j = 1}^m {{{(Q_{ij}^{} - O_{ij}^{})}^2}} | (12) |
步骤2. 对蚁群执行选择交叉变异的操作. 执行蚁群算法时, 首先构造蚂蚁搜索空间, 蚂蚁移动并更新信息素浓度且计算出适应度, 在不满足设置的适应度条件时, 依次执行遗传算法的3步操作. 满足设置的适应度条件时, 进行步骤3.
步骤3. 对步骤2中的蚂蚁计算状态转移概率、更新信息素.
| \tau _j^{}(I_{wi}^{}) = (1 - \rho ) \cdot \tau _j^{}(I_{wi}^{}) + \Delta \tau _j^{}(I_{wi}^{}) | (13) |
| \Delta \tau _j^{}(I_{wi}^{}) = \sum\limits_{k = 1}^m {\Delta \tau _j^k(I_{wi}^{})} | (14) |
其中,
步骤4. 将步骤2, 步骤3获得的寻优结果作为BP神经网络的参数进行训练; 计算网络的输出误差.
步骤5. 根据获得的结果, 判断是否满足目标要求. 记录误差最小的一组权值、阈值, 判断是否满足要求. 直到满足时退出条件.
2.2 混合预测模型的实施步骤首先, 剔除无效数据并将采集到的有效数据进行归一化处理.
其次, 确定最佳隐藏层个数, 并确定神经网络结构. 将数据应用在本文所构建的混合模型中.
最后, 分别采用BP网络模型、GA-BP网络模型、ACO-BP网络模型、GA-ACO-BP网络模型对空气质量指数进行预测, 并对不同模型的预测结果进行对比分析.
3 基于组合模型的空气质量预测 3.1 数据预处理本篇文章采用的是西安市2021年1月–2022年5月的空气质量指数日历史数据, 数据来源于环境专业知识服务系统和中国气象局官网. 根据《环境空气质量标准》可知, 用来测量空气质量的污染物主要有6种, 分别为SO2、NO2、PM10、PM2.5、O3、CO. 本文数据包含上述6种污染物数据以及AQI数据信息. 剔除问题数据(2022年3月3日–13日数据丢失)之外共502条数据, 如表2所示.
数据首先需要采用mapminmax()函数进行归一化处理, 目的在于消除因量纲不同对预测结果造成的影响, 如式(15)所示:
| x* = \frac{{(x - x_{{\rm{min}}}^{})(y_{{\rm{max}}}^{} - y_{{\rm{min}}}^{})}}{{x_{{\rm{max}}}^{} - x_{{\rm{min}}}^{}}} + y_{{\rm{min}}}^{} | (15) |
其中,
| 表 2 西安市空气质量指数数据(部分) |
3.2 仿真条件及结果分析 3.2.1 实验条件及评价指标
本文的仿真实验是在Matlab 2016a平台上进行的, 首先选择了单隐藏层的BP神经网络, 并根据实际需要选取网络模型的所有参数, 其中输入层结点为6, 输出层结点为1, 隐藏层结点根据经验公式来确定, 如式(16):
| l = \sqrt {m + n} {\kern 1pt} {\kern 1pt} {\kern 1pt} + {\kern 1pt} {\kern 1pt} {\kern 1pt} a | (16) |
其中,
| MAE {\text{ = }} \frac{1}{n}\sum\limits_{i = 1}^n {|y_i^{} - y_i^*|} | (17) |
| {\textit{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{(y_i^{} - y_i^*)}^2}} } | (18) |
| MAPE {\text{ = }} \frac{1}{n}\sum\limits_{i = 1}^n {\frac{{|y_i^{} - y_i^*|}}{{y_i^{}}}} | (19) |
| EC = 1 - \frac{{\sqrt {\displaystyle\sum\limits_{i = 1}^n {{{(y_i^{} - y_i^*)}^2}} } }}{{\sqrt {\displaystyle\sum\limits_{i = 1}^n {{{(y_i^{})}^2}} } + \sqrt {\displaystyle\sum\limits_{i = 1}^n {{{(y_i^*)}^2}} } }} | (20) |
其中,
采用本文模型预测空气质量指数时, 将502条数据按7:3的比例分为训练集和测试集. 随后将数据分别输入到BP、GA-BP、ACO-BP、GA-ACO-BP模型中进行实验. 其中, 根据上述隐藏层结点数的经验公式并结合准确率公式, 可得表3, 准确率公式为:
| 准确率= \left(1{{ - }}\frac{1}{n}\sum\limits_{i = 1}^n \frac{{|y_i^{} - y_i^*|}}{{y_i^{}}} \right) \times 100{\text{%}} | (21) |
| 表 3 不同隐层节点数的GA-ACO-BP神经网络对应的准确率 |
通过表3可知, 当隐藏层节点个数为10时, 准确率最高.下面依次对GA-BP、ACO-BP对比模型进行实验, 首先根据实验经验, 通过使用控制变量的方式, 分别在遗传算法和蚁群算法中对所需参数在一定范围内进行调试, 将调试10次之后所获得的MAE、MASE、MAPE、EC值进行取平均值, 通过比较选择出最优的参数.
通过表4、表5中GA-BP、ACO-BP的参数调试性能对比, 筛选出以上两个模型中评价指标较为优秀的参数, 并应用到本文所提的混合模型中, 得到的参数性能对比结果如表6所示.
| 表 4 GA-BP参数调试性能对比 |
根据表6中筛选出的不同参数的运行结果对比, 最终可以确定混合模型的最优参数值见表7.
将BP、GA-BP、ACO-BP与本文提出的GA-ACO-BP模型进行对比, 如图3. 对比图3(a)和图3(b)可以看出在GA-BP、ACO-BP模型使用的测试集数据中, 预测值和实际值在图像上所反映的仍有很多天的AQI数据值差距比较明显. 但是通过图3(c)可以看出, GA-ACO优化的BP神经网络模型大大减小了这种差距, 使得预测值和实际值的拟合度变得更高, 效果也是这几种模型中最好的.
| 表 5 AC0-BP参数调试性能对比 |
| 表 6 GA-ACO-BP参数调试性能对比 |
| 表 7 GA-ACO-BP模型参数设置 |
通过引入的评价指标, 对各个模型的预测结果进一步分析. 根据设定的参数值, 从表8中可以看出本文所提出的GA-ACO-BP混合模型的ave-MAE、ave-MSE、ave-MAPE在4种模型中都是最小的, 分别为2.3759、12.0764、0.0238; ave-EC值较对比模型来说是最大的, 为0.9858; 说明效果最佳. 因此用本文提出的模型对空气质量指数进行预测是更加合适的.
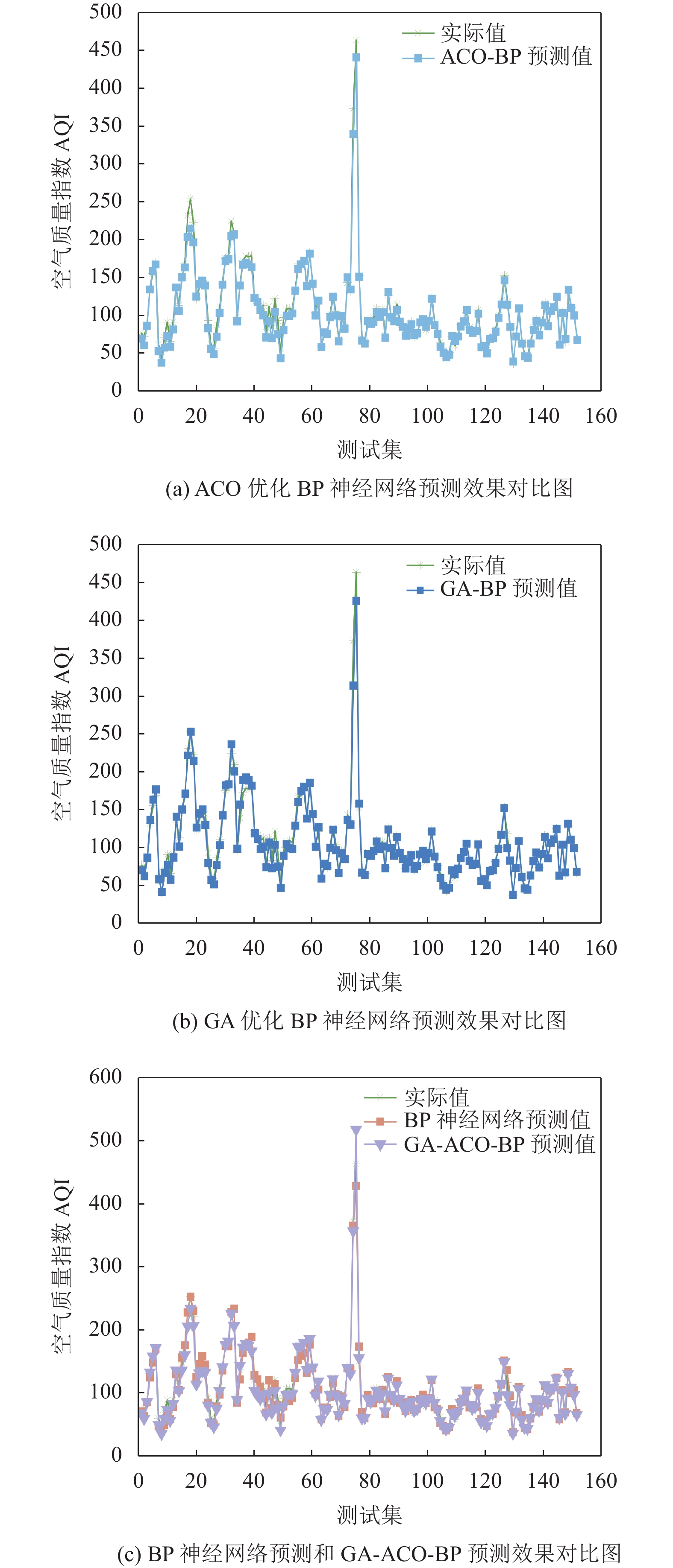
|
图 3 不同模型的预测结果对比图 |
| 表 8 模型在不同评价指标下的误差对比 |
4 结论
本文主要利用混合遗传蚁群算法优化BP神经网络来预测空气质量指数, 通过使用西安市的空气质量指数日历史数据对所提模型进行验证, 结合预测对比图以及误差评价指标可知, 混合遗传蚁群算法优化的BP神经网络预测效果更好, 拟合能力更加突出. 可见该模型在分析空气质量指数方面具有一定优势, 对相关部门判断空气质量具有重要意义.
虽然本文提出的模型在一定程度上提高了预测精度, 但是空气质量指数受很多因素的影响, 其中很大一部分因素是与人类活动有关的, 比如汽车的尾气排放、工厂的有害气体排放、城市的发展密度、各个地区的地形地貌等. 所以在后续的研究工作中, 应更加全面的考虑其他影响因素, 进一步提高预测精度.
| [1] |
雷明丽, 张艳飞. 浅析空气质量的影响因素和防治措施. 城市建设理论研究(电子版), 2012, (14).
|
| [2] |
刘闽, 王帅, 林宏, 等. 沈阳市冬季环境空气质量统计预报模型建立及应用. 中国环境监测, 2014, 30(4): 10-15. DOI:10.3969/j.issn.1002-6002.2014.04.002 |
| [3] |
齐甜方, 蒋洪迅, 石晓文. 面向多源数据沈阳市PM2.5 浓度预测研究及实证分析
. 系统工程, 2018, 36(5): 104-115. |
| [4] |
甘露情, 刘媛华. 基于BP-SVR组合模型的空气质量指数预测. 软件导刊, 2020, 19(10): 80-83. |
| [5] |
史学良, 李梁, 赵清华. 基于改进LSTM网络的空气质量指数预测. 统计与决策, 2021, 37(16): 57-60. DOI:10.13546/j.cnki.tjyjc.2021.16.012 |
| [6] |
Yang RJ, Hu XQ, He LJ. Prediction of Shanghai air quality index based on BP neural network optimized by genetic algorithm. Proceedings of the 2020 13th International Symposium on Computational Intelligence and Design (ISCID). Hangzhou: IEEE, 2020. 205–208.
|
| [7] |
Chen Z, Cai DW. Based on a prediction method for improving WOA-Elman air quality prediction. Proceedings of the 2nd International Conference on Computing and Data Science. Stanford: ACM. 2021. 43.
|
| [8] |
许毅蓉, 连金海, 张小蓉, 等. 运用智能型算法预测空气综合质量指数的研究. 福建电脑, 2022, 38(6): 17-21. DOI:10.16707/j.cnki.fjpc.2022.06.005 |
| [9] |
Gilik A, Ogrenci AS, Ozmen A. Air quality prediction using CNN+LSTM based hybrid deep learning architecture. Environmental Science and Pollution Research, 2022, 29(8): 11920-11938. DOI:10.1007/s11356-021-16227-w |
| [10] |
Nurcahyanto H, Prihatno AT, Alam MM, et al. Multilevel RNN-based PM10 air quality prediction for industrial Internet of things applications in cleanroom environment
. Wireless Communications and Mobile Computing, 2022, 2022: 1874237. |
| [11] |
陈峰. 基于蚁群算法和支持向量机的空气质量指数预测模型研究[硕士学位论文]. 金华: 浙江师范大学, 2017.
|
| [12] |
Septiawan WM, Endah SN. Suitable recurrent neural network for air quality prediction with backpropagation through time. Proceedings of the 2018 2nd International Conference on Informatics and Computational Sciences (ICICoS). Semarang: IEEE, 2018. 1–6.
|
| [13] |
李长安, 卢雪琴, 吴忠强, 等. 基于蚁群算法优化反向传播神经网络的港口吞吐量预测. 计量学报, 2020, 41(11): 1398-1403. DOI:10.3969/j.issn.1000-1158.2020.11.14 |
| [14] |
杨客. 遗传算法优化的BP神经网络在连云港港口吞吐量预测中的应用研究[硕士学位论文]. 深圳: 深圳大学, 2017.
|
| [15] |
吴慧静, 赫晓慧. 基于GA-BP神经网络的空气质量指数预测研究. 安徽师范大学学报(自然科学版), 2019, 42(4): 360-365. DOI:10.14182/J.cnki.1001-2443.2019.04.011 |
| [16] |
杨云, 杨毅. 基于GA-BP神经网络的供暖期空气质量指数预测分析. 陕西科技大学学报, 2016, 34(4): 171-176, 186. DOI:10.19481/j.cnki.issn1000-5811.2016.04.032 |
| [17] |
Ding MJ, Zhang SZ, Zhong HD, et al. A prediction model of the sum of container based on combined BP neural network and SVM. Journal of Information Processing Systems, 2019, 15(2): 305-319. |
| [18] |
Irani R, Nasimi R. An evolving neural network using an ant colony algorithm for a permeability estimation of the reservoir. Petroleum Science and Technology, 2012, 30(4): 375-384. DOI:10.1080/10916466.2010.483442 |
| [19] |
杨锐锐, 王颖. 蚁群算法的基本原理及参数设置研究. 南方农机, 2018, 49(13): 38-39. DOI:10.3969/j.issn.1672-3872.2018.13.023 |
| [20] |
吴铁锋. 改进BP神经网络的城市交通流预测研究. 交通科技, 2010(5): 92-94. DOI:10.3963/j.issn.1671-7570.2010.05.031 |
| [21] |
孟飞, 兰巨龙, 胡宇翔. 基于改进的量子粒子群优化小波神经网络的网络流量预测. 计算机应用研究, 2015, 32(5): 1450-1453. DOI:10.3969/j.issn.1001-3695.2015.05.042 |
 2023, Vol. 32
2023, Vol. 32



