1 前言

自2020年初新冠疫情爆发以来, 在疫情防控常态化的背景下, 线上与线下相结合的混合式教学成为各高校的首选教学方式^{[1, 2]}. 如果能够在复杂繁琐的混合式学习数据中提取有用的信息, 结合机器学习算法对学生的学习结果进行早期预测, 可以帮助教师及时对有挂科风险的学生实施干预, 这对于教学工作具有重要意义^[3-8].

近年来, 国内外学者在学生成绩分析预测方面进行了大量研究^[9-11]. 在预测方法上, Akçapınar等^[12]采用KNN对在线学习中学生期末成绩进行分类预测. 刘博鹏等^[13]采用学生的行为、个人属性和历史成绩等数据通过支持向量机对学生成绩进行预测. 但以上算法较为单一, 在数据量较大情况下模型的预测效果欠佳. 为此, 部分学者采用随机森林^{[14, 15]}、CatBoost^[16]、XGBoost^[17]等集成树模型提升预测效果. 还有学者采用Stacking^[18-20]集成策略将多个单一算法进行集成预测, 相比与单一算法预测效果有一定提升. 但在模型训练前需要对稀疏的数据进行大量人工特征工程工作, 较为费时费力. 此外, 由于学生成绩数据存在不平衡性, 类别占比较多的一类预测效果较好, 而类别较差的一类相对较差, 易造成模型的整体预测效果变差^[21], 而大部分学生成绩预测模型缺乏对不平衡数据均衡处理.

综合上述研究工作, 虽然目前在成绩预测领域已取得一定进展, 但仍然存在一些问题有待解决: (1) 学生行为特征依赖人工特征工程提取和需要领域专家的参与, 容易忽略一些对分类预测目标造成影响的因素; 如在数据预处理过程中, 需要根据学生的学习特征分布, 主观对部分学习特征进行分箱操作^[22], 如果分箱不合理, 可能会造成学生的特征信息丢失; (2) 没有考虑对数据集的学生成绩类别不平衡性对模型的影响. 针对以上问题, 为减小不平衡数据对模型分类预测效果的影响, 并进一步提高对学生成绩分类预测模型的泛化能力, 本文开展了以下工作, 并区别于已有研究.

1) 通过SMOTE算法对数据集进行过采样, 以降低不平衡数据对模型的影响.

2) 采用SHAP (Shapley additive explanation) 模型对影响学生成绩的因素进行分析、特征选择, 增强预测模型的泛化能力.

3) 通过融合XGBoost和因子分解机(FM)建立学习成绩分类预测模型, 减少传统成绩预测基线模型对人工特征工程的依赖.

2 SMOTE-XGBoost-FM 分类预测模型 2.1 问题定义

学习成绩预测的目的是根据学生历史行为数据预测未来的学习结果, 在混合式学习环境下, 学生历史行为数据主要包括个人基本信息、线上和线下学习数据等. 下面给出问题的定义.

学习行为特征: 行为特征 $ {X_m} = \left\{ {x_m^1, x_m^2, \cdots , x_m^t} \right\} $ 定义为某个学生的所有学习行为数据集合, 其中 $ x_m^t $ 为学生m的第t个教学周的历史行为数据, 为了实现对学生学习结果进行早期预测, 以 $ x_m^t = \left\{ {x_{m1}^t, x_{m2}^t, \cdots , x_{mn}^t} \right\} $ 作为样本特征, 其中 $ x_{mn}^t $ 为学生m的第t个教学周的第n个行为特征数据.

学习成绩分类预测: 给定学生m的第t周学习行为特征 $ x_m^t = \left\{ {x_{m1}^t, x_{m2}^t, \cdots , x_{mn}^t} \right\} $ 预测 $y{'_m}$ . $y{'_m}$ 表示学生的期末学习成绩类别标签, $y{'_m}$ 有1和0两个状态, 分别表示学生m能和未能通过期末检测.

2.2 SMOTE-XGBoost-FM模型

以混合式学习下学习行为数据为研究对象, 本文结合SMOTE、XGBoost和FM提出SMOTE-XGBoost-FM分类预测模型, 用于均衡样本不平衡类别、提取数据中深度隐藏的信息和提高整体模型的泛化性能. 如图1所示, SMOTE-XGBoost-FM分类预测模型主要分为4个核心阶段.

1) SMOTE采样阶段, 通过对原始数据集中学生类别较少的一类进行SMOTE过采样, 弥补两个类别间的数量差异均衡数据.

2) 特征交叉阶段, 采用XGBoost树结构模型对类别均衡的特征数据进行训练, 通过树分裂的方式进行特征交叉, 最终生成树结构. XGBoost对特征数据的训练可以看作是XGBoost中每棵决策树对特征的交叉组合, 其中从每棵树的根节点到叶子节点的这条路径可以看作是不同特征之间交叉组合. 叶子节点数可看作为新特征数, 每个样本在所有叶子节点的编码为新的样本特征值.

3) 特征转换阶段, 计算每个样本在每棵树各叶子节点所得到的预测概率值, 将每个样本的预测概率值所属的叶子节点独热编码, 通过以上方式将原始特征重新变换, 获得新稀疏特征矩阵.

4) 模型训练阶段, 将新特征数据输入因子分解机(FM)进行训练, 最后通过Sigmoid函数将结果分为两类.

2.3 SMOTE-XGBoost-FM 分类预测算法

假设融合模型SMOTE-XGBoost-FM的输入训练数据集为 $ D = \left\{ {\left( {{x_1}, {y_1}} \right), \left( {{x_2}, {y_2}} \right), \cdots , \left( {{x_m}, {y_m}} \right)} \right\} $ , 实例样本的特征为 $ x_m^t = \left\{ {x_{m1}^t, x_{m2}^t, \cdots , x_{mn}^t} \right\} $ , 样本特征对应的标签为 $ {y_m} $ , 样本的特征维度为n, 记期末考试中学生能通过检测的样本集为 $ {D_p} $ , 未能通过检测的样本集为 $ {D_f} $ , 其中p和f分别为多数类别与少数类别样本数量, p < f且p + f = m, XGBoost学习器为 $ \hat y\left( x \right) $ , FM学习器为 $y\left( x \right)$ . 经过SMOTE采样后所产生的新数据集为 ${D_{{\rm{new}}}} = \{ \left( {{x_1}, {y_1}} \right), \left( {{x_2}, {y_2}} \right), \cdots , \left( {{x_s}, {y_s}} \right) \}$ 然后经过XGBoost学习器 $\xi $ 的训练, 最终生成j个叶子节点, 然后获取各叶子节点对应索引 ${u_{{s}}} = \left\{ {{u_{s1}}, {u_{s2}}, \cdots , {u_{sj}}} \right\}$ , 如果叶子节点 ${u_{{{s}}j}}$ 为学生样本 $ {x_m} $ 最终分裂所在位置, 则记叶子节点 ${u_{{{s}}j}}$ 所对应值 ${q_{{{s}}j}} = 1$ , 否则记 ${q_{mj}} = 0$ . 最终获得新特征集合 ${Q_{{s}}} = \left\{ {{q_{{{s}}1}}, {q_{s2}}, \cdots , {q_{sj}}} \right\}$ , 将新特征构建新数据集 $D' = \{ \left( {{q_1}, {y_1}} \right), \left( {{q_2}, {y_2}} \right), \cdots , \left( {{q_s}, {y_s}} \right) \}$ , 并将其输入FM学习器 $\psi $ 训练预测, 最后得出每个样本最终预测结果 $y{'_{{s}}}$ . 具体融合算法伪代码如算法1所示.

算法1. 融合算法

输入: 原始数据集 $\scriptstyle D = \left\{ {\left( {{x_1}, {y_1}} \right), \left( {{x_2}, {y_2}} \right), \cdots , \left( {{x_m}, {y_m}} \right)} \right\} $ , 样本特征值 $\scriptstyle {x_m} = \{ {x_{m1}}, \scriptstyle {x_{m2}}, \cdots , {x_{mn}} \}$ , XGBoost学习器为 $\scriptstyle \xi $ , FM学习器为 $\scriptstyle \psi $

过程:

1. 　 $\scriptstyle {D_{{\text{new}}}} \leftarrow {{{\rm{SMOTE}}}}\left( D \right)$

2.　 for $\scriptstyle i = 1, 2, \cdots , {{s}}$ do

3.　　 $\scriptstyle {u_{{s}}} \leftarrow {\xi _{{s}}}\left( D \right)$

4.　　 $\scriptstyle {u_s} = \left\{ {{u_{s1}}, {u_{s2}}, \cdots , {u_{sj}}} \right\}$

5.　　　 if u_sj ← x_s

6.　　　　　 q_sj = 1

7.　　　 else q_sj = 0

8.　　 $\scriptstyle {Q_{{s}}} = \left\{ {{q_{s1}}, {q_{s2}}, \cdots , {q_{{{s}}j}}} \right\}$

9. 　end for

10.　 $\scriptstyle D' = \left\{ {\left( {{q_1}, {y_1}} \right), \left( {{q_2}, {y_2}} \right), \cdots , \left( {{q_s}, {y_s}} \right)} \right\} $

11. 　for $\scriptstyle i = 1, \cdots , {{s}}$ do

12. 　　 $\scriptstyle y{'_{{s}}} = {\psi _s}\left( {D'} \right)$

13.　 end for

输出: 每个样本最终预测结果 $\scriptstyle y{'_{{s}}}$

SMOTE-XGBoost-FM算法具体步骤如下.

1) 根据样本类别权重, 通过公式 $ N = {\text{int}}\left(\dfrac{{p - f}}{f}\right) $ 对未能通过期末检测的学生样本设置一个采样倍率N, 其中N为整数, 且大于0. 由采样倍率N和少数类别样本数量f, 计算出未能通过期末检测的样本集D_f需要合成的样本数量为Nf.

2) 对样本集D_f中每个样本 ${x_i}$ 采用欧式距离计算其到D_f中其他所有样本的距离, 得到k近邻, 在 ${x_i}$ 的k近邻中随机选择样本 $ {x_j} $ , 按照 ${x_n} = {x_i} + rand(0, 1)\times|{x_i} - {x_j}|$ 计算方式得出新样本 ${x_n}$ , rand(0, 1)表示区间(0, 1)的随机数.

3) 根据数据集中未能通过期末检测样本类别的采样倍率N重复进行采样过程, 直到满足步骤1)中所需要合成的新样本数量. 数据集D经过平衡后生成数据集记为 ${D_{{\rm{new}}}} = \left\{ {\left( {{x_1}, {y_1}} \right), \left( {{x_2}, {y_2}} \right), \cdots , \left( {{x_s}, {y_s}} \right)} \right\}$ , 其中s = m + Nf.

将经过SMOTE采样平衡后的新数据集 ${D_{{\rm{new}}}} = \left\{ {\left( {{x_1}, {y_1}} \right), \left( {{x_2}, {y_2}} \right), \cdots , \left( {{x_s}, {y_s}} \right)} \right\}$ 输入XGBoost学习器 $ \hat y\left( x \right) $ 中进行迭代训练, 并通过网格搜索调整学习器参数, 迭代训练公式如下:

$ \hat y_i^{(t)} = \sum\limits_{k = 1}^t {{f_k}} \left( {{x_i}} \right) = \hat y_i^{(t - 1)} + {f_t}\left( {{x_i}} \right) $

(1)

其中, $\hat y_i^{(t)}$ 表示树结构模型的第t次迭代预测结果, 在每一次梯度提升迭代中, 通过损失函数处理残差来修正前一次迭代预测的结果, f_k(x_i)表示第k棵树给第i个样本的预测值.

模型每次以式 (2) 为求解最小化目标函数进行迭代:

$ {\textit{obj}}^{(t)} = \sum\limits_{i = 1}^n l \left( {{y_i}\hat y_i^{(t)}} \right) + \sum\limits_{i = 1}^n \Omega \left( {{f_i}} \right) $

(2)

其中, $\displaystyle\sum\limits_{i = 1}^n l \left( {{y_i}\hat y_i^{(t)}} \right)$ 为损失函数部分, 其用来衡量预测值 $\hat y_i^{}$ 和目标值 ${y_i}$ 之间的差异. $\Omega \left( {{f_i}} \right) = \gamma T + \dfrac{1}{2}\lambda \displaystyle\sum\limits_{j = 1}^T {{w_{j2}}} $ 为正则化项, 式中 $\gamma $ 为L1正则项, $\lambda $ 为L2正则项.

4) 经过步骤4)迭代训练后建立树结构, 记树结构的叶子节点个数为j, 获取各叶子节点对应索引 $ {u_s} = \left\{ {{u_{s1}}, {u_{s2}}, \cdots , {u_{sj}}} \right\} $ , 如果叶子节点u_sj为样本x_s最终分裂所在的位置, 则记叶子节点u_sj所对应值q_sj = 1, 否则记q_sj = 0, 最终获得新样本特征集合 ${q_s} = \left\{ {{q_{s1}}, {q_{s2}}, \cdots , {q_{sj}}} \right\}$ .

5) 将步骤5)获得的样本特征集 $ {q_s} = \left\{ {{q_{s1}}, {q_{s2}}, \cdots , {q_{sj}}} \right\} $ 构建新的数据集 $ D' = \left\{ {\left( {{q_1}, {y_1}} \right), \left( {{q_2}, {y_2}} \right), \cdots , \left( {{q_s}, {y_s}} \right)} \right\} $ , 将其按一定比例切分为训练集 $D{'_{{\rm{train}}}}$ 和测试集 $D{'_{{\rm{test}}}}$ .

6) 将训练集 $D{'_{{\rm{train}}}}$ 送入因子分解机学习器 $\psi \left( x \right)$ 进行训练, $y\left( x \right)$ 算法函数如式 (3) 所示:

$ y(x) = \sigma \left( {{w_0} + \sum\limits_{i = 1}^n {{w_i}} {x_i} + \sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^n \lt } {v_i}, {v_j} \gt {x_i}{x_j}} \right) $

(3)

其中, $ {x_i} $ 为样本x的第i个特征值, n为样本特征的维度. $ {w_0} \in R $ 为全局偏差, $ {w_i} \in {R^n} $ 表示第i个特征的影响因子, $ \lt {v_i}, {v_j} \gt = \displaystyle\sum\limits_{f = 1}^k {{v_{i, f}}} \cdot {v_{j, f}} $ 表示两k维向量的内积, 隐向量长度k为一超参数, k<<n. $\sigma $ 为Sigmoid函数, 设置在模型的输出上, 将模型输出分类转换.

7) 将因子分解机学习器 $y\left( x \right)$ 通过网格搜索和5折交叉验证来调整学习器参数, 使其获最佳效果, 最后得出每个样本最终预测结果 $y{'_m}$ , 并利用测试集 $D{'_{{\rm{t}}{\text{est}}}}$ 验证SMOTE-XGBoost-FM模型的泛化能力.

3 实验与结果分析

本文实验环境为CPU Inter i7-9700, RAM为12 GB, 编译软件PyCharm 2021.3.3, 算法模型使用Python实现. 为了展示均衡不平衡数据集的必要性和验证融合XGBoost与FM算法在学生成绩分类预测中的优越性, 随机将数据集按7:3切分为训练集与测试集用来训练与测试, 设置两组对比实验, 对比logistic regression(LR)、gradient Boosting decision tree (GBDT)、random forest (RF)、XGBoost、FM、XGBoost+FM在数据集上的准确率、召回率、AUC值等评价指标, 以及对比未采用SOMTE采样与采用SOMTE采样的模型效果.

3.1 数据集介绍

本文所研究的数据采集自学校超星学习通平台与教务系统, 共129名学生, 一个学期18个教学周, 共提取出16个学习行为特征, 通过按周进行样本数据提取, 最终共获2 322个样本. 数据集中各学生学习行为特征含义如表1所示.

3.2 数据预处理

将原始数据集按周划分并集成新的数据集, 新的数据集中共有2 322个样本数据, 通过Python中pandas库的describe函数对新的数据集进行描述性统计, 结果如表2所示. 可以发现, 各特征的最小值除了interactive、sign_in等几个特征外几乎全为0, 数据集中各特征数据的25%分位中仍然存在大量的0值特征, 特征数据的75%分位中部分特征依然为0, 因此可以看出数据较为稀疏. Final_mark为期末考试卷面成绩, 由于存在缺考同学, 所以存在零分现象, 因此需要缺失值填充. video_progress、questions等特征由于系统统计问题而存在负值, 对其置0处理. 由于本文采用的预测方式为分类预测, 预测问题为识别学生是否存在课程学业风险, 因此将学生的期末成绩分为failed与pass两类. 经处理后共获得failed类别839例, pass类别1 483例, 两个类别占比情况如图2所示, 从图中可以看出两个类别的分布占比较不平衡, pass类别占比更大.

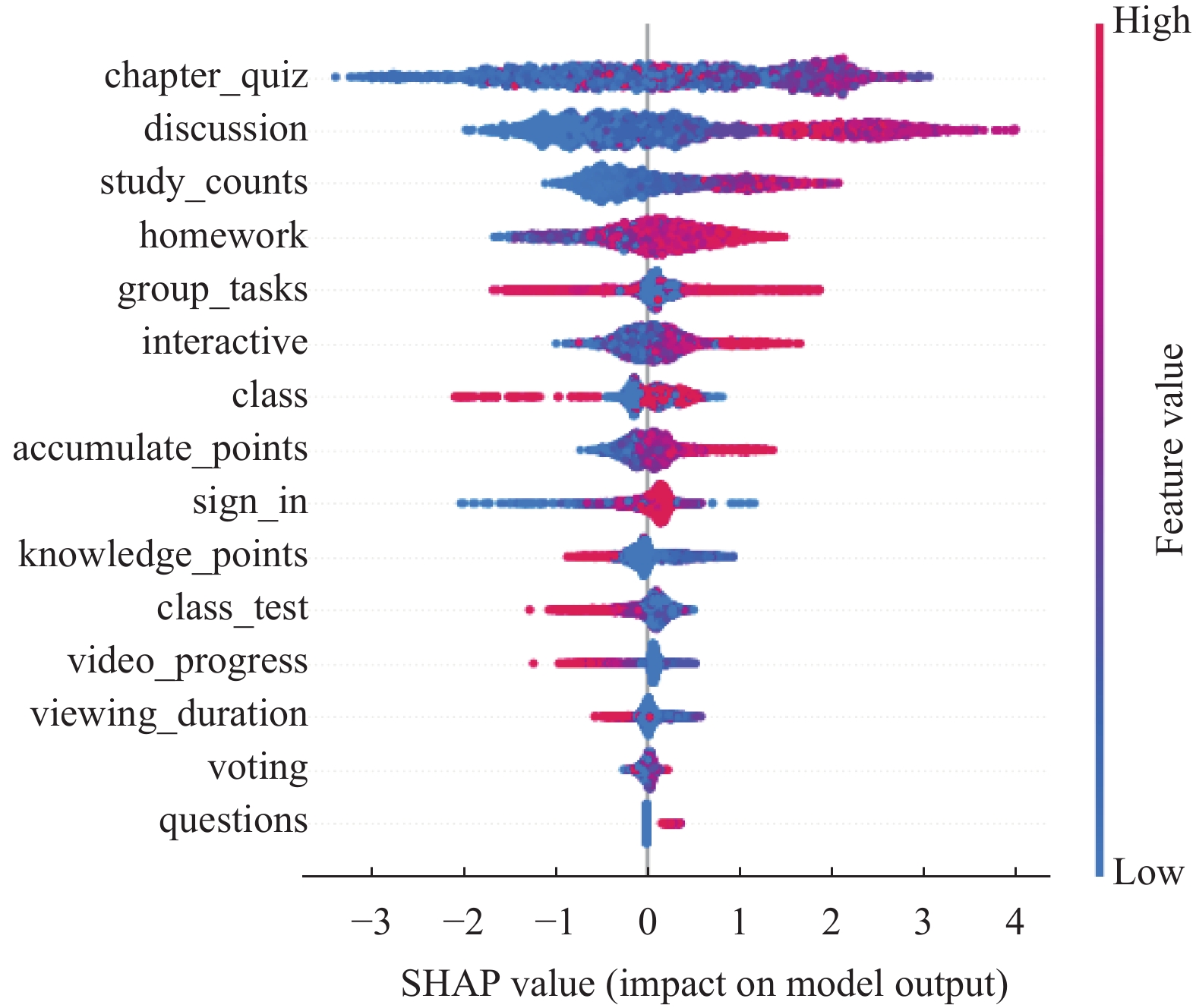
3.3 特征选择

特征选择可以减少冗余特征, 提高模型建立的速度, 增强模型泛化能力, 减少模型过拟合问题. 本文采用SHAP值来描述和评估特征的重要性, 基于XGBoost模型利用SHAP值选择最终输入模型训练的特征. SHAP值可以将每个特征中的所有样本整体可视化^[23]. 如图3所示, 图中表示特征对每个样本的影响, 每一行是一个特征, 每个点表示一个样本, 横坐标为SHAP值, 颜色表示特征值的强弱, 红色和蓝色分别表示高值和低值. 图3中所示, chapter_quiz、discussion等特征的较低值会增加学生挂科风险的概率, 而knowledge_points、video_progress、viewing_duration等特征的较高值会增加学生挂科风险的概率(可能的原因是个别学生为了获得更好的平时成绩, 将未来需要完成的任务提前刷完, 从而造成个别样本的knowledge_points、video_progress、viewing_duration等特征值异常高). 每个特征的平均SHAP值表示其特征的重要性, 特征重要性排序如图4所示, 从图中可以看出chapter_quiz特征最重要, voting和questions特征的重要性几乎为零. 因此, 在模型训练时采用前13个特征, 将最后两个voting和questions特征删除.

3.4 模型的泛化能力评估指标

预测学生能否通过期末检测, 即将预测结果分为通过(pass)和挂科(failed)两类, 这是一个二分类预测问题, 其混淆矩阵分析表如表3所示, 其中TP、TN、FP和FN分别代表真阳性、真阴性、假阳性和假阴性.

本文选择了准确率A (accuracy)、召回率R (recall)、精确率P (precision)、F1 (F1 score)得分和接收器工作特性(ROC)曲线作为评估标准. 精确率的通过假阳性来衡量模型的准确性, 即被误判为不能通过期末考试的学生数量, 假阳性越低, 模型的精确率越高. 召回率则通过假阴性来衡量模型的性能, 即真正挂科学生中预测为挂科学生的数量. 在学习预测的背景下, 真正挂科学生的预测准确性被认为比能通过期末考试的学生更重要. 因此, 就评估模型而言, 召回率比精确率更重要. ROC曲线为真阳性率和假阳性率的对比图, 用来进一步评估模型的性能. AUC定义为ROC曲线下的面积, 面积值越大, 模型的效果越好. 准确率、召回率、精确率和F1得分定义如下:

$ A = \frac{{TP + TN}}{{TP + TN + FP + FN}} $

(4)

$ P = \frac{{TP}}{{TP + FP}} $

(5)

$ R = \frac{{TP}}{{TP + FN}} $

(6)

$ F1 = \frac{{2P \times R}}{{P + R}} $

(7)

3.5 模型参数设置

选择合适模型参数可以进一步优化模型, 充分发挥模型的性能, 网格搜索法是机器学习中有效的调整模型参数方法. 本文采用5折交叉验证验证方式将训练集进一步划分为5份, 循环选取其中一份作为最优参数的验证集, 以准确率作为模型预测效果的评价指标, 通过网格搜索法选取各模型的最有参数. 本文中采用的模型最终参数设置如表4所示.

3.6 结果对比分析

采用SMOTE算法对原始数据集过采样, 原始数据集的不平衡标签类别经过均衡后生成新数据集, 利用XGBoost对新特征数据进行特征交叉, 充分挖掘特征数据信息, 最后采用因子分解机(FM)预测学生能否通过期末考试. 融合XGBoost与因子分解机(FM)的目的是在较少人工特征工程情况下充分挖掘数据集的信息, 提高模型的泛化能力. 为验证所提模型的有效性, 本文设置了相关对比实验, 根据设置的两组对比实验对所有的预测结果进行定性和定量分析比较.

(1) 基础模型泛化性能对比分析

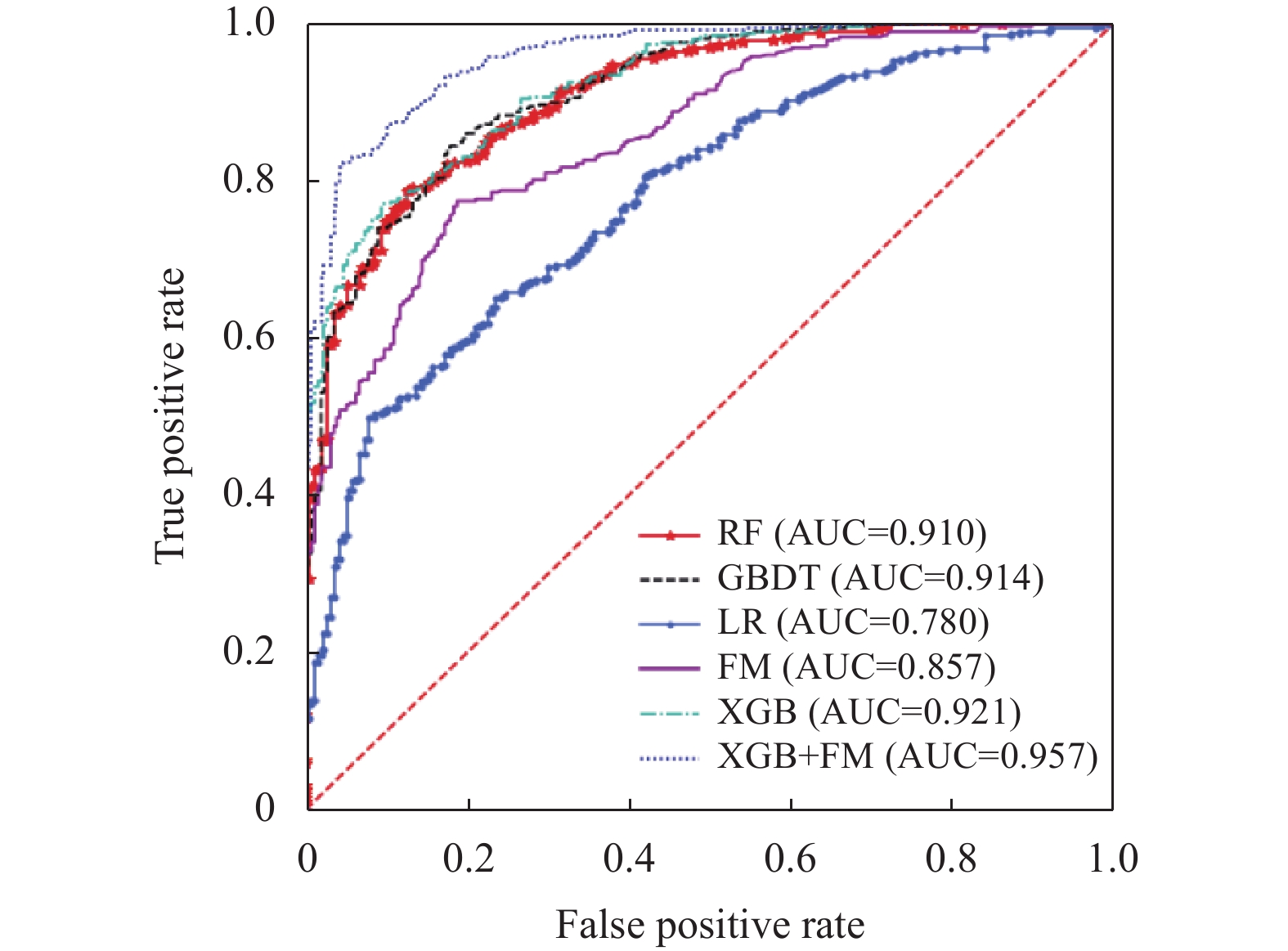
图5为各模型在未SMOTE采样情况下根据预测结果绘制的ROC曲线, 从图中可以看出, XGBoost+FM的AUC达到了95.7%, 预测效果最好. 表5为各模型在未SMOTE采样与SMOTE采样情况下各模型预测的精确率、召回率、F1得分等结果. 从表5中可以看出, 在未SMOTE采样的情况下, 各模型的failed类别预测的精确率、召回率、F1得分相对于pass类别皆较偏低. 其中, LR模型预测的failed类别精确率、召回率分别为29.0%和41.6%, pass类别的精确率、召回率分别为94.5%和81.1%, 相差最大. 可以看出样本类别较少的failed类别预测效果较差, 数据集的不平衡性对模型的预测效果有一定的影响. 此外, 从表5可以看出在6个模型中XGBoost+FM各项预测效果最优.

(2) 不平衡过采样后各模型对比分析

图6为原始数据集经过SMOTE采样后根据各模型预测结果绘制的ROC曲线, 可以看出, SOMTE+XGBoost+FM模型的AUC在SMOTE采样情况下达到了97.5%, 预测效果最好. 对比图5可以看出, 在SMOTE采样后SOMTE+XGBoost+FM模型的AUC提升了1.8%. 表6为各模型在SMOTE采样情况下各模型预测的精确率、召回率、F1得分等结果. 通过对比表5和表6中的各项结果可以看出, 经过SMOTE采样后, 各模型failed类别预测的精确率、召回率、F1得分都得到了一定的提升, 各模型failed类别与pass类别预测的精确率、召回率、F1得分之间差异变小, 且各模型整体的预测准确率和AUC值等都有一定提升, 其中SOMTE+XGBoost+FM的准确率达到了92.7%, AUC达到了97.5%, 效果最好, 相比于SOMTE+XGBoost高出4.3%, 相比于SOMTE+FM高出11.7%.

综上所述, 通过SMOTE算法对原始数据集进行过采样能够有效均衡数据集中不平衡类别, 对XGBoost和FM进行融合可以取得较好的分类预测效果, 这是因为FM是一个复杂度为线性的模型, 可以很容易地处理大量数据. 但是尽管FM存在二阶特征交叉, 却无法进行更高阶特征交叉, 需要通过大量的特征工程才能得到改进. 特征决定了算法模型的预测效果上限, 不同的算法模型只是在逼近该上限的距离上有所不同. 然而, 人工特征工程既耗时又费力, 且最后效果往往不太理想. 因此, 本文通过XGBoost进行特征交叉, 生成新的高阶特征, 以弥补人工经验的不足, 充分挖掘特征之间的信息, 最后为避免特征信息丢失, 将新的特征与原始特征一起输入FM进行训练. 如图4, 图5以及表5, 表6所示, 相比于单一算法模型以及主流的机器学习模型, 本文所采用的SMOTE-XGBoost-FM模型分类预测效果更佳, 进一步验证了其在混合式教学下学生成绩分类预测中的适用性.

4 总结

本文针对混合式教学下产生的学习行为数据, 基于SHAP模型进行特征选择, 采用SMOTE算法平衡数据集不平衡类别, 融合XGBoost和FM模型, 并设置了6组对照实验对学生成绩分类预测进行了实证研究. 实验结果表明:

(1)采用SHAP模型特征选择和通过SMOTE算法平衡数据集不平衡类别可以有效提高模型的分类预测性能.

(2)相比与单一算法模型, XGBoost和FM融合模型对于学生成绩分类预测的效果更好, XGBoost+FM能够充分挖掘变量之间复杂的相互作用和非线性关系, SMOTE-XGBoost-FM分类预测的准确率和AUC值分别为92.7%和97.5%, 取得了最好的预测效果.

本文的研究成果可以帮助教育工作者提前发现未来可能出现学业问题的学生, 以及帮助学生在早期发现自己的不足. 考虑到学生学习行为数据具有时间序列因素, 从学习行为数据中挖掘出时序因素对学习效果的影响是下一步的工作.