复杂网络的经典定义, 是将具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络称为复杂网络[1]. 在现实生活中, 通信网络, 电力网络, 生物网络, 社会网络和经济网络等实际网络, 都可以称之为复杂网络, 它们都具有上述复杂网络的5种特性中的一种或多种. 这些网络系统中的成员可以表示为节点, 成员之间的交互关系可以表示为连接复杂网络因其节点, 连边, 以及其连接关系的复杂性而与现实中大量的物理系统相匹配. 例如, 神经系统可以看作大量神经细胞通过神经纤维相互连接形成的网络[2], 计算机网络可以看作是自主工作的计算机通过通信介质如光缆、双绞线、同轴电缆等相互连接形成的网络[2]. 复杂网络领域的研究关注于看上去互不相同的复杂网络之间的共性和处理它们的普适方法, 着眼于复杂网络的定量和定性特征的分析, 其中包含了统计力学、博弈论、动力系统等分支的概念、理论与方法, 常用的分析方法和工具包括图论、组合数学、矩阵理论、概率论、随机过程、优化理论等. 研究内容主要体现在网络结构复杂性, 节点复杂性, 结构与节点之间的相互影响以及网络之间的相互影响这4个方面[3].
(1) 网络结构复杂性可以理解为网络处于一个演化过程, 网络连接和网络拓扑结构会随着时间发生变化.
(2) 节点复杂性一方面可以理解为在一个网络中节点也存在复杂的时间演化行为; 另一方面, 在一个同质网络中相同类型的节点存在不同的重要程度和不同的类别; 再者, 在异质网络中, 类似于知识图谱, 则存在不同类型的节点.
(3) 结构与节点之间的相互影响意为网络结构会影响节点的行为, 同样, 节点的行为也会影响网络的结构.
(4) 网络之间的相互影响则表示在一个网络化社会中不同网络之间的相互联系. 如电网故障不仅会影响电力网络的稳定性, 也可能造成供水网络的故障, 金融机构的关闭等.
目前, 复杂网络领域的研究方向包括但不局限于复杂网络模型、网络性质、网络博弈、网络传播、网络同步与控制等.
为了理解网络结构与网络行为之间的关系使网络指导现实系统的规划和建设, 首先我们需要对网络的拓扑和特征结构有一定了解, 其关键在于对网络拓扑结构进行建模, 进而辅助更加深入的研究. 20世纪50年代末由Erdös和Rényi建立的随机图理论(random graph theory)被公认为是在数学上开创了复杂网络拓扑结构的系统性研究[4]. 随机图理论中的核心是随机图模型(ER随机图模型), 其建立在任意两点之间产生连边概率相同的前提下, 是第1个以概率描述复杂网络系统的模型. 1998年, Watts及其导师Strongatz针对实际网络中具有的小世界(small world, SW)数值特性[2]和聚类特征构建了WS小世界网络模型(SWWS)[2], 通过在规则初始环结构上对连边进行随机重连得到. 1999年, Newman和Watts提出的NW小世界网络模型(SWNW)则是在规则环结构的基础上通过随机添加连边得到的[5]. 同年, Barabási和Albert针对实际网络的幂律度分布特性(或无标度性)提出了BA无标度网络模型[6]. 无标度(scale free, SF)网络具有严重的异质性, 其各节点之间的连接状况(度数)具有严重的不均匀分布性: 网络中少数称之为Hub点的节点拥有极其多的连边, 而大多数节点只有很少量的连边. 少数Hub点对无标度网络的运行起着主导的作用, 该特性与大量的现实系统高度相似, 如互联网[7, 8]、蛋白质分子网络、科研合作网络等, 其度分布可用适当的幂律形式来描述. 而前述ER随机图和小世界模型其网络的度分布则可近似用泊松分布来表示.
网络性质的研究目前已经十分完善, 如无标度性[6]、小世界性[2]、社团性[9]. 这些研究不仅用于网络模型的构建, 也应用于实际网络中, 反映了社会现象, 如社交网络的小世界特性[2].
通过复杂网络建模, 模拟进化博弈, 可以将复杂网络应用于模拟人类社会中的竞争合作现象, 演化竞争与合作关系. 为了表达经济学和社会学中的利他主义和利己主义[10, 11], 研究人员提出的经典的进化博弈场景有: 囚徒困境、雪堆博弈、鹰鸽博弈、猎鹿博弈等. 以往的研究中发现不同结构的网络保持合作的能力不同, 如在博弈双方收益关系符合囚徒困境时, 正则三角形网格网络倾向于保持合作. 这些研究为某些社会现象提供了一定的解释.
复杂网络传播理论的研究涉及基本的流行病(生物病毒、计算机病毒、信息等)的传播模型的构建、网络传播动力学方程和传播临界值的构建与计算[12]、研究不同网络结构对于传播临界值的影响和本质原因等. 网络传播理论的研究有助于人们设计免疫策略, 鉴别超级传播节点, 预防并阻断流行病的传播等.
同步现象分为两种, 一种是大自然中存在的同步现象, 称为耦合作用形成的同步; 另一种是添加了控制之后形成的同步现象. 网络同步是网络科学中一个受到较多关注的研究领域[13-15]. 对复杂网络中同步现象的研究基于复杂动力网络模型. 复杂动力网络是刻画多个个体耦合的复杂系统模型, 每个个体均是一个动力系统, 并且个体之间存在特定的耦合关系. 因此, 模型有两个主要部分, 一是节点动力学, 二是网络结构. 控制复杂系统是人们对复杂系统模型结构及相关动力学进行研究的最终目标, 反映人们对复杂系统的认识能力[16]. 因此, 对于复杂网络的控制研究在近年来越来越受关注[16-21]. 宏观上讲, 控制表示指导和调节一个系统达到预期目标的功能或力量, 复杂网络的控制理论和方法源于经典控制理论与复杂系统研究的结合, 由于自身的复杂性特点使其又不同于经典控制论[22]. 网络控制技术和计算、通信技术的融合共同助力大型互联系统的形成.
在现有的研究中, 启发式算法被广泛用于解决复杂网络优化问题中, 如社团检测, 鲁棒性优化等. 且其依然有广大的研究与应用前景.
进化算法(evolutionary algorithm, EA)是一类模拟生物自然选择与自然进化的随机搜索算法, 因其适用于求解高度复杂的非线性问题而得到了非常广泛的应用, 同时它又具有较好的通用性. 在解决单个目标的复杂系统优化问题时, 进化算法的优势得以充分展现.
进化算法的研究可以追溯到20世纪60年代, 早期的研究旨在解决黑盒问题, 如设计自适应系统[23]、模式识别任务[24]和功能优化[25]. 这些问题没有明确答案甚至没有明确的定义. 1975年, De Jong等人对进化算法的概念进行了总结[26, 27]. 自此, 进化算法被广泛应用, 包括机器学习[28]、计算智能[29]和并行系统[30]等工程领域.
经典的优化算法中, 最普通的优化策略为穷举, 但计算成本十分昂贵. 爬山算法是一种基于贪心策略的算法, 简单但易陷入局部最优解中. 随机搜索算法中, 如模拟退火算法和禁忌搜索算法, 能避免陷入局部最优, 但是不能利用进化种群提供的信息实现并行搜索.
进化算法依赖于一组候选解. 这些候选解之间经过多代进化, 通过信息交换产生新的适应度更高的候选解. 进化算法的基本要素是: (1)变量编码; (2)初始种群集合; (3)适应度函数的设计; (4)遗传算子的设计; (5)控制参数的设置, 包括种群规模、进行遗传算子的概率等.
进化算法中的候选解称为个体, 一组个体称为一个种群. 算法循环执行以下步骤: (1)对种群中所有个体进行适应度评估; (2)从种群中选择进行繁殖的父代个体; (3)父代个体间进行信息交换, 生成子代个体; (4)通过幸存者选择机制(survivor selection mechanism)确定保留到下一代的个体. 如果此时满足终止条件, 则终止循环, 否则继续. 该过程类似于生物进化论中的“物竞天择, 适者生存”, 能够保留更适合解决方案的个体, 而淘汰哪些不具有竞争力的个体. 上述信息交换通过遗传算子执行, 包括选择、交叉和变异算子. 这些算子有助于搜索过程的收敛性, 并引导个体靠近最优解. 上述进化算法基本要素和遗传算子的具体内容如下[31].
(1) 编码: 经典的进化算法通过编码将需要优化的变量转换成可操作的表示形式. 如遗传算法中常用二进制编码, 可以加快处理速度. 但是, 大多数进化算法的实现并不依赖于这一特性. 其他编码方案包括使用实数和字符串. 一些实现要求编码字符串(也称为染色体)的长度是固定的, 而另一些实现允许可变长度的编码.
(2) 初始化: 初始种群通常是通过随机初始化创建的. 这样能减少初始种群中的偏差, 使候选解具备多样性. 由于种群的大小的有限的, 初始化偏差随着种群大小的减小而增大. 工程人员会针对具体问题具体分析, 使用领域知识设计更好的初始化方法.
(3) 适应度评估: 适应度通常被称为个体相对于整体的表现. 优化问题包括一个或多个目标函数, 这些目标函数用于测量单个个体的性能. 以不同的方式计算适应度, 来评估候选解相对于种群中其他个体的质量.
(4) 选择算子: 选择的目的是择优, 受达尔文进化论的启发, 通过选择更优秀的个体作为双亲, 使它们通过交叉算子得到的子代个体具有更高的适应度值. 经典的选择策略有适应度占比选择(fitness proportional selection)、排序选择(ranking selection)、轮盘赌(roulette wheel)和锦标赛选择(tournament selection). 最简单的实现方法是适应度占比选择, 首先计算种群中所有适应度值的总和
(5) 交叉算子: 交叉的概念可以被理解为信息的交换, 通常需要一对个体(双亲), 这对个体通过交换信息生成子代个体(类似于“基因重组”). 在经典的进化算法中, 交叉起着重要作用.
(6) 变异算子: 变异算子的实质是向个体注入新信息. 但是, 要确保引入新信息的来源, 以避免个体陷入局部最优状态. 以二进制编码为例, 随机选择个体的一位执行变异算子, 即改变该位的值(二进制编码中, 0变为1或1变为0), 生成一个新的个体.
(7) 幸存者选择: 通常根据个体的适应度值决定哪些个体可以进入下一代. 由于进化算法执行过程中, 种群大小一般固定不变, 所以, 常见的策略分为两种: 第1种策略直接从生成的子代个体中进行选择, 第2种策略则是从父代和子代中共同决定.
上述操作组成经典进化算法的基本成分. 单目标无约束优化问题的简单实现即为: 随机初始化种群; 对单个个体进行适应度评估; 通过选择算子选出一对双亲个体; 每一对双亲个体执行交叉算子生成子代个体; 子代个体执行变异算子; 评估子代个体的适应度值, 然后执行幸存者选择, 确定下一代的个体并重复上述步骤.
本文第1节为相关基础知识, 第2节针对不同任务详述其相关优化目标及实例, 第3节为多目标进化算法的性能评价指标, 第4节为实验, 第5节为总结与展望.
1 复杂网络和进化算法基本概述 1.1 复杂网络目前, 许多系统可以被抽象出来用复杂网络表示. 这既包含自然系统, 如蛋白质分子网络, 也包括人工系统, 如互联网、引文网络等. 在进行复杂网络建模时, 通常使用图论的知识来描述一个网络, 一个网络(或者一个图)由边集合和节点集合构成. 一般, 用符号
| aij={1,if存在连边(i,j)0,otherwise | (1) |
有权网络通过三元组
符号网络属于特殊的有权网络, 在符号网络中, 用+和–标记连边的两种相反的类型, 如社交网络中, 这两种连边被赋予“朋友”和“敌人”的含义.
1.2 经典单目标进化算法近年来, 在进化算法领域中, 一个流行的分支是模因算法(memetic algorithms, MA). “模因”的概念来自于Dawkins等人提出的“meme”, 它代表一个文化进化的单位, 可以表现出局部的精细化[32, 33]. 在进化算法中, 模因通常被认为是一个能够进行局部细化的个体学习过程. 因此, 进化算法成功地将全局搜索和局部搜索结合起来, 在许多问题上都比传统的进化算法更加高效和有效[34, 35]. 相比较进化算法, 模因算法增加了局部搜索算子. 一个简单的模因算法的流程如算法1所示.
算法1. 模因算法
输入: 初始个体
输出: 最佳候选解
初始化: 生成初始种群;
适应度评估: 对初始种群中每个个体进行适应度评估;
REPEAT
选择算子: 选择双亲个体;
交叉算子: 双亲个体进行信息交换;
局部搜索算子: 优化子代个体;
适应度评估: 评估新生成个体的适应度值;
幸存者选择: 选择保留到下一代的个体;
UNTIL (满足终止条件)
在进化算法中, 另一个常用的算法为粒子群优化算法(particle swarm optimization, PSO), 属于群体智能(swarm intelligence, SI)领域, 是一种启发式的全局优化算法. 粒子群算法通过一群粒子来搜索解空间. 这些粒子通过迭代更新它们的位置. 在每次迭代中, 粒子的移动方向由之前已知的最佳位置(
| {pbest(i,t)=argmink=1,2,⋯,tf(Pi(k)),i∈[1,2,⋯,Np]gbest=argmink=1,2,⋯,ti=1,2,⋯,Npf(Pi(k)) | (2) |
其中,
| {Vi(t+1)=ωVi(t)+c1r1(pbest(i,t)−Pi(t))+c2r2(gbest(i,t)−Pi(t))Pi(t+1)=Pi(t)+Vi(t+1) | (3) |
其中,
算法2. PSO算法
输入: 最小化目标函数
输出: 全局最优值
FOR 每个粒子
用
用
END FOR
REPEAT
FOR 每个粒子
在
IF
IF
END IF
END IF
UNTIL (满足终止条件)
1.3 经典多目标进化算法通常, 现实中的优化问题往往是多目标的, 且多个目标之间是相互作用且相互冲突的, 需要对相互冲突的子目标进行折衷(tradeoffs). 由此, 出现了多目标进化算法(multi-objective evolutionary algorithm, MOEA). 在不同的文献中, 将MOEA亦称为多目标遗传算法(multi-objective genetic algorithm, MOGA)以及进化多目标优化(evolutionary multi-objective optimization, EMOO)等[37].
多目标优化问题定义如下:
| minx∈ωF(x)=minx∈ω(f1(x),f2(x),⋯,fm(x)) | (4) |
其中,
| PS={x′∈ω|∄x∈ω,且F(x)≺F(x′)} | (5) |
同时, Pareto最优解集的映射称为Pareto最优前沿(Pareto-optimal front, PF),
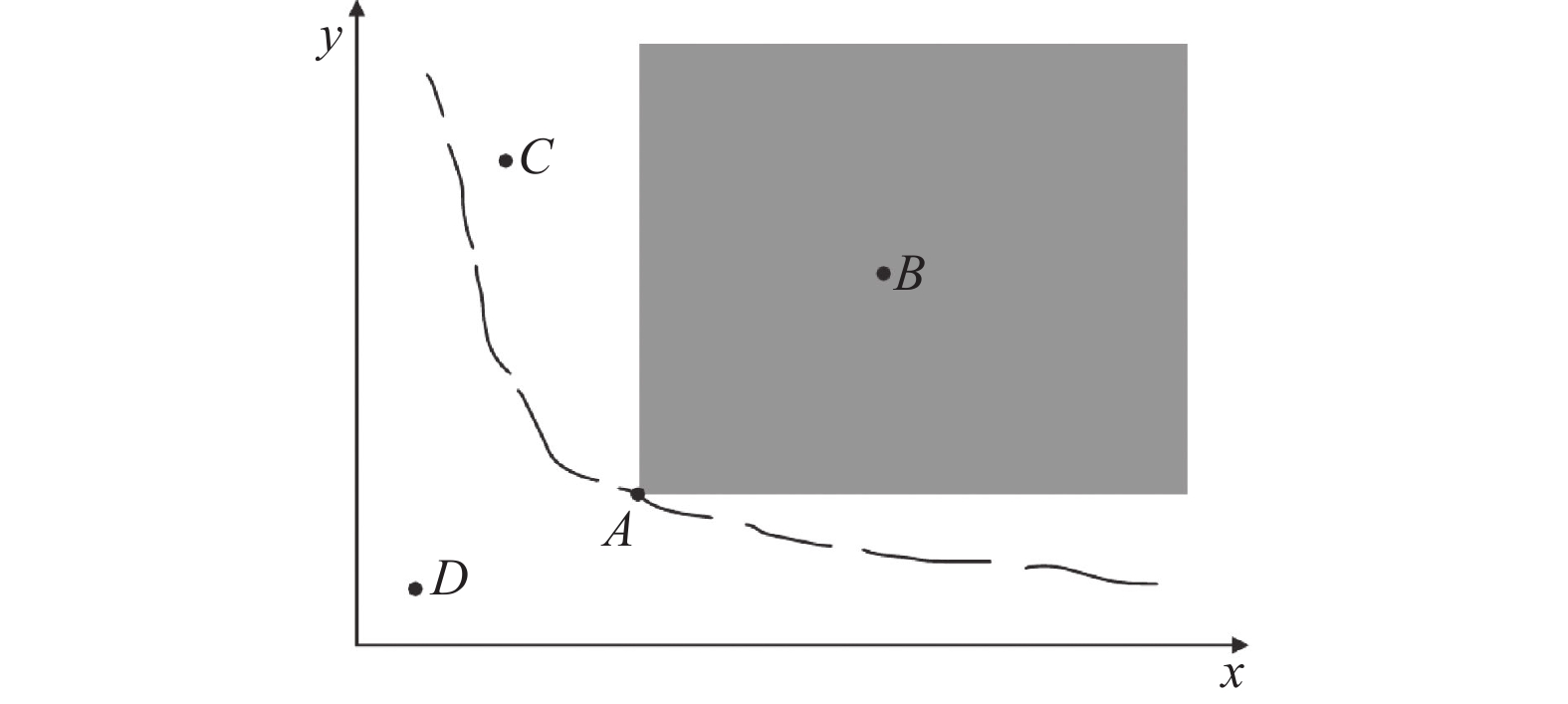
|
图 1 Pareto前沿示例 |
按进化机制的不同, MOEA可分为3类: 基于分解的MOEA (decomposition-based MOEA)、基于支配关系的MOEA (domination-based MOEA)和基于指标的MOEA (indicator-based MOEA)[37].
基于分解的MOEA: 其思想是将多目标问题通过组合函数(combine)或聚集函数(aggregate)转换为单目标问题. 聚集函数可以是线性的也可以是非线性的. 但聚集函数是线性的时候会出现很难找到非凸解的问题. 代表的算法有向量评价遗传算法(VEGA)[38]、MOEA/D[39]、MOEA/D-ACO[40].
基于支配关系的MOEA: 利用基于Pareto的适应度的分配策略, 从当前进化群体中找出所有的非支配个体, 该方法由Goldberg等人[41]提出. 代表进化算法有NSGA[42]、NSGA-II[43]、NSGA-III[44]、SPEA[45]、SPEA2[46]、MOGA[47]、NPGA[48]、PAES[49]、PESA[50]等.
基于指标的MOEA: 使用性能评价指标来引导搜索过程和对解的选择过程. 如Zitzler等人提出的IBEA[51], 使用一个任意的指标来评价并比较一对候选解的性能, 以及Bader和Zitzler提出的针对高维优化的一个快速计算的基于超体积指标的算法[52].
在上述算法中, MOEA/D得到了广泛的应用和改进, 其核心思想是将多目标优化问题分解为一组单目标子问题或多个多目标子问题, 利用子问题之间的邻域关系, 通过协作的方式同时优化所有子问题, 从而找到整个Pareto前沿的逼近. 一般, 子问题(
算法3. MOEA/D算法
输入: 初始个体
输出: 最优非支配解集
初始化精英种群
为权重向量集合
并标记其邻域为
初始化种群
初始化参考点
REPEAT
FOR每个
交叉算子: 从邻域
根据约束修正解
FOR每个
IF
更新邻域中的个体;
END IF
END FOR
更新
END FOR
UNTIL (满足终止条件)
算法3中,
目前, 多目标进化优化的研究方向主要包括方法研究, 理论研究和应用研究. 方法研究的内容包括但不限于高维MOP, 基于偏好的MOP, 动态MOP. MOEA的理论研究的内容有如收敛性分析, Pareto最优解集的构造方法, MOEA性能评价方法, MOEA测试及测试函数的构造方法等. MOEA应用研究则是将MOEA应用到不同的领域. 已有的研究成果中, MOEA已经应用到了机器学习、优化控制、数据挖掘、通信与网络优化等领域中[37].
2 进化算法在复杂网络中的应用进化算法常用于复杂网络中的3类任务: 社团检测、鲁棒性优化以及其他任务. 本节将根据不同任务进行详述.
2.1 社团检测任务及其相关优化目标在网络科学研究中, 如果某个网络中的节点可以轻易地被划分为若干个内部紧密连接的节点集(集合间可能重合), 那么就可以说这个网络具有社团结构[8]. 社团结构存在于各种不同的网络中, 如社交网络、生物网络、信息网络等. 网络中社团结构的检测问题称为社团检测问题(community detection problems, CDPs). 社团结构分为两类: 分离社团结构(separated community structure)和重叠社团结构(overlapped community structure). 其中分离社团结构中每个节点只会被划分到一个社团中, 而重叠社团结构中每个节点允许被划分到多个社团中.
社团检测是一个常用的分析策略, 复杂网络中的社团检测可以帮助人们更好地了解网络的组织结构. 其实际应用场景有如商品推荐[53], 疾病的预测和预防[54], 为高维数据集降维[55], 以及流行病的传播和控制[56, 57]. 通常, 社团检测问题被建模为优化问题. 由于优化问题一般为NP难问题. 因此, 出现了许多元启发式算法, 如遗传算法、模拟退火算法和协同进化算法.
通常的社团检测任务针对无向无权网络, 对于有向网络通常选择忽略连边方向, 但与此同时也丢失了有向边提供的额外信息. 在有权网络中, 连边权重被认为是两个节点之间关系强弱的度量, 因此社团检测任务可以轻松地适应有权网络.
社团检测任务的常见优化目标如下.
(1)标准化互信息(normalized mutual information,
| NMI(X,Y)=−2∑cXi=1∑cYj=1Nijlog(NijNNi.N.j)∑cXi=1Ni.log(Ni.N)+∑cYj=1N.jlog(N.jN) | (6) |
其中,
(2)模块化值(modularity,
| Q=12M∑i,j(Aij−Pij)δ(Ci,Cj) | (7) |
其中,
有向网络的社团结构模块化值[61]定义如下:
| QD=12M∑i,j(Aij−koutikinjM)δ(Ci,Cj) | (8) |
其中,
对于有权的无符号网络, 使用权重和代替度数, 公式定义如下:
| QW=12M∑i,j(wij−wiwj2w)δ(Ci,Cj) | (9) |
其中,
对于符号网络, 文献[62]中提出如下公式, 其正边和负边需要分别计算.
| QS=12w++2w−∑i,j(wij−(w+iw+j2w+−w−iw−j2w−))δ(Ci,Cj) | (10) |
其中,
文献[63]将模块化值的概念扩展到了重叠社团结构中, 公式定义如下:
| QO=12M∑C∑i,j∈C1OiOj(Aij−kikj2M) | (11) |
其中,
此外, 文献[64]提出了适用于具有重叠社团结构的符号网络的模块化值, 定义如下:
| QSO=12w++2w−∑C∑i,j∈C1OiOj(wij−(w+iw+j2w+−w−iw−j2w−)) | (12) |
但是模块化值被文献[65]证实具有局限性, 当模块化值无法识别小于一定规模的社团结构, 而该规模的大小取决于网络自身的大小和社团结构之间的互连程度.
(3) Ratio association (
| {RA=m∑i=1L(Vi,Vi)|Vi|RC=m∑i=1(L(Vi,¯Vi)|Vi|) | (13) |
(4)核K均值(kernel K-means,
| KKM=2(N−m)−m∑i=1(L(Vi,Vi)|Vi|) | (14) |
(5)模块化密度(modularity density, D): 针对模块化值没有考虑到社团中节点的数量的问题, Li等人提出了一种新的评价网络社团划分的量化指标, 称为模块化密度[67]. 其公式定义如下:
| D=m∑i=1L(Vi,Vi)−L(Vi,¯Vi)|Vi|=RA−RC | (15) |
最大化
(6)紧密度(tightness,
| T(C)=SinCSinC+SoutC | (16) |
其中,
| {SinC=∑u∈C,v∈C,u,v∈Es(u,v)SoutC=∑u∈C,v∈¯C,u,v∈Es(u,v)s(u,v)=∑x∈Γ(u)∩Γ(v)wux×wvx√∑x∈Γ(u)w2ux√∑x∈Γ(v)w2vx |
其中,
文献[64]基于社会平衡理论[69]将紧密度扩展到符号网络中, 公式定义如下:
| TS(C)=Sin+C−Sin−CSin+C−Sin−C+Sout+C | (17) |
其中,
| {Sin+C=∑u,v∈C,(u,v)∈Emax(ssigned(u,v),0)Sout+C=∑u∈C,v∈¯C,(u,v)∈Emax(ssigned(u,v),0)Sin−C=∑u,v∈C,(u,v)∈Emin(ssigned(u,v),0)ssigned(u,v)=∑x∈Γ(u)∩Γ(v)ψ(x)√∑x∈Γ(u)w2ux√∑x∈Γ(v)w2vxψ(x)={0,if wux⩽0,wvx⩽0wux×wvx,otherwise |
其中,
单目标优化方法是现有研究中解决社团检测问题的一个关键思路. 如, Pizzuti[70]提出了一种基于遗传算法的方法, 称为GA-Net, 用于社交网络中的社团检测. Gong等人提出了一种社团检测方法, 称为Meme-Net, 通过模因算法来优化网络模块化密度[71]. Cai等人[72, 73]设计了用于社团检测的离散粒子群优化(discrete particle swarm optimization)算法. 为提高遗传算法的空间搜索能力, Bui等人提出了一种基于模式预处理阶段的图划分遗传算法[74]. Talbi等人针对图划分问题提出了一种并行遗传算法, 该算法具有超线性加速[75]的特性. Tasgin等人使用一种基于模块化值的遗传算法来检测社团[76]. Gog等人提出了一种基于种群中个体间信息共享极值的新型协作进化算法[77].
为了避免单目标优化算法陷入局部最优的缺点, 许多多目标社团检测方法被提出. 如Pizzuti提出的多目标遗传算法(MOGA-Net)通过两个目标函数分别最大化社团内部连接和最小化社团间的连接来发现社团结构[78]. Shi等人提出了一个两阶段的多目标社团检测的框架(MOCD), 并基于此框架提出一种多目标进化算法寻找有效解[79]. Shi等人同样分析了11种与社团检测任务相关的目标函数间的相关性, 并指出对一对负相关的目标进行多目标优化的结果要优于对任意一个原始目标进行单目标优化的结果[80]. Gong等人使用基于分解的多目标进化算法, 提出了用于社团检测的方法(MOEA/D-Net), 将
本节的鲁棒性优化任务中, 鲁棒性分为连通性鲁棒性和能控性鲁棒性两种, 二者对于复杂网络的不同应用场景均有重要意义. 复杂网络通过演化动力学研究网络的鲁棒性, 鲁棒性是指发生蓄意攻击或内部错误时, 系统保持其原有功能的能力. 鲁棒性的研究对于系统设计而言具有指导意义, 能够有效抵抗未知错误和攻击的健壮系统已经成为迫切的需要. 近年来, 人们已经从不同的角度提出了评估网络的鲁棒性的方法. 1994年, Merris提出了基于拉普拉斯矩阵[89]特征值的方法; 2000年, Albert等人[90]从图论的角度提出了鲁棒性度量方法, 利用网络解体(network disintegration)过程中最大联通分支的数值表现来评价网络在去除部分顶点或连边后的性能. 此外, 针对不同攻击方式, 也提出了相应的评级指标. 如, 在随机攻击中, 每次以等概率删除一个节点或一条连边[90]; 在蓄意攻击中, 节点或连边按照某种性质进行排序, 然后删除最重要的节点或连边, 最后根据实际情况判断删除后是否需要重新计算重要度[91].
鲁棒性优化任务相关的目标具体如下.
(1)连通性鲁棒性(connectivity robustness,
| R=1N∑NQ=1s(Q) | (18) |
现有的研究中, 针对网络鲁棒性的优化通常在某种结构约束(如保持节点度分布不变)下, 通过拓扑重连来提高网络的鲁棒性. 常用的算法包括贪心算法[92]、模拟退火算法[93]和进化算法[94].
(2)能控性(controllability): 复杂网络能控性的概念由Kalman在1960年首先提出[95, 96], 目前已成为复杂网络研究的一个核心问题. 能控性的概念是指在有限时间内, 通过适当的控制输入, 控制网络从任意初始状态到达一个目标状态的能力[22]. 对于一个复杂网络系统或线性时不变(linear time-invariant, LTI)系统, 满足
控制节点数(
复杂网络能控性一般可以通过控制节点的密度
(3)能控性鲁棒性(controllability robustness,
通常, 能控性鲁棒性计算基于能控性曲线, 它由一组能控性值的序列组成, 通过计算系统遭受节点或连边攻击后, 剩余网络的能控性得到. 由于伴随攻击过程, 网络能控性是动态变化的. 因此, 网络整体的能控性鲁棒性为控制节点密度(
| Rc=1N∑N−1i=0nND(i) | (19) |
网络拥有较小的
(4)可控的鲁棒性(controllable robustness,
| CR=1N∑Nq=1s(q)ND(q) | (20) |
其中,
(5)社团鲁棒性(community robustness,
| Rcom=1N∑Nq=1[1k∑kp=1SpqSp] | (21) |
其中,
(6)互依网络中的社团鲁棒性(
| Rintercom=1LmaxLmax∑l=1fcom(Gl)=1LmaxLmax∑l=1Nl∑q=11Nl[1klkl∑p=1SpqSp] | (22) |
其中,
(7)针对连边攻击的社团鲁棒性(
| Rl=1M∑Ml=1s(l) | (23) |
其中,
| RlNMI=1M∑Ml=1NMI(Cl,Cori) | (24) |
其中,
(8)节点抵御级联故障的能力: 文献[110]根据节点度提出节点的负载
| {Ci=βLiLi=kαi | (25) |
其中, 参数
(9)网络抵抗级联故障的能力: 在以往的研究中, 为了提高网络抗级联故障的鲁棒性, 一种方法是区分系统中最脆弱的节点并保护它们不受故障影响. 另一种方法则是拓扑重连, 在文献[111]中通过进化算法得到对级联故障具有更好抵御能力的网络. 文献[112]中设计了一种模因算法(memetic algorithm), 并发现以高概率连接负载相似的节点有助于增强网络对级联故障的鲁棒性. 文献[109]中扩展了网络抵抗级联失效模型的衡量指标, 定义如下:
| Rcf=1N∑Tt=1st | (26) |
其中,
(10)结构平衡的网络的鲁棒性: 文献[113]提出了基于社会心理学领域的结构平衡理论, 文献[114]将其扩展为广义的图论版本, 指出当一个网络可以被划分为几个簇(cluster), 簇内节点之间是正的连接关系, 簇间节点之间是负的连接关系时, 这个网络被认为是平衡的. 通常基于符号网络来研究网络的结构平衡, 平衡网络中的有效连边同时被分为两类: 簇间负关系连边和簇内正关系连边. 文献[115]中通过攻击网络中簇间有效连边后, 最大连通分量的大小来衡量结构平衡的网络簇间鲁棒性, 公式定义如下:
| Rinter=1M∑e∈Enegas(e) | (27) |
同样, 文献[115]中通过攻击网络中簇内有效连边后, 最大连通分量的大小来衡量结构平衡的网络簇内鲁棒性, 公式定义如下:
| Rintra=1M∑e∈Eposis(e) | (28) |
其中,
针对鲁棒性优化任务, 有许多单目标优化的文章. 如, 文献[116]使用代理模型辅助完成网络连通性鲁棒性的优化, 目的是减少网络鲁棒性优化过程的计算成本, 提出了GE-SU-EAnet. 首先, 通过图嵌入方法训练网络的数值化表示, 同时, 使用3种代理模型完成网络的性能预测过程, 得到网络适应度估计器. 在模型管理策略的帮助下, 分别对网络的初始化, 变异, 决策(局部搜索)过程进行管控. 结合图嵌入信息和鲁棒性评价指标, 利用代理模型对鲁棒性进行预测, 既考虑了真实评估因子, 也考虑了代理模型来引导整个优化过程. 在互依网络中, 由于存在多层结构, 不同层之间存在连接, 导致某层遭到蓄意攻击时, 会造成整个互依网络上的级联故障. 针对互依网络面临的蓄意攻击, 文献[117]提出了一种模因算法通过优化网络内部连接增强互依网络的连通性鲁棒性. 对于互依网络中的社团鲁棒性优化问题, 文献[103]设计了一个鲁棒性评测方法, 即
同时, 也有许多文章对网络的鲁棒性进行多目标优化. 文献[109]综合考虑了系统可能遇到的蓄意攻击和级联故障, 提出MAGA-NetR算法. 优化过程在一个网格网络(lattice)中实现. 优化目标中, 网络抵抗蓄意攻击的能力通过
本节介绍了两种复杂网络中的优化任务, 其一是博弈论中的合作能力, 其二是寻找网络中最具传播影响力的节点集合. 以下为二者的详述.
(1)合作: 合作是指人类社会在进化博弈过程中的合作现象. 合作性就是指在网络博弈演化趋于稳定时, 网络保存合作者的能力. 合作强调了个体行为, 其广泛存在于社会困境和经济活动中. 保持合作者和叛逃者之间的平衡不仅对系统的稳定和和谐很重要, 对于决策者来说也是必要的. 如在经济学上, 不同的公司可以选择相互合作或竞争. 合作过多可能会导致缺乏创新, 导致行业在海外市场中的竞争力下降, 对金融动荡的抵抗力下降, 而合作过少可能会形成恶性竞争, 也不利于行业的健康发展[120]. 因此, 对于行业监管机构来说, 合作和竞争之间达到平衡是相当重要的. 此前的研究将进化博弈与复杂网络理论结合在一起[121-124], 通过仿真模拟博弈演化过程, 并发现不同结构的网络具有不同的能力来保存合作者.
(2)节点的影响力: 为了模拟网络中节点的影响力传播过程, 许多研究提出了影响力传播模型, 如IC (independent cascade)模型[125]、WC (weighted cascade)模型[126]以及LT (linear threshold)模型[127]. 针对社交网络中的影响力最大化问题(influence maximization problem), 文献[128]基于IC模型设计了一种算法, 通过寻找k-种子集(k-seed set), 最大化社交网络中的影响力. 即在给定参数
由于复杂网络中的鲁棒性和合作性在现实应用和理论分析中都具有重要意义. 然而, 已有研究表明, 在网络结构上, 鲁棒性和合作性是相互冲突的. 因此, 在演化博弈模型的基础上, 许多文章对合作能力与鲁棒性进行共同优化. 对于鲁棒性而言, 同配的网络结构或异质性低的网络结构对于攻击和错误有更高的抵御能力[92,129], 但这种结构限制了合作者的出现[122, 123]. 为了构建鲁棒且能保证合作能力的网络系统, 文献[130]对
关于寻找最具影响力的节点集合任务, 文献[132]在文献[125]的基础上, 将模拟影响力传播过程的模型扩展到复用网络(multiplex networks)中, 利用模因算法寻找复用网络中影响力最大的节点集合. 该实验有助于在复用网络中识别潜在的传播者, 为深入了解和分析网络提供了思路.
2.4 优化目标替代指标在复杂网络中, 除了上述优化目标外, 还有其他性能评价指标, 有时也可以作为优化目标的替代指标.
(1)谱分析方法(spectral measures): 基于网络拉普拉斯矩阵或邻接矩阵特征值的谱分析方法是一种经典的鲁棒性评价方法. 本文将详细介绍谱半径(spectral radius,
| SR=λ1 | (29) |
| SG=λ1−λ2 | (30) |
| ACo=μ2,μ1⩽μ2⩽⋯⩽μN | (31) |
其中,
| NCo=ln(1N∑Ni=1eλi) | (32) |
在给定节点数的情况下, 孤立图(没有连边)的自然连通度最小, 完全图的
| ERe=12N∑i,jEReij=NN∑i=21μi | (33) |
| STC=1N∏Ni=2μi | (34) |
(2)同配性(assortativity,
| r=|E|−1∑∀⟨i,j⟩∈Ekikj−[|E|−1∑∀⟨i,j⟩∈E12(ki+kj)]2|E|−1∑∀⟨i,j⟩∈E12(k2i+k2j)−[|E|−1∑∀⟨i,j⟩∈E12(ki+kj)]2 | (35) |
(3)异质性(heterogeneity,
| H=∑Ni=1∑Nj=1|ki−kj|2N2⟨k⟩ | (36) |
在对复杂网络进行进化优化时, 不同网络在不同情境下的表示方式有所不同.
(1)普通的无权网络通常用邻接矩阵
(2)有权网络中则用权重矩阵
(3)社团检测任务中通常采用直接表示方式, 每个社团由
(4)使用图嵌入方法获取图中节点的特征表示时, 通常可以得到节点特征的降维表示, 将输出结果喂入下游学习任务可以大大减少参数量. 文献[148]中提出, 网络表示学习方法从算法的角度可以归纳为5类: 基于矩阵分解的算法, 如HOPE[149], LANE[150]; 基于游走启发的算法, 如DeepWalk[151], node2vec[152]; 基于连边建模的方法, 如LINE[153]算法, 直接从顶点与顶点的连边中学习顶点表示; 基于深度学习的算法, 如SDNE[154], 为了提取复杂结构的特称, 学习高度非线性的定点表示; 最后一种是混合方法, 混合使用上述方法来学习顶点表示, 如HARP[155]利用了基于随机游走的方法(DeepWalk和node2vec)和基于连边建模的方法(LINE)学习从小样本网络到原始网络的顶点表示.
3 MOEA性能评价指标通常评价一个多目标进化算法的性能从两个方面: 算法的效果与算法的效率. 算法的效果通过其所求Pareto最优解集的质量进行判断, 主要看算法的收敛性和分布; 算法效率是指其求解多目标优化问题的时间复杂度和空间复杂度. 此外, 多目标优化算法的鲁棒性、泛化能力等也是衡量其性能的重要指标. 同样, 评价MOEA的性能有两类方法: 理论分析和实验分析. 理论分析可以解决算法的运行效率和收敛性; 实验分析可以对算法的性能进行测试和比较. 实践中, 两种方法可以结合使用来评价一个MOEA的性能[37].
目前, 研究者归纳出来的MOEA性能评价方法或工具主要分为3类: 第1类用于评价所求解集和真正Pareto最优面的趋近程度, 即评价MOEA的收敛性; 第2类用于评价解集的分布性; 第3类综合考虑解集的收敛性和分布性, 作为综合评价指标. 表1为MOEA性能评价指标分类表.
| 表 1 MOEA性能评价指标分类表 |
3.1 收敛性评价指标
收敛性评价方法主要通过
(1)错误率(error ratio,
| ER=∑ni=1ein | (37) |
其中,
| ei={0,if向量Xi∈PFtrue(i∈{1,2,⋯,n})1,otherwise |
(2)覆盖率(coverage,
| C(P(1),P(2))=|{a(2)∈P(2)}|∃a(1)∈P(1),a(1)≺a(2)||P(2)| | (38) |
若
(3)世代距离(generational distance,
| GD=(∑ni=1dpi)1pn | (39) |
其中,
(4)高维空间及其比率(hyperarea,
| HA={∪iai|vi∈PFknown} | (40) |
其中,
| HAR=H1H2 | (41) |
其中,
多样性评价指标衡量解集的分布性和延展性. 当解集分布均匀时, 称其具有良好的分布性; 若解集在Pareto前沿分布过于稀疏, 称其具有较差的延展性.
(1)空间评价方法(spacing metric,
| Δ=∑|PF|i=1di−¯d|PF| | (42) |
其中,
| Δ′=√1n−1∑ni=1(¯d−di)2 | (43) |
其中,
(2)分布广度指标(spread indicator,
综合评价指标能同时反应MOEA的收敛性和多样性, 最为广泛应用的综合评价指标为超体积评价指标(hypervolume,
(1)
| HV=λ(|PF|∪i=1vi) | (44) |
其中,
(2)
| IGD=∑ˉj∈PFdˉj′n | (45) |
其中,
实验部分由3部分组成: 多目标优化实验、单目标优化与多目标优化对比实验以及部分鲁棒性相关目标的皮尔森相关性实验. 具体内容详述如下.
4.1 多目标优化实验多目标优化实验在Wang等人提出的SP-RV-MOEANet[119]的基础上完成. 实验将网络在节点度攻击下的连通性鲁棒性(
SP-RV-MOEANet利用图自编码器(SDNE[154])获得网络的数值化表示, 通过代理模型对网络的性能进行评价, 获得鲁棒性预测值, 利用3个代理模型(RBF[164], LS[165], IDW[166])提供的不确定信息选择更优的解. MOEA/D0模型则是仅使用MOEA/D多目标进化算法, 不使用任何代理模型. MOEA/DRBF, MOEA/DLS和MOEA/DIDW则是仅使用一种代理模型. 上述5个模型分别对节点数为200, 平均度为5的SF网络和SW网络进行优化, 最终得到的Pareto前沿如图2所示,
| 表 2 多目标优化实验设计 |
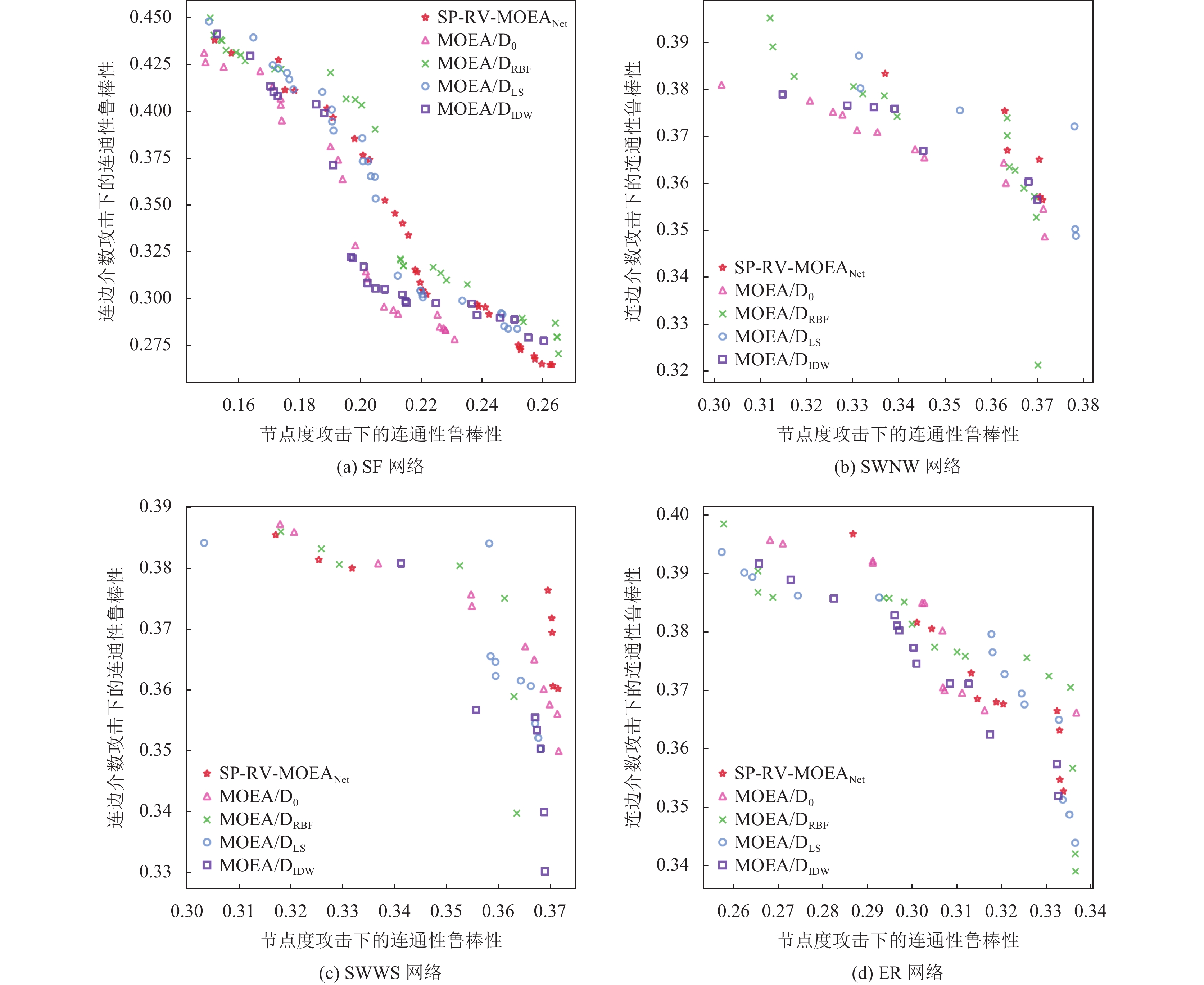
|
图 2 多目标优化Pareto前沿 |

|
图 3 |
结果表明: 在使用代理模型之后, 目标优化过程所需要的运行时间大大缩短, 而且最终得到的非支配解集比不使用代理模型得到的结果更优MOEA/DRBF, MOEA/DLS和MOEA/DIDW虽然仅使用一个代理模型, 不能提供不确定信息, 但是结果表现并不逊色于使用了3个代理模型的SP-RV-MOEANet.
4.2 单目标优化与多目标优化对比实验实验以BA模型构建的SF网络为例, 同样将
分别对
图5将多目标优化
在复杂网络的目标优化的研究中, 文献[130, 131]将优化目标之间的皮尔森相关性为强负相关作为多目标优化的依据. 据此, 本实验分别对以BA模型构建的SF网络、ER网络以及WS模型构建的SW网络进行优化目标之间的皮尔森相关性系数的研究. 选用的优化目标及其符号说明如表5所示, 实验结果如图6所示. 结果显示, 这些优化目标之间并不存在完全的正相关关系, 但是也没有强负相关的关系, 大部分目标间的皮尔森相关性都小于0.4. 然而从单目标优化与多目标优化对比实验结果中, 可以看出多目标优化可以在一对相关性不那么强的目标中找到它们的权衡解. 因此, 于研究人员而言可以对任意一对目标进行多目标优化, 均能得到Pareto前沿, 且能为决策者带来更多选择, 但其是否具有现实意义, 要求研究人员从实际出发, 具体情况具体分析.
| 表 3 多目标优化实验运行时间 |
| 表 4 实验参数 |
5 总结与展望
本文阐述了复杂网络领域的前沿发展以及进化算法在复杂网络优化领域的应用. 具体来说包括复杂网络与进化算法的概述、常用的算法框架及其进展、针对不同任务的单目标优化和多目标优化的应用、多目标算法的性能评价指标. 实验部分则是进一步让读者对进化算法在复杂网络中的应用有更加深入的了解, 3个实验循序渐进, 希望能够对读者带来一定的思考和启发. 本文对进化算法在复杂网络中的应用有以下几点的展望.

|
图 4 单目标优化的连通性鲁棒性 |

|
图 5 多目标优化vs. 单目标优化 |
| 表 5 优化目标及其对应符号 |
(1)应用场景: 目前, 优化算法在复杂网络中已经有了很多的应用, 但是当前研究的方向大多着眼于网络社团检测, 网络合作与传播能力优化和网络结构鲁棒性优化, 并没有拓展到更多具有现实意义的目标中. 因此, 结合现实的复杂系统需求, 寻找更多具有现实意义的网络结构依然有很大的研究空间.
(2)优化目标: 本文中复杂网络优化目标间皮尔森相关性实验探究了以连通性鲁棒性和能控性鲁棒性为主的多种目标之间的数值相关性, 可以发现不同拓扑结构的复杂网络的各目标间都有不同的相关性表现, 使得设计满足不同现实需求. 实验结果中尽管没有强负相关的两个目标, 但是通过多目标优化, 仍能找到Pareto前沿, 这保证了优化工作的可行性.
(3)代理模型: 由于优化过程需要大量计算, 时耗很高, 因此有许多研究通过代理模型来减少大量的计算. 在今后的研究中, 也可以尝试通过深度学习来加速优化过程. 在文献[167]中, Lou等人首次设计了一个卷积神经网络结构(convolutional neural network, CNN), 称为PCR, 以用于复杂网络能控性鲁棒性的计算, 该方法保证了极低计算误差的同时, 将能控性鲁棒性的计算速度提高了近一百倍. 同时文献[167]也验证了深度学习方法论在复杂网络能控性鲁棒性研究中的可行性. 后续Lou等人在实验中发现复杂网络的能控性鲁棒性表现和其拓扑结构相对独立. 但不同的高阶网络模型表现了不同的鲁棒性. 因此提出iPCR[168], 设计了一个由多个CNN结构组成的鲁棒性预测器, 在PCR的基础上应用更多的网络的先验知识, 进一步提高了鲁棒性预测的精度. 后续, 深度学习方法也被应用到了连通性鲁棒性的预测等方面[169], 取得了不错的成果. 然而鉴于深度神经网络对输入大小固定的局限, 以上方法难以用于处理具有不同大小的网络. 因此Lou等人改进了Patchy-SAN算法[170], 提出了LFR-CNN[171], 通过对关键节点的采样, 邻域构建等步骤对网络建立特征图以进行鲁棒性预测, 在不同输入大小的网络上依然保证了较高的准确度. 基于此, 可以将上述工作作为代理模型来加速优化过程中涉及的大量计算的任务.
在之后的研究中, 不仅可以对优化目标进行扩展以优化现有复杂网络的拓扑结构, 同样可以对启发式进化算法框架进行设计, 也可以使用不同的策略来加速目标的优化过程, 如加入代理模型以降低大量重复的高计算消耗过程, 以及优化前进行图嵌入降低数据处理维度等. 当前进化算法已有了一个比较普遍的框架, 但其中各部分步骤依然存在优化的潜力, 在MOEA系算法中各类优化向我们展示了进化算法的研究空间和领域的活力. 基于多目标进化算法的复杂网络优化问题的研究已经建立起一定的理论基础, 但同时仍有更多的研究方向可供探索.

|
图 6 皮尔森相关性系数 |
| [1] |
佘振苏, 倪志勇. 钱学森复杂系统思想的理论探索与实践. 党政干部学刊, 2011(1): 8-13. DOI:10.3969/j.issn.1672-2426.2011.01.002 |
| [2] |
Watts DJ, Strogatz SH. Collective dynamics of ‘small-world’ networks. Nature, 1998, 393(6684): 440-442. DOI:10.1038/30918 |
| [3] |
汪小帆, 李翔, 陈关荣. 网络科学导论. 北京: 高等教育出版社, 2012.
|
| [4] |
Erdős P, Rényi A. On the evolution of random graphs. Publications of the Mathematical Institute of the Hungarian Academy of Sciences, 1960, 5(1): 17-60. |
| [5] |
Newman MEJ, Watts DJ. Renormalization group analysis of the small-world network model. Physics Letters A, 1999, 263(4–6): 341–346.
|
| [6] |
Barabási AL, Albert R. Emergence of scaling in random networks. Science, 1999, 286(5439): 509-512. DOI:10.1126/science.286.5439.509 |
| [7] |
Adamic LA, Huberman BA. Power-law distribution of the world wide Web. Science, 2000, 287(5461): 2115-2115. DOI:10.1126/science.287.5461.2115a |
| [8] |
Doyle JC, Alderson DL, Li L, et al. The “robust yet fragile” nature of the Internet. Proceedings of the National Academy of Sciences of the United States of America, 2005, 102(41): 14497-14502. DOI:10.1073/pnas.0501426102 |
| [9] |
Girvan M, Newman MEJ. Community structure in social and biological networks. Proceedings of the National Academy of Sciences of the United States of America, 2002, 99(12): 7821-7826. DOI:10.1073/pnas.122653799 |
| [10] |
Axelrod R, Hamilton WD. The evolution of cooperation. Science, 1981, 211(4489): 1390-1396. DOI:10.1126/science.7466396 |
| [11] |
Nowak MA, May RM. Evolutionary games and spatial chaos. Nature, 1992, 359(6398): 826-829. DOI:10.1038/359826a0 |
| [12] |
Pastor-Satorras R, Vespignani A. Immunization of complex networks. Physical Review E, 2002, 65(3): 036104. DOI:10.1103/PhysRevE.65.036104 |
| [13] |
Wang XF. Complex networks: Topology, dynamics and synchronization. International Journal of Bifurcation and Chaos, 2002, 12(5): 885-916. DOI:10.1142/S0218127402004802 |
| [14] |
Chen GR, Wang XF, Li X, et al. Some recent advances in complex networks synchronization. In: Kyamakya K, Halang WA, Unger H, et al., eds. Recent Advances in Nonlinear Dynamics and Synchronization. Berlin: Springer, 2009. 3–16.
|
| [15] |
Arenas A, Dı́az-Guilera A, Kurths J, et al. Synchronization in complex networks. Physics Reports, 2008, 469(3): 93-153. DOI:10.1016/j.physrep.2008.09.002 |
| [16] |
Liu YY, Slotine JJ, Barabási AL. Controllability of complex networks. Nature, 2011, 473(7346): 167-173. DOI:10.1038/nature10011 |
| [17] |
Lombardi A, Hörnquist M. Controllability analysis of networks. Physical Review E, 2007, 75(5): 056110. DOI:10.1103/PhysRevE.75.056110 |
| [18] |
Wang XF, Chen GR. Pinning control of scale-free dynamical networks. Physica A: Statistical Mechanics and Its Applications, 2002, 310(3–4): 521–531.
|
| [19] |
Chen GR. Pinning control and controllability of complex dynamical networks. International Journal of Automation and Computing, 2017, 14(1): 1-9. DOI:10.1007/s11633-016-1052-9 |
| [20] |
陈关荣. 复杂动态网络环境下控制理论遇到的问题与挑战. 自动化学报, 2013, 39(4): 312–321.
|
| [21] |
Chen GR. Pinning control and synchronization on complex dynamical networks. International Journal of Control, Automation and Systems, 2014, 12(2): 221-230. DOI:10.1007/s12555-014-9001-2 |
| [22] |
侯绿林, 老松杨, 肖延东, 等. 复杂网络可控性研究现状综述. 物理学报, 2015, 64(18): 188901. DOI:10.7498/aps.64.188901 |
| [23] |
Bagley JD. The behavior of adaptive systems which employ genetic and correlation algorithms [Ph.D. thesis]. Pittsburgh: University of Michigan, 1967.
|
| [24] |
Cavicchio DJ. Adaptive search using simulated evolution [Ph.D. thesis]. Ann Arbor: University of Michigan, 1970.
|
| [25] |
Hollstien RB. Artificial genetic adaptation in computer control systems [Ph.D. thesis]. Ann Arbor: University of Michigan, 1971.
|
| [26] |
De Jong KA. An analysis of the behavior of a class of genetic adaptive systems [Ph.D. Thesis]. Ann Arbor: University of Michigan, 1975.
|
| [27] |
Holland JH. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence. Cambridge: MIT Press, 1992.
|
| [28] |
Shapiro J. Genetic algorithms in machine learning. In: Paliouras G, Karkaletsis V, Spyropoulos CD, eds. Advanced Course on Artificial Intelligence. Berlin: Springer, 2001. 146–168.
|
| [29] |
De Castro LN, Von Zuben FJ. Artificial immune systems: Part I–Basic theory and applications. Technical Report, São Paulo: Universidade Estadual de Campinas, 1999.
|
| [30] |
Stender J. Parallel Genetic Algorithms: Theory and Applications. Amsterdam: IOS Press, 1993. 14.
|
| [31] |
Liu J, Abbass HA, Tan KC. Evolutionary Computation and Complex Networks. Cham: Springer, 2019.
|
| [32] |
Moscato P. On evolution, search, optimization, genetic algorithms and martial arts: Towards memetic algorithms. Caltech concurrent computation program, C3P Report, 1989, 826(1989): 37.
|
| [33] |
Dawkins R, Davis N. The Selfish Gene. Macat Library, 2017.
|
| [34] |
Krasnogor N, Smith J. A tutorial for competent memetic algorithms: Model, taxonomy, and design issues. IEEE Transactions on Evolutionary Computation, 2005, 9(5): 474-488. DOI:10.1109/TEVC.2005.850260 |
| [35] |
Ong YS, Keane AJ. Meta-Lamarckian learning in memetic algorithms. IEEE Transactions on Evolutionary Computation, 2004, 8(2): 99-110. DOI:10.1109/TEVC.2003.819944 |
| [36] |
Zhang YD, Balochian S, Agarwal P, et al. Artificial intelligence and its applications. Mathematical Problems in Engineering, 2014, 2014: 840491. |
| [37] |
郑金华, 邹娟. 多目标进化优化. 北京: 科学出版社, 2017.
|
| [38] |
Schaffer JD. Some experiments in machine learning using vector evaluated genetic algorithms [Ph.D. thesis]. Nashville: Vanderbilt University, 1984.
|
| [39] |
Zhang QF, Li H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712-731. DOI:10.1109/TEVC.2007.892759 |
| [40] |
Ke LJ, Zhang QF, Battiti R. MOEA/D-ACO: A multiobjective evolutionary algorithm using decomposition and antcolony. IEEE Transactions on Cybernetics, 2013, 43(6): 1845-1859. DOI:10.1109/TSMCB.2012.2231860 |
| [41] |
Goldberg DE, Korb B, Deb K. Messy genetic algorithms: Motivation, analysis, and first results. Complex Systems, 1989, 3(5): 493–530.
|
| [42] |
Deb K. Nonlinear goal programming using multi-objective genetic algorithms. Journal of the Operational Research Society, 2001, 52(3): 291-302. DOI:10.1057/palgrave.jors.2601089 |
| [43] |
Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. DOI:10.1109/4235.996017 |
| [44] |
Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: Solving problems with box constraints. IEEE Transactions on Evolutionary Computation, 2014, 18(4): 577-601. DOI:10.1109/TEVC.2013.2281535 |
| [45] |
Zitzler E, Thiele L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Transactions on Evolutionary Computation, 1999, 3(4): 257-271. DOI:10.1109/4235.797969 |
| [46] |
Zitzler E, Laumanns M, Thiele L. SPEA2: Improving the strength Pareto evolutionary algorithm. TIK-report, 2001, 103. |
| [47] |
Murata T, Ishibuchi H. MOGA: Multi-objective genetic algorithms. Proceedings of 1995 IEEE International Conference on Evolutionary Computation. Perth: IEEE, 1995. 289–294.
|
| [48] |
Horn J, Nafpliotis N, Goldberg DE. A niched Pareto genetic algorithm for multiobjective optimization. Proceedings of the 1st IEEE Conference on Evolutionary Computation. Orlando: IEEE, 1994. 82–87.
|
| [49] |
Knowles J, Corne D. The Pareto archived evolution strategy: A new baseline algorithm for Pareto multiobjective optimisation. Proceedings of the 1999 Congress on Evolutionary Computation-CEC99. Washington DC: IEEE, 1999. 98–105.
|
| [50] |
Corne DW, Knowles JD, Oates MJ. The Pareto envelope-based selection algorithm for multiobjective optimization. Proceedings of the 6th International Conference on Parallel Problem Solving from Nature. Paris: Springer, 2000. 839–848.
|
| [51] |
Zitzler E, Künzli S. Indicator-based selection in multiobjective search. Proceedings of the 8th International Conference on Parallel Problem Solving from Nature. Birmingham: Springer, 2004. 832–842.
|
| [52] |
Bader J, Zitzler E. HypE: An algorithm for fast hypervolume-based many-objective optimization. Evolutionary Computation, 2011, 19(1): 45-76. DOI:10.1162/EVCO_a_00009 |
| [53] |
Moradi P, Ahmadian S, Akhlaghian F. An effective trust-based recommendation method using a novel graph clustering algorithm. Physica A: Statistical Mechanics and Its Applications, 2015, 436: 462-481. DOI:10.1016/j.physa.2015.05.008 |
| [54] |
Cantini L, Medico E, Fortunato S, et al. Detection of gene communities in multi-networks reveals cancer drivers. Scientific Reports, 2015, 5(1): 17386. DOI:10.1038/srep17386 |
| [55] |
Moradi P, Rostami M. Integration of graph clustering with ant colony optimization for feature selection. Knowledge-based Systems, 2015, 84: 144-161. DOI:10.1016/j.knosys.2015.04.007 |
| [56] |
Deng XL, Wen Y, Chen YH. Highly efficient epidemic spreading model based LPA threshold community detection method. Neurocomputing, 2016, 210: 3-12. DOI:10.1016/j.neucom.2015.10.142 |
| [57] |
Shang JX, Liu LC, Li X, et al. Epidemic spreading on complex networks with overlapping and non-overlapping community structure. Physica A: Statistical Mechanics and Its Applications, 2015, 419: 171-182. DOI:10.1016/j.physa.2014.10.023 |
| [58] |
Danon L, Díaz-Guilera A, Duch J, et al. Comparing community structure identification. Journal of Statistical Mechanics: Theory and Experiment, 2005, 2005: P09008. |
| [59] |
Lancichinetti A, Fortunato S, Kertész J. Detecting the overlapping and hierarchical community structure in complex networks. New Journal of Physics, 2009, 11(3): 033015. DOI:10.1088/1367-2630/11/3/033015 |
| [60] |
Newman MEJ. Fast algorithm for detecting community structure in networks. Physical Review E, 2004, 69(6): 066133. DOI:10.1103/PhysRevE.69.066133 |
| [61] |
Leicht EA, Newman MEJ. Community structure in directed networks. Physical Review Letters, 2008, 100(11): 118703. DOI:10.1103/PhysRevLett.100.118703 |
| [62] |
Gómez S, Jensen P, Arenas A. Analysis of community structure in networks of correlated data. Physical Review E, 2009, 80(1): 016114. DOI:10.1103/PhysRevE.80.016114 |
| [63] |
Shen HW, Cheng XQ, Cai K, et al. Detect overlapping and hierarchical community structure in networks. Physica A: Statistical Mechanics and Its Applications, 2009, 388(8): 1706-1712. DOI:10.1016/j.physa.2008.12.021 |
| [64] |
Liu CL, Liu J, Jiang ZZ. A multiobjective evolutionary algorithm based on similarity for community detection from signed social networks. IEEE Transactions on Cybernetics, 2014, 44(12): 2274-2287. DOI:10.1109/TCYB.2014.2305974 |
| [65] |
Fortunato S, Barthélemy M. Resolution limit in community detection. Proceedings of the National Academy of Sciences of the United States of America, 2007, 104(1): 36-41. DOI:10.1073/pnas.0605965104 |
| [66] |
Angelini L, Boccaletti S, Marinazzo D, et al. Identification of network modules by optimization of ratio association. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2007, 17(2): 023114. DOI:10.1063/1.2732162 |
| [67] |
Li ZP, Zhang SH, Wang RS, et al. Quantitative function for community detection. Physical Review E, 2008, 77(3): 036109. DOI:10.1103/PhysRevE.77.036109 |
| [68] |
Huang JB, Sun HL, Liu YG, et al. Towards online multiresolution community detection in large-scale networks. PLoS One, 2011, 6(8): e23829. DOI:10.1371/journal.pone.0023829 |
| [69] |
Tang J, Lou TC, Kleinberg J. Inferring social ties across heterogenous networks. Proceedings of the 5th ACM International Conference on Web Search and Data Mining. Seattle: ACM, 2012. 743–752.
|
| [70] |
Pizzuti C. GA-Net: A genetic algorithm for community detection in social networks. Proceedings of the 10th International Conference on Parallel Problem Solving from Nature. Dortmund: Springer, 2008. 1081–1090.
|
| [71] |
Gong MG, Fu B, Jiao LC, et al. Memetic algorithm for community detection in networks. Physical Review E, 2011, 84(5): 056101. |
| [72] |
Cai Q, Gong MG, Ma LJ, et al. Greedy discrete particle swarm optimization for large-scale social network clustering. Information Sciences, 2015, 316: 503-516. DOI:10.1016/j.ins.2014.09.041 |
| [73] |
Cai Q, Gong MG, Shen B, et al. Discrete particle swarm optimization for identifying community structures in signed social networks. Neural Networks, 2014, 58: 4-13. DOI:10.1016/j.neunet.2014.04.006 |
| [74] |
Bui TN, Ro Moon B. Genetic algorithm and graph partitioning. IEEE Transactions on Computers, 1996, 45(7): 841-855. DOI:10.1109/12.508322 |
| [75] |
Talbi EG, Bessière P. A parallel genetic algorithm for the graph partitioning problem. Proceedings of the 5th International Conference on Supercomputing. Cologne: ACM, 1991. 312–320.
|
| [76] |
Tasgin M, Herdagdelen A, Bingol H. Community detection in complex networks using genetic algorithms. arXiv:0711.0491, 2007.
|
| [77] |
Gog A, Dumitrescu D, Hirsbrunner B. Community detection in complex networks using collaborative evolutionary algorithms. Proceedings of the 9th European Conference on Artificial Life. Lisbon: Springer, 2007. 886–894.
|
| [78] |
Pizzuti C. A multiobjective genetic algorithm to find communities in complex networks. IEEE Transactions on Evolutionary Computation, 2012, 16(3): 418-430. DOI:10.1109/TEVC.2011.2161090 |
| [79] |
Shi C, Yan ZY, Cai YN, et al. Multi-objective community detection in complex networks. Applied Soft Computing, 2012, 12(2): 850-859. DOI:10.1016/j.asoc.2011.10.005 |
| [80] |
Shi C, Yu PS, Cai YN, et al. On selection of objective functions in multi-objective community detection. Proceedings of the 20th ACM International Conference on Information and Knowledge Management. Glasgow: ACM, 2011. 2301–2304.
|
| [81] |
Gong MG, Ma LJ, Zhang QF, et al. Community detection in networks by using multiobjective evolutionary algorithm with decomposition. Physica A: Statistical Mechanics and Its Applications, 2012, 391(15): 4050-4060. DOI:10.1016/j.physa.2012.03.021 |
| [82] |
Gong MG, Cai Q, Chen XW, et al. Complex network clustering by multiobjective discrete particle swarm optimization based on decomposition. IEEE Transactions on Evolutionary Computation, 2013, 18(1): 82-97. |
| [83] |
Zhou YL, Wang JH, Luo NB, et al. Multiobjective local search for community detection in networks. Soft Computing, 2016, 20(8): 3273-3282. DOI:10.1007/s00500-015-1706-5 |
| [84] |
Li LL, Jiao LC, Zhao JQ, et al. Quantum-behaved discrete multi-objective particle swarm optimization for complex network clustering. Pattern Recognition, 2017, 63: 1-14. DOI:10.1016/j.patcog.2016.09.013 |
| [85] |
Liu XR, Du YZ, Jiang M, et al. Multiobjective particle swarm optimization based on network embedding for complex network community detection. IEEE Transactions on Computational Social Systems, 2020, 7(2): 437-449. DOI:10.1109/TCSS.2020.2964027 |
| [86] |
Zhang ZW, Cui P, Wang X, et al. Arbitrary-order proximity preserved network embedding. Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. London: ACM, 2018. 2778–2786.
|
| [87] |
Ghaffaripour Z, Abdollahpouri A, Moradi P. A multi-objective genetic algorithm for community detection in weighted networks. Proceedings of the 8th International Conference on Information and Knowledge Technology. Hamedan: IEEE, 2016. 193–199.
|
| [88] |
Liu J, Zhong WC, Abbass HA, et al. Separated and overlapping community detection in complex networks using multiobjective evolutionary algorithms. Proceedings of the 2010 IEEE Congress on Evolutionary Computation. Barcelona: IEEE, 2010. 1–7.
|
| [89] |
Merris R. Laplacian matrices of graphs: A survey. Linear Algebra and Its Applications, 1994, 197–198: 143–176.
|
| [90] |
Albert R, Jeong H, Barabási AL. Error and attack tolerance of complex networks. Nature, 2000, 406(6794): 378-382. DOI:10.1038/35019019 |
| [91] |
Cohen R, Erez K, Ben-Avraham D, et al. Breakdown of the Internet under intentional attack. Physical Review Letters, 2001, 86(16): 3682-3685. DOI:10.1103/PhysRevLett.86.3682 |
| [92] |
Schneider CM, Moreira AA, Andrade JS, et al. Mitigation of malicious attacks on networks. Proceedings of the National Academy of Sciences of the United States of America, 2011, 108(10): 3838-3841. DOI:10.1073/pnas.1009440108 |
| [93] |
Buesser P, Daolio F, Tomassini M. Optimizing the robustness of scale-free networks with simulated annealing. Proceedings of the 10th International Conference on Adaptive and Natural Computing Algorithms. Ljubljana: Springer, 2011. 167–176.
|
| [94] |
Zhou MX, Liu J. A memetic algorithm for enhancing the robustness of scale-free networks against malicious attacks. Physica A: Statistical Mechanics and Its Applications, 2014, 410: 131-143. DOI:10.1016/j.physa.2014.05.002 |
| [95] |
Kalman RE. Contributions to the theory of optimal control. Boletin de la Sociedad Matematica Mexicana, 1960, 5(1): 102-119. |
| [96] |
Kalman RE. On the general theory of control systems. Proceedings of the 1st International Conference on Automatic Control. Moscow: USSR. 1960. 481–492.
|
| [97] |
Yuan ZZ, Zhao C, Di ZR, et al. Exact controllability of complex networks. Nature Communications, 2013, 4(1): 2447. DOI:10.1038/ncomms3447 |
| [98] |
楼洋, 李均利, 李升, 等. 复杂网络能控性鲁棒性研究进展. 自动化学报, 2022, 48(10): 2374-2391. |
| [99] |
Wang BB, Gao L, Gao Y, et al. Maintain the structural controllability under malicious attacks on directed networks. Europhysics Letters, 2013, 101(5): 58003. DOI:10.1209/0295-5075/101/58003 |
| [100] |
Xiao YD, Lao SY, Hou LL, et al. Optimization of robustness of network controllability against malicious attacks. Chinese Physics B, 2014, 23(11): 118902. DOI:10.1088/1674-1056/23/11/118902 |
| [101] |
Nie S, Wang XW, Zhang HF, et al. Robustness of controllability for networks based on edge-attack. PLoS One, 2014, 9(2): e89066. DOI:10.1371/journal.pone.0089066 |
| [102] |
Ma LJ, Gong MG, Cai Q, et al. Enhancing community integrity of networks against multilevel targeted attacks. Physical Review E, 2013, 88(2): 022810. DOI:10.1103/PhysRevE.88.022810 |
| [103] |
Wang S, Liu J. Community robustness and its enhancement in interdependent networks. Applied Soft Computing, 2019, 77: 665-677. DOI:10.1016/j.asoc.2019.01.045 |
| [104] |
Buldyrev SV, Parshani R, Paul G, et al. Catastrophic cascade of failures in interdependent networks. Nature, 2010, 464(7291): 1025-1028. DOI:10.1038/nature08932 |
| [105] |
Gao JX, Buldyrev SV, Havlin S, et al. Robustness of a network of networks. Physical Review Letters, 2011, 107(19): 195701. DOI:10.1103/PhysRevLett.107.195701 |
| [106] |
Kenett DY, Perc M, Boccaletti S. Networks of net-works—An introduction. Chaos, Solitons & Fractals, 2015, 80: 1-6. |
| [107] |
Di Muro MA, La Rocca CE, Stanley HE, et al. Recovery of interdependent networks. Scientific Reports, 2016, 6(1): 22834. DOI:10.1038/srep22834 |
| [108] |
Zeng A, Liu WP. Enhancing network robustness against malicious attacks. Physical Review E, 2012, 85(6): 066130. DOI:10.1103/PhysRevE.85.066130 |
| [109] |
Wang S, Liu J. Designing comprehensively robust networks against intentional attacks and cascading failures. Information Sciences, 2019, 478: 125-140. DOI:10.1016/j.ins.2018.11.005 |
| [110] |
Wang JW, Rong LL, Zhang L, et al. Attack vulnerability of scale-free networks due to cascading failures. Physica A: Statistical Mechanics and Its Applications, 2008, 387(26): 6671-6678. DOI:10.1016/j.physa.2008.08.037 |
| [111] |
Ash J, Newth D. Optimizing complex networks for resilience against cascading failure. Physica A: Statistical Mechanics and Its Applications, 2007, 380: 673-683. DOI:10.1016/j.physa.2006.12.058 |
| [112] |
Tang XL, Liu J, Hao XX. Mitigate cascading failures on networks using a memetic algorithm. Scientific Reports, 2016, 6: 38713. DOI:10.1038/srep38713 |
| [113] |
Cartwright D, Harary F. Structural balance: A generalization of Heider’s theory. Psychological Review, 1956, 63(5): 277-293. DOI:10.1037/h0046049 |
| [114] |
Easley D, Kleinberg J. Networks, Crowds, and Markets: Reasoning About a Highly Connected World. Cambridge: Cambridge University Press, 2010.
|
| [115] |
Wang S, Liu J, Jin YC. Robust structural balance in signed networks using a multiobjective evolutionary algorithm. IEEE Computational Intelligence Magazine, 2020, 15(2): 24-35. DOI:10.1109/MCI.2020.2976183 |
| [116] |
Wang S, Liu J, Jin YC. Surrogate-assisted robust optimization of large-scale networks based on graph embedding. IEEE Transactions on Evolutionary Computation, 2020, 24(4): 735-749. DOI:10.1109/TEVC.2019.2950935 |
| [117] |
Chen JY, Liu J. A memetic algorithm for optimizing inter-links to enhance the robustness of interdependent networks against malicious attacks. Proceedings of the 2021 IEEE Congress on Evolutionary Computation. Kraków: IEEE, 2021. 327–334.
|
| [118] |
Wang S, Liu J. Constructing robust community structure against edge-based attacks. IEEE Systems Journal, 2019, 13(1): 582-592. DOI:10.1109/JSYST.2018.2835642 |
| [119] |
Wang S, Liu J, Jin YC. A computationally efficient evolutionary algorithm for multiobjective network robustness optimization. IEEE Transactions on Evolutionary Computation, 2021, 25(3): 419-432. DOI:10.1109/TEVC.2020.3048174 |
| [120] |
Bensaid B, Encaoua D, Winckler A. Competition, cooperation and mergers: Economic and policy issues. European Economic Review, 1994, 38(3–4): 637–650.
|
| [121] |
Yang HX, Wu ZX, Du WB. Evolutionary games on scale-free networks with tunable degree distribution. Europhysics Letters, 2012, 99(1): 10006. DOI:10.1209/0295-5075/99/10006 |
| [122] |
Santos FC, Pacheco JM. Scale-free networks provide a unifying framework for the emergence of cooperation. Physical Review Letters, 2005, 95(9): 098104. DOI:10.1103/PhysRevLett.95.098104 |
| [123] |
Rong ZH, Li X, Wang XF. Roles of mixing patterns in cooperation on a scale-free networked game. Physical Review E, 2007, 76(2): 027101. DOI:10.1103/PhysRevE.76.027101 |
| [124] |
Zimmermann MG, Eguı́luz VM. Cooperation, social networks, and the emergence of leadership in a prisoner’s dilemma with adaptive local interactions. Physical Review E, 2005, 72(5): 056118. DOI:10.1103/PhysRevE.72.056118 |
| [125] |
Kempe D, Kleinberg J, Tardos É. Maximizing the spread of influence through a social network. Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Washington DC: ACM, 2003. 137–146.
|
| [126] |
Chen W, Wang YJ, Yang SY. Efficient influence maximization in social networks. Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Paris: ACM, 2009. 199–208.
|
| [127] |
Rahimkhani K, Aleahmad A, Rahgozar M, et al. A fast algorithm for finding most influential people based on the linear threshold model. Expert Systems with Applications, 2015, 42(3): 1353-1361. DOI:10.1016/j.eswa.2014.09.037 |
| [128] |
Lee JR, Chung CW. A fast approximation for influence maximization in large social networks. Proceedings of the 23rd International Conference on World Wide Web. Seoul: ACM, 2014. 1157–1162.
|
| [129] |
Herrmann HJ, Schneider CM, Moreira AA, et al. Onion-like network topology enhances robustness against malicious attacks. Journal of Statistical Mechanics: Theory and Experiment, 2011, 2011: P01027. |
| [130] |
Wang S, Liu J. Constructing robust cooperative networks using a multi-objective evolutionary algorithm. Scientific Reports, 2017, 7(1): 41600. DOI:10.1038/srep41600 |
| [131] |
Wang S, Liu J. A multi-objective evolutionary algorithm for promoting the emergence of cooperation and controllable robustness on directed networks. IEEE Transactions on Network Science and Engineering, 2018, 5(2): 92-100. DOI:10.1109/TNSE.2017.2742522 |
| [132] |
Wang S, Liu J, Jin YC. Finding influential nodes in multiplex networks using a memetic algorithm. IEEE Transactions on Cybernetics, 2021, 51(2): 900-912. DOI:10.1109/TCYB.2019.2917059 |
| [133] |
Tong H, Prakash BA, Eliassi-Rad T, et al. Gelling, and melting, large graphs by edge manipulation. Proceedings of the 21st ACM International Conference on Information and Knowledge Management. Maui: ACM, 2012. 245–254.
|
| [134] |
Estrada E. Network robustness to targeted attacks. The interplay of expansibility and degree distribution. The Euro-pean Physical Journal B—Condensed Matter and Complex Systems, 2006, 52(4): 563-574. DOI:10.1140/epjb/e2006-00330-7 |
| [135] |
Malliaros FD, Megalooikonomou V, Faloutsos C. Fast robustness estimation in large social graphs: Communities and anomaly detection. Proceedings of the 2012 SIAM International Conference on Data Mining. Anaheim: SIAM, 2012. 942–953.
|
| [136] |
Fiedler M. Algebraic connectivity of graphs. Czechoslovak Mathematical Journal, 1973, 23(2): 298-305. DOI:10.21136/CMJ.1973.101168 |
| [137] |
Wu J, Barahona M, Tan YJ, et al. Spectral measure of structural robustness in complex networks. IEEE Transactions on Systems, Man, and Cybernetics—Part A: Systems and Humans, 2011, 41(6): 1244-1252. DOI:10.1109/TSMCA.2011.2116117 |
| [138] |
Ghosh A, Boyd S, Saberi A. Minimizing effective resistance of a graph. SIAM Review, 2008, 50(1): 37-66. DOI:10.1137/050645452 |
| [139] |
Klein DJ, Randić M. Resistance distance. Journal of Mathematical Chemistry, 1993, 12(1): 81-95. DOI:10.1007/BF01164627 |
| [140] |
Buekenhout F, Parker M. The number of nets of the regular convex polytopes in dimension≤4. Discrete Mathematics, 1998, 186(1–3): 69–94.
|
| [141] |
Baras JS, Hovareshti P. Efficient and robust communication topologies for distributed decision making in networked systems. Proceedings of the 48h IEEE Conference on Decision and Control (CDC) Held Jointly with 2009 28th Chinese Control Conference. Shanghai: IEEE, 2009. 3751–3756.
|
| [142] |
Newman MEJ. Assortative mixing in networks. Physical Review Letters, 2002, 89(20): 208701. DOI:10.1103/PhysRevLett.89.208701 |
| [143] |
Newman MEJ. Mixing patterns in networks. Physical Review E, 2003, 67(2): 026126. DOI:10.1103/PhysRevE.67.026126 |
| [144] |
Ma LL, Liu J, Duan BP, et al. A theoretical estimation for the optimal network robustness measure R against malicious node attacks
. Europhysics Letters, 2015, 111(2): 28003. DOI:10.1209/0295-5075/111/28003 |
| [145] |
Hu HB, Wang XF. Unified index to quantifying heterogeneity of complex networks. Physica A: Statistical Mechanics and Its Applications, 2008, 387(14): 3769-3780. DOI:10.1016/j.physa.2008.01.113 |
| [146] |
Andrews GE. The Theory of Partitions. Cambridge: Cambridge University Press, 1998.
|
| [147] |
Park YJ, Song MS. A genetic algorithm for clustering problems. Proceedings of the 3rd Annual Conference on Genetic Programming. Madison: University of Wisconsin, 1998. 568–575.
|
| [148] |
Zhang DK, Yin J, Zhu XQ, et al. Network representation learning: A survey. IEEE Transactions on Big Data, 2020, 6(1): 3-28. DOI:10.1109/TBDATA.2018.2850013 |
| [149] |
Ou MD, Cui P, Pei J, et al. Asymmetric transitivity preserving graph embedding. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco: ACM, 2016. 1105–1114.
|
| [150] |
Huang X, Li JD, Hu X. Label informed attributed network embedding. Proceedings of the 10th ACM International Conference on Web Search and Data Mining. Cambridge: ACM, 2017. 731–739.
|
| [151] |
Perozzi B, Al-Rfou R, Skiena S. DeepWalk: Online learning of social representations. Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: ACM, 2014. 701–710.
|
| [152] |
Grover A, Leskovec J. node2vec: Scalable feature learning for networks. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco: ACM, 2016. 855–864.
|
| [153] |
Tang J, Qu M, Wang MZ, et al. Line: Large-scale information network embedding. Proceedings of the 24th International Conference on World Wide Web. Florence: International World Wide Web Conferences Steering Committee, 2015. 1067–1077.
|
| [154] |
Wang DX, Cui P, Zhu WW. Structural deep network embedding. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco: ACM, 2016. 1225–1234.
|
| [155] |
Chen HC, Perozzi B, Hu YF, et al. HARP: Hierarchical representation learning for networks. Proceedings of the 32nd AAAI Conference on Artificial Intelligence. New Orleans: AAAI Press, 2018. 2127–2134.
|
| [156] |
Van Veldhuizen DA, Lamont GB. Multiobjective evolutionary algorithm test suites. Proceedings of the 1999 ACM Symposium on Applied Computing. San Antonio: ACM, 1999. 351–357.
|
| [157] |
Zitzler E, Thiele L. Multiobjective optimization using evolutionary algorithms—A comparative case study. Proceed-ings of the 5th International Conference on Parallel Problem Solving from Nature. Amsterdam: Springer, 1998. 292–301.
|
| [158] |
Van Veldhuizen DA, Lamont GB, et al. Evolutionary computation and convergence to a Pareto front. Proceedings of the 1998 Genetic Programming Conference. Madison: Stanford University Bookstore, 1998. 221–228.
|
| [159] |
Van Veldhuizen DA. Multiobjective evolutionary algorithms: Classifications, analyses, and new innovations [Ph.D. thesis]. Patterson: Air Force Institute of Technology, 1999.
|
| [160] |
Deb K, Agrawal S, Pratap A, et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II. Proceedings of the 6th International Conference on Parallel Problem Solving from Nature. Paris: Springer, 2000. 849–858.
|
| [161] |
李密青, 郑金华. 一种多目标进化算法解集分布广度评价方法. 计算机学报, 2011, 34(4): 647-664. |
| [162] |
Coello CAC, Cortés NC. Solving multiobjective optimization problems using an artificial immune system. Genetic Programming and Evolvable Machines, 2005, 6(2): 163-190. DOI:10.1007/s10710-005-6164-x |
| [163] |
Schott JR. Fault tolerant design using single and multicriteria genetic algorithm optimization [Master’s thesis]. Cambridge: Massachusetts Institute of Technology, 1995.
|
| [164] |
Hardy RL. Multiquadric equations of topography and other irregular surfaces. Journal of Geophysical Research, 1971, 76(8): 1905-1915. DOI:10.1029/JB076i008p01905 |
| [165] |
Shepard D. A two-dimensional interpolation function for irregularly-spaced data. Proceedings of the 1968 23rd ACM National Conference. New York: ACM, 1968. 517–524.
|
| [166] |
Zhou ZZ, Ong YS, Nguyen MH, et al. A study on polynomial regression and Gaussian process global surrogate model in hierarchical surrogate-assisted evolutionary algorithm. Proceedings of the 2005 IEEE Congress on Evolutionary Computation. Edinburgh: IEEE, 2005. 2832–2839.
|
| [167] |
Lou Y, He YD, Wang L, et al. Predicting network controllability robustness: A convolutional neural network approach. IEEE Transactions on Cybernetics, 2022, 52(5): 4052-4063. DOI:10.1109/TCYB.2020.3013251 |
| [168] |
Lou Y, He YD, Wang L, et al. Knowledge-based prediction of network controllability robustness. IEEE Transactions on Neural Networks and Learning Systems, 2022, 33(10): 5739-5750. DOI:10.1109/TNNLS.2021.3071367 |
| [169] |
Lou Y, Wu RZ, Li JL, et al. A convolutional neural network approach to predicting network connectedness robustness. IEEE Transactions on Network Science and Engineering, 2021, 8(4): 3209-3219. DOI:10.1109/TNSE.2021.3107186 |
| [170] |
Niepert M, Ahmed M, Kutzkov K. Learning convolutional neural networks for graphs. Proceedings of the 33rd International Conference on International Conference on Machine Learning. New York: JMLR.org, 2016. 2014–2023.
|
| [171] |
Lou Y, Wu RZ, Li JL, et al. A learning convolutional neural network approach for network robustness prediction. IEEE Transactions on Cybernetics, 2022, 1-14. DOI:10.1109/TCYB.2022.3207878 |
 2023, Vol. 32
2023, Vol. 32



