1 概述

Kubernetes是Google公司开源的一个容器编排与调度管理框架, 该项目最初是Google内部面向容器的集群管理系统, 现在由云原生计算基金会托管开源平台, 由Google、AWS等主要参与者支持, 其目标是通过创建一组新的通用容器技术来推进云原生技术和服务的开发^[1]. 在Kubernetes平台中调度是进行容器编排工作重要的一环, 其中Scheduler又是这一环中的核心组件, 其功能是根据调度策略将待调度的Pod匹配到最合适的节点上^[2]. Pod在Kubernetes集群中进行调度时需要经历Predicates和Priorities两个阶段: 在预选阶段, Kubernetes会遍历所有的计算节点, 排除那些完全不能符合对应Pod的基本运行节点; 而在优选阶段由Scheduler组件按照相应的优选算法对通过第一阶段筛选合格的节点进行打分, 最后决定出分数最高的节点进行Pod调度.

Kubernetes中Scheduler模块在整个平台中有着举足轻重的地位, 不合适的预选和优选策略会对集群的资源利用率产生不利的影响, 会对用户部署请求缺乏快速响应, 服务质量下降, 增加服务商开销成本.

现阶段, 国内外学者针对Kubernetes平台中Pod调度做了大量的研究工作, 并且已经产生较多的研究成果. 胡程鹏等^[3]在原有的资源指标上增加了带宽和磁盘IO, 并将改进的遗传算法运用在Kubernetes调度策略中, 该算法优化了集群的负载均衡, 但是没有考虑到不同类型的应用对Pod中资源的消耗是不同的, 容易导致节点单个资源的瓶颈; Zhang等^[4] 将蚁群算法和粒子群优化算法相结合, 提出基于启发式算法的Kuber-netes调度算法, 实验表明该算法相较于原有调度算法, 降低了节点总成本和最大负载, 使负载更加均衡, 但是只考虑了CPU和内存两种资源, 忽略了其他资源对节点的影响, 易导致其他类型的资源过载; 孔德瑾等^[5]面向5G边缘计算的资源调度场景, 提出一种基于CPU、内存、带宽和磁盘4种指标的自适应权重调度策略WSLB, 避免了节点中带宽和磁盘资源的过载, 提高了资源利用率; Li等^[6]提出了BDI (balanced-disk-IO-priority)和BCDI (balanced-CPU-disk-IO-priority)动态算法, 两种算法分别改善了节点之间磁盘I/O平衡和解决单个节点的资源不平衡问题, 但是没有考虑到Pod中的应用在不同时刻对节点资源消耗是不同的, 可能导致节点资源耗尽; 常旭征等^[7]针对 Kubernetes默认调度算法没有考虑到节点本身的资源利用率, 且没有考虑到网络和IO指标, 提出了相应的改进算法, 实验证明改进的算法可以提高进群的负载; Dua等^[8]实现可以将任务替换的算法, 通过对每个作业打上标签, 将其分到不同特定类型任务集群; 何龙等^[9]实现了基于应用历史记录的 Kubernetes调度方法, 该方法在提升节点资源均衡程度和减少资源浪费相比原有算法均有一定提升, 但是该算法仅考虑了CPU和内存指标, 对于磁盘容量以及网络带宽等指标等方面研究不足; 张可颖等^[10]通过将OpenStack和Kubernetes相结合提出一种基于容器的弹性调度策略, 实验表明在数据中心能耗和资源利用率方面得到了提高.

虽然国内外学者针对Kubernetes资源调度取得了一定的成果, 但是忽略了不同时刻节点中的应用对资源的消耗是不同的, 如果节点中的应用处于低消耗状态, 此时节点满足Pod调度条件并调入, 当节点中的应用处于高消耗的状态, 可能导致节点出现资源耗尽杀死Pod, 同时也没有考虑到应用的资源类型对Pod的影响是各异的^[11]. 针对上述问题, 本文在Kubernetes原有指标基础上, 增加带宽和磁盘容量两种指标, 根据Pod中应用的资源需求将待调度的Pod分类, 并为不同种类的Pod设置相应的权重, 并且选择节点某个时刻的最大的资源利用率作为计算指标, 最后利用改进的秃鹰算法寻找出最优节点进行调度.

2 默认调度算法分析

Kubernetes Scheduler是Kubernetes关键模块, 其职责通过Kubernetes watch机制从集群中获取待调度Pod的相关信息, 通过Pod和节点的相关信息计算出集群中最合适的工作节点信息进行捆绑, 并将相关的绑定内容写入ETCD中^[12]. 接着Kubelet会接收到Pod的调度消息, 从ETCD中获取Pod配置文件并完成相关资源和容器的创建.

Kubernetes中Pod调度主要经过两个流程, Predicates和Priorities. Predicates算法通过遍历集群中全部节点, 将满足要求的节点记录并作为Priorities的输入, 如果全部节点都不满足, 则Pod一直处于悬挂阶段. 而优选阶段是对预选阶段的筛选出的节点按照优选策略进行节点打分, 通过分数进行优先级排序, 选出优先级最高的节点进行Pod部署. 在Kubernetes的优选阶段中, 主要提供BalancedResourcesAllocation、LeastRequestedPriority等策略对节点进行优先级排序.

1)默认的LeastRequestedPriority算法, 该算法从Predicates筛选出来的节点中, 选择CPU和内存剩余最多的节点及资源消耗最少的节点进行Pod调度, 如式(1)所示:

$ {{score}} = {\left[ \dfrac{S_{\rm{CPU}}-N_{\rm{CPU}}}{S_{\rm{CPU}}}\times 10+\dfrac{S_{\rm{mem}}-N_{\rm{mem}}}{S_{\rm{mem}}}\times 10 \right] \mathord{\left/ {\vphantom {{[\dfrac{{Scpu - Ncpu}}{{Scpu}} \times 10 + \dfrac{{Smem - Nmem}}{{Smem}} \times 10]} 2}} \right. } 2} $

(1)

2)默认的BalancedResourceAllocation算法, 该算法从Predicates筛选出来的节点中, 选择CPU和内存利用率相差最小的节点进行Pod调度, 如式(2)所示:

$ {{score}} = 10 - abs\left( {\dfrac{{N_{\rm{CPU}}}}{{S_{\rm{CPU}}}} - \dfrac{{N_{\rm{mem}}}}{{S_{\rm{mem}}}}} \right) \times 10 $

(2)

其中, $S_{\rm{CPU}}$ 和 $S_{\rm{mem}}$ 分别代表节点所拥有的CPU和内存的总资源, $N_{\rm{CPU}}$ 和 $N_{\rm{mem}}$ 则代表节点已用的资源(Pod需要的资源和节点已被使用的资源之和). 通过分析 Kubernetes 调度器的默认算法可以发现其默认算法对节点的评价指标中只考虑了CPU和内存的使用率, 没有考虑磁盘容量和网络带宽的使用. 并且 Kubernetes 调度器是一种静态调度策略, 该调度机制虽然简单, 但是缺乏灵活性, 且只能在 Pod 初次部署时进行资源配置. 还忽略了应用对资源的消耗是不均匀的, 容易导致节点对不同资源的使用不均衡, 从而造成节点对某一资源的性能瓶颈. 同时默认调度策略调度的优先级是根据应用的请求量来衡量的, 不能很好地反映节点的实际资源情况, 容易使节点的资源失衡.

3 秃鹰搜索算法改进与实验验证

在Pod调度过程中, 若将m个Pod分配到n个节点中, 根据排列组合可得出共有n^m种情况, 这是一个NP Hard 问题, 在解决这类问题上, 如果问题的固有知识不能被用来减少搜索空间, 很容易产生搜索的组合爆炸.

针对 NP Hard问题, 常用启发式算法来解决, 秃鹰搜索算法(bald eagle search, BES)^[13]是2020年马来西亚学者Alsatter等提出的一种模仿秃鹰捕食过程的新型元启发式算法. 该算法相较于传统的启发式算法具有较强的全局搜索能力, 在应对各类复杂数值优化问题都能够有效的解决. 该算法可分为3个阶段, 即选择搜索猎物的区域、在选择的搜索区域内搜索猎物和俯冲捕猎.

3.1 秃鹰搜索算法介绍 3.1.1 选择搜索空间

在选择阶段, 秃鹰寻找并挑选所选搜索区域内它们可以捕食最理想的空间(就食物数量而言), 式(3)在数学上描述了这种行为.

$ {P_{i, {\rm{new}}}} = {P_{{\rm{best}}}} + \alpha \times \lambda \left( {{P_{{\rm{mean}}}} - {P_i}} \right) $

(3)

其中, $ \alpha $ 是用于控制位置更改的参数, 该参数的值介于1.5到2之间; $ \lambda $ 是一个随机数, 取值在0到1之间; ${P_{{\rm{best}}}}$ 表示秃鹰表示当前选择的搜索空间, 该搜索空间是由秃鹰根据它们之前搜索时确定的最佳位置选择的; ${P_{{\rm{mean}}}}$ 表示这些秃鹰已经用完了之前各点的所有信息; $ {P_i} $ 为第 $ i $ 只秃鹰所处位置.

3.1.2 搜索空间猎物(探索)

在搜索阶段, 秃鹰在挑选好的搜寻区域内搜索猎物, 并在螺旋形区域内不断向不同地方移动, 以加快搜索速度. 俯冲的最佳位置如式(10)所示:

$ \theta \left( i \right) = \alpha \times \pi \times rand $

(4)

$ r\left( i \right) = \theta \left( i \right) + R \times rand $

(5)

$ xr\left( i \right) = r\left( i \right) \times \sin\left( {\theta \left( i \right)} \right) $

(6)

$ yr\left( i \right) = r\left( i \right) \times \cos \left( {\theta \left( i \right)} \right) $

(7)

$ x\left( i \right) = {{xr\left( i \right)} \mathord{\left/ {\vphantom {{xr\left( i \right)} {\max \left( {|xr|} \right)}}} \right. } {\max \left( {|xr|} \right)}} $

(8)

$ y\left( i \right) = {{yr\left( i \right)} \mathord{\left/ {\vphantom {{yr\left( i \right)} {\max \left( {|yr|} \right)}}} \right. } {\max \left( {|yr|} \right)}} $

(9)

$ {P_{i, {\rm{new}}}} = {P_i} + x\left( i \right) \times \left( {{P_i} - {P_{{\rm{mean}}}}} \right) + y\left( i \right) \times \left( {{P_i} - {P_{i + 1}}} \right) $

(10)

其中, $ \theta \left( i \right) $ 与 $ r\left( i \right) $ 分别表示螺旋方程的极角与极径; $ \alpha $ 与 $ R $ 是控制螺旋轨迹的参数, 取值范围分别为(5, 10)、(0.5, 2); $ x\left( i \right) $ 与 $ y\left( i \right) $ 表示在极坐标下秃鹰的位置, 取值均为(−1, 1); $ {P_{i + 1}} $ 表示第 $ i $ 只秃鹰下一次更新的位置.

3.1.3 俯冲捕获猎物(利用)

在俯冲阶段, 秃鹰从最佳位置向目标猎物所摇摆, 其他秃鹰也都朝着最优点移动. 利用极坐标方式来描述运动状态, 如第2.1.2节式(4)–式(9)所示.

秃鹰的位置更新方式如式(11)和式(12)所示:

$ \left\{ {\begin{array}{*{20}{c}} {{\delta _x} = x\left( i \right) \times \left( {P{}_i - {C_1} \times {P_{{\rm{mean}}}}} \right)} \\ {{\delta _y} = y\left( i \right) \times \left( {P{}_i - {C_2} \times {P_{{\rm{mean}}}}} \right)} \end{array}} \right. $

(11)

$ {P_{i, {\rm{new}}}} = rand \times {P_{{\rm{best}}}} + {\delta _x} + {\delta _y} $

(12)

3.2 秃鹰搜索算法的改进

与其他智能优化算法一样, 秃鹰搜索算法也存在容易陷入局部最优和收敛精度低的问题^[14]. 因此本文提出了一种基于混沌映射和t分布改进的秃鹰搜索算法(TBESK). 首先, 为了增强种群的多样性, 本文在初始化种群时, 使用Tent混沌映射来提高秃鹰的全局搜索能力; 其次在搜寻阶段, 算法陷入局部最优, 使用t分布扰动跳出局部最优, 增强整体寻优能力.

3.2.1 Tent混沌映射

秃鹰搜索算法(BES)在进行种群初始化时, 通常将随机产生的数据用作初始种群信息, 遗失了种群多样性, 使得算法寻优能力降低. 由于混沌变量包含随机性、遍历性和规律性等特性^[15], 很多学者将其应用于初始化种群, 增强了种群的多样性, 改善算法的全局搜索能力. 目前常用于群体智能领域的混沌序列有Tent映射、Logistic 映射、Singer 映射等, 但是, 不同的混沌序列有着不同的特点, 对算法的优化效果也不一样. 单梁等^[16]研究验证了Tent映射在均匀分布和收敛速度方面均优于 Logistic 映射, 通过严格的数学推理, 在[0, 1]区间内Tent映射可以产生优化算法的混沌序列.

本文使用 Tent 映射来初始化种群, Tent 映射的表达式如下所示:

$ {x}_{i+1}=\left\{ {\begin{array}{l}2{x}_{i}{, }\;0\leqslant x\leqslant \dfrac{1}{2}\\ 2\left(1-{x}_{i}\right),\; \dfrac{1}{2}\lt x\leqslant 1\end{array}} \right. $

(13)

即经过贝努利移位变换后表达式如下:

$ {x_{i + 1}} = \left( {2{x_i}} \right)\;{\rm{mod}}\;1 $

(14)

利用Tent混沌映射对种群进行初始化的步骤如下.

Step 1. 在(0, 1)之间生成随机数 $ {x_0} $ , 记 $ j $ = 0.

Step 2. 根据式(13)计算得到新的 $ x $ 序列, $ j $ = $ j $ +1.

Step 3. 当j达到设置最大迭代次数, 则停止迭代, 保存好 $ x $ 序列.

3.2.2 自适应t分布

学生t分布简称t分布, 是以0为中心, 左右对称的单峰分布. t分布是一簇曲线, 其形态变化与自由度n有关, n的值越小, 其曲线越低平;n值越大, 其曲线越接近标准正态分布曲线, t(n→∞)→N(0, 1), t(n=1)=c(0, 1), 其中N(0, 1)为高斯分布, c(0, 1)为柯西分布, 由此可以看出t分布的两个边界特例分布为标准高斯分布和柯西分布^[17]. 对秃鹰选择搜索空间的位置 $P_{i, {\rm{new}}}^t$ 定义见式(15):

$ P_{i, {\rm{new}}}^t = {P_{i, {\rm{new}}}} + {P_{i, {\rm{new}}}} \times t\left( n \right) $

(15)

其中, $P_{i, {\rm{new}}}^t$ 为变异后的搜索空间, ${P_{i, {\rm{new}}}}$ 为第 $ i $ 个秃鹰的搜索空间, $ t\left( n \right) $ 表示自由度为n的t分布, 其中n为迭代次数. 该定义式在秃鹰进行搜索空间选择时增加了t分布扰动 ${P_{i, {\rm{new}}}} \times t\left( n \right)$ , 使搜索空间陷入局部最优时, 能够跳脱出来, 提升了搜索精度, 同时加快了收敛速度.

自适应t分布变异使用算法的迭代次数作为t分布的自由度参数, 在算法运行初期, 迭代次数的值较小, t分布变异近似于柯西分布变异, 算法具有良好的全局搜索能力; 在算法运行后期, t分布近似于高斯分布变异, 算法具有良好的局部开发能力; 在算法运行中期,t分布变异介于柯西分布变异和高斯分布变异之间. t分布的变异算子结合高斯算子和柯西算子的优势, 同时提高了算法的全局探索性和局部开发性.

3.2.3 TBESK算法描述

基于Tent混沌映射和t分布对BES算法的改进, TBESK算法具体实现流程如下所示.

Step 1. 设置种群的规模N, 迭代次数t_max, 搜索空间维度以及初始边界条件.

Step 2. 使用第3.2.1节中Tent混沌映射对种群进行初始化, 根据适应度函数求出秃鹰种群个体的适应度值, 对秃鹰种群进行排序, 找出全局最优的个体.

Step 3. 在秃鹰选择搜索阶段, 使用t分布对式(15)进行位置更新.

Step 4. 在秃鹰搜索空间猎物阶段, 按照式(10)进行位置更新.

Step 5. 在俯冲阶段, 按照式(12)进行秃鹰的位置更新.

Step 6. 不断更新种群最优位置以及适应度值, 更新迭代次数. 判断算法是否达到设置的迭代次数或者精度要求, 若满足, 则终止算法, 输出适应度最优位置及最优解; 若没有, 则返回 Step 3 进行循环.

3.3 实验验证

本文选取秃鹰搜索算法作为Kubernetes资源调度算法, 主要是因其具有较高的收敛精度. 而收敛精度的优劣则可以通过一些基本的测试函数来测试对比. 并且本文主要工作在于将改进的秃鹰算法用于Kubernetes资源调度, 因此后文主要将原秃鹰搜索算法与TBESK算法在Kubernetes环境中对比验证. 本文选取了常见的4个测试函数进行实验对比, 详细的测试函数信息见表1.

为了验证本文改进的秃鹰搜索算法的收敛性和稳定性, 选取了秃鹰搜索算法(BES)、使用t分布改进后的麻雀算法(tSSA)^[18]、使用t分布改进的缎蓝园丁鸟算法(tSBO)^[19]和t分布改进的粒子群算法(tPSO)^[20]进行对比实验. 为了降低随机性, 本文选取5种算法分别在4个测试函数上独立运行10次. 表2分别列出了TBESK、BES、tSSA、tSBO、tPSO独立运行10次所得的最优值、最差值以及平均迭代次数.

根据实验结果可知, 在所有的测试函数中, 本文提出的融合Tent混沌映射和t分布的秃鹰搜索算法全部优于BES、tSSA、tSBO、tPSO.

4 TBESK调度策略 4.1 划分Pod资源类型

在集群中, Pod中的应用对资源的不同需求影响了节点的性能, 比如有的租户对CPU需求比较大, 会加大节点的CPU负载, 有的租户则对内存需求比较大, 会加大内存的负载, 因此需要对Pod类型进行划分. 由于CPU和带宽超出配额后可以通过软性限制避免超额使用, 而对于内存和磁盘容量超出配额后只能通过内核抛出out-of-memory错误地将Pod杀死, 并将Pod重新调度^[21], 本文按照Pod中应用对CPU、内存、带宽、磁盘容量资源的请求, 将Pod分为可压缩资源消耗型、不可压缩资源消耗型和均衡型.

在 Kubernetes 集群中, 租户把对CPU、内存、带宽、磁盘容量的资源需求写在Pod的yaml文件中. 本文根据yaml文件中资源配置, 计算出Pod部署后对相应节点上的资源消耗程度 $ {C_r} $ , 定义 $ {R_r} $ 为yaml文件中应用对资源r的需求量, $ {T_r} $ 为某一节点上资源r的总量, 该Pod对节点资源的消耗大小如式(16)所示:

$ {C_r} = {{{R_r}} \mathord{\left/ {\vphantom {{{R_r}} {{T_r}}}} \right. } {{T_r}}} $

(16)

其中, 资源r代表着节点上CPU、内存、带宽和磁盘容量. 根据式(16)可计算出 ${C_{{\rm{CPU}}}}$ 、 ${C_{{\rm{mem}}}}$ 、 ${C_{{\rm{net}}}}$ 和 ${C_{{\rm{disk}}}}$ . 如果 ${{{C_{{\rm{CPU}}}}}/{{C_{{\rm{mem}}}}}} > 1$ 和 ${{{C_{{\rm{net}}}}} / {{C_{{\rm{disk}}}}}} > 1$ , 规定该Pod资源相对于该节点为可压缩资源消耗型; 如果 ${{{C_{{\rm{CPU}}}}} / {{C_{{\rm{mem}}}}}} < 1$ 和 ${{{C_{{\rm{net}}}}} / {{C_{{\rm{disk}}}}}} < 1$ , 规定该Pod资源相对于该节点为不可压缩资源消耗型; 如果 ${{{C_{{\rm{CPU}}}}} / {{C_{{\rm{mem}}}}}} < 1$ 、 ${{{C_{{\rm{net}}}}} / {{C_{{\rm{disk}}}}}} > 1$ 或 ${{{C_{{\rm{CPU}}}}} / {{C_{{\rm{mem}}}}}} > 1$ 、 ${{{C_{{\rm{net}}}}} \mathord{\left/ {\vphantom {{{C_{net}}} {{C_{disk}}}}} \right. } {{C_{{\rm{disk}}}}}} < 1$ , 规定该Pod资源相对于该节点属于均衡型.

4.2 适应度函数的选择

启发式算法最重要的是适应度函数选择, 本文选取节点的负载均衡度和节点的可用资源剩余率作为打分标准.

1) 可用资源剩余率

当Pod在集群中任意节点上部署时, 对应节点会获取Pod中应用的需求, 为Pod分配相应的资源. 随着Pod部署的逐渐增多, 节点当前的可用资源在逐渐减少. 定义Pod的各个资源需求量与节点上可用资源的比为可用资源剩余率, 公式如下所示:

$ {{{R}}_{{\rm{CPU}}}} = 1 - \dfrac{{{P_{{\rm{CPU}}}}}}{{{N_{{\rm{CPU}}}} - {S_{{\rm{CPU}}}}}} $

(17)

$ {{{R}}_{{\rm{mem}}}} = 1 - \dfrac{{{P_{{\rm{mem}}}}}}{{{N_{{\rm{mem}}}} - {S_{{\rm{mem}}}}}} $

(18)

$ {{{R}}_{{\rm{net}}}} = 1 - \dfrac{{{P_{{\rm{net}}}}}}{{{N_{{\rm{net}}}} - {S_{{\rm{net}}}}}} $

(19)

$ {{{R}}_{{\rm{disk}}}} = 1 - \dfrac{{{P_{{\rm{disk}}}}}}{{{N_{{\rm{disk}}}} - {S_{{\rm{disk}}}}}} $

(20)

$ {{{R}}_N} = {\mu _1}{R_{{\rm{CPU}}}} + {\mu _2}{R_{{\rm{mem}}}} + {\mu _3}{R_{{\rm{net}}}} + {\mu _4}{R_{{\rm{disk}}}} $

(21)

其中, ${P_{{\rm{CPU}}}}$ 、 ${P_{{\rm{mem}}}}$ 、 ${P_{{\rm{net}}}}$ 和 ${P_{{\rm{disk}}}}$ 分别表示Pod中应用对CPU、内存、带宽和磁盘容量的需求; ${S_{{\rm{CPU}}}}$ 、 ${S_{{\rm{mem}}}}$ 、 ${S_{{\rm{net}}}}$ 和 ${S_{{\rm{disk}}}}$ 表示节点上已经使用的CPU、内存、带宽和磁盘容量的资源量; ${N_{{\rm{CPU}}}}$ 、 ${N_{{\rm{mem}}}}$ 、 ${N_{{\rm{net}}}}$ 、 ${N_{{\rm{disk}}}}$ 则表示节点所拥有的总资源量; ${{{R}}_{{\rm{CPU}}}}$ 、 ${{{R}}_{{\rm{mem}}}}$ 、 ${{{R}}_{{\rm{net}}}}$ 和 ${{{R}}_{{\rm{disk}}}}$ 反映了Pod所需资源部署在节点上的可用CPU剩余率可用内存剩余率、可用带宽剩余率和可用磁盘容量剩余率. ${{{R}}_N}$ 为调度器将Pod部署在某个节点后, 该节点的可用资源剩余率, 其值越大, 该节点分数越高; $ \;{\mu _1} $ 、 $ \;{\mu _2} $ 、 $\; {\mu _3} $ 和 $\; {\mu _4} $ 分别表示 ${{{R}}_{{\rm{CPU}}}}$ 、 ${{{R}}_{{\rm{mem}}}}$ 、 ${{{R}}_{{\rm{net}}}}$ 和 ${{{R}}_{{\rm{disk}}}}$ 的权重, $ \;{\mu _1} $ + $ \;{\mu _2} $ + $ \;{\mu _3} $ + $\; {\mu _4} $ =1. 权重根据Pod的资源类型划分相应的大小.

2) 负载均衡度

当集群中的应用处于低峰期时, 此时应用对节点的资源使用比较低, 此时去选择节点部署Pod, 容易在应用处于高峰期时, 对节点资源的使用增大导致节点的资源过载, 影响集群的负载均衡. 本文选择当集群处于高峰期时的节点资源指标, 用来衡量集群负载大小. 为了预防节点因资源过载而影响节点中的Pod正常运行, 本文为节点上的资源设置最大负载率, 即由(最大负载率–(Pod资源量+高峰期已用资源量)/总资源量)确定, 计算公式如下:

$ {L_{{\rm{CPU}}}} = \frac{{{P_{{\rm{CPU}}}} + {S_{{\rm{CPU}}}}}}{{{N_{{\rm{CPU}}}}}} $

(22)

$ {L_{{\rm{mem}}}} = \frac{{{P_{{\rm{mem}}}} + {S_{{\rm{mem}}}}}}{{{N_{{\rm{mem}}}}}} $

(23)

$ {L_{{\rm{net}}}} = \frac{{{P_{{\rm{net}}}} + {S_{{\rm{net}}}}}}{{{N_{{\rm{net}}}}}} $

(24)

$ {L_{{\rm{disk}}}} = \frac{{{P_{{\rm{disk}}}} + {S_{{\rm{disk}}}}}}{{{N_{{\rm{disk}}}}}} $

(25)

$ \begin{split} {L_N} =& {v_1}\left( {{T_{{\rm{CPU}}}} - {L_{{\rm{CPU}}}}} \right) + {v_2}\left( {{T_{{\rm{mem}}}} - {L_{{\rm{mem}}}}} \right) \\& +{v_3}\left( {{T_{{\rm{net}}}} - {L_{{\rm{net}}}}} \right) + {v_4}\left( {{T_{{\rm{disk}}}} - {L_{{\rm{disk}}}}} \right) \end{split} $

(26)

其中, ${L_{{\rm{CPU}}}}$ 、 ${L_{{\rm{mem}}}}$ 、 ${L_{{\rm{net}}}}$ 和 ${L_{{\rm{disk}}}}$ 分别代表Pod部署在节点上, 该节点的CPU、内存、带宽和磁盘容量负载率; ${T_{{\rm{CPU}}}}$ 、 ${T_{{\rm{mem}}}}$ 、 ${T_{{\rm{net}}}}$ 和 ${T_{{\rm{disk}}}}$ 表示资源的临界负载, 其取值为(0, 1); 式(26)中, $ {L_N} $ 代表着节点的负载均衡度; $ {v_1} $ 、 $ {v_2} $ 、 $ {v_3} $ 和 $ {v_4} $ 为自定义均衡度权重, 其权重大小是根据资源对节点的均衡度的影响程度设置, 其中 $ {v_1} + {v_2} + {v_3} + {v_4} = 1 $ .

节点N的优选总得分计算公式如下:

$ {S_N} = \left( {{R_N} + {L_N}} \right) $

(27)

其中, $ {S_N} $ 表示节点的总得分, 当节点的剩余资源越多 $ {R_N} $ 值越大, 资源综合负载均衡度越高 $ {L_N} $ 值越大, 从而 $ {S _N} $ 值越大, 节点部署Pod的优先越高.

4.3 TBESK调度模型

假设Kubernetes集群由m个配置不尽相同的节点服务器, 有n个待调度的Pod需要调度至m个节点上. 初始种群有x个秃鹰, 秃鹰在m维空间搜索最优解, 最优解即为Pod寻找最优的部署节点. 第k个秃鹰的可行解表示为 $Po{s_k} = \left( {Po{s_k}_1, Po{s_k}_2,\cdots, Po{s_{ki}}, \cdots,Po{s_{kn}}} \right)$ , k∈[1, x], $Po{s_{ki}}$ 表示第i个Pod被调度部署的所在节点, 其取值区间为[1, m]; TBESK策略先根据Pod中资源的需求将Pod分类, 然后则通过3个筛选阶段来确定Pod最终分配节点.

TBESK在选择阶段, 从m个节点中选择最佳搜索区域进行Pod调度, 定义的公式为:

$ {P_{ki, {\rm{new}}}} = {P_{{\rm{best}}}} + \alpha \times \lambda \left( {{P_{{\rm{mean}}}} - Po{s_{ki}}} \right) $

(28)

$ P_{ki, {\rm{new}}}^t = {P_{ki, {\rm{new}}}} + {P_{ki, {\rm{new}}}} \times t\left( n \right) $

(29)

其中, ${P_{ki, {\rm{new}}}}$ 为第k个秃鹰中第i个待调度Pod所在的新节点, ${P_{{\rm{best}}}}$ 为通过自定义的适应度函数计算出上次迭代Pod部署在节点上的最优位置, $ \alpha $ 是用于控制位置更改的参数, 该参数的值介于1.5到2之间; $ \lambda $ 是一个随机数, 取值在0到1之间; ${P_{{\rm{mean}}}}$ 表示这些秃鹰已经用完了之前各点的所有信息; $P_{ki, {\rm{new}}}^t$ 为经过t分布变异后待部署Pod所在新的节点.

TBESK策略在搜索阶段, 秃鹰在选择好的节点区域内选择合适的节点部署Pod, 并在螺旋形区域内不断向不同地方移动, 定义的公式如下:

$ {P_{ki, {\rm{new}}}} = {P_{ki}} + x\left( i \right) \times \left( {{P_{ki}} - {P_{{\rm{mean}}}}} \right) + y\left( i \right) \times \left( {{P_{ki}} - {P_{ki + 1}}} \right) $

(30)

其中, $ x\left( i \right) $ 与 $ y\left( i \right) $ 表示在极坐标下秃鹰的位置, 取值均为(−1, 1); $ {P_{ki + 1}} $ 表示第k只秃鹰下一次Pod更新的位置.

TBESK策略在俯冲阶段, 秃鹰从搜索空间的最佳位置摇摆到它们的目标猎物. 所有的秃鹰也都朝着Pod被调度到最合适的节点移动, 定义公式如下:

$ {P_{ki, {\rm{new}}}} = rand \times {P_{{\rm{best}}}} + {\delta _x} + {\delta _y} $

(31)

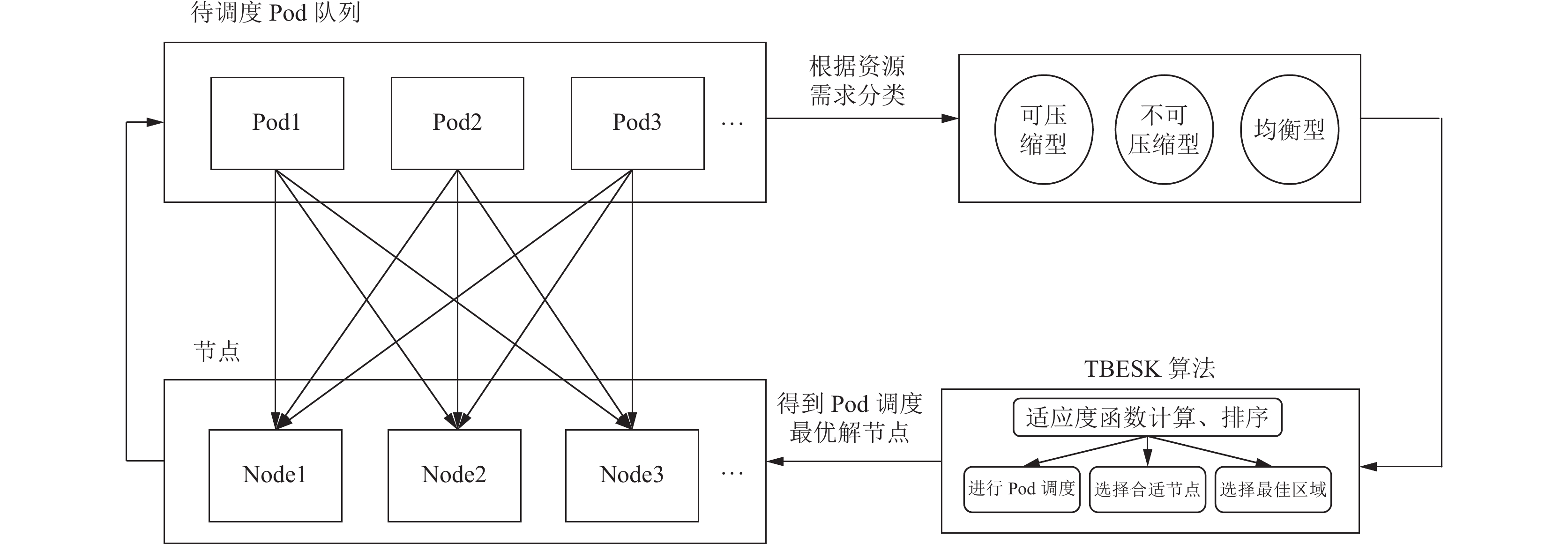
通过3个阶段筛选迭代, TBESK算法选择出最合适Pod分配方案, 调度器将Pod调度到相应的节点上. TBESK调度模型图如图1所示.

5 实验验证与分析

为测试本文提出的TBESK算法在Kubernetes集群的性能, 进行实验验证. 所有实验均由 PyCharm 2020.2编程实现, 并基于平台: Windows 10, AMD Ryzen 5 3550H with Radeon Vega Mobile Gfx 2.10 GHz, 16 GB内存.

5.1 实验环境

本文数据集采用文献[22]中的数据集. 在仿真环境下, 模拟一个包含31个节点的Kubernetes集群, 节点具体信息如表3.

同时, 考虑到节点对不同资源的敏感程度, 将应用需求分为3类: 可压缩消耗型、不可压缩消耗型以及均衡型. 表4显示了部分应用程序请求信息.

5.2 实验评价指标

假定Kubernetes集群是由n台服务器搭建, 其中每台服务器有m种资源. 定义服务器上单个资源的资源利用率为 $ A\left( {i, j} \right) $ , 其中 $ i $ 表示不同的服务器, j表示服务器上的资源; 定义服务器上所有资源利用率总和的平均值为 ${A_{{\rm{avg}}}}$ ; $ Z\left( i \right) $ 代表着服务器 $ i $ 资源失衡度, 即服务器 $ i $ 上的资源标准差之和; ${Z_{{\rm{avg}}}}$ 为集群的平均资源失衡度, 其值越小, 表明集群中资源的分布越均匀, 服务器上的资源不易出现倾斜, 可以为集群提供更多资源去部署Pod:

$ {A_{{\rm{avg}}}} = \sum\limits_{j = 1}^m {\dfrac{{A\left( {i, j} \right)}}{m}} $

(32)

$ Z\left( i \right) = \sqrt {\displaystyle \sum\limits_{j = 1}^m {{{\left( {A\left( {i, j} \right) - {A_{{\rm{avg}}}}\left( i \right)} \right)}^2}} } $

(33)

$ {Z_{{\rm{avg}}}} = \displaystyle \sum\limits_{i = 1}^n {\dfrac{{Z\left( i \right)}}{n}} $

(34)

5.3 实验结果和分析

本文使用Kubernetes平台自带的两种调度的策略: LeastRequestedPriority (LRA)算法、Balanced-ResourceAllocation (BRA) 算法和本文中提出的改进的秃鹰搜索算法(TBESK), 从资源失衡度、CPU、内存、带宽、磁盘容量利用率角度来对比3种算法的表现; 本文还使用了组合权重TOPSIS调度算法(CWT)^[22]以及原始的BES算法与TBESK算法在集群资源失衡度上对比3种算法的表现.

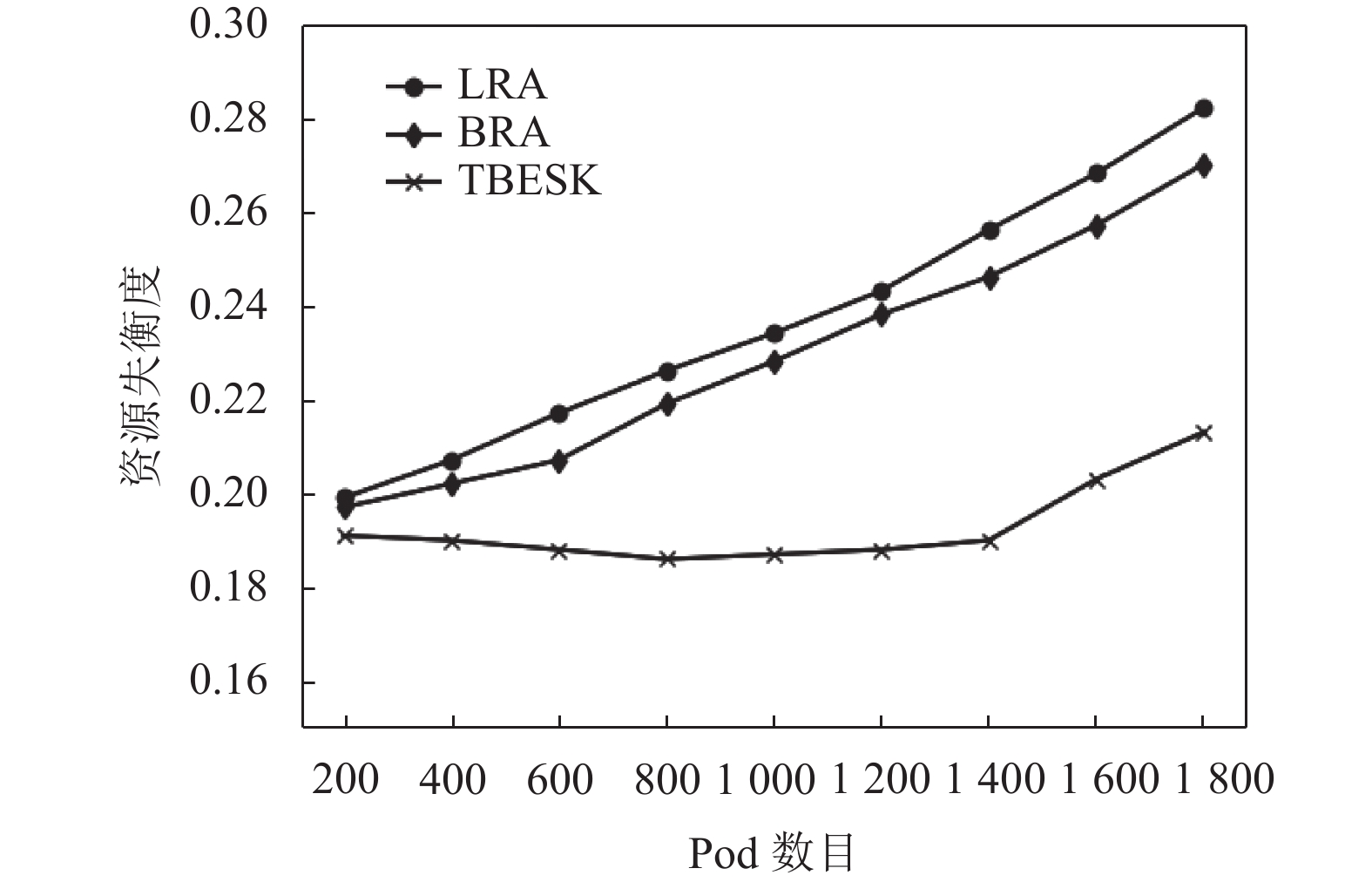
5.3.1 集群资源失衡度

图2为集群资源失衡度曲线, 在Pod应用部署初期阶段, 可以发现TBESK集群失衡度在下降, 这是由于TBESK算法在对Pod进行调度时, 相对于自带的调度算法, 不仅考虑了带宽和磁盘容量两种资源指标、还考虑了Pod资源类型并设置相应的权重, 使节点资源更加均衡, 降低了集群失衡度. 整体上来看, TBESK算法的资源失衡度与LRA算法、BRA 算法相比, 分别下降24%和21%, 这表示TBESK算法可以有效地调节集群负载, 有效降低了节点出现资源使用出现失衡的情况.

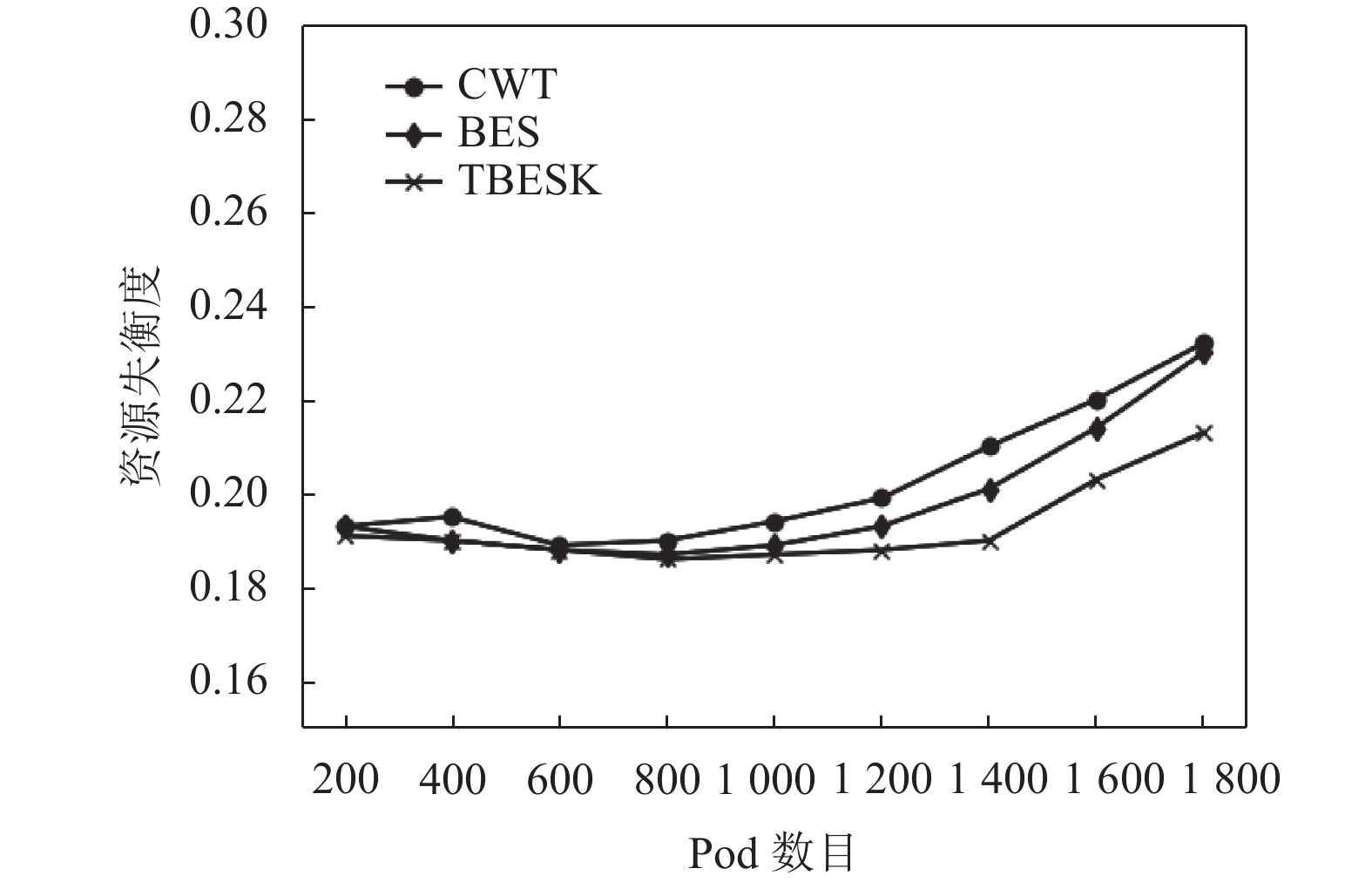
图3为CWT算法、BES算法以及TBESK算法的资源失衡度曲线, 可以发现在Pod数目较少的情况下, 资源失衡度相差不大, 但是随着Pod数目的增多, TBESK相较于其他两种算法在资源失衡度上有着明显的优势

5.3.2 集群资源失衡度

图4和图5体现了当Kubernetes集群中的Pod 数量为1800时, 各个节点分别在TBESK算法、LRA算法和BRA算法作用下, CPU和内存资源利用率. 3种算法都考虑到CPU和内存, 因此在CPU和内存的资源利用率上没有很大的差异.

5.3.3 带宽、磁盘容量资源利用率

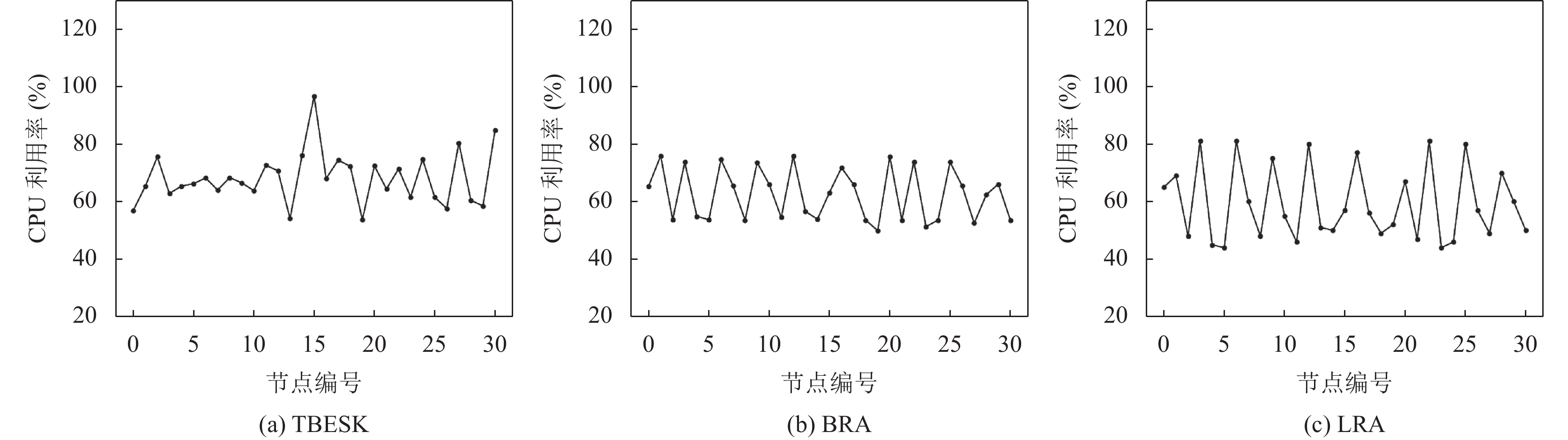
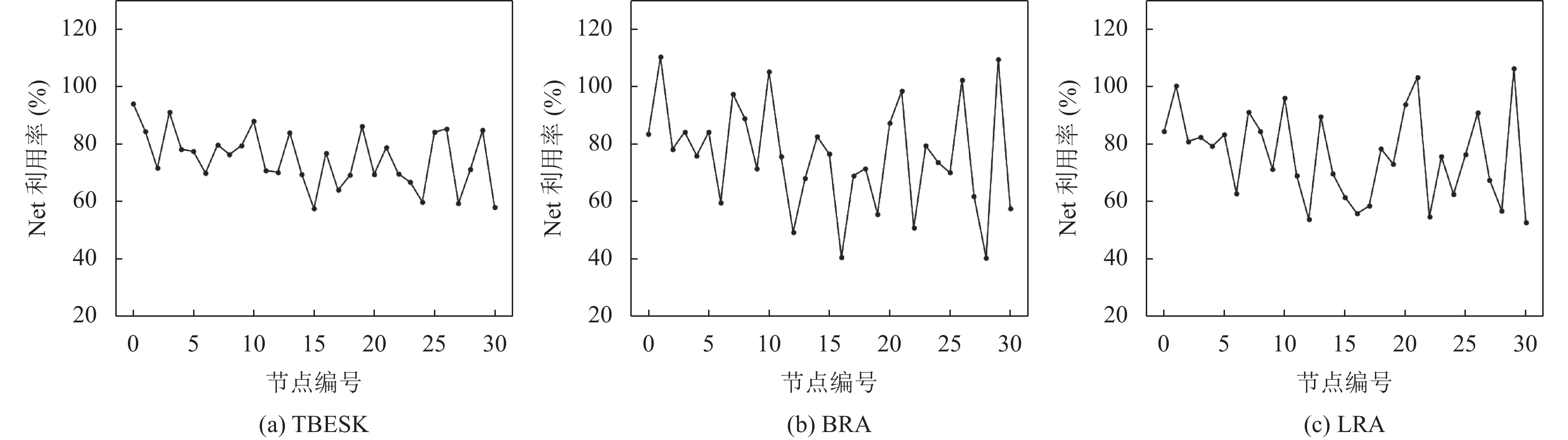
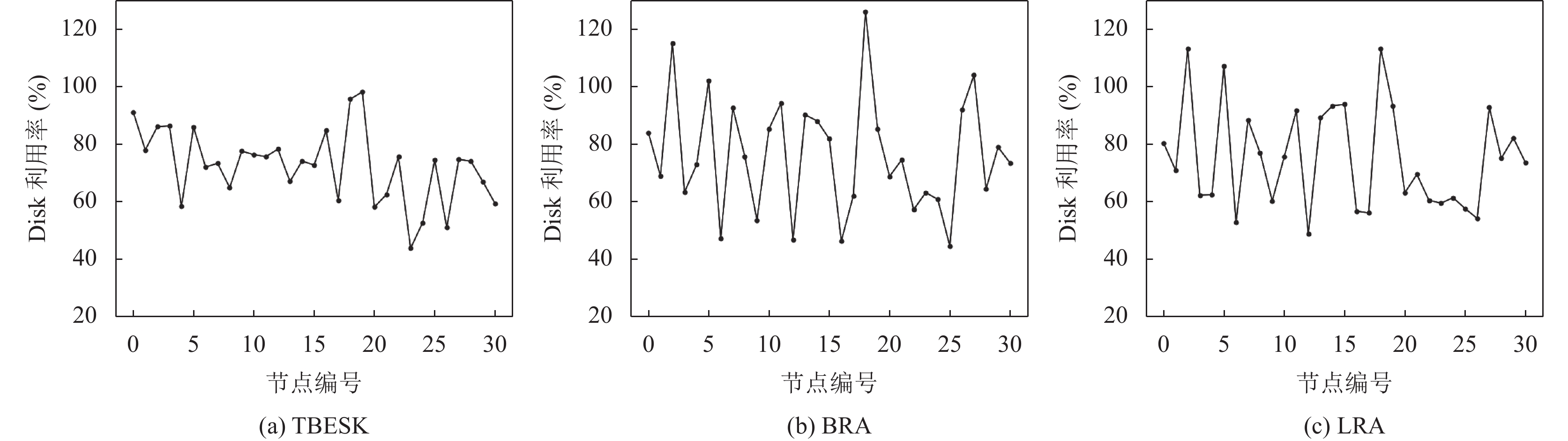
图6和图7展示了在 Pod 数量为1800时, 集群分别在TBESK算法、LRA算法和BRA算法作用下节点的带宽利用率和磁盘容量的资源利用率. 在LRA算法和BRA算法下集群中部分节点网络带宽和磁盘容量出现倾斜, TBESK算法相对于其他两种算法, 集群中节点的带宽利用率和磁盘容量利用率的波动相对较小.

在 LRA 算法下, 集群中不同节点的带宽利用率最大相差54%, 不同节点的磁盘容量利用率最大相差65%, 而在BRA算法下, 集群中不同节点的带宽利用率最大相差60%, 磁盘容量利用率相差80%. 同时可以明显看到集群中部分节点的带宽和磁盘容量的资源利用率已超过100%, 如果继续将相同需求Pod调度这些节点上, 可能导致应用出现一些问题.

在TBESK算法下, 集群中各个节点的带宽资源利用率都在55%到95%的区间内波动, 节点中带宽没有发生超分的情况; 磁盘容量利用率都处在43%到98%的区间内波动, 没有出现磁盘容量超过100%情况, 和LRA算法、BRA算法对比, 集群带宽和磁盘容量在TBESK算法下更加稳定.

6 结论与展望

在Kubernetes集群中, 默认调度算法忽略了应用对不同的资源消耗是不同的, 易导致某一资源到达瓶颈, 同时还忽略了带宽和磁盘容量对节点的影响. 针对上述问题, 本文根据Pod的资源需求, 将Pod分为可压缩消耗型、不可压缩消耗型以及均衡型, 为每种类型Pod的资源自定义相应的权重, 并在CPU、内存资源指标的基础上考虑了带宽、磁盘容量对节点的影响. 考虑秃鹰搜索算法易陷入局部最优和收敛精度低问题, 本文通过Tent映射和自适应t分布来改进秃鹰搜索算法. 最后结合改进的秃鹰搜索算法(TBESK)将待调度的Pod分配在最优节点上, 加强了集群的负载能力, 有效提升了节点的资源利用率. 实验证明改进的秃鹰搜索调度算法的有效性合理性. 下一阶段将考虑Pod的部署速度、成本, 提高集群中Pod在节点的部署速度, 降低集群中Pod的部署成本.