2. 东莞理工学院 计算机科学与技术学院, 东莞 523808
2. School of Computer Science and Technology, Dongguan University of Technology, Dongguan 523808, China
近年来, 深度强化学习算法被广泛应用于解决各类复杂问题. 2014年, DeepMind团队推出深度Q学习算法[1], 在2600个雅达利游戏上实现了人类水平的控制. 2016年, DeepMind团队结合卷积神经网络[2], 蒙特卡洛树搜索[3]和强化学习理论, 推出人工智能机器人AlphaGo[4], 并在围棋项目上以4:1的比分击败了人类世界冠军李世石. 此后, AlphaGo Zero[5]在不使用任何先验知识的前提下以100:0的比分击败AlphaGo, 宣告了人工智能在围棋项目上的全面胜利. 2018年, OpenAI团队推出了OpenAI Five[6], 在Dota2游戏传统的5v5模式下击败了两届世界冠军OG战队. 2019年DeepMind团队基于多智能体强化学习推出AlphaStar[7], 在星际争霸2游戏中达到了人类大师级别的水平, 并于该游戏的官方排名中超越了99.8%的人类玩家. 在上述困难项目中的成功表明, 未来针对深度强化学习领域的研究有着广阔的前景.
一般而言, 深度强化学习算法可分为值函数算法和策略梯度算法(policy gradient, PG)[8]. 值函数算法对回报建模, 在每次迭代中按当前最优策略更新. 策略梯度算法对策略建模, 在每次迭代中小幅修正策略使其收敛. 策略梯度算法相较于值函数算法更为稳定, 但受限于样本使用率低的困境. 策略梯度算法中, 一类解决样本效率问题的算法是确定性策略梯度(deterministic policy gradient, DPG)[9], 这类算法将策略网络由状态的函数修改为状态-动作对的函数, 并通过双价值网络和延迟学习提升稳定性[10, 11]. 另一类算法在随机策略的基础上增加数据复用次数, 最有代表性的包括置信域优化算法(trust region policy optimization, TRPO)[12]和近端策略优化算法(proximal policy optimization, PPO)[13]. TRPO算法提出一种代理目标, 通过优化该代理目标并限制更新前后策略分布的KL散度(Kullback-Leibler divergence)实现优化过程. PPO算法使用近似点优化替代TRPO算法中的置信域优化, 降低了计算过程的复杂性[14]. PPO的具体实现算法包括PPO-Clip和PPO-Penalty. 其中PPO-Clip在代理目标中引入了裁切方法, 在实际应用中适用性更广. 一些研究通过细化裁切理论改进PPO-Clip算法.
PPO-
早期停止的近端策略优化算法(PPO with early stopping)[18]和使用衰减裁切边界的近端策略优化算法(PPO with decaying clipping range)[19]在注重保留PPO-Clip算法简洁性的同时提升性能. 早期停止算法选择在KL散度首次到达边界的时候停止更新, 直接进入下一轮采样. 而边界衰减算法在整个更新过程中不断收窄裁切边界, 从而保证算法的稳定性.
PPO-Clip算法的理论部分基于TRPO算法, 但是基于近似点的优化并不能保证TRPO算法中提出的置信域. 反过来, 如果直接将TRPO优化目标中的置信域约束条件直接引入则会使PPO-Clip算法失去简洁性. 一个兼顾两者的方案是赋予裁切边界一定的灵活度, 并通过对裁切边界的调整将参数约束在置信域范围中. 基于以上观点, 本文提出双裁切近端策略优化算法(proximal policy optimization with double clipping boundaries, PPO-DC). 该算法继承了PPO-Clip算法的主体, 不同的是PPO算法使用单一且固定的裁切边界, PPO-DC算法使用双裁切边界. 在一次更新中, 每个样本依概率选择其中一个裁切边界, 该概率值是一个正态分布累计分布函数的输出. 而该累计分布函数的输入为采样簇上的平均KL散度的对数. PPO-DC的理论部分基于TRPO论文提出的置信域优化目标, 其基本思路是将当前策略网络参数尽可能地置于置信域边界, 以保证样本数据得到充分利用. 而使用双裁切的一个优势在于, 算法可以通过选择任意一条边界自适应的调整KL散度, 并且依概率的决策方式可以保证以上调整的平滑性.
本文的第1节介绍了策略梯度算法的相关知识以及一些基于PPO裁切方法的研究. 第2节通过一些小规模实验探讨了裁切机制的作用原理, 并在此基础上提出PPO-DC算法. 第3节使用OpenAI的Gym作为测试环境[20], 在Mujoco[21]和Box2d的多个连续控制任务中对比了多个算法的性能. 实验结果表明, PPO-DC算法拥有较好的性能.
1 相关工作 1.1 马尔可夫决策过程强化学习中, 常使用有限马尔可夫决策过程对连续控制任务建模. 一个完整的马尔科夫决策过程包括状态空间
深度强化学习算法一般分为值函数算法和策略梯度算法[8]. 值函数方法中, 智能体对累计回报建立神经网络模型, 并在决策中根据贪心参数选择是否试探. 在试探决策中选择随机动作, 在非试探决策中选择值函数最大动作, 最后根据反馈更新值函数模型. 在实际应用中, 值函数方法只能处理动作空间离散且低维的情况.
在策略梯度方法中, 智能体对决策方案建立神经网络模型, 根据输出概率分布选择动作, 在收到环境反馈的序列后, 通过贝尔曼方程计算各节点蒙特卡洛回报值, 最后使用策略梯度方法更新决策函数模型. 策略梯度的表达式如下:
| ∇J(θ)=∑Qst,at∇θlogπθ(at|st) | (1) |
其中,
策略梯度算法是单步更新的, 每一次迭代都会淘汰用过的样本, 这是因为策略梯度定理中的优化目标建立在目标策略的状态分布上. 而改进这一点需要把优化目标建立在当前或过去策略的状态分布上, 故有策略改进下界:
| {J(π)−J(πk)⩾11−γE(s,a)∼dπk[π(a|s)πk(a|s)Aπk(s,a)]−2γCπ,πk(1−γ)2Es∼dπk[TV(π,πk)(s)]Cπ,πk=maxs∈S|Ea∼π(⋅|s)[Aπk(s,a)]| | (2) |
其中,
| {maxθEs∼ρθold,a∼q[πθ(a|s)q(a|s)Qθold(s,a)]subjecttoEs∼ρθold[DKL((πθold⋅|s)||(πθ⋅|s))]⩽δ | (3) |
其中,
| LCLIP(θ)=E[min(rt(θ)At,(rt(θ),1−ε,1+ε)At)] | (4) |
其中,
| {ˆAt=δt+(γλ)δt+1+⋯+(γλ)T−t+1δT−1δt=rt+γV(st+1)−V(st) | (5) |
其中,
在实际训练中,
| LCLIP+VF+St(θ)=ˆEt[LCLIPt(θ)−c1LVFt(θ)+c2S[πθ](st)] | (6) |
其中,
| {LVFt=(Vθ(st)−Vtargt)2Vtargt=rt+γVθ(st+1) | (7) |
其中,
PPO-Clip算法通过引入裁切机制完成TRPO的优化目标中对KL散度的约束, 但是论文没有在理论上给出裁切的作用原理, 本节内容将从实验的角度对此进行探讨.
图1(a)对比了使用不同裁切系数的PPO-Clip算法在Hopper任务上的训练曲线. 随着裁切系数的增加, 训练曲线变得更不稳定. 从第1.3节中式(2)的策略改进下界可知保持训练稳定的前提是将更新前后的策略分布间距限制在一定范围内, 该间距可通过KL散度衡量.

|
图 1 使用不同裁切系数的PPO-Clip算法在Hopper任务上的训练结果 |
图1(b)和图1(c)分别对比了训练过程中的KL散度的平均值和最大值. 可以看到
以上实验得出的一个结论是, 使用经验较优的裁切系数
从第2.1节实验可知较宽松的裁切系数只对KL散度有限制性, 却不具备严格定义其上界的能力. 而式(3)明确了约束KL散度是稳定优化过程的前提, 这也是置信域优化算法的核心思想. 改进PPO算法的一个思路是使裁切方法实现对KL散度的严格约束, 同时尽可能保留算法对样本的重复利用率. 图1(b)表明收窄裁切边界会对KL散度进行更严格的限制, 因此一个直观的想法是动态调整裁切边界, 使KL散度保持在合理范围内. 该范围下的参数须满足两个条件: 一是落在置信域内, 二是尽量靠近置信域边界. 前者是置信域优化的核心, 后者是提升样本利用率的核心.
PPO-DC算法基于以上思路被提出. 该算法确定两个裁切边界, 按概率选择其中一个使用. 上述概率随当前状态下的KL散度动态调整, 目的是将KL散度限制在一个合理范围内. 两段裁切系数虽然是超参数, 但是它们应具有以下特点: 内边界应当严格限制更新幅度, 侧重于保证置信域; 外边界应当放宽更新幅度, 侧重于提升样本利用率.
2.3 PPO-DC算法内容PPO-DC算法使用双裁切系数, 生成两段裁切边界. 若KL散度偏高, 则增加样本被内边界裁切的概率, 减小被外边界裁切的概率, 若偏低则反之. 算法的总体优化目标如下:
| LDclip(θ)=E(st,at)∼τ,εt∼Dm[min(rt(θ)At,clip(rt(θ),1−εt,1+εt)At)] | (8) |
其中,
| {P{εt=εL}=pmP{εt=εU}=1−pm(0⩽pm⩽1) | (9) |
其中, 超参数
| X∼N(μ,σ) | (10) |
其中, 超参数
| pm=F(xm)=P(X⩽xm)=1√2πσ∫xm−∞e−(t−μ)22σ2dtxm→ln[Es∼τ[DKL(π0,πm)]+ω] | (11) |
其中,
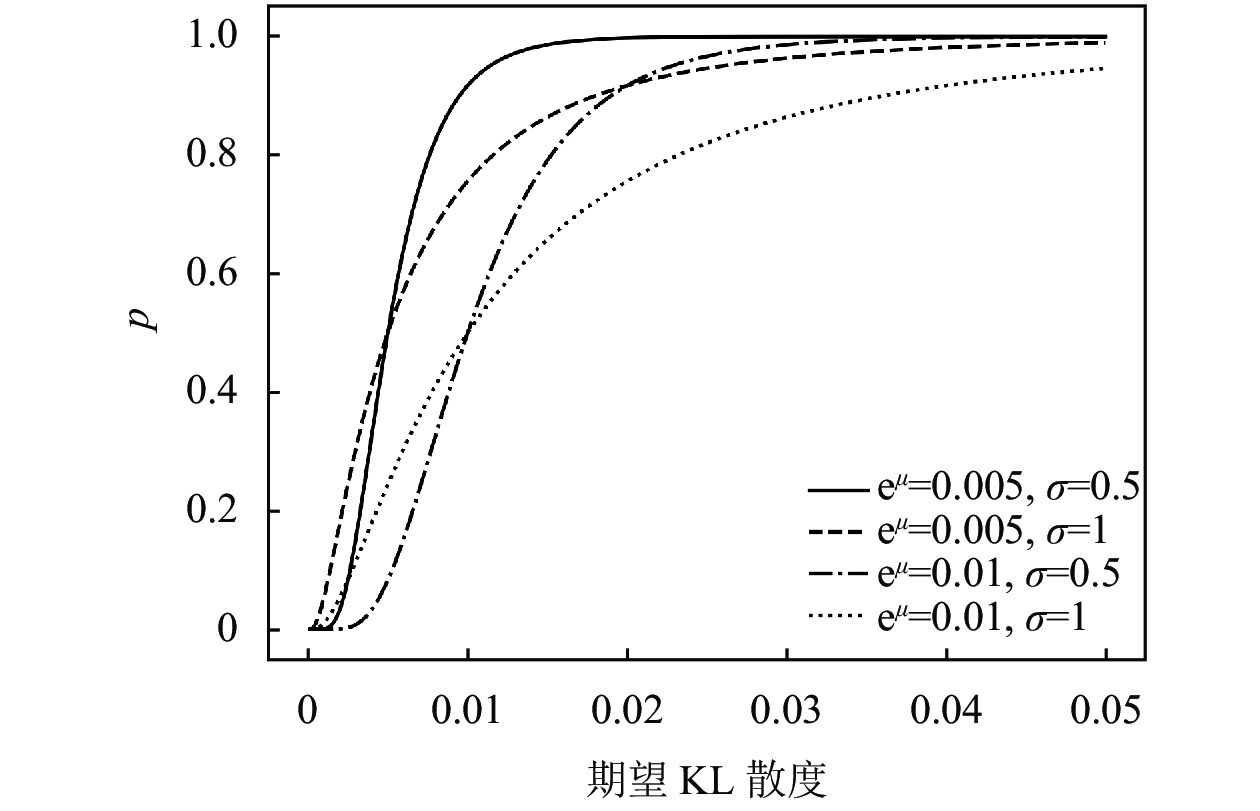
|
图 2 不同
|
式(11)中期望KL散度的表达式如下:
| Es∼τ[DKL(π0,πm)]=Es∼τ,a∼π0[logπ0(a|s)πm(a|s)] | (12) |
式(12)的计算有两种方法, 一种是在采样簇上对每个样本的动作分布积分后求均值:
| Es∼τ,a∼π0[logπ0(a|s)πm(a|s)]=1TT−1∑t=0∫ahighalowlogπ0(u|st)πm(u|st)du | (13) |
其中, 超参数T为单轮更新采样步数,
| Es∼τ,a∼π0[logπ0(a|s)πm(a|s)]≈1TNT−1∑t=0N−1∑n=0,at,n∼π0(⋅|st)[logπ0(at,n|st)πm(at,n|st)] | (14) |
其中, 超参数N是动作抽样次数, 通常根据计算资源决定. 蒙特卡洛法获得当前采样簇上的近似解, 使用该方法的好处在于能够通过超参数自由平衡计算资源与计算精度.
PPO-DC算法的具体流程见算法1. 该算法引入4个超参数, 分别是式(9)中的双裁切系数
| 算法1. PPO-DC |
| 1. 初始化策略网络
|
本文使用OpenAI的强化学习环境库Gym作为实验平台, 在标准控制任务和Box2d环境中对比了几种算法的性能. 测试采用PyTorch作为深度学习框架, 并选择ElegantRL[25]作为强化学习基线.
第3.4节实验在Mujoco环境上进行, 包括5个控制任务Walker2d, Swimmer, Ant, Hopper, Half-Cheetah. Mujoco是DeepMind公司开发的物理仿真引擎. 以HalfCheetah任务为例, 智能体接收17维的状态输入, 并输出6维动作控制仿真机器人的不同关节. 算法在二维仿真环境内训练双足机器人前进, 训练得分与前进速度成正比. 图3为可视化的Mujoco环境.

|
图 3 Mujoco引擎上的连续控制任务 |
第3.5节的实验在Box2d环境上进行, 环境包括2个连续控制任务BipedalWalker和LunarLander. 在BipedalWalker任务中, 智能体接收24维状态并输出6维动作, 以此控制一个双足机器人前进, 并被要求能够行走得更为快速和稳健. 该环境被认为是连续控制任务里较难的一个. LunarLander任务则模拟了宇宙飞船在月球的着陆过程. 智能体接收8维状态并输出2维动作, 分别控制两个不同位置的推进器. 训练的总体目标为调整宇宙飞船双足平稳着陆在目标区域内, 并在接触地面的瞬间速度小于一个阈值. 若飞船顺利着陆环境将反馈一个+100的奖励, 反之若撞毁则反馈一个−100的奖励.图4为可视化的Box2d环境.

|
图 4 Box2d环境上的连续控制任务 |
本节实验的评价方法如下: 在Mujoco和BipedalWalker任务中, 通过计算所有幕的平均回报评价算法的训练速度, 计算最后100幕的平均回报评价算法的最终性能. 在LunarLander任务中, 由于飞船完成着陆后的回报基本恒定, 故通过计算首次成功着陆的采样轮数评价训练速度.
3.2 超参数PPO-DC算法主干部分与PPO-Clip算法一致, 因此继承了原算法的主要超参数. 表1列出了通用超参数的取值, 这些取值同时被应用于对比算法中. 除此以外PPO-DC算法引入了4个超参数, 其中
| 表 2 通用超参数取值表 |
两段裁切系数
表2对比了超参数
|
表 3 超参数
|
3.3 参与对比的算法
参与对比的算法除PPO-DC与PPO-Clip[9]外, 还包括PPO-Penalty[9], PPO-S[13]以及PPO-Decay[15]. 一些算法引入了新的超参数, 本节内容将介绍这些算法的核心内容并给出超参数的取值.
3.3.1 PPO-PenaltyPPO-Penalty是将KL散度作为罚项引入优化目标的方法, 优化目标如下:
| Lpenalty(θ)=E[πθ(at|st)πθold(at|st)ˆAt−βKL[πθold(⋅|st),πθ(⋅|st)]] | (15) |
其中, 超参数
PPO-S是PPO-RB的一种改进算法, 其裁切方法如下:
| ratioPPOS={−αtanh(rs,a(π)−1)+1+ε+αtanh(ε),rs,a(π)⩽1−ε−αtanh(rs,a(π)−1)+1−ε+αtanh(ε),rs,a(π)⩾1+εrs,a(π),otherwise | (16) |
其中,
PPO-Decay则是一种在单轮训练中不断衰减裁切边界的算法. 其边界衰减方式有两种, 分别为线性衰减与指数衰减. 对比实验选择线性衰减方式, 其表达式如下:
| εt=T−tTε0 | (17) |
其中, T是单轮更新采样步数, t是当前更新步数,
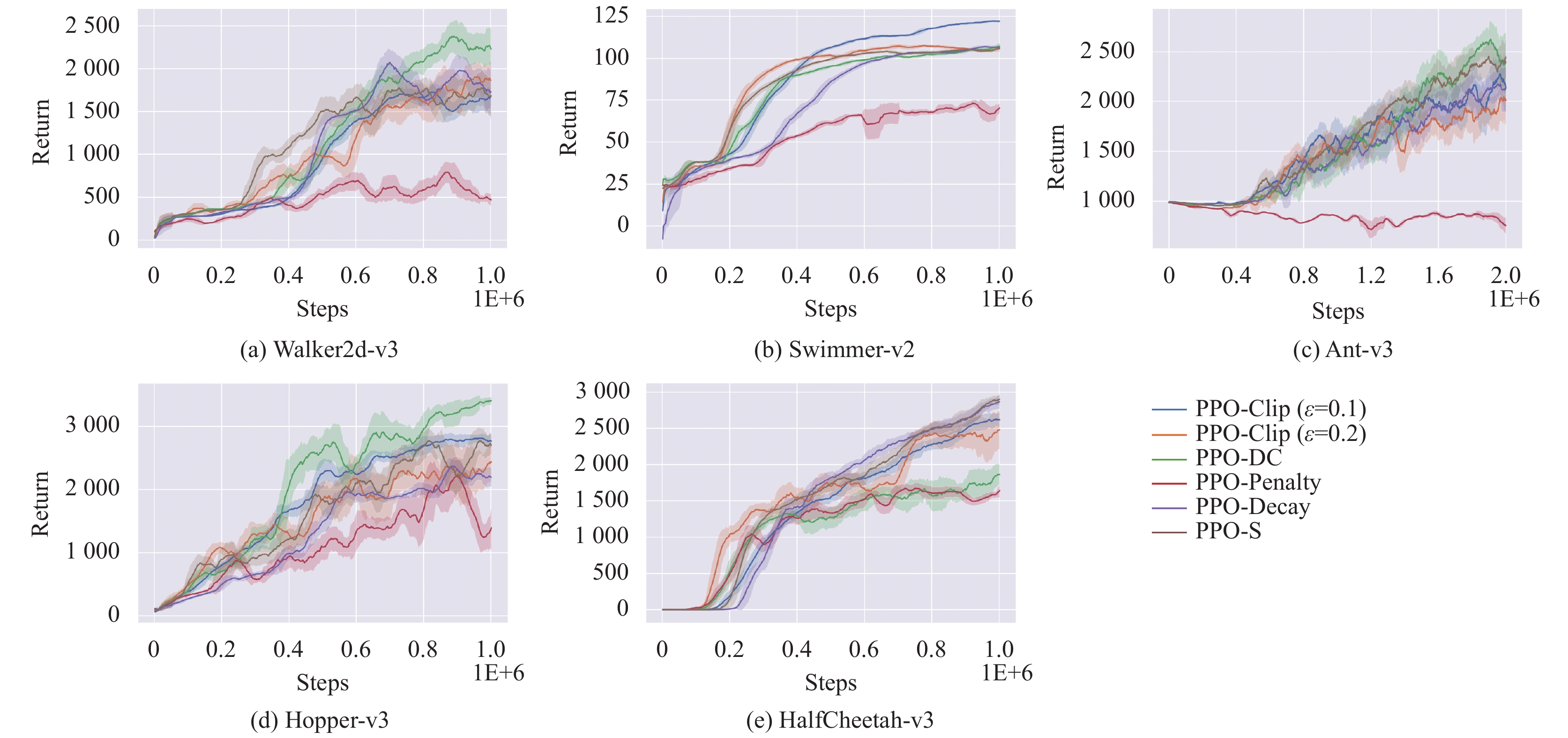
本节实验对比了不同算法在Mujoco环境上的运行结果, 环境包括5个标准控制任务Walker2d, Swimmer, Ant, Hopper, HalfCheetah. 由于Ant是三维控制环境, 接收111维状态并输出8维动作, 学习难度较高, 故训练在Ant任务上运行2E+6步, 在其余任务上运行1E+6步. 评价在完成一轮更新后进行, 选择策略网络输出分布的均值作为每步动作, 在完成一整幕后计算总回报, 取5次实验的平均值作为结果. 训练曲线见图5. 通过计算所有幕的平均回报评价算法的训练速度, 计算最后100幕的平均回报评价算法的最终性能. 评价数据见表3.
|
图 5 不同算法在5个Mujoco任务上的训练曲线 |
首先, 无论采用两种指标的哪一种评价, PPO-DC算法在Walker2d和Hopper两个任务下的分数都是6个对比算法中最高的. 尤其是在Hopper任务中, 该算法的得分远超其他算法. 而在Ant任务中, PPO-DC算法展现了优秀的最终性能, 并在180万步后超越了其余所有算法. 在Swimmer任务中, 最好的结果来自
其次, PPO-DC与PPO-Clip的对比能帮助我们判断双裁切是否真正有效, 因为PPO-DC依概率采用
另一个观察角度是置信域. 图6对比了训练过程中平均KL散度的变化, 参与对比的算法包括PPO-Clip和PPO-DC. PPO-Clip算法采用
| 表 4 Mujoco环境下的对比实验结果 |

|
图 6 PPO-Clip和PPO-DC算法在5个Mujoco任务上的平均KL散度 |
3.5 不同算法在Box2d任务上的对比实验
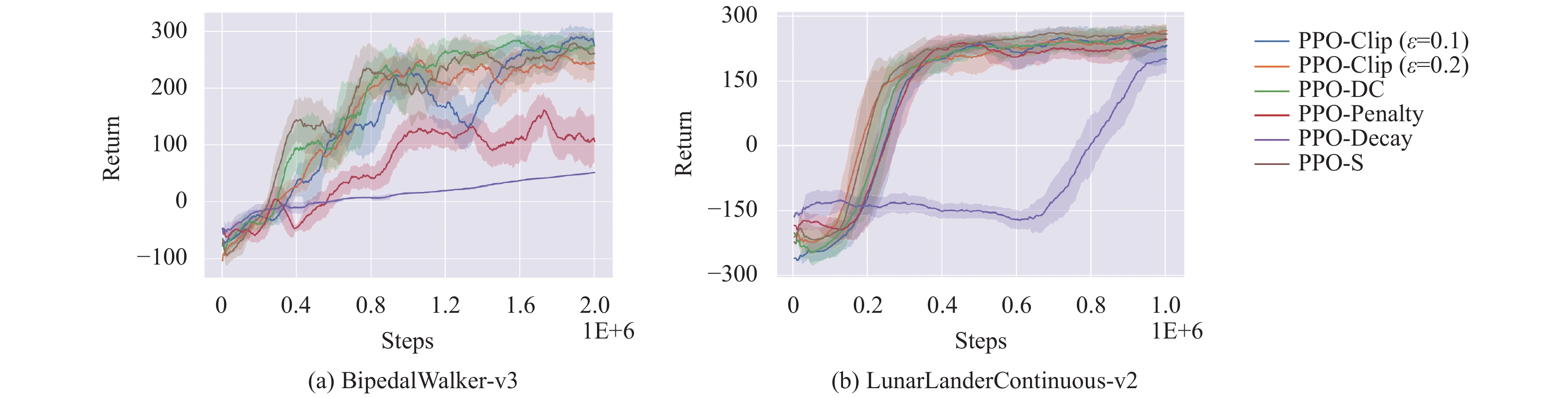
本节实验对比了不同算法在Box2d任务上的运行结果, 环境包括2个连续控制任务BipedalWalker和LunarLander. 训练在BipedalWalker任务上运行2E+6步, 在LunarLander上运行1E+6步. 评价在完成一轮更新后进行, 选择策略网络输出分布的均值作为每步动作, 在完成一整幕后计算总回报, 取5次实验的平均值作为结果. 训练曲线见图7. 由于LunarLander任务目标为宇宙飞船稳定着陆, 故使用首次成功着陆时的采样轮数作为评价指标. 评价数据见表4.
BipedalWalker任务中表现较好的算法包括PPO-DC和PPO-S. 虽然PPO-Clip在
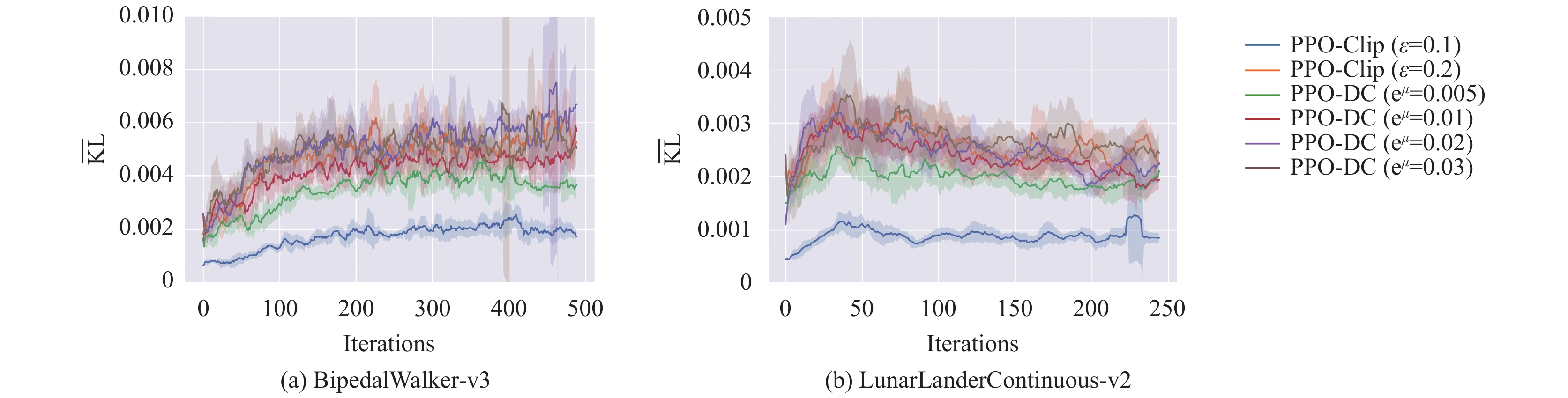
图8对比了两类算法在训练过程中的平均KL散度变化. 由于使用了较大的更新批次, KL散度的波动相对前一节实验稳定, 而各曲线随超参数变化的排列顺序较为明显. LunarLander任务的KL散度曲线在初始阶段上升并在其后缓慢下降, 这是因为算法在早期已达成了训练目标.
|
图 7 不同算法在2个Box2d任务上的训练曲线 |
| 表 5 Box2d环境下的对比实验结果 |
4 结论
虽然PPO算法本身的设计理念是使用近似点替代置信域, 并不严格要求参数落在置信域内, 但是更新后的参数也应当被限制在合理的范围内. PPO-Clip算法无法保证这一点, 实验表明当使用较宽松裁切系数时, KL散度的上界无法被确立, 这有悖于置信域优化目标. 基于以上缺陷, 本文对经典PPO-Clip算法改进, 提出了PPO-DC算法. 该算法使用两段裁切的代理目标, 每段边界被选择的概率随训练轮数的迭代而变化. 其中内边界被选择的概率是一个正态分布累计分布函数的输出, 该函数的输入为采样簇上平均KL散度的对数, 外边界被选择的概率与之相反. 这样做的优势在于, 当参数越过置信域边界, PPO-DC算法能通过提升内边界的概率严格约束KL散度. 反之, 当置信域得到保证, 外边界被选择的概率提升, 样本更有可能得到宽幅的更新.
|
图 8 PPO-Clip算法和PPO-DC算法在2个Box2d任务上的平均KL散度 |
在Mujoco和Box2d环境的多个连续控制任务上, 本文对比了不同算法的训练曲线, PPO-DC算法的性能是所有算法中是最优的. 同时, 本文也对比了改进前后算法在训练过程中的KL散度变化, 结果表明PPO-DC算法可以在使用较宽松裁切系数的情况下完成对KL散度的约束.
| [1] |
Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning. Nature, 2015, 518(7540): 529-533. DOI:10.1038/nature14236 |
| [2] |
He KM, Zhang XY, Ren SQ, et al. Deep residual learning for image recognition. Proceedings of the 2016 IEEE conference on Computer Vision and Pattern Recognition. Las Vegas: IEEE, 2016. 770–778.
|
| [3] |
Browne CB, Powley E, Whitehouse D, et al. A survey of monte carlo tree search methods. IEEE Transactions on Computational Intelligence and AI in Games, 2012, 4(1): 1-43. DOI:10.1109/TCIAIG.2012.2186810 |
| [4] |
Silver D, Huang A, Maddison CJ, et al. Mastering the game of Go with deep neural networks and tree search. Nature, 2016, 529(7587): 484-489. DOI:10.1038/nature16961 |
| [5] |
Silver D, Schrittwieser J, Simonyan K, et al. Mastering the game of go without human knowledge. Nature, 2017, 550(7676): 354-359. DOI:10.1038/nature24270 |
| [6] |
Berner C, Brockman G, Chan B, et al. Dota 2 with large scale deep reinforcement learning. arXiv:1912.06680v1, 2019.
|
| [7] |
Vinyals O, Babuschkin I, Czarnecki WM, et al. Grandmaster level in StarCraft II using multi-agent reinforcement learning. Nature, 2019, 575(7782): 350-354. DOI:10.1038/s41586-019-1724-z |
| [8] |
Sutton RS, Barto AG. Reinforcement Learning: An Introduction. Boston: MIT Press, 2018. 216–320.
|
| [9] |
Silver D, Lever G, Heess N, et al. Deterministic policy gradient algorithms. Proceedings of the 31st International Conference on International Conference on Machine Learning. Beijing: JMLR.org, 2014. I-387–I-395.
|
| [10] |
Lillicrap TP, Hunt JJ, Pritzel A, et al. Continuous control with deep reinforcement learning. arXiv:1509.02971, 2015.
|
| [11] |
Fujimoto S, van Hoof H, Meger D. Addressing function approximation error in actor-critic methods. Proceedings of the 35th International Conference on Machine Learning. Stockholmsmässan: PMLR, 2018. 1582–1591.
|
| [12] |
Schulman J, Levine S, Abbeel P, et al. Trust region policy optimization. Proceedings of the 32nd International Conference on Machine Learning. Lille: PMLR, 2015. 1889–1897.
|
| [13] |
Schulman J, Wolski F, Dhariwal P, et al. Proximal policy optimization algorithms. arXiv:1707.06347, 2017.
|
| [14] |
Engstrom L, Ilyas A, Santurkar S, et al. Implementation matters in deep RL: A case study on PPO and TRPO. 8th International Conference on Learning Representations. Addis Ababa: OpenReview.net, 2020. 1–14.
|
| [15] |
Chen G, Peng YM, Zhang MJ. An adaptive clipping approach for proximal policy optimization. arXiv:1804.06461, 2018.
|
| [16] |
Wang YH, He H, Tan XY. Truly proximal policy optimization. Proceedings of the 35th Uncertainty in Artificial Intelligence Conference. Tel Aviv: PMLR, 2020. 113–122.
|
| [17] |
Zhu WS, Rosendo A. A functional clipping approach for policy optimization algorithms. IEEE Access, 2021, 9: 96056-96063. DOI:10.1109/ACCESS.2021.3094566 |
| [18] |
Dossa RFJ, Huang SY, Ontañón S, et al. An empirical investigation of early stopping optimizations in proximal policy optimization. IEEE Access, 2021, 9: 117981-117992. DOI:10.1109/ACCESS.2021.3106662 |
| [19] |
Farsang M, Szegletes L. Decaying clipping range in proximal policy optimization. Proceedings of the 2021 IEEE 15th International Symposium on Applied Computational Intelligence and Informatics (SACI). Timisoara: IEEE, 2021. 521–526.
|
| [20] |
Brockman G, Cheung V, Pettersson L, et al. OpenAI gym. arXiv:1606.01540v1, 2016.
|
| [21] |
Todorov E, Erez T, Tassa Y. MuJoCo: A physics engine for model-based control. Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems. Vilamoura-Algarve: IEEE, 2012. 5026–5033.
|
| [22] |
Kakade SM. A natural policy gradient. Proceedings of the 14th International Conference on Neural Information Processing Systems: Natural and Synthetic. Vancouver: MIT Press, 2001. 1531–1538.
|
| [23] |
Schulman J, Moritz P, Levine S, et al. High-dimensional continuous control using generalized advantage estimation. arXiv:1506.02438, 2015.
|
| [24] |
Haarnoja T, Zhou A, Abbeel P, et al. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. Proceedings of the 35th International Conference on Machine Learning. Stockholmsmässan: PMLR, 2018. 1861–1870.
|
| [25] |
Liu XY, Li ZC, Yang ZR, et al. ElegantRL-Podracer: Scalable and elastic library for cloud-native deep reinforcement learning. arXiv:2112.05923, 2021.
|
 2023, Vol. 32
2023, Vol. 32



