道路交通安全是交通工程领域的热点研究问题, 路面抗滑性能是道路交通安全的保障. 路面抗滑性能取决于车辆轮胎与路面之间的摩擦力, 摩擦力的不足使得车辆不能及时刹车, 从而引发交通事故[1], 由于抗滑能力不足导致的车辆侧翻被归为一大交通事故原因[2], 因此摩擦系数被选作衡量路面抗滑性能的关键指标[3-5]. 目前, 已经开发出许多不同的摩擦系数检测设备[6]. 主要根据标准轮胎与路面之间的相互作用力衡量摩擦系数, 可分为定点式摩擦测试设备和连续式摩擦测试设备[7]. 其中, 定点式摩擦测试设备有摆式摩擦系数测试仪、动态摩擦系数测试仪等. 连续式摩擦测试设备有小型移动式摩擦测试仪、横向力系数测试车等. 《公路路基路面现场测试规程》JTG 3450-2019中规定了若干用于评定路面表面抗滑性能的摩擦测试设备, 然而, 使用摩擦测试设备检测摩擦系数的检测效率较低, 结果受主观性因素影响, 且稳定性差[8]. 因此, 有必要探究路面抗滑性能的影响因素, 并通过影响因素分析预测出路面抗滑性能.
针对路面抗滑性能影响因素, 《公路沥青路面设计规范》JTG D50-2017中提到, 路面材料的选择, 路基湿度状态以及等效温度等因素的改变均会破坏路面结构的安全性与耐久性, 从而影响路面表面的抗滑性能. 国内外也已有许多相关研究. Liu等人[9]使用激光扫描设备获取路面纹理, 计算出SMTP, Ssk, Sku, Sq共4类统计学纹理特征参数用于表征纹理, 并与环道仪(CTM)以及高速纹理分析器(HSTP)得到的纹理进行对比. Hu等人[10]依照ISO25178标准由路面宏观纹理提取出Sa、Ssk、Sku、Sq、Sdq、Sdr、Spd、Spc共8类统计学纹理特征参数用于表征纹理. 钱振东等人[11]通过差分盒维数法计算出理分形维数, 研究分形维数与抗滑性能的关系. 徐粒[12]使用软件计算出综合统计学特征参数、横向纹理特征参数及几何特征参数用于表征纹理相关性分析筛选有效特征. 刘林等人[13]综合ISO25178标准中的高度参数, 空间参数与符合参数, 并通过二维傅里叶频谱计算出二维功率密度以及波长用于表征纹理. 以上文献主要研究了路面纹理表征以及路面纹理与抗滑性能的关联, 然而大多数研究止步于计算纹理特征与抗滑性能的线性相关性, 而忽视了多维特征间的非线性关系, 且没有对多维特征进行特征工程分析, 无法较好地体现纹理特征与抗滑性能的关联.
针对路面抗滑性能预测研究, 彭毅等人[14]使用动态摩擦系数测试仪(DFT)采集70 km/h和15 km/h时的动态摩擦系数, 分别用于衡量高速与低速状态下的路面抗滑性能, 并构建多元线性回归模型, 使用多个区域纹理特征参数预测路面抗滑性能. 杨跃琴[15]使用DFT采集20 km/h、40 km/h及60 km/h时的动态摩擦系数, 分别计算了统计特征参数、横向宏观纹理参数及几何特征参数, 构建线性回归模型与基于B-P算法的多元感知模型预测路面抗滑性能. Fwa[16]分析了不同水膜厚度和车辆速度条件下的路面抗滑性的关系, 并提出了一个从力学角度推导的三维有限元抗滑性模拟模型来预测抗滑性. 黄正伟[17]通过运用摆式摩擦系数仪对制作的AC-13C、AK-13A、SMA-13三种不同类型沥青路面试块进行了在不同潮湿度、温度、砂砾覆盖量条件下的路面抗滑性研究, 并设计了缩尺车模实验, 反应出动态情况下路面影响因素的变化对车辆的摩擦系数的影响. 战友等人[18]分别获取行车道轮迹带路面摩擦数据、宏观纹理以及集料表面三维微观纹理数据, 构建随机森林模型预测路面抗滑性能. 以上文献的研究中构建的预测模型较为传统, 而随着人工智能技术的发展, 机器学习中回归预测模型在道路工程领域的发展应用愈加广泛[19-21], 为路面抗滑性能的预测提供了新的技术手段. 本文基于机器学习领域的前沿研究, 构建基于IGWO-XGBoost融合的抗滑性能预测模型.
本文的主要工作如下.
(1)选取由加速加载设备磨耗的沥青混合料试件, 使用Gocator 3110三维智能传感器、电动铺砂仪及摆式摩擦仪分别采集表面纹理、构造深度及摩擦系数.
(2)使用基于RBF的邻域插值算法对采集的三维纹理点云数据进行数据质量提升, 并对采集的数据进行特征筛选, 去除冗余特征.
(3)构建基于IGWO-XGBoost融合的抗滑性能预测模型, 预测沥青路面的摩擦系数.
1 沥青混合料试件数据采集本文选取由加速加载设备磨耗的沥青混合料试件, 选用的沥青混合料包含AC、SMA以及OGFC, 混合料集配类型如表1所示.
首先使用Gocator 3110高精度三维智能传感器采集路面三维纹理点云数据, 使用电动铺砂仪采集路面构造深度. 其次, 使用摆式摩擦仪进行实验以获取不同含水量下路面摩擦系数. 接着, 对采集的三维纹理点云数据进行质量提升. 在此基础上, 表征并计算并三维纹理特征. 最后, 建立多特征条件下的路面抗滑性能预测模型.
| 表 1 混合料集配类型 |
1.1 高精度三维纹理点云数据采集
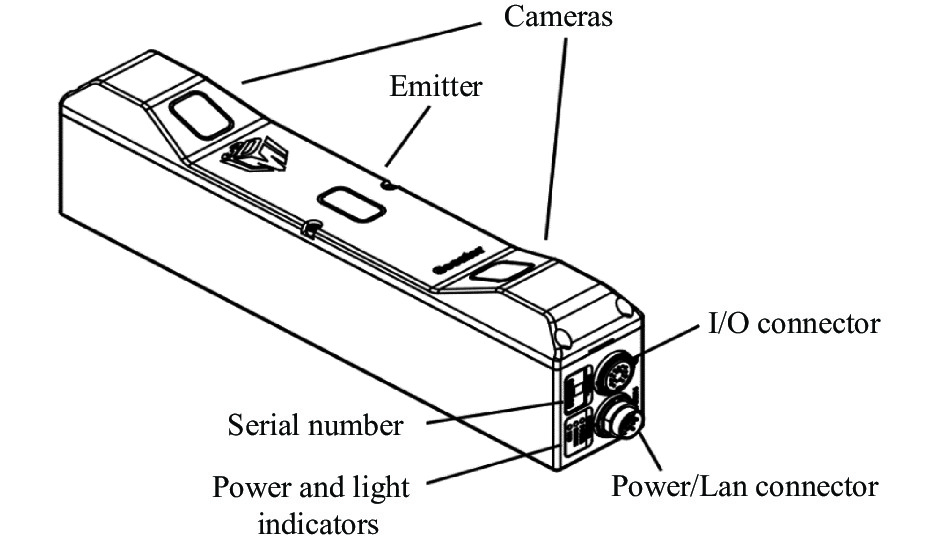
本文采用沥青路面混合料试件作为实验数据采集对象, 并使用Gocator 3110三维智能传感器进行高精度纹理数据采集. Gocator 3110三维智能传感器使用蓝结构光投射到被测对象上的高对比度图案的反射来创建物体表面的三维点云数据, 并使用基于横向色相差的光学扫描法以极高的分辨率和极快的测量速度获取三维形貌. Gocator 3110三维智能传感器由相机模块、蓝色LED结构光模块、IO输入输出接口模块以及电源系统模块组成, 其结构如图1所示.
|
图 1 三维智能传感器结构图 |
Gocator 3110三维智能传感器的各项性能参数如表2所示.
| 表 2 Gocator 3110三维智能传感器性能参数 |
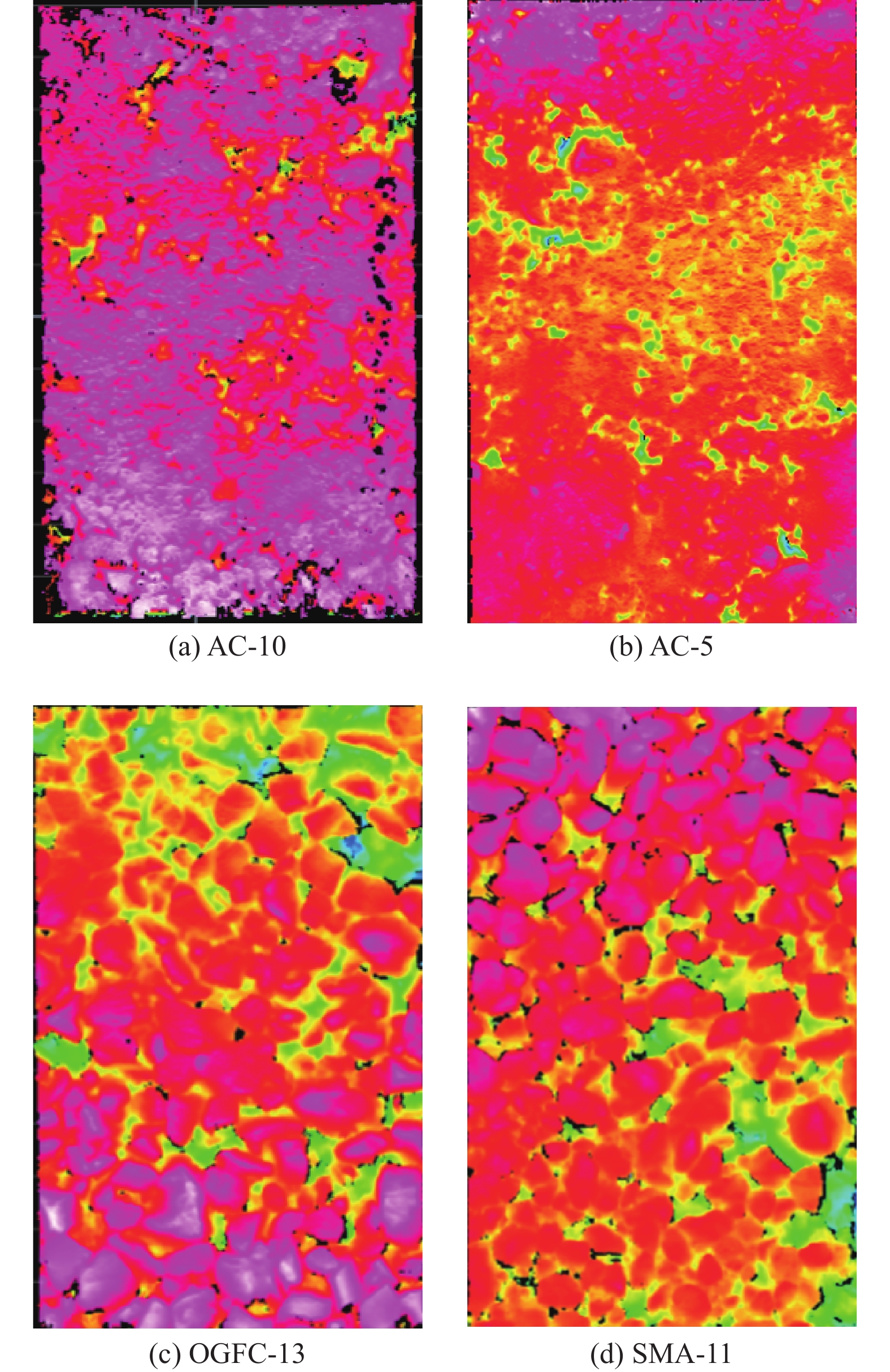
使用Gocator采集的高精度三维纹理点云数据热力图如图2所示.
|
图 2 三维纹理点云数据热力图 |
由图2可以看出, 不同混合料集配试件间粗细集料含量不同, 纹理形貌差异较大. 受纹理的影响, 试件间的抗滑性能也有较大差异.
1.2 构造深度数据采集传统的手工铺砂法测量构造深度数据易受人为因素影响, 难以保证采集结果的准确性. 因此, 本文使用电动铺砂仪采集试件构造深度. 使用的电动铺砂仪如图3所示.

|
图 3 电动铺砂仪 |
依照《公路路基路面现场测试规程》JTG 3450-2019规定, 采用平均粒径位于区间[0.15, 0.3] mm内的特细砂. 量取50 mL砂砾量, 并使用电动铺砂仪将其均匀摊铺在试件表面, 取3次特细砂均匀铺洒距离的测量均值为
| MTD=L0−LL0⋅L×1000 | (1) |
依照《公路路基路面现场测试规程》JTG 3450-2019规定, 摆式摩擦仪用于测试沥青路面的摆式摩擦系数值BPN, 测试结果可以评定路面表面的抗滑性能. 本文使用量筒测量出试件区域的含水量, 并使用洒水器均匀泼洒在区域内, 不断增加试件表面的含水量, 使用工业温度测试仪与摆式摩擦仪测试不同潮湿状态下试件表面温度及表面摩擦系数, 测试一块试件时, 在相同潮湿状态与相同试件表面温度条件下将5次试件测试结果的均值作为一条记录. 本文选取面积为200 mm×100 mm的矩形BPN测试区域, 对每块沥青混合料试件进行11轮不同潮湿状态下BPN的测试区域, 每轮测试所需喷洒水的体积分别为0 mL, 2 mL, 4 mL, 6 mL, 8 mL, 10 mL, 12 mL, 14 mL, 16 mL, 18 mL, 20 mL.
2 三维纹理点云数据特征工程由Gocator 3110采集的三维纹理点云数据, 由电动铺砂仪采集的构造深度数据以及由摆式摩擦仪采集的摩擦系数数据无法直接输入模型进行预测, 需要通过三维纹理点云数据特征工程构造筛选出合适的数据特征, 从而保证预测模型的预测精度.
首先, 三维纹理点云数据由于数据缺失、采集倾角和干扰噪声等原因, 会降低纹理特征分析与计算的准确性. 因此, 需要对三维纹理点云数据进行数据质量提升.
其次, 由三维纹理提取出的用于表征纹理的多维特征中, 存在与摩擦系数不相关以及可从其他特征包含的信息中推导出的冗余特征. 去除不相关特征以及冗余特征可以使得模型的训练效果更好, 因此需要进行特征相关性分析与特征筛选.
2.1 三维纹理点云数据质量提升由于试件表面纹理的波动, 可能导致激光传感器无法感应反射的蓝色LED结构光, 使得采集的三维纹理数据产生部分缺失. 因此, 本文使用基于径向基函数(RBF)的邻域插值算法[22]进行三维纹理点云数据修复. RBF插值法是一种基于逼近理论的非结构化数据多维度精确插值法, 其原理为径向基函数的加权和, 例如高斯分布. RBF插值法以最小曲率面不断逼近采样点, 具有无网格、无量纲的特点, 适合于多维离散数据. RBF插值法首先计算多维空间中两点的距离, 如式(2)所示:
| f(x)=N∑i=1λiφ(r) | (2) |
其中, N为采样点的数量,
| φ(r)=√r2+c2 | (3) |
其中, r为插值点与数据集点间的距离, c为形貌因子.
设点云数据集为
| hi=f(xi)=N∑i=1λiφ(‖x−xi‖)+Pk(xi) | (4) |
其中,
| [λ1λ2⋮λN]=[φ(‖x1−x1‖)φ(‖x1−x2‖)⋮φ(‖x1−xN‖)φ(‖x2−x1‖)φ(‖x2−x2‖)⋮φ(‖x2−xN‖)⋯⋯⋱⋯φ(‖xN−x1‖)φ(‖xN−x2‖)⋮φ(‖xN−xN‖)]−1[h1h2⋮hN] | (5) |
形貌因子c的计算如式(6)所示:
| c={c1,c1(1−5(μd−0.1))+5c2(μd−0.1),5c3(μd−0.3)+c2(1−5(μd−0.3)),c3(1−5(μd−0.5))+5c4(μd−0.5),5c5(μd−0.7)+c2(1−5(μd−0.7)),c5,0⩽ | (6) |
其中,
| {\mu _d} = \left\{ {\begin{array}{*{20}{l}} 0,&{}&{S(i) \lt 0} \\ {\dfrac{1}{2}{{ - }}\dfrac{1}{2}\cos \left(\dfrac{\pi }{2}S(i)\right)},&{}&{0 \leqslant S(i) < 2} \\ 1,&{}&{ S(i) \geqslant 2} \end{array}} \right. | (7) |
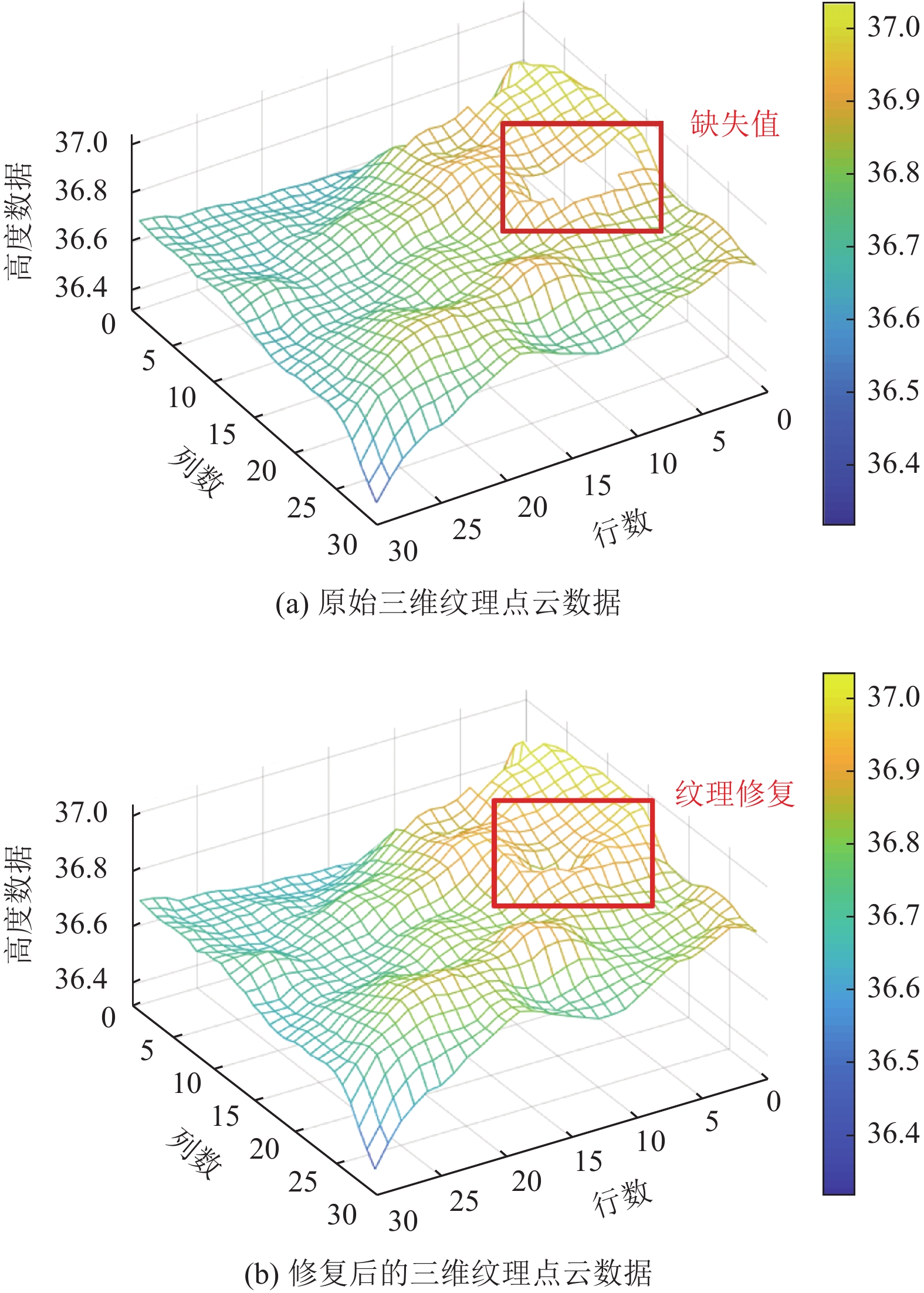
由于三维纹理点云数据量较大, 使用全部数据计算插值点将会产生极大的时间复杂度. 考虑到插值点主要受其空间临近点的影响, 且缺失区域的面积较小. 因此, 本文选取插值坐标邻域的60个点作为插值集. 带有缺失值的原始纹理点云数据以及修复后的纹理点云数据分别如图4(a)与图4(b)所示.
|
图 4 三维纹理点云数据缺失值修复 |
为验证插值算法的精度, 采用基于RBF的邻域插值算法对随机100个点云高度数据进行预测, 并将预测值与实际值对比, 分析点云数据修复的吻合度. 使用
| {R^2} = 1 - \frac{{\displaystyle\sum {{{(\widehat {{y_i}} - {y_i})}^2}} }}{{\displaystyle\sum {{{(\overline {{y_i}} - {y_i})}^2}} }} | (8) |
| {\textit{RMSE}} = \sqrt {\frac{1}{m}\sum {{{(\widehat {{y_i}} - {y_i})}^2}} } | (9) |
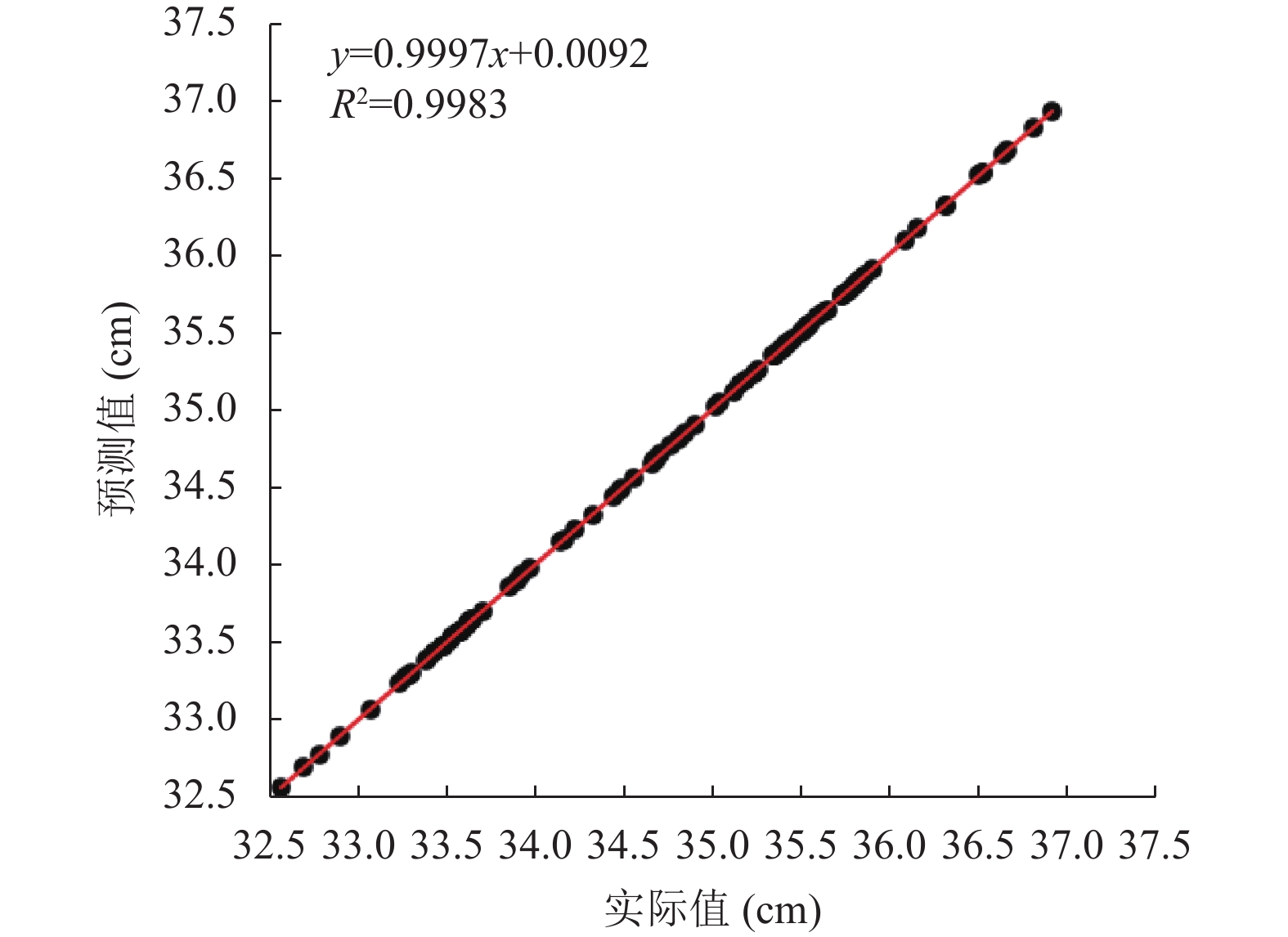
RBF插值法评估结果如图5所示,
|
图 5 基于RBF的邻域插值算法预测值与实测值对比 |
由于采集的纹理数据不可避免的带有倾角, 本文使用最小二乘法拟合三维纹理点云数据的平面方程, 通过变换矩阵计算实现基准面的矫正, 如式(10)和式(11)所示:
| R(\theta ) = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ - \sin \theta }&0 \\ {\sin \theta }&{\cos \theta }&0 \\ 0&0&1 \end{array}} \right] | (10) |
| T({t_x}, {t_y}) = \left[ {\begin{array}{*{20}{c}} 1&0&{{t_x}} \\ 0&1&{{t_y}} \\ 0&0&1 \end{array}} \right] | (11) |
其中,
最后, 为了提取出水平波长位于
宏观纹理与路面抗滑性能密切相关[23], 常用的表征宏观纹理的特征参数分别为平均断面深度(MPD)与平均构造深度(MTD). 相关研究[24]表明, 虽然这两个参数概念清晰合理, 但难以描述足够的宏观纹理特征细节, 并不能反映出路面抗滑性能. 为了进一步研究宏观纹理对路面抗滑性能的影响机理, 需要其他构造的宏观纹理特征参数, 并通过相关性分析提取出能有效反映路面抗滑性能的参数. 本文使用GB/T 131-2006标准中规定的若干参数作为表征宏观纹理的备选特征, 如表3所示.
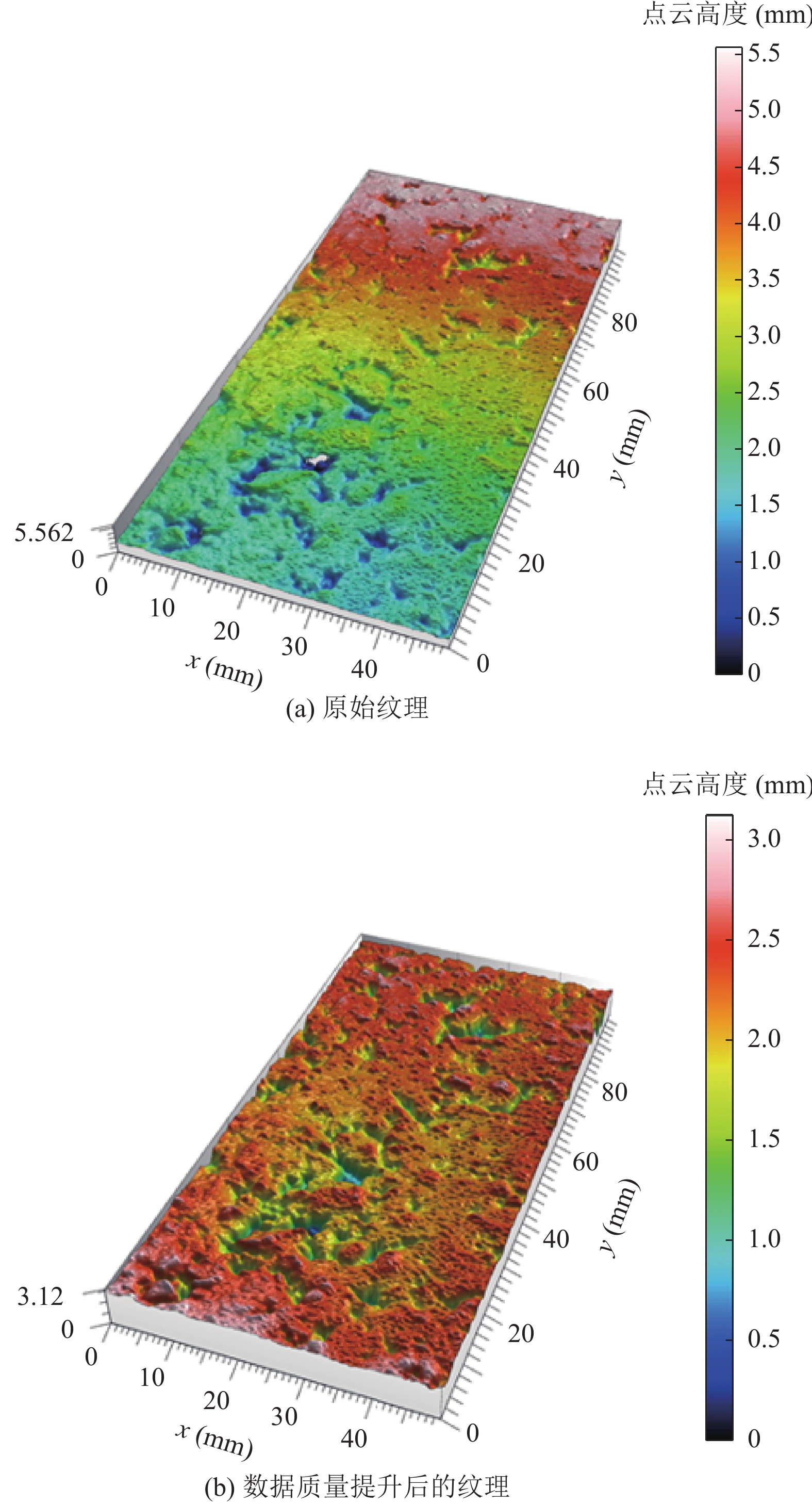
|
图 6 三维纹理点云数据质量提升图 |
为了研究三维纹理特征与摩擦系数之间的关联性, 使用Pearson系数对上述参数进行相关性分析, Pearson系数计算如式(12)所示:
| {\rho _{XY}} = \frac{{\displaystyle\sum {({x_i} - \overline x )({y_i} - \overline y )} }}{{\sqrt {{{\displaystyle\sum {{{({x_i} - \overline x )}^2}\sum {({y_i} - \overline y )} } }^2}} }} | (12) |
其中, Pearson系数
| 表 3 纹理特征参数 |
Pearson系数相关性分析的结果如图7所示. 由相关性分析可知, MTD与
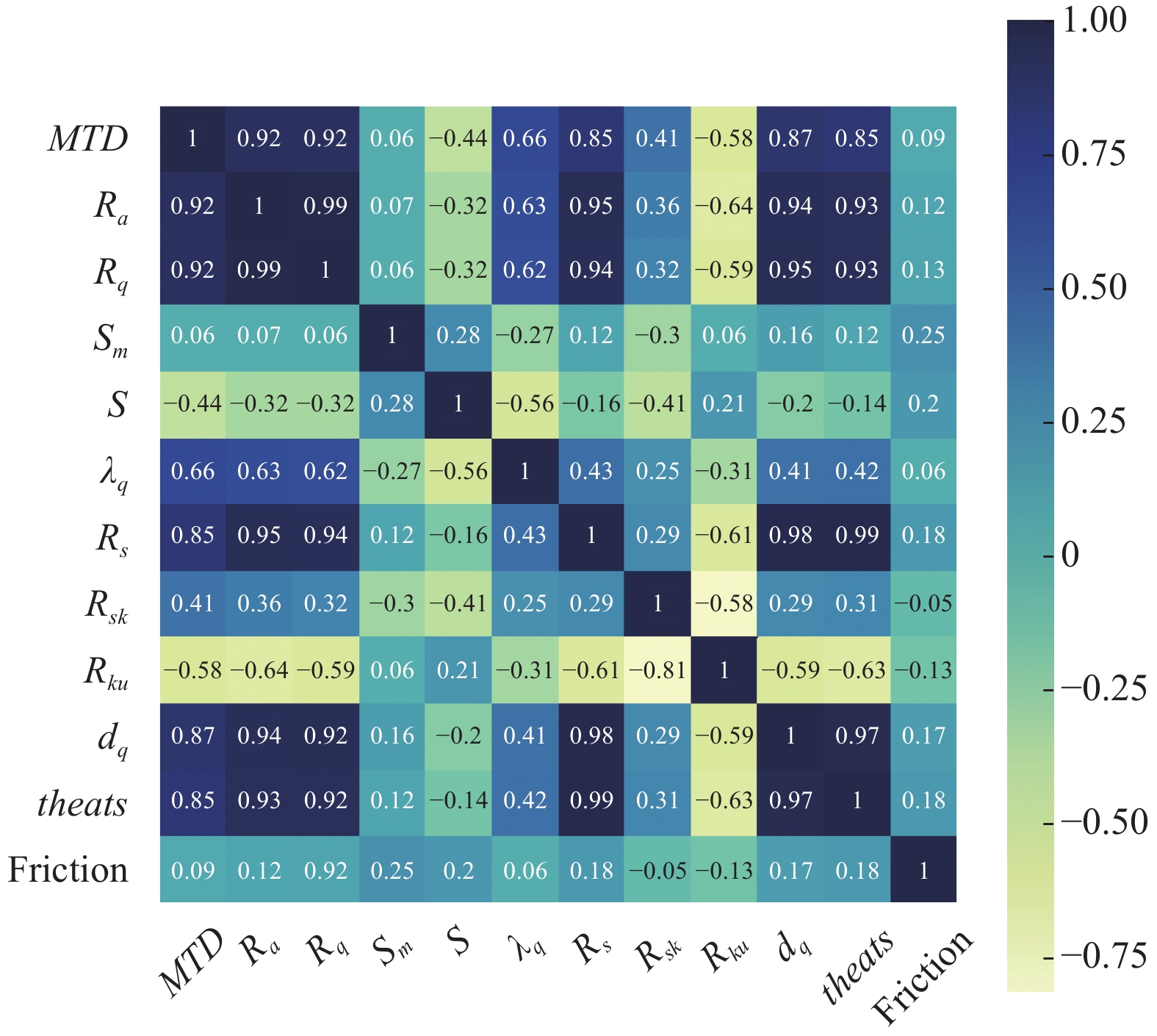
|
图 7 Pearson系数相关性分析结果 |
3 基于IGWO-XGBoost融合的路面抗滑性能预测模型构建 3.1 XGBoost工作原理
XGBoost模型以回归决策树为基础, 通过逐渐特征分裂增添新的决策树, 集成多个回归树的叶子节点得分以优化目标函数[25]. XGBoost的目标函数如式(13)所示:
| Obj = {\sum\limits_i {({y_i} - {{\widehat y}_i})} ^2} + \sum\limits_i {\Omega ({f_i})} | (13) |
其中,
| \Omega ({f_i}) = \frac{1}{2}\lambda \sum\limits_{j = 1}^K {\omega _j^2} + \gamma T | (14) |
其中, K为回归决策树叶子节点的数量,
XGBoost通过不断迭代拟合当前预测值与真实值的残差, 不断趋近真实值. XGBoost每次迭代的结果如式(15)所示:
| {\widehat y_i}^{(t + 1)} = {\widehat y_i}^{(t)} + \sum\limits_{j = 1}^N {{f_j}({x_i})} | (15) |
其中, t为当前迭代次数.
为了确定树的最佳结构, XGBoost选取
| Gain = \frac{1}{2}\left[\frac{{G_L^2}}{{{H_L} + \lambda }} + \frac{{G_R^2}}{{{H_R} + \lambda }} - \frac{{{{({G_L} + {G_R})}^2}}}{{{H_L} + {H_R} + \lambda }}\right] - \gamma | (16) |
其中, 式(16)右侧4项分别为左节点与右节点的得分, 节点不分裂时的得分以及正则化系数. 回归树将会持续分裂, 直至
传统的超参数搜索方法有网格化搜索法以及随机搜索法[26]. 网格化搜索法通过枚举搜索, 在指定的参数取值范围内改变步长, 遍历参数的每一种组合, 并分别使用这些参数组合训练模型, 最终找到在验证集上精度最高的参数. 随机搜索法则不再枚举取值范围内的所有值, 而是为每个参数定义了一个分布函数并在该空间中随机采样. 由于本文使用的模型超参数较多, 且超参数的调整极大影响模型精度, 因此需要搜索出合适的超参数值. 传统的网格化搜索法的搜索空间十分庞大而搜索时间过长, 随机搜索法无法保证搜索结果是最优参数, 且容易获取到局部最优的参数, 因此需要使用一种搜索结果较好且搜索时间较短的算法. 本文使用改进灰狼优化算法对模型超参数进行寻优. 灰狼优化(GWO)算法[27]是一种启发式群体智能优化算法, 通过模拟狼群社会活动以及捕猎行为以优化搜索, 具有全局寻优能力强、时间复杂度低、编程复现性好等优点. IGWO算法流程如图8所示.
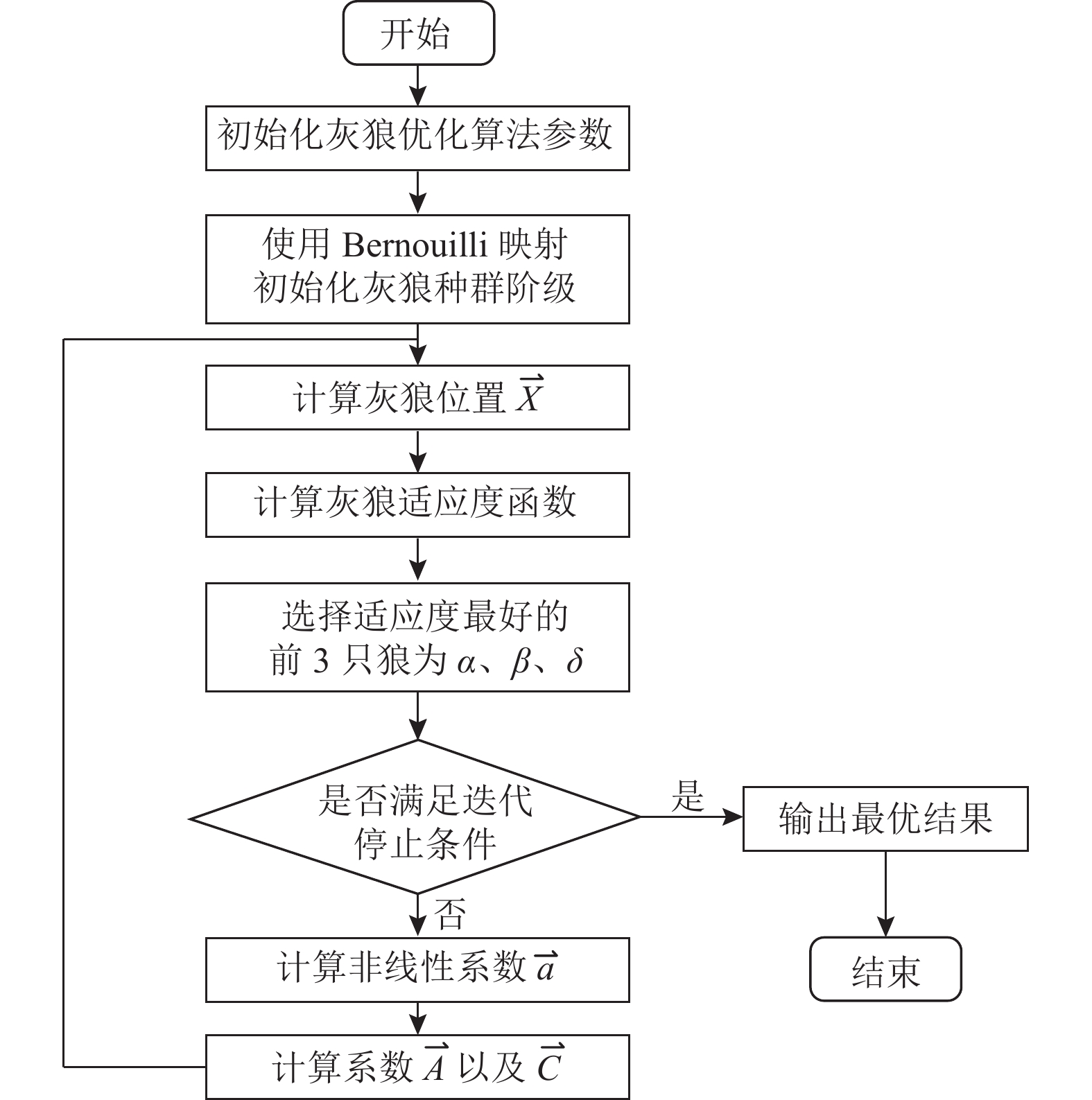
|
图 8 IGWO算法流程图 |
算法首先模拟狼群社会阶级, 随机将狼划分为α、β、δ、ω四类, 其中α为适应度最佳的顶层阶级, 且阶级按从左到右的顺序依次递减, 其适应度也随之递减. 寻优结果由α、β、δ三者共同决定, 通过迭代位置, 优化路径, 不断缩短捕猎距离, 确定最优值.
设
| {\rightharpoonup{D}}=\left|{\rightharpoonup{C}}\cdot {{\rightharpoonup{X}}_{p}}(t)-{\rightharpoonup{X}}(t)\right| | (17) |
| {\rightharpoonup{X}}(t)={{\rightharpoonup{X}}_{p}}(t)-{\rightharpoonup{A}}\cdot {\rightharpoonup{D}} | (18) |
其中,
| {\rightharpoonup{A}}=2\cdot {\rightharpoonup{a}}\cdot {\rightharpoonup{r}}-{\rightharpoonup{a}} | (19) |
| {\rightharpoonup{C}}=2\cdot {\rightharpoonup{r}} | (20) |
接着, 狼群开始捕猎. 其中,
| {\rightharpoonup{D}}_{ki}=\left|{\rightharpoonup{C}}\cdot {{\rightharpoonup{X}}_{k}}(t)-{{\rightharpoonup{X}}_{t}}(t)\right| | (21) |
其中, k分别为α、β、δ, i为当前遍历的灰狼, t为当前迭代次数,
| {\rightharpoonup{X}}_{\alpha i}={{\rightharpoonup{X}}_{\alpha }}-{\rightharpoonup{A}}\cdot {{\rightharpoonup{D}}_{\alpha i}} | (22) |
| {\rightharpoonup{X}}_{\beta i}={{\rightharpoonup{X}}_{\beta }}-{\rightharpoonup{A}}\cdot {{\rightharpoonup{D}}_{\beta i}} | (23) |
| {\rightharpoonup{X}}_{\delta i}={{\rightharpoonup{X}}_{\delta }}-{\rightharpoonup{A}}\cdot {{\rightharpoonup{D}}_{\delta i}} | (24) |
| {\rightharpoonup{X}}_{i}(t+1)=\frac{{{\rightharpoonup{X}}_{\alpha i}}+{{\rightharpoonup{X}}_{\beta i}}+{{\rightharpoonup{X}}_{\delta i}}}{3} | (25) |
在初始阶段, 对狼群阶级的随机划分无法保证搜索空间内个体尽可能均匀的分布, 可能会导致算法的效率大大降低. 而混沌映射算法能够生成位于0与1间的混沌数, 代替伪随机数的生成. 本文使用Bernoulli映射[28]对狼群的阶级进行随机划分. Bernoulli映射的公式如式(26)所示:
| {x_{i + 1}} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{{x_i}}}{{1 - \lambda }}},&{0 < {x_i} \leqslant 1 - \lambda } \\ {\dfrac{{{x_i} - 1 + \lambda }}{\lambda }},&{1 - \lambda < {x_i} \leqslant 1} \end{array}} \right. | (26) |
本文选取
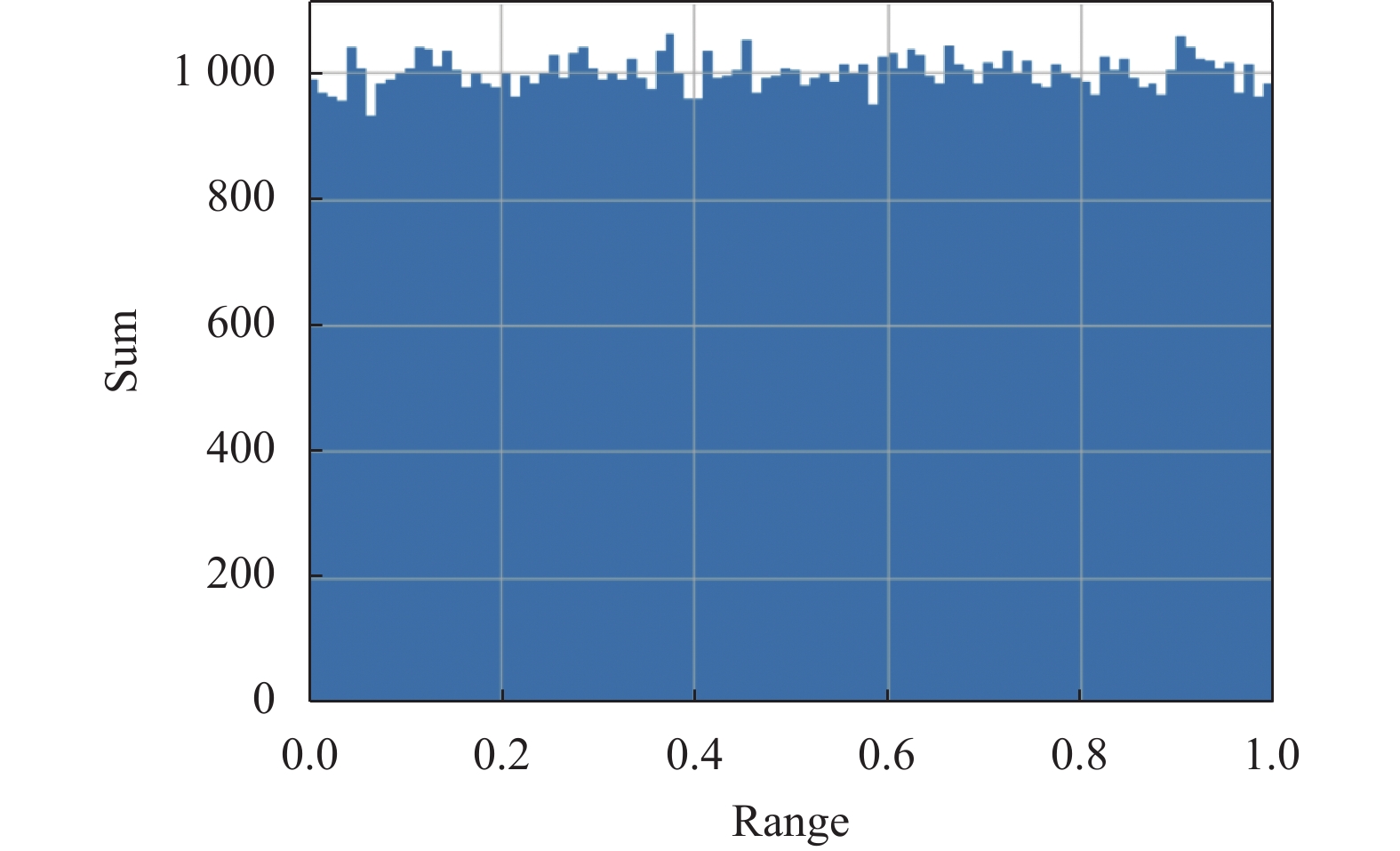
|
图 9 Bernoulli映射分布直方图 |
图9中, 混沌数结果方差为0.083, 可以认为混沌数的分布较为均匀.
由式(19)可知, 向量系数
为增强算法全局搜索能力, 受文献[29]的启发, 将
| {\rightharpoonup{a}}(t)=2\left(1-\mathrm{sin}\left(\frac{\pi t}{2T}\right)\right) | (27) |
其中, T为最大迭代次数, t为当前迭代次数.
3.3 基于IGWO-XGBoost融合的抗滑性能预测模型建立本文以800组包含纹理特征, 温度以及表面潮湿程度的数据为基础, 在三维纹理点云数据质量提升基础上, 选取70%的数据作为样本集训练模型, 30%的数据作为测试集评价模型性能. 设置需要优化的XGBoost超参数如表4所示.
| 表 4 XGBoost超参数及寻优区间 |
使用改进灰狼优化算法对上述超参数进行优化, 以训练集训练XGBoost模型, 并以测试集的预测结果
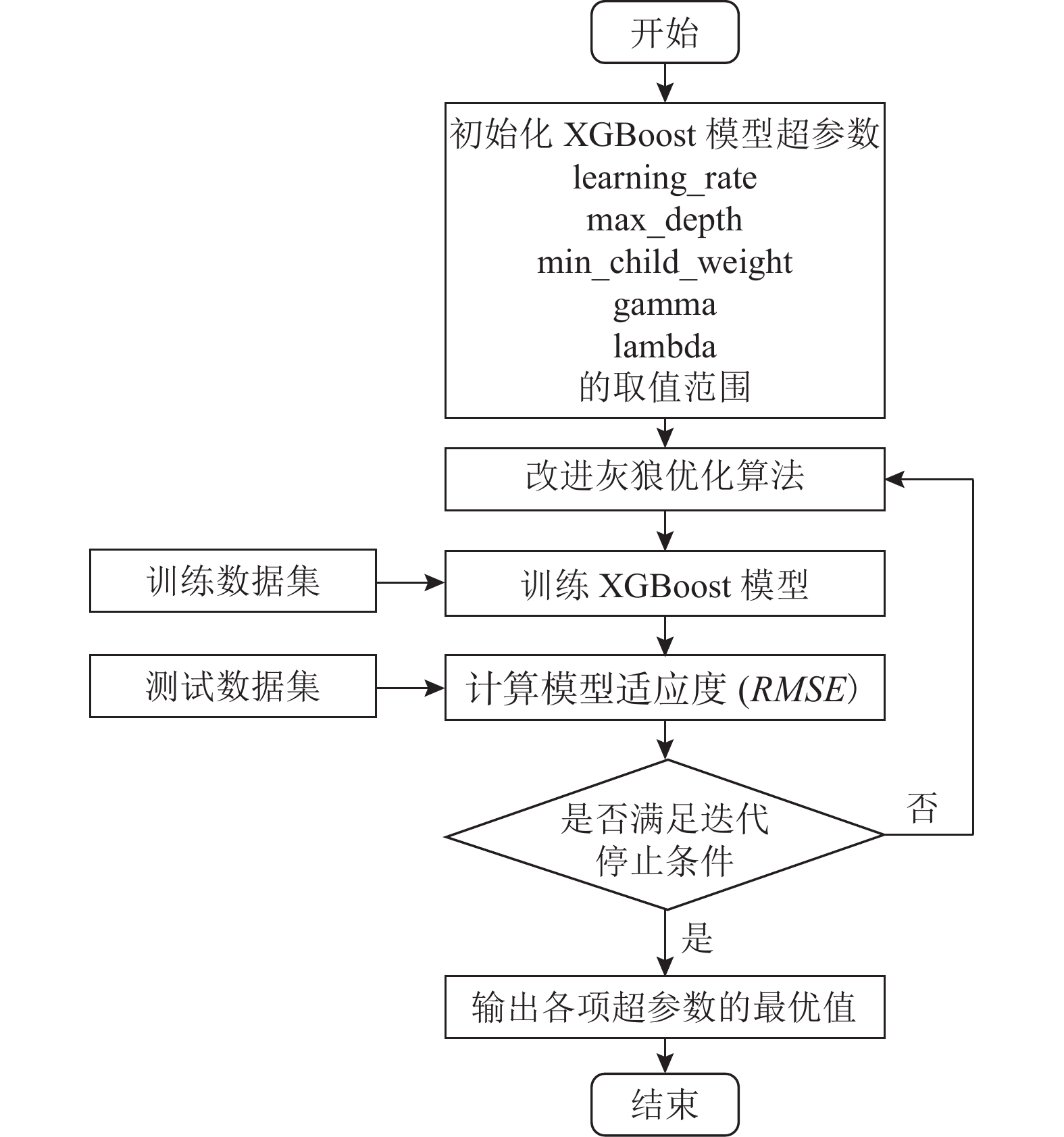
|
图 10 基于IGWO-XGBoost融合模型构建流程图 |
使用IGWO算法与传统网格化搜索方法获取XGBoost模型超参数最优值的时间如表5所示.
| 表 5 超参数搜索算法用时对比 (s) |
由表5可知, IGWO算法的用时较网格化搜索法用时降低了69%, 有效地缩短了超参数寻优的时间, 提高了参数优化效率. 使用网格化搜索与IGWO算法搜索的XGBoost模型超参数如表6所示.
| 表 6 XGBoost模型最优超参数值搜索结果 |
由表6可知, IGWO算法搜索结果在个别参数与网格化搜索算法的结果相近, 而IGWO算法搜索在连续参数的取值上精度更高, 搜索时间更短.
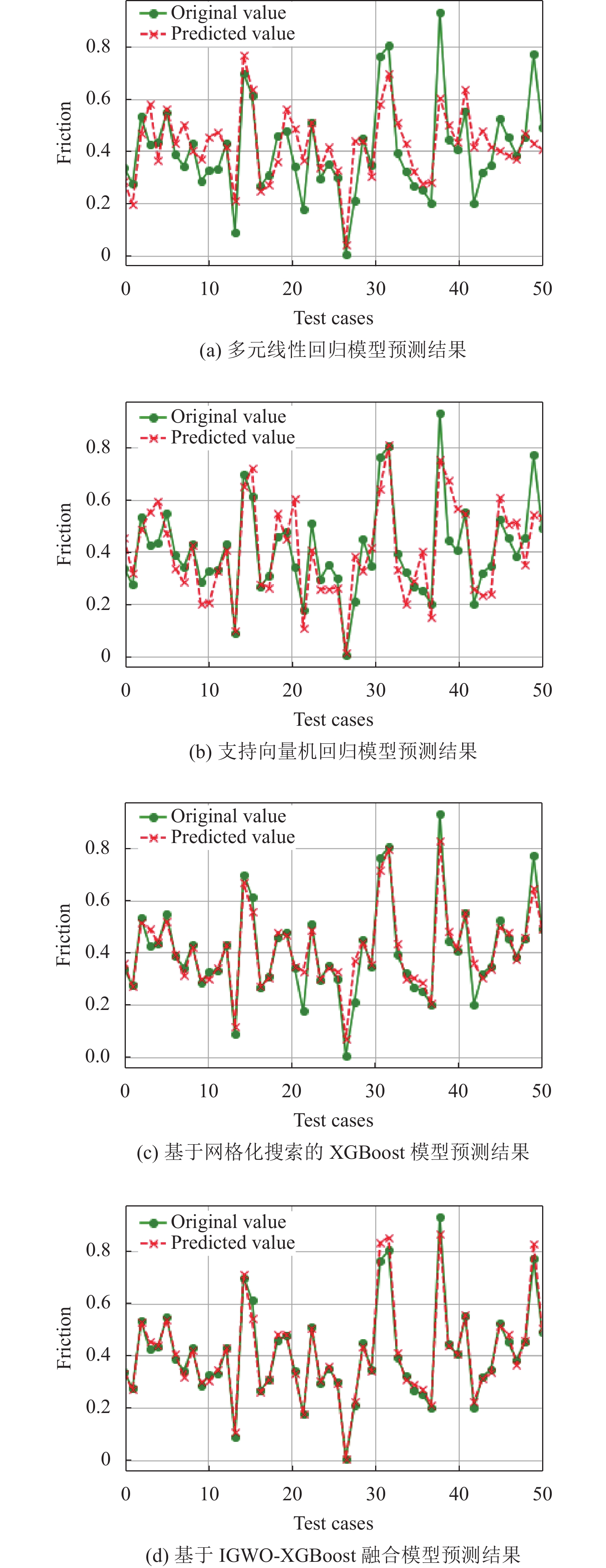
4 基于IGWO-XGBoost融合模型预测结果对比分析为评估模型性能, 本文采用
图11中, 实线曲线表示真实值, 虚线曲线表示不同模型对应的预测值. 由图11可知, 传统抗滑性能预测研究中使用的多元线性回归模型以及传统机器学习领域使用的支持向量机回归模型, 其预测值与真实值差距较大, 难以准确预测抗滑性能. 相较基于网格化搜索的XGBoost模型, 本文提出的基于IGWO-XGBoost融合模型能够更好地拟合实际结果, 预测效果更佳.
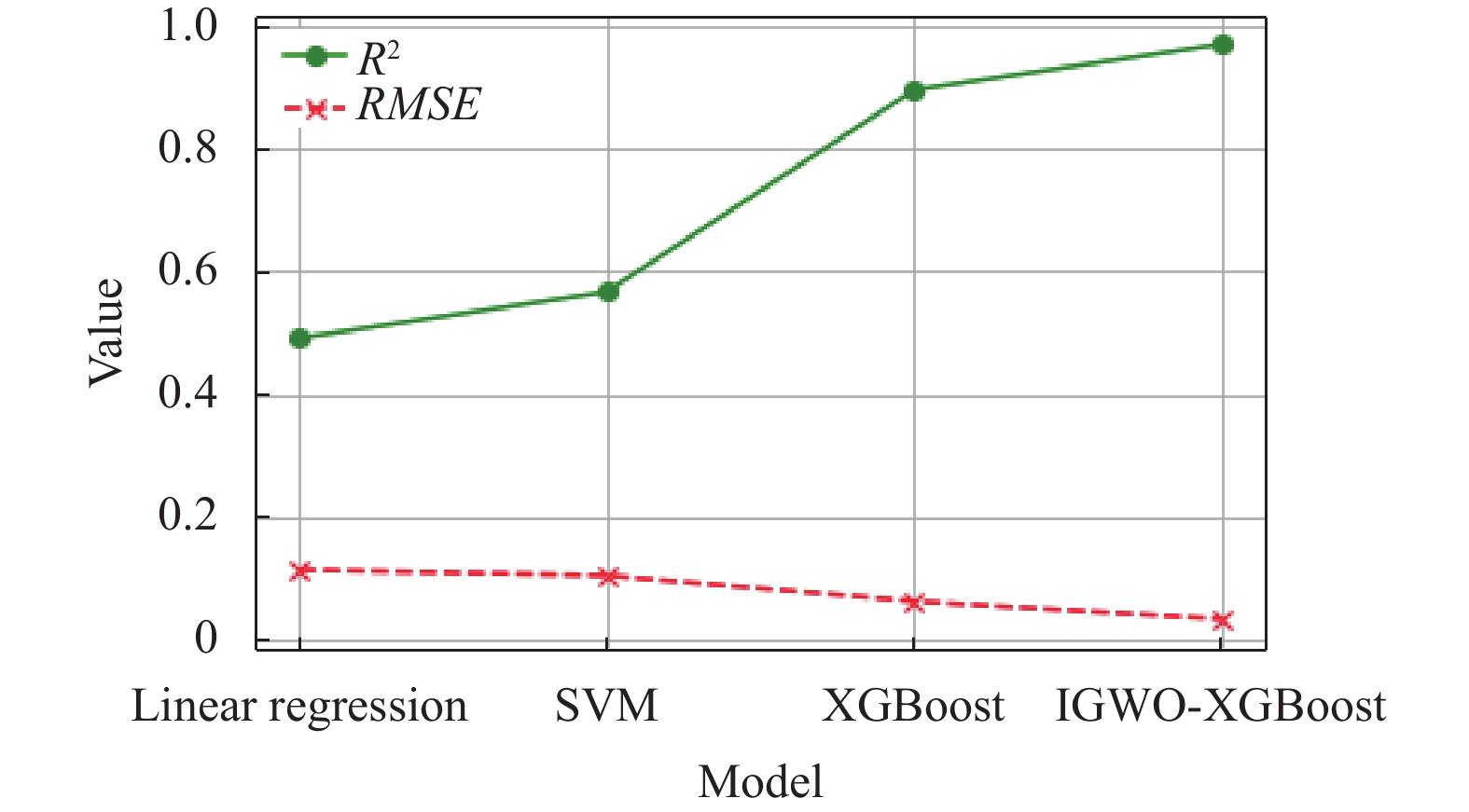
由图12和表7可知, 相较于多元线性回归模型预测结果, 基于IGWO-XGBoost融合模型的
|
图 11 不同模型预测结果对比 |
|
图 12 不同模型预测结果对比 |
| 表 7 不同模型预测性能对比 |
5 结语
(1)本文使用Gocator 3110采集试件表面高精度三维点云纹理数据, 并使用基于RBF的邻域插值算法对纹理点云缺失数据进行修复. 相比于传统的中值插值算法与均值插值算法, 基于RBF的邻域插值算法对于数据的局部化特征拟合效果更优, 能够精确修复纹理点云缺失数据, 修复准确率为90.2%.
(2)构造能够表征三维纹理的多因素纹理特征参数, 使用Pearson系数对纹理特征参数进行相关性分析, 剔除了其中的冗余特征, 避免输入相关性高的冗余特征对模型预测结果的影响.
(3)使用IGWO算法对XGBoost模型超参数搜索进行优化, 构建基于IGWO-XGBoost融合模型, IGWO算法较传统的网格化搜索算法的用时大大降低.
(4)基于IGWO-XGBoost融合模型综合了三维纹理特征参数、表面温度、潮湿状态, 并深入挖掘了多因素影响因子与表面摩擦系数的内在关联. 相较多元线性回归模型、支持向量机回归模型和基于网格化搜索的XGBoost模型, 本文提出的模型拥有更优的模型性能, 能够精确的预测表面摩擦系数, 对路面抗滑性能的评估提供更加精准的科学依据.
| [1] |
黄绍龙, 沈凡, 付军, 等. 路面抗滑性能与交通安全的相关性研究. 交通科技, 2011(2): 98-101. DOI:10.3963/j.issn.1671-7570.2011.02.033 |
| [2] |
王磊, 余功新, 王朝辉, 等. 面向降低路面湿滑事故率的交通量与抗滑阈值确定. 长安大学学报 (自然科学版), 2019, 39(5): 106-114. |
| [3] |
孙政. 沥青路面横向力摩擦系数影响因素研究. 城市建筑, 2016(29): 283. DOI:10.3969/j.issn.1673-0232.2016.29.261 |
| [4] |
赵雪涛. 公路路面摩擦系数检测与评价方法研究. 交通世界(中旬刊), 2019(8): 56-58. |
| [5] |
职雨风, 苏堪祥. 南方多雨地区SMA路面摩擦系数变化规律研究. 公路工程, 2019, 44(3): 176-180. DOI:10.19782/j.cnki.1674-0610.2019.03.034 |
| [6] |
谭忆秋, 肖神清, 熊学堂. 路面抗滑性能检测与预估方法综述. 交通运输工程学报, 2021, 21(4): 32-47. DOI:10.19818/j.cnki.1671-1637.2021.04.002 |
| [7] |
陈文英. 公路沥青路面抗滑性能检测方法. 交通科技与管理, 2021(21): 103-104. |
| [8] |
黄晓明, 郑彬双. 沥青路面抗滑性能研究现状与展望. 中国公路学报, 2019, 32(4): 32-49. |
| [9] |
Liu QF, Shalaby A. Relating concrete pavement noise and friction to three-dimensional texture parameters. International Journal of Pavement Engineering, 2017, 18(5): 450-458. DOI:10.1080/10298436.2015.1095897 |
| [10] |
Hu LQ, Yun D, Liu ZZ, et al. Effect of three-dimensional macrotexture characteristics on dynamic frictional coefficient of asphalt pavement surface. Construction and Building Materials, 2016, 126: 720-729. DOI:10.1016/j.conbuildmat.2016.09.088 |
| [11] |
钱振东, 薛永超, 张令刚. 沥青路面三维纹理分形维数及其抗滑性能. 中南大学学报(自然科学版), 2016, 47(10): 3590-3596. |
| [12] |
徐粒. 路表三维纹理重构及其与路面抗滑性能的关联性研究[硕士学位论文]. 乌鲁木齐: 新疆大学, 2021.
|
| [13] |
刘林, 呙润华, 李梦茹, 等. 沥青路面三维纹理构造特征研究. 公路交通科技(应用技术版), 2019, 15(4): 46-50. |
| [14] |
彭毅, 李强, 战友, 等. 基于区域三维纹理特征的路面抗滑性能评估. 东南大学学报(自然科学版), 2020, 50(4): 667-676. DOI:10.3969/j.issn.1001-0505.2020.04.010 |
| [15] |
杨跃琴. 沥青路面宏观纹理的精确表征及抗滑性能衰减规律研究[硕士学位论文]. 北京: 北京建筑大学, 2021.
|
| [16] |
Fwa TF. Skid resistance determination for pavement management and wet-weather road safety. International Journal of Transportation Science and Technology, 2017, 6(3): 217-227. DOI:10.1016/j.ijtst.2017.08.001 |
| [17] |
黄正伟. 不同潮湿状态下沥青路面附着系数及行车安全影响研究[硕士学位论文]. 重庆: 重庆交通大学, 2017.
|
| [18] |
战友, 李强, 马啸天, 等. 基于宏微观纹理特征融合的路面摩擦性能预测. 浙江大学学报 (工学版), 2021, 55(4): 684-694. |
| [19] |
张瑞, 贾虎. 基于多变量时间序列及向量自回归机器学习模型的水驱油藏产量预测方法. 石油勘探与开发, 2021, 48(1): 175-184. DOI:10.11698/PED.2021.01.16 |
| [20] |
寇雯博, 董灏, 邹岷强, 等. 混杂复合材料等效热传导性能预测的小波-机器学习混合方法. 物理学报, 2021, 70(3): 57-68. |
| [21] |
肖立华, 张博, 胡伟, 等. 基于机器学习的电网工程量计价预测模型. 沈阳工业大学学报, 2021, 43(3): 241-246. DOI:10.7688/j.issn.1000-1646.2021.03.01 |
| [22] |
冯佰威, 王首茗, 冯梅. 改进的径向基插值方法在船型优化中的应用. 华南理工大学学报(自然科学版), 2022, 50(3): 57-64. |
| [23] |
牛亚东, 张思祥, 田广军, 等. 机场跑道摩擦系数影响因素研究. 应用力学学报, 2021, 38(2): 715-720. DOI:10.11776/cjam.38.02.D158 |
| [24] |
沈小俊, 黄维蓉, 杨玉柱, 等. 高速公路沥青路面抗滑性能影响因素及衰减规律分析. 公路交通技术, 2021, 37(5): 12-16, 23. DOI:10.13607/j.cnki.gljt.2021.05.003 |
| [25] |
Chen TQ, Guestrin C. XGBoost: A scalable tree boosting system. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco: ACM, 2016. 785–794.
|
| [26] |
卢光跃, 吴洋, 吕少卿, 等. 基于聚类分析和XGBoost算法的换机预测模型. 西安邮电大学学报, 2019, 24(2): 94-97, 104. DOI:10.13682/j.issn.2095-6533.2019.02.018 |
| [27] |
宋玉生, 刘光宇, 朱凌, 等. 改进的灰狼优化算法在SVM参数优化中的应用. 传感器与微系统, 2022, 41(9): 151-155. DOI:10.13873/J.1000-9787(2022)09-0151-05 |
| [28] |
孙中廷. 基于Logistic混沌Bernoulli测量矩阵的压缩感知研究. 电脑知识与技术, 2019, 15(27): 250-252. DOI:10.14004/j.cnki.ckt.2019.3260 |
| [29] |
陈暄, 顾锦, 毛科技, 等. 一种改进鲸鱼算法的无线传感器网络定位优化研究. 传感技术学报, 2021, 34(10): 1366-1373. |
 2023, Vol. 32
2023, Vol. 32



